Long-wavelength (reddish) hues induce unusually large gamma oscillations in the primate primary visual cortex

Significance

Electrophysiological signals recorded from the brain exhibit prominent gamma oscillations (∼30–80 Hz) under sensory stimulation. These oscillations are modulated by stimulus properties and behavioral state, and implicated to play a role in cognitive functions, such as attention and object-binding. In visual areas, gamma oscillations have mainly been studied using achromatic gratings/gabors. Here we show that color stimuli generate unprecedented levels of gamma oscillations in the local field potentials recorded from primate area V1. The strongest oscillations are induced by long-wavelength (reddish) hues. Importantly, their strength depends on color saturation but not on luminance, and is strongly correlated with the L−M cone contrast produced by stimuli, suggesting that gamma oscillations may represent key components of the processing of visual chromatic information.

Abstract

Gamma oscillations (∼30–80 Hz) are a prominent signature of electrophysiological signals, with a purported role in natural vision. Previous studies in the primary visual cortex (area V1) have shown that achromatic gratings or gabor stimuli generate salient gamma oscillations, whose strength and frequency depend on stimulus properties such as their size, contrast, and orientation. Surprisingly, although natural images are rarely achromatic, the effect of chromatic input on gamma has not been thoroughly investigated. Recording from primate V1, we show that gamma oscillations of extremely high magnitude (peak increase of ∼300-fold in some cases), far exceeding the gamma generated by optimally tuned achromatic gratings, are induced in the local field potentials by full-field color stimuli of different hues. Furthermore, gamma oscillations are sensitive to the hue of the chromatic input, with the strongest oscillations for long-wavelength (reddish) hues and another, smaller gamma response peak for hues in the short-wavelength (bluish) range, which lie approximately on the two cardinal chromatic response axes of the upstream lateral geniculate nucleus neurons. These oscillations depended critically on the purity of the hue, decreasing with hue desaturation, but remained robust for pure hue stimuli even at reduced luminance. Importantly, the magnitude of gamma oscillations was highly correlated with positive L−M cone contrast produced by the stimuli, suggesting that gamma could be a marker of the specific mechanisms underlying this computation. These findings provide insights into the generation of gamma oscillations, as well as the processing of color along the visual pathway.

Over the past 3 decades, studies of the visual pathway, particularly in the primary visual cortex (V1), have shown that gamma oscillations in the local field potential (LFP) are highly dependent on the properties of the visual stimuli (1–3), although whether they play a role in binding or communication is a matter of debate (2, 4–6). Recently, two electrocorticography (ECoG) studies have presented disparate views regarding the role of gamma for natural vision. One study showed that narrow-band gamma is highly stimulus-dependent and is strongly induced by achromatic luminance gratings, but not by noise patterns or many natural images (7). However, another study reported the presence of robust gamma even for natural images, both colored and achromatic (8).

Interestingly, although color is an indispensable component of natural vision, whether gamma in V1 is sensitive to the chromaticity of the stimulus is not well understood, as previous studies have mainly used achromatic gratings, gabors, or bars that are known to elicit vigorous spiking as well as gamma oscillations in V1 (1, 2, 9). To address this question, we recorded LFPs and spikes using chronically implanted microelectrode arrays inserted in area V1 of three awake monkeys while they viewed full-field color stimuli, and studied whether gamma oscillations depend on stimulus hue, saturation, and luminance.

Results

To capture the full range of colors present in natural images, we used the hue-saturation-value (HSV) color model, and first presented hues at their maximum saturation and value (Figs. 1–3; here value, in italics, refers specifically to the “V” parameter in the HSV color notation). To resolve potential issues due to differences in absolute luminance/saturation levels of different hues in the HSV color model (see ref. 10 and references therein for a detailed discussion of some confounders in the HSV model), we subsequently presented hues at varying value and saturation levels (Fig. 4). Results are presented such that long-wavelength (reddish) hues, corresponding to 0° in the standard HSV nomenclature, lie in the middle of each plot for better visualization of power changes and peak frequency shifts.

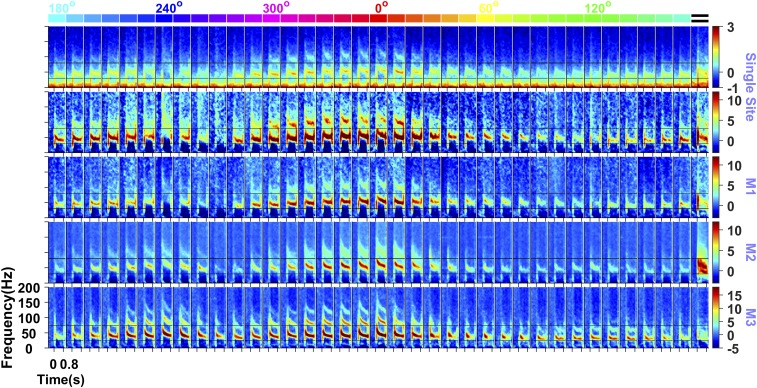
Fig. 1.

Gamma oscillations induced by hue and grating stimuli. Time frequency spectra showing the power [Top, in log₁₀(µV²)] and changes in power from the baseline period (−0.5 s to 0 s, where 0 indicates stimulus onset; other rows, in dB) for 36 full-screen (subtending a visual angle of ∼56° in the horizontal direction and ∼33° in the vertical direction) hues (indicated at the top) and full-screen static grating (extreme right; presented at an orientation of 90° and spatial frequency of 2 cycles/degree) for an example site in monkey (M) 1 and average across the population for M1, M2, and M3 (number of sites: 64, 32, and 16, respectively). The black lines indicate the gamma band limits. Hue angles of 0°, 60°, 120°, 180°, 240°, and 300° are indicated at the top for reference.

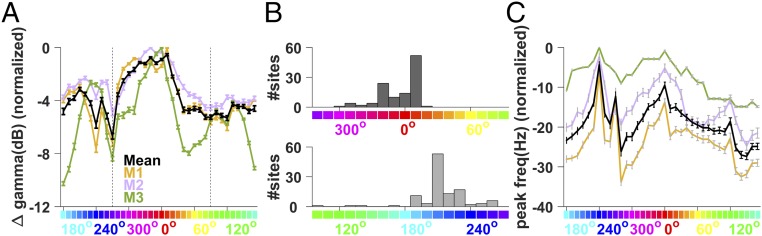
Fig. 3.

Hue tuning of gamma oscillations. (A) Change in gamma power from the baseline to the stimulus period, normalized for each electrode by subtracting the maximum change across hues, such that the trace for each electrode has a maximum of 0. These traces were subsequently averaged across all electrodes. Individual monkey traces are shown in different colors, as indicated in the plot. Error bars denote the SEM across electrodes. (B) Histogram of peak hue across electrodes in two hue ranges separated by 270° and 90° hues (represented by the dotted black lines in A). (C) Variation in peak frequency, normalized in the same way as in A by subtracting the maximum peak frequency value for each electrode, followed by averaging across electrodes and monkeys.

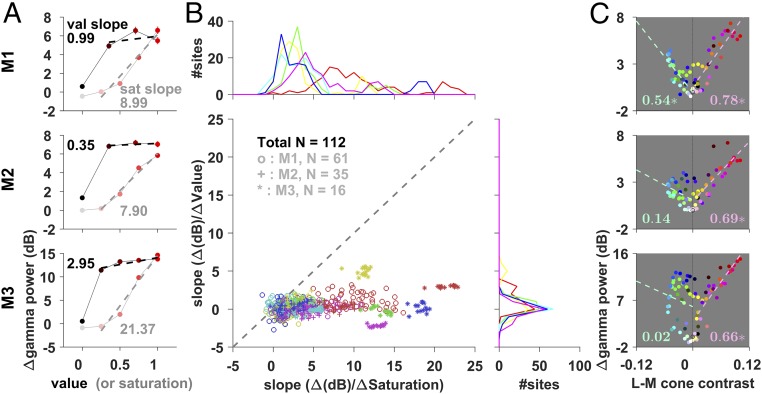
Fig. 4.

Effects of saturation, value, and L−M cone contrast. (A) Average change in gamma power for varying levels of saturation and value for 0° hue stimulus. The dashed lines show the linear fit for the non-0 saturation (or value) conditions, and their slope is indicated alongside. Note that although the black and white stimuli are shown in the plots at 0 value and 0 saturation levels, respectively, they are not used to estimate the slopes, since chromatic information is completely lost for these colors. (B) Scatterplot of the slopes with saturation and value variations. Each data point represents an electrode. The marginals (Top and Right) show the distribution of slopes across electrodes separately for saturation and value variations. Color indicates the hue used. (C) L−M cone contrast with respect to the adapting gray (details in Materials and Methods) and the corresponding change in gamma power for the different stimuli (shown in the corresponding color; data point for gray shown as an open black circle) for the three monkeys. The numbers indicate the goodness-of-fit (R²) values for linear regression between the change in gamma power and positive (shown in red, at a precision of two decimal places) and negative (in green) L−M cone contrast values; the dashed line represents the corresponding line of regression. Asterisks indicate significant R² values (P < 0.01).

Hue Tuning.

Stimuli of almost any hue, shown full screen at their maximum saturation and value, produced strong gamma oscillations in V1 LFP consistently across sites in the three monkeys (Fig. 1). Gamma was most prominent for long-wavelength (reddish) hues, typically much stronger than achromatic full-screen gratings presented at optimal orientation and spatial frequency (Fig. 1, extreme right). A comparison of power spectral density during stimulus presentation (computed during 250 to 750 ms, where 0 indicates stimulus onset; Fig. 2A) and the change in power from spontaneous activity (–500 to 0 ms; Fig. 2B) showed that hue-induced gamma was much stronger than grating-induced gamma. Note that the use of full-screen gratings induced a prominent gamma rhythm between 25 and 40 Hz in addition to the traditional gamma rhythm between 40 and 60 Hz, as reported recently (11). These two gamma rhythms, termed “slow” and “fast,” have different tuning preferences for size, contrast, temporal frequency, and orientation (11); the gratings were optimized to produce the strongest fast gamma (full screen, 100% contrast, static, orientation of 90°, and spatial frequency of 2 cycles per degree for all monkeys; see ref. 11 for a detailed comparison of tuning properties for the first two monkeys). On the other hand, hues did not induce slow gamma. The hue-induced gamma was more narrow-band than the grating-induced gamma and also exhibited stronger harmonics. The narrower bandwidth, higher gamma peaks, and prominent harmonics suggest a stronger and cleaner oscillatory structure in hue-induced gamma. Unlike gamma, the firing rates were variable or weak due to the use of full-screen, nonoptimized color stimuli without luminance or chromatic contrast (Fig. S1).

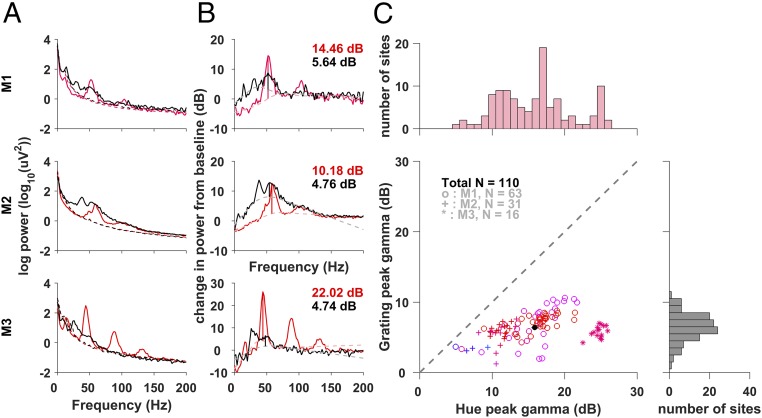
Fig. 2.

Gamma induced by long-wavelength (reddish) hues vs. achromatic gratings. (A) Power spectrum (A) and average change in spectral power from the baseline (B) (−0.5 s to 0 s, dashed lines in A) during the stimulus period (0.25–0.75 s) for the hue that produced the maximum change in the gamma range (shown in that hue) and a grating stimulus (shown in black). The height of the gamma peak (colored and black vertical lines) is estimated as the elevation of the PSD above the fitted underlying broadband pedestal of the PSD (dashed line; details in Materials and Methods). (C) Scatterplot of the peak gamma for hue and grating across common sites. Color denotes the hue that produced the largest gamma; the black dot indicates the grand mean. The marginal histograms show the distribution of peak change in gamma power for hue and grating separately.

Grating-induced gamma had a larger broadband component (most prominent in monkey 2), probably reflecting higher overall firing rates (12). A comparison of the peak gamma power increase from the broadband “pedestal” for the grating vs. the hue that generated the strongest gamma, which was typically a long-wavelength (reddish) hue showed that hue-induced gamma was on average ∼9.45 dB (or ∼8.83-fold) larger than grating-induced gamma (Fig. 2C); uncorrected increases showed similar trends, as shown in Fig. S2. Optimal hues increased gamma by as much as ∼25 dB, or ∼300-fold in some cases.

The total increase in gamma power was strongest for long-wavelength (reddish) hues (around 0° in standard HSV nomenclature), followed by short-wavelength (bluish) hues (around 210°; Figs. 1 and 3A), exhibiting an overall bimodal nature across the hues for all the sites across monkeys. For monkey 3, a third mode was also observed near the middle wavelength (greenish) hues (around 130°). The valley between the long- and short-wavelength peaks occurred at ∼270° (purple hue), falling on the line joining the long- and short-wavelength extremes of the horseshoe curve on the International Commission on Illumination (CIE) chromaticity diagram. The other trough in gamma response occurred near 60° (yellowish hue). To visualize the distribution of hues for peak gamma response across all electrodes, we divided the hues into two ranges of equal length, separated by 270° (purple) and 90° (yellowish-green), owing to the predominantly bimodal form of the hue tuning curve (Fig. 3A). The peak hues clustered tightly around 0° (reddish) and 210° (bluish) hues in the resulting histograms (Fig. 3B).

To further characterize the gamma band responses, we determined the peak frequency (i.e., the frequency showing the maximum change in power from spontaneous activity) of the gamma rhythm (Fig. 3C). Interestingly, the peak frequency of the rhythm across hues exhibited local maxima at 240°, 0°, and 120° hues (bluish, reddish, and greenish ranges, respectively), which correspond to the monitor primaries. Generally, the peak frequency varied as a function of the hue, shifting higher with higher gamma power. This effect is qualitatively similar to the effect of increasing the contrast of achromatic gratings, which increases both the strength and the center frequency of gamma (2, 3).

Unlike the gamma band, power in the other bands, such as alpha (8–12 Hz), beta (15–25 Hz), and high-gamma (250–500 Hz) did not show a strong dependence on hue (Fig. S3). We chose a higher range of frequencies for high-gamma, which has been associated with multiunit firing of the neurons around the microelectrode tip (12), because prominent harmonics of the gamma rhythm occurring in the intermediate range (110–250 Hz) caused the hue tuning to trivially follow that of the gamma rhythm.

Dependence on Saturation, Luminance, and Cone Contrast.

To understand the dependence of gamma on the purity and luminance of the hue, we progressively reduced the saturation (effectively adding white) and value (adding black; see Table S1 for the corresponding luminance, Y, values in cd/m²) of the pure hues (Fig. 4A). Desaturation effectively reduces the excitation purity of the stimulus and also shifts the effective hue even though the dominant wavelength is the same. In contrast, reducing the value does not affect the purity of the stimulus wavelength, but just makes it less bright. We observed across sites in all monkeys that the gamma strength dropped drastically with a reduction in saturation but remained high for reduced levels of value. Slopes of the linear fits between saturation level and change in gamma power were significantly greater than 0 for all hues in all monkeys (P = 10⁻¹¹⁰, t test). In contrast, slopes between value level and change in power were small and were significantly greater than 0 for only 9 out of 18 hues for the three monkeys (P < 0.05, Bonferroni- corrected, t test), and significantly smaller than the corresponding slopes between saturation levels and power in almost all cases (P = 10⁻¹⁰⁶, t test) (Fig. 4B).

Of note, shifting from a pure hue to white actually increased the stimulus luminance. Indeed, monkey pupil dilation faithfully tracked the changes in overall luminance, being largest for the short-wavelength (bluish) and smallest for the middle-wavelength (greenish and yellowish) hues, and expanding with decreasing value for all hues (Fig. S4). In addition, we observed that the gamma was stronger for black than for white, as reported previously (13), although the difference was subtle compared with the difference between pure hues and achromatic stimuli.

To understand the mechanisms underlying these results, we computed the L, M, and S cone contrasts (i.e., relative change in cone activation with respect to the adapting gray stimulus before the onset of the hue stimulus; details in Materials and Methods); cone contrasts along the cardinal axes [L−M and S−(L+M)]; and luminance (L+M) for all the stimuli and plotted them against the corresponding change in gamma power (Fig. 4C and Fig. S5; details in Materials and Methods). Gamma power depended very strongly on positive L−M cone contrast (P < 10⁻⁹ for all three monkeys; Fig. 4C), but not on other parameters (Fig. S5). This strong dependence of power on positive L−M cone contrast was not observed in the high-gamma range (Fig. S6) or in any other frequency ranges.

We further tested the dependence of gamma power on hue, saturation (defined as the ratio of distance between the stimulus and the adapting gray and the distance between the spectral locus of the stimulus and the adapting gray in xyY space), or luminance (Y value for each color represented in xyY coordinates; Table S1) using linear regression with change in gamma power as the regressand. For hue, we used the cosine and sine of the hue angle as regressors to account for the circular nature of hue angles (14). Although gamma power was clearly hue-dependent, the weights were not significantly different from 0, mainly because of the multimodal (nonlinear) nature of the hue dependence curve on gamma (Fig. 3A). Although simple linear regression with saturation or luminance as the regressors yielded significant weights for all three monkeys (Fig. S7), a multiple linear regression with luminance, saturation, and the sine and cosine of the hue value as regressors showed that the weights associated with saturation remained significantly greater than 0 for all monkeys, but were not different from 0 for luminance for monkeys 1 and 3. Similar results were obtained using partial correlation, for which gamma power significantly depended on the saturation (P = 0.009, 0.01, and 1.7 × 10⁻⁹ for monkey 1, 2, and 3, respectively), while luminance showed a significant partial correlation with gamma only in monkey 2 (P = 1.35 × 10⁻⁴ for monkey 2 and P > 0.2 for monkeys 1 and 3). This analysis revealed no consistent effect of luminance variation on gamma power.

Gamma power did not significantly depend on the eccentricity of the receptive field except in monkey 1, although this could be due to the limited span of eccentricities for the other two monkeys (Fig. S8).

Discussion

Color processing in V1 has mostly been studied by analyzing evoked spiking responses due to chromatic stimuli (reviewed in refs. 15–17), with only a few recent studies looking at LFP responses, although not at gamma oscillations (18–20). We show that the gamma band of V1 LFP is highly sensitive to hue and saturation and largely invariant to luminance, with power increases far exceeding those reported in previous studies that used achromatic stimuli. Importantly, by computing the activation of different cone types, we show that the strength of gamma oscillations depends most significantly on the difference in the activation of the M pathway relative to the L pathway.

Our results are consistent with a previous report in which ECoG signals recorded over V1 of anesthetized macaques exhibited stronger gamma oscillations for isoluminant red stimulus than for green, yellow, or white stimuli (21). Such a dependence on color could be one reason why the image of an orange generated very strong gamma oscillations in ECoG in the dataset used by Brunet et al. (8; figures 2 and 3).

Gamma Generated by Gratings vs. Hues.

The almost 10-fold increase in gamma generated by long-wavelength (reddish) hues compared with gratings is surprising, since these uniformly illuminated hue stimuli did not appear to consistently drive the neurons (Fig. S1). However, since gamma oscillations in LFP are thought to emerge from excitation–inhibition interactions in the network (22), the key factor determining the strength of gamma could be the spatial and temporal overlap of excitation and inhibition. Receptive fields in the LGN are dominated by color opponent mechanisms, namely red-green (L−M or vice versa) and blue-yellow [S − (L+M)] transformations of the cone inputs, which, along with an achromatic axis (L+M), constitute the three cardinal response axes (23, 24). Cells in V1 also show receptive field structures ranging from single opponency (center and surround excited by different cone types, e.g., an L+ center and M− surround) to double (both spatial and chromatic) opponency (e.g., an L+M− center and L−M+ surround) (16, 25). Therefore, uniformly illuminated hues could produce homogenous, balanced, and spatially and temporally aligned central excitation and surround inhibition in a large fraction of neurons, leading to large gamma oscillations. In contrast, achromatic gratings would generate variable excitation across the neural population depending on the orientation preference, and the suppression (e.g., through a normalization mechanism) may have a different tuning and spatial spread (26).

Although gamma has been linked to excitation–inhibition interactions (reviewed in ref. 22), the precise nature of such computations remains relatively unknown and is a topic of active research. Models that attempt to explain changes in gamma power due to variations in stimulus properties (e.g., Wilson–Cowan model) often use lumped excitation and inhibition, which, while useful for explaining some aspects of gamma generation, often lack important biophysical details (3, 27). Furthermore, gamma rhythms often show peculiar properties that cannot be easily accounted for using a simple excitation-inhibition mechanism. For example, nearly all of the sites recorded from a monkey often show stronger gamma for a single orientation (which, interestingly, varies from monkey to monkey), even though single units show preference for different orientations (figure 1 of ref. 11; figure 5 of ref. 28; figure 2C and D of ref. 29). Similarly, gamma power continues to increase with stimulus size even up to several degrees of visual space, far greater than the size of the receptive field of the units recorded from the same electrode (figure 2A of ref. 3; figure 4 of ref. 11). Incredibly, large stimulus sizes can induce a second gamma rhythm that is tuned to a completely different orientation (11). These results suggest that gamma rhythm could depend on the complex dynamics of the entire network, not merely of the cells near the microelectrode tip.

To make concrete models of gamma rhythms generated by hues, the first step would be to better characterize the dependence of gamma power on luminance and saturation, using pure hues along more controlled color spaces, such as DKL (24), or using cone- isolating stimuli (25), as well as using stimuli that have chromatic contrast of varying spatial/temporal frequencies (similar to, say, the stimuli used in ref. 24) and of varying size. But even after characterizing gamma responses to various features of chromatic gratings, integrating these findings into a biophysical model of excitation and inhibition may pose a considerable challenge.

Preference for Long-Wavelength (Reddish) Hues.

Strong gamma oscillations for long-wavelength (reddish) and short-wavelength (bluish) hues in V1 could simply be due to stronger inputs from LGN, preferential nonlinear processing along the cardinal directions in V1 (30), or stronger feedback from other visual areas where the response to primary hues remains strong even though the overall representation becomes more widely distributed (31–34). Stronger gamma for red vs. green hues, or positive L−M as opposed to negative L−M cone contrast, could be because of higher absolute (L−M) cone contrast (∼0.10 vs. ∼0.05; Fig. 4C), the presence of a larger number of L cones compared with M or S cones (L:M:S = 10:5:1) (35), or a high proportion of L+M− cells in retinal ganglion cells (36). Previous studies using achromatic gratings or gabors (1–3, 12, 29) have shown that inhibition in the magnocellular pathway, which is involved in the processing of achromatic visual information, strongly modulates gamma. Notably, it has been reported that sustained inhibition is produced in the magnocellular layer by long wavelengths, but not by white light (37). This may also lead to an increase in gamma power with positive L−M contrast and a reduction in gamma power at lower saturation. Finally, the laminar position of our microelectrodes (most likely in layer 2/3 or upper layer 4) could also determine the strength of gamma, since the achromatic magnocellular inputs preferentially terminate at 4Cα and the parvocellular L/M afferents terminate at 4Cβ, whereas the koniocellular S/L+M afferents terminate at more superficial layers 2/3 and 4A, particularly in the cytochrome oxidase-rich “blobs” (reviewed in ref. 38). Further testing with recordings from several layers using stimuli that excite only one type of cone (25) or specifically target one of the three cardinal LGN axes (24), as discussed above, and other visual areas are needed to better understand the relationship between color and gamma.

Materials and Methods

Animal Preparation and Training.

All monkey experiments were carried out in adherence to the guidelines approved by the Institutional Animal Ethics Committee of the Indian Institute of Science and the Committee for the Purpose of Control and Supervision of Experiments on Animals. Three adult female monkeys (Macaca radiata; 13 y, ∼3.3 kg; 17 y, ∼4 kg; and 13 y, ∼3.5 kg) were used in this study. In each monkey, a titanium headpost was surgically implanted over the anterior/frontal region of the skull under general anesthesia. After adequate recovery, the monkey was trained on a visual passive fixation task. Once the monkey was satisfactorily trained, another surgery was performed under general anesthesia to insert a microelectrode array [Utah array, 96 active platinum microelectrodes (81 for monkey 3), 1 mm long, 400 µm interelectrode distance; Blackrock Microsystems] in the primary visual cortex (right hemisphere, centered ∼10–15 mm rostral from the occipital ridge and ∼10–15 mm lateral from the midline, with location varying slightly in the three monkeys). The receptive fields of the recorded neurons were located in the lower left quadrant of the visual space with respect to fixation (at an eccentricity of ∼3°–4.5° in monkey 1, ∼1.4°–1.8° in monkey 2, and ∼3.5°– 4.5° in monkey 3). The recordings are unlikely to be entirely from blobs/cytochrome oxidase patches, which are thought to be involved in color processing in V1, because the microelectrode array dimensions far exceed the dimensions of blobs. Moreover, we confirmed that the units show orientation selectivity. Following a period of postsurgery care and monitored recovery of at least 2 wk, the monkeys performed the experimental task regularly while microelectrode data were recorded.

Experimental Setup and Behavior.

For the task, each monkey sat with its head fixed by the headpost in a monkey chair and viewed a monitor (BenQ XL2411, LCD, 1,280 × 720 resolution, 100-Hz refresh rate, gamma-corrected and calibrated to a mean luminance of 60 cd/m² on the monitor surface using i1Display Pro; x-rite PANTONE) placed ∼50 cm from its eyes. The monkey and the display setup were housed in a Faraday enclosure with a dedicated grounding separate from the main supply ground to provide isolation from external electrical noise.

Each monkey performed a passive fixation task in which fixation had to be maintained at a small dot (0.05°–0.10° radius) at the center of the screen for the duration of a trial, which varied between 3.3 and 4.8 s. Each trial began with fixation, and following an initial blank gray screen of 1,000 ms, two to three stimuli were shown for 800 ms each, with an interstimulus interval of 700 ms. The monkey was rewarded with juice for successfully holding its fixation within 2° of the fixation spot, which remained visible throughout this period. The monkey were able to hold their fixation well within these limits (SD <0.4° across all sessions for all monkeys) during the task. Since the stimuli were all full screen, the small deviations are unlikely to affect the results.

Stimuli.

All stimuli were presented on a monitor that was gamma-corrected to obtain a gamma of 1 for each of the three primaries of the color gamut, which had the following CIE chromaticity xy coordinates: red, (0.644, 0.331); green, (0.327, 0.607); blue, (0.160, 0.062). The white point was at (0.345, 0.358). The xyY coordinates of all the stimuli are listed in Table S1 and also shown in Fig. S7A, along with the spectrum locus.

For the hue tuning experiment, the stimuli consisted of 36 equally spaced hues along the circular hue space (0° hue to 350° hue, with 0°, 120°, and 240° corresponding to red, green, and blue, respectively, in accordance with the standard HSV nomenclature), shown on full screen at full saturation and value (intensity or luminance). Full-screen stimuli produced stimulation of a visual angle of ∼56° in the horizontal direction and ∼33° in the vertical direction.

Large visual stimuli do not drive neurons effectively, but gamma oscillations increase in magnitude with stimulus size (1, 3, 12) and thus are most salient for full-screen gratings. We found that hue patches showed a similar trend as gratings: increasing the size of the patch increased the magnitude of gamma. Thus, we used full-screen hues. Since our main goal was to study the effect of hues observed in natural scenes, we used hues at full saturation and value instead of using, say, equiluminant hues that do not span the color space effectively, especially bright green and red hues. Because of this, the overall physical luminance varied with hue, which was highest for greenish hues and lowest for bluish hues (as confirmed by pupil diameter, as shown in Fig. S4). Furthermore, since the prestimulus background color was fixed at gray at 50% luminance, presentation of each hue effectively introduced a different luminance step, which could by itself trigger neural or oscillatory responses. Therefore, additional experiments were conducted in which the saturation or value was varied parametrically (see below). We found that magnitude of gamma oscillations changed little with the value of the hue (Fig. 4), suggesting that the issues described above with using hues at varying luminances did not affect the major results presented here in any important way.

For the hue saturation (HS) tuning experiment and the hue value (HV) tuning experiment, six equally spaced hues (0°–300°, in steps of 60°) were used. For HS, the value was fixed to the maximum of 1 while saturation was varied from 0 to 1 in steps of 0.25. Likewise, for HV, the saturation was fixed to 1 while value was varied from 0 to 1 in steps of 0.25 for monkey 3. For monkeys 1 and 2, values of 0, 0.35, 0.71, and 1 were used.

The full-screen grating stimuli used for comparison were shown similarly, either in the same session or in a separate session. The gratings were static, at 100% contrast and at a spatial frequency of 2 cycles per degree and an orientation of 90°, which elicited strong gamma oscillations in the LFP signal in all three monkeys. (More detailed tuning experiments in monkeys 1 and 2 are described in ref. 11.)

Data Recording.

Raw signals were recorded on 96 channels using the 128-channel Cerebus neural signal processor (Blackrock Microsystems). To derive the LFP signals, the raw signals were filtered online between 0.3 Hz (Butterworth filter, first-order, analog) and 500 Hz (Butterworth filter, fourth-order, digital), sampled at 2 kHz, and digitized at 16-bit resolution. Spikes (multiunits) were extracted separately from the raw signals using another online filter between 250 Hz (Butterworth filter, fourth-order, digital) and 7.5 kHz (Butterworth filter, third-order, analog) and then subjecting the filtered signal to a threshold (amplitude threshold of ∼5 SD of the signal). No further offline filtering was done on these data before the analyses.

Eye position data (horizontal and vertical coordinates/positions) and pupil diameters were recorded throughout the task using the ETL-200 Primate Eye Tracking System (ISCAN) and monitored using custom software running on MacOS that controlled the task flow, stimulus generation, and pseudorandom stimulus presentation.

Electrode Selection.

The suitability of electrodes for use in analyses was determined using a receptive field mapping protocol run across multiple days, in which small sinusoidal gratings were flashed at equally spaced locations within a rectangular grid on the visual space that approximately covered the aggregate receptive field of the entire microelectrode array. Electrodes with consistent stimulus-induced changes and reliable receptive field estimates across sessions were chosen for further analysis. In addition, electrodes with unusable or inconsistent signals, a high degree of crosstalk with other electrodes, or impedances outside the range of 250–2,500 KΩ (125–2,500 KΩ for monkey 3) were discarded. This yielded 62–64, 32–35, and 16 electrodes for the three monkeys. For the scatterplots shown in Figs. 2C and 4B and Fig. S2B, data for the common electrodes (numbers indicated by N on the plots) across the analyzed conditions are shown.

Data Analysis.

Stimulus presentations for which excessive electrical artifacts were observed were discarded (<2% for all monkeys) for every session, yielding on average between 12.4 and 29.9 stimulus repeats per condition across different sessions and monkeys (overall range for number of repeats for a condition, a minimum of 10 to a maximum of 43 repeats; the noninteger value of the average number of repeats arises due to an unequal number of repeats across conditions for any session owing to pseudorandom stimulus presentation and removal of some repeats from analyses after artifact rejection). Spectral analyses were done using the Multitaper method using functions in the Chronux toolbox (39) (chronux.org/) developed for MATLAB. Time-frequency power spectra were obtained with a single taper with a sliding window of 0.25 s to obtain a 4-Hz frequency resolution. Power spectral densities (PSDs) were computed for period 0.25 to 0.75 s after stimulus onset and compared with the PSD during the spontaneous period (–0.5 to 0 s). The change in power was calculated by subtracting the logarithm of power during stimulus period and spontaneous activity and multiplying by 10 to obtain units of decibels.

Unlike the hue stimuli, the full-field grating stimuli induced a broadband increase in power around the gamma range of frequencies, increasing the overall power in the gamma band. A pedestal fit (Fig. 2) was done to remove the contribution of the broadband effect. A log-log fit to the raw power spectral density during the baseline period did not give a satisfactory fit, since the slope of this fit is typically not constant across frequencies (e.g., figure 1B of ref. 40), and is more difficult to estimate in the presence of gamma oscillations and associated harmonics. Thus, we used a heuristic fitting procedure to estimate the shape of the “pedestal” over which the gamma rhythm was riding in the difference PSD. Specifically, we fitted a linear curve to the difference PSD in two ranges: 0–30 Hz [0–25 Hz for difference PSD due to grating stimuli, to avoid the influence of the slow gamma peak observed in this case (11)] and 40–150 Hz, barring two bands of 30-Hz width centered at the peak frequency of the gamma and its first harmonic. A cubic spline was then fitted over the entire range interpolating the two linear curves. We estimated the maximum change in gamma power from baseline in decibels as the height of the gamma peak above the fitted curve, as shown in Fig. 2; however, the results remained qualitatively similar when the uncorrected gamma power changes were used (Fig. S2).

In addition to the broadband effect, large full-field grating stimuli induced two distinct gamma rhythms, which we term “slow” and “fast,” that are not cotuned and thus should not be confused for gamma and its harmonic (11). We used the grating that maximized the fast gamma occurring above 40 Hz for comparison with the hue-induced gamma (11).

To calculate the change in power in a particular spectral band (Fig. 3), we computed the total power in the band during the stimulus epoch and divided it by the total power in the band during the baseline epoch as described above and then converted it to a decibel change in power. These quantities were calculated separately for each electrode, and an average across electrodes was taken wherever applicable. The peak frequency within a spectral band was defined as the frequency within the band that showed the maximum decibel change from the baseline condition (Fig. 3C). The gamma band ranges for the three monkeys were chosen as [30 80] Hz for monkey 1, [30 80] Hz for monkey 2, and [25 75] Hz for monkey 3, based on inspection of the difference PSD. The results were qualitatively similar when we used the peak gamma change (estimated from the curve-fitting procedure used for Fig. 2) as the metric to determine the tuning to hues.

For cone contrast calculations, the monitor emission spectrum for each stimulus was first measured in the form of intensity (count) for wavelengths of light from 194.61 nm to 1,056.3 nm in steps of 0.2 nm using a spectrometer (USB4000-UV-VIS; Ocean Optics), which was subsequently smoothed using a spline fit to obtain intensities for wavelengths between 390 and 830 nm in steps of 5 nm. Cone activation was calculated for each stimulus by taking a dot product of the stimulus spectrum with the corresponding cone absorption spectrum (Stockman and Sharpe 10-degree human cone fundamentals based on the Stiles & Burch 10-degree color matching functions, obtained from Colour and Vision Research Laboratory Database, www.cvrl.org/). Cone activations for the interstimulus gray stimulus (adaptation state) were obtained similarly. The Michelson cone contrast was obtained as the difference in cone activations between the stimulus and gray divided by the sum, (X − X_AD)/(X + X_AD), where X is the L, M, or S cone activation and X_AD is the corresponding cone activation for gray. Qualitatively similar results were obtained using the Weber contrast, (X − X_AD)/(X_AD).