Harmonics added to a flickering light can upset the balance between ON and OFF pathways to produce illusory colors

Significance

By varying the temporal waveforms of complex flickering stimuli, we can produce alterations in their mean color that can be predicted by a physiologically based model of visual processing. The model highlights the perceptual effects of a well-known feature of most visual pathways, namely the early separation of visual signals into increments and decrements. The role of this separation in improving the efficiency and sensitivity of the visual system has been discussed before, but its effect on perception has been neglected. The application of a model incorporating half-wave rectification offers an exciting psychophysical method for investigating the inner workings of the human visual system.

Abstract

The neural signals generated by the light-sensitive photoreceptors in the human eye are substantially processed and recoded in the retina before being transmitted to the brain via the optic nerve. A key aspect of this recoding is the splitting of the signals within the two major cone-driven visual pathways into distinct ON and OFF branches that transmit information about increases and decreases in the neural signal around its mean level. While this separation is clearly important physiologically, its effect on perception is unclear. We have developed a model of the ON and OFF pathways in early color processing. Using this model as a guide, we can produce imbalances in the ON and OFF pathways by changing the shapes of time-varying stimulus waveforms and thus make reliable and predictable alterations to the perceived average color of the stimulus—although the physical mean of the waveforms does not change. The key components in the model are the early half-wave rectifying synapses that split retinal photoreceptor outputs into the ON and OFF pathways and later sigmoidal nonlinearities in each pathway. The ability to systematically vary the waveforms to change a perceptual quality by changing the balance of signals between the ON and OFF visual pathways provides a powerful psychophysical tool for disentangling and investigating the neural workings of human vision.

An image of the outside world is formed on the rear, inner surface of the eye, the retina, on which a patchwork of light-sensitive photoreceptors generates a neural representation of the image. Before being transmitted to the brain, however, this neural representation is substantially processed and recoded by the other retinal neurons: the horizontal, bipolar, amacrine, and ganglion cells. An important step in the recoding is the partitioning of information about different aspects of the image, such as color and luminance, into distinct parallel pathways. Although this early processing allows neural activity to represent the information in the retinal image efficiently (1–4), it makes the neural threads that eventually lead to perception difficult to unravel.

Information about color is first represented by a trichromatic or three-variable code that corresponds to the responses of the three classes of cone photoreceptor: the long (L)-, middle (M)-, and short (S)-wavelength sensitive cones, which peak in sensitivity near 566, 541, and 441 nm, respectively (5). At the first neural junction in the visual system, the synapses at the photoreceptor outputs, the three cone signals feed into several pathways that selectively encode different aspects of the image. In the major pathways, the signals are additionally subdivided into parallel “ON” and “OFF” branches, each of which is an approximately half-wave rectified version of the cone output—with the ON pathway carrying signals corresponding to changes in the light stimulus above the average intensity (increments) and the OFF pathway carrying signals corresponding to changes below the average intensity (decrements).

The main focus of this paper is on the primary signals that lead to the perception of “red” and “green” colors—the cone-opponent signals formed by differencing L- and M-cone outputs. The cone-opponent ON and OFF pathways that carry these signals remain separate at least through to the primary visual cortex (6, 7). Individual neural elements in these pathways each respond to a limited region of the external visual field called the receptive field. The centers of the receptive fields of cone-opponent “midget” bipolar cells in the central retina (the “fovea”) have single L- or M-cone inputs, so that there are four varieties of foveal midget bipolar cells: receptive fields with centers that are L-ON, M-ON, L-OFF, or M-OFF, with the two ON varieties carrying information about increments and the two OFF varieties carrying information about decrements. Each receptive field has an opponent surround that derives from lateral connections made between horizontal cells and surrounding cones (8).

Having parallel ON and OFF pathways has major advantages in terms of sensitivity and efficiency, since it allows neurons to maintain a low resting level or firing rate while roughly doubling the response range (9, 10). A major disadvantage, however, is that splitting visual signals into increments and decrements is an inherently nonlinear process that substantially distorts the input signal and produces distinct signals in the ON and OFF pathways.

The distortion can be clearly seen in physiological recordings: whereas cones and horizontal cells respond approximately linearly to light stimulation (11), the responses of ON and OFF retinal ganglion cells clearly show the effects of half-wave rectification (12–14). Half-wave rectification is not entirely complete in the retina, since the responses of ON and OFF neurons can fall below their resting levels to a lower limit of the cell’s response (15), but it is nearly complete in the cortex (16–18).

The extent to which the distortion introduced by segregating signals into ON and OFF pathways affects visual perception remains unclear. If the ON and OFF pathways are balanced and approximately linear after half-wave rectification, then their subsequent recombination will cancel the distortion. If, however, the ON and OFF signals are distorted after half-wave rectification (by some additional nonlinear process or processes), then some distortion will remain, even if the signals are recombined. In particular, a compressive nonlinearity will decrease the mean signal level in each pathway, while an expansive nonlinearity will increase it. Thus, the most likely perceptual effect of the segregation into ON and OFF pathways will be a change in the mean appearance of a flickering light. For many of the waveforms used in experimental studies of visual perception, such as sinusoids and square waves, changes in the mean levels in balanced ON and OFF pathways will be identical, because for such stimuli, the ON and OFF signals are identical in shape (i.e., the waveforms are “half-wave symmetric”) and thus will be similarly distorted. Consequently, there will be no net change in the mean if the ON and OFF signals are subsequently recombined. By contrast, a change in the mean output (and thus, in mean appearance) would be expected if the stimuli are not half-wave symmetric, because the positive and negative parts of the asymmetrical stimuli will be unequally affected by matching nonlinearities in the ON and OFF pathways. Examples of changes in mean appearance found for such stimuli include the illusory change in mean brightness produced by the eye moving across a black and white sawtooth pattern (19) and the illusory changes in mean color when red and green lights are flickered around the mean using asymmetrical patterns (20–22).

Here, we use these illusory red–green color shifts to reveal some of the properties of the early stages of color processing and develop a physiologically based model that can account for the dependence of the color shifts on the shape of the temporal waveform. The model’s predictions depend on the half-wave rectification of the visual signals into ON and OFF pathways and on a later saturating nonlinearity that is similar in form to the way in which neurons respond to contrast (23). Crucially in the model, the size and direction of the color shifts are initially determined by the shape of the waveform at the input to the half-wave rectifiers (i.e., before subsequent processing reduces sensitivity to higher temporal frequencies). Consequently, the color shifts can be altered by high-frequency components of the visual input that are themselves invisible (or nearly so). The way in which the color shifts vary with the shape of the waveform at the visual input then provides useful information both about the linear processes before the rectifying stages and about subsequent linear and nonlinear processing.

To test the model, we presented pairs of flickering red–green stimuli side by side on a cathode ray tube (CRT). The two flickering stimuli had identical means and Fourier amplitude spectra, but they had opposite phases (i.e., each was a contrast inversion of the other). Observers were required to judge which of the pair appeared redder on average. Our model accurately predicts the red–green color shifts that the observers reported and can be applied to a variety of other color and luminance phenomena, providing a straightforward psychophysical method for examining properties of the ON and OFF pathways in the human visual system.

Results

To examine the perceptual effects of the early separation of information into ON and OFF pathways, we presented flickering lights on a CRT display that generated either (i) time-varying signals in the L-cones while holding the signals from the M-cones constant or (ii) time-varying signals in the M-cones while holding those from the L-cones constant. At the temporal frequencies that we used, these L- or M-cone “isolating” flickering waveforms are perceived mainly as variations in color rather than in brightness. L-cone or M-cone isolating stimuli were used in separate experimental runs. Our approach was to use different time-varying, cone-isolating waveforms that, despite having the same time-averaged mean, produced very different signals when split into ON and OFF pathways. Rather than using arbitrary waveform shapes in our experiments, we used combinations of harmonically related sinusoids, which allowed us to measure systematically the effects of varying the harmonic content and, in addition, substantially simplified the analysis and modeling.

In the experiments, we presented pairs of visual stimuli on a carefully calibrated and linearized CRT monitor in two semicircular 5.7° of visual angle half-fields separated by a 0.6° gap as shown in Fig. 3, Upper Left Inset. A temporal waveform of a particular shape was presented in one half-field, chosen at random, and its inverse (i.e., the same temporal waveform multiplied by −1) was presented in the other. One of the stimuli was usually described as redder, and the other was usually described as greener; we simply asked observers to report which side appeared redder.

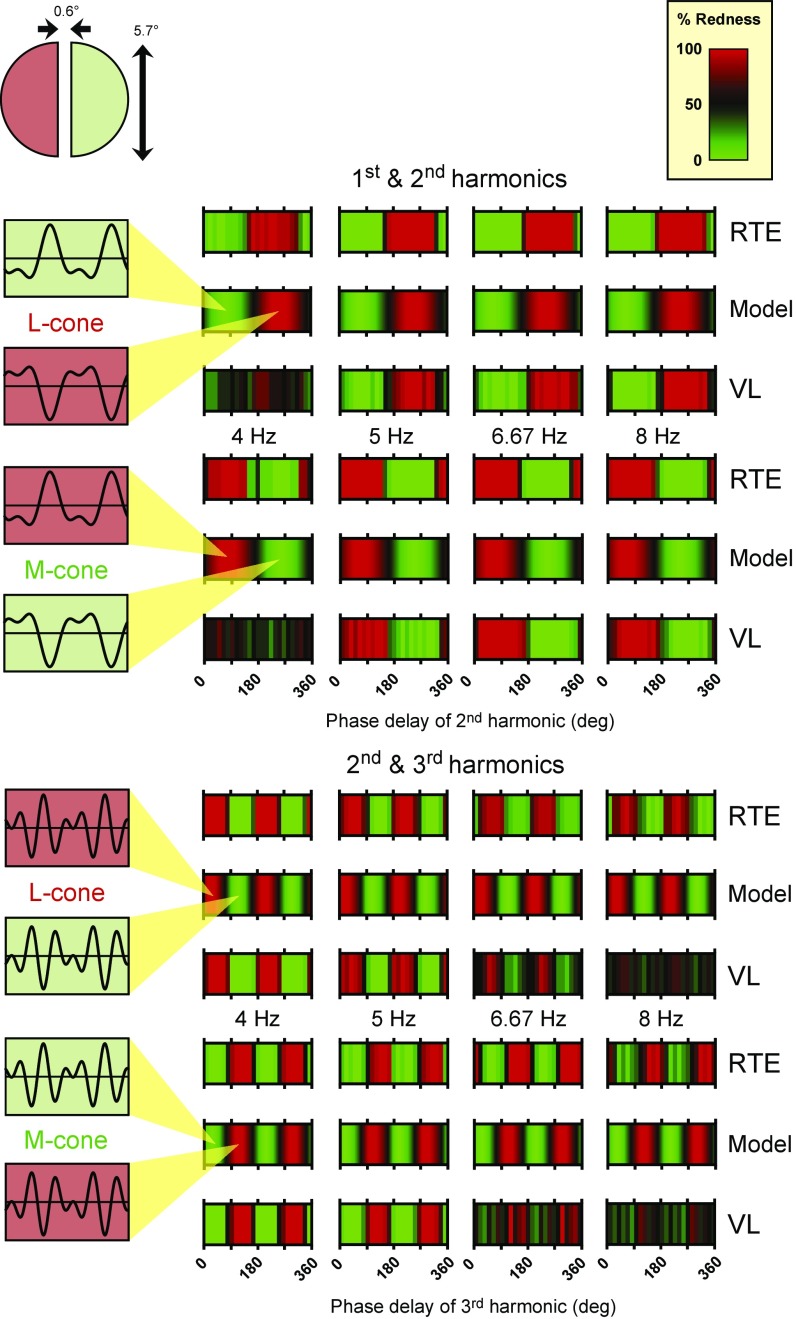
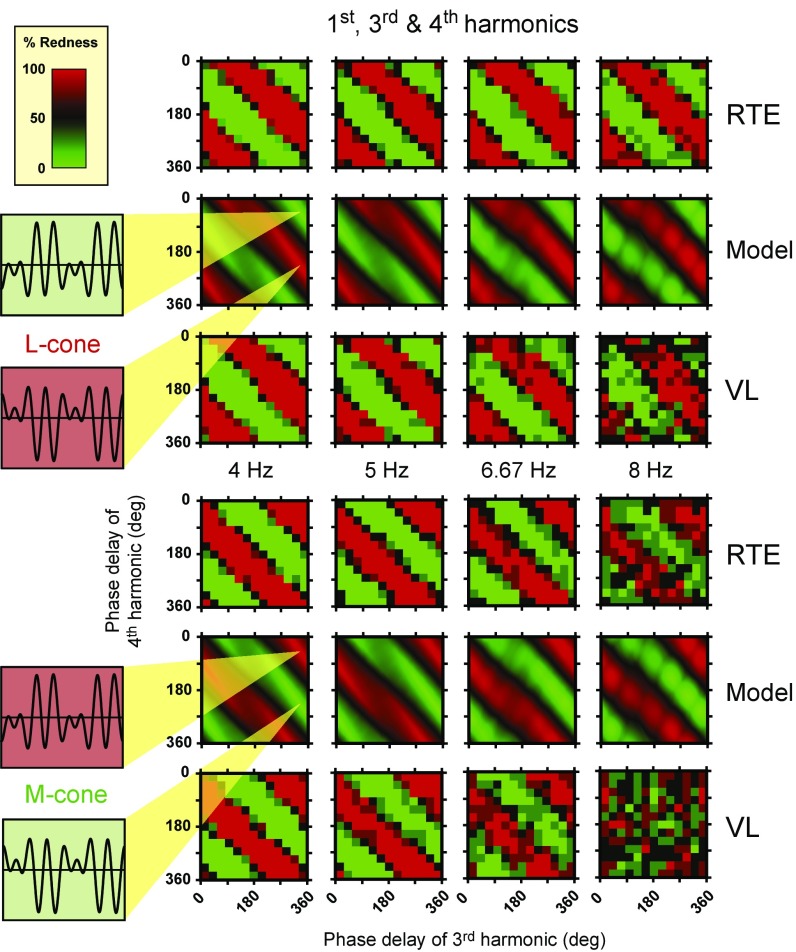
Fig. 3.

The illustration in the top left corner shows the stimulus configuration: 5.7° hemifields separated by a 0.6° gap. Data for two observers R.T.E. and V.L. and predictions for two different two-component waveforms are shown in four columns, with each column corresponding to a different fundamental frequency. Upper shows results for a fundamental and second harmonic in the amplitude ratio 1.0:0.5. Rows 1–3 in Upper are for L cone-isolating stimuli, and rows 4–6 in Upper are for M cone-isolating stimuli. The colors in the panels correspond to the scale labeled as “percent redness”. In the data panels, the colors indicate the percentage of times that each phase combination was indicated by the observer as appearing redder than its inverse. Black here corresponds to 50%, which we take to mean no reliable color shift between the two waveforms (i.e., one waveform and its inverse were equally likely to be chosen as redder). The colors in the model panels indicate the predicted color shift given by our model. The predictions have been scaled so that the largest shift toward red corresponds to a score of 100 and the largest shift toward green corresponds to 0, with 50 (shown as black) meaning no color shift. Each panel in Upper has the phase delay (in degrees) of the second harmonic on the abscissa. Lower shows results and model predictions for second and third harmonics of equal amplitude (the optimal modulation ratio of these harmonics according to the model) in the same format as Upper. Each panel has the phase delay (in degrees) of the third harmonic on the abscissa. Measurements were made at 15° intervals; the model’s predictions are given at 1° intervals. The waveforms in the Left Insets illustrate the optimal waveforms for producing red and color shifts according to the model, which have the harmonic phase delays indicated by the tips of the yellow cones.

By varying the content of the harmonically related sinusoids that make up the visual stimuli, we could manipulate signals at different stages in the chromatic pathway for reasons that will become clearer when we explain the model more fully. In the experiments, we focused on four different harmonic combinations, each of which was designed to answer a particular question. The combinations in the order in which the corresponding data are presented below were as follows.

• i)The first (called the fundamental) and second harmonics in amplitude ratio 2:1 (Fig. 1, Right).
• ii)The second and third harmonics in amplitude ratio 1:1 (Fig. 2, Left).
• iii)The first, third, and fourth harmonics in the amplitude ratio 0.5:1.0:1.0 (Fig. 2, Center).
• iv)The first, second, and fourth harmonics in the amplitude ratio 0.5:1.0:1.0 (Fig. 2, Right).

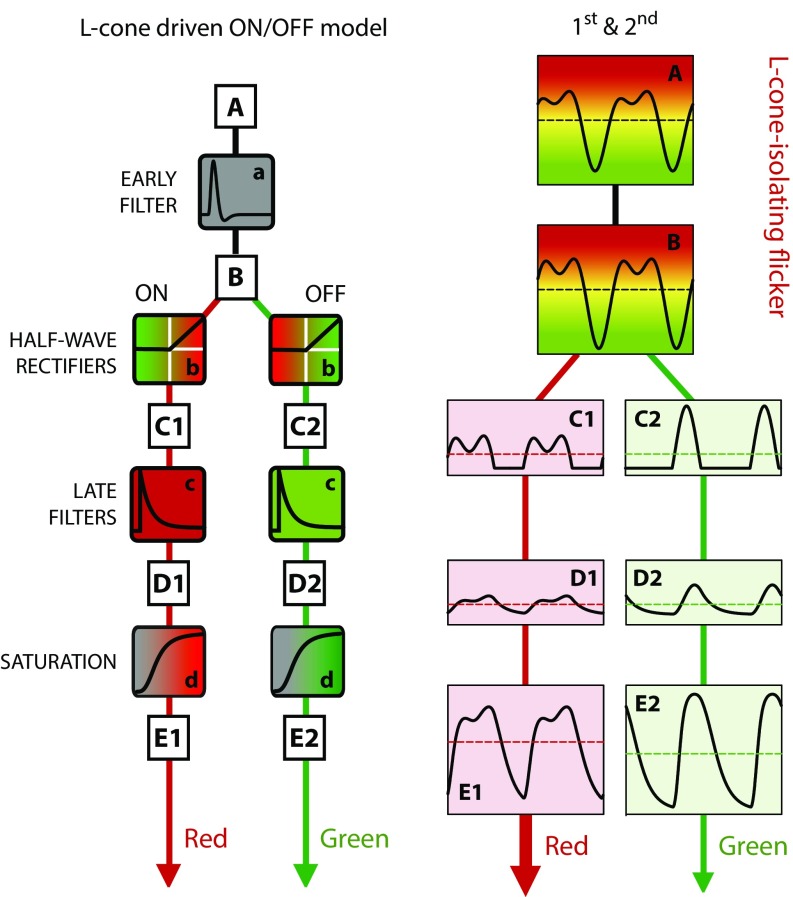
Fig. 1.

Left shows a model of the sequence of signal processing steps in L cone-driven ON and OFF pathways, and Right shows the processing through the model of an L cone-isolating waveform that is the sum of a fundamental and its second harmonic in the amplitude ratio 1.0:0.5, with a second harmonic phase delay of 256°. In Left, the stimulus, A, feeds an early band-pass filter, a, and its output, B, is split into ON and OFF channels by half-wave rectifiers, b. They produce two outputs, C1 and C2, that are low-pass filtered, c, and then compressed at d. Right takes the input waveform in A (two cycles of a 4-Hz fundamental frequency are shown) through the model and shows the final signals scaled up at E1 and E2. The mean values, shown as dashed horizontal red and green lines, are identical after rectification (C1 and C2) and after the late filter (D1 and D2) but differ in E1 and E2 because of the compression at d. It is the larger of the two means that determines the predicted color, which, in this case, is red.

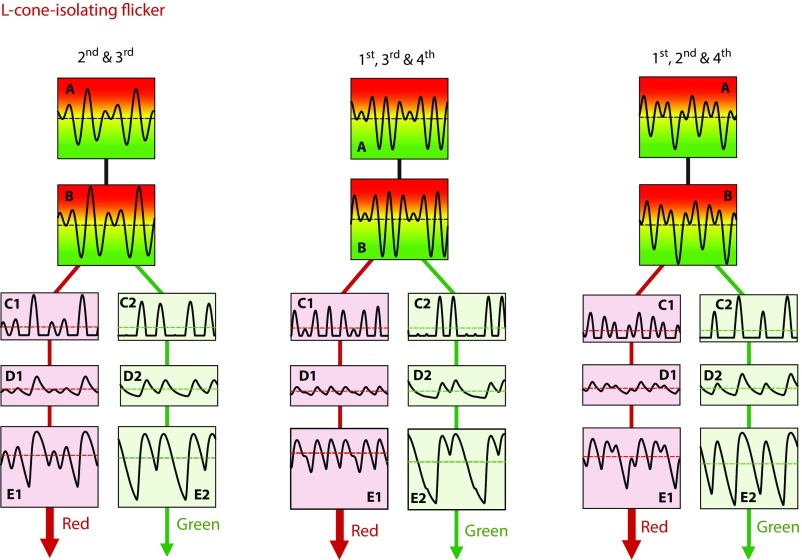
Fig. 2.

Illustrations of three waveforms passing through the sequence of steps of the model shown in Fig. 1. Each panel represents two cycles of the fundamental frequency. Left shows the processing of an L cone-isolating waveform that is the sum of a second and third harmonic in the amplitude ratio 1:0:1.0, with a third harmonic phase delay of 27° and no fundamental. Center shows the processing of an L-cone waveform that is the sum of first, third, and fourth harmonics in the amplitude ratio 0.5:1.0:1.0, with a third harmonic phase delay of 333° and a fourth of 226°. Right shows the processing of an L-cone waveform that is the sum of first, second, and fourth harmonics in the amplitude ratio 0.5:1.0:1.0, with second and fourth harmonic phase delays of 268° and 57°, respectively. Details are the same as in Fig. 1. In each illustrated case, the flickering light appears predominantly red.

The amplitude ratio used in i was chosen to be consistent with our previous work (22), being the ratio of first and second harmonic components of the sawtooth waveforms used in that work. The amplitude ratios for the other three combinations were predicted by our model (22) to produce large color shifts. The two-component stimuli (i and ii) were used, because they provide useful information about relative phase changes produced by the early filter in our model (to be discussed below); the results can be used to constrain the parameters of that filter (22). Combination iii (the first, third, and fourth harmonics) was chosen to examine the effect of high-frequency components—as we note below, the crucial component here is the fourth harmonic. Combination iv was chosen because the model predicted that the pattern of results would vary significantly with frequency, providing a stringent test of the model.

We used four different fundamental frequencies (4, 5, 6.67, and 8 Hz) in separate blocks for each combination of harmonics. On each trial, the relative phases of the harmonics were chosen at random from a set that was equally spaced between 0° and 360°. In each trial, the selected waveform was presented in one half-field chosen at random, and its inverse was presented in the other; the observers were asked to indicate which appeared redder on average.

Before presenting the results, we describe the model that emerged and show how its operation affects the different waveforms that we used.

Model.

To see how the splitting of the waveforms into ON and OFF pathways determines the mean color of each stimulus, consider the model illustrated in Fig. 1, Left. The predictions come from this relatively simple, physiologically based model of the red–green chromatic pathway. The model derives in part from Petrova et al. (24) and Stockman et al. (25), and it was formalized in the work by Stockman et al. (22). Fig. 1, Left shows the stages of an L cone-driven model, and Fig. 1, Right illustrates the effect of each stage of the processing on the representation of a flickering L cone-isolating stimulus comprising a 4-Hz fundamental frequency and its second harmonic in the amplitude ratio 2:1 (A in Fig. 1, Right). The phase delays of the harmonics are defined relative to their all being in sine phase (given as 0°). In the example waveform shown in Fig. 1, the phase delay of the second harmonic was 256°; the first harmonic was always taken to be in sine (0°) phase. [Note that, although the model and stimuli shown in Figs. 1 and 2 are L-cone examples that produce L-ON (red) and L-OFF (green) responses, there are analogous M-cone examples that produce M-ON (green) and M-OFF (red) responses.]

The stimulus (A in Fig. 1, Right) is first filtered by a slightly band-pass filter, with the biphasic impulse response a in Fig. 1, Left, to produce a slightly altered signal (B in Fig. 1, Right); the change in shape is relatively small in this case, because the early filter (a in Fig. 1, Left) has little effect near the 4-Hz fundamental frequency and its second harmonic. This early band-pass filter reflects the photoreceptor’s response and some low-frequency attenuation assumed to result from horizontal cell surround inhibition. The output of the early filter (B in Fig. 1, Right) is separated by half-wave rectifiers (b in Fig. 1, Left) that split the photoreceptor outputs into positive- and negative-signaling pathways. The half-wave rectification reflects the bifurcation of cone photoreceptor signals into ON and OFF cone-driven bipolar cells, which occurs at the cone-bipolar synapses at the cone pedicles (15, 26–30). The outputs of the half-wave rectifiers (C1 and C2 in Fig. 1, Right) are filtered by the late low-pass filters shown as exponentially decaying impulse responses (c in in Fig. 1, Left). The late filters represent neural temporal filtering, most of which seems likely to occur in the visual cortex [because physiological recordings show that high temporal frequencies produce strong responses in subcortical structures, such as the lateral geniculate nucleus (31)]. The early (a in Fig. 1, Left) and late (c in Fig. 1, Left) filters are designed such that their combined operation is consistent with previously measured psychophysical chromatic temporal contrast-sensitivity functions (22).

The late filters’ outputs (D1 and D2 in Fig. 1, Right) feed the final saturating nonlinearities (d in Fig. 1, Left), which we represent as sigmoidal Naka–Rushton-like nonlinearities (32), to produce the final outputs (E1 and E2 in Fig. 1, Right).

In each panel in Fig. 1, Right, the waveforms are represented by solid lines, and their time-averaged means are shown by the dashed lines. The means of the ON and OFF signals are the same until after the final compression by the sigmoidal nonlinearity, after which they differ, because the signal with greater amplitude is compressed more than the signal with lower amplitude. We assume that the color reported by our observers is determined by the larger of the mean signals at E in Fig. 1, Right, so that, for this L-cone example, the reported color shifts toward red, although the input stimulus modulates around a mean yellow-appearing chromaticity. The shift is toward red, because as indicated in Fig. 1, the mean in the L-OFF (green) pathway is reduced compared with the mean in the L-ON (red) pathway. An M cone-isolating stimulus would produce analogous results but with the roles of ON and OFF reversed: M-ON signaling green, and M-OFF signaling red. For simplicity, we take the absolute difference of the means of E1 and E2 in Fig. 1, Right as the size of the predicted color shift (but any monotonic function of the mean difference would produce qualitatively similar results).

One of the key features of the model is that the color shifts depend on the phase alignments of the harmonic components in the signal at the input to the half-wave rectification (b in Fig. 1, Left), where the half-wave rectification significantly affects the relative size of the harmonic components in the subsequent ON and OFF pathways (i.e., the waveforms at C1 and C2 in Fig. 1, Right must be clearly different to produce the mean color shift).

Fig. 2 shows how the 4-Hz fundamental L-cone waveforms for harmonic combination ii [the second and third harmonics (Fig. 2, Left)], combination iii [the first, third, and fourth harmonics (Fig. 2, Center)], and combination iv [the first, second, and fourth harmonics (Fig. 2, Right)] are affected by each stage of the model. The waveforms are shown with the phases predicted by the model to produce the largest color shifts. In each illustration, the mean color shift is toward red.

Model Predictions and Psychophysical Data.

The experimental results and the details of the model’s predictions are shown in Figs. 3–8. In Fig. 3, we consider harmonic combinations with just two components. Fig. 3, Upper shows the model’s predictions and data for the first and second harmonics, and Fig. 3, Lower shows the predictions and data for the combination of the second and third harmonics. In Fig. 3, Left Insets, we show the four stimuli that should produce the largest mean color shifts according to the model. The horizontal bars in Fig. 3 show the measured color shifts for observers R.T.E. and Vy Luong (henceforth abbreviated to V.L.) and the bars between them show the model’s predictions for L cone-isolating stimuli (Fig. 3, Upper, rows 1–3) and M cone-isolating stimuli (Fig. 3, Upper, rows 4–6). Each column corresponds to a different fundamental frequency. This format is also used in Figs. 4–7. Each bar plots along the abscissa the phase delay of the second relative to the first harmonic (Fig. 3, Upper) or third relative to the second harmonic (Fig. 3, Lower) in degrees from 0° to 360°. Since there are only two frequency components in each case and only the phase of one component is varied relative to a fixed phase of the other, the results and predictions vary along only one dimension of phase, so that the results and predictions form vertical stripes. The colors in the data bars indicate the percentages of time that each phase combination was reported by the observers as appearing redder than its inverse. The color scale (upper right of Fig. 3) shows how color in the data bars is related to the percentage of time that a stimulus was reported as red. Note that black indicates that the waveform was chosen as redder or greener with equal frequency (i.e., there was no consistent color shift). The colors in the bars showing the model’s predictions, presented at a much finer resolution, represent the color shifts predicted by the model using the same color scale as for the data. The predictions have been scaled so that the largest predicted shift toward red corresponds to 100 and the largest shift toward green corresponds to 0, with 50 (black) denoting no color shift; inspection of the data and corresponding model bars shows how well the model predicts the results.

Fig. 8.

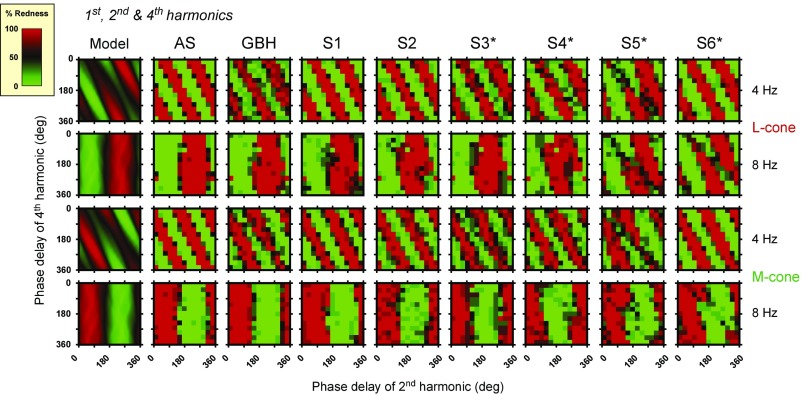
Results for eight additional observers: the authors G.B.H. and A.S. and six naïve observers, S1–S6. Data are for L-cone (rows 1 and 2) and M-cone (rows 3 and 4) stimulus waveforms comprising the fundamental, second, and fourth harmonics in the amplitude ratio 0.5:1.0:1.0 at fundamental frequencies of 4 Hz (rows 1 and 3) and 8 Hz (rows 2 and 4). Column 1 shows the model predictions. Comparable data for R.T.E. and V.L. can be seen in columns 1 and 4 in Fig. 5.

Fig. 4.

The panels show results for two observers, R.T.E. and V.L., on separate rows and model predictions in the rows between them. Upper shows an L cone-isolating stimulus waveform comprising the fundamental, third, and fourth harmonics in the amplitude ratio 0.5:1.0:1.0, and Lower shows the equivalent M-cone stimulus. Each column corresponds to a different fundamental frequency (first harmonic) ranging from 4 to 8 Hz. Each panel has the phase delay (degrees) of the third harmonic on the abscissa and the phase delay of the fourth harmonic on the ordinate. Measurements were made at 30° intervals; the model’s predictions are given at 1° intervals. Insets illustrate the L-cone or M-cone stimulus waveforms at the input that correspond to the third and fourth harmonic phases indicated at the points of the yellow cones at 333° and 46° or 333° and 226°. Two cycles of the 4-Hz fundamental are illustrated. At a fundamental frequency of 4 Hz, the yellow cones indicate the optimal input stimuli, according to the model, for producing red and green color shifts. The red or green vertical stripes show the colors indicated by the observers or the model, the intensity of which denotes the percentage of times that the observer or model selected each waveform as appearing redder than its inverse (coded from red to black) or greener than its inverse (coded from green to black).

Fig. 7.

(A) Each adjacent pair of panels in A shows data from V.L. (in the left-hand member of each pair) and model predictions (in the right-hand member of each pair) for L cone-isolating stimuli. (B) Each pair of panels in B shows data from V.L. and model predictions for M cone-isolating stimuli. Other details are the same as in Fig. 6.

If our model is correct and the most significant factor in determining the color shift is the shape of the waveform at the input to the half-wave rectifiers, then the maximum ON vs. OFF difference for a two-component waveform should occur when the peaks or troughs of the two sinusoids align (B in Figs. 1 and 2, Left), but there will be no shifts when the phases are 90° away from these alignments. We can then compare measured color shifts at the phases of the visual input as shown in Fig. 3 with the expected phases at the half-wave rectifiers that produce the largest and smallest shifts, and therefore infer how the relative phases of the two components change as they pass through the early filter. Thus, the importance of the experiment with two components is that it allows us to measure and then constrain the parameters of the early filter.

Comparing the L- and M-cone results in Fig. 3 reveals that they are, as expected, the reverse of one another: where a particular temporal waveform produces red with an L cone-isolating stimulus, the same waveform produces green with an M cone-isolating stimulus. This finding is precisely what our model predicts given that L-ON and M-OFF are red pathways and the L-OFF and M-ON are green pathways.

The data in Fig. 3 also reveal that there is very little dependence on fundamental frequency for the two-component waveforms, except that observer V.L. found the task difficult with the 4-Hz combination of the first and second harmonics, because the apparent flicker was too strong and obscured the mean color shift; he also had difficulty with the second and third combination at higher fundamental frequencies. The overall lack of frequency dependence suggests that, over this range of frequencies, the early filter produces approximately the same phase delay between the two components, regardless of fundamental frequency. It is of interest to note that the model predicts that the optimal stimulus phases for producing large differences in the ON and OFF pathways are 76° and 256° and not 0° and 180°, which are the phases of the second harmonics in sawtooth waveforms. Sawtooth waveforms are often used under the assumption that they should be optimal for producing the largest ON or OFF responses (33–35), but according to our model, this is clearly not the case. Waveforms in which the peaks or troughs of the first and second harmonics align at the input to the half-wave rectifiers should produce larger differential signals in the ON and OFF pathways (22).

The color shift varies over 360° through one cycle of red and green for the first and second harmonic combination as shown by the red and green bands in Fig. 3, Upper. However, the expected pattern is different for the combination of second and third harmonics, because advancing the third harmonic by 180° relative to the second produces the same-shaped waveform, except for an absolute time shift of half a cycle. Therefore, as expected, the number of red and green bands doubles with the second and third harmonic combinations. The waveforms illustrated Fig. 3, Left Insets show the waveforms predicted by the model to produce the largest color shifts—those on a red background toward red and those on a green background toward green. The corresponding best phases are indicated by the tips of the yellow cones.

Next, we show in Fig. 4 the slightly more complicated results and predictions for combinations of the first, third, and fourth harmonics. This combination was chosen to examine the effect of the highest-frequency (fourth) harmonic. A waveform composed of only the first and third harmonics (or any waveform composed of only odd harmonics) is half-wave symmetric (i.e., when the waveform is inverted about its mean, it retains the same shape, except for a shift in time by half a cycle). According to the model, for half-wave symmetric stimuli, there should be no color difference between the waveforms that we ask observers to discriminate. Consequently, for stimuli made up of first, third, and fourth harmonics to produce a mean color shift, the presence of the fourth harmonic is vital, and indeed, our model requires that the fourth harmonic be transmitted through the early filter at least as far as the half-wave rectifier, where it can change the balance of signals in the ON and OFF pathways.

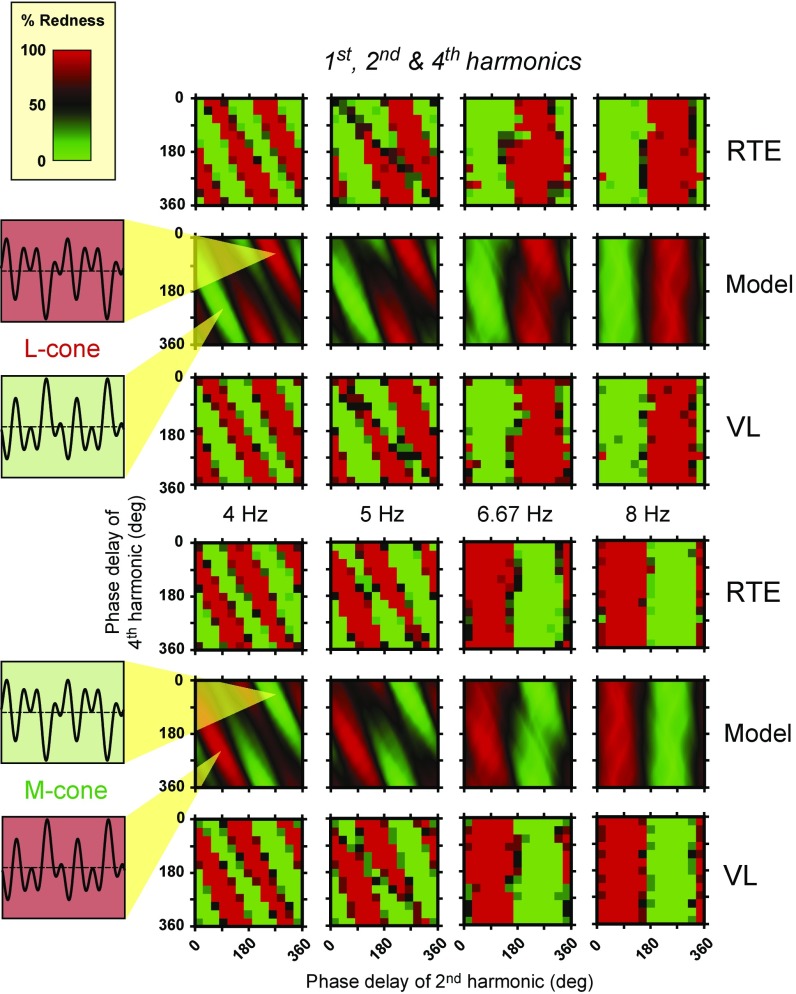
In Fig. 4, Left Insets, we again show the first, third, and fourth harmonic combinations that, according to the model, should produce the largest mean color shifts. Fig. 4 shows the measured color shifts for observers R.T.E. and V.L. and the predictions of the model for L-cone stimuli (Fig. 4, Upper) and M-cone stimuli (Fig. 4, Lower) in a format analogous to that of Fig. 3; since there are two higher harmonics, the results and predictions in Fig. 4 (and also, Figs. 5–8) vary along two dimensions of phase. Thus, relative to the first harmonic, each panel shows the phase delay of one harmonic along the abscissa and the phase delay of the other harmonic along the ordinate from (0°, 0°) in the top left-hand corner to (360°, 360°) in the bottom right-hand corner.

Fig. 5.

Results for two observers, R.T.E. and V.L., on separate rows and model predictions in the rows between them. Upper shows an L-cone stimulus waveform comprising the fundamental, second, and fourth harmonics in the amplitude ratio 0.5:1.0:1.0, and an equivalent M-cone stimulus is shown in Lower. The optimal waveforms at 4 Hz shown in Insets (two cycles of the fundamental are shown) have second and fourth harmonics in the phases indicated by the tips of the yellow cones at 333° and 46° or 333° and 226°. Details are the same as in Fig. 4.

The results in Fig. 4 show a clear dependence on the phase of both the third and fourth harmonics, with the red and green stripes forming patterns that slope diagonally downward from top left to bottom right with two red and green cycles. The patterns are roughly independent of fundamental frequency—the different panels are very similar—but become noisier as the fundamental frequency increases. Even so, there is a clear effect of the fourth harmonic even at the highest frequency tested (at 32 Hz for the fourth harmonic in the 8-Hz fundamental condition), particularly for L-cones: if the 32-Hz component had had no effect, it would be impossible to discriminate the waveforms, and observers should have been equally likely to call either stimulus redder. Although the red–green chromatic pathway is extremely insensitive to 32-Hz flicker (36–38), the 32-Hz component strongly influences the mean color of our multicomponent waveforms as can be seen in Fig. 4. The insensitivity to 32-Hz flicker is accounted for by the late filter in our model, but that filter is unimportant to the color shift, because the 32-Hz component initiates the color shift early at the input to the rectifiers. In general, the data patterns are again in very good agreement with the model’s predictions.

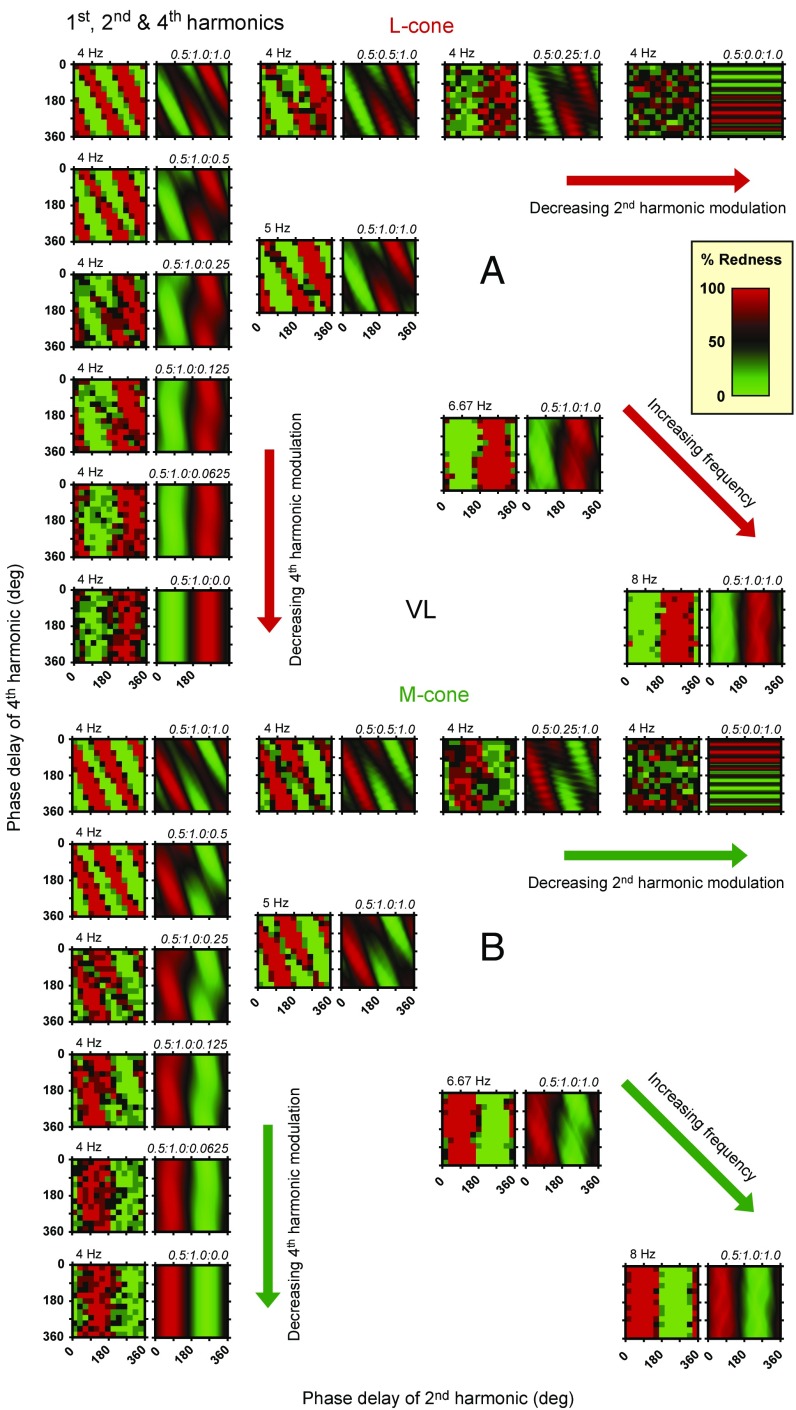
Predictions and data for the combination of the first, second, and fourth harmonics, are shown in Fig. 5. Although the model is exactly the same, the results in Fig. 5 are very different from those in Fig. 4, since the results in Fig. 5 clearly depend on fundamental frequency. The pattern of results is more complex, because either of the even (second and fourth) harmonics, when combined with the first harmonic, can produce a color shift, unlike the combination shown in Fig. 4, where only the fourth can be effective. At lower fundamental frequencies, Fig. 5 shows three red and three green alternating diagonal stripes that fall from top left to bottom right, with a slope of about twice that found for the first, third, and fourth harmonics of Fig. 4. At higher fundamental frequencies in Fig. 5, unlike Fig. 4, there is just a single pair of vertical red and green stripes (Fig. 8). The model’s predictions, which agree remarkably well with the data, provide a straightforward explanation of these results. At the low fundamental frequencies of 4 and 5 Hz, both the second and fourth harmonics have a marked effect on the perceived color as shown by the diagonal stripes in columns 1 and 2 in Fig. 5. At 8 Hz, the effect of the fourth harmonic has been lost, while at 6.67 Hz, there is a transition between the two patterns. Since the results in Fig. 4 rule out the possibility that the fourth harmonic at 32 Hz is too weak to affect the mean color, it must be that, for the first, second, and fourth combination shown in Fig. 5, the second harmonic dominates the smaller effect of the fourth harmonic. Again, the model predicts this change, and its predictions are generally in very good agreement with the data.

In the examples shown so far, we chose harmonic combinations with fixed amplitude ratios, varied the fundamental frequency, and predicted the effects of the early and late filters on the harmonic components at different stages of processing (Figs. 1 and 2). Another experimental approach is to fix the fundamental frequency and vary the modulation of one of the harmonic components. A particularly revealing case is to vary the modulation of either the second or the fourth harmonic in the combination of first, second, and fourth harmonics. As explained above, as the fundamental frequency is increased, the color shift changes from being dependent on the three components to being dependent only on the first and second, and as a result, the phase patterns rotate from diagonal to vertical.

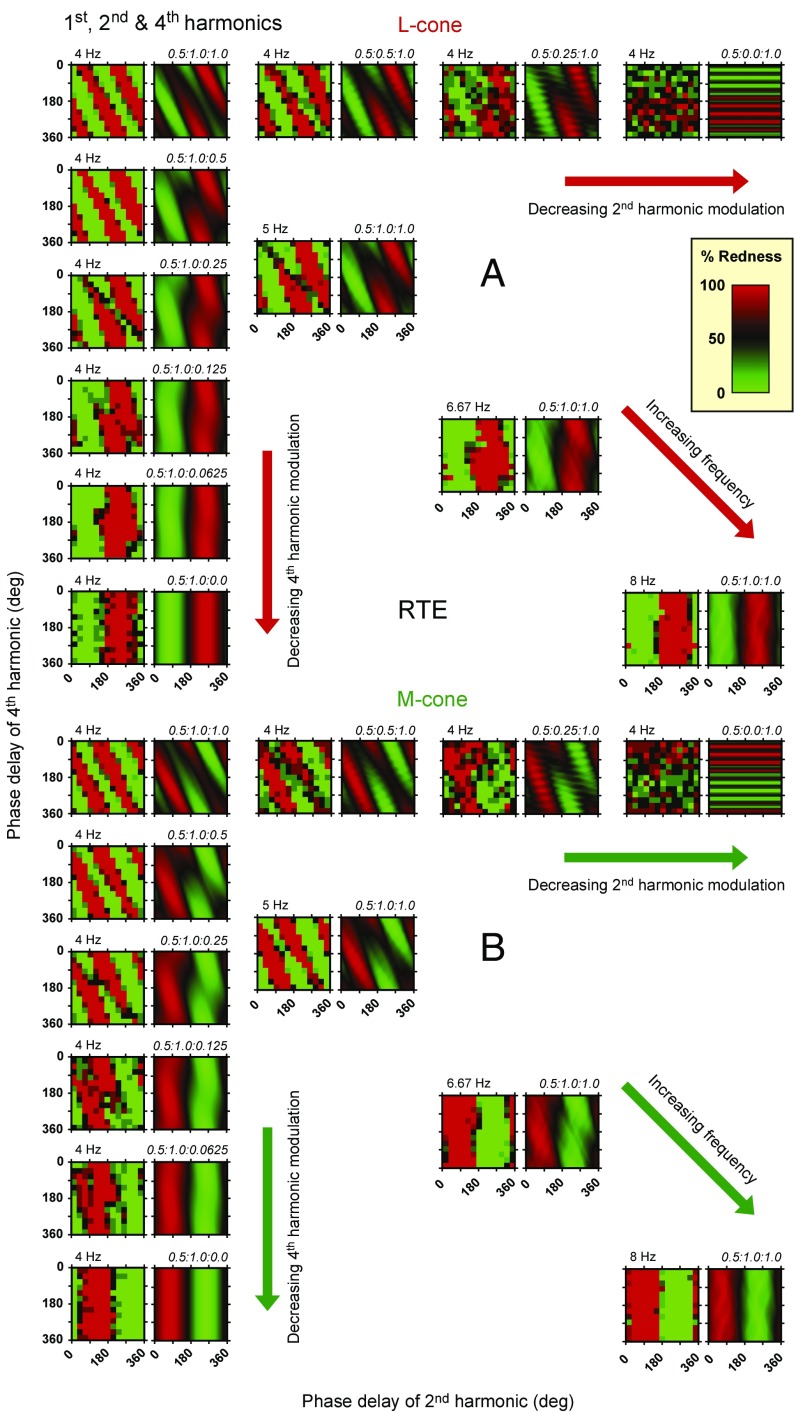
Figs. 6 and 7 show the results for observers R.T.E. and V.L., respectively, and the predictions for stimuli comprising the first, second, and fourth harmonics for L cone-isolating stimuli above in rows 1–6 and M cone-isolating stimuli below in rows 7–12. Different pairs of panels show different ratios of the amplitudes of the second and fourth harmonics, all with the amplitude of the fundamental set at 0.5; the ratios are given above the model prediction panels. In Figs. 6 and 7, the amplitude of the second harmonic decreases across rows 1 and 7 of panel pairs, the amplitude of the fourth harmonic decreases down column 1 of pairs, and the fundamental frequency increases down the main diagonals with the stimulus amplitudes fixed (replotted from Fig. 5).

Fig. 6.

(A) Each adjacent pair of panels shows data from R.T.E. (in the left-hand member of each pair) and model predictions (in the right-hand member of each pair) for L cone-isolating stimuli comprising the fundamental, second, and fourth harmonics in different amplitude ratios. The phase delay (in degrees) of the second harmonic is shown on the abscissa of each panel, and that of the fourth is shown on the ordinate. In column 1, the ratio of the amplitude of the fundamental and second harmonics is fixed at 0.5:1, but the amplitude of the fourth decreases from equality with the second at the top to zero at the bottom. Along row 1, the amplitude ratio of the fundamental to the fourth is fixed at 0.5:1, but the ratio of the second decreases from equality with the fourth harmonic on the left to zero on the right. In column 1 and along row 1, the fundamental frequency is 4 Hz. Along the diagonal, the amplitude ratio of the components is fixed at 0.5:1.0:1.0, but the fundamental frequency increases from 4 to 8 Hz; the diagonal panels are reproduced from Fig. 5. (B) Each pair of panels shows data from R.T.E. and model predictions for M cone-isolating stimuli. Other details are the same as in A.

As the relative amplitude of the fourth harmonic decreases (down column 1 in Figs. 6 and 7), the diagonal stripes that indicate that both second and fourth harmonics are contributing to the color gradually change to vertical stripes, indicating that the fourth harmonic has ceased to contribute (as indeed must be the case in columns 1 and 2, rows 6 and 12 of Figs. 6 and 7 for stimuli with no fourth harmonic). As the amplitude of the second harmonic is reduced (across rows 1 and 7 in Figs. 6 and 7), the diagonal stripes switch to horizontal stripes, indicating that the second harmonic has ceased to contribute to the color (as indeed must be the case in columns 7 and 8, rows 1 and 7 of Figs. 6 and 7 for stimuli with no second harmonic). Interestingly and somewhat counterintuitively, the data in the third pair along rows 1 and 7 in Figs. 6 and 7 (with the ratio 0.5:0.25:1.0) seem more dependent on the second than on the fourth harmonic (i.e., the data seem more like vertical than horizontal stripes). This is also seen in the model, which indicates that the second harmonic influences the color shift in two ways: first by its interaction with the first harmonic and second by its interaction with the fourth harmonic. As we reduce the amplitude of the second harmonic, its interaction with the fourth harmonic is more impaired than its interaction with the first, leading to the unexpected finding with this combination that, relative to the influence of the fourth harmonic, reducing the second harmonic actually increases its net influence on the color shift.

The four pairs of panels down the diagonals of Figs. 6 and 7 (replotted from Fig. 5) have first, second, and fourth harmonics in the ratio 0.5:1.0:1.0 but with fundamental frequencies that increase from 4 to 8 Hz. As discussed above, with increasing fundamental frequency, the diagonal stripes of color that indicate that both the second and fourth harmonics are contributing to color become vertical, indicating that the fourth harmonic has ceased to contribute. This change reflects the early filter’s increasing attenuation of the fourth harmonic relative to the second harmonic before the half-wave rectifiers and hence, the dominance of the second harmonic on the postrectification waveforms in the ON and OFF channels.

Note that increasing the fundamental frequency until the fourth harmonic is at 32 Hz (columns 7 and 8, rows 6 and 12 in Figs. 6 and 7) has the same effect on the pattern of results as decreasing the amplitude of the fourth harmonic at a constant 16 Hz (column 1, rows 6 and 12 in Figs. 6 and 7). In both cases, the key is that the influence of the fourth harmonic is reduced: in one case, because we lowered its amplitude and in the other, because we raised its frequency and the early filter reduced its amplitude.

Overall, the results for R.T.E. and V.L. in Figs. 6 and 7 (as well as in Figs. 3–5) are remarkably consistent with each other and with the predictions of the model. To assess the extent of individual differences, we also tested eight additional observers (G.B.H., A.S., and six naïve volunteers: S1–S6) on a subset of conditions chosen to show clear frequency-dependent changes in the dependence of the perceived color on harmonic phase. The conditions that we used were the 4- and 8-Hz L- and M-cone combinations of the fundamental, second, and fourth harmonic shown in Fig. 5 for R.T.E. and V.L., the results for which change from three diagonally falling red–green stripes at 4 Hz to a single vertical red–green stripe at 8 Hz as the relative influence of the fourth harmonic at 32 Hz drops out. Each additional observer performed three repeats of each condition. The results are shown in Fig. 8. Column 1 in Fig. 8 shows the model predictions. Columns 2–9 in Fig. 8 show the data for the eight observers. The four female observers are denoted by the asterisks. The 4-Hz L- and M-cone fundamental data are remarkably consistent across observers, with each set showing the same three diagonally falling red–green stripes also found for R.T.E. and V.L. The 8-Hz fundamental data show some interesting individual variations. The 8-Hz M-cone datasets for all observers and the 8-Hz L-cone datasets for all four male observers and two female observers, S3 and S4, show the single red–green stripe also found for R.T.E. and V.L. By contrast, the 8-Hz data for the other two female observers, S5 and S6, show patterns that are intermediate in form between the diagonally falling three-stripe pattern and the vertical one-stripe pattern. The intermediate patterns for these two observers can be accounted for by slight modifications to the parameters of the model that govern the shape of the early filter denoted as a in Fig. 1 (Methods), such that the 32-Hz fourth harmonic component is slightly less attenuated relative to the 16-Hz second harmonic component. The finding that the variability is found in two of four female observers (S4 also shows some rotation of the 8-Hz L-cone contour) but none of the male observers suggests that the difference might be sex-linked and thus perhaps related to females having two different copies of the L- and M-cone photopigment genes on their two X chromosomes. If the gene copies are different, then X-chromosome inactivation (or “lyonization”) would result in different L- or M-cone photopigments being expressed in different parts of the female retina (39–41), which could lead to imbalances because of L- or M-cone spectral sensitivity changes or changes in L- and M-cone numerosity across the retina.

Conclusions

We can reliably predict differences in the illusory colors of flickering red–green stimuli with identical time-averaged chromaticities and luminance. The predictions are based on a relatively simple model of chromatic processing that is consistent with known physiology, which is shown schematically in Fig. 1. The model’s predictions depend on two nonlinearities. The first is half-wave rectification that, depending on the shape of the waveforms going into the half-wave rectifiers, produces very different signals in the ON and OFF pathways after the rectification. The second nonlinearity is a static compression that reduces the time-averaged value in the pathway; it has a greater effect on a larger-amplitude signal than a smaller-amplitude signal, thus affecting the means of the signals in the two pathways. It is the change in the balance of the means in the ON and OFF pathways that accounts for the shift in color toward whichever pathway has the smaller-amplitude signal at the input to the compression. The fact that we can predict complex color changes from our model suggests that it captures the significant details of the L–M chromatic pathways and in particular, the stage at which visual signals are split into ON and OFF pathways. We therefore have a means of controlling the relative strengths of signals in the two pathways and thus, a way of separately probing the ON and OFF pathways.

The model shows how the effect of higher harmonics in the input are “piggy-backed” on the amplitudes of lower-frequency components after half-wave rectification to produce a significant color shift, although the high-frequency components are largely filtered out before the signal reaches the late compressive nonlinearity; thus input components that are of too high a frequency to be visible themselves can still affect the mean color of the stimulus. This observation is one example of how the model provides a framework within which combinations of visual signals with particular frequency and phase relationships can be used to dissect early vs. late stages of processing in human vision.

The distortion produced by splitting visual signals into ON and OFF pathways is unavoidable; so, why is the resulting distortion not usually visible? One reason, as discussed above, might be that, if the ON and OFF signals are recombined late in visual processing (and the preceding pathways are approximately linear except for the rectification), the distortion products will largely cancel. This might happen when ON and OFF signals from both L- and M-cone types are summed into a single pathway before any late nonlinearities, so that L-ON distortions cancel L-OFF distortions and M-ON distortions cancel M-OFF distortions. However, in the red–green pathway, the separation of L-ON and M-OFF signals into a red channel and the M-ON and L-OFF signals into a green channel (e.g., figure 7 in ref. 22) precludes this within cone-type cancellation so that the distortion products remain. Our model also predicts that the distortions produced by half-wave rectification would cancel were it not for the later nonlinearity, which introduces unbalanced distortions when half-wave asymmetric waveforms are used. As also discussed above, our model does not produce a difference in the mean levels of the ON and OFF signals for half-wave symmetric waveforms, such as sinusoids, square waves, or triangle waves, which are commonly used in vision research.

The elements of the model are not unique to red–green color vision. Splitting cone signals into ON and OFF pathways is a consistent property of the cone-to-cone bipolar synapse, and nonlinear input–output functions are a common feature of neuronal responses. Thus, we expect our model to have applications to other time-varying stimuli and tasks, including brightness flicker and incremental/decremental flashes, but particularly in cases where the recombination of ON and OFF signals may not cancel the distortion introduced by rectification. ON and OFF S-cone pathways, for example, differ physiologically (42) and psychophysically (43, 44). Another interesting case is a form of congenital stationary night blindness, in which mutations in the GRM6 gene render ON pathways nonfunctional (45).

Except where noted, the patterns of results for our two observers are very similar, and therefore, we have used the same model parameters—based in part on previous measurements (22)—to account for their data. Individual differences, such as those revealed in Fig. 8, will lead to refinements to the model. Models with a single nonlinearity have been exploited before to parse visual processing into separate stages (46–48). Our model, with two distinct and separable nonlinearities separating two stages of temporal filtering, offers exciting possibilities for understanding more about how vision works.

Methods

Observers.

One of the authors (R.T.E.; male, age 62 y old) and a naïve volunteer [Vy Luong (V.L.); male, age 39 y old] were the main observers in these experiments, while two authors (G.B.H. and A.S.; both male, ages 77 and 61 y old, respectively) and another six naïve volunteers participated in a subset of experiments carried out to assess the extent of individual differences. S1 and S2 were male and ages 24 and 38 y old, respectively; S3–S6 were female and ages 46, 26, 37, and 43 y old, respectively. All observers have normal color vision according to standard tests. Research protocol was approved by the University College London Research Ethics Committee. Informed consent was obtained from all participants.

Apparatus.

Experiments were programmed in MATLAB with the Cambridge Research Systems toolbox and presented via a Visual Stimulus Generator (VSG 2/5) system (Cambridge Research Systems Ltd.) on a carefully linearized and calibrated 21-inch Sony FD Trinitron CRT display (20, 21). The spectral power distributions of the three CRT primaries were measured at 1-nm steps using a Radoma spectroradiometer (Gamma Scientific), and the measured distributions were multiplied by the Stockman and Sharpe (5) cone fundamentals wavelength by wavelength. The resulting product was integrated over wavelength and used to determine the phosphor combinations that would isolate either L- or M-cones. [The technique of producing stimuli that modulate only one cone type is sometimes called “silent substitution” (49).] M- and L-cone modulations of up to about 25% could be achieved for both cone types with the CRT and VSG system.

Stimuli.

Observers viewed the display binocularly at a 1-m viewing distance in an otherwise dark room. We presented flickering red–green temporal waveforms in two half circles with diameters subtending 5.7° at the observer’s eyes and separated by 0.6° of visual angle (Fig. 3). Each waveform was calculated as variations about a mean yellow field [CIE (Commission Internationale de l′ Éclairage) x,y color coordinates = 0.410, 0.514; luminance = 43.8 cd/m²]. On each trial, a zero mean temporal waveform was added to the mean in one half-field (chosen at random) and subtracted from the mean in the other (equivalent to a 180° phase shift in all components). Thus, the stimuli were vertically opposite around their common mean, such that we call one the inverse of the other. The stimuli were ramped on with a raised cosine window over 1 s to avoid transients and remained on for up to a maximum of 12 s (including the 1-s raised cosine off ramp) or until the observer responded. The identical mean (yellow) half circles remained steady on the screen during the 3 s between trials.

In a two-alternative spatial force choice paradigm, the observers pressed buttons to indicate which of the two flickering half-fields appeared redder. The fundamental frequency was fixed within a block of trials at 4, 5, 6.67, or 8 Hz. These frequencies were chosen based on preliminary observations and prior published work; at still lower frequencies, the red–green color alternation dominates perception and obscures any mean color shifts, while at higher frequencies, the color shifts become much less visible (20). Thus, the highest-frequency component used (the fourth harmonic of the 8-Hz fundamental) was 32 Hz, well below the Nyquist frequency of the monitor (which was refreshed 160 times per second). Different combinations of harmonics (at fixed amplitudes) were presented in different blocks of trials. We used four different waveform types. (i) We used the same ratio as used in our previous work (20, 21): the fundamental and second harmonics in the modulation ratio 1.0:0.5. (ii) The second and third harmonics alone with equal modulation: 1.0: 1.0. (iii) The fundamental, third, and fourth harmonics in the modulation ratio 0.5:1.0:1.0. (iv) The fundamental, second, and fourth harmonics in modulation ratio 0.5:1.0:1.0. The modulation ratios for ii–iv were chosen, because the model predicts relatively large color changes with these values. In the final experiment, we presented the first, second, and fourth harmonics and decreased the modulation of either the second or the fourth harmonic (to obtain the results shown in Figs. 6 and 7).

For the first and second harmonic judgements (condition i) and the second and third harmonic judgements (condition ii), the phase of the higher harmonics (measured relative to the lower harmonic in sine phase) was chosen in random order from 1 of 24 equal steps spaced 15° apart, giving a total of 12 distinct waveform pairs per block. In conditions iii and iv, in which there were two relative phases to vary, on each trial, the phase of the higher harmonics (measured relative to the fundamental in sine phase) was chosen in random order from 1 of 12 equal steps spaced 30° apart, giving a total of 72 distinct waveform pairs per block. Each waveform pair was presented six times for R.T.E. and four times for V.L.

In addition to the extensive experimental results obtained for our two main subjects, we collected additional data on eight observers (G.B.H., A.S., and S1–S6) under a subset of conditions to assess the extent of individual differences. The experimental setup for these observers was as described above for R.T.E. and V.L. The subset of conditions was as for condition iv described above: the fundamental, second, and fourth harmonic were presented in amplitude ratio 0.5:1.0:1.0 at fundamental frequencies of 4 and 8 Hz for both L and M cone-isolating stimuli. These conditions were chosen, because they showed the clearest frequency-dependent changes in perceived color in our two original observers (Fig. 5, columns 1 and 4). The results are shown in Fig. 8.

Model Details.

The model consists of a linear–nonlinear–linear–nonlinear sequence sometimes referred to as a “sandwich” model (46, 47), although in this case, it is a double-decker sandwich. The model is based on the work by Stockman et al. (25), which estimated the characteristics of an early and a late chromatic filter. It was elucidated in the work by Stockman et al. (22). The first filter is composed of a cascade of four identical low-pass filters (leaky integrators) and two identical stages of subtractive inhibition (lead–lag filters). The net result is a slightly band-pass filter that attenuates both low and high frequencies. The attenuation characteristics, $A\left(f\right)$, and phase response, $\phi \left(f\right)$, of this early band-pass filter are given by

$$A\left(f\right)=\frac{{\sqrt{\left(f^2+{\left(f_{ce}(1-k)\right)}^2\right)}}^2}{{\sqrt{\left(f^2+f_{ce}^2\right)}}^6},\text{and}\hspace{0.17em}\phi \left(f\right)=6\arctan \left(\frac{f}{f_{ce}}\right)-2\arctan \left(\frac{f}{f_{ce}\left(1-k\right)}\right),$$ [1]

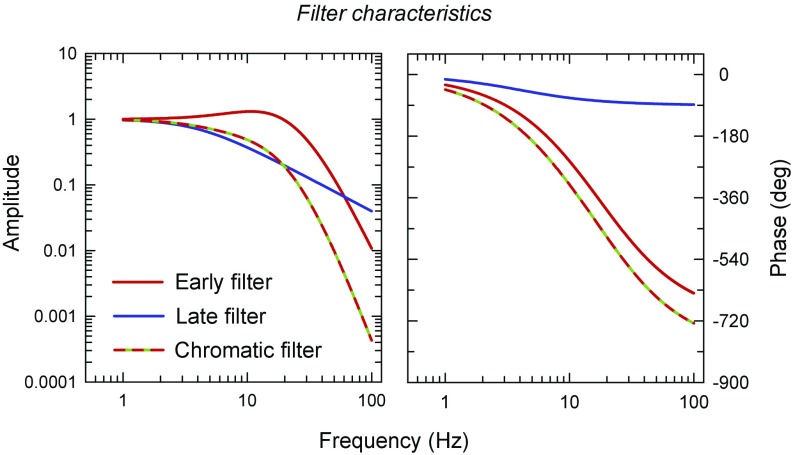
where $f$ is frequency (hertz), $f_{ce}$ is the corner frequency (hertz), and k is the gain of the feedforward inhibition of the lead–lag filters. (Different values of k change the lead–lag filters from all-pass to high-pass filters.) Based on our previous measurements (20, 21), we used values of $f_{ce}$ = 21 Hz and k = 0.6. The continuous red lines in Fig. 9 show the attenuation (Fig. 9, Left) and phase characteristics (Fig. 9, Right) of the early filter.

Fig. 9.

Amplitude and phase characteristics of the early filter (red lines), the late filter (blue lines), and their combination in the overall chromatic filter (red–green dashed lines). Left shows the filters’ amplitude response on a logarithmic scale as a function of frequency (logarithmic scale). The amplitude characteristics have been normalized to one at low frequencies. Right shows the phase (in degrees; linear scale) also as a function of frequency on a logarithmic scale.

The first nonlinear stage is half-wave rectification that partitions the temporal variations into ON and OFF pathways. In the model, the half-wave rectification occurs at the time-averaged signal mean, which is highly plausible given that observers adapt to the mean chromaticity (50). The second linear stage, the late filter, is identical in the ON and OFF pathways. It is modeled as a one-stage low-pass filter. The attenuation characteristics, $A\left(f\right)$, and phase response, $\phi \left(f\right)$, of the late low-pass filter are given by

$$A\left(f\right)=\frac{1}{\sqrt{\left(f^2+f_{cl}^2\right)}},\text{and}\hspace{0.17em}\phi \left(f\right)=\arctan \left(\frac{f}{f_{cl}}\right),$$ [2]

where $f$ is frequency (hertz) and $f_{cl}$ is the corner frequency (hertz); it indicates the frequency above which the filter attenuation begins to increase significantly. Also, based partly on our previous measurements (20, 21), we used values of $f_{cl}$ = 4 Hz. The continuous blue lines in Fig. 9 show the attenuation (Fig. 9, Left) and phase characteristics (Fig. 9, Right) of the late filter. The cascade of the early and late filter is assumed to be equivalent to the overall chromatic filter (red–green dashed lines in Fig. 9).

The second nonlinearity is static compression, r(x), which we model according to a modified Naka–Rushton equation (32): r(x) = x³/(x³ + x₅₀³), where x is the instantaneous signal intensity at the late nonlinearity and $x_{50}$ is the intensity at which the compressed response is 50% of its maximum. The exact choice of nonlinearity does not materially affect the results (we tried several examples). The exponent of three in the equation above has been shown to provide a good approximation to contrast response functions of cat and monkey cortical neurons (51).

Finally, we take the difference of the time-averaged means in the ON and OFF pathways after the compression. The sign of the difference predicts whether a stimulus will appear red or green. The magnitude of the difference indicates the size of color shift and should, therefore, correlate with the probability of discriminating the two half-fields. As we do not know a priori the function relating the color shifts to discriminability, we have chosen simply to scale each panel of model predictions so that the largest predicted shift in that condition is shown as the same saturated red or green and the smaller shifts are scaled linearly toward black (which indicates no color shift).