Comparisons of Superiority, Non-inferiority, and Equivalence Trials

Summary

Efficacy of a new drug or treatment is usually established through randomized clinical trials. However, specifying hypotheses remains a challenging problem for biomedical researchers. In this survey we discuss superiority, non-inferiority, and equivalence trials. These three types of trials have different assumptions on treatment effects. We compare the assumptions underlying these trials and provide sample size formulas.

1. Introduction

In medical research, randomized clinical trials are the gold standard for establishing efficacy of a newly developed drug/treatment method.^[1-5] A well designed clinical trial should clearly specify the kind of hypothesis to be tested and procedures to be used for analysis of primary outcomes. For example, depending on the purpose of the trial, we need to specify whether the study is to test superiority (i.e., better than), non-inferiority, or equivalence, between different treatment conditions. Sample size calculation, data analysis, and interpretation of analysis results all depend on the type of hypothesis specified. From our interactions with biomedical and psychosocial researchers, these issues do not seem to be clear and appreciated in the research community. In this report, we attempt to clarify different types of hypothesis testing and rationales for each, and show how to calculate sample size in each case.

Hypotheses in most clinical trials can be stated in terms of differences in the mean response of an outcome of interest such as group means. For example, prostate-specific antigen (PSA) level is a common outcome for prostate cancer patients^[6] (or the Hamilton Depression Rating Scale (HAM-D) is a popular scale for depression severity). In this case, PSA level is a continuous measure and the hypothesis is stated to compare mean PSA levels between two groups. Sometimes, an outcome of interest may be categorical. For example, the outcome may be the survival status of the patient by the end of the follow-up (or diagnosis of clinical depression). In this case, for each patient we can use a binary outcome variable X with value 1 (0) to denote the survival (death) of the patient. The proportion of survival in each group is just the mean value of X for patients in the corresponding group. The hypothesis to compare differences in prevalence of depression between two study populations can be stated in terms of difference between the means of X for the two groups.

We think technical difficulty may likely be responsible for the confusion. Thus, we will try to make our presentation as non-technical as possible. Also, for simplicity we assume two groups with i = 0, 1, denoting the control and treatment groups. For group i, let X_ii denote the primary outcome of the jth subject in the ith group. Let µ_i and σ_i² denote the mean and variance of X_ij in group i. They are also loosely called the group mean and variance. We further assume higher value mean of X_ij means better outcome. Hence the treatment group is said to be ‘better’ than the control group if µ₁>µ₀.

In the following sections, we introduce the three types of trials: superiority, non-inferiority, and equivalence trial. We start with the most popular superiority.

2. Superiority trial

In a superiority trial, we want to show that the new treatment intervention (drug, psychotherapy) is superior to (better than) the control condition. For example, we want to know if a new drug can significantly increase CD4 counts for HIV patients or a novel psychosocial therapy will increase social activities for lonely old adults.

For many researchers, a challenging problem is how to specify the null and alternative hypotheses for the specific trial. A rule of thumb is to specify the null hypothesis opposite to what we expect for the outcome. For example, if we want to test if treatment A is better than treatment B, the null hypothesis is that A is not better than or same as B. We anticipate that the data from the trial will tell us otherwise and reject the null hypothesis in support of the anticipated superiority of treatment A. Based on this idea, the null and alternative hypotheses of a superiority trial are specified as

(1)

where δ≥0.

Under the null hypothesis, the mean value of the treatment group is less than or equal to that of the control group plus a nonnegative number δ. Sometimes we may not feel so confident that the treatment is better than the control, even if the mean value of the treatment group is really greater than the control, but the difference is small. For example, suppose that we want to test if a new instructional method improves the performance of students in a math test. If the new method increases the average score from 75 to 76, we may be reluctant to say that the new method is better than the current one. However, if the new method can increase the average score by at least 6 points, then we may think that the new method is superior to the current one. These 6 points is the superiority margin of the new instructional method. If the improvement of the new method is less than this value, we may not care much about it even if it has a higher group mean.

The value δ in (1) is called margin of clinical significance.^[4] For a given study, the larger the δ, the harder to reject the null hypothesis, as reflected in the sample size formula in (2) and (3) below. Therefore, this margin is the threshold for which we claim the superiority of the new treatment. For different studies, choices of δ depend on the contexts of the study and scale of measures. For example, for a study on suicide rate, even a small δ in reducing the rate of suicide will have a significant impact on the lives of those at risk for suicide. For a new method to improve scores on a math test, a difference of 6 points or higher may be a reasonable threshold for adopting the new method. There is no general rule to specify the margin. It depends on the purpose of the study.

In most studies, different groups typically have equal sample sizes. However, sometimes we may want assign more subjects to one or more groups. For example, for a study with two active treatments and one control, we may want to have a larger sample size for the control for more power to compare the treatment with the control. Below, we consider a general situation and provide formulas of sample size calculations for unequal sample sizes for the two groups. We assume that n₁ = rn₀, where r is a fixed positive constant.

For a constant η ∈ (0,1), let z_n denote the ηth upper-quantile of standard normal distribution. For example, if η = 0.1, then z_n = 1.2816, which means that for a random variable with standard normal distribution, it is greater than 1.2816 with 10% probability. For each real number x, let [x] denote the least integer greater than or equal to x. For example, [8]=8 and [8.1]=9.

Sample size depends on the true mean difference, d, standard deviations for the two groups, and a level of significance α (type | error), and the power. Given all these parameters, required sample sizes for the treatment and control groups are as follows:

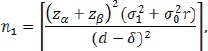(2)

(3)

where β = 1– power and is called the type II error. For example, if power = 80%, then β = 0.2. The total sample size n=n₁+n₀ is minimized when r = σ₁/σ₀. In most studies, we assume equal group variance, i.e., σ₁ = σ₀, the minimum overall sample achieves when r = 1. This fact may explain why most clinical trials use equal sample sizes in two groups.

Given d, sample sizes increase with δ. Therefore, it becomes more difficult to reject the null hypothesis if the margin of clinical significance δ is set higher.

Remark. Although the hypotheses in (1) are very natural and intuitive for the superiority trial, there are many discussions about the establishment of superiority from regulatory agencies, see for example Dunnett and Gent ^[3], Lesaffre ^[7], Sackett ^[8], and Sackett.^[9] According to Chow and Liu,^[1] testing of superiority is usually done in two steps. The first step is to show the treatment and groups are significantly different by testing the hypotheses

(4)

If the null hypothesis in (4) is rejected, then check if the sample mean value in the treatment group is larger than the control. If it is, then we claim that the treatment group is superior to the control. According to Chow and Liu^[1], this two-step procedure is equivalent to testing the superiority based on the following special form of (1)

with significance level α/2.

3. Non-inferiority trial

A non-inferiority trial is to show that treatment A is not worse than the treatment B. Although these kinds of trials are not used to establish better treatment efficacy, the new method may have advantages over current methods in other aspects. For example, the new intervention may be less costly, less invasive, and have less side effects.

The hypotheses of non-inferiority clinical trials are

(5)

where δ ≥ 0 and is also called the margin of clinical significance which is usually small.

The non-inferiority of the treatment to the control can be easily understood form the alternative hypothesis. If the mean difference between the treatment and control group is greater than δ, then the treatment is non-inferior to the control. Unlike the superiority trial, we don’t need the treatment to be better than the control. For example, if δ > 0, the treatment may be ‘worse’ than the control (i.e. µ₁ – µ₀ < 0). However, as long as µ₁ – µ₀ > - δ, the treatment is the non-inferior.

By comparing (1) and (5), we may see that it is generally easier to establish the non-inferiority than superiority. This is true if we compare the sample size formulas in these two cases. Suppose the true mean difference µ₁ – µ₀ is d. Given significance level a and power 1-β, the required sample sizes in the treatment and control groups in a non-inferiority trial are

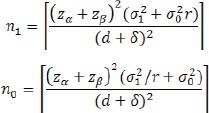It’s easy to see that given d, n₀ increases with δ. This is very intuitive. The larger the δ, the easier to reject the null hypothesis.

4. Equivalence trial

‘Equivalence’ does not mean ‘equal’ or ’same’ as in practice. When we say the treatment and the control are equivalent, we mean that they are ‘similar’. By quantifying ‘Similarity’ using a tolerance range, the hypotheses for an equivalence trial are specified as

(6)

where δ > 0 is a pre-specified tolerance margin. If the null hypothesis is rejected, then the mean difference of two groups is within the tolerance range and the treatment and control are equivalent.

A closer look at (6) shows the hypotheses in an equivalence trial are the same as

Comparing (5) and (6) we can see that the equivalence trial is the intersection of two non-inferiority trials. Intuitively, the treatment and control are equivalent, if and only if neither one is inferior to the other.

Suppose the true mean difference µ₁ – µ₀ is d. Given significance level and power 1-β, the required sample sizes in the treatment and control groups in an equivalence trial are

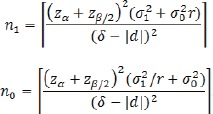It’s easy to see that given d, n₀ increases with δ. Thus, the larger the δ, the easier to reject the null hypothesis.

5. Conclusion

Superiority, non-inferiority, and equivalence trials are three types of widely used clinical trials. By a close examination of these hypotheses we can see that there are some similarities between trials. For example, superiority is a special case of non-inferiority. It is much easier to establish non-inferiority than superiority. Equivalence is the combination of two non-inferiority trials. On the analytic side, as different types of trials entail quite different interpretations and sample sizes, we must pay close attention to their different uses and use the right type of study in a given situation.

Biography

Bokai Wang obtained his BS in Statistics from the Nankai University in 2010 and his MS in Applied Statistics from the Bowling Green State University (Bowling Green, OH) in 2012. He is currently a PhD student in Statistics at the University of Rochester. His research interests include Survival Analysis, Causal Inference, and Variable Selection. Currently, he has published 6 papers in peer reviewed journals.