Summary
Comparison of groups is a common statistical test in many biomedical and psychosocial research studies. When there are more than two groups, one first performs an omnibus test for an overall difference across the groups. If this null is rejected, one then proceeds to the next step of post-hoc pairwise group comparisons to determine sources of difference. Otherwise, one stops and declares no group difference. A common belief is that if the omnibus test is significant, there must exist at least two groups that are significantly different and vice versa. Thus, when the omnibus test is significant, but no post-hoc between-group comparison shows significant difference, one is bewildered at what is going on and wondering how to interpret the results. At the end of the spectrum, when the omnibus test is not significant, one wonders if all post-hoc tests will be non-significant as well so that stopping after a nonsignificant omnibus test will not lead to any missed opportunity of finding group difference. In this report, we investigate this perplexing phenomenon and discuss how to interpret such results.
Key words: Omnibus test, post-hoc test, F test, Tukey’s test
概述
多组比较在许多生物医学和心理社会学研究中是一种常见的统计检验。当组数为两个以上时,首先对组间的整体差异进行全局检验。如果零假设被拒绝,则接着进行下一步的事后两两组间比较,以确定差异的来源。相反,第一步停止即可声明没有组间差异。一个共同认识是如果全局检测结果是显著的,那么至少存在两个组之间是有显著差异的,反之亦然。因此,当全局检测结果显著,但没有事后组间两两比较没有显著差异,人们会感到困惑发生了什么并想知道如何来解释该结果。总之,当全局检测结果不显著时,人们会想知道是否所有的事后检测也都不显著?同样,全局检测结果不显著而停止事后检测是否会导致发现组差差异的丢失?在这篇报告中,我们研究了这个令人费解的现象,并且讨论了如何解释这样的结果。
关键词: 全局检测, 事后检验、, F 检验、, 图基(Tukey)检验
1. Introduction
Comparison of groups is a common issue of interest in most biomedical and psychosocial research studies. In many studies, there are more than two groups, in which case the popular t-test for two (independent) groups no longer applies and models for comparing more than two groups must be used, such as the analysis of variance, ANOVA, model.[1] When comparing more than two groups, one follows a hierarchical approach. Under this approach, one first performs an omnibus test, which tests the null hypothesis of no difference across groups, i.e., all groups have the same mean. If this test is not significant, there is no evidence in the data to reject the null and one then concludes that there is no evidence to suggest that the group means are different. Otherwise, post-hoc tests are performed to find sources of difference.
During post-hoc analysis, one compares pairs of groups and finds all pairs that show significant difference. This hierarchical procedure is predicated upon the premise that if the omnibus test is significant, there must exist at least two groups that are significantly different and vice versa.
The hierarchical procedure is taught in basic as well as advanced statistics courses and built into many popular statistical packages. For example, when performing the analysis of variance (ANOVA) model for comparing multiple groups, the omnibus test is carried out by the F-statistic.[1] For post-hoc analyses, one can use a number of specialized procedures such as Tukey’s and Scheffe’s tests.[1] Special statistical tests are needed for performing post-hoc analyses, because of potentially inflated type I errors when performing multiple tests to identify the groups that have different means. Tukey’s, Scheffe’s and other post-hoc tests are all adjusted for such multiple comparisons to ensure correct type I errors in the fact of multiple testing.
In practice, however, it seems quite often that none of the post-hoc tests are significant, while the omnibus test is significant. The reverse seems to occur often as well; when the omnibus test is not significant, although some of the post-hoc tests are significant. To the best of our knowledge, there does not appear a general, commonly accepted approach to handle such a situation. In this report, we examine this hierarchical approach and see how well it performs using simulated data. We want to know if a significant omnibus test guarantees at least one post-hoc test and vice versa. Although the statistical problem of comparing multiple groups is relevant to all statistical models, we focus on the relatively simpler analysis of variance (ANOVA) model and start with a brief overview of this popular model for comparing more than two groups.
2. One-Way Analysis of Variance (ANOVA)
2.1 The Statistical Model
The analysis of variance (ANOVA) model is widely used in research studies for comparing multiple groups. This model extends the popular t-test for comparing two (independent) groups to the general setting of more than two groups.[1]
Consider a continuous outcome of interest, Y, and let I denote the number of groups. We are interested in comparing the (population) mean of Y across the I groups. The classic analysis of variance (ANOVA) model has the form:
| (1) |
where Yij is the outcome from the j th subject within the i th group, µi = E(Yij) is the (population) mean of the i th group, εiJ is the error term, N(µ,σ2) denotes the normal distribution with mean µ and variance σ2, and ni is the sample size for the i th group.
With the statistical model in Equation (1), the primary objective of group comparison can be stated in terms of statistical hypotheses as follows. First, we want to know if all the groups have the same mean. Under the ANOVA above, the null and alternative hypothesis for this comparison of interest is stated as:
| (2) |
Thus, under the null H0, all groups have the same mean. If H0 is rejected in favor of the alternative Ha, there are at least two groups that have different means.
When performing ANOVA, one first tests the hypothesis in Equation (2). If this omnibus test is not rejected, then one concludes that there is evidence to indicate different means across the groups. Otherwise, there is evidence against the null in favor of the alternative and one then proceeds to the next step to identify the groups that have different means from each other. For I groups, there are a total of I(I-1)/2 pairs of groups to examine. In the post-hoc testing phase, one performs I(I-1)/2 tests to identify the groups that have different group means µi. This number I(I-1)/2 can be large, especially where there is a large number of groups. Thus, performing all such tests can potentially increase type I errors. The popular t-test for comparing two (independent) groups is inappropriate and specially designed tests must be used to account for accumulated type I errors due to multiple testing to ensure correct type I errors. Next we review the omnibus and some post-hoc tests, which will later be used in our simulation studies.
2.1 The Omnibus F Test for No Difference Across Groups
The omnibus test for comparing all group means simultaneously within the context of ANOVA is the F-test. The F-test is defined by quantities in the so-called ANOVA table. To set up this table, let us define the following quantities:
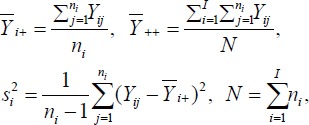 |
where N is the total sample size, 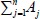 denotes sum of all
denotes sum of all 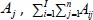 denotes sum of Aij over both indices i and j, i.e.,
denotes sum of Aij over both indices i and j, i.e.,
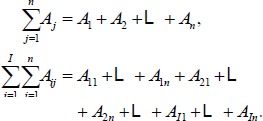 |
The ANOVA table is defined by:
| Source | degree of freedom ¢df) | Sum of Squares ¢SS) | Mean Squre (MS) |
|---|---|---|---|
| Groups | I – 1 | 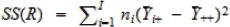 |
MS(R) = SS(R)/(I – 1) |
| Error | N – I | 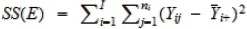 |
MS(E) = SS(E)/(N – I) |
| Total | N – 1 | 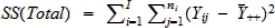 |
In the ANOVA table above, SS(R) is called the regression sum of squares, SS(E) is called the error sum of squares, SS(Total) is called the total sum of squares, MS(R) is called the mean regression sum of squares, and SS(E)is called the mean error sum of squares. These sums of squares characterize variability of all the groups (1) when ignoring differences in the group means (SS(Total)), and (2) after accounting for such differences (SS(R)). For example, it can be shown that
| SS(Total) = SS(R) + SS(E). |
Thus, if the group means help explain a large amount of variability in group differences, SS(R) will be close to SS(Total), resulting in small SS(E), in which case groups means are likely to be different. Otherwise, SS(R) will be small and SS(E) will become close to SS(Total), in which case group means are unlikely to be different. By normalizing SS(R) with respect to the number of groups and SS(E) with respect to the total sample size, the mean squares MS(R) and MS(E) can be used to quantify the relative difference between SS(R) and SS(E) to help discern where the group means are different.
Under the null hypothesis H0, the ratio, or F statistic, 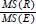 , follows the F-test:
, follows the F-test:
where Fi–1,N-i denotes the F-distribution with I – 1 (numerator) degrees of freedom and N – I (denominator) degrees of freedom. As noted earlier, a larger MS(R) relative to MS(E) indicates evidence against the null and vice versa. This is consistent with the fact that a larger value of the F-statistic 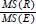 leads to rejection of the null and vice versa.
leads to rejection of the null and vice versa.
2.2 Tests for Post-hoc Group Comparison
If the null of no group mean difference is rejected by the F-test, one then proceeds to the next step to identify groups that have different group means. Multiple specialized procedures are available to perform such post-hoc tests by preserving the type I error. For example, if the group size is the same for all groups, i.e., n1 = n for all 1 ≤ i ≤ I, we can use Tukey’s procedure. We first rank the sample group means Ȳi+ and then test if two groups with sample group means, Ȳi+ and Ȳk+, have different (population) group means, i.e., µi = µk, by the following criteria:
where s2=MS(E), qα(1,N-1) is the upper-tail critical value of the Studentized range for comparing I groups and N is the common group size.
2.3 Simulation Study
When applying the ANOVA for comparing multiple groups, we first perform the omnibus F test and then follow with post-hoc pairwise group comparisons if the omnibus test is significant. Otherwise, we stop and draw the conclusion that there is no evidence of rejecting the null of no group difference. Implicit in the procedure is the assumption that a significant omnibus test implies at least one significant pairwise comparison and vice versa. If this assumption fails, this procedure will either (1) yield false positive (significant omnibus test, but no significant pairwise test) or (2) false negative (no significant omnibus test, but at least one significant post-hoc test) results. In the first scenario, it is difficult to logically reconcile such differences and report findings, while the second scenario also leads to missed opportunity to find group difference. In this section, we use simulated data to examine this assumption upon which this popular hierarchical procedure is predicated.
For brevity and without loss of generality, we consider four groups and assume a common group size n. Then the ANOVA model for the simulation study setting is given by:
| (3) |
We assume the first three groups have the same mean, i.e., µ1 =µ2 =µ3 = µ, which differs from the mean of the fourth group by d, i.e., µ4 = µ + d, with d > 0. For the simulation study, we set µ = 1 and σ2 = 1 in all the simulations, but vary the group size n and type I error level α to see how the performance of the hierarchical procedure changes when these parameters vary.
To compare group means using the hierarchical procedure, we first test the null of no group mean difference across the four groups:
| (4) |
If the above null is rejected, then we proceed to performing pairwise comparison of the four groups to identify groups that are significantly different from each other, i.e., H0 : µi=µk v.s. Ha : µi≠µk, for all pairs (i,k), 1≤i <k ≤4.
| (5) |
Within the simulation study setting, there are a total of 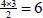 post-hoc tests.
post-hoc tests.
To see how well the hierarchical procedure performs for the simulated data, we use Monte Carlo replications and set the Monte Carlo sample size to M= 1,000. Thus, for a given group size n, we simulate data Yij from the ANOVA in Equation (3) and then perform the F test to test the null of no group mean difference in Equation (4). If the F test is significant, we proceed to the post-hoc phase by performing six pairwise group comparisons in Equation (5).
Shown in Table 1 under “F” is the percent of times the F test is significant for testing the null of no group mean difference and under “Tukey” is the percent of times at least one of the post-hoc Tukey’s tests is significant based on M = 1,000 Monte Carlo replications, as a function of sample size n, difference d, and type I error level α. The percent is actually an estimate of power, or empirical power, for rejecting the respective null when the null is false. Since power increases with sample size as well as differences between the means, the percent increased as sample size n grew from 20 to 40 and the difference between the group means d increased from 0.5 to 1 for both α = 0.05 and α = 0.001. Also, as expected, the percent became smaller as α reduced from α = 0.05 to α = 0.001.
Table 1.
p-values from the F test and Tukey’s test (at least one of the pairs is significant), rates of false positive (FP) and rates of false negative (FN) based on M=1000 Monte Carlo replications.
| Sample | α = 0.05 | α = 0.001 | |||||||
|---|---|---|---|---|---|---|---|---|---|
| size | F | Tukey | FP | FN | F | Tukey | FP | FN | |
| n=20 | d=0.5 | 0.318 | 0.313 | 0.091 | 0.035 | 0.032 | 0.033 | 0.188 | 0.007 |
| n=40 | d=0.5 | 0.597 | 0.585 | 0.059 | 0.057 | 0.143 | 0.126 | 0.196 | 0.013 |
| n=20 | d=0.8 | 0.718 | 0.711 | 0.039 | 0.074 | 0.220 | 0.197 | 0.182 | 0.022 |
| n=40 | d=0.8 | 0.969 | 0.967 | 0.004 | 0.065 | 0.466 | 0.448 | 0.079 | 0.042 |
The objective of comparing multiple groups is to find the groups that have different group means. The hierarchical procedure is intended to facilitate this task by first performing a “screening” test to see if it is necessary to further delve into comparisons of all pairs of groups. In this sense, we may characterize the performance of the hierarchical procedure using the “false positive” (FP) and “false negative” (FN) rates defined by:
where Pr(B | A) denotes the probability that event B occurs given event A. Thus, FP is the proportion that none of the post-hoc tests is significant given a significant F test, while FN is the proportion that at least one post-hoc test is significant given a nonsignificant F test. In the case of FP, we have a false alarm, while in the case of FN, we miss the opportunity to find group differences.
Shown in Table 1 under “FP” is an estimate of FP by the percent of non-significant post-hoc test among the significant F tests. It is interesting that FP increased substantially when α changed from α = 0.05 to α = 0.001. For example, for n = 20 and d = 0.5, FP is about 10% when α = 0.05, but increased to nearly 20% when α = 0.001. In other words, we have about 10% false alarm when α = 0.05, but nearly 20% false alarm when α = 0.001.
Shown in Table 1 under “FN” is an estimate of FN by the percent of significant post-hoc test among the non-significant F tests. As in the case of FP, FN also varied as a function of α. But, unlike FP, FN decreased when α changed from α = 0.05 to α = 0.001. Also, FN is smaller compared to FP. For example, for n = 20 and d = 0.5, FN is about 4% when α = 0.05 and less than 1% when α = 0.001. In other words, we have about 10% false alarm when α = 0.05, but nearly 20% false alarm when α = 0.001.
3. Discussion
In this report, we investigated performance of the omnibus test using simulated data. The hierarchical procedure is a widely used approach for comparing multiple (more than two) groups.[1] The omnibus test is intended to preserve type I errors by eliminating unnecessary post-hoc analyses under the null of no group difference. However, our simulation study shows that the hierarchical approach is not guaranteed to work all the time. The omnibus and post-hoc tests are not always in agreement. As our goal of comparing multiple groups is to find groups that have different means, a significant omnibus test gives a false alarm, if none of the post-hoc tests are significant. But, most important, we may also miss opportunities to detect group differences, if we have a non-significant omnibus test, since some or all post-hoc tests may still be significant in this case.
Although we focus on the classic ANOVA model in this report, the same considerations and conclusions also apply to more complex models for comparing multiple groups, such as longitudinal data models [2]. Since for most models, post-hoc tests with significant levels adjusted to account for multiple testing do not have exactly the same type I error as the omnibus test as in the case of ANOVA, it is more difficult to evaluate performance of the hierarchical procedure. For example, the Bonferroni correction is generally conservative.
Given our findings, it seems important to always perform pairwise group comparisons, regardless of the significance status of the omnibus test and report findings based on such group comparisons.
Biography

Tian Chen obtained a PhD from University of Rochester in 2015. She has been working at University of Toledo since 2015, and now is working as an assistant professor in the department of Mathematics and Statistics. Her research interests are Missing data, longitudinal data analysis, variable selection and zero-inflated count model.
Footnotes
Funding statement
This study received no external funding.
Conflict of interest statement
The authors have no conflict of interest to declare.
Authors’ contributions
Tian CHEN conceived the initial idea and performed the numerical simulations.
Manfei XU participated in the discussion of the statistical issues in mental health research and turning it into a manuscript, and wrote part of the manuscript.
Justin TU participated in the discussion of the statistical problems in biomedical research, wrote part of the manuscript and helped finalized the manuscript.
Hongyue WANG researched the statistical issues in the statistical literature and helped developed the simulation examples.
Xiaohui NIU researched the statistical issues, and helped with the simulation study and finalize the manuscript.
All authors provided critical feedback and helped shape the research, analysis and manuscript.
References
- 1.Kutner MH, Nachtsheim CJ, Neter J, Li W. Applied Linear Models, 5th ed. New York: McGraw-Hill/Irwin; 2005 [Google Scholar]
- 2.Tang W, He H, Tu XM. Applied Categorical and Count Data Analysis. FL: Chapman & Hall/CRC; 2012 [Google Scholar]


