Missing value imputation for LC-MS metabolomics data by incorporating metabolic network and adduct ion relations

Abstract

Motivation

Metabolomics data generated from liquid chromatography-mass spectrometry platforms often contain missing values. Existing imputation methods do not consider underlying feature relations and the metabolic network information. As a result, the imputation results may not be optimal.

Results

We proposed an imputation algorithm that incorporates the existing metabolic network, adduct ion relations even for unknown compounds, as well as linear and nonlinear associations between feature intensities to build a feature-level network. The algorithm uses support vector regression for missing value imputation based on features in the neighborhood on the network. We compared our proposed method with methods being widely used. As judged by the normalized root mean squared error in real data-based simulations, our proposed methods can achieve better accuracy.

Availability and implementation

The R package is available at http://web1.sph.emory.edu/users/tyu8/MINMA.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Metabolomics aims to comprehensively identify and quantify all metabolites in a system and to study their changes in relation to diet, environment, disease status, genetic effects, pharmaceutical interventions, etc. (Lindon et al., 2007). By profiling and analyzing metabolite abundance, it can be helpful for unveiling the etiology of diseases and providing a functional readout of the physiological state of the human body. Liquid chromatography-mass spectrometry (LC-MS) is a commonly used metabolomics platform due to its feasibility to measure complex samples, such as human plasma and urine (Jones et al., 2012).

The quality of the LC-MS data influences the downstream analysis, including metabolite quantitation, functional interpretation, pathway analysis for disease mechanisms. The datasets normally contain large portions of metabolites with missing observations in some samples. The underlying missingness mechanism is complex. As discussed by Gromski et al. (2014), the missingness can be the result of one or any combination of the following factors: (i) the failure in computational detection, (ii) measurement error, (iii) signals are of low intensity which cannot be distinguished from background noise, (iv) imperfection of the detection algorithms used and (v) deconvolution that may result in false negatives. They also argued that imputation techniques should be favored over other methods of handling missingness in LC-MS metabolomics studies.

Various imputation techniques have been developed and applied in metabolomics studies (Armitage et al., 2015; Gromski et al., 2014; Hrydziuszko and Viant, 2012; Taylor et al., 2016), many of which were carried over from the field of microarray gene expression. They do not utilize two pieces of valuable information that are unique to metabolomics data. The first piece of information is the known metabolic network, such as the Kyoto Encyclopedia of Genes and Genomes (KEGG) database (Kanehisa and Goto, 2000). There are plenty of literature supporting the idea of utilizing network information in data analysis procedures to improve variable selection and functional interpretation (Aggio et al., 2010; Barupal et al., 2012; Cai et al., 2017; Kessler et al., 2013; Li et al., 2013; Ravasz et al., 2002; Stelling et al., 2002; Xia and Wishart, 2010). Given their close co-regulation, features matched to neighboring metabolites on the network could help predict each other’s abundance in the sample. This may only be true for a subset of the metabolites, and the relation could be non-linear, creating a challenge in utilizing such information. However advanced machine learning techniques such as support vector regression (SVR) can utilize non-linear relations, as well as resist the impact of nuisance variables, i.e. those included in the model but have no true predictive power. With the help of such techniques, network information could contribute to missing value imputation.

The second piece of information that we try to utilize is the relationship between features that are likely derived from the same metabolite. Grouping and annotating features based on their mass-to-charge ratio (m/z) and retention time (RT) characteristics have been utilized in feature identification (Kuhl et al., 2012; Silva et al., 2014; Uppal et al., 2017). Potentially features derived from the same metabolite, even if the identity of the metabolite is unknown, can help the imputation of each other. For example, if the monoisotopic weight of a hypothetical molecule M is 100.000, then in data from positive ion mode with ESI ionization, the theoretical m/z values of two of its likely adduct ions are: ${[\mathrm{M}+\mathrm{H}]}^{+},101.007276$ and ${[\mathrm{M}+\text{Na}]}^{+},122.989218$. Here ‘M’ represents the metabolite, the element after the plus sign represents the adduct, and the ‘+’ outside the bracket represents the charge state. The difference between the two m/z values does not change with the molecular weight of M. That is, even if a chemical is not in the database, its adduct ions still follow the same pattern in terms of the difference between their m/z values. For example, if we observe two m/z values in the data, and $|m/z_1-m/z_2|$ is different from $22.989218-1.007276$ by no more than $m/z_2\times {10}^{-5}$, and the two features have close RT values, then we consider they are highly likely to be derived from the same metabolite. We note that this relation is likely but not definitive. We will again rely on the SVR’s capability to resist nuisance variables when a false relation is included in the imputation.

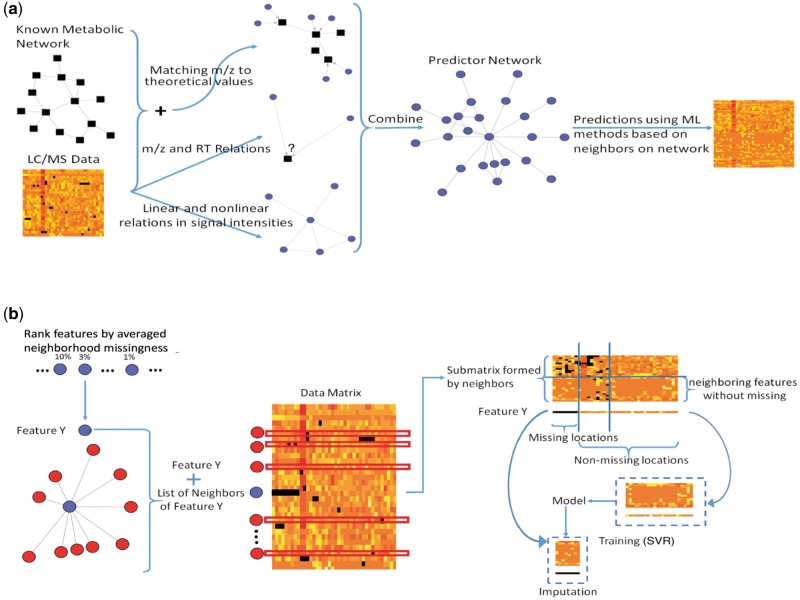
Combining the afore-mentioned information and traditional approaches, we propose a missing value imputation algorithm for LC-MS metabolomics data by applying the support vector regression (SVR) algorithm to a predictor network newly constructed among the features. To be specific, the predictor network is built by incorporating the metabolic network and adduct ion relations, together with linear and nonlinear associations between feature abundance levels calculated directly from the data (Fig. 1a). And then we impute each feature with missing values by fitting an SVR model on the dataset where the neighboring features on the predictor network are utilized (Fig. 1b). An R package called MINMA (Missing data Imputation incorporating Network and adduct ion information in Metabolomics Analysis) has been developed to implement the algorithm.

Fig. 1.

The workflow of the proposed method. (a) Building the predictor network for imputation; (b) the imputation procedure given the predictor network

2 Materials and methods

2.1 Building the predictor network

The predictor network was constructed on the feature level. The purpose of this network was to represent the feature relations. Essentially, every node on this network was a feature. If two features were considered as ‘potentially helpful in imputing each other’s missing values’, they were connected by an edge between them in the network. To define the ‘potentially helpful’ features, we mainly considered the feature relations from three sources (Fig. 1a):

• Metabolic Network The metabolic network we used in this paper was extracted from the KEGG database (Kanehisa and Goto, 2000). If two metabolites are involved in the same reaction, then they are linked in the metabolic network. Features matched to these two metabolites were considered connected. The matching of features to metabolites was based on matching the theoretical m/z of some common adduct ions of the metabolites to the observed m/z values of the features at a certain tolerance level (10 ppm in this study). In this proof-of-concept study, as the data were generated from positive ion mode with electrospray ionization (ESI), we considered five adduct ions that are common in this type of data: ${[\mathrm{M}+\mathrm{H}]}^{+},\hspace{0.17em}{[\mathrm{M}+\text{NH}4]}^{+},\hspace{0.17em}{[\mathrm{M}+\text{Na}]}^{+},\hspace{0.17em}{[\mathrm{M}+\mathrm{K}]}^{+},\hspace{0.17em}{[\mathrm{M}+2\text{Na}-\mathrm{H}]}^{+}$. The specification of ion types can easily be done by user choice of the package.

• m/z value differences of common adduct ions First we determined what adduct ion forms were included. Then the m/z differences between the adduct ions of the same charge were calculated. Pairwise m/z differences were calculated for all features in the data. When the m/z difference between two features match closely with the theoretical difference between two adduct ions (10 ppm in this study), and their RT difference was less than a pre-defined threshold (100 es in this study), the two features were considered likely to be derived from the same metabolite. They were connected in the feature level network. The same set of five common adduct ions as mentioned above were used in this study.

• Correlation Inferred from Data Matrix We consider two features ‘neighbors’ if they were highly correlated base on the following correlation measures:

  1. Linear correlation: consider ‘neighbors’ based on n₁ largest pairwise Pearson correlations ($n_1=10$ in this study).
  2. DCOL correlation: consider ‘neighbors’ based on n₂ largest pairwise nonlinear correlations defined by Distance based on Conditional Ordered List (DCOL) (Yu and Peng, 2013). ($n_2=10$ in this study)
  3. dCov dependency: consider ‘neighbors’ based on n₃ largest pairwise general dependencies defined by Brownian distance covariance (Kosorok, 2009). ($n_3=10$ in this study) These three criteria might generate overlapping feature pairs.

By building the predictor network from multiple sources, it was guaranteed that each feature had at least k connections in the network.

2.2 The imputation procedure

The imputation was based on the predictor network. In the following discussions when network neighborhood is mentioned, we refer to the predictor network. In the imputation of every feature, only its connected features on the predictor network were used as predictors. We firstly introduce some mathematical notations here: $e_{(i,j)}$ represents the value at location (i, j) in data matrix $E=\{e_{(i,j)},i=1,\dots ,m,j=1,\dots ,n\}$, i represents the ith feature (row) and j represents the jth sample (column). If the ith row, feature $e_i=\{e_{(i,j)},j=1,\dots ,n\}$ has missing locations, we denote: $e_{i,mis}=\{e_{(i,j)},j=1,\dots ,n,\text{where}\hspace{0.17em},e_{(i,j)}=\text{NA}\}$, similarly, we denote $e_{i,obs}=\{e_{(i,j)},j=1,\dots ,n,\text{where},e_{(i,j)}\ne \text{NA}\}$ as the observed locations in feature e_i, here the mis and obs only indicate locations instead of the values. All the neighboring features of feature i are indexed as nbr(i).

For feature i, we selected the non-missing locations of feature i and used $e_{i,obs}$ as response vector and those neighboring features where they were fully observed in these observed locations denoted as $e_{nbr\left(i\right),obs}$ were formed as the predictor matrix. Then we trained the SVR model using $e_{i,obs}\sim e_{nbr\left(i\right),obs}$ and extracted the predicted value ${\widehat{e}}_{i,mis}$ when $e_{nbr\left(i\right),mis}$ was used as the testing data for imputation.

Before imputation, the sequence for imputing the features with missing locations needs to be decided first or to be updated along the way. In this paper, we utilized a pre-fixed imputation sequence scheme for computation consideration. Specifically speaking, features were firstly ranked by a measure called averaged neighborhood missingness. The averaged neighborhood missingness of one feature was defined as the average number of missing locations of its neighboring features. Then the features with smaller averaged neighborhood missingness were imputed first. After imputing the feature, the imputed values were filled in the original missing locations and were treated as non-missing locations in the following iterations (Fig. 1b). However, the imputation sequence still stayed the same.

2.3 Performance comparision

We compared the proposed imputation algorithm (denoted as Net_SVR) with other commonly used imputation algorithms in metabolomics studies, including the K-Nearest Neighbors (KNN) (Troyanskaya et al., 2001), the Bayesian Principal Component Analysis (BPCA) (Oba et al., 2003), the imputation based on Simple Linear Regression (SLR), the imputation based on Singular Value Decomposition (SVD), the imputation by inserting Single Values (SVI: Min/2, Mean, Median). We briefly describe those methods:

• The K-Nearest Neighbors (KNN) (Troyanskaya et al., 2001) finds the k nearest neighboring features $\{e_j,j=l_1,\dots ,l_k\}$ by a Euclidean metric calculated among those whose feature columns are not missing at location mis, and then takes the average values of non-missing locations $e_{j,mis}$ calculated as $\frac{1}{k}{\sum }_{j=l_1}^{l_k}{e}_{j,mis}$ for imputation.

• The Bayesian Principal Component Analysis (BPCA) (Oba et al., 2003) simultaneously estimates a probabilistic model for the data matrix and estimates some latent parameter sets within the framework of Bayesian inference, and then impute the missing values in the data matrix by the expectation with respect to the estimated posterior distribution.

• The imputation based on Simple Linear Regression (SLR) is conducted by first fitting a series of univariate simple linear regression models and collecting the predicted value from each SLR model, and then imputing $e_{i,mis}$ by a weighted summation of all these predicted values, where the weights are decided by their pairwise Pearson correlation only using observed data.

• The imputation based on Singular Value Decomposition (SVD) (Troyanskaya et al., 2001) firstly initializes all missing values by their row means. Each time, given a complete observed matrix, it conducts a SVD procedure that obtains a set of mutually orthogonal expression patterns (eigen-features). And then it imputes the missing values by regressing the features with missing values against the nPC eigen-features (nPCs need to be pre-specified). This imputation is repeated until the total change of two successive imputations is less than the tolerance value.

• The imputation by inserting a Single Value (SVI: Min/2, Mean, Median). These methods replace all missing values by a pre-calculated value. Common choices are: half of the minimum (Min/2), the mean (Mean) and the median (Median) calculated from all the observed values in the data matrix.

In order to evaluate the performance of each method, we calculated the normalized root mean squared error (NRMSE) of the imputed values. The NRMSE was calculated for all the simulated missing locations that were non-zero in the original data matrix.

Suppose the total number of locations we use in calculation is K, the imputed values are $\widehat{e}=\{{\widehat{e}}_k,k=1,\dots ,K\}$ and the ground-truth from the original observed data matrix are $e=\{e_k,k=1,\dots ,K\}$. The NRMSE is defined as follows:

$$\text{NRMSE}(\widehat{e},e)=\sqrt{\frac{\sum _{k=1}^K{({\widehat{e}}_k-e_k)}^2/K}{Var\left(e\right)}}.$$

The smaller NRMSE is, the lower the prediction errors and the better the imputation method. For better illustration, we further used a metric called ‘NRMSE Ratio’ for algorithm comparison, such that the plot is on similar scale for all missing rates. For every missing imputation method (MI), it is defined as the ratio of its NRMSE taken over the NRMSE of KNN. Due to the popularity of KNN in this field, we chose to use KNN in the denominator for calculation.

$$\text{NRMSE}\hspace{0.17em}\text{Ratio}\left(\text{MI}\right)=\text{NRMSE}({\widehat{e}}_{\text{MI}},e)/\text{NRMSE}({\widehat{e}}_{\text{KNN}},e).$$

Based on the definition, if we compare two methods, the smaller the $\text{NRMSE}\hspace{0.17em}\text{Ratio}$ is, the better imputation performance.

In summary, the pseudocodes for the proposed algorithm are listed in the following:

Algorithm 1 .

BUILD_NET

1: Input data matrix $E_{m\times n}$; metabolite network G; adduct info-matrix $A=(A_{mz},A_{rt})$; reference ions names I; tolerance level $tol.mz,\hspace{0.17em}tol.rt$; number of neighbors: $n_1,n_2,n_3$;

2:  procedure Create the feature-level predictor network

3:   neighbors $N=list\left(\right)$

4:   for feature i in $1:m$do

5:    nbrs.net=$\{j:i\sim j$ in $G\}$

6:    nbrs.ion=$\{j:\exists p,q\in I,s.t$

7:    $\frac{\left|\right|A_{mz}\left[i\right]-A_{mz}\left[j\right]|-|A_{mz}\left[p\right]-A_{mz}\left[q\right]\left|\right|}{\left|A_{mz}\right[p]-A_{mz}[q\left]\right|}\le tol.mz$

8:    and $\left|\right|A_{rt}\left[i\right]-A_{rt}\left[j\right]|-|A_{rt}\left[p\right]-A_{rt}\left[q\right]\left|\right|\le tol.rt\}$

9:    nbrs.corr = c()

10:    nbrs.corr1={n₁ largest linear-correlated features with i}

11:     nbrs.corr2={n₂ largest DCOL-correlated features with i}

12:    nbrs.corr3={n₃ largest dCov-correlated features with i}

13:   nbrs.corr = nbrs.corr1 $\cup$ nbrs.corr2 $\cup$ nbrs.corr3

14:   $N\left[\right[i\left]\right]$=nbrs.net $\cup$ nbrs.ion $\cup$ nbrs.corr

15:  ReturnN

Algorithm 2 .

IMP_SEQ

1:  Input data matrix E; predictor network denoted as neighbors list N

2:   procedure Rank features by averaged neighborhood missigness

3:   impseq = c()

4:   avemiss = c()

5:   E.nmiss = apply(E, 1, function(e){sum(is.na(e))})

6:   for feature i in $1:m$do

7:    nbrs.i = N[[i]]

8:    avemiss[i]=mean(E.nmiss[nbrs.i])

9:   impseq = rank ($1:m$) by avemiss

10:   Return impseq

Algorithm 3 .

NET_SVR

1:  Input data matrix E; metabolite network G; adduct info-matrix $A=(A_{mz},A_{rt})$; reference ions names I; tolerance level $tol.mz,\hspace{0.17em}tol.rt$; number of neighbors: $n_1,n_2,n_3$;

2:  procedure Build predictor network

3:   N = BUILD_NET($E,G,A,I,tol.mz,tol.rt,n1,n2,n3$)

4:  procedure Creat an imputation sequence

5:   impseq = IMP_SEQ(E, N)

6:  procedure Imputation

7:   Initialize $\widehat{E}=E$

8:   for feature i in impseqdo

9:    create $e_i=E[i,],\hspace{0.17em}{e}_{i,obs},e_{i,mis}$

10:    extract neighbor locations from $N\left[\right[i\left]\right]$ as nbr(i)

11:    train a SVR model $e_{i,obs}\sim e_{nbr\left(i\right),obs}$

12:    predict $e_{i,mis}$ as ${\widehat{e}}_{i,mis}$ using $e_{nbr\left(i\right),mis}$

13:    set $\widehat{E}[i,mis]={\widehat{e}}_{i,mis}$

14:  Return$\widehat{E}$

3 Results

3.1 Datasets and simulation setup

In this study, we used two metabolomics datasets denoted as CAD and CHD to assess the performance of different methods. The CAD dataset is from the Emory Cardiovascular Biobank, which consists of patients who have undergone coronary angiography to document the presence/absence of coronary artery disease. Demographic characteristics, medical histories, behavioral factors and fasting blood samples have been documented and details about risk factor definitions and coronary angiographic phenotyping have been described previously (Patel et al., 2012). Each sample was analyzed in triplicate with high-resolution liquid chromatography-mass spectrometry (LC-MS), using anion exchange column combined with the Thermo-Orbitrap-Velos (Thermo Fisher, San Diego, CA) mass spectrometer in positive ion mode, with a m/z range of 85 to 850.

The CHD dataset is a dataset from the Emory-Georgia Tech Predictive Health Initiative Cohort of the Center for Health Discovery and Well Being. This is a cohort of generally healthy university employees aged 18 and older (http$:$//predictivehealth.emory.edu) (Brigham, 2010). The data was generated by C18 column combined with the Thermo-Orbitrap-Velos mass spectrometer in positive ion mode, with a m/z range of 85 to 850.

Both datasets were pre-processed using xMSAnalyzer (Uppal et al., 2013) in combination with apLCMS (Yu et al., 2009, 2013). Each sample was run in triplicates in the datasets. For each feature, there were three readings per subject. An average feature intensity value was calculated from the non-zero readings of the three. For filtering the data matrix, rows with more than 20% of zeros were removed. Finally, the data matrix was log-transformed by the function $y=\text{log}(1+x)$. The CAD dataset contains 18 434 features and 489 samples with 41.34% of the locations being zero. We removed rows with over 20% zeros, resulting in a data matrix of 7033 rows with an overall missing rate of 2%. The CHD dataset contains 8942 features and 415 samples with 43.54% zeros. We removed rows with over 20% zeros, resulting in a data matrix of 3187 rows with an overall missing rate of 7%. In the following simulation procedure, the non-zero values in these matrices served as ground truth. They were knocked out and then imputed, and the imputation accuracy was assessed by NRMSE over these non-zero ground truth values.

As described in the Materials and methods section, we built the predictor network using: (1) linear correlation, (2) DCOL correlation, (3) dCov dependency, (4) difference in m/z (relative difference is less than 10 ppm) and RT values (difference less than 100) between any pair of features, indicating high likelihood of them being derived from the same metabolite, (5) m/z matching to neighboring metabolites on the KEGG metabolic network. For all KEGG metabolites, we first computed the theoretical m/z values of common adduct ions, and then computed the difference between these m/z values and the feature m/z values. A relative difference less than 10 ppm suggests a potential match. Two features matched to connected metabolites on the KEGG network are connected in the predictor network. For (4) and (5), five adduct ions were considered in this study: ${[\mathrm{M}+\mathrm{H}]}^{+},\hspace{0.17em}{[\mathrm{M}+\text{NH}4]}^{+},\hspace{0.17em}{[\mathrm{M}+\text{Na}]}^{+},\hspace{0.17em}{[\mathrm{M}+\mathrm{K}]}^{+},\hspace{0.17em}{[\mathrm{M}+2\text{Na}-\mathrm{H}]}^{+}$. The MINMA package provides the option of using other adduct ions.

3.2 Computation

As indicated by Hrydziuszko and Viant (2012), the missingness may not occurr randomly in metabolomics data based on the analysis of DI FT-ICR MS metabolomics datasets. As a result, assuming a complete random missing mechanism may not be appropriate for imputation. Inspired by their work, we created the simulated datasets by knocking out a portion of locations from the ground-truth matrix by mimicking real missing patterns, and then evaluated each of the algorithms. To be specific, when we simulated a missing rate of r, each time we randomly selected one feature a from this ground-truth matrix, and one feature b from the original input matrix (before removing rows with $>20\%$ missing). We knocked out the locations (encoded as NA) in feature a where there were observed zero values in the corresponding location in feature b, until the simulated dataset hit the missing rate of r. Similar approach has been taken in microarray missing value imputation study (Yu et al., 2011). In this way, without any assumptions of missing mechanism, imputation algorithms were all evaluated based on the real data missing pattern.

We simulated the datasets with various missing rates: 1, 5, 10, 15, 20, 25, 30, 35 and 40%. For each of them, we generated 50 datasets and used the averaged NRMSE Ratio for evaluation. For each missing percentage, we tested various parameter settings for each method, i.e. k = 5, 10, 15 for KNN and $n_1,n_2,n_3=5,10,15$ for Net_SVR and nPCs = 5, 10, 15 for BPCA and SVD, using 5 simulations, and then used the best parameter setting in the full simulation of 50 datasets.

All computations were run under R version 3.3.1. KNN was implemented using the function ‘impute.knn’ from the package ‘impute’; BPCA was performed using the function ‘bpca’ from the package ‘pcaMethods’ (Stacklies et al., 2007); SVD was applied using function ‘impute.svd’ in the package ‘bcv’. For our mehtod Net_SVR, the SVR model was fitted using the function ‘svm’ from the package ‘e1071’ (Meyer et al., 2017). The packages ‘impute’ and ‘pcaMethods’ are Bioconductor packages.

3.3 Simulation results

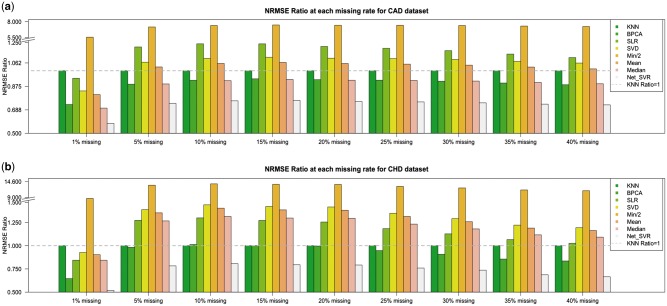
The simulation results are presented in Figure 2, where we applied all the candidate algorithms for imputation to two real datasets: CAD and CHD. For the simulation results of CAD dataset (Fig. 2a), at each missing rate ranging from 1 to 40%, BPCA, Median Imputation and Net_SVR were below the dash line of 1, which means all three methods outperformed KNN (recall that NRMSE Ratio of KNN is always 1). The averaged NRMSE Ratio for them were 0.893, 0.890 and 0.727, respectively. SLR, SVD and Mean Imputation outperformed KNN only when missing rate was 1% and performed worse than KNN when missing rate was increased. Among all top three methods: BPCA, Median and Net_SVR, when missing rate was as low as 1%, all three of them performed significantly better than KNN, as the missing rate increased, the gap compared to KNN shrank. Across all missing rates, our proposed algorithm Net_SVR performed the best as it obtained the smallest NRMSE Ratio compared to others with a minimum of 0.579 and maximum of 0.762.

Fig. 2.

Simulation results. (a) CAD (AE) data; (b) CHD (C18) data

The Net_SVR method also outperformed others when we applied all algorithms to the CHD dataset (Fig. 1b). It was the only algorithm that achieved an NRMSE Ratio below 1 across all missing rates. The averaged NRMSE Ratio of Net_SVR was 0.726 with a minimum of 0.518 and a maximum of 0.806. BPCA performed slightly better than KNN in most of the cases, but still yielded larger NRMSE Ratio at missing rate 10% (1.013), and was very close to KNN at missing rates 15% (NRMSE Ratio 1.000) and 20% (NRMSE Ratio 0.996). Median performed worse than KNN for the CHD dataset while it performed better in the CAD dataset, but the overall NRMSE Ratio of Median is around 1.

Additionally, of all the algorithms evaluated, imputing the missing locations by half of the minimum value yielded the largest NRMSE values, even though the data was already log-transformed. It is because the Min/2 approach takes a different assumption than all the other methods. It assumes the unobserved values are missed only when the signal is below a detection threshold, which largely doesn’t hold true in metabolomics data, thus, it is the worst among all the imputation algorithms. Our results are generally consistent with previous studies. The studies were somewhat diverse in terms of the data used, as well as the objectives used in judging the performance. Overall they showed a mixed performance between KNN, BPCA and SVD, while simple imputation methods such as Min/2 are in general unfavorable (Armitage et al., 2015; Gromski et al., 2014; Hrydziuszko and Viant, 2012; Taylor et al., 2016). Given the methods’ performance may depend on the data type, sample size and missing mechanisms, it is most likely that no method is universally better. On the other hand, the knockout-impute simulation approach can be helpful. Given a specific dataset, a simulation similar to the current manuscript or those previously reported may be helpful in determining which imputation method best suites the data.

In metabolomics data, the underlying missing data pattern is unclear, and the assumptions needed for modeling missing mechanism is hard to justify. Thus in these two simulation studies, the missing locations were generated in a way to mimic the real data missing pattern, which is not in favor of any of the algorithms tested. The results indicated that Net_SVR may be a safer choice given it utilizes diverse information.

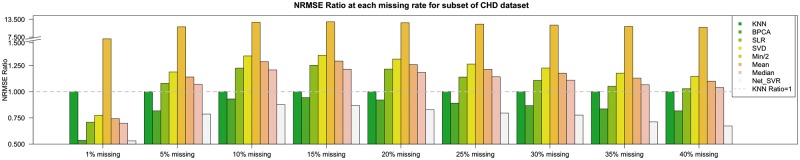
The two datasets used both contained over 400 samples. However, some datasets in real-world applications may contain fewer samples. In order to evaluate how the methods perform under the situation of smaller sample sizes, we randomly subsampled the columns of the CHD dataset. The simulation result when we subsampled 100 columns is presented in Figure 3. All the algorithms performed similarly to the results in Figure 2b. With the sample size reduction, BPCA had better relative performance compared to itself but still worse than Net_SVR. Our proposed method still outperformed the others at most missing rates. Further reduction of sample size produced similar results (see Supplementary materials for details).

Fig. 3.

Simulation results from a subset of the CHD data with 100 columns

4 Discussion and conclusion

Imputation techniques are widely used for handling missing data in metabolomics studies. In this paper, we proposed a missing data imputation algorithm where a feature-level predictor network is constructed and then utilized for imputation. We incorporated different information for constructing the predictor network: the existing metabolic network structure, adduct ion relations among features and various linear/nonlinear pairwise correlations calculated from feature abundance levels. They are believed to be potentially helpful in depicting related features which may help in imputing each other’s missing values. As this predictor network may include some false edges, hence noise in the imputation model, we applied the SVR model for reducing the influence of possible nuisance variables in the imputation process.

In real-world metabolomics studies, missing mechanism is hard to ascertain and the assumptions needed for modeling real data missing pattern is sometimes hard to justify. In order to better compare some of the widely-used algorithms in this field, we randomly sampled missing patterns from real features to mimic the real data missing pattern in the simulation studies. Simulation results showed that in high-resolution LC-MS data, the proposed algorithm Net_SVR outperforms the others at most missing rate settings.

In the application of the Net_SVR method, correctly specifying the types of adduct ions is important. Using too few adduct ion types causes the loss of valuable links that could contribute to imputation, while using adduct ions that are uncommon in the specific experimental platform may add many false edges in the predictor network. MINMA provides a function to match feature m/z values to 32 positive adduct ions, or 13 negative adduct ions. Alternatively, xMSannotator provides matching to more adduct ions (Uppal et al., 2017). Although m/z matching can always yield some false positives, nonetheless the frequency of adduct ion in the match can indicate which types of adduct ions are more common in the data, which can serve as the basis for selecting adduct ions to use.

To summarize, by constructing a feature-level predictor network and then imputing missing values using a SVR model that uses neighborhood predictors on the network, the Net_SVR is an effective imputation method. The method can be extended in several directions: 1. other machine learning methods that are better resistant to nuisance variables can be used in place of the SVR; 2. when constructing the predictor network, different sources of information could be weighted differently based on the user’s prior knowledge; 3. other feature relations can be incorporated; 4. if computationally feasible, the imputation sequence can be constantly updated along the way for better utilizing the network information.