Power Analysis for Genetic Association Test (PAGEANT) provides insights to challenges for rare variant association studies

Abstract

Motivation

Genome-wide association studies are now shifting focus from analysis of common to rare variants. As power for association testing for individual rare variants may often be low, various aggregate level association tests have been proposed to detect genetic loci. Typically, power calculations for such tests require specification of large number of parameters, including effect sizes and allele frequencies of individual variants, making them difficult to use in practice. We propose to approximate power to a varying degree of accuracy using a smaller number of key parameters, including the total genetic variance explained by multiple variants within a locus.

Results

We perform extensive simulation studies to assess the accuracy of the proposed approximations in realistic settings. Using these simplified power calculations, we develop an analytic framework to obtain bounds on genetic architecture of an underlying trait given results from genome-wide association studies with rare variants. Finally, we provide insights into the required quality of annotation/functional information for identification of likely causal variants to make meaningful improvement in power.

Availability and implementation

A shiny application that allows a variety of Power Analysis of GEnetic AssociatioN Tests (PAGEANT), in R is made publicly available at https://andrewhaoyu.shinyapps.io/PAGEANT/.

Supplementary information

Supplementary data are available at Bioinformatics online.

1 Introduction

Over the last decade, genome-wide association studies (GWAS) of common variants of increasingly large sample sizes have been the main driving force for discovery of susceptibility loci associated with complex diseases and traits. While analysis of heritability suggests that common variants have further ability to explain additional variation of these traits (Park et al., 2010; Yang et al., 2010; Lee et al., 2011, 2012; Stahl et al., 2012; Visscher et al., 2012; Dudbridge 2013; Wood et al., 2014; Bulik-Sullivan et al., 2015; Locke et al., 2015; Sampson et al., 2015), the focus of the field is inevitably shifting towards studies of less common and rare variants with the rapidly decreasing cost of sequencing technologies and increasing sophistication of imputation algorithms (Huang et al., 2015; Kreiner-Moller et al., 2015; Davies et al., 2016). However, limited or lack of findings from early studies (Purcell et al., 2014; Tang et al., 2014; Cheng et al., 2015; UK10K Consortium et al., 2015; Huang et al., 2015; Mahajan et al., 2015; Wessel et al., 2015; Xu et al., 2015; Zheng et al., 2015; Fuchsberger et al., 2016; Ganna et al., 2016; CHARGE Consortium Hematology Working Group, 2016; Haddad et al., 2016; Liu et al., 2016; Luo et al., 2017) indicate that effect sizes of rare susceptibility variants in general are likely to be modest and discovery of underlying loci will require large sample size in future studies (Park et al., 2011; Zuk et al., 2014; Moutsianas et al., 2015).

Testing of associations at the level of genetic loci or regions using various aggregate-level statistics have been proposed as a strategy to improve power of discovery in association studies of rare variants (Li and Leal, 2008; Madsen and Browning, 2009; Liu and Leal, 2010; Morris and Zeggini, 2010; Price et al., 2010; Ionita-Laza et al., 2011; Lin and Tang, 2011; Neale et al., 2011; Wu et al., 2011; Lee et al., 2012; Derkach et al., 2013; Sun et al., 2013). Simulation studies have been used under various anticipated genetic architectures of the traits for the demonstration of potential power of these procedures (Neale et al., 2011; Wu et al., 2011; Lee et al., 2012; Moutsianas et al., 2015). In particular, analysis of power for variance component-based tests, such as the popular SKAT method, can be complex as they require specification of many different parameters including a number of genetic variants under study, proportion of causal variants, allele frequency and effect size distributions. Use of various functional and annotation information to identify likely pathogenic variants a priori has also been proposed as a strategy to improve the power of rare variant association tests (Kosmicki et al., 2016; Richardson et al., 2016). To the best of our knowledge, however, there has been no systematic study of the effect of the use of such extraneous information on power of the association tests.

In this report, we first describe approximations that allow analytic characterizations of power for popular aggregate-level association tests based on a few key parameters, thus dramatically reducing the complexity of power calculations. We perform simulation studies using allele frequency distribution observed in Exome Aggregation Consortium (ExAC) (Lek et al., 2016) under various models for effect size distributions to assess the accuracy of the proposed approximations in realistic settings. We then develop a framework for genome-wide power calculations based on the underlying genetic architecture of a trait characterized by a number of underlying causal loci and total variability they explain. We assess the power of a number of recently reported association studies of rare variants using the proposed framework and provide insights into the implications for lack of discoveries on bounds of genetic architecture of the underlying traits.

We also use the proposed framework to characterize power of association tests that may preselect variants based on prior functional/annotation information. These derivations provide important insights into the required quality of annotation/functional information for identification of likely causal variants to make meaningful improvement in the power of subsequent association tests. Finally, to facilitate convenient and rapid power calculations for rare variant association tests, we make a shiny app PAGEANT (Power Analysis for GEnetic AssociatioN Test) available in R.

2 Materials and methods

2.1 Existing power calculations

A variety of statistics have been proposed for testing genetic associations at the levels of genetic loci or regions by aggregating association statistics over multiple genetic variants (Li and Leal, 2008; Madsen and Browning, 2009; Liu and Leal, 2010; Price et al., 2010; Lin and Tang, 2011; Neale et al., 2011; Wu et al., 2011; Lee et al., 2012; Derkach et al., 2013). Multiple studies (Lin and Tang, 2011; Derkach et al., 2014; Moutsianas et al., 2015) have shown that existing methods can be classified as sum-based (Li and Leal, 2008; Madsen and Browning, 2009; Morris and Zeggini, 2010; Price et al., 2010), variance component (Neale et al., 2011; Wu et al., 2011; Derkach et al., 2014), and hybrid tests that are functions of both classes (Lin and Tang, 2011; Lee et al., 2012; Derkach et al., 2013). Here, we focus on sum-based and variance component tests. We do not consider hybrid tests because their power is usually close to one of the two components. Sum-based tests aggregate variant-level association statistics by a linear combination in the forms

$$T_{ST}=\sum _{j=1}^J{w}_j{T}_j,$$

and variance component tests aggregate by quadratic combination in the forms

$$T_{VC}=\sum _{j=1}^J{w}_j{T}_j^2,$$

where $w_j$s are weights that depend on minor allele frequency (MAF) and $T_j$s are score statistics for associations for individual SNPs$(j=1,\dots ,J)$, the latter of which are typically derived from a regression model, such as the linear or logistic regression (Lin and Tang, 2011; Lee et al., 2012; Derkach et al., 2014).

Existing analytic power formulas for sum-based and variance component tests are complex functions of many parameters including number of genetic variants under study, proportion of causal variants, allele frequencies and effect size distributions (Derkach et al., 2014). The analytic power of a single-variant statistic

$$Z_j^2=\frac{T_j^2}{Var\left(T_j\right)}\sim {\chi }_{1,{nc}_j}^2,$$

can be derived based on one degree-of-freedom chi-square distribution with a non-centrality parameter of the form ${nc}_j=2p_j(1-p_j){{\beta }_j}^{2}N=\hspace{0.5em}{EV}_{j}N$, which depends on two parameters: effective sample size ($N$) and proportion of phenotypic variation explained by the j^th variant [${EV}_j=2p_j(1-p_j){{\beta }_j}^2$], a function of MAF ($p_j$) and genetic effect (${\beta }_j$), measured in the unit of per copy of an allele (Park et al., 2010).

Under assumption of low LD between rare variants and high probabilities of observing the variant in a sample Derkach et al. (2014) derived analytical power formulas for rare variant association tests. They showed that analytic power for a sum-based test statistic ${ Z}_{ST}$,

$$Z_{ST}^2=\frac{T_{ST}^2}{Var\left(T_{ST}\right)}\sim {\chi }_{1,{nc}_L}^2,$$

depends on the non-centrality parameter

$${nc}_{ST}=N\frac{{\left({\sum }_{j=1}^J{w}_{j}sign\left({\beta }_j\right)\sqrt{p_j\left(1-p_j\right){EV}_j}\mathrm{ }\right)}^2}{\sum _{j=1}^J{w}_j^2{p}_j(1-p_j)},$$

which depends on coefficients of explained variations associated with individual variants. Previous studies (Ionita-Laza et al., 2011; Derkach et al., 2014) have shown that a variance component statistic is asymptotically distributed as a linear combination of non-central chi-square random variables,

$$T_{VC}\sim \sum _{j=1}^J{\lambda }_j{\chi }_{1,{nc}_j}^2,$$

with non-centrality parameters ${nc}_j=\hspace{0.5em}{EV}_{j}N$ and weights ${\lambda }_j=w_j{p}_j(1-p_j)N$. It has been suggested that analytic power calculations for variance component tests be done by approximating the asymptotic distribution of $T_{VC}$ by a single non-central chi-square distribution matched up to four cumulants (Wu and Pankow, 2016). There are also several modifications of this method matching higher moments to improve the tail probability approximation (Wu et al., 2011; Wu and Pankow, 2016); however, power differences seem to be marginal. The cumulants ${ c}_k$of the test statistic $T_{VC}$can be written as

$${\mathrm{ }c}_k=\sum _{j=1}^J{\lambda }_j^k+kN\sum _{j=1}^J{\lambda }_j^k{EV}_j\mathrm{ }for\mathrm{ }k=1,\dots ,\mathrm{ }4,\mathrm{ }$$ (1)

which require specification of effect sizes $\left({EV}_j\right)$ and allele frequencies of individual variants. The power calculations for aggregate-level tests requiring specification of MAFs and genetic effects for individual variants have been implemented in several statistical packages (Wu et al., 2011; Wang et al., 2014; Wu and Pankow, 2016).

2.2 Approximate power calculations for aggregate tests

In the following, we describe simple formulae for approximating power for different aggregate-level tests using a limited number of key parameters. First, we show that for the sum-based test, under an assumption of independence between coefficients of explained variations and MAFs [e.g. genetic effect of a variant ${\beta }_j$ is inversely proportional to $\sqrt{2p_j(1-p_j)}$], we can roughly estimate non-centrality parameter as

$${nc}_{ST}\approx \mathrm{ }N\frac{|J_D-J_P|}{J}\frac{|J_D-J_P|}{J_D+J_P}TEV,$$

where $J_D$ and $J_P$ are numbers of deleterious and protective variants in a locus and ${\sum }_{j=1}^J{EV}_j=TEV$is the total proportion of variation explained by all $J$ variants in the locus (see Supplementary Appendix S1). If all of the causal variants in a locus are deleterious (or protective), then the non-centrality parameter can be characterized by $TEV$ and the proportion of causal variants. In Supplementary Appendix S1, we state approximations for other two common relationships between genetic effects and MAFs.

Next, we consider simplified power calculations for variance component tests $T_{VC}$ by approximating cumulants ${ c}_k$ in (1) as a function of the total proportion of variance explained by all variants within a locus ($TEV$). For example, if we assume independence between MAF and proportion of variation explained across individual variants, we can obtain a first-order approximation in the form

$${\mathrm{ }c}_k=\sum _{j=1}^J{\lambda }_j^k+kN\sum _{j=1}^J{\lambda }_j^k{EV}_j\mathrm{ }\approx \sum _{j=1}^J{\lambda }_j^k+kN\frac{\sum _{\mathrm{j}=1}^J{\lambda }_j^k}{J}TEV$$

In Supplementary Appendix S2, we derive approximations of ${ c}_k$ for three commonly assumed relationships between genetic effects and MAFs and summarize them in Supplementary Table S1. The first-order approximations, which implicitly treat all variants in a locus to be causal, can be inaccurate when the number of true causal variants is small. To improve accuracy, we propose second-order approximations to estimate the sum ${\sum }_{j=1}^J{\lambda }_j^k{EV}_j$ in (1) as function of $TEV$ and number of underlying casual variants ($J_C$) (see Supplementary Appendix S2 and Table S1). For example, if we assume the same hypothesis of independence between proportion of variation explained and MAF across individual variants, then we approximate ${\sum }_{j=1}^J{\lambda }_j^k{EV}_j$ in $c_k$ as $\frac{1}{J_C}{\sum }_{j=1}^{J_C}{\lambda }_j^k$.

2.3 Genome-wide power calculations and bounds on genetic architecture

Using the proposed first-order power calculation framework, we further develop a mathematical framework to study bounds on genetic architecture of underlying traits from limited findings reported in a GWAS. We first characterize the probability of a number of discoveries in a given study as a function of sample size $N$, the number of underlying causal loci $K$ and the distribution of their effect sizes, $TEVs$. Let $P\left(TEV,J,p\right)$ be a power of a test to detect a locus explaining $TEV$ of phenotypic variation. Then in Supplementary Appendix S3, we show that probability of $M$ discoveries in a study of sample size N is

$$P\left(\mathrm{M}\mathrm{ }\mathrm{D}\mathrm{i}\mathrm{s}\mathrm{c}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{i}\mathrm{e}\mathrm{s}|\hspace{0.17em}|\hspace{0.17em}\mathrm{G}\mathrm{e}\mathrm{n}\mathrm{e}\mathrm{t}\mathrm{i}\mathrm{c}\mathrm{ }\mathrm{M}\mathrm{o}\mathrm{d}\mathrm{e}\mathrm{l}\right)\approx \approx \left(\genfrac{}{}{0pt}{}{K}{M}\right){{E\left[P\left(TEV,J,p\right)\right]}^{M}e}^{\left(K-M\right)E\left\{\log \left[1-P\left(TEV,J,p\right)\right]|\}\right\}},\mathrm{ }$$ (2)

which depends on average power of the underlying association tests over the different causal loci in the genome and can be calculated by specifying number of underlying causal loci and distributions of proportion of phenotypic variations they explain ($TEV$), number of SNPs within a locus ($J$) and MAF $p$ across the causal loci (see Supplementary Appendix S3). This formula can be extended using the second-order approximations by specifying distribution for a number of causal variants per locus. Because of limited information about this parameter, we do not focus on it.

Now, if $M=m$ is the number of discoveries reported based on a given GWAS of sample size $N$, we can calculate $P(M\le m)$ using the above formula based on empirical distributions for MAFs ($p_k$), size of genes ($J_k$) observed in real data and various hypothesized values for number of causal loci ($K$) and parameters for underlying effect size distributions for $TEV$. Specifically, we generated a class of L-shaped effect size distribution using a two-parameter gamma distribution: Gamma(α, γ) with $\mathrm{\alpha }\hspace{0.5em}\le \hspace{0.5em}$1 and restriction that the total variance of a trait explained by causal loci, $GEV$ is smaller than 50%. Under this model, $GEV$ is given by $K\mu$ where $\mu \approx \alpha \gamma$. For various combination of $K$ and $\mu$, we evaluate the maximum value of P(M ≤ m) over different values of the dispersion parameter ($\mathrm{\alpha }/\mathrm{\gamma }=\hspace{0.5em}{\mathrm{\alpha }}^2/\mathrm{\mu }$) determined from wide range of possible values of $\mathrm{\alpha }$.

When this probability is low (e.g. <5%), we conclude that the underlying model for genetic architecture is unlikely. For example, many recent studies have reported no discoveries based on gene-level association tests. In these studies, the probability of no discoveries, $m=0$, can be used to provide bound on genetic architecture of the underlying trait.

2.4 Effects of filtering variants by extraneous information

We use the proposed framework to study the effects of filtering of variants based on prior functional/annotation information on the power of association tests. Here, power of association tests can be summarized as a function of sensitivity and specificity of the underlying filtering method. Sensitivity ($Se$) is the probability of selecting a variant given that it is truly causal, while specificity ($Sp$) is the probability of filtering a variant out given that is non-causal. If selection/filtering is independent of MAFs and proportions of variations explained, then the number of remaining variants after filtering in a locus is $J_S=Se{\hspace{0.17em}·\hspace{0.17em}J}_C+(1-Sp)·(J-J_C)$ and the proportion of variation explained by them is ${TEV}_S=Se·TEV$. Now, with new values of $J$ and $TEV$, we estimate power for aggregated tests and compare them to corresponding base values if no filtering was applied (e.g. $Se=100\mathrm{\%}\mathrm{ }$but specificity is $Sp=0\mathrm{\%}$).

If only a small subset of variants is selected, then sensitivity may be reduced as some true causal variants could be missed while specificity may improve because of removal of non-causal variants. If one takes a random subset of the variants, then $Se=1-Sp$ as the casual and non-causal variants are selected at the same rate. If the functional/annotation information used for screening is predictive of whether the SNPs are likely to be causal for the trait of interest, then one would expect specificity > 1 − sensitivity. Using the proposed framework, we explore the power of aggregated tests for various combinations of sensitivity and specificity of the underlying filtering algorithm. Furthermore, we assume that the functional/annotation information for the variants is measured by underlying normally distributed continuous score and variants are included in association test if their score is above a specified threshold. For example, several functional/annotation tools (Wang et al., 2010; Grant et al., 2011; Asmann et al., 2012) summarize multiple sources into one continuous score. Under these assumptions, we evaluate receiver operating characteristic curves generated by the combination of sensitivity and specificity at different thresholds for SNP selection. We track power of different methods along different combinations of sensitivity and specificity parameters that lead to specific values of the area under the curve (AUC), which is an overall summary of the ability of the underlying score to discriminate between causal and non-causal variants (see Fig. 3).

Fig. 3.

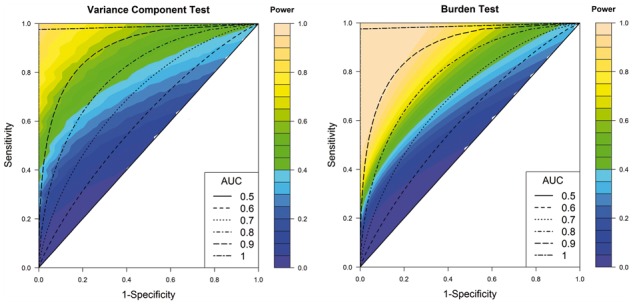
Effects of sensitivity and specificity for a priori variant screening on power of aggregate-level tests. Power of variance component test (SKAT) and burden test are studied under simulation Scenario S1 (MAF-independent EV). Number of variants in a locus is set to J = 50 and number of causal variants to J_C = 10. The setting corresponds to a baseline power (i.e. if all variants were included in the study) of 40% and 36% for variance component and sum-based tests, respectively

2.5 Empirical investigations

2.5.1 Properties of the first- and second-order approximations

We conduct extensive simulation studies to evaluate accuracy of the proposed power calculations for variance component tests in comparison to exact theoretical methods that require specification of effect sizes of individual variants. Here, we focus on the SKAT test statistics as a representative of variance component tests, and in Supplementary Material, we present results for the burden and simple sum test statistics (Li and Leal, 2008; Madsen and Browning, 2009) as a representatives of sum-based tests and C-alpha (Neale et al., 2011) as other variance component test. For each fixed combination of the size of a region ($J$) and the total variance explained ($TEV$), the two key parameters that determine the approximate power of the SKAT test, we simulate various possible values of allele frequencies and effect sizes for individual markers ${EV}_j$. Then the power based on the first- and second-order approximations averaged over empirically derived distribution of allele frequencies is compared with power based on exact theoretical calculations averaged over distribution of allele frequencies and distribution of effect sizes for individual markers ${EV}_j$ (see Fig. 1 and Supplementary Appendix S4 for more detail). Additional to evaluation of accuracy of the proposed power calculations, in Supplementary Material, we evaluate accuracy of estimation of sample size required to achieve 80% of power for variance component tests in comparison to exact theoretical method (see Supplementary Appendix S4). We consider three types of simulation scenarios: S1 (‘MAF-independent EV’) assumes that coefficients of explained variations $\left(EV\right)$ is independent of MAF; S2 (‘MAF-independent ${\beta }_j$’) assumes that size of genetic effect ($\beta$), measured in the unit of per copy of an allele [${\beta }^2=EV/2MAF(1-MAF)$] is independent of MAF and S3 [‘MAF-log-dependent ${\beta }_j$’] assumes that genetic effect is related to MAF through log₁₀ function (as defined in Supplementary Table S1). For each type of simulation scenario, we estimate the power for a locus of size $J=50, 100, 200 \mathrm{a}\mathrm{n}\mathrm{d}\mathrm{ }400$ with the number of underlying causal variants $J_C=10, 20, 30 \mathrm{a}\mathrm{n}\mathrm{d}\mathrm{ }50$. In Supplementary Appendix S4, we describe simulation mechanisms in detail and we summarize simulation models and parameters required for each method in Supplementary Table S2.

Fig. 1.

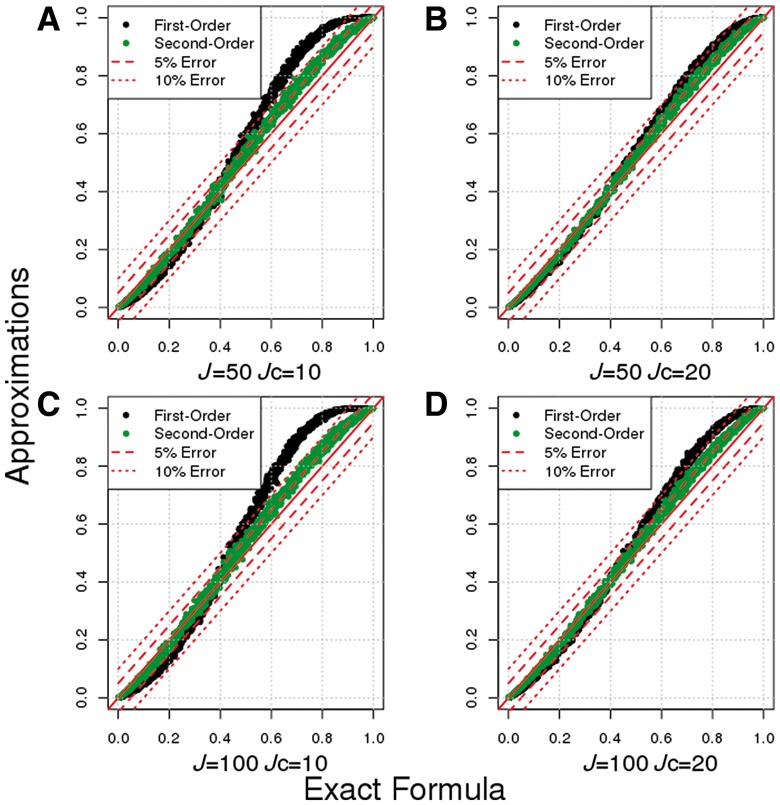
Evaluation of the accuracy of the first-and second-order approximations to the power of SKAT test under simulation scenario S1 (MAF-independent EV). Exact Formula represents estimated average power over empirical distribution of MAFs and genetic effect sizes using exact theoretical formulas for the SKAT test statistic. First-order represents estimated average power over empirical distribution of MAFs using the first-order approximation for the SKAT test statistic. Second-order represents estimated average power over empirical distribution of MAFs using the second-order approximation for the SKAT test statistic. 5% and 10% error represents 5% and 10% error bounds over exact power calculations. Number of variants in a locus (J) and number of causal variants (Jc): A) J = 50, Jc = 10; B) J = 50, Jc = 10; C) J = 100, Jc = 10 and D) J = 100, Jc = 20.

2.5.2 Bounds on variation explained by a causal locus

In Supplementary Table S3, we provide key parameters that summarize a variety of recently published association studies of rare variants (Purcell et al., 2014; UK10K Consortium et al., 2015; Wessel et al., 2015; Xu et al., 2015; Zheng et al., 2015; Fuchsberger et al., 2016; Ganna et al., 2016; CHARGE Consortium Hematology Working Group, 2016; Liu et al., 2016; Luo et al., 2017). Typically, studies on Human Exome BeadChip (Exome Chip) had larger sample sizes than studies on sequencing platform; however, the latter covered a much smaller number of rare variants. We use our mathematical framework to obtain bounds on genetic architecture implied by the results from two of the largest studies, one of which studied educational attainment with exome sequencing and the other studied blood pressure employing exome chip (Ganna et al., 2016; Liu et al., 2016) (see 5th and 9th rows of the Supplementary Table S3).

For ease of illustration, we assume that analysis in these studies was conducted by the SKAT statistic with a gene as a unit, although the study of educational attainment (Ganna et al., 2016) did not explicitly report results from gene-based analysis. We used the publicly available ExAC database (Lek et al., 2016) to obtain empirical distributions for number of rare variants in a gene ($J_k$) and vector of MAFs $p_k$ across exome. The average numbers of rare variants per gene ($J$) were 35.5 and 13 in the studies of educational attainment and blood pressure, which used exome sequencing and Exome Chip platforms, respectively. We provide empirical distributions and other key parameters in Supplementary Figures S11 and S12. Finally, we set Type 1 error threshold $T1=\frac{0.05}{20,\hspace{0.17em}000}=2.5\times ·{10}^{-6}$. To estimate genetic bounds from the results of study on educational attainment, we estimate the probability of no discoveries ($m=0$) given a genetic model from (2) by using the sample size $N=14,\hspace{0.17em}000$, the number of sequenced individuals. To ensure validity of asymptotic power formulas, we assume that MAF of rare variant ranges between 0.0001 and 0.01 (e.g. no singletons and doubletons).

To estimate genetic bounds from the study of blood pressure outcome, we calculate probability of at most three discoveries ($m=3$) under a sample size of $N=140,\hspace{0.17em}000$ to match the number of discoveries reported and number of individuals genotyped in this study (see 9th row of Supplementary Table S3). In contrast to the previous study, here we did not put any lower bound for MAFs.

For each combination of the number underlying of causal loci $\left(K\right)$ and parameters of effect size distributions, we calculate the probability of less than or equal to m discoveries using (2) with study-specific parameters. Expectations in (2) are estimated using 100 000 Monte Carlo simulations. In this report, we calculate power of the SKAT test statistic under the assumption of independence between proportion of variations explained and MAF of individual variants. Results for other genetic architecture are also discussed and presented in the Supplementary Material.

2.5.3 Effects of variant filtering on power of aggregated tests

We consider two values of a size of a locus $J=50, 100\mathrm{ }$and two values of a number of causal variants in a locus, $J_C=\hspace{0.5em}10, 20$. Initial values of $TEV$ are selected so that power of the SKAT test is equal to 40% at Type 1 error $T1\hspace{0.5em}=\hspace{0.5em}0.05/20,\hspace{0.17em}000\hspace{0.5em}=\hspace{0.5em}2.5·{10}^{-6}\mathrm{ }$and sample size $N=10,\hspace{0.17em}000$. For every combination of sensitivity and specificity, we estimate average power for the SKAT and burden tests. For this study, we also assume independence between proportion of variations explained and MAF for the individual variants. Results for other genetic architectures are presented in the Supplementary Material.

3 Results

3.1 Properties of the first- and second-order approximations

We evaluate the accuracy of first- and second-order approximations compared to exact power calculations of the variance component test under variety of genetic models (see Supplementary Table S2). The first-order approximations match exact calculations better as the number of causal variants in a locus $J_C$ increases (Fig. 1). Particularly, we observe that with more than 20 causal variants in a locus ($J_C\ge 20$), difference in power between those two methods is small regardless of the total number of variants in a locus $J=50, 100$ (see Fig. 1B and D and Supplementary Fig. S1). Similar conclusion holds also for very large loci $J=200, 400$and other relationships between genetic effect and MAF (see Supplementary Figs S2–S4). With lower number of causal variants in a locus (e.g. $J_C=10$), we observe upward bias in first-order estimates when exact power is high and downward bias when exact power is low (see Fig. 1A and C).

We also observe that the second-order approximation is more accurate at estimating the exact power (Fig. 1). Now, difference in power between approximate and exact calculations is small even when the number of causal variants in a locus is small, (see also Supplementary Figs S1–S4). Overall, our simulations demonstrate that the first-order approximation accurately estimates exact power when the number of causal variants in a locus is not too small. However, if the number of causal variants in a locus is small, then the first-order approximation may produce biased results. On the other hand, the second-order approximation estimates exact power more accurately regardless of underlying generic architecture, but it requires specification of an additional parameter, namely the number of causal variants in a locus ${(J}_C)$. Very similar results hold for another type of variance component test, C-alpha (see Supplementary Fig. S5).

We also observe that the accuracy of the proposed approximations for sample size calculations is consistent with what is expected from power calculations (see Supplementary Figs S8–S10). The second-order approximation provides unbiased estimates for average sample size, while accuracy of the first-order approximation improves as the number of causal variants in a locus $J_C$ increases.

As for sum-based statistic, we observe that the accuracy of the proposed approximations does not drastically depend on number of causal variants in a locus (Supplementary Figs S6 and S7). However, the accuracy depends on the variation in SNP-specific coefficients of variations as we take square inside of expectation (see Supplementary Appendix S1). Particularly accuracy should improve if causal variants have similar generic effects.

3.2 Bounds on effect size distribution

Genome-wide power analysis of the educational attainment study (Ganna et al., 2016) (see Fig. 2A), which implemented whole-exome sequencing, shows implausibility of models that correspond to a small number of underlying causal loci explaining significant total phenotypic variance. For example, the probability of observing no discovery is less than 5% under genetic models that involve less than 250 loci to explain a total of 20% or more phenotypic variation. If we assume independence between genetic effects and MAFs across variants, a scenario under which SKAT test has higher power, then even larger number of loci will be needed to explain the same total variance (see Supplementary Fig. S13A).

Fig. 2.

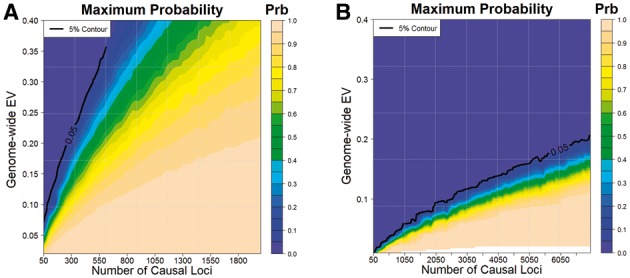
Bounds for genetic architecture based on results reported in studies of education attainment (EA) and blood pressure (BP). (A) Maximum probability of observing no discoveries in the EA study, which used whole-exome sequencing platform, as a function of the number of underlying causal loci K and the total variation explained by them with a sample size of 14 000. (B) The maximum probability of observing three statistical significant discoveries in the BP study, which used exome chip, as a function of the number of underlying causal loci K and the total variation explained by them with a sample size of 140 000. In both cases, it is assumed that gene-based tests have been performed using the SKAT test statistics at the level of T1 = 2.5 × 10⁻⁶. Probabilities are estimated by (2) and assumption of independence between minor allele frequency and explained variations. Maximum probability was calculated over a set of possible effect size distributions. The black line shows approximate contours (bounds) corresponding to the probability of 5%

Genome-wide power analysis of the study of blood pressure (Liu et al., 2016) (see Fig. 2B), which is much larger in sample size but implements the Exome Chip platform, provides a very sharp bound on the relationship between number of underlying causal loci and total heritability explained by the underlying variants. We estimate, for example, at least 6000 causal loci will need to be involved if the variants included in the study could explain 20% of phenotypic variance of blood pressure. Identical to results for the WES study, genetic bound is even sharper if independence between MAFs and genetic effects is assumed (see Supplementary Fig. S13B).

3.3 Effects of a priori SNP screening on power of aggregated test

A priori SNP selection does not improve the power of variance component test substantially (e.g. by 10%) unless the underlying algorithm has very high accuracy to discriminate between causal and non-causal SNPs (AUC between 80% and 90%) (see Fig. 3). In contrast, power for sum-based test can improve substantially with more modest discriminatory accuracy of the SNP selection algorithm (AUC between 70% and 80%). Furthermore, we observe that the roles of sensitivity and specificity are not symmetric on power of these tests. For both tests, substantial improvement of power is possible only if sensitivity is at the minimal 30–40%. On the other hand, substantial improvement in power is possible with fairly poor specificity (e.g. about 20%) as along as sensitivity is high (e.g. 90%). We observe similar results in studies with different genetic architecture and large number of SNPs in a locus (see Supplementary Figs S14 and S15).

4 Discussion

Although large GWAS of low frequency and rare variants are now becoming increasingly feasible due to technological advances, the likely yield of such studies in the future remains uncertain as studies conducted to date have only reported limited number of findings (Purcell et al., 2014; Tang et al., 2014; Cheng et al., 2015; UK10K Consortium et al., 2015; Huang et al., 2015; Mahajan et al., 2015; Wessel et al., 2015; Xu et al., 2015; Zheng et al., 2015; Fuchsberger et al., 2016; Ganna et al., 2016; CHARGE Consortium Hematology Working Group, 2016; Haddad et al., 2016; Liu et al., 2016; Luo et al., 2017). For studies of common variants, which have mostly relied on association testing at the level of individual variants, we and others have shown that the yield of GWAScritically depend on distribution of phenotypic variances explained by individual variants across the genome (Park et al., 2010; Chatterjee et al., 2013; Dudbridge, 2013). For studies of rare variants, it has been suggested that tests for genetic associations be performed at an aggregated level by combining signals across multiple variants for powerful detection of underlying susceptibility loci (Li and Leal, 2008; Madsen and Browning, 2009; Neale et al., 2011; Wu et al., 2011; Moutsianas et al., 2015). In this report, we show that how power for some of these more complex tests critically relates to total genetic variances explained by multiple variants within a locus. Based on such power calculations, we assess bounds on distributions of locus-level genetic variances that are consistent with limited findings reported in current studies. Furthermore, based on these simplified power calculations, we evaluate the potential for improving power for aggregated tests by preselection of likely causal variants based on functional/annotation information.

Power analysis of current studies of large sample sizes may provide important bounds on genetic architecture of the underlying traits. Our analysis suggests that rare variants investigated in current studies could explain significant fraction of heritability of the underlying traits only under highly polygenic models in which causal variants are distributed over hundreds or even thousands of different genetic loci. These results are intuitive given that if a relatively small number, e.g. a few dozens, of genetic loci could explain a substantial fraction of heritability of these traits, then at least some of these loci will be detected by the sample size achieved so far in the current studies.

A number of rare variant studies that have conducted both individual-variant and aggregated tests have detected more genetic loci using the former than the latter approach (UK10K Consortium et al., 2015; Fuchsberger et al., 2016; CHARGE Consortium Hematology Working Group, 2016; Liu et al., 2016) (see Supplementary Table S3). The analytic formula we propose for calculating probability of a certain number of discoveries under various models for genetic architecture can also be applied for single-variant tests. Genetic bounds based on the results from single SNP analysis for the same two studies also show that only under highly polygenic architecture the variants included in these studies can explain a substantial fraction of heritability of the underlying traits (see Supplementary Fig. S16). These genetic bounds based on single SNP analysis are also consistent with corresponding genetic bounds from gene-based analysis and assumption of clustering of multiple causal variants per causal locus. Large studies with more accurate estimates of genetic bounds will provide additional information on the degrees of clustering of multiple rare variants within causal locus.

A variety of studies have studied genetic architecture of common variants by characterization of underlying heritability, number of susceptibility variants and effect size distributions (International Schizophrenia et al., 2009; Park et al., 2010; Yang et al., 2010; Lee et al., 2011, 2012; Park et al., 2011; Stahl et al., 2012; Visscher et al., 2012; Dudbridge, 2013; Zhou et al., 2013; Huang et al., 2015; Loh et al., 2015; Speed et al., 2017). All of these studies consistently point toward a highly polygenic model where disease etiology may involve thousands or even tens of thousands of common susceptibility variants, each conferring only a modest association, but in combinations they can explain substantial phenotypic variations. Some recent studies have reported that low frequency and rare variant studies have the potential to explain significant fraction of heritability for selected traits (UK10K Consortium et al., 2015; Mancuso et al., 2016; Speed et al., 2017). Further insights into genetic architecture of these traits can be obtained by comparing observed number discoveries in these studies with those from simulated studies under different models for genetic architecture (Price et al., 2010; Zuk et al., 2014). The proposed analytic framework provides an alternative fast and simple way of evaluating expected discoveries for a large variety of genetic models and quantification of their plausibility given results from a given study.

Power calculations for aggregated tests with a selected subset of variants point towards challenges for use of functional and annotation information for pre-screening. Overall, it appears that preselection of variants can significantly improve the power of aggregated tests only if the underlying functional/annotation information have a fairly high accuracy to discriminate (AUC > 70–80%) between causal and non-causal variants for the underlying disease of interest. In particular, the algorithm should be highly sensitive to capture the underlying causal variants of a disease. Use of a too stringent criterion for variant selection may increase specificity but will lead to decreased sensitivity and hence could lead to loss of power in aggregated tests. More empirical studies are needed to assess the impact of variant selection on power of aggregated tests.

Sophisticated imputation algorithms (Huang et al., 2015; Kreiner-Moller et al., 2015) and increasing sample size of reference datasets (Huang et al., 2015) are allowing imputation of low frequency and rare variants with increasing accuracy. Many association studies are now being conducted based on imputation in existing large GWAS. A limitation of our method is that it currently cannot account for imputation accuracy, which is expected to reduce with decreasing allele frequency. At the level of individual variants, it is possible to characterize reduction of power based on formula for effect size attenuation due to imputation (Huang et al., 2009). Further studies are needed to understand the impact of imputation on aggregated tests encompassing variants of different allele frequency spectra.

Our simulation results demonstrated that analytical power formulas presented in Section 2.1 match empirical power very well for quantitative trait (see Supplementary Fig. S17). Under case–control settings, exact power calculations are biased due to reliance on asymptotic normal distribution (see Supplementary Fig. S18). As a result, these calculations may not be adequate for low Type 1 thresholds or low MAFs. Further development in an improvement of the accuracy by incorporating of LD structure and sparsity is needed.

In this report, we have illustrated the application of the framework in exome-based analysis where aggregated tests can be applied across largely non-overlapping genes. For whole-genome sequencing studies, where aggregated tests may be applied in a sliding window fashions (UK10K Consortium et al., 2015; Zheng et al., 2015), more work is needed for genome-wide power calculations in terms of underlying models for genetic architecture.

In conclusion, in this report, we provide simple analytic approaches to power calculations for rare variant association tests at the levels of individual loci and whole genome in terms of a few key parameters of the underlying models for genetic architecture. These methods, which we implement in a shiny application in R, will provide useful design tools for planning next-generation GWAS.