Limb Position Tolerant Pattern Recognition for Myoelectric Prosthesis Control with Adaptive Sparse Representations from Extreme Learning

Abstract

Myoelectric signals can be used to predict the intended movements of an amputee for prosthesis control. However, untrained effects like limb position changes influence myoelectric signal characteristics, hindering the ability of pattern recognition algorithms to discriminate among motion classes. Despite frequent and long training sessions, these deleterious conditional influences may result in poor performance and device abandonment.

Goal

We present a robust sparsity-based adaptive classification method that is significantly less sensitive to signal deviations resulting from untrained conditions.

Methods

We compare this approach in the offline and online contexts of untrained upper-limb positions for amputee and able-bodied subjects to demonstrate its robustness compared against other myoelectric classification methods.

Results

We report significant performance improvements (p < 0.001) in untrained limb positions across all subject groups.

Significance

The robustness of our suggested approach helps to ensure better untrained condition performance from fewer training conditions.

Conclusions

This method of prosthesis control has the potential to deliver real-world clinical benefits to amputees: better condition-tolerant performance, reduced training burden in terms of frequency and duration, and increased adoption of myoelectric prostheses.

I. Introduction

Electromyogram (EMG) is produced as the direct result of force-generating electrical activity in the underlying muscle and can be used as a means to decode the intended movements of an amputee for prosthesis control [1]. EMG pattern recognition methods have emerged as a means to intuitively operate prosthetic devices through the extraction of EMG feature data that are informative enough to encode specific desired movement patterns or classes [2][3]. Linear Discriminant Analysis (LDA) [4] is commonly used as a classification method to decode these movement patterns. The objective of LDA is to determine a subspace projection that maximizes the distance between class data clusters while minimizing the scatter of each cluster such that linear class-separation boundaries can be drawn. The available movement classes and training conditions are often carefully selected to enforce this separation.

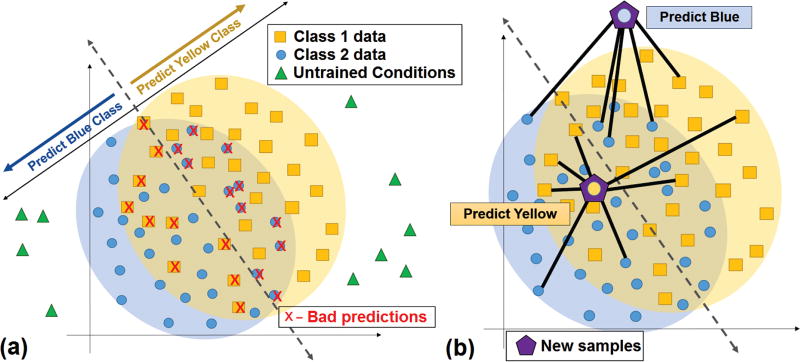
Many classification methods are excellent at discriminating large numbers of classes when the testing conditions closely mirror the training conditions [3][5], what we refer to as symmetric evaluations. Symmetric evaluations artificially enforce class data separation, contributing somewhat to the known disparity between offline and online performances of EMG control strategies [6][7]. Classification performance can degrade substantially when new data samples differ from the training conditions [8][9], which is likely to occur in asymmetric evaluations like testing in untrained (unseen) conditions and real-time online assessments. Specifically, it is understood that movement classification performance declines when the user is exposed to real-world conditions that were not explored during training such as new arm positions [10][11] and load changes [12]. The untrained effects previously mentioned introduce changes to the size and shape of the class data clusters which, in turn, have the effect of increasing cluster size and reducing inter-cluster distances (Fig. 1a). From an algorithmic perspective, this problem is two-fold: (1) condition-invariant training data may not perform well in untrained conditions, and (2) too much condition-variant training data can crowd or intersperse data within the feature space, diminishing the returns from additional training [13]. Both cases can negatively affect the utility of EMG control schemes in a real-world setting.

Fig. 1.

Boundary-based classification and the need for more robust algorithms. (a) Real-world prosthesis use introduces untrained conditions which may not cluster in a separable way. Boundary classifiers cannot fully discriminate interspersed data. (b) In SRC methods, incoming test data are reconstructed from a minimal explanatory subset of the training data and the reconstruction is classified rather than the original input. SRC allows data from all classes to compete for membership in this subset at runtime, providing flexibility to classify interspersed data near class boundaries as well as outliers resulting from untrained effects.

Recently, myoelectric pattern recognition research has centered on improving robustness in order to mitigate the disparity between training and testing data resulting from nonideal conditions [9]. Classifier modifications like fault-detection [14] and confidence-based rejection [15] probabilistically reduce erroneous decisions by requiring a class candidate to achieve a minimum posterior ratio with respect to its alternative candidates [16]. Unsupervised techniques for adaptive classifier self-enhancement have been developed to account for changes and drift in the EMG signal properties over time [5][17]. Frequent retraining or training in more conditions can also improve robustness up to a point [6][10], but this process is burdensome for a user and is therefore impractical as a guard against poor performance. Promising surgical solutions like osseointegration and implantable EMG electrodes can significantly reduce or eliminate user retraining while improving task completion in real-world conditions [18]. All of these solutions and algorithmic extensions stand to benefit from improvements in the robustness of their underlying pattern recognition strategy.

For myoelectric pattern recognition to be robust in a practical sense, especially in noninvasive approaches, it is critical to devise methods that are resilient to the noise-producing and use-dependent effects generated during arm movement. To this end, new strategies from other fields are emerging to deal with analogous problems. Research in face recognition has produced algorithms which achieve robustness to the corruption of test data samples by estimating reconstructions of those samples from limited (sparse) subsets of the training data. These sparse representation classification (SRC) methods demonstrate high recognition accuracy on image data that is 70% noise-corrupted, 30% occluded [19], or even misaligned [20]. In addition to these error-tolerance properties, SRC methods allow inter-class competition among data samples in their reconstructions. As a result, these methods are more robust at classifying interspersed data samples from multiple classes (Fig. 1b), whereas boundary-based classifiers may be unable to discriminate well for these cases.

The work herein significantly expands our preliminary work [21] through the adoption of an enhanced SRC method, the inclusion of amputee subjects in our position-variant offline analysis, and a position-variant online performance assessment for a group of able-bodied subjects.

II. Methods

A. Paradigm for Limb Position Tolerance

1) SRC

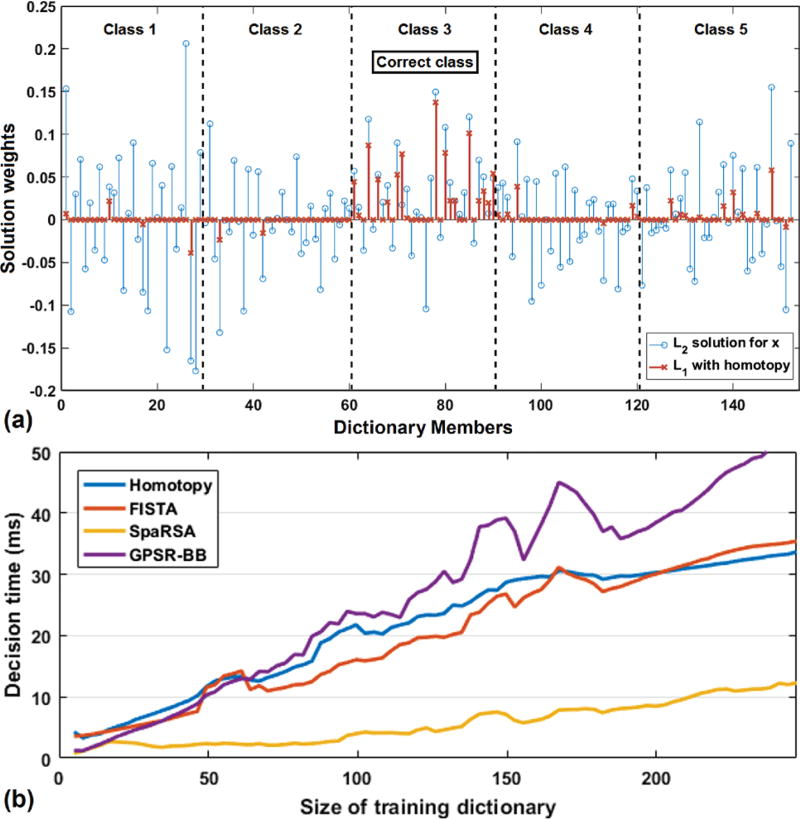
Rather than model class boundaries through algorithm training, each class can be exactly defined by its vector members, forming a single training data matrix partitioned by class, A = [A₁|A₂|…|A_C], called the training dictionary. A new data sample, y, can then be reconstructed from a linear combination, Ax, of the data where x = [x₁|x₂|…|x_C]^T are the specific contribution weights from each of the training set samples. A sparsity constraint limits this linear combination to a minimal explanatory subset of the training data, reducing the influence of noise and outliers. In the typical case, members from the correct class provide the greatest contributions (Fig. 2a). The sparsity constraint is imposed by finding the ℓ₁ basis pursuit solution for x

$$({\ell }_1)\mathbf{x}=\underset{\mathbf{x}}{\text{argmin}}{\Vert \mathbf{x}\Vert }_1\text{ such that }\mathbf{A}\mathbf{x}=\mathbf{y}$$ (1)

which can be alternatively posed as the following convex optimization problem:

$$\mathbf{x}=\underset{\mathbf{x}}{\text{argmin}}\{\frac{1}{2}{\Vert \mathbf{\text{Ax}}-\mathbf{y}\Vert }_2^2+\lambda {\Vert \mathbf{x}\Vert }_1\}$$ (2)

where λ > 0 is an appropriately chosen regularization parameter influencing sparsity. After determining x from (2) and computing residuals r_i = ‖A_ix_i − y‖₂ for each class, the class i of minimum residual is the chosen class. Herein, we utilize SRC as described above; however, additional extensions have been proposed for confidence rejection, enhanced error-tolerance, and feature reduction [19][20].

Fig. 2.

(a) The ℓ₁ sparse reconstruction of weights x vs. ℓ₂ least-squares, x = (A^T A)⁻¹ A^T y. With a sparsity constraint, contributions to x tend to come primarily from dictionary members of the correct class, making it well-suited for classification. The ℓ₁ solution can reduce the influence of noise or untrained effects which may be present in test sample y. (b) Computation time comparison of ℓ₁ solvers for SRC classification (computed on EMG time-frequency features of length 1064). SRC can be used for real-time classification, but limits must be placed on the training dictionary size.

2) Problems with Real-time SRC

The primary drawback of SRC is the ℓ₁ computation speed [22]. Given our real-time need to classify quickly, we exhaustively compared various ℓ₁ solvers from literature to find the following fast and accurate methods for use on EMG data (Fig. 2b): homotopy [23], fast iterative shrinkage thresholding (FISTA) [24], and gradient projection for sparse reconstruction (GPSR) [25]. Even in the best case, limits must be imposed on the training dictionary size for SRC to be practical for real-time EMG classification. The fastest ℓ₁ solver, sparse reconstruction by separable approximation (SpaRSA) [26], tested poorly in terms of accuracy.

In preliminary testing, we found that homotopy was well-balanced in terms of computation speed, error-tolerance, and accuracy. Homotopy iteratively drives an initial estimate x⁽⁰⁾ towards ℓ₁ according to the following update procedure:

$$\mathbf{x}=\underset{\mathbf{x}}{\text{argmin}}\{\frac{1}{2}{\Vert \mathbf{\text{Ax}}-\mathbf{y}\Vert }_2^2+\lambda {\Vert \mathbf{x}\Vert }_1+(1-\epsilon ){\mathbf{u}}^T\mathbf{x}\}.$$ (3)

For the nth iteration, u⁽ⁿ⁾ = −λz⁽ⁿ⁾ − A^T (Ax⁽ⁿ⁻¹⁾ − y) where z⁽ⁿ⁾ is the sign sequence of x⁽ⁿ⁻¹⁾, and x is updated with (3) from its previous estimate. Changes in x at each iteration are used to update the step-size of parameter ε as it increases from 0 to 1, diminishing the last term in (3), and converging to the ℓ₁ solution for x. Convergence is faster when initial estimate x⁽⁰⁾ is near the final solution, so least-squares (ℓ₂) x⁽⁰⁾ = (A^T A)⁻¹ A^T y is recommended to initialize.

3) Extreme Learning for Fast Adaptive SRC

Extreme learning machine (ELM) with adaptive sparse representation classification (EASRC) was developed for image recognition problems to combine speed and accuracy benefits from ELM in noise-free conditions with the error-tolerance properties of SRC in noisy conditions or near inter-class boundaries [22]. We summarize the EASRC method, but encourage exploration of the source material for specific details.

ELM is a feed-forward network containing a single hidden layer with randomly assigned weights w_i and biases b_i connecting input neurons to hidden nodes:

$$\sum _{i=1}^L{\beta }_{i}g({\mathbf{w}}_i·{\mathbf{y}}_j+b_i)={\mathbf{o}}_j,j=1,2,\dots N$$ (4)

where L is the number of hidden nodes, N is the number of training data vectors, g(·) is a sigmoid activation function, β_i are the weights connecting hidden nodes to output neurons, and o_j is the network output from a given input vector y_j. The output weights β_i are learned via iterative regularization from Leave-One-Out (LOO) cross-validation over the training data.

After training the ELM, a new input data sample y will generate output vector o to be used for classification. Defining T_diff as the difference between the two largest entries in o, this metric is a good indicator of the noisiness of y with respect to the training data [27]. For an appropriately chosen α, T_diff > α indicates that y is well-represented by one class in the training data and can therefore be classified by ELM with high confidence. If T_diff ≤ α, likely resulting from noise or a boundary case, the slower SRC is used instead. However, to improve the ℓ₁ computation speed, the dictionary A′ passed to SRC is adaptively reduced by selecting the classes associated with the n-largest entries in o. For example, if the n entries represent only members from classes 3 and 5, then A′ = [A₃|A₅] resulting in faster classification of this reduced set of candidate classes. From [22], we use α = 0.1, n = 60, and L = 1000.

B. Offline Limb Position Experiment

This study was conducted in accordance with protocols approved by the Johns Hopkins Medicine Institutional Review Board. Eight able-bodied and two transradial amputee subjects participated in the offline experiment. The able-bodied subjects (6 male, 2 female) are ages 18 to 45, and specific traits of amputee subjects are: Subject A1 is four years status post bilateral upper and lower extremity amputations due to extensive tissue necrosis from septicemia, and A2 is eight years status post right upper-extremity amputation due to a work-related trauma. The offline experiment generally involved prompting subjects to move their arm to random endpoint locations uniformly distributed in their reaching space to perform certain hand movements while EMG and arm position data were recorded. In order to create the asymmetric offline conditions detailed in our results, we regulated which of these limb position data were used for classifier training and evaluated various classifiers and feature combinations in the untrained positions.

Subject ID	Age	Sex	Status	Arm used	Residual length
A1	69	F	bilateral	right	12 cm
A2	64	M	unilateral	right	16 cm

1) Offline Protocol

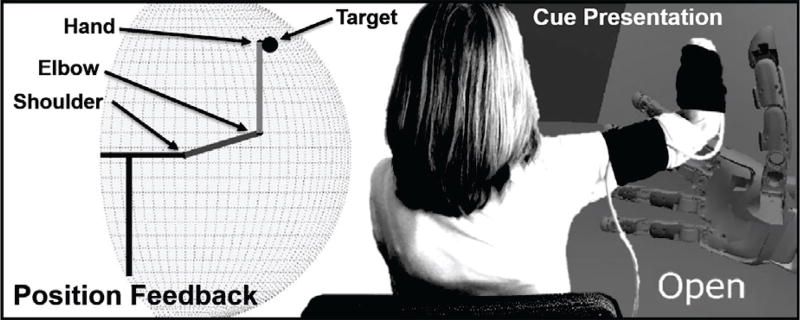
A user interface (UI) developed in MATLAB Simulink (Mathworks, Natick, MA) was used to show the target hand locations and provide the subject with a real-time display of their current hand location as measured by inertial sensors (Fig. 3). The radial boundary of the subject’s reaching space was calculated by measuring the subject’s arm (including prosthesis for amputee subjects) from tip of the middle finger to the center of the shoulder joint at maximum extension. The angular boundaries for this reaching space were set between 15° ≤ θ ≤ 165° and 10° ≤ ϕ ≤ 120°. θ is the vertical polar angle with 0° referencing the arm pointing down, and ϕ is the azimuth with 0° referencing the shoulder abducted 90° from neutral.

Fig. 3.

Asymmetric offline limb position experiment. The subject was shown a position indicator randomly chosen within his 3-dimensional reaching space. Once the position was acquired, the subject was presented movement cues, and executed each while data were collected. This process was repeated for 81 random positions, or 54 in the case of subject A2.

After setup, the UI prompted the subject to reach a random arm endpoint target within their reaching space. The subjects were instructed to use the visual feedback of their current endpoint position to reach the target location with a natural, comfortable posture. After dwelling at the target location for 3 s, image cues of five wrist and hand movement classes (rest, hand open/close, wrist pronate/supinate) were presented to the user via the UI. The cues were presented in random order for 4 s each and the subject was asked to use their existing or phantom hand to mimic the cued movement. The recording phase of cue presentation began 1.5 s after initial cue prompt and continued for an additional 2.5 s. Hereafter, we refer to this performance and recording process as “executing the movement classes.”

We define a single trial as the successful acquisition of one random arm endpoint position and execution of the movement classes at that position. Every subject, except A2, completed a total of 81 trials. Subject A2 opted to perform 54 trials due to fatigue. The subjects were allowed as much time as needed to acquire each target or, optionally, to rest. The experiment and set-up time required between 45 min and 1 h depending on the subjects variable intertrial rest times and skill in acquiring position targets. Able-bodied subjects completed the experiment once, whereas each amputee conducted the experiment twice, first with the subject’s own prosthetic limb donned to provide a real-world loading condition, and a second time with no prosthesis load.

2) Data Acquisition and Feature Extraction

For all subjects, eight channels of raw EMG were obtained through differentially amplified electrode pairs placed roughly equidistant around the circumference of proximal forearm muscle of greatest mass and held onto the limb using a compressive band. We did not target specific muscles with the surface electrodes nor prepare the skin surface for maximal contact. Raw EMG input data were amplified using 13E200 MYOBOCK amplifiers (Ottobock, Plymouth, MN). The amplified signal was sampled using the NI USB-6009 (National Instruments, Austin, TX) at 1000 Hz and subsequently filtered through a 20–500 Hz digital bandpass and 60 Hz digital notch filter. Limb position data were recorded using three 9-axis MPU-9150 inertial sensors (InvenSense, San Jose, CA) mounted on the upper back just below the cervicothoracic junction, on the upper arm, and on the forearm.

Features of the EMG signals were extracted with a 200 ms sliding window, computing a new feature vector every 50 ms. For each of the eight EMG signals, we extract the following feature sets: In our preliminary work [21], we found that FT of length 256 per EMG signal yielded good classification performance. FT magnitude sequences possess even symmetry across their half-lengths; therefore, the last 128 of these values are redundant for classification purposes and are discarded.

TD5: mean absolute value, waveform length, variance, slope sign change, and zero crossings [1]

TDAR: concatenation of TD5 with 6th order auto-regressive (AR) coefficients [28]

TDFT: concatenation of TD5 with discrete-time Fourier transform (FT) magnitudes [29]

When dealing with mixed feature types, some classification methods can benefit from feature scaling [30]. We used the feature-wise range information from the training set to perform min-max feature scaling [30] on the training data (new range: [0,1]). We then used these training data ranges to similarly scale all input test data (new range: [0−δ,1+δ]). Depending on the classifier, the effects on our data ranged from beneficial in nearly all cases to, at worst, no appreciable change. We, therefore, recommend feature scaling and present our results accordingly. The combined extraction time for all scaled features was 1.4 ms per window of 8-channel EMG.

3) Offline Classifier Comparison

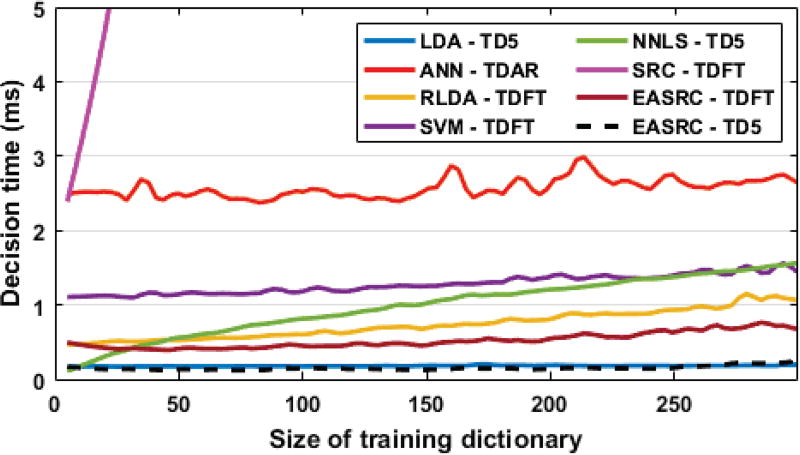
We compared EASRC, λ = 0.01, against the following classifiers: We chose this set of classifiers to emphasize those which either (a) are commonly used in myoelectric pattern recognition applications or (b) consistently performed well on our data. A computation time comparison (Fig. 4) shows that EASRC-TDFT requires about 0.7 ms to classify, and the fastest method was typically EASRC-TD5. In order to present fair one-to-one comparisons, each classifier’s parameters/kernels were adjusted to optimize overall performance. We excluded feature decomposition or principal component methods to avoid competing influences in our analyses. In offline cases, we computed performances from each pairing of classifier and feature set. We report and indicate only the best performing (lowest global error) classifier-feature pairs for the specified subject group. For example, when showing ANN-TDAR results, we imply that ANN-TD5 and ANN-TDFT performed worse for that group. We computed the following offline performance metrics in our analyses: global accuracy; global error; and the classwise averages for accuracy, precision, sensitivity, specificity, negative predictive value, and F₁ score [35].

LDA: Linear discriminant analysis [4]

ANN: Artificial neural network [31], 15 hidden layers

RLDA: Regularized LDA [32], with γ = 0.01

SVM: Support vector machine [33], gaussian radial basis function

NNLS: Non-negative least squares [34]

SRC: Sparse representation classification [19], with λ = 0.01

For classifier and feature combinations, we use the format LDA-TD5 to denote “LDA using the TD5 feature set.”

Fig. 4.

A speed comparison of classifiers using typical feature sets shows EASRC-TDFT is faster than most other methods, the fastest being EASRC-TD5 and LDA-TD5. The slow SRC decision time highlights the need for EASRC modification.

C. Online Limb Position Experiment

Three male able-bodied subjects, ages 23 to 37, participated in the online experiment. The preparation of the EMG sensors was identical to the offline preparation previously described. The online protocol generally involved prompting subjects to perform movement tasks at specific untrained arm endpoint locations within their reaching space. They used the MyoTrain virtual prosthesis environment (Infinite Biomedical Technologies, Baltimore, MD) to perform modified asymmetric target achievement control (TAC) tasks [36] in those positions (Fig. 5), wherein the subject attempted to drive an animated virtual hand from an initial posture to a target posture using real-time classifier output and visual feedback for control. We limited the classifiers in our online performance evaluation to establish a baseline comparison of EASRC against the commonly used LDA-TD5, as opposed to our exhaustive offline comparison. Virtual online experiments with able-bodied subjects are no substitute for more comprehensive, real-world functional assessments with amputee subjects using a prosthesis. Therefore, our objective is to determine if further explorations into comprehensive functional assessments are warranted.

Fig. 5.

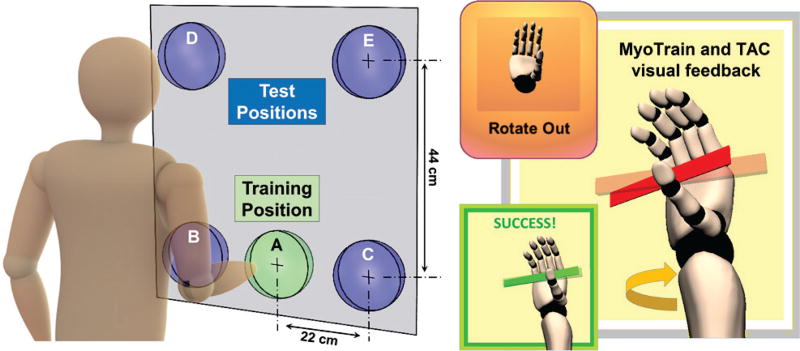
Asymmetric online limb position experiment. The subject trained in neutral arm position A, and then performed 3 target achievement control tasks (wrist supination task shown at right) with the MyoTrain interface in untrained position B. The subject then repeated these 3 tasks in untrained positions C,D,E to complete a single trial. For each target task, the subject attempted to activate a cued movement to drive an animated virtual hand’s real-time posture (solid red plane) to a given target posture (semitransparent red) and continuously dwell in the target for 1 s within a 15 s timeframe. Each trial was repeated 8 times, 4 each for LDA and EASRC in a random order unknown to the subject.

1) Real-time Classification Output

Each classifier was programmed to generate a real-time stream of predictions by performing feature extraction and classification every 8 ms from the most recent 200 ms window of incoming raw EMG. To temper some spurious classifications without forcefully manipulating the outputs, we applied a majority filter of length 3 on this prediction stream, resulting in a new decision every 24 ms. During the experiment, the MyoTrain environment accessed this prediction stream for sequential, constant-velocity virtual prosthesis control.

2) Online Protocol

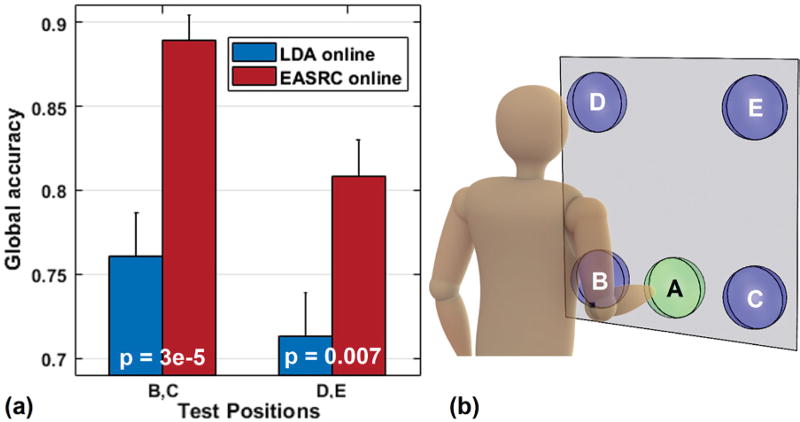
A planar surface showing circular target locations (A,B,C,D,E) was placed in front of the standing subject, parallel to his coronal plane, such that a neutral arm position (arm at side, elbow at 90°) with fingers extended was at the center of training target A, roughly 5 cm away from the surface. Testing targets B and C were located 22 cm to the left and right, respectively, of A. Testing targets D and E were located 44 cm directly above B and C, respectively. Each subject executed 3 repetitions of five movement classes (rest, hand open/close, wrist pronate/supinate) at limb position A to obtain the training dataset used throughout the remainder of the experiment. One of the two classifiers was then selected randomly, unknown to the subject, trained using his training data, and its real-time prediction stream was activated.

After this setup, the subject was instructed to reach to untrained limb position B without moving his legs or torso. While maintaining that limb position, the subject performed modified TAC tests using visual feedback from the MyoTrain virtual environment to perform 3 target hand posture tasks: hand 75% closed (HC), wrist pronated 67.5° from neutral (WP), and wrist supinated 67.5° from neutral (WS). The subject then repeated these 3 tasks in the remaining positions C,D,E. For clarity, the target postures correspond the positional orientations of the constant-velocity ( $\frac{\pi }{2}$ rad/s) virtual hand as opposed to proportional orientations based on muscle contraction level. During each target task, a visual cue indicated to the subject the appropriate movement class to complete the task (Fig. 5). All five trained movements were available to the subject during each task to correct for overshooting or, in the case of “rest,” to cease movement. To reduce fatigue, the subject chose when to initiate each task, which was triggered by the full opening the virtual hand from a neutral posture. Once initiated, a pair of indicator objects appeared superimposed on the virtual hand showing both the current hand/wrist posture (solid red) and the desired target posture (semitransparent red). The subject then attempted to match his virtual hand posture with the target posture as quickly as possible. For additional visual feedback, when the subject was able to dwell in the target posture for any amount of time, the two aligned indicator objects would appear as green. Successful target acquisition was defined as 1 s of continuous dwelling time at the target posture (±5%) within 15 s. The index of difficulty [37] for each task was 3.09.

We define a trial as the performance of the 3 target tasks in each of the untrained limb positions B,C,D,E using one classifier. Each subject completed 8 total trials, 4 for each classifier, in random order. The subjects were blind to which classifier they were using at all times during the experiment. The experiment required approximately 20 min to complete depending on a subject’s rest times and skill. We computed the following online performance metrics in our analyses: global accuracy, completion rate, completion time, overshoot, and throughput [36][37]. Performance evaluations for each task began at the moment of subject initiation.

D. Experiment Analysis and Evaluation

All classifications and analyses were performed using MATLAB 2016a (Mathworks, Natick, MA). Statistical p-values reported were calculated using two-sample t-test comparisons of EASRC-TDFT performance metrics against the other algorithm-feature combinations for the specified conditions and subject groups. Homotopy [23] was used to compute ℓ₁ solutions for SRC and EASRC. Error bars in all figures represent 1 standard error of the mean. Explanations of all performance evaluation metrics and their methods of computation can be found in the referenced literature. In all offline cases, the raw EMG training and testing data used to compare each classification method were identical.

III. Results

The objective of our limb position experiments is to quantify the robustness of EASRC in untrained limb positions. In general, EASRC yielded significant global accuracy improvement over other classification methods for all subject groups, across all offline and online conditions examined, and lower variation with respect to the training conditions.

A. Offline Limb Position Results

1) Train 1, Test 1

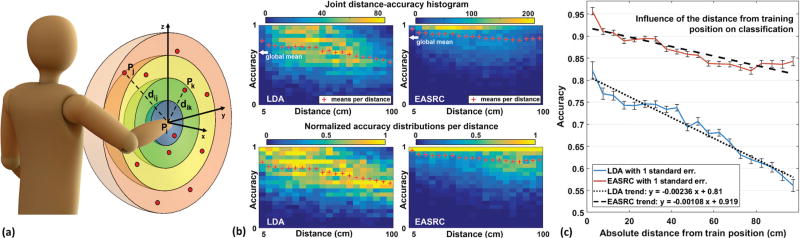
By choosing any 2 of the 81 trials at a time, one as training data and one as testing data, we used all possible such train-test set combinations to demonstrate how the distance from the training position affected the classifier performance of amputee subjects A1 and A2 wearing a prosthesis (Fig. 6). Disallowing the training and testing data to originate from the same position, there were 81 × 80=6480 (or 2862 for subject A2) such combinations per subject. As described in Fig. 6b, we use the combined data from both amputee subjects to map the accuracy distributions of EASRC-TDFT and LDA-TD5 for discrete train-test distance regions in 5 cm increments. We also plot the decay in mean accuracy as a function of train-test distance (Fig. 6c). EASRC was more resilient to per-distance decay than LDA, in particular, and its comparative advantage grew as such distance increased. To emphasize this point, we fit lines to each classifier’s performance decay and report that the per-distance decay rate of EASRC from our experiment was 54.2% less than the decay rate of LDA.

Fig. 6.

(a) For each of the 81 random positions P_i for subject A1 and 54 for subject A2 (subjects wearing prosthesis), we used data collected in P_i to train a classifier, and tested that classifier on data from each of the remaining 80 (or 53) untrained positions P_j≠i. There are 81 × 80=6480 (or 2862) “train 1, test 1” combinations per subject, and for each combination we computed euclidean train-test distance d_ij and accuracy a_ij. Discrete train-test distance regions or bins are illustrated as colored rings concentric to a given P_i. (b) By combining results from both amputee subjects, we obtain joint distance-accuracy histograms (LDA and EASRC shown) with bin sizes Δd=5 cm and Δa=0.05. The global and per-distance accuracy means are also shown. We divided each histogram column by its maximum frequency (bottom) to normalize the per-distance accuracy distributions. Normalization highlights the relative frequencies of accuracies at each distance without affecting their mean values. Regardless of distance, the most frequently occurring accuracies for EASRC were in the interval [0.95,1]. (c) Plot of per-distance means, or accuracy as a function of train-test distance for the two amputee subjects wearing a prosthesis. Using least-squares linear regression to fit our data, we show that the per-distance decay rate of EASRC was less than half that of LDA.

2) Train k, Test All Others

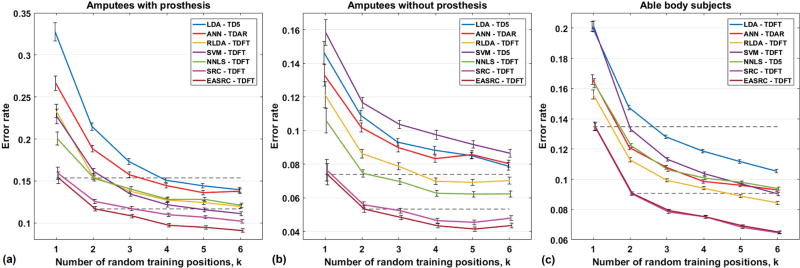
To show the effect that training in multiple random positions has on classifier performance, we regulated the number of positions used for the training data, and tested the classifiers in all other untrained positions (Fig. 7). A desired quantity k ∈ {1,2, …, 6} positions were randomly selected from all 81 (or 54 for subject A2) and used for training, and then tested on data from the remaining untrained 81-k positions (54-k for A2). For k > 1 this process was repeated for 200 random k-of-81 (k-of-54 for A2) position combinations to obtain aggregate results within each subject group. For k = 1 there were 81 (54 for A2) such combinations. Across all subject groups, for all k, EASRC yielded significantly lower global errors (p < 0.001) than all other non-SRC methods tested. In most cases, EASRC performed better when trained in only 2 random positions than other methods trained in up to 6 positions (Table I).

Fig. 7.

Classifier comparison from our offline limb-position experiment for (a) amputee subjects A1 and A2 wearing prostheses, (b) amputees A1 and A2 with no prosthesis load, and (c) eight able-bodied subjects. Random combinations of k positions were used for training and the classifiers were tested in the untrained 81 – k positions (54 – k for subject A2). At no point were the limb positions used for training the same as those used for testing. For all k, EASRC significantly (p < 0.001) outperformed other non-SRC classifiers in untrained positions, and EASRC required fewer training positions to achieve superior performance (Table I). The two dashed lines in each plot are visual aids for comparing EASRC, k ∈ {1,2}, with other classifiers where k ≥ 2. For all subject groups, EASRC achieved better performance after training in just 2 random positions than most of the other methods after training in up to 6.

TABLE I.

Classifier comparisons with two EASRC train positions ^†

Group	Method	k = 3	k = 4	k = 5	k = 6
A1,2††	LDA	p < 0.001	p < 0.001	p < 0.001	p < 0.001
	ANN	p < 0.001	p < 0.001	p < 0.001	p < 0.001
	RLDA	p < 0.01	p < 0.05	p = 0.12	p = 0.55
	SVM	p < 0.01	p = 0.31	–	–
	NNLS	p < 0.01	p < 0.05	p < 0.05	p = 0.37

^†k_EASRC = 2 < k_Method.

^††A1 and A2 wearing prosthesis.

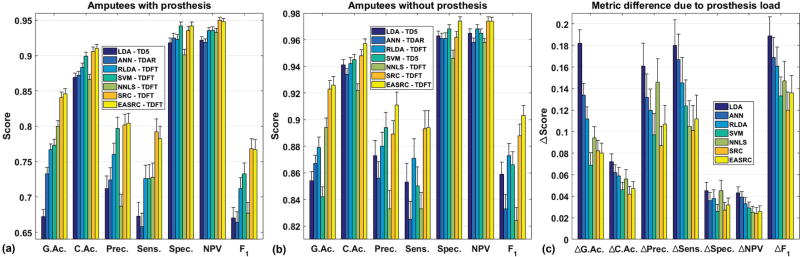
EASRC was among the top scorers for many additional classification performance metrics [35] across all subject groups (amputee data shown in Fig. 8). Furthermore, by subtracting the performance metrics of subjects A1 and A2 wearing a prosthesis (Fig. 8a) from A1 and A2 under no load (Fig. 8b), we observe that SRC and EASRC were among the least affected by the presence of the prosthesis load (Fig. 8c). We emphasize that the non-SRC classifiers possessing similar resilience to the prosthesis load performed significantly worse in terms of global error.

Fig. 8.

Across all subject groups in the “train 1, test all others” scenario (able-bodied results not shown), SRC and EASRC were among the top scorers in every offline performance metric [35], typically achieving the two best. The abbreviated metrics on each horizontal axis are (from left to right) global accuracy, and classwise averages for accuracy, precision, sensitivity, specificity, negative predictive value, and F₁ score. Subjects A1 and A2 performed the experiment both (a) with prosthesis attached and (b) without prosthesis load. (c) By subtracting score distributions (ΔScore) from the two load condition groups (a and b), we can observe the influence of the prosthesis load on classification performance. For simplicity, we treat these distributions as Gaussian and represent each resulting difference distribution as having mean μ_Δ = μ_b − μ_a and variance ${\mathrm{\sigma }}_{\mathrm{\Delta }}^2={\mathrm{\sigma }}_a^2+{\mathrm{\sigma }}_b^2$. The lower ΔScores of EASRC, SRC, and SVM show they were among the least affected by the presence of a prosthesis load.

B. Online Limb Position Results

In the online context of performing target achievement in untrained limb positions, EASRC had significantly higher global accuracies than LDA in the overall sense (p < 0.001). By further refining these results into two groups (B,C and D,E) based on train-to-test distance (Fig. 9), we likewise observe that global accuracy was significantly higher using EASRC: p < 0.001 in positions B,C and p < 0.01 in D,E. Additional performance metrics and statistical comparisons for the classifiers are shown in Table II. When using EASRC for online control, all subjects fully completed every target task, in all positions, within each 15 s time limit. In contrast, when using LDA, failures did occur, particularly when attempting the hand close posture in positions D,E. On average, the subjects using EASRC performed each task faster, with less overshoot, and greater throughput than when using LDA. Across all evaluation criterion measured, we report better performance from EASRC significant within p < 0.05.

Fig. 9.

(a) Online classifier accuracy in untrained limb positions, and (b) position reference illustration. Able-bodied EASRC users performed significantly better at task completion in untrained limb positions (Table II).

TABLE II.

Online classifier comparisons for 3 able-bodied subjects

Test positions	Method	GA*	CR	CT (s)	OS	TP
B,C,D,E	LDA	0.746	0.937	4.36	0.853	1.069
	EASRC	0.849	1.000	3.22	0.458	1.161
	p <	0.001	0.01	0.001	0.01	0.05

^*GA: global accuracy, CR: completion rate, CT: completion time OS: overshoot, TP: throughput [36][37]

IV. Discussion

One of the biggest clinical hurdles with respect to adoption of current myoelectric control paradigms and training procedures is the need to train in many conditions to ensure that the training data captures as much conditional information as possible. However, such extensive, often daily, training does not ensure faithful classification performance and is burdensome for amputees. Much of the related EMG pattern recognition literature has focused on the testing of various classifier control strategies under the same conditions that were used during classifier training, typically in a static and neutral arm position. In this symmetric context, many strategies can generate high accuracies with a large number of movement classes, but there is a well-documented disparity between those outcomes and actual real-world performance [6][7]. With only five basic movement classes, asymmetric testing in untrained positions is generally very disruptive to the performance of commonly-used classifiers such as ANN, LDA, and SVM. Therefore, the focus of this work is to establish a classification strategy which is less vulnerable to untrained conditions to promote minimal user training and increase myoelectric prosthesis adoption.

By examining the adverse effect of untrained limb positions on EMG prosthesis control in both offline and online contexts, we show that EASRC is significantly more robust to this effect than other commonly used classification methods. When training in a single position and testing in another, our offline analysis (Fig. 6) shows that EASRC is less vulnerable than LDA to a decay in decoding performance as the person moves away from the initial training position. To our knowledge, this is the first such mapping of this decaying effect for amputee subjects wearing prostheses. Our offline results are reinforced by our online results (Table II), which show that subjects using EASRC performed significantly better regardless of evaluation metric over the conventional LDA algorithm in untrained positions. These offline and online results generally show that EASRC provides greater high-performance coverage throughout a user’s reaching space.

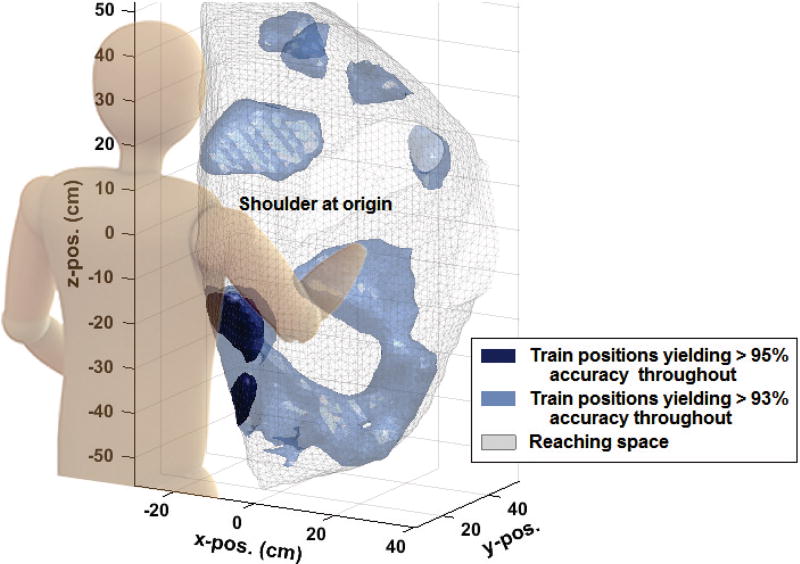
In our previous work [13], we showed that an LDA classifier required training data from at least 5 random positions to create stable decoding performance across the reaching space. Herein, we found that, across all subject groups, the EASRC classifier trained in 2 random positions significantly outperformed other classifiers trained in 6 positions (Table I). These results imply users may not need to train in as many positions to retain stable, high performance, thereby reducing the burden of long classifier training sessions. Furthermore, we show (Fig. 10) how user-specific high-yield training positions can be localized. If it is determined that such regions persist across time, an amputee could target these specific locations to reduce their daily training regimen.

Fig. 10.

Using “train 1, test all others” analysis for amputee A1 wearing a prosthesis, it is possible to construct a training position-dependent mapping of the average testing accuracies resulting from each training position. This mapping allows the localization of subject-dependent regions for optimal training. The darkest blue areas represent A1’s training regions which yielded >95% average accuracy throughout the other 80 untrained positions.

There is a notable performance reduction for amputee subjects when wearing their prostheses as opposed to bearing no prosthesis load. Causal factors which could contribute to this reduction include changes in the supporting muscle contributions required to achieve different limb positions and/or changes in skin-electrode contact. Despite these root causes, we show that EASRC, SRC, and SVM are less sensitive to the prosthesis load than other classifiers. When the subjects are wearing their prosthesis, the offline performance error of EASRC is significantly less than the other non-SRC classifiers we tested. We have begun investigations isolating untrained loads and electrode-shifts, and have observed that sparse representation classifiers also appear to be more robust to these conditional effects than other methods for able-bodied and amputee subjects. Given the inherent noise-tolerant properties of SRC and EASRC, such an outcome would not be surprising.

Our results show promise for the online use of EASRC, and justify its further exploration to discover how well it will aid amputees in performing real-world functional assessment tasks using their prostheses. At present, we have integrated EASRC and related methods into a real-time embedded prosthesis controller. We are experimenting with these methods in a variety of functional assessment protocols using commercially available myoelectric prostheses. Going forward, we will report on any modifications that we incorporate into our approach as we continue to pursue an optimal solution for condition-tolerant myoelectric prosthesis control.

V. Conclusions

Our suggested EASRC approach is a limb position tolerant paradigm for myoelectric control that significantly outperforms other movement classification methods in both offline and online contexts of untrained upper-limb positions. EASRC also requires fewer training positions than these other methods to achieve better performance, which, in a practical sense, means that our findings could lead to significant reductions in overall patient training times. We have demonstrated additional tolerance to the prosthesis load itself, and can begin to assert that EASRC is likely more robust across a variety of real-world condition spaces. Therefore, we expect our approach to continue to achieve high performance when applied to the unpredictable conditions a person encounters during online myoelectric prosthesis use. Our findings have the potential to deliver real-world clinical benefits to amputees by greatly enhancing the utility and reliability of EMG prosthesis control in performing activities of daily living.