Abstract
Objective
Several studies have suggested that cancer is associated with a reduced risk of the development of Alzheimer’s disease (AD). This study seeks to improve our understanding of the association between cancer and the development of AD by showing how mortality selection alters this relationship.
Method
A retrospective cohort study was carried out examining 92,425 individuals (47,873 women and 44,552 men) from the Utah Population Database with and without a history of any primary cancer identified by the Utah Cancer Registry. All individuals were aged 65–79 years and free of dementia in 1992 and followed for upwards of 18 years (1992–2009) for AD ascertainment, which was identified using diagnostic information from Medicare claims data.
Results
We replicate previous results suggesting that cancer is associated with reduced risk of subsequent AD under specific statistical model specifications. However, these results should not be interpreted as evidence of an etiological association. We conclude that higher rates of overall mortality among individuals with cancer relative to those without cancer induce the widely reported putative protective association with cancer.
Conclusion
Careful consideration of model specification and the profound effects of mortality selection in the older adult population is essential when investigating the relationship between aging-related diseases such as cancer and AD. We show that cancer does not provide protection from AD as previously described in the literature. Social scientists seeking to understand social disparities in disease outcomes among older adults may therefore want to strongly consider the role of mortality selection which, if uncorrected, may generate biased associations.
Keywords: Alzheimer’s disease, Competing risks, Dementia, Mortality selection
Geriatric researchers studying age-related health and mortality often confront the problem of competing risks. It is common for investigators to study diseases in an aging population by focusing on a single disease outcome while ignoring the complexity of comorbid conditions and the competing risk of death associated with aging. Broadening our focus to study the interrelationship between common complex diseases may provide important insights into the etiological processes of disease. Investigating how one disease relates to other diseases, as part of a biologic system or through shared social determinants, will contribute to our understanding of aging and longevity. Social scientists seeking greater understanding of the socioenvironmental mechanisms associated with disease risk among the older adult population have taken careful consideration of validity threats such as residual confounding and endogeneity problems (Austin, Lee, & Fine, 2016; Berry, Ngo, Samelson, & Kiel, 2010; de Glas et al., 2016). We argue in this analysis the need to further emphasize the importance of competing risks for investigations focused on survival and duration-related outcomes among older individuals.
A possible link between two such aging-related diseases, Alzheimer’s disease (AD) and cancer, has recently piqued the interest of the public, clinicians, and the research community (Demetrius & Simon, 2013; Driver, 2014; Plun-Favreau, Lewis, Hardy, Martins, & Wood, 2010; Tabares-Seisdedos & Rubenstein, 2013). Cancer and AD are both multifactorial diseases that are found to be affected by fundamental psychosocial factors such as educational attainment, socioeconomic status, social networks, and health behaviors (Clegg et al., 2009; Fratiglioni, Paillard-Borg, & Winblad, 2004; Fratiglioni, Wang, Ericsson, Maytan, & Winblad, 2000; Reiche, Nunes, & Morimoto, 2004). These findings would therefore lead investigators to conclude that these psychosocial risk factors lead to increased risk of both diseases. However, several epidemiological studies have examined the association between cancer and AD and have concluded that there may be an inverse association between these two diseases—specifically, that a cancer diagnosis reduces the risk of subsequent AD (Driver et al., 2012; Frain et al., 2013; Musicco et al., 2013; Roe, Behrens, Xiong, Miller, & Morris, 2005; Roe et al., 2010; White, Lipton, Hall, & Steinerman, 2013). The authors of these studies and subsequent reviews have suggested a possible biological mechanism underpinning both diseases that leads to two opposite cellular functions—cellular proliferation (predisposing to cancer) or cellular apoptosis (predisposing to AD) (Behrens, Lendon, & Roe, 2009; Driver, 2014; Tabares-Seisdedos & Rubenstein, 2013).
However, any analysis of an association between two morbid medical conditions in an elderly population must introduce aggressive controls to assess the effects of competing risks. In the case of cancer incidence altering the risk of dementia, it is plausible that dementia risks are low for those diagnosed with cancer because their mortality rates are higher than those of unaffected controls and hence have less opportunity to develop dementia. This article will examine this problem specifically through the use of competing risks with dependent and independent hazards and cumulative incidence curves.
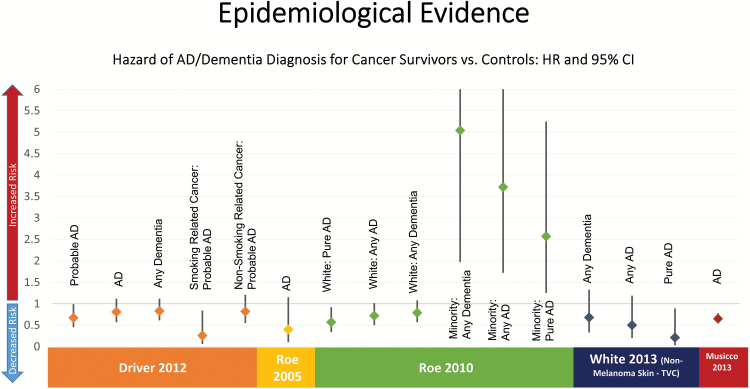
The epidemiologic literature to support an inverse association is not as straightforward as it may seem (Bennett & Leurgans, 2010). These studies are limited by relatively short follow-up periods (Frain et al., 2013; Musicco et al., 2013; Roe et al., 2005, 2010; White et al., 2013), small sample sizes (Driver et al., 2012; Roe et al., 2005, 2010; White et al., 2013), reliance primarily upon prescription data for AD diagnoses (Musicco et al., 2013), and in one case a predominantly (98%) male patient population (Frain et al., 2013). Figure 1 displays the hazard rate ratios (HRs) and 95% confidence intervals (CIs) for the five published studies examining this association. In addition, choice of statistical model and study design issues raise questions about the validity of the results. For example, in the article published by Driver and colleagues (2012), cancer diagnosis is treated as a time-independent covariate (i.e., ever/never), with all individuals with a cancer diagnosis at any time counted in the exposure category for the entire period of follow-up (Driver et al., 2012). When cancer is measured this way, it is unclear which diagnosis occurred first, the cancer or the AD. Individuals with cancer diagnosed after a dementia diagnosis will be incorrectly counted as exposed to cancer, even though the dementia diagnosis preceded the cancer diagnosis (i.e., the event sequence is reversed). The time-varying nature of cancer diagnosis can be corrected through the sample selection process (i.e., individuals with dementia prior to cancer diagnosis are excluded from the sample) or by ignoring cancer diagnoses that occur after baseline (Roe et al., 2005, 2010), although this latter strategy will bias the sample.
Figure 1.
Summary of previous findings showing a protective relationship between cancer and Alzheimer’s disease.
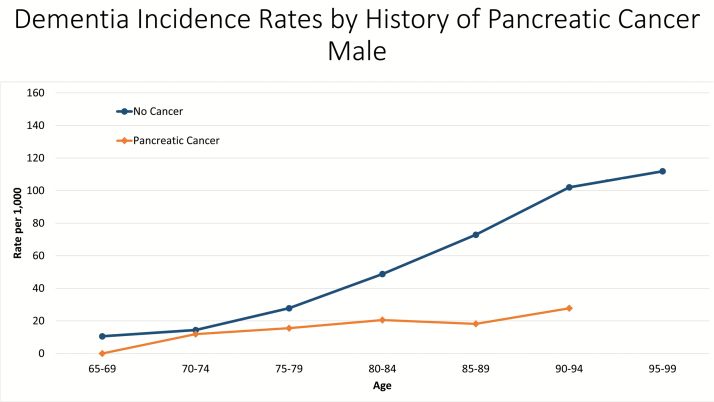
Musicco and colleagues (2013) use a population-based sample from Italy to assess the relationship between cancer and AD. AD diagnosis was inferred by prescriptions. They stratify the sample in several ways in an attempt to account for bias. They find a strong protective effect of cancer on subsequent AD diagnosis (HR = 0.65; 95% CI = 0.56–0.76), and this rate does not significantly differ between survivors and nonsurvivors. However, they are only able to follow the cohort for a 5-year period, which may decrease the probability of having multiple disease state transitions—particularly because AD diagnoses after cancer may be regarded as treatment-related dementia and remain undiagnosed for a longer period of time. In addition, they find no difference in AD risk between breast, lung, bladder, and prostate cancer patients and the general population, which suggests that the underlying link between the two diseases may not be biological. Diagnosis of age-related diseases, such as AD, is dependent upon an individual surviving to an age where the onset of disease can occur. The average age of onset for AD is 72.8 years (Li et al., 2002). If we select a cancer site with a particularly dismal survival rate, such as pancreatic cancer, we see large differences in dementia rates between cancer survivors and cancer-free individuals (Figure 2). Pancreatic cancer deaths are the highest among people aged 75–84 years, with the median age at death being 73 years and a 5-year survival rate of 7.2% (“SEER Stat Fact Sheets: Pancreas Cancer,” 2015). This strongly suggests that pancreatic cancer patients do not live long enough for a subsequent incidence case of AD to occur. Under this formulation, the observed association between cancer and dementia would be due to mortality selection, but not etiologic. Failing to account for the increased rates of mortality in cancer survivors (i.e., mortality selection) as a significant contributor to the protective effect of cancer on incidence dementia can lead to incorrect conclusions about the nature of this relationship.
Figure 2.
Dementia incidence rates by history of pancreatic cancer in Utah. Source: Utah Population Database.
In addition to modeling choice mortality selection, information on health behaviors and sociodemographic variables related to cancer and AD should be considered. Cancer and AD are both complex diseases, linked by underlying social determinants of health that arguably increased the risk for both diseases as well as mortality. Smoking and obesity are risk factors for both cancer and AD (Anstey, von Sanden, Salim, & O’Kearney, 2007; De Pergola & Silvestris, 2013; Ott et al., 1998; Rusanen, Kivipelto, Quesenberry, Zhou, & Whitmer, 2011; US Department of Health and Human Services, 2014). Active affiliation with the Church of Jesus Christ of Latter-day Saints (LDS or Mormon) church is associated with increased life expectancy (Enstrom & Breslow, 2008), decreased cancer risk (Lyon, Gardner, & Gress, 1994; Merrill & Lyon, 2005), and decreased risk of dementia (Norton et al., 2012). Individuals actively affiliated with the LDS church are more likely to abstain from alcohol and tobacco use, fast once a month, and participate in church-related social activities (Mineau, Smith, & Bean, 2002). Parity is associated with cancer risk and risk for dementia (Beeri et al., 2009; Key, Verkasalo, & Banks, 2001), particularly for women. Socioeconomic status is also associated with cancer and dementia risk (Evans et al., 1997; Ward et al., 2004). Understanding the role of social determinants in the interplay between cancer and AD is essential to understanding health inequalities and identifying subpopulations that are at increased risk for disease.
A fundamental question remains: Is there a causal association between the two diseases (etiological) or is the observed effect related to the excess risk of mortality in individuals with cancer (mortality selection) (Koller, Raatz, Steyerberg, & Wolbers, 2012)? This study seeks to improve our understanding of the association between cancer and the development of AD by showing how model specifications affect the interpretation of results.
Method
The Utah Population Database (UPDB) is a premiere and unparalleled database mandated to support biomedical research. It provides in-depth demographic and genealogical information on the majority of the historical and current population of Utah (for more details see http://www.hci.utah.edu/groups/ppr). Due to longstanding and ongoing efforts to add new sources of data and update records as they become available, the full UPDB contains data on more than 8 million individuals (e.g., including all state-wide death certificate records [1904 to the present], all Medicare claims [1992–2009], and the Utah Cancer Registry, an NCI Surveillance, Epidemiology, and End Results [SEER] Program member). The infrastructure developed by the UPDB enables the linkage of distinct records for a specific person, which creates a portrayal of the life history of an individual based on these (and other) medical and administrative data.
The sample inclusion criteria for this study is outlined in Supplementary Figure 1. First, Medicare-eligible individuals not enrolled in a managed care organization (MCO) and linked to the UPDB were eligible for sample selection (N = 217,476). Those in an MCO will not have medical care episodes visible in the Medicare data; their exclusion accounts for 29%.
Incidence dates per se are not available in the Medicare claims data. To identify highly probable incident cases, we imposed a 2-year blackout period after 1992 (i.e., baseline) to exclude prevalent AD diagnoses. During this blackout period, individuals with an AD diagnosis during the first 2 years (1992 or 1993) were excluded from the sample because we considered them to be a prevalent case and any AD diagnosis after that time was assumed to be an incident case. All individuals with a dementia diagnosis (see Supplementary Table 1 for a list of ICD-9 codes) or death within 2 years of enrollment were excluded from the analyses (n = 18,403). For the purposes of these analyses, we also excluded individuals older than 80 years at baseline and individuals aging into the program or enrolling after 1992 (n = 106,648). These restrictions provided us with a final sample of 92,425 Medicare enrollees aged 65–79 years in 1992.
This study was approved by the Institutional Review Boards of the University of Utah and by the Utah Resource for Genetic and Epidemiologic Research (www.research.utah.edu/rge/), an administrative board that oversees access to the UPDB (IRB_00043524).
Identification of Cancer Cases
The Utah Cancer Registry (UCR) is a population-based registry and an original member of the SEER program that has collected all incident primary cancer diagnoses in the state of Utah since 1966. Incident cases of cancer were identified among Utah residents based on systematic and routine review of medical records, pathology reports, radiation therapy records, hospital discharge lists, and vital records. Primary cancer cases were coded using the World Health Organization international classification of disease (ICD-O). Non-malignant neoplasms and nonmelanoma skin cancers are not included in this analysis. UCR data are linked to the UPDB, which holds the Medicare data from 1992 to 2009.
Identification of AD
Two sources of data linked to the UPDB allow for the identification of individuals with AD. Medicare records from 1992 to 2009 were used to identify incident AD cases. Cause of death information from Utah Death Certificates was also used as a source of AD ascertainment. International Classification of Disease Codes (ICD-9) code 331.0 was used to identify AD cases. To minimize the rate of false positives, two or more AD diagnosis codes during the follow-up period or a single diagnosis during the year of death were required to classify an individual as having AD. Time to AD onset was defined as the month during which an individual first received their diagnosis.
Covariates
Personal information on smoking history, obesity, religious status, and parity were collected at baseline. Previous studies have shown that ICD-9 tobacco use codes (305.1 and V15.82) can be used effectively to identify smoking status (Wiley, Shah, Xu, & Bush, 2013), and any smoking-related ICD-9 code during the blackout period was coded as having smoked at baseline. Similarly, individuals with ICD-9 code 278.0 during the blackout period were coded as being obese at baseline. The UPDB contains information on baptism and endowment dates from family history records, and these were used to classify individuals as active followers, inactive, or nonmembers of the LDS religion. Individuals with an endowment date have pledged to live their lives following the doctrine of the LDS church and were considered active church followers if endowed before age 40. Individuals with a baptism date but no endowment date were considered inactive, and individuals with no baptism or endowment date were considered nonmembers of the LDS church (reference category). Parity was derived from a combination of sources collected from genealogical records obtained from the Genealogical Society of Utah and linked birth certificate records, including birth certificate data from 1915 to 1921 and 1936 to the present. All eligible women in the sample completed their fertility by definition because they were required to survive to at least age 65 to be visible in the Medicare data.
Dual-eligible Medicare beneficiaries are also covered by Medicaid services. These individuals must meet certain income and resource requirements to become eligible for dual enrollment, and eligibility is subject to change every year. We used dual-eligibility status during the previous year as a proxy for later life socioeconomic circumstances and treated it as a time-varying covariate.
Area-level demographics were also included in all models to control for additional indicators of socioeconomic status (SES) and access to care (Evans et al., 1997). Information about an individual’s county of residence in 1992, based on Centers for Medicare and Medicaid Services residential data, was derived from the 1990U.S. Census. Total population and median family income at the county level were included as covariates in the final models.
Statistical Analyses
Cox regression methods were used to assess the relationship between cancer diagnosis and dementia or AD onset. Individuals were followed up to 18 years from baseline to the development of dementia or death. Because we excluded individuals enrolled in a managed care plan during any period of a given year, our only sources of censorship were death and the end of the follow-up period, 2009. Given the cohort differences in mortality and quickly changing morbidity risks by age and sex, we conducted all analyses by sex and three 5-year age categories (65–69, 70–74, and 75–79 years). Age was measured in 1992, the first year in which UPDB has been linked to Medicare data. Separating samples by age categories effectively held 5-year cohort effects constant and allowed us to analyze the trends by birth cohort for an 18-year period. In addition, we aggressively controlled for birth year within age groups by stratifying analyses by birth year. Stratification by birth year within the Cox model allowed the unspecified hazard function to vary by birth year.
We carried out several analyses to show that the relationship between cancer and AD was sensitive to model choice and was affected by the competing risk of mortality. Supplementary Figure 2 shows a diagram of statistical models considered for the analyses. Models 1–3 are cause-specific models that censor individuals experiencing the competing event, death, at the point of occurrence, the classic approach that assumes independence of death and AD risk. Model 1 treats cancer as a time-independent covariate, with all individuals with a cancer diagnosis pre- or post-1992 contributing person years to the cancer group only. In Model 2, an extension of the Cox proportional hazards (PH) model was used to model cancer diagnosis as a time-varying covariate where individuals with a prevalent cancer diagnosis (in 1992) contributed to person years in the cancer group. Individuals with no cancer diagnosis at baseline contributed person years to the noncancer group until diagnosis of an incident cancer, after which they contributed person years to the cancer group. Model 3 is nested within Model 2 and further considers the effect of time since diagnosis on the risk of AD. In this model, separate indicator variables were added to the model for prevalent cancer diagnoses 0–4 years prior to baseline, 5–9 years prior to baseline, and 10 or more years prior to baseline. Cancer diagnosis after baseline was continued to be treated as a time-varying covariate.
The standard Cox PH model assumes that censoring is uninformative (i.e., the censoring event death is unrelated to the event in question, incident AD), an assumption widely adopted but infrequently examined; however, death is an important competing event for this population that may preclude observing future diagnoses of AD. Competing risk models can be used to adjust the hazard ratios for the competing risk of mortality and rely on a standard modification to the PH model. Two formulations of competing risk models were used to further elucidate the mortality selection versus etiological nature of the association between cancer and AD: Fine and Gray (FG) and Kalbfleisch and Prentice (KP).
The FG regression approach (Model 4) is used to estimate the effect of cancer diagnosis on the subdistribution hazard of specific causes of failure (Jason & Gray, 1999), a common method for competing risk analyses. This model calculates the absolute risk of AD by allowing individuals experiencing the competing risk of death to contribute person years after the time of death. With the FG method, absolute risk simply means that the calculation of hazard rates for a given exposure group relies on a denominator fixed in size at the start of the follow-up period that never changes despite depletions due to death. This is different from the standard cause-specific relative hazard from Models 1–3, where individuals who have experienced the competing event are removed from the risk set. The results from the FG method should not be interpreted necessarily as etiological in nature, but rather as a function of the absolute risk of AD in cancer patients.
We consider the event of interest (AD) and the competing risk of death. In this model, the cumulative incidence function is defined as the joint probability that an individual is diagnosed with AD given that the individual has survived to time t without an event or has died prior to time t. The subdistribution hazard can be defined as follows:
where “*” indicates an improper (the subdensity function integrates to <1), T = min(TAD, TDeath, or censoring time), j is an index for event type (in our case AD or death), is the subdistribution cumulative incidence, is the subsurvivor function, and is the subdensity function. The proportional subdistribution hazards model is as follows:
where λ0j is the unspecified baseline subdistribution hazard, φj is the corresponding regression coefficient, and exp(φj) is the relative change in the subdistribution hazard for a 1-unit increase in the corresponding covariate.
The relationship between the cause-specific relative hazard (csHRj = 1) and the subdistribution relative hazard (sdHRj = 1) is a function of the cause-specific relative hazard of death (csHRj = 2; the competing event), the unspecified baseline cause-specific hazard for AD and death (h01(t) and h02(t)), and time (refer to the appendix in Lau, Cole, & Gange (2009) and Beyersmann & Schumacher (2008)):
where is the subdistribution cumulative incidence of death for individuals with cancer and is the subdistribution cumulative incidence of death in individuals without cancer.
Therefore, when the cause-specific relative hazard of death (the competing event) between those with cancer and those without cancer is not equal to 1, the risk sets for AD are modified differentially. Therefore, the proportion of individuals with AD will be different by cancer status if mortality differs between groups even if the rates are the same. This is a crucial point to consider when interpreting the results from this model because if individuals in the cancer or noncancer group have higher mortality than those in the other group (mortality varies by exposure group), the risk set will be artificially inflated in this group with higher mortality and the subdistribution hazard will be lower by definition.
One alternate method for accounting for the competing risk of mortality while still investigating the etiological association between cancer and AD is the KP method (2002; chapter 8.2.5) presented in Model 5. This method uses internal time-varying covariates that are strong indicators of the competing event (death), which can be measured regularly throughout the follow-up period. We used a modified version of the Charlson Comorbidity Index (CCI) (Charlson, Pompei, Ales, & MacKenzie, 1987; Klabunde, Potosky, Legler, & Warren, 2000), where higher scores are associated with an increased risk of death. Because both cancer and dementia are normally included in the CCI calculation, a variant of the CCI (based on the SEER-Medicare comorbidity SAS (Klabunde et al., 2000; Klabunde, Warren, & Legler, 2002) macros) was created with cancer and dementia removed from the score. A list of conditions included in the CCI can be found in Supplementary Table 2. CCI scores were calculated on an annual basis, lagged by a single year, and included in Model 5 as a time-varying covariate. A significant association between the CCI score and the outcome of AD will provide evidence consistent with nonindependence between the two competing events. This method relies on wisely selecting the measure that can serve as a proxy for the competing event; we consider CCI to be an excellent candidate.
Model 6 is an extension of Model 5 and tests for site-specific associations between cancer and later life AD risk. This model is used to illustrate the mortality selection effect between cancer and AD in a cancer with a late age at onset, prostate (men only) cancer. We also compare the effects of localized and regional/metastatic stage at diagnosis, which have lower 5-year survival rates relative to localized. These models include a lagged time-dependent measure of CCI, familial excess longevity (FEL), Medicare–Medicaid dual eligibility, smoking history at baseline, obesity at baseline, neighborhood measures for population and income, LDS status, and parity.
In addition to including a time-varying measure of the propensity of death, we used a time-independent measure of genetic proclivity for longevity. FEL was developed using the in-depth genealogical data in the UPDB (Kerber, O’Brien, Smith, & Cawthon, 2001) to represent familial predisposition. We have used this measure in multiple studies and have previously demonstrated its robustness as a predictor of increased life span (O’Brien et al., 2007; Smith, Hanson, Norton, Hollingshaus, & Mineau, 2014; Smith, Mineau, Garibotti, & Kerber, 2009). A more complete description can be found in the Supplementary Appendix. We also controlled for Medicare–Medicaid dual eligibility, smoking history at baseline, obesity, neighborhood measures for population and income, LDS status, and parity.
Results
The age- and sex-specific means of all key variables are displayed in Supplementary Table 3. Most cancer incidence cases occur after the time of enrollment for the individuals aged 65–69 years, with 69% being women and 77% being men. There is a similar pattern for individuals aged 70–74 and 75–79 years, however as expected, due to the age distribution of cancer diagnoses, the proportion of cancers diagnosed after baseline decreases with each age group. For example, 64% of the cancer diagnoses for women aged 70–74 years occur after baseline, and this number decreases to 57% for women aged 75–79 years. The most common sites for women and men are breast and prostate, respectively. Our sample is predominately non-Hispanic white and LDS, with younger cohorts being slightly more heterogeneous, which is consistent with the demography of Utah. Younger men had the highest percentage of ever smokers, and we observed the expected decline in percentage of ever smokers with older cohorts and lower rates in women with respect to men. Women were nearly twice as likely as men to be obese at baseline, and the proportion of obese individuals in the sample decreases with age. Dual Medicaid–Medicare enrollment and CCI scores increase over time and with age. A measure of FEL was available for more than half of our sample, and area-level census data were available for more than 99% of individuals.
The absolute risk of cancer by sex and age group is displayed in Table 1. Absolute risk is calculated using two different ways to compute the denominator. First, denominators were calculated by classifying individuals as cancer survivor or cancer free and then counting the total number of person years. In the second version, the time-varying nature of the denominator was accounted for by forcing the individual to change risk set after a cancer diagnosis. AD rates are higher for the noncancer group when cancer status is treated as time invariant but are lower when it is allowed to vary over time.
Table 1.
Absolute Risk of Alzheimer’s Disease (AD) by Sex and Age Group
| AD diagnosis | Ever/never had a cancer diagnosis | Time-varying classification of cancer status | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Person years | Rate per 1,000 | Person years | Rate per 1,000 | |||||||
| Cancer diagnosis | ||||||||||
| Female | No | Yes | No | Yes | No | Yes | No | Yes | No | Yes |
| Age 65–69 | 1,512 | 334 | 161,702 | 50,849 | 9.4 | 6.6 | 182,488 | 30,063 | 8.3 | 11.1 |
| Age 70–74 | 2,581 | 569 | 171,332 | 53,410 | 15.1 | 10.7 | 194,056 | 33,957 | 13.3 | 16.8 |
| Age 75–79 | 2,234 | 445 | 121,245 | 34,570 | 18.4 | 12.9 | 134,332 | 21,483 | 16.6 | 20.7 |
| Male | ||||||||||
| Age 65–69 | 1,077 | 349 | 136,019 | 59,968 | 7.9 | 5.8 | 162,030 | 33,957 | 6.6 | 10.3 |
| Age 70–74 | 1,627 | 510 | 134,400 | 60,589 | 12.1 | 8.4 | 160,651 | 34,338 | 10.1 | 14.9 |
| Age 75–79 | 1,457 | 423 | 82,011 | 36,768 | 17.8 | 11.5 | 95,315 | 23,464 | 15.3 | 18.0 |
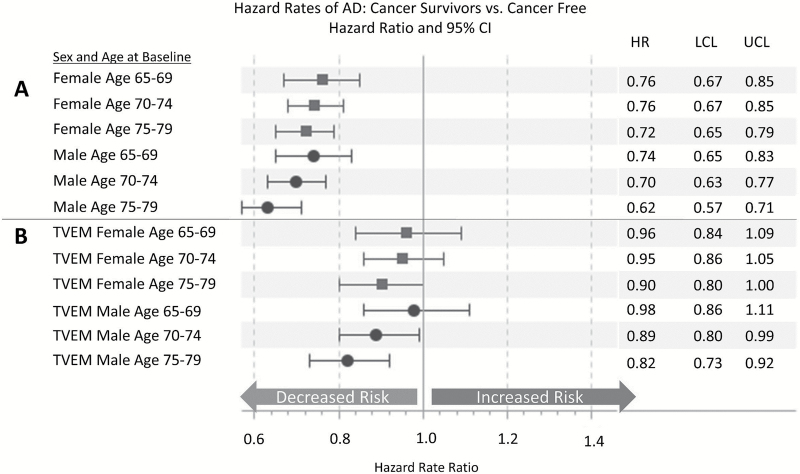
Figure 3 shows the relationship between cancer and later life AD when cancer is modeled as a time-invariant predictor (Figure 3A; Model 1) and time-varying predictor (Figure 3B; Model 2). Sex-specific models are estimated and stratified by birth year. As reported in other published studies, we find a significant protective effect of cancer on the risk of incident AD for men and women of all ages in Model 1. However, we show that when cancer is modeled as a time-varying covariate (Model 2), there is no significant protective association between cancer and AD with the exception of men aged 70–79 years at baseline (HR = 0.82; 95% CI = 0.73–0.92). The change in the magnitude and the precision of the estimate is related to the manner in which individuals at risk of AD are counted. In the time-invariant model, individuals with a cancer diagnosis after baseline are incorrectly included in the denominator of those diagnosed with cancer for the entire period of observation. Therefore, cancer survivors have lower rates of AD by definition in Model 1. Allowing the effect of cancer to vary over time if it is diagnosed after baseline corrects this bias because individuals are not counted in the cancer category until the incident cancer diagnosis occurs. Note that in the latter, there is a pattern of a stronger inverse association between cancer and AD with age, when the forces of mortality are stronger, although these age differences are not statistically significant. In summary, failure to properly specify the model can lead to an inverse association between cancer and AD that is an artifact and not related to the etiology of cancer or AD.
Figure 3.
Modeling cancer as a time-varying predictor eliminates the inverse relationship between cancer and Alzheimer’s disease (AD). Hazard rate ratios for the effect of cancer diagnosis on AD estimated using Cox regression. Panels A and B are run separately by sex and stratified by birth year. No additional covariates are included in the models. Panel (A) treats cancer as time-independent predictor and Panel (B) treats cancer diagnosis as time-varying predictor. TVEM = time-varying effect model (Models 1 and 2 in Figure 4). Source: Utah Population Database, Utah Cancer Registry, Centers for Medicare and Medicaid Services.
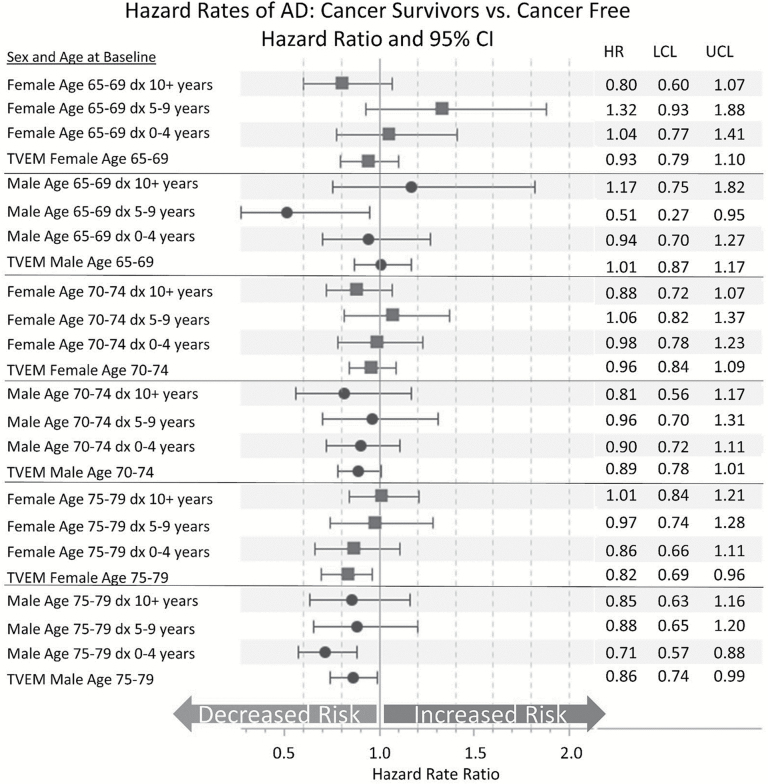
Figure 4 shows the relationship between cancer and AD when further separated into prevalent cancer and incident cancer at baseline (Model 3). The results show little association between cancer diagnosis and AD risk, particularly for prevalent cancer cases. As with the previous set of models, we see the inverse association between cancer and AD strengthening with age. Men and women aged 75–79 years at baseline with a cancer diagnosis after baseline have a decreased risk of AD (HR = 0.82; 95% CI = 0.69–0.96 and HR = 0.86; 95% CI = 0.74–0.99, respectively). Again, these findings are consistent with the influences of mortality selection because these individuals will generally not live long enough to be diagnosed with AD.
Figure 4.
Considering the time since diagnosis when evaluating the relationship between cancer and Alzheimer’s disease (AD). Hazard rate ratios for the effect of cancer diagnosis on AD estimated using Cox regression. Models displayed are run separately by sex and stratified by birth year. No other covariates are included in the models. Results displayed have separate variables for prebaseline (prevalent) and postbaseline (incident) cancer diagnosis (Model 3 in Figure 4). dx 10+years = cancer diagnosis 10 or more years prior to baseline; dx 5–9 years = cancer diagnosis 5–9 years prior to baseline; dx 0–4 years = cancer diagnosis 0–4 years prior to baseline; TVEM = time-varying effect for cancer diagnosed after baseline. Source: Utah Population Database, Utah Cancer Registry, Centers for Medicare and Medicaid Services.
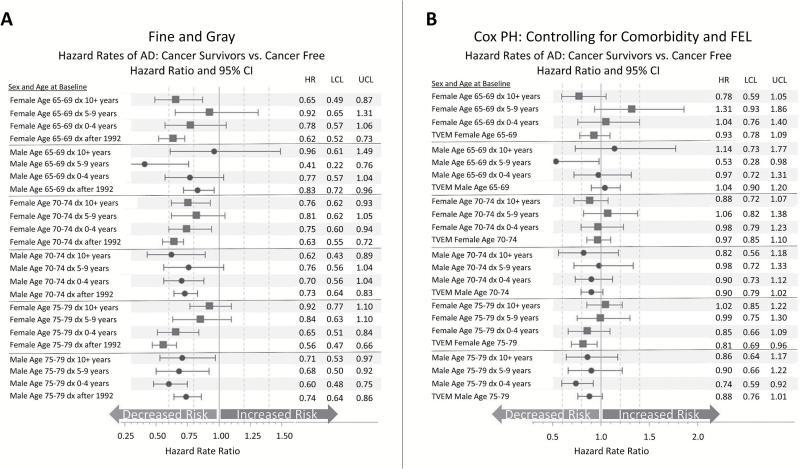
The FG models are used to further test the role of mortality as a competing event. Figure 5A displays the results from the FG competing risk models (Model 4). When accounting for the competing risk of death using FG models, individuals with prevalent and incident cancer have decreased rates of AD, and the magnitude of the effect increases with age. This is a crucial point to consider when interpreting the results from this model, because if individuals in the cancer group have higher mortality than the noncancer group, the set of persons deemed to be at risk will be artificially inflated in the group with higher mortality and the (subdistribution) hazard for AD will be lower by definition.
Figure 5.
(A) The Fine and Gray method to control for the competing risk of death: a misspecified model with useful information. Hazard rate ratios for the effect of cancer diagnosis on Alzheimer’s disease (AD) estimated using the Fine and Gray method for competing risks. Models are run separately by sex and stratified by birth year. No other covariates are included in the models. (B) The Kalbfleisch and Prentice approach: a useful method for correcting for mortality selection. Hazard rate ratios for the effect of cancer diagnosis on AD estimated using Cox regression. Models are run separately by sex and stratified by birth year. Models are controlling for a lagged Charlson Comorbidity Index score, familial excess longevity, religious status, obesity, smoking history, and neighborhood measures of population and median family income. Results are nested within models displayed in Figure 6 with the addition of the aforementioned covariates. dx 10+years = cancer diagnosis 10 or more years prior to baseline; dx 5–9 years = cancer diagnosis 5–9 years prior to baseline; dx 0–4 years = cancer diagnosis 0–4 years prior to baseline; TVEM = time-varying effect for cancer diagnosed after baseline (Model 5 in Figure 4). Source: Utah Population Database, Utah Cancer Registry, Centers for Medicare and Medicaid Services.
Finally, we applied the KP approach to investigate the etiological relationship between cancer and AD while controlling for the competing risk of death using a lagged internal time-varying covariate (CCI) that is predictive of the competing event, death (Model 5). In this approach, we also use FEL as a proxy for an individual’s risk of mortality based on family history. Models also include statistical controls for Medicare–Medicaid dual-enrollment eligibility (a measure of SES), smoking history, obesity, LDS status, neighborhood population and average income, and number of children ever born. The results are not displayed in the interest of space but available upon request. We find a significant and positive association between CCI and AD for men and women of all ages, and the magnitude of the effect is attenuated as age increases. The effect of FEL is less clear, with effects that vary across age group and sex, and does not reach significance in all models. Smoking history and obesity at baseline are both inversely associated with AD with HRs ranging from 0.63 to 0.90 when significant. Smoking has a larger protective effect than obesity. The effects of the Medicaid–Medicare enrollment, neighborhood measures of population and average family income, LDS status, and parity are not displayed, but as mentioned earlier, these are available upon request. We find that dual eligibility is positively associated with AD with HRs ranging from 1.6 to 2.2. Neighborhood population and median family income are both positively associated with AD risk in the 70–79 age groups, and there is no effect for the area-level measures in the 65–69 age group. There is no significant relationship between the number of children ever born and later life AD risk.
Figure 5B displays the exposure (cancer/no cancer) results from the KP approach. We find that once controlling for confounders, the precision of the estimates declines, as expected. There is little change in the largely null association between cancer and AD when the additional covariates are added to the model (Figure 5A compared with Figure 3). Again, this finding supports the conclusion that cancer is not associated with a decreased risk in AD.
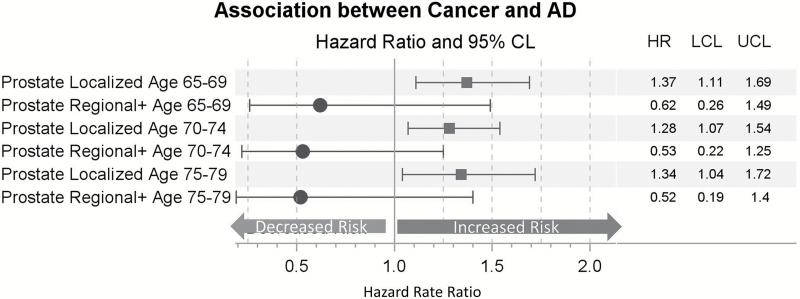
Figure 6 displays the prostate cancer results from the KP approach. We find that men with localized prostate cancer have an increased risk of AD at all ages of diagnosis (HR = 1.3–1.4), compared with men with no history of prostate cancer. As predicted due to higher mortality rates, men with regional/metastatic stage prostate cancer have lower rates of AD than men without a history of cancer, however, the differences are not significant.
Figure 6.
The Kalbfleisch and Prentice approach: prostate cancer risk by stage at diagnosis. Hazard rate ratios for the effect of prostate cancer diagnosis on Alzheimer’s disease estimated using Cox regression. Models are controlling for a lagged Charlson Comorbidity Index score, familial excess longevity, religious status, obesity, smoking history, and neighborhood measures of population and median family income and stratified by birth year. Cancer diagnosis is treated as a time-varying effect.
Discussion
We conclude that cancer is not protective against AD when appropriate model specifications that control for mortality selection are utilized. We show that under certain model specifications, we can replicate the inverse association between cancer and AD reported in the literature. The effects of differential mortality in the cancer and noncancer groups play an important role in the observed association between these two aging-related diseases. Our results demonstrate a dependence between AD diagnosis and mortality. Careful consideration of model specifications and interpretation of results is imperative when investigating the relationship between aging-related diseases where elevated mortality is omnipresent.
A recent meta-analysis reported the existence of an inverse association between cancer and AD (Ma et al., 2014). We offer several cautions about this analysis. The findings are heavily weighted by a single study (Musicco et al., 2013), and therefore, their conclusions largely reflect this one study’s findings. In addition, the meta-analysis does not correct for model misspecification or ignoring potential confounders, and the time-varying nature of cancer diagnosis relative to an AD diagnosis.
Consideration of mortality selection is important for several reasons. We show that the pattern of decreased risk of AD due to cancer increases with age, a finding consistent with the effects of mortality selection. This conclusion is clearly illustrated with the prostate cancer findings, where it is shown that men with less lethal forms of prostate cancer have higher rates of AD. Older individuals who have a cancer diagnosis must live long enough to be diagnosed with AD but generally do not, because their mortality rates are higher. Our findings suggest that the association between cancer and AD is attributable to mortality selection, or due to increased mortality in individuals with cancer, rather than for biological reasons. Future research should further investigate these findings by comparing site-specific cancers with differential survival rates with respect to AD risk. If mortality selection underlies this association, a stronger inverse association should be observed for more lethal cancers.
There are also clear age and sex patterns in the effects of cancer on AD risk. Individuals in the youngest age group generally have higher risks of AD relative to the older age group, and women have higher risks than men. In those instances when cancer is protective, it is less protective for younger individuals and women. Again, this pattern supports our conclusion that the competing risk of mortality plays an important role in the observed association between cancer and AD. Five-year cancer survival is highest in the youngest age groups and decreases with age. Women also have higher 5-year survival rates than men (National Cancer Institute, 2014). Both of these age and sex patterns of cancer survival strengthen the case for mortality selection as a fundamental mechanism.
Indeed, the strategy implemented in this study speaks to the general problem of linking social factors to disease risk in elderly individuals, because mortality selection creates the underlying population architecture of health at more advanced ages, and all estimated associations are constrained by the strength of this selection. Increasing the amount of time spent without major morbid conditions is a significant public health goal, and further elucidation of interplay between morbid conditions is key to understanding the aging process. Any analysis of an association between two morbid medical conditions in the older adult population should introduce robust statistical controls to address competing risks. As other authors have pointed out, the FG model is not a panacea for addressing competing risk problems (Beyersmann & Schumacher, 2008; Latouche, Porcher, & Chevret, 2005; Lau et al., 2009). Differential rates of the competing event between the exposed and unexposed group result in a misspecified model with misleading results; it is noteworthy that this information is very useful when combined with the results from cause-specific hazard models. Examining both the cause-specific and subdistribution (FG) hazard models and understanding the relationship between the estimates lead us to conclude that an observed inverse association between cancer and AD is likely due to mortality selection. Further research to investigate other related associations, such as cancer and Parkinson’s disease, is warranted. In addition, future research should quantify how ignoring competing risks of disease affects interpretation of findings across a range of age-related diseases with different ages of onset.
Two types of future investigations of the relationship between cancer and AD are justified. First, there is keen interest in better understanding the increased risk of acute dementia during cancer treatment (e.g., “Chemo brain”), a topic that parallels the present study but deserves further examination. Second, the analysis here relies on the Cox PH model. Other models, such as parametric mixture models (Lau, Cole, & Gange, 2009) and multistate models (Cortese & Andersen, 2010), have been used to account for mortality selection but were not implemented in this study. More insight may be gained into the dependence of these disease-related processes by exploring these and other alternative methods.
There are two noteworthy limitations to this study. First, the use of administrative claims data to identify AD diagnoses is not without error. Previous studies have shown that the agreement between clinical diagnoses and administrative records diagnoses is imperfect. Fallible phenotyping of AD may contribute to a null finding for association between cancer and AD. We attempted to increase the sensitivity of our measure by requiring two or more instances of an AD-related code for an AD diagnosis. The ability to replicate previous findings suggests that AD measurement error is not responsible for the observed null association between cancer and AD. Second, and relatedly, the diagnosis of AD would have to differ systematically between cancer patients and individuals without a cancer diagnosis for this to influence the findings, which is an unlikely scenario.
This population-based study advances our knowledge about the association between AD and cancer based upon its use of a range of models and its use of a large, high quality population database. The ability to study site- and stage-specific results is important because it allow us to observe a robust association across alternative types of models. Replications of this research are now needed using other national-based samples, such as the SEER-Medicare files.
Supplementary Material
Supplementary data is available at The Journals of Gerontology, Series B: Psychological Sciences and Social Sciences online.
Funding
This work was supported by the National Institutes of Health – National Institute of Aging (1R21AG036938-01 and 2R01 AG022095) and Department of Health and Human Services, National Institutes of Health, Eunice Kennedy Shriver National Institute of Child Health & Human Development (1K12HD085852-01). Partial support for all data sets within the UPDB was provided by the HCI Cancer Center Support Grant (P30 CA42014) from National Cancer Institute.
Supplementary Material
Acknowledgments
The authors thank the Huntsman Cancer Foundation for database support provided to the Pedigree and Population Resource of the HCI, University of Utah. They also thank Alison Fraser, Site Li, Diana Lane Reed, and Jennifer West for valuable assistance in managing the data and Jennifer Majersik and Richard Kryscio for valuable comments during the preparation of the manuscript. All authors listed have contributed sufficiently to the project to be included as authors, have approved the manuscript, and agree with its submission to The Journals of Gerontology, Series B: Psychological Sciences and Social Sciences. H. A. Hanson designed the statistical analysis plan, cleaned and analyzed the data, and drafted and revised the paper. She is guarantor. K. P. Horn, K. M. Rasmussen, and J. M. Hoffman revised the paper. . K. R. Smith commented on the statistical analysis plan and drafted and revised the paper.
To the best of our knowledge, no conflict of interest, financial or other, exists. The lead author affirms that this manuscript is an honest, accurate, and transparent account of the study being reported; that no important aspects of the study have been omitted; and that any discrepancies from the study as planned (and, if relevant, registered) have been explained.
References
- Anstey K. J. von Sanden C. Salim A., & O’Kearney R (2007). Smoking as a risk factor for dementia and cognitive decline: A meta-analysis of prospective studies. American Journal of Epidemiology, 166, 367–378. doi:10.1093/aje/kwm116 [DOI] [PubMed] [Google Scholar]
- Austin P. C. Lee D. S., & Fine J. P (2016). Introduction to the analysis of survival data in the presence of competing risks. Circulation, 133, 601–609. doi:10.1161/CIRCULATIONAHA.115.017719 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beeri M. S. Rapp M. Schmeidler J. Reichenberg A. Purohit D. P. Perl D. P., … Silverman J. M (2009). Number of children is associated with neuropathology of Alzheimer’s disease in women. Neurobiology of Aging, 30, 1184–1191. doi:10.1016/j.neurobiolaging.2007.11.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Behrens M. I., Lendon C., Roe C. M. (2009). A common biological mechanism in cancer and Alzheimer’s disease? Current Alzheimer Research, 6, 196–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bennett D. A., Leurgans S. (2010). Is there a link between cancer and Alzheimer disease? Neurology, 74, 100–101. doi:10.1212/WNL.0b013e3181cbb89a [DOI] [PubMed] [Google Scholar]
- Berry S. D. Ngo L. Samelson E. J., & Kiel D. P (2010). Competing risk of death: An important consideration in studies of older adults. Journal of the American Geriatrics Society, 58, 783–787. doi:10.1111/j.1532-5415.2010.02767.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beyersmann J., & Schumacher M (2008). Time-dependent covariates in the proportional subdistribution hazards model for competing risks. Biostatistics, 9, 765–776. doi:10.1093/biostatistics/kxn009 [DOI] [PubMed] [Google Scholar]
- Charlson M. E. Pompei P. Ales K. L., & MacKenzie C. R (1987). A new method of classifying prognostic comorbidity in longitudinal studies: Development and validation. Journal of Chronic Diseases, 40, 373–383. doi:10.1016/0021-9681(87)90171-8 [DOI] [PubMed] [Google Scholar]
- Clegg L. X. Reichman M. E. Miller B. A. Hankey B. F. Singh G. K. Lin Y. D., … Edwards B. K (2009). Impact of socioeconomic status on cancer incidence and stage at diagnosis: Selected findings from the surveillance, epidemiology, and end results: National Longitudinal Mortality Study. Cancer Causes & Control, 20, 417–435. doi:10.1007/s10552-008-9256-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cortese G., & Andersen P. K (2010). Competing risks and time-dependent covariates. Biomedical Journal, 52, 138–158. doi:10.1002/bimj.200900076 [DOI] [PubMed] [Google Scholar]
- de Glas N. A. Kiderlen M. Vandenbroucke J. P. de Craen A. J. M. Portielje J. E. A. van de Velde C. J. H., … Le Cessie S (2016). Performing survival analyses in the presence of competing risks: A clinical example in older breast cancer patients. Journal of the National Cancer Institute, 108, djv366 doi:10.1093/jnci/djv366 [DOI] [PubMed] [Google Scholar]
- De Pergola G., & Silvestris F (2013). Obesity as a major risk factor for cancer. Journal of Obesity, 2013, 291546 doi:10.1155/2013/291546 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demetrius L. A., & Simon D. K (2013). The inverse association of cancer and Alzheimer’s: A bioenergetic mechanism. Journal of the Royal Society Interface, 10, 20130006. doi:10.1098/rsif.2013.0006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Driver J. A. (2014). Inverse association between cancer and neurodegenerative disease: Review of the epidemiologic and biological evidence. Biogerontology, 15, 547–557. doi:10.1007/s10522-014-9523-2 [DOI] [PubMed] [Google Scholar]
- Driver J. A. Beiser A. Au R. Kreger B. E. Splansky G. L. Kurth T. … Wolf P. A (2012). Inverse association between cancer and Alzheimer’s disease: Results from the Framingham Heart Study. The British Medical Journal, 344, e1442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Enstrom J. E., & Breslow L (2008). Lifestyle and reduced mortality among active California Mormons, 1980–2004. Preventive Medicine, 46, 133–136. doi:10.1016/j.ypmed.2007.07.030 [DOI] [PubMed] [Google Scholar]
- Evans D. A. Hebert L. E. Beckett L. A. Scherr P. A. Albert M. S. Chown M. J., … Taylor J. O (1997). Education and other measures of socioeconomic status and risk of incident Alzheimer disease in a defined population of older persons. Archives of Neurology, 54, 1399–1405. doi:10.1001/archneur.1997.00550230066019 [DOI] [PubMed] [Google Scholar]
- Frain L. Swanson D. Betensky R. Cho K. Gagnon D. Kowall N., … Driver J (2013). A reduced risk of Alzheimer’s disease is associated with the majority of cancers in a national cohort of veterans. Alzheimer’s & Dementia, 9, P617 doi:10.1016/j.jalz.2013.05.1247 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fratiglioni L., Paillard-Borg S., Winblad B. (2004). An active and socially integrated lifestyle in late life might protect against dementia. The Lancet Neurology, 3, 343–353. doi:10.1016/S1474-4422(04)00767-7 [DOI] [PubMed] [Google Scholar]
- Fratiglioni L. Wang H. X. Ericsson K. Maytan M., & Winblad B (2000). Influence of social network on occurrence of dementia: A community-based longitudinal study. Lancet, 355, 1315–1319. doi:10.1016/s0140-6736(00)02113-9 [DOI] [PubMed] [Google Scholar]
- Jason P. F., & Gray R. J (1999). A proportional hazards model for the subdistribution of a competing risk. Journal of the American Statistical Association, 94, 496–509. doi:10.2307/2670170 [Google Scholar]
- Kerber R. A. O’Brien E. Smith K. R., & Cawthon R. M (2001). Familial excess longevity in Utah genealogies. The Journals of Gerontology, Series B: Psychological Sciences and Social Sciences, 56, 130–139. [DOI] [PubMed] [Google Scholar]
- Key T. J. Verkasalo P. K., & Banks E (2001). Epidemiology of breast cancer. The Lancet Oncology, 2, 133–140. doi:10.1016/S1470-2045(00)00254-0 [DOI] [PubMed] [Google Scholar]
- Klabunde C. N. Potosky A. L. Legler J. M., & Warren J. L (2000). Development of a comorbidity index using physician claims data. Journal of Clinical Epidemiology, 53, 1258–1267. doi:10.1016/S0895-4356(00)00256-0 [DOI] [PubMed] [Google Scholar]
- Klabunde C. N. Warren J. L., & Legler J. M (2002). Assessing comorbidity using claims data: An overview. Medical Care, 40, IV-26–IV-35. [DOI] [PubMed] [Google Scholar]
- Koller M. T. Raatz H. Steyerberg E. W., & Wolbers M (2012). Competing risks and the clinical community: Irrelevance or ignorance? Statistics in Medicine, 31, 1089–1097. doi: 10.1002/sim.4384 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latouche A. Porcher R., & Chevret S (2005). A note on including time-dependent covariate in regression model for competing risks data. Biometrical Journal, 47, 807–814. doi:10.1002/bimj.200410152 [DOI] [PubMed] [Google Scholar]
- Lau B. Cole S. R., & Gange S. J (2009). Competing risk regression models for epidemiologic data. American Journal of Epidemiology, 170, 244–256. doi:10.1093/aje/kwp107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y.-J. Scott W. K. Hedges D. J. Zhang F. Gaskell P. C. Nance M. A., … Pericak-Vance M. A (2002). Age at onset in two common neurodegenerative diseases is genetically controlled. The American Journal of Human Genetics, 70, 985–993. doi:10.1086/339815 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyon J. Gardner K., & Gress R (1994). Cancer incidence among Mormons and non-Mormons in Utah (United States) 1971–85. Cancer Causes & Control, 5, 149–156. doi:10.1007/bf01830261 [DOI] [PubMed] [Google Scholar]
- Ma L. L., Yu J. T., Wang H. F., Meng X. F., Tan C. C., Wang C., Tan L. (2014). Association between cancer and Alzheimer’s disease: Systematic review and meta-analysis. Journal of Alzheimer’s Disease, 42, 565–573. doi:10.3233/JAD-140168 [DOI] [PubMed] [Google Scholar]
- Merrill R. M., & Lyon J. L (2005). Cancer incidence among Mormons and non-Mormons in Utah (United States) 1995–1999. Preventive Medicine, 40, 535–541. doi:10.1016/j.ypmed.2004.10.011 [DOI] [PubMed] [Google Scholar]
- Mineau G. P. Smith K. R., & Bean L. L (2002). Historical trends of survival among widows and widowers. Social Science & Medicine, 54, 245–254. doi:10.1016/S0277-9536(01)00024-7 [DOI] [PubMed] [Google Scholar]
- Musicco M. Adorni F. Di Santo S. Prinelli F. Pettenati C. Caltagirone C., … Russo A (2013). Inverse occurrence of cancer and Alzheimer disease: A population-based incidence study. Neurology, 81, 322–328. doi:10.1212/WNL.0b013e31829c5ec1 [DOI] [PubMed] [Google Scholar]
- National Cancer Institute (2014). Table 2.8 5-year relative and period survival: All cancer sites (invasive) Retrieved from http://seer.cancer.gov/csr/1975_2012/browse_csr.php?sectionSEL=2&pageSEL=sect_02_table.08.html
- Norton M. C. Dew J. Smith H. Fauth E. Piercy K. W. Breitner J. C. S., … for the Cache County Investigators. (2012). Lifestyle behavior pattern is associated with different levels of risk for incident dementia and Alzheimer’s disease: The Cache County Study. Journal of the American Geriatrics Society, 60, 405–412. doi:10.1111/j.1532-5415.2011.03860.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- O’Brien E., Kerber R., Smith K., Mineau G., Boucher K., Reed D. L. (2007). Familial mortality in the Utah population database: Characterizing a human aging phenotype. The Journals of Gerontology, Series A: Biological Sciences and Medical Sciences, 62, 803–812. doi:10.1093/gerona/62.8.803 [DOI] [PubMed] [Google Scholar]
- Ott A. Slooter A. J. C. Hofman A. van Harskamp F. Witteman J. C. M. Van Broeckhoven C., … Breteler M. M. B (1998). Smoking and risk of dementia and Alzheimer’s disease in a population-based cohort study: The Rotterdam Study. The Lancet, 351, 1840–1843. doi:10.1016/S0140-6736(97)07541-7 [DOI] [PubMed] [Google Scholar]
- Plun-Favreau H., Lewis P. A., Hardy J., Martins L. M., Wood N. W. (2010). Cancer and neurodegeneration: Between the devil and the deep blue sea. PLoS Genetics, 6, e1001257 doi:10.1371/journal.pgen.1001257 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reiche E. M. V. Nunes S. O. V., & Morimoto H. K (2004). Stress, depression, the immune system, and cancer. The Lancet Oncology, 5, 617–625. doi:10.1016/S1470-2045(04)01597-9 [DOI] [PubMed] [Google Scholar]
- Roe C. M., Behrens M. I., Xiong C., Miller J. P., Morris J. C. (2005). Alzheimer disease and cancer. Neurology, 64, 895–898. doi:10.1212/01.WNL.0000152889.94785.51 [DOI] [PubMed] [Google Scholar]
- Roe C. M. Fitzpatrick A. L. Xiong C. Sieh W. Kuller L. Miller J. P., … Morris J. C (2010). Cancer linked to Alzheimer disease but not vascular dementia. Neurology, 74, 106–112. doi:10.1212/WNL.0b013e3181c91873 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rusanen M., Kivipelto M., Quesenberry C. P., Jr, Zhou J., Whitmer R. A. (2011). Heavy smoking in midlife and long-term risk of Alzheimer disease and vascular dementia. Archives of Internal Medicine, 171, 333–339. doi:10.1001/archinternmed.2010.393 [DOI] [PubMed] [Google Scholar]
- SEER Stat Fact Sheets: Pancreas Cancer (2015) Retrieved February 24, 2015, from http://seer.cancer.gov/statfacts/html/pancreas.html
- Smith K. R. Hanson H. A. Norton M. C. Hollingshaus M. S., & Mineau G. P (2014). Survival of offspring who experience early parental death: Early life conditions and later-life mortality. Social Science & Medicine, 119, 180–190. doi:10.1016/j.socscimed.2013.11.054 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith K. R. Mineau G. P. Garibotti G., & Kerber R (2009). Effects of childhood and middle-adulthood family conditions on later-life mortality: Evidence from the Utah Population Database, 1850–2002. Social Science & Medicine, 68, 1649–1658. doi:10.1016/j.socscimed.2009.02.010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tabares-Seisdedos R., & Rubenstein J. L (2013). Inverse cancer comorbidity: A serendipitous opportunity to gain insight into CNS disorders. Nature Reviews Neuroscience, 14, 293–304. doi:10.1038/nrn3464 [DOI] [PubMed] [Google Scholar]
- US Department of Health and Human Services (2014). The health consequences of smoking—50 years of progress: A report of the Surgeon General (Vol. 17) Atlanta, GA: US Department of Health and Human Services, Centers for Disease Control and Prevention, National Center for Chronic Disease Prevention and Health Promotion, Office on Smoking and Health. [Google Scholar]
- Ward E. Jemal A. Cokkinides V. Singh G. K. Cardinez C. Ghafoor A., & Thun M (2004). Cancer disparities by race/ethnicity and socioeconomic status. CA: A Cancer Journal for Clinicians, 54, 78–93. [DOI] [PubMed] [Google Scholar]
- White R. S., Lipton R. B., Hall C. B., Steinerman J. R. (2013). Nonmelanoma skin cancer is associated with reduced Alzheimer disease risk. Neurology, 80, 1966–1972. doi:10.1212/WNL.0b013e3182941990 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wiley L. K. Shah A. Xu H., & Bush W. S (2013). ICD-9 tobacco use codes are effective identifiers of smoking status. Journal of the American Medical Informatics Association, 20, 652–658. doi:10.1136/amiajnl-2012-001557 [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.