More than Counting: An Intraindividual Variability Approach to Categorical Repeated Measures

Abstract

Objectives

Age-related differences in daily experiences are often described using summaries of categorical repeated measures, including typologies of stressors, activities, social partners, and coping strategies. This paper illustrates how an intraindividual variability (IIV) framework can be used to extract additional meaning from categorical IIV data.

Method

Using 8-occasion categorical data on daily stressors from the National Study of Daily Experiences (N = 1,499, M_Age = 46.74, SD_Age= 12.91), we derive and compute six IIV metrics that invoke numeric and nominal measurement of the central tendency, dispersion, and asymmetry of individuals’ stressor experiences and examine how these metrics, relative dominance, diversity, log-skew and mode, spread, order, are related to age and interindividual differences in negative affect.

Results

Results demonstrate the utility of the numeric and nominal categorical IIV metrics, with theoretically meaningful age gradients in the three numeric IIV stressor metrics and five of six IIV metrics mapping differences in negative affect.

Discussion

Findings highlight how the unique constructs measured by these six metrics of categorical IIV may be used to examine dynamic process, study interindividual and age-related differences, and expand the variety of developmental research questions that may be answered using categorical repeated measures data.

Intraindividual variability (IIV) is fluctuation of an individual’s repeated measures over micro time-scales. Within the life-span developmental framework, studying IIV can illuminate individuals’ dynamic characteristics and how they change over the life span (Nesselroade, 1991). Indeed, IIV methodology provides a window into important developmental processes (Ram & Gerstorf, 2009). For example, moment-to-moment or day-to-day affective variability can reflect personality traits (e.g., emotional stability; Eid & Diener, 1999; Fleeson, 2001), and age-related changes in emotion regulation (Liu, Bangerter, Rovine, Zarit, & Almeida, 2016; Röcke, Li, & Smith, 2009). Most IIV-based studies of aging have focused on continuous variables, but there is also a need to capture age-related changes in categorical IIV constructs (van Dijk & van Geert, 2015). In this paper, we apply general IIV principles to study variability in types (i.e., categories) of events, activities, or social interactions over time (e.g., during a typical week). Based on principles underlying the statistical moments of continuous IIV distributions (iMean, iSD, iSkew), we develop and illustrate how six categorical IIV metrics may capture novel and important age-related processes. Specifically, we demonstrate how categorical IIV metrics and constructs can help articulate developmental and aging theories.

Stressor Experience as an Ecosystem

Our exploration into categorical IIV is motivated by daily stress research, where key variables are categorical—“Did a stressful event happen today? (yes/no); What type? (argument, home overload, work/education overload, etc.).” Repeated measurements from daily diary studies has enabled study of interindividual and age-related differences in stressor exposure (the total number of stressors an individual experiences) and stressor reactivity (intraindividual covariation between daily stressors and daily negative affect). Generally, both greater stressor exposure and reactivity are associated with poorer well-being, while stressor reactivity also relates to compromised health, and increased mortality risk (Almeida, 2005; Charles, Piazza, Mogle, Sliwinski, & Almeida, 2013; Mroczek et al., 2015). Developmentally, stressor exposure decreases across adulthood, while stressor reactivity has no clear, consistent age gradient (Bellingtier & Neupert, 2016). Invoking parallelism between biological and human ecology, Koffer and colleagues (Koffer, Ram, Conroy, Pincus, & Almeida, 2016) characterized individuals’ daily stressor experiences as a stressor ecosystem that could be quantified using metrics from biology: abundance (number of organisms/stressor types) and diversity (relative abundance across species/stressor types). They found individuals with higher stressor exposure and lower stressor diversity had lower positive affect and higher negative affect (see also Brose, Scheibe, & Schmiedek, 2013). Stressor diversity decreased with age, with older adults being particularly vulnerable to chronic stressors. Theoretically, these findings provided a new operationalization of chronic stressors, demonstrated the usefulness of an ecosystem analogy for stressors and resource use, and examined how stressors influence individuals’ daily well-being across the life span. Methodologically, these findings demonstrated the utility of quantifying categorical IIV in the study of successful aging. We now reach further into the biological literature—a literature with established need and methods for examining categorical data—to identify metrics that systematically extract more information from categorical IIV data.

The Statistical Moments of IIV Distributions

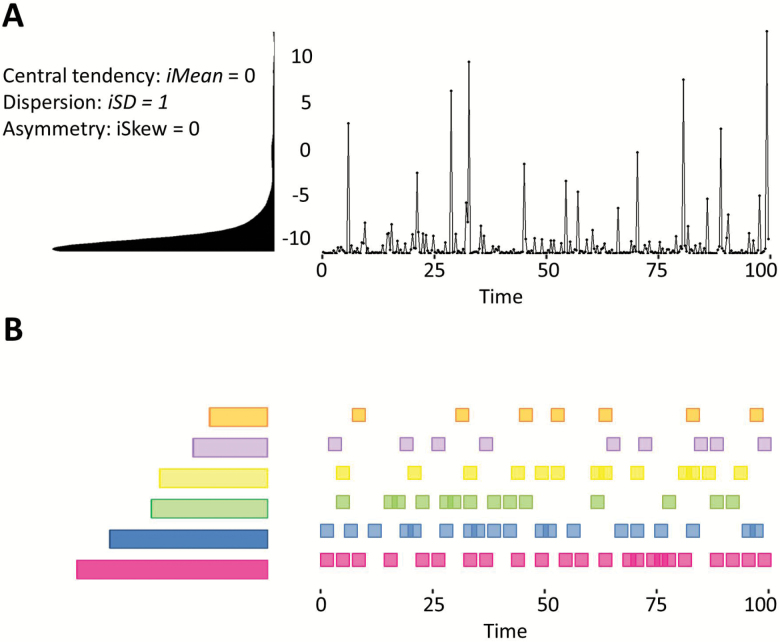
IIV research often summarizes intensive repeated measures obtained on continuous scales. In the upper panel of Figure 1, T = 100 simulated repeated measures from a hypothetical individual are summarized in the (IIV) distribution on the left. The statistical moments of the distribution—mean, variance, and skew—represent specific features that might differ across distributions: interindividual differences in IIV (e.g., Newell & Hancock, 1984). Our proposal is that, with categorical time-series, metrics for the first three statistical moments of categorical distributions—central tendency, dispersion, and asymmetry—will also hold value as interindividual difference measures. In the lower panel of Figure 1, T = 100 repeated measures of a multicategory variable (e.g., for stressor or activity type, colored squares would represent when particular types of stressors or activities were reported) are summarized in the (categorical IIV) distribution on the left, the features of which (e.g., height of bars, color of bars, order of bars) might be indicators of IIV constructs. Borrowing from ecological literature, we explore the utility of three numeric metrics and three nominal metrics that describe both quantitative and qualitative aspects of the central tendency, dispersion, and asymmetry of categorical IIV distributions. In the sections that follow, we walk through the Figure 2 flowchart, defining each distributional attribute of interest, describing associated research questions, articulating mathematical details of the categorical IIV metrics, and providing an empirical example using categorical IIV stressor distributions.

Figure 1.

Continuous and categorical IIV data and distributions. A simulated continuous IIV time series with T = 100 occasions (top right) is collected into an intraindividual distribution (top left), and summarized by measures of central tendency (mean), dispersion (SD), and asymmetry (skew). A simulated categorical IIV time series with T = 100 occasions (bottom right) is collected into an intraindividual distribution (bottom left). Each colored square represents when a particular category was reported. The categorical intraindividual distribution arranges the categories in height order by frequency. Like the continuous intraindividual distribution, categorical intraindividual distributions can be summarized by descriptions of central tendency, dispersion, and asymmetry.

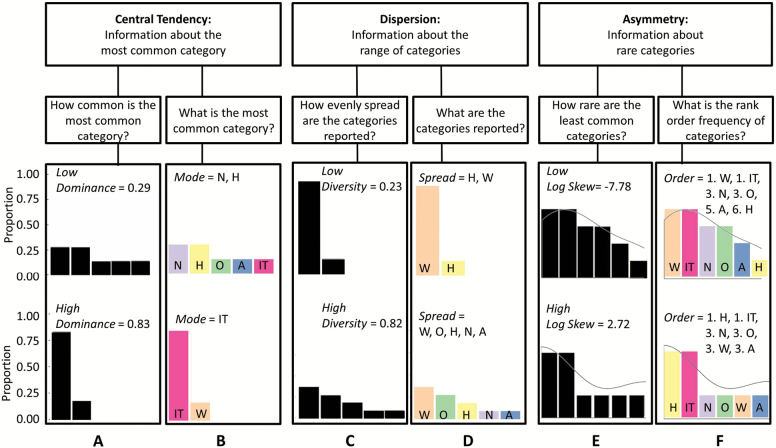
Figure 2.

Flow chart guiding researchers from the distributional characteristic of interest (i.e., central tendency, dispersion, asymmetry) on the top row, to research questions on the middle row, to metrics that describe such characteristics on the bottom row. Categorical IIV distributions that differ in central tendency (Panel A: with numeric relative dominance, Panel B: with nominal mode metrics), dispersion (Panel C: with numeric diversity, Panel D: with nominal spread metrics), and asymmetry (Panel E: with numeric log-skew, Panel F: with nominal order metrics). The distributions at the top and bottom of each Panel represent a different individual’s stressor experiences; the six individuals’ distributions are displayed either in in black and white (B, D, F), indicating a numeric approach, or in color (A, C, E), representing a nominal approach. Gray line is a smoothed density curve highlighting asymmetry of distribution. Note: IT = nonargument interpersonal tensions (pink), A = argument stressors (blue), W = work stressors (orange), H = home stressors (yellow), N = network stressors (purple), O = other stressors (green).

Numeric Metrics for Categorical IIV

We begin by examining utility of numeric metrics (depicted in Figure 2, Panels A, C, and E) that describe the first three statistical moments of the categorical IIV distributions.

Central Tendency

The central tendency of categorical distributions, the mode, is a nominal category, but a numerical counterpart, relative dominance, quantifies how dominant that mode is using the proportion of observations in the modal category. Figure 2, Panel A depicts IIV stressor distributions from two persons, histogram bars ordered left to right by proportion of stressors in each category. Looking only at the height of the equally tallest bars, we see that the person at the top of the panel experiences the dominant stressor only slightly more frequently than other stressor types (low relative dominance; p_i1 = .286). In contrast, the person at the bottom experiences the dominant stressor much more frequently than other stressor types (high relative dominance; p_i1 = .833).

Stressor relative dominance indicates the extent to which the dominant stressor drives an individual’s stressor experiences. A variety of aging-related hypotheses might be invoked using this metric. For example, life course role change theory (Pearlin, 1989) suggests stressor relative dominance will be lowest in midlife, when individuals simultaneously serve in multiple roles.

Dispersion

The dispersion of a categorical distribution quantifies how evenly observations are distributed across categories. Ecologists describe an ecosystem’s species diversity with a variety of metrics, the most popular being Shannon’s (1948) entropy metric, which quantifies relative abundance of different species in terms of evenness (Magurran & McGill, 2011). Looking at the relative height of the bars in Panel C of Figure 2, we see that the person at the top of the panel has relatively low diversity (diversity_i = .23), with most observations concentrated in one category. In contrast, the person below has high diversity (diversity_i = .82), with observations relatively evenly distributed across five of the six possible categories.

In the stressor ecosystem, stressor diversity indicates heterogeneity of stressor experience. As previously mentioned, researchers have begun to test developmental hypotheses with stressor diversity metrics. For example, age-related selective pruning and regulation of experiences suggest stressor diversity decreases with age (Brose et al., 2013; Koffer et al., 2016).

Asymmetry

Skew describes the asymmetry of probability distributions. For categorical distributions, skew is quantified in terms of “rarity”—how much the least common categories influence the distribution structure. In particular, log-skew indicates the proportion of observations in rare categories (the tail of the distribution) relative to the proportion of observations in common categories. Looking at the relative heights of the tallest and shortest bars in Panel E of Figure 2, we see that the person at the top of the panel has proportionally more observations in “rare” categories (log-skew_i = −7.78) compared to the person at the bottom (log-skew_i = 2.72). Generally, negative log-skew indicates that all types are fairly common while higher positive log-skew indicates that some types are very rare.

In the stressor ecosystem, stressor log-skew reflects whether an individual experiences stressors that are atypical for him/herself. Thus, stressor log-skew allows for testing of age-related changes in the rarity of stressor types. For example, socioemotional aging theories (Carstensen, Isaacowitz, & Charles, 1999; Charles, 2010) suggest that older adults may, because of selective engagement with activities and social partners, have a few commonly experienced stressor types and very few rarely experienced stressor types (higher log-skew).

Nominal Metrics for Categorical IIV

Numeric metrics compress the complexity of the categorical distribution that, by definition, is already a concise multidimensional representation of taxonomic abundance (Li, Bihan, Yooseph, & Methé, 2012). When describing the visual depictions of low and high relative dominance, diversity, and log-skew, we only referred to the heights of the bars in Figure 2 (i.e., global quantifiable properties), without considering the colors of the bars (i.e., content differences). To capture the content information we outline three nominal metrics (depicted in Figure 2, Panels B, D, and F) as qualitative counterparts to the quantitative metrics above.

Central Tendency

The central tendency of categorical distributions is the mode—the most abundant category. Parallel to Panel A of Figure 2, Panel B depicts categorical IIV stressor distributions obtained from two persons, histogram bars ordered left to right by proportion of stressors in each category. Looking now only at the color of the tallest bar, we see the person at the top of Panel B has a dual mode, purple and yellow (equivalent number of network and home stressors), while the person at the bottom has a pink mode (nonargument interpersonal tensions). In our 6-category example, the nominal mode has 6 possible values (or, when allowing for potential ties like the person at the top of Panel B, 2⁶ = 64 possible values).

In the stressor ecosystem, modal stressor is the expected stressor type an individual will encounter. Hypotheses regarding age-related differences in expected stressor type can then be tested with this nominal metric. For example, Socioemotional Selectivity Theory (Carstensen et al., 1999) suggests older adults are less likely than younger adults to report arguments as their modal stressor.

Dispersion

From a qualitative perspective, the nominal spread or range of a categorical distribution is a list of the categories that have one or more observations. Looking again only at the colors of the bars in Panel D of Figure 2, we see the person at the top has a spread of orange and yellow (i.e., [work, home]), while the person at the bottom has a spread of orange, green, yellow, purple, and blue (i.e., [work, other, home, network, and argument]). In our 6-category example, nominal spread has 2⁶ = 64 possible values.

In the stressor ecosystem, stressor spread indicates the specific stressor types an individual experiences and across which coping resources must be deployed. Again, a variety of developmental hypotheses might be invoked using stressor spread. For example, life course role change theory (Pearlin, 1989) suggests stressor spreads experienced by older and younger adults differ, with younger adults’ spreads including work, home, and argument, and older adults’ spreads including nonargument interpersonal tension and network stressors.

Asymmetry

Finally, the asymmetry of nominal categories—the nominal order—can be derived by rank-ordering the elements of the categories according to frequency of occurrence. Consider the bars in Panel F of Figure 2, which have been ordered left to right based on height, tallest to shortest. The person at the top of the panel has nominal order of (1. orange, 1. pink, 3. purple, 3. green, 5. blue, 6. yellow) (i.e., [1. work, 1. non-argument interpersonal tension, 3. network, 3. other, 5. argument, 6. home], while the person at the bottom has nominal order of [1. yellow, 1. pink, 3. purple, 3. green, 3. orange, 3. blue] (i.e., [1. home, 1. non-argument interpersonal tension, 3. network, 3. other, 3. work, 3. argument]). In our 6-category example nominal order has 6! + 5! + 4! + 3! + 2! + 1! = 873 possible values, and even more when adjusting rank numbers to reflect ties (i.e., equivalent frequencies) as above.

In the stressor ecosystem, stressor order indicates the relative frequency of stressor types, possibly reflecting the relative demands stressor types make on psychosocial resources. For example, for the person at the top of Panel F, work stressors occur more frequently than home stressors, whereas for the person at the bottom, home stressors occur more frequently than work stressors. Given such differences, stressor order might be used to articulate hypotheses derived from socioemotional theories of aging (Carstensen et al., 1999; Charles, 2010). In particular, such theories suggest arguments should appear later (i.e., relatively less frequently) in the stressor order for older adults than for younger adults.

The Present Study

Using a national study of individuals’ daily stressor experiences, we demonstrate how an intraindividual variability framework can parse additional information from categorical repeated measures in three steps. First, we calculate six metrics that describe features of individuals’ categorical IIV distributions following the examples in Figure 2. Second, we examine age-gradients in the numeric metrics, expecting that older age is associated with more stressor dominance, less stressor diversity, and more stressor skew. Third, in the context of daily stress models, we assess the relation between interindividual differences in each categorical IIV metric and interindividual differences in negative affect. We expect higher stressor relative dominance, lower stressor diversity, and higher stressor skew to each be associated with higher negative affect, and we explore age-moderation of those associations. Similarly, but without directional specificity, we expect negative affect differences across groups defined by modal stressor, stressor spread, and stressor order. Working from these initial demonstrations, we speculate how categorical IIV metrics may contribute to theory development or revision in multiple domains.

Method

Data are from Wave 1 of the National Survey of Daily Experiences (NSDE), the daily diary component of the Midlife in the U.S. Survey (MIDUS). Details relevant to the current analysis are given below (see also Almeida, Wethington, & Kessler, 2002).

Participants

As part of MIDUS 1 (1995–1996), 7,108 participants completed a telephone psychosocial battery (Brim, Ryff, & Kessler, 2004), with 1,843 of these individuals randomly selected to participate in the NSDE (Wave 1, 1996–1997), an 8-day daily diary study. Of these, 1,499 respondents (81% of those contacted) provided data on their daily experiences. Participants ranged from age 24–74 years (M = 46.74, SD = 12.91), and approximately half were women. The majority were White (91.45%), married or living with a romantic partner (77%), with an average of two children (M = 2.30, SD = 3.01), median income of $55,000, and “very good” physical health (M = 3.60, SD = 0.96).

Procedure

Participants were compensated $20 in advance and asked to complete 8 consecutive days of semistructured telephone interviews. They reported their experiences that day, including stressor events and affect (Almeida et al., 2002). Participants provided between 1 and 8 days of data (M = 7, SD = 1.41), with 87.19% providing 6 or more daily reports and 50.63% providing all 8 daily reports.

Measures

Daily stressors

Individuals’ stressor experiences were assessed using the Daily Inventory of Stressor Events (DISE; Almeida et al., 2002). Assessments of arguments, nonargument interpersonal tensions, and network stressors probed the experience of such occurrences as judged by the individual: “Did you have an argument or disagreement with anyone since (this time/we spoke) yesterday?”; “Since (this time/we spoke) yesterday, did anything happen that you could have argued about but you decided to let pass in order to avoid a disagreement?”; and “Since (this time/we spoke) yesterday, did anything happen to a close friend or relative (other than you’ve already mentioned) that turned out to be stressful for you?” Assessments of work stressors, home stressors, and other stressors were framed in terms of events that most people would consider stressful: “Since (this time/we spoke) yesterday, did anything happen at (question domain) (other than what you already have mentioned) that most people would consider stressful?” Assessment of discrimination was prefaced with: “Many people experience discrimination on the basis of such things as race, sex, or age. Did anything like this happen to you since (this time/we spoke) yesterday?” Each day participants indicated whether they had (=1) or had not (=0) experienced each of the seven stressor types. On average, participants reported one or more stressors on 39.53% of study days, with M = 0.55 (SD = 0.47) stressors per day. The most common stressor type was nonargument interpersonal tensions (27.29% of stressor days), followed by arguments (18.13%), work (17.83%), home (14.94%), network (10.54%), other (9.39%), and discrimination (1.97%). For parsimony, categories with less than 5% of the total observations (discrimination) were removed, leaving m = 6 categories. Stressor exposure was calculated as the sum total number of stressors over the study period.

Negative affect

Each day, participants indicated “How much of the time today did you feel _________?” on a 0–4 scale, where 0 = “none of the time,” 1 = “a little of the time,” 2 = “some of the time,” 3 = “most of the time,” and 4 = “all of the time.” Daily negative affect (NA) was calculated as the average of responses to 12 items (Mroczek & Kolarz, 1998): depressed, restless or fidgety, so restless that you could not sit still, nervous, so nervous that you could not calm down, worthless, so sad that nothing could cheer you up, tired out for no good reason, that everything takes an effort, hopeless, angry or irritable. The eight daily NA scores were averaged to obtain a single negative affect interindividual differences variable (Cronbach’s α = 0.89).

Data Analysis

Our analytical goals were to (1) describe the first three statistical moments of categorical stressor type distributions by computing three numeric metrics (a) relative dominance of the modal stressor (b) stressor diversity, and (c) stressor log-skew, and three nominal descriptives (d) modal stressor, (e) stressor range, and (f) stressor order, and (2) assess age-differences in numeric metrics, and examine how interindividual differences in the numeric and nominal metrics related to individuals’ NA.

Preliminaries

To preprocess the data, we computed, for each individual i, the total number, n_ij, of stressors reported in each type, j = 1 to m (where m = 6), and the proportion of stressors in each type (p_ij = $\left(p_{ij}=\frac{n_{ij}}{{\displaystyle \sum _j^{n_{ij}}{1}^{n_{ij}}}}\right)$ We then ordered the proportions from largest to smallest (e.g., p_i1 to p_i6 with p_ij ≥ p_ij+1) and retained the corresponding stressor type as a linked variable, rank. type_i1 to rank. type_i6, (e.g., 1. arguments, 2. nonargument interpersonal tensions, 3. home stressors, 4. network stressors, 5. work stressors, 6. other stressors). In cases where proportions were equal, the linked ordering was adjusted to reflect equality in rankings (e.g., 1. arguments, 1. nonargument interpersonal tensions, 1. home stressors, 4. network stressors, 5. work stressors, 6. other stressors).

Numeric Metrics for Categorical IIV

Using the counts (n_ij) and ordered proportion scores (p_i1 to p_i6) described above, we compute relative dominance, diversity, and log-skew indices for each individual’s repeated measures of daily stressors.

Relative dominance (central tendency)

The stressor relative dominance score is the modal stressor’s proportion of individual i’s total stressor experiences, p_{i1 =}p_max (Berger & Parker, 1970). Using the proportion instead of the number of modal stressor events corrects for differences in total number of observations and allows for comparisons across individuals with differing total exposure to stressors (Magurran & McGill, 2011).

Diversity (dispersion)

The diversity of each individual’s stressor experiences across all study days is quantified using Shannon’s (1948) entropy index. Specifically,

$$Diversit{y}_i=-(\frac{1}{ln(m)}){\displaystyle \sum _{j=1}^m{p}_i{}_{j}1n{p}_{ij}}$$ (1)

where m is the number of available stressor categories (m = 6), and p_ij is the proportion of individual i’s stressors that were in each category, j = 1 to m. Entropy scores can range from 0.0 (no diversity; all daily stressor experiences are of a single type), to 1.0 (maximum diversity; all six stressor types are evenly represented).

Log-skew (asymmetry)

The rarity metric, log-skew indicates extent of the stressor distribution’s asymmetry, with the assumption that nonmodal stressor experiences are rare compared to the modal stressor and thus approximate a log-normal distribution. Stressor log-skew for each individual, i, is computed as

$$\log ske{w}_i=\left[\frac{\frac{{{\displaystyle \sum }}^{\text{}}(\text{log}{(n_{ij})}^3}{m}}{{\left(\frac{{{\displaystyle \sum }}^{\text{}}{(\log \left(n_{ij}\right)-{\mu }_{\text{log}(n_{ij})})}^2}{m}\right)}^{\frac{3}{2}}}\right]*\frac{m}{m-2}*\sqrt{\frac{m-1}{m}}$$ (2)

Where m = 6 is the total number of stressor types, and n_ij is the number of stressors within each category.

Nominal Metrics for Categorical IIV

Using the ordered category labels, type_i1 to type_i6 from preliminary processing, we extract the nominal metrics, mode, spread, and order, for each individual’s repeated measures of daily stressors.

Mode (central tendency)

The stressor type, type_i1, with the largest p_ij is the individual’s mode. Where there were ties (e.g., p_i1 = p_i2 = p_max), a new category was created to reflect the mixed-type mode.

Spread (dispersion)

Each individual’s unordered list of reported stressor types indicates the nominal spread of stressors. These lists are determined via each individual’s unordered type indicators (e.g., derived from the binary lists indicating whether = 1 or not = 0 an individual experienced each of the j = 1 to m stressor types during the study period). For example, in our m = 6 situation, one individual’s spread may be spread_i = (type_i1, type_i2, type_i3, type_i4, type_i5, type_i6) * (0,0,0,1,0,1) = (type_i4, type_i6) while another individual may have spread_i = (type_i1, type_i2, type_i3, type_i4, type_i5, type_i6) * (1,1,1,1,1,1) = (type_i1, type_i2, type_i3, type_i4, type_i5, type_i6).

Order (asymmetry)

The rank order of stressor types indicates the relative influence of each stressor type, from most abundant to least abundant. Each individual retains a concatenated string of the rank ordered type_ij variables. Stressor types with p_ij = 0 remain in the string, as the lowest rank for the particular individual. Rank numbers are attached to the stressor type in order to reflect exact ranking and ties (e.g., [1. home stressors, 1. nonargument interpersonal tensions, 3. network stressors, 3. Other stressors, 3. work stressors, 3. arguments]). For programming purposes, we additionally maintained an implicit ordering when stressor types were equal. Specifically, when frequencies were equivalent, ordering was given by sample-level frequency (an arbitrary choice for ordering within ties).

Interindividual Differences in Categorical IIV: Age Gradients and Associations with Negative Affect

With the six categorical IIV metrics calculated/derived, these new interindividual differences variables (and the constructs they measure) can be examined for relations with age and other interindividual differences. For the numeric metrics, age gradients were determined by regressing each metric on age and quadratic age:

$$Numeric IIV Metri{c}_i= {\beta }_0+{\beta }_{1}Ag{e}_i+{\beta }_{2}Ag{e}_i^2+{\epsilon }_i$$ (3)

Subsequent associations with negative affect were examined using three regressions (each numeric metric separately) of the form,

$$\begin{array}{ll}{\mathit{\text{Negative Affect}}}_i& ={\beta }_0+{\beta }_1{\mathit{\text{Numeric IIV Metric}}}_i\\ & +{\beta }_2{\mathit{\text{Stressor Exposure}}}_i+{\beta }_3{\mathit{\text{Age}}}_i\\ & +{\beta }_4{\mathit{\text{Numeric IIV Metric}}}_i*{\mathit{\text{Stressor Exposure}}}_i\\ & +{\beta }_5{\mathit{\text{Numeric IIV Metric}}}_i*{\mathit{\text{Age}}}_i\\ & +{\beta }_6{\mathit{\text{Stressor Exposure}}}_i*{\mathit{\text{Age}}}_i\\ & +{\beta }_7{\mathit{\text{Numeric IIV Metric}}}_i*{\mathit{\text{Stressor Exposure}}}_i*{\mathit{\text{Age}}}_i+{\epsilon }_i\end{array}$$ (4)

where, with all grand-mean centered predictors, β₀ is the prototypical NSDE participant’s expected negative affect, β₁ is the unique association between the numeric IIV metric (i.e., stressor relative dominance, stressor diversity, or stressor log-skew) and NA, β₂ is the unique association between stressor exposure and NA, β₃ is the unique association between age and NA, β₄ is the extent to which the numeric IIV metric moderates the association between stressor exposure and negative affect, β_5–7 are the extent to which the age moderates the above associations, and ε_i is unexplained residual that is assumed independent and normally distributed. Stressor exposure, an established predictor of negative affect in the stress literature, is included as a covariate here in order to evaluate the contribution of the categorical IIV metrics above and beyond the simple “counting” of exposure to stressors.

For the nominal metrics, individual differences in negative affect were examined as group differences in an analysis of variance (ANOVA) framework (each nominal metric separately),

$$Negative Affec{t}_i= {\alpha }_0+{\alpha }_{1}NominalMetri{c}_i+{\epsilon }_i$$ (5)

where α₀ is the mean level of negative affect in the reference category and the vector α₁ indicates how average negative affect at each level of the nominal metric differs from the reference category. All models were fit using R (e.g., lm function; R Core Team, 2016), with missing data treated as missing completely at random. Code and an illustrative tutorial can be found on the Penn State Quantitative Developmental Systems website (http://quantdev.ssri.psu.edu).

Results

Numeric Metrics of Categorical IIV

Descriptives

Descriptive statistics of the numeric categorical IIV metrics are displayed in Table 1. Stressor relative dominance ranged from 0.17 to 1 (M = 0.59, SD = 0.26), and was negatively associated with both stressor exposure (r = −.57), which ranged from 0 to 4.14 (M = 0.55, SD = 0.48), and stressor diversity (r =−.95), which ranged from 0 to 1 (M = 0.44, SD = 0.30). Note that with 6 stressor types assessed over 8 days, stressor dominance and stressor diversity are inherently highly negatively associated. Consistent with NSDE Wave 2 (see Koffer et al., 2016), stressor exposure and stressor diversity were positively correlated (r = .70). Stressor log-skew ranged from −56.18 to 50.31 (M = 2.61, SD = 13.88), and was correlated with stressor relative dominance (r = .49), stressor diversity (r = −.51), and stressor exposure (r = −.33). The associations among the numeric metrics support their conceptual definitions: higher stressor relative dominance indicates a more recurrent modal stressor type, higher stressor diversity indicates more stressor type heterogeneity, and higher stressor log-skew indicates fewer rare stressors.

Table 1.

Descriptive Statistics of and Correlations Among the Numeric Metrics of the Stressor Type Distribution in NSDE Wave 1

	N	Mean	(SD)	1.	2.	3.	4.	5.	6.
1. Stressor Relative Dominance	1,336	0.59	(0.26)	--
2. Stressor Diversity	1,336	0.44	(0.30)	−0.95	--
3. Stressor Log-Skew	1,335	2.61	(13.88)	0.49	−0.51	--
4. Stressor Exposure	1,471	0.55	(0.48)	−0.57	0.70	−0.33	--
5. Age	1,498	46.21	(23.87)	0.11	−0.13	0.06	−0.20	--
6. Negative Affect	1,486	0.20	(0.28)	−0.17	0.20	−0.04	0.34	−0.14	--

Note: NSDE = National Survey of Daily Experiences; SD = Standard deviation. Missing cases for stressor exposure variable are individuals who did not have stressor data across the entire reporting period. Missing cases for stressor diversity and relative dominance are individuals who reported no stressors (n = 132) or only discrimination stressors (n = 3) across the entire reporting period. Bold highlighted the values we were most interested in.

Relations with age and negative affect

As seen in Table 1, older age is associated with higher stressor relative dominance (r = .11), lower stressor exposure (r = −.20), and lower stressor diversity (r = −.13). Individuals with higher overall negative affect (NA) tended to have lower stressor relative dominance (r = −.17), and higher stressor diversity (r = .20) and stressor exposure (r = .34). Stressor log-skew was very weakly associated with age (r = .06) and NA (r = −.04).

Age differences in stressor relative dominance were described by a decreasing linear gradient, β₁ = −0.01 (p = .04) with upward curvature, β₂ = 0.0001 (p = .01). Stressor diversity demonstrated an increasing linear age gradient, β₁ = 0.01 (p = .02) with downward curvature, β₂ = −0.0001 (p = .002). Stressor log-skew was described by a decreasing linear age gradient β₁ = −0.48 (p = .03) with upward curvature, β₂ = 0.006 (p = .01). Thus, older adults experienced more stressor dominance, less stressor diversity, and more stressor skew than their younger counterparts.

Models regressing NA on each of the three numeric metrics are shown in Table 2. In Model 1, where stressor relative dominance is the numeric IIV metric of interest, the prototypical NSDE participant’s NA was estimated as β₀ = 0.21 (p < .001) on the 0 to 4 scale. Stressor relative dominance and stressor exposure were both associated with higher NA, β₁ = 0.09 (p = .03) and β₂ = 0.25 (p < .001), within the context of a significant Stressor relative dominance × Stressor exposure interaction β₄ = 0.21 (p = .01). That is, the relation between stressor relative dominance and NA was moderated by level of stressor exposure. Older age was associated with lower NA β₃ = −0.002 (p = .002), and damped associations between stressor relative dominance and NA, β₅ = −0.007 (p = .04) and stressor exposure and NA, β₆ = −0.004 (p = .03). The interaction between stressor relative dominance and stressor exposure was age invariant.

Table 2.

Negative Affect Regressed on Numeric Metrics of the Stressor Type IIV Distributions from NSDE Wave 1

	Model 1: Numeric metric = Stressor Dominance		Model 2: Numeric metric = Stressor Diversity		Model 3: Numeric metric = Stressor Log-skew
	Est	(SE)	Est	(SE)	Est	(SE)
Intercept	0.21*	(.01)	0.21*	(0.01)	0.20*	(0.01)
Numeric IIV Metric	0.09*	(0.04)	−0.11*	(0.04)	<0.01*	(<0.01)
Stressor Exposure	0.25*	(0.02)	0.28*	(0.03)	0.22*	(0.02)
Age	>−0.01*	(<0.01)	>−0.01*	(<0.01)	>−0.01*	(<0.01)
Numeric IIV Metric × Stressor Exposure	0.21*	(0.09)	−0.20*	(0.07)	<0.01*	(<0.01)
Numeric IIV Metric × Age	−0.01*	(<0.01)	0.01*	(<0.01)	>−0.01	(<0.01)
Stressor Exposure × Age	>−0.01*	(<0.01)	>−0.01*	(<0.01)	>−0.01	(<0.01)
Numeric IIV Metric × Stressor Exposure × Age	−0.01	(0.01)	0.01	(0.01)	>−0.01	(<0.01)
R 2	0.12		0.13		0.12

Note: NSDE = National Survey of Daily Experiences; SE = Standard error. Negative Affect is computed as a person-specific mean on a 0 to 4 scale for T= 8 days. Missing cases for stressor exposure variable are individuals who did not have stressor data across the entire reporting period. N_Model1 = 1,312; N_Model2 = 1,312; N_Model3 = 1,311. Missing cases are individuals who did not have stressor and negative affect data (n = 28), or reported no stressors (n = 155) or only discrimination (n = 3) across the entire reporting period. *indicates p < .05.

In Model 2, stressor diversity was associated with lower NA, β₁ = −0.11 (p = .002), and stressor exposure was associated with higher NA, β₂ = 0.29 (p < .001), within the context of a significant Stressor diversity × Stressor exposure interaction; with higher stressor diversity, the link between stressor exposure and NA was weaker, β₃ = −0.20 (p = .002). Older age damped the association between stressor exposure and NA, β₆ = −0.005 (p = .03), and trended toward enhancing the association between stressor diversity and NA, β₅ = 0.005 (p = .08). The interaction between stressor diversity and stressor exposure was age invariant.

In Model 3, stressor log-skew was associated with higher NA, β₁ = 0.002 (p = .002) and stressor exposure, β₂ = 0.23 (p < .001), within the context of a significant Stressor log-skew × Stressor exposure interaction, β₃ = 0.003 (p = .02). These associations were age invariant, β₅ to β₇ all not significantly different than zero (ps > .30).

Both stressor relative dominance and stressor diversity capture the (lack of) heterogeneity of stressors, so at average levels of stressor exposure, greater stressor heterogeneity is associated with lower negative affect. Heterogeneity is protective. However, the presence of “rare” stressors (e.g., high log-skew) contributes to higher negative affect. Overall, the evidence of both main effects and moderation suggest that the numeric categorical IIV metrics offer new information about how the stressor ecosystem contributes to individuals’ well-being.

Nominal Metrics of Categorical IIV

Descriptives

While in principle there are six possible modes, accommodating for ties provided 59 modal stressor combinations. Of the total N = 1,336 sample, n = 325 (24.33%) individuals’ modal stressor was nonargument interpersonal tensions, for n = 174 (13.02%) it was work stressors, for n = 148 (11.08%) arguments, for n = 101 (7.56%) home stressors, for n = 72 (5.39%) network stressors, and for n = 49 (3.67%) other stressors. In addition to those who had one modal stressor, n = 55 (4.12%) had equally-proportioned arguments and nonargument interpersonal tensions modes, and n = 43 (3.22%) had equally-proportioned work stressor and nonargument interpersonal tension modes, with all other combinations being very rare. In sum, modal stressor types are extremely heterogeneous across the sample.

Of the 64 possible stressor spreads that might manifest in 6-category data, 63 were represented in the empirical data. The most frequent stressor spreads consist of only other stressors (n = 148, 11.08%); network stressors and other stressors (n = 81, 6.06%); nonargument interpersonal tensions and other stressors (n = 62, 4.64%); only nonargument interpersonal tensions (n = 53, 3.97%); only network stressors (n = 47, 3.52%); network, work, and other stressors (n = 38, 2.84%); network, work, nonargument interpersonal tensions, and other stressors (n = 35, 2.62%); network, work, arguments, and other stressors (n = 32, 2.40%); and network, work, home, nonargument interpersonal tensions, and other stressors (n = 30, 2.25%). Again, there are lots of heterogeneity in how 8 days of stressor experiences are dispersed across categories.

Of the 873 possible orders that might manifest in 6-category data, only 395 different rank-ordered sequences were represented in the empirical data. The most prevalent sequences, though still quite rare were: n = 150 (11.23%) experienced the rank ordered sequence 1. nonargument interpersonal tensions, with all other stressor types equally ranked at 2.; n = 53 (3.97%) had order with 1. work stressors, with the all other stressor types equally ranked at 2.; n = 47 (3.53%) had order with 1. arguments, with all other stressor types equally ranked at 2.; and n = 41 (3.07%) had order with 1. nonargument interpersonal tensions, 2. arguments, and all other stressor types equally ranked at 3. Again, there is substantial heterogeneity in how the stressors individuals experience are ordered with respect to relative frequency. In sum, all three nominal metrics reveal extremely abundant, unique IIV distributional attributes—even for a simple 6-category measurement scheme—highlighting both the value and difficulty inherent in categorical heterogeneity.

Relations with negative affect

Results from an ANOVA indicated that the 59 mode groups did not significantly differ on NA, F(58, 1,268) = 0.96, p = .56. Descriptive information for mean and standard deviation NA of most frequent mode types are displayed in Panel A of Figure 3.

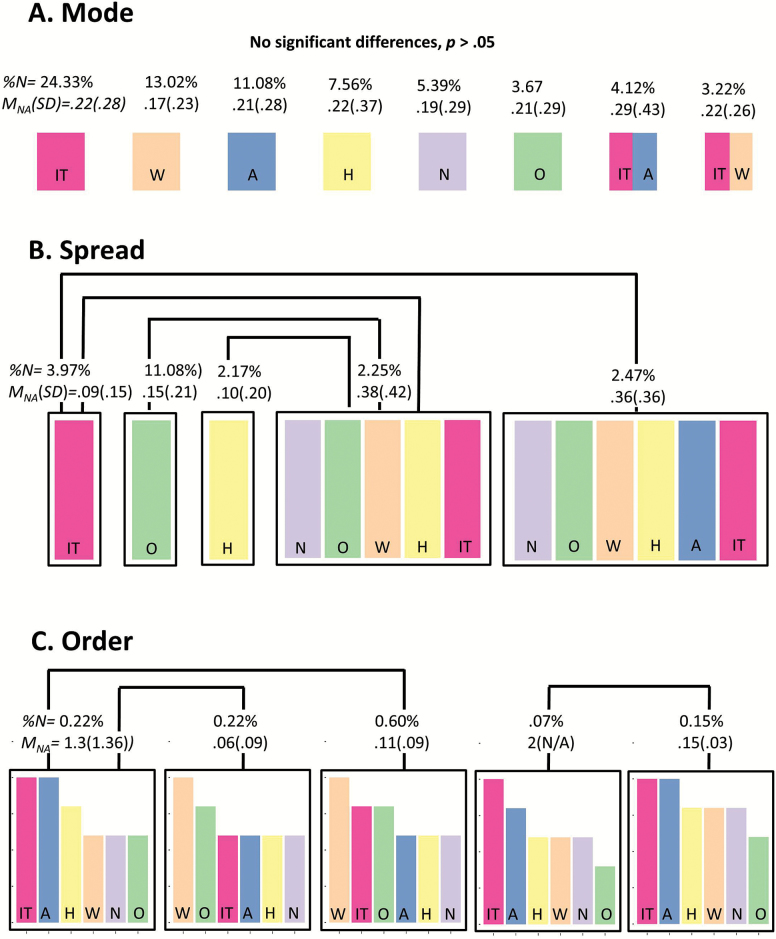
Figure 3.

Panel A: Most frequent mode types in NSDE Wave 1 stressor data. Panel B: Stressor Spreads (individual spread represented as colors within each black box). Panel C: Sample of order sequences, represented as relative heights of the bar chart. 518 pairwise comparisons (0.007% of total possible comparisons) were significant (Tukey adjusted p < .05). Note for all panels: For each group (mode type, spread group, and order sequence), the percentage of total population (N = 1,336), mean (M_NA) and SD of negative affect are displayed. IT = nonargument interpersonal tensions (pink), A = argument stressors (blue), W = work stressors (orange), H = home stressors (yellow), N = network stressors (purple), O = other stressors (green).

Results from an ANOVA testing whether the 63 spread groups differed on average NA revealed significant group differences, F(62, 1,264) = 2.07, p < .001. Post-hoc (Tukey’s HSD adjusted) tests depicted in Panel B of Figure 3 indicated that the (network, other, work, home, argument, nonargument interpersonal tensions) spread group (M_NA = 0.36, SD_NA = 0.36) had significantly higher average NA than the (nonargument interpersonal tensions) spread group (M_NA = 0.09, SD = 0.15; p = .02). The (network, other, work, home, nonargument interpersonal tensions) spread group (M_NA = 0.38, SD_NA = 0.42) also had significantly higher NA than the (other) spread group (M_NA = 0.15, SD_NA = 0.21; p = .01), the (home) spread group (M_NA = 0.10, SD_NA = 0.20; p = .045), and the (nonargument interpersonal tensions) spread (M_NA = 0.09, SD_NA = 0.15; p = .001).

ANOVA and Tukey HSD adjusted post-hoc tests also revealed NA differences among the 395 stressor order groups, F(393, 936) = 1.38, p < .001 (one group removed for complete missingness on NA). From all possible order sequence comparisons, 518 (.007%) were significant (Tukey adjusted), of which we present a few sample cases. For instance, as shown in Panel C of Figure 3, stressor order of (1. nonargument interpersonal tensions, 1. arguments, 3. home, 4. work, 4. other, 4. network) (M_NA = 1.30, SD_NA = 1.36) had higher average NA than stressor orders of (1. work, 2. other, 3. nonargument interpersonal tensions, 3. arguments, 3. home, 3. network) (M_NA = 0.06, SD_NA = 0.09; p < .001) and (1. work, 2. nonargument interpersonal tensions, 2. other, 4. arguments, 4. home, 4. network) (M_NA = 0.11, SD_NA = 0.09; p < .001). As well, stressor order of (1. nonargument interpersonal tensions, 2. arguments, 3. home, 3. work, 3. network, 6. other) (M_NA = 2.00, SD_NA = N/A; one individual) had higher NA than stressor order of (1. home, 1. work, 3. nonargument interpersonal tensions, 3. arguments, 3. network, 6. other) (M_NA = 0.15, SD_NA = 0.03; p < .001). Significant differences in average NA among stressor order groups suggest that nominal asymmetry in the relative frequency of stressor types impacts individuals’ affective well-being.

In sum, we find that the modal stressor is not associated with negative affect, but that stressor spread and stressor order are indeed associated with negative affect. While difficult to parse, there appears to be value in trying to understand the differences measured by the nominal metrics.

Discussion

This study introduced six metrics for examining interindividual differences in IIV of categorical data. Our approach summarized categorical intensive repeated measures using the same principles applied to their continuous scale counterparts (i.e., description of statistical moments of the IIV distribution). Specifically, we identified three numeric metrics to quantify distributional features: relative dominance describes the frequency of the central tendency, diversity measures dispersion, and log-skew measures asymmetry; and three nominal metrics to capture categorical content of the statistical moments: mode as a measure of central tendency, spread as dispersion across categories, and order as asymmetry across categories. We illustrated how these metrics can be used in analysis of large-scale daily diary data to measure dynamic characteristics of individuals’ stressor experiences and examine how those characteristics are related to age and individual differences in negative affect. Results suggest the six metrics capture meaningful aspects of individuals’ stressor ecosystems and should be further incorporated into stressor theory. By systematically applying IIV principles to categorical variables, we hope that the six categorical IIV metrics provided here can expand the variety of research questions that may be answered using experience sampling data.

Individual Differences in Stressor-type IIV

Our exploration into categorical IIV metrics was situated in study of daily stress; particularly, IIV in daily reports of the types of stressors individuals experienced. Analysis of such data has typically summed across types and/or days to quantify total stressor exposure or used multilevel models to examine stressor reactivity (Almeida, 2005). Although conceived as distinct, the different stressor types (arguments, work stressors, etc.) are often treated as fully interchangeable. Only a handful of studies have made use of stressor category information in experience sampling data. For example, Hay and Diehl (2010) and Neupert, Almeida, and Charles (2007) examined how protective factors, such as control beliefs and self-concept differentiation, interact uniquely with interpersonal, work, home, network, and health stressors, while Stawski, Cichy, Piazza, and Almeida (2013) examined whether day-to-day differences in diurnal cortisol were related to experience of specific types of stressors. Recent studies have also begun to quantify and examined differences in stressor diversity (relative abundance of different stressor types; Brose et al., 2013; Koffer et al., 2016). These prior studies clearly indicate both the empirical value of across-category information (e.g., increased prediction of well-being) and its theoretical importance for identifying mechanisms through which stressor experiences influence well-being (e.g., cross-domain resource depletion; (Hobfoll, 1989; Lazarus & Folkman, 1984). Here, we expand the ways stressor category information can be summarized and used in analysis.

The value of the three numeric metrics, relative dominance, diversity, and log-skew, was demonstrated by their theoretically meaningful age gradients and the additional precision they contributed to prediction of individual differences in negative affect (above stressor exposure). In line with life course theory, stressor relative dominance is at its minimum in early midlife, when individuals are likely balancing multiple roles, and thus less likely to experience one stressor type far more than others (Pearlin, 1989). Similarly, stressor diversity reaches its maximum during midlife, indicating stressors are spread across several types, as opposed to concentrated in a few types. Finally, in line with socioemotional selectivity theory, older adults indeed have proportionally more stressors in common rather than rare stressor types (Carstensen et al., 1999). Replicating previous analysis of NSDE Wave 2 data (Koffer et al., 2016), we found that greater heterogeneity is associated with lower overall NA, suggesting that stressor diversity allows for resource replenishment (Hobfoll, 1989; Lazarus & Folkman, 1984). The link between higher log-skew (fewer rare stressors) and higher NA, corroborates the notion that spread across a variety of stressors, even those that are rare, may offer opportunity for resource replenishment.

We also found value with the nominal metrics, mode, spread, and order. In these data, modal stressor was not associated with negative affect. However, this may be due to high number of p_max ties, which requires considering 59 stressor modal combinations. The study design, with only 8 days and 6 stressor types, might not have enabled the most preponderate category to assert itself. Longer time series will likely reduce ties for easier comparison. Significant group differences emerged for both stressor spread and stressor order. In line with stress and appraisal theory (Lazarus & Folkman, 1984), the differences among stressor spread and stressor order groups highlight the value of theorizing about and studying interindividual differences in both dispersion across the stressor space, and relative asymmetry in frequency of individuals’ sources of stress.

Notably, difficulties interpreting the nominal IIV metrics arise from comparing across many identified groups. Our 6-category data, for example, provides 64 possible configurations of spread and 873 possible configurations of order. Consequently, coherent interpretation of individual differences (e.g., NA differences, age differences, or even age-moderated NA differences) among a large number of sparsely observed configurations is challenging (see Horn, 1967). Encouragingly, the study of IIV is meant to capture idiosyncratic experience throughout development (see Molenaar, 2004). Furthermore, rich literatures in other fields (e.g., bioinformatics, chemistry, and big data enterprises more generally), make use of combinatorial lists (e.g., in DNA sequencing, microbial diversity sequencing, text analysis). Moving forward, there are good examples to follow as we continue to untangle the nominal summaries of categorical experience sampling data.

Application to Developmental/Gerontological Research

The numeric and nominal metrics for categorical IIV allow for several theoretically important applications for developmental and aging research. Many theories of aging highlight developmental changes that manifest as differences in categorical IIV. For example, Selective Optimization and Compensation (Baltes & Baltes, 1990) and Socioemotional Selectivity Theory (Carstensen et al., 1999) suggest that older adults selectively interact with specific types of social partners (e.g., family, friend, coworker). We can now test for age differences in social partner distributions using either numeric or nominal metrics (older adults should have higher relative dominance, and spread lists that are less likely to include strangers). Furthermore, we can potentially use categorical IIV metrics as indicators of (un)successful aging. For example, greater activity diversity might be indicative of successful aging (Lee et al., 2016). Relatedly, the categorical IIV metrics may offer specificity for intervention targets—directing support toward individuals with distributional characteristics associated with negative outcomes—an approach already being used to identify intervention targets in ecology (Magurran & McGill, 2011). Next steps include validating the categorical IIV metrics and associated constructs through empirical studies associate those constructs with other constructs (e.g., well-being, personality) and developmental change. Recent examples include studies of how activity diversity, stressor diversity, and emotional diversity are related to physical and mental well-being, and age (Benson, Ram, Almeida, Zautra, & Ong, 2017; Brose et al., 2013; Koffer et al., 2016; Lee et al., 2016). Using typical methods (e.g., SEM, multilevel models) these papers begin establishing theoretically informative findings regarding convergent validity, divergent validity, and stability/change of the diversity constructs. As this body of works extends to cover the other five metrics introduced here, the push into categorical IIV may help us articulate, operationalize, and test long-standing tenets of developmental theory.

Cautionary Notes

Our study of categorical IIV constructs of course has some caveats. Notably, our analysis of 8-day daily diary data underscored the need for study designs with more occasions. High correlation between the numeric relative dominance and diversity metrics, and the abundant ties in the nominal metrics hamper the study of individual differences in IIV in this T = 8, m = 6 design. Simulations and empirical studies both suggest that (continuous) IIV metrics require 25+ sampling occasions, depending on the construct of interest (Mejía, Hooker, Ram, Pham, & Metoyer, 2014). Similarly, biologists have highlighted the difficulty small samples pose for studying categorical IIV with diversity metrics (Magurran & McGill, 2011).

Several approaches may be helpful in our smaller, currently available data. While our analytical framework (ANOVA) kept all 59 modes/combinations of modes as separate factors, one could instead use a theory-based ranking system to deal with equal proportions, or a data-driven data reduction approach (e.g., with dissimilarity matrices and clustering) to obtain a more manageable number of comparisons. Similarly, the nominal metrics capture some information also captured in numeric IIV metrics; for example, the individual on the top of panel D may experience greater negative affect than the individual on the bottom due to the greater number of stressor types experienced along with nominal differences in specific types experienced. Complexity might be reduced by examining metrics in combination (e.g., among individuals with equivalent stressor diversity, does stressor spread predict negative affect differences?).

However, it is important to understand and address the nonlinear relations among the numeric metrics. Mathematically, the measure of relative dominance (p_ij = p_max; Equation 1) is a component of the measure of stressor diversity (i.e., Equation 2 includes p_ij). Thus, and particularly at extreme values of stressor dominance, the dominance and diversity metrics are highly related (see Supplementary Figure 1). In fact, each of the three numeric metrics is derived in some way from, and correlates with, both the total number of categories (m) and the total number of observations in all categories ($N={\displaystyle {\sum }_{j=1}^m{n}_{ij}}$ ). That is, the metrics are mathematically related to each other in known ways. As such, we encourage careful consideration of the time-series lengths, number of categories, and inherent relations/properties of the score calculations before treating them as indicators of independent constructs and/or including more than one metric in a regression (inherent multicollinearity). Specifically, we recommend first using theory to choose an appropriate metric(s), followed by empirical examination of how the metrics are correlated, and if necessary, multivariate analytical approaches and/or computation of alternative dominance and diversity indices (see Magurran & McGill, 2011) that are of theoretical interest.

More broadly, we note that net IIV metrics, like those forwarded here, allow researchers to study interindividual differences, but do not explicitly describe dynamic processes (i.e., the metrics do not consider time dependencies; see Ram & Gerstorf, 2009). Careful consideration of the measurement methods along with theoretical and analytical consideration of the source of IIV (person, context, and/or person-context interaction; see Koffer & Ram, 2016) will be useful for understanding the meaning of categorical IIV.

Synopsis

Developmental research on stress, activity engagement, and emotion complexity (to name only a few) has begun to demonstrate theoretically meaningful age differences using categorical IIV. The additional metrics introduced here provide an opportunity to expand the range of developmental questions that may be asked with categorical repeated measures. In the same way that metrics and models of continuous IIV have continued to advance our understanding of micro-time scale processes through the life span (Diehl, Hooker, & Sliwinski, 2015), we hope further development of categorical IIV metrics will help uncover the information embedded in the plethora of categorical repeated measures being collected in psychological and aging research.

Supplementary Material

Supplementary data are available at The Journals of Gerontology, Series B: Psychological Sciences and Social Sciences online.

Funding

This work was supported by the National Science Foundation (IGERT 1144860), National Institutes of Health (R01 HD076994, P2C HD041025, UL TR000127, T32 AG049676, R01 AG19239, P01 AG0210166), and the Penn State Social Science Research Institute.

Conflict of Interests

The authors have no conflicts of interest to disclose.