The Use of Growth Mixture Modeling for Studying Resilience to Major Life Stressors in Adulthood and Old Age: Lessons for Class Size and Identification and Model Selection

Abstract

Objectives

Growth mixture modeling (GMM) combines latent growth curve and mixture modeling approaches and is typically used to identify discrete trajectories following major life stressors (MLS). However, GMM is often applied to data that does not meet the statistical assumptions of the model (e.g., within-class normality) and researchers often do not test additional model constraints (e.g., homogeneity of variance across classes), which can lead to incorrect conclusions regarding the number and nature of the trajectories. We evaluate how these methodological assumptions influence trajectory size and identification in the study of resilience to MLS.

Method

We use data on changes in subjective well-being and depressive symptoms following spousal loss from the HILDA and HRS.

Results

Findings drastically differ when constraining the variances to be homogenous versus heterogeneous across trajectories, with overextraction being more common when constraining the variances to be homogeneous across trajectories. In instances, when the data are non-normally distributed, assuming normally distributed data increases the extraction of latent classes.

Discussion

Our findings showcase that the assumptions typically underlying GMM are not tenable, influencing trajectory size and identification and most importantly, misinforming conceptual models of resilience. The discussion focuses on how GMM can be leveraged to effectively examine trajectories of adaptation following MLS and avenues for future research.

Major life stressors (MLS) have the potential to influence the course of development across the adult life span (Baltes & Nesselroade, 1979; Hultsch & Plemons, 1979). However, not all individuals succumb to the detrimental consequences of MLS. The resilience literature is built on the premise that there is heterogeneity in individuals’ ability to adapt following adversity, with some being able to maintain psychological functioning, whereas others show declines, followed by gradual improvement to near-previous levels (Bonanno, 2004; Infurna & Luthar, 2016a; Luthar, Cicchetti, & Becker, 2000; Zautra, Hall, Murray, & The Resilience Solutions Group, 2008). This is especially pertinent in adulthood and old age as the likelihood of confronting significant adversity, such as spousal loss or chronic illness increases.

The past decade has seen an influx of research in the adulthood and old age literature that has utilized a resilience perspective to study individual variations in response to a wide range of adversities (for overview, see Bonanno & Diminich, 2013). Trajectories that have been observed include resilience, recovery, growth, and chronic low, with debates recently as to whether resilience or recovery is the most common trajectory (Galatzer-Levy & Bonanno, 2016; Infurna & Luthar, 2016a, 2016b). Resilience is broadly defined as exhibiting stable, healthy levels of psychological functioning before and after the adversity; a recovery trajectory is characterized by individuals showing declines as a function of the adversity, followed by gradual improvements to near-previous levels; growth refers to improvements in psychological functioning that is enduring; chronic low refers to individuals exhibiting sustained declines in psychological functioning following the adversity.

The explosion of research on resilience has been coupled with advancements in longitudinal research methodology, in particular the utilization of growth mixture modeling (GMM). GMM combines aspects of latent growth curve modeling and finite mixture modeling to identify discrete trajectories in longitudinal data (more details below). However, the use of GMM and its methodological assumptions have come under scrutiny and this is the crux of our study. Our objectives are to evaluate whether and how commonly applied methodological assumptions of GMM influence findings when using GMM, namely, homogeneity of variance across trajectories and non-normality in the data. Our interest is in examining whether these methodological assumptions influence class size and identification. The use of GMM has recently been heavily utilized in the study of resilience to MLS (Bonanno & Diminich, 2013; Infurna & Luthar, 2016a), but also has wider applicability in other literatures, including the examination of substance use trajectories in adolescence and young adulthood (see Chassin, Sher, Hussong, & Curran, 2013) and disability in adulthood and old age (see Liang, Xu, Bennett, Ye, & Quiñones, 2010; Martin, Zimmer, & Lee, 2017). To carry out the objectives of our study, we use GMM to examine resilience to spousal loss across dimensions of subjective well-being (life satisfaction and positive affect) and mental health (depressive symptoms).

Approaches to Studying Resilience to MLS in Adulthood and Old Age

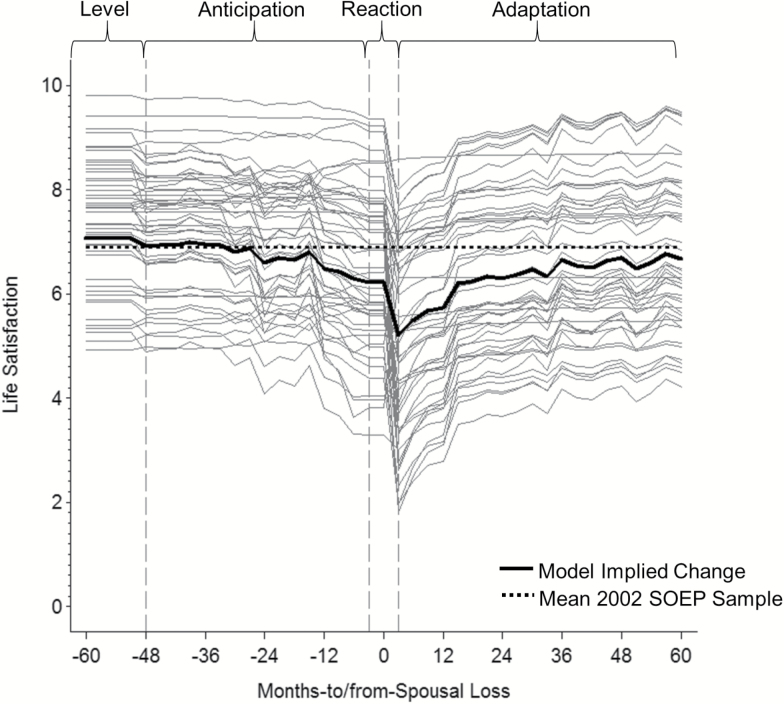
There are various approaches to studying whether and how MLS influence developmental change across the adult life span. One approach is to use latent growth curve (multilevel) modeling to examine changes in, for example, life satisfaction before and after adversity. Latent growth curve modeling allows for studying the sample as a single population, with the ability to examine model-implied changes and assessing whether there are between-person differences in level and rates of change over time (Grimm, Ram, & Estabrook, 2017). For example, Lucas (2007) has found that changes in life satisfaction before and after MLS are typically represented by a multiphase process; on average, individuals exhibit declines as a result of the MLS, followed by gradual improvement to near-previous levels in the years thereafter. This is exemplified in Figure 1, which shows that, on average, life satisfaction shows a multiphase change process before and after spousal loss, with declines occurring in the 2 years prior to spousal loss, substantial declines surrounding the year of spousal loss, followed by gradual improvements to near-previous levels in the years thereafter (see Infurna et al., in press). The gray lines in Figure 1 represent a subset of individuals’ model-implied change and, most importantly, signify the great deal of heterogeneity in levels and rates of change in life satisfaction; this demonstrates that not all individuals show the same levels and rates of change. One way to target these between-person differences is the inclusion of moderators. Infurna and colleagues (in press) did this and found that individuals who were younger reported stronger declines in life satisfaction at the year of spousal loss, but showed quicker adaptation in the years thereafter. An additional factor found to be predictive of better adaptation was higher levels of social participation.

Figure 1.

Within-person changes and between-person variation in life satisfaction before and after spousal loss (from Infurna et al., in press). The solid black line represents the model-implied average taken from the sample under study and the gray lines represent model-implied changes from a subset of participants. One can observe that there is a great deal of between-person variation in the extent to which life satisfaction changes before and after spousal loss. Reprinted with permission from Infurna et al. (in press).

This approach has clear advantages in its ability to examine the nature of change in a large sample and identifying factors that are associated with better (or worse) changes following the adversity. However, this approach inhibits the ability to extract discrete trajectories of change. Looking more closely at Figure 1, one can observe that there are certain subgroups or classes of individuals who show stable, high levels of life satisfaction, whereas others show more substantial and sustained changes, relative to others. One way to examine this further is through the use of GMM, which we next discuss in detail.

The use of GMM to study resilience

The resilience literature has been instrumental in illuminating individual variations following adversity. Early work by Bonanno (2004) showed that resilience was the modal response to most significant life adversities encountered (see Bonanno & Diminich, 2013). This evolved together with the advent of GMM. GMM, as an extension of latent growth curve (multilevel) modeling, allows researchers the ability to extract discrete trajectories from the sample that are unobserved, such as resilience, recovery, growth, and chronic low.

The use of GMM allows for new research questions to be asked, such as are there different paths that individuals follow in the months and years following spousal loss? An initial study by Mancini, Bonanno, and Clark (2011) found that 59% of individuals who experienced spousal loss showed stable, high levels of life satisfaction that is characteristic of resilience. Other trajectories that were found included recovery (21%), improvement (5%), and chronic low levels (15%). Similarly, Galatzer-Levy and Bonanno (2012) found 66% of individuals belonged to a resilient trajectory of stable, low levels of depressive symptoms following spousal loss, with additional trajectories being that of chronic grief (9%), chronic depression (15%), and improvement (10%). Stable low levels of depressive symptoms following spousal loss was the most commonly observed trajectory by Maccallum, Galatzer-Levy, and Bonanno (2015), with 71% of the sample likely to comprise this trajectory. More recently, Infurna and Luthar (2016a), in a reanalysis of data from Mancini and colleagues (2011), found that a recovery class was largest (53%) followed by the resilient class (47%), with the models indicating that a single class model may best represent the data. Furthermore, Infurna and Luthar (in press) took a multidimensional approach to examining resilience to spousal loss that involved the simultaneous examination of five key indicators, with results showing that 66%, 19%, 26%, 37%, and 29% were resilient in life satisfaction, negative affect, positive affect, general health, and physical functioning, respectively. When Infurna and Luthar (in press) considered all five outcomes collectively, only 8% showed across the board resilience, whereas 20% were not resilient across all five outcomes. Contrasting findings could be the result of incorporating multiple outcomes and most pertinent for this study, differences in methodological assumptions underlying the application of GMM in each study.

Key assumptions underlying model specifications in GMM

Research studies that have applied GMM to study resilience to MLS have overwhelmingly assumed two key methodological assumptions. The first consideration revolves around homogeneity of variance across trajectories and setting the slope variances to 0 (for discussion, see Infurna & Luthar, 2016a, 2016b). A second consideration that has received less attention is whether the outcome is normally distributed. In the case of depressive symptoms and post-traumatic stress symptoms, the data typically are not normally distributed.

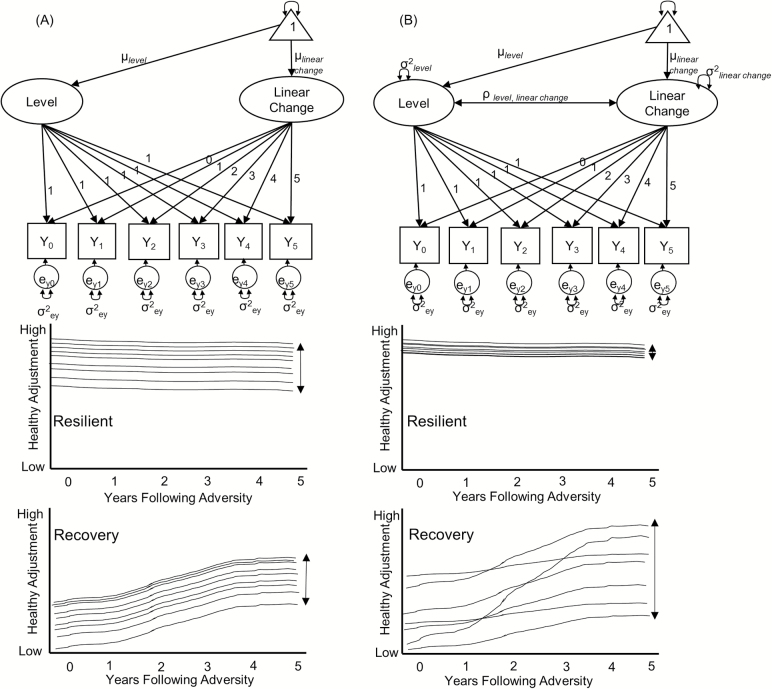
The implications of these methodological assumptions are shown in Figure 2. Figure 2A displays the restrictive methodological assumptions, commonly referred to as a latent class growth analysis approach (LCGA; Nagin, 1999), where researchers are assuming that the latent variable variances and covariances (i.e., intercept and slope), the structure of changes over time, and residual variances are assumed to be equal across trajectories. LCGA forces all of the between-person differences in the change trajectories to be attributable to having multiple latent classes. Relaxing these assumptions has been shown to change the relative size and nature of the latent classes (Infurna & Luthar, 2016a) and implies different conceptual considerations of the observed classes (see Figure 2B).

Figure 2.

Conceptual representation of assumptions underlying the latent class growth analysis (A) and growth mixture model (B). The key differences between the approaches are the assumption of homogeneity of variance across trajectories (A) and allowing the variances to differ across trajectories (B).

Supporting claims by Infurna and Luthar (2016a, 2016b) of relaxing the homogeneity of variance assumption, a rigorous simulation study by Diallo, Morin, and Lu (2016) showed that relaxing this methodological assumption protects against over-extraction of trajectories and increases the ability to recover the proper number of trajectories underlying the data. More specifically, using simulated data, Diallo and colleagues (2016) demonstrated that when only one trajectory was known to encompass the data, the use of these restrictive assumptions led to four trajectories being found in over 95% of the simulations. Furthermore, Diallo and colleagues (2016) showed that when three trajectories were known to encompass the data, the model with the relaxed methodological assumptions found three trajectories to best represent the data in over 90% of the simulations. These discrepant findings based on methodological assumptions and coupled with the wide-spread use of GMM across adversities in the literature signifies the importance of thoroughly testing the implications of these assumptions for the number of trajectories identified and the proportion of individuals in each trajectory.

Non-normality and its causes

As shown by Bauer and Curran (2003), the GMM, and the finite mixture model more generally, is one way to account for non-normality in the distribution of observed variables. That is, a summation of normal distributions can account for non-normal data better than a single normal distribution. The distribution of observed variables in a GMM is a combination of multiple mixture distributions because there are often two (or more) latent variables (e.g., intercept and slope) in a GMM, as well as the unique factors, which may come from a mixture distribution.

Non-normality of outcome measures, which is common in the social and behavioral sciences, can be seen as a reason why mixture models have become so popular. Mixture models can provide a rationale (i.e., multiple classes) for the non-normality of outcome scores (one related to sampling multiple populations). As discussed by Grimm and Ram (2009), there are multiple reasons why outcome data may be non-normal. For example, researchers may select participants who meet some criteria, which often eliminates individuals from a specific part of the distribution. As a second example, researchers may be interested in certain types of negatively valenced behaviors, such as externalizing behaviors, and the nature of the scale does not differentiate between people who show differing levels of positive behaviors.

Researchers may not fully consider whether a more appropriate outcome distribution may be necessary for the data. For example, GMMs are often applied to negatively valenced behaviors (e.g., behavior problems, depressive symptoms), and the distribution of these types of behaviors is typically non-normal. Moreover, the measurement of these constructs may be counts. For example, scores on the Center for Epidemiologic Studies-Depression (CES-D) in the Health and Retirement Study are counts of the frequency of certain depressive symptoms. In these situations, it would be important to model the data as having a Poisson or negative binomial distribution. Thus, there would be a nonlinear relationship between the observed variables and the latent variables. Importantly, for our discussion of GMM, the link function between the observed and latent variable may affect the nature of latent classes in both the number of classes and the composition of the latent classes. Furthermore, incorrectly treating count data (or ordinal data) as having a normal distribution may suggest there are latent classes when, in fact, no latent classes exist.

The Present Study

Given the overall state of the literature in adulthood and old age that has applied GMM to examine resilience to MLS (see Infurna & Luthar, 2016a, 2016b), we believe that there are several questions/issues that need to be openly discussed and require further consideration in the implementation of GMM. Researchers need to better understand (a) the reasons for differences in findings when utilizing different methodological approaches (i.e., LCGA vs GMM); (b) what goes into the implementation of these models—if the same data are used and specifications of the model are changed, then why are dramatically different findings observed; and (c) the distribution of the outcome and how it potentially influences model specifications. To address these open questions/issues, we examine how model assumptions, namely in the across trajectories constraints, and the link function affect the results and conclusions garnered from the use of LCGA and GMM. For this, we utilize an illustrative example (as opposed to simulated data), data on changes in life satisfaction and positive affect following spousal loss from the Household, Income, and Labour Dynamics of Australia and data on changes in depressive symptoms following spousal loss from the HRS.

Method

Participants and Procedure

HILDA

The HILDA is a nationally representative annual panel study of private households and their inhabitants initiated in 2001 that includes residents of Australia. We use data from 13 annual waves (2001–2013). Within a household, all persons aged 15 and older were invited to participate. Data are collected annually via a combination of face-to-face and telephone interviews and self-completed questionnaires. Comprehensive information about the design, participants, variables, and assessment procedures in the study are reported in Dyrenforth, Kashy, Donnellan, and Lucas (2010) and Watson (2010). For the present study, we included 396 participants who experienced spousal loss over the course of the study.

HRS

The HRS is a longitudinal panel survey conducted in the United States that surveys a large, nationally representative sample of older adults. The HRS began in 1992 by surveying participants’ ages 51–61 years who have been reinterviewed biennially since then with data being collected jointly with the Asset and Health Dynamics Among the Oldest Old (AHEAD) study beginning in 1998 and refresher cohorts being included in 1998, 2004, and 2010 (the AHEAD began in 1993; for details, see McArdle, Fisher, & Kadlec, 2007; Soldo, Hurd, Rodgers, & Wallace, 1997). For the present study, we use data from 1992 and 2010 and included 3,533 participants who experienced spousal loss over the course of the study.

Measures

HILDA: Life satisfaction

Participants’ reported on their life satisfaction annually, answering the question “How satisfied are you with your life, all things considered?” using a 0 (totally unsatisfied) to 10 (totally satisfied) rating scale. This item is considered a measure of cognitive-evaluative (as opposed to emotional) aspects of well-being and it has been used widely used in psychological research and shows high reliability to multiple item indicators of life satisfaction (see Cheung & Lucas, 2014; Gerstorf et al., 2008). On average, participants provided 4.26 (SD = 1.66, range: 1–6) observations.

HILDA: Positive affect

Positive affect was assessed at each wave using questions starting with the stem “How much of the time during the past 4 weeks…” and answered on a scale from 1 (all of the time) to 6 (none of the time; see Anusic, Yap, & Lucas, 2014; Infurna & Luthar, in press). Specific items were “Did you feel full of life?”, “Have you felt calm and peaceful?”, “Did you have a lot of energy?”, and “Have you been a happy person?”. On average, participants provided 3.96 (SD = 1.77, range: 1–6) observations.

HRS: depressive symptoms

Eight items from the CES-D scale (Radloff, 1977) were used to assess depressive symptoms. Items asked participants whether they had (=1) or had not (=0) experienced the following symptoms “much of the time during the past week”: feeling depressed, everything was an effort, restless sleep, was not happy, felt lonely, did not enjoy life, felt sad, and could not get going. The sum across items was taken as an indicator of the number of depressive symptoms an individual experienced frequently. On average, participants provided 2.77 (SD = 1.19, range: 1–4) observations.

Statistical Analysis

GMM, combining latent growth curve and mixture models, simultaneously estimates trajectories of change and provides the opportunity to observe subgroups of individuals with distinct multivariate normal distributions (for discussion, see Grimm & Ram, 2009; Muthén, 2004; Ram & Grimm, 2009). A longitudinal model of change needs to first be established to allow for GMM to subsequently identify distinct subgroups or classes underlying the sample. To do so, each individual’s time series was realigned to year of spousal loss.

We used observations from the year of reported spousal loss to 5 years following for HILDA (i.e., participants could have provided up to six observations) and up to 6 years following for HRS (i.e., participants could have provided up to four observations) for the GMM analyses conducted for this report. A linear model of change was used to examine changes in life satisfaction, positive affect, and depressive symptoms following spousal loss. We acknowledge that this is a simplified model of change, with previous research indicating a multiphase process in regards to changes following spousal loss. We use the linear model of change for illustration purposes as more complex models, such as latent basis introduces additional factors to consider (i.e., estimation of slope factor loadings). When we used a quadratic model of change, substantively similar findings to those reported were observed. Our longitudinal model allowed for variations in individuals’ life satisfaction and positive affect levels at the year of the reported spousal loss (i.e., year 0; spousal loss level). Because the intercept was set to year 0, the spousal loss change parameter is interpreted as the amount of change in each outcome in the years following spousal loss.

Steps for model fitting

We estimated a series of models for one more than the best fitting model with up to six classes estimated in certain instances. To select the best fitting model for each outcome, we used multiple fit statistics, including information criteria (e.g., Bayesian information criterion [BIC]—better fitting models have a lower BIC; see Nylund, Asparouhov, & Muthén, 2007), entropy (higher values indicate more distinct classes and that individuals are grouped into classes that describe their functional configuration well), approximate likelihood ratio tests (LRTs) that compare the relative fit of models to similarly structured models with one fewer class (Lo, Mendell, & Rubin, 2001), the class size (classes identified should not comprise less than 5% of the sample), and interpretation of the class parameters through the plotting of group trajectories for their theoretical sensibility and distinctiveness (see Ram & Grimm, 2009). Along the lines suggested (see Muthén, 2004; Nylund et al., 2007; Ram & Grimm, 2009), we used a combination of these fit statistics. All models were estimated using Mplus 7.1 (see Muthén & Muthén, 2012), with incomplete data accommodated using full information maximum likelihood.

Results

The results are organized into two sections. We first fit LCGA models and second, fit growth mixture models; each analysis, respectively, corresponds to the conceptual layout illustrated in Figure 2. For data from the HRS, we additionally estimated whether different findings emerged when taking into consideration the Poisson distribution. With all types of models, we increased the number of classes until convergence issues were encountered or the BIC plateaued. Supplementary Figure S1 shows the raw data for each outcome for a subset of the participants included in the study. We see that there is a great deal of heterogeneity in levels and rates of change in each outcome following spousal loss, precluding the use of GMM.

Latent Class Growth Analysis

We began with the LCGA model, where the residual variances were estimated and assumed to be homogeneous between classes, and the intercept and slope variances were fixed at 0 (Figure 2A; see Nagin, 1999). We note that the LCGA model that estimates the variances to be homogenous across classes is the default setting in Mplus. Table 1 contains the fit statistics, class sample sizes, and entropy (measure of classification quality) for the LCGA and GMM models for life satisfaction and positive affect. Table 2 contains the fit statistics, class sample sizes, and entropy for the LCGA and GMM models for depressive symptoms.

Table 1.

Fit Statistics for Latent Class Growth Analysis (LCGA) and Growth Mixture Models (GMM) for Data on Life Satisfaction and Positive Affect

	Class sizes	Parameters	BIC	LMR LRT	aLMR LRT	BLRT	Entropy
Life satisfaction—LCGA
1-Class	396	3	6,955	—	—	—	—
2-Class	72, 324	6	6,494	<0.01	<0.01	<0.01	0.883
3-Class	15, 112, 269	9	6,352	0.08	0.08	<0.01	0.837
4-Class	5, 210, 134, 47	12	6,308	0.32	0.33	<0.01	0.759
5-Class	54, 12, 5, 150, 175	15	6,288	0.02	0.02	<0.01	0.750
6-Class	5, 26, 1, 144, 187, 33	18	6,300	0.64	0.64	0.09	0.777
Life satisfaction—GMM
1-Class	396	6	6,347	—	—	—	—
2-Class	129, 267	13	5,914	<0.01	<0.01	<0.01	0.723
3-Class	43, 131, 222	20	5,915	0.17	0.17	0.01	0.631
Positive affect—LCGA
1-Class	393	3	4,667	—	—	—	—
2-Class	228, 165	6	4,035	<0.01	<0.01	<0.01	0.809
3-Class	61, 177, 155	9	3,880	0.01	0.01	<0.01	0.795
4-Class	43, 120, 113, 117	12	3,834	0.24	0.25	<0.01	0.709
5-Class	112, 4, 43, 117, 116	15	3,849	0.44	0.45	0.50	0.730
6-Class	64, 42, 73, 118, 5, 91	18	3,836	0.46	0.47	0.50	0.678
Positive affect—GMM
1-Class	393	6	3,820	—	—	—	—
2-Class	289, 104	13	3,661	<0.01	<0.01	<0.01	0.763
3-Class	97, 216, 80	20	3,651	0.02	0.03	<0.01	0.550
4-Class	104, 84, 9, 196	23	3,656	0.04	0.05	0.07	0.611

Note: BIC = Bayesian information criterion; BLRT = bootstrapped likelihood ratio test; CFI = comparative fit index; LMR LRT = Vuong-Lo-Mendell-Rubin likelihood ratio test; aLMR LRT = adjusted Vuong-Lo-Mendell-Rubin likelihood ratio test; RMSEA = root mean square error of approximation. LCGA models: model fit for one-class model: life satisfaction: CFI = 0.000, RMSEA = 0.272; positive affect: CFI = 0.000, RMSEA = 0.312. GMM models: model fit for one-class model: life satisfaction: CFI = 0.884, RMSEA = 0.098; positive affect: CFI = 0.939, RMSEA = 0.082. Bold values indicate the model that was selected as being most appropriate or best fitting to the data.

Table 2.

Fit Statistics for Latent Class Growth Analysis (LCGA) and Growth Mixture Models (GMM) for Data on Depressive Symptoms

	Class sizes	Parameters	BIC	LMR LRT	aLMR LRT	BLRT	Entropy
LCGA
1-Class	3,533	3	42,382	—	—	—	—
2-Class	2,610; 923	6	39,674	<0.01	<0.01	<0.01	0.793
3-Class	930; 2,263; 340	9	39,260	<0.01	<0.01	<0.01	0.741
4-Class	2,156; 343; 441; 593	12	39,007	<0.01	<0.01	<0.01	0.716
5-Class	2,105; 391; 558; 326; 152	15	38,966	<0.01	<0.01	<0.01	0.708
LCGA—Count
1-Class	3,533	2	41,618	—	—	—	—
2-Class	2,017; 1,516	5	36,631	<0.01	<0.01	<0.01	0.700
3-Class	915; 1,098; 1,520	8	36,223	<0.01	<0.01	<0.01	0.570
4-Class	862; 937; 971; 762	11	36,121	<0.01	<0.01	<0.01	0.492
5-Class	745; 467; 904; 545; 872	14	36,090	<0.01	<0.01	<0.01	0.457
GMM
1-Class	3,533	6	40,021	—	—	—	—
2-Class	1,314; 2,219	13	37,759	<0.01	<0.01	<0.01	0.702
3-Class	1,285; 527; 1,721	14	37,204	<0.01	<0.01	<0.01	0.675
4-Class	231; 1,520; 1,272; 509	19	37,046	<0.01	<0.01	<0.01	0.698
GMM—Count
1-Class	3,533	5	36,370	—	—	—	—
2-Class	1,444; 2,089	11	36,110	<0.01	<0.01	<0.01	0.478

Note: BIC = Bayesian information criterion; BLRT = bootstrapped likelihood ratio test; CFI = comparative fit index; LMR LRT = Vuong-Lo-Mendell-Rubin likelihood ratio test; aLMR LRT = adjusted Vuong-Lo-Mendell-Rubin likelihood ratio test; RMSEA = root mean square error of approximation. LCGA: model fit for one-class model: CFI = 0.000, RMSEA = 0.256; GMM: model fit for one-class model: CFI = 0.936, RMSEA = 0.075. When taking into consideration the count nature of the data, CFI and RMSEA values are not given. Bold values indicate the model that was selected as being most appropriate or best fitting to the data.

For the three-class solution in the GMM model, the intercept and slope variances and the covariance needed to be set to 0 for the first and second class to allow for model convergence. For the four-class solution in the GMM model, the intercept variance needed to be set to 0 for the second class, the intercept and slope variance needed to be set to 0 for the third and fourth class to ensure for model convergence.

Life satisfaction

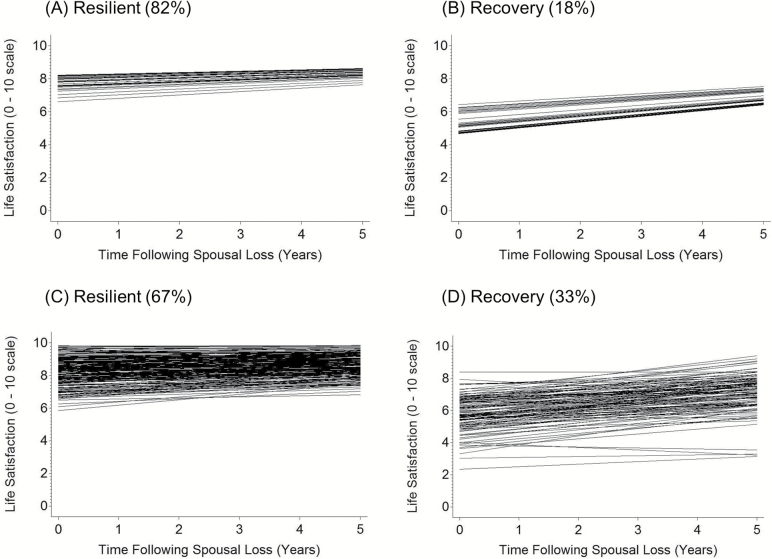
For life satisfaction, we observed that there was consistent improvement in the BIC until six classes were specified. In considering all of the fit information, the number of people in each class, and the entropy, we decided that the two-class model was most appropriate. Although the BIC was lowest in the five-class model, and the LRTs were statistically significant, the models contains multiple classes that comprise less than 5% of the sample; this was also true of the three- and four-class solutions. In the two-class solution, 82% were likely to belong to a resilient trajectory of steady, high levels of life satisfaction, whereas 18% were likely to belong to a recovery trajectory that was characteristic of gradual improvements in life satisfaction following spousal loss. Supplementary Table S1 in the supplemental materials shows the fixed and random effects for these two classes, and Figure 3A and B shows the trajectories from this model. Figure 3A and B shows that within-each class there was a homogenous change process (i.e., all participants show the same amount of change) and the within-class variability (residual) was the same.

Figure 3.

Selected models for life satisfaction for the LCGA and GMM analyses. Model implied trajectories for a subset of participants in the two classes for life satisfaction in the LCGA analysis (A, B) and two classes for life satisfaction in the GMM analysis (C, D).

Positive affect

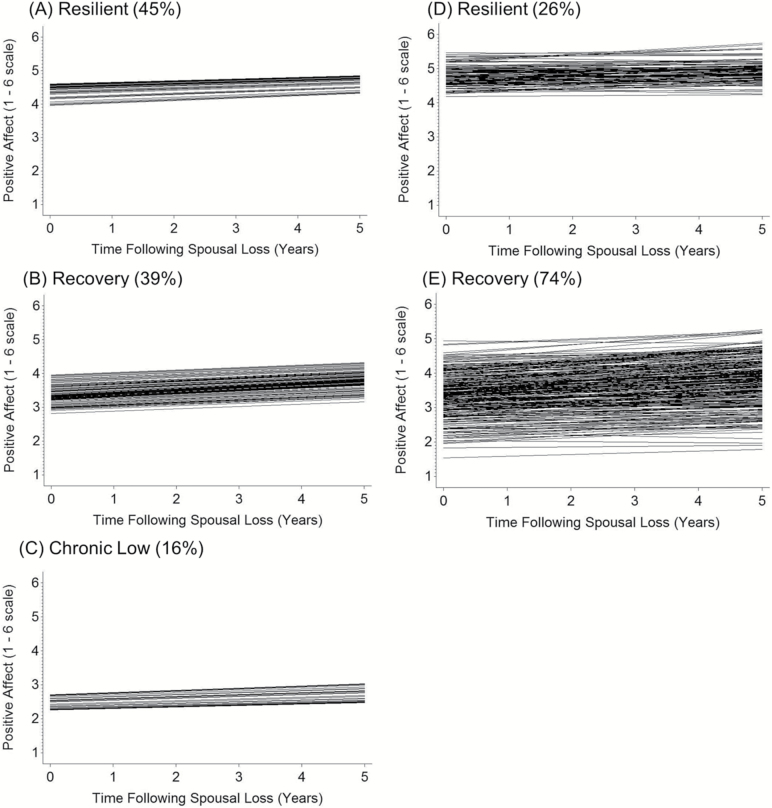
We observed that there was consistent improvement in the BIC through the four-class model for positive affect. However, based on the LMR and aLMR LRTs not being statistically significant in the four-class model, we decided that the three-class model fit best. In the three-class solution, 45% were likely to belong to a resilient trajectory of steady, high levels of positive affect, whereas 39% were likely to belong to a recovery trajectory that was characteristic of gradual improvements in positive affect and 16% belonged to a class that showed steady, low levels of positive affect. Supplementary Table S2 in the supplemental materials shows the fixed and random effects for these three classes, and Figure 4A, B, and C shows the trajectories from this model. Similar to life satisfaction, within-each class, there was a homogenous change process and that the differences between groups were due to the levels of the classes.

Figure 4.

Selected models for positive affect for the LCGA and GMM. Model implied trajectories for a subset of participants in the three classes for positive affect in the LCGA analysis (A, B, C) and two classes for positive affect in the GMM analysis (D, E).

Depressive symptoms

Results for the LCGA model for depressive symptoms are shown in the top of Table 2. The LCGA model showed improvements in the BIC until the five-class model, with the six-class model not converging due to a nonpositive definite first-order derivative product matrix. We selected the four-class model as being best fitting because the five-class model had a class that contained less than 5% of the sample and overlap in class characteristics. Supplementary Table S3 in the supplemental materials shows the fixed and random effects for the four classes. In the four-class solution, 61% were likely to belong to a resilient trajectory of steady, low levels of depressive symptoms; 10% were likely to belong to a trajectory showing stable, high levels of depressive symptoms (chronic high); 12% displayed increasing levels of depressive symptoms; and 17% showed high levels of depressive symptoms at the time of spousal loss, but declines in depressive symptoms over time (recovery).

In an additional step, we estimated the LCGA model, but assumed a Poisson distribution. This was done because the measure of depressive symptoms in the HRS is a count variable, with a large number of zeroes. When doing this, we found that the BIC steadily dropped with the inclusion of each additional class, with the six-class model not converging due to a nonpositive definite first-order derivative product matrix. Additionally, the entropy value steadily dropped beginning with the three-class solution. Given this, we selected the two-class solution as providing the best fit to the data. In the two-class solution, 57% of participants were likely to belong to the resilient trajectory and 43% likely to belong to the recovery trajectory. Supplementary Table S4 in the supplemental materials shows the fixed and random effects for the two classes.

Growth Mixture Models

Linear GMMs were specified where we estimated the intercept, slope, and residual variances to differ between the trajectories estimated. This model is analogous to what is presented in Figure 2B. Table 1 contains the fit statistics, class sample sizes, and entropy (measure of classification quality) for the GMMs for life satisfaction and positive affect, with results for depressive symptoms shown in the bottom half of Table 2.

Life satisfaction

For life satisfaction, we selected the two-class model as fitting the data best. This was due to the BIC not improving in the three-class model and the LMR and aLMR LRTs were not statistically significant and the entropy level dropped. The two classes were not evenly distributed with 33% likely belonging to a recovery class, indicative of gradual improvements following spousal loss and 67% likely belonging to a resilient class, indicative of stable, high levels of life satisfaction. Supplementary Table S5 in the supplemental materials displays the fixed and random effects for each of the classes and Figure 3C and D graphically illustrates the classes. We observe that the distribution of scores differed across the two trajectories and within-each class, individuals show differing rates of change in life satisfaction.

Positive affect

Based on the models shown in Table 1, we selected the two-class model as fitting the data best for positive affect. Although the BIC improved in the three- and four-class solutions and each of the LRT tests are statistically significant, the entropy level dropped below acceptable levels, indicating the trajectories are less distinct from one another. The two classes were not evenly distributed, with 74% of the sample likely belonging to the recovery trajectory and 26% of the sample likely belonging to the resilient trajectory. Supplementary Table S6 in the supplemental materials displays the fixed and random effects for each of the classes and Figure 4D and E graphically illustrates the classes. Similar to life satisfaction, the distribution of scores and within-class variability differs across the two classes.

Depressive symptoms

The bottom half of Table 2 shows our findings for the two sets of GMM models that we estimated for depressive symptoms. Based on the various fit statistics, we selected the two-class model as being the best fitting model to the data. The three- and four-class models had a lower BIC value and the LRTs are significant. However, the entropy values dropped below acceptable values and in the three- and four-class solutions, and the variance parameters had to be set to zero for convergence (see note in Table 2). Also, the four-class model contained a class with less than 10% of the sample. Thirty-seven percent of the sample were likely to belong to a resilient trajectory, whereas a larger proportion, 63% were likely to belong to a recovery trajectory. Supplementary Table S7 in the supplemental materials displays the fixed and random effects for each of the classes.

In the next step, we estimated the same models, but took into consideration the count nature of the depressive symptoms data. When doing so, we observed that the one-class solution represented the data best. Although the BIC dropped and each of the LRTs are statistically significant for the two-class solutions, the entropy value was not in the acceptable range and in the three-class solution, variance parameters needed to be set to zero (see note in Table 2). Supplementary Table S8 in the supplemental materials displays the fixed and random effects for the one class.

Comparison of Findings Between LCGA and GMM

We observed stark differences when comparing across the tested models for LCGA and GMM and for taking into consideration non-normality in the data. Focusing on our findings for life satisfaction and positive affect, we found that using the restrictive methodological assumptions (LCGA) led to a poorer fitting model and overextraction of classes/trajectories in the data. This is exemplified when comparing the BIC between the LCGA models and the GMMs, with the values being lower for the GMMs, compared with the LCGA models (i.e., life satisfaction: two-class LCGA model, BIC = 6,494 vs two-class GMM = 5,914; positive affect: three-class LCGA model, BIC = 3,880 vs two-class GMM = 3,661). Furthermore, across the LCGA and GMMs, resilient and recovery trajectories were observed with a fewer proportion of individuals belonging to the resilient trajectory in the GMM analyses (life satisfaction: LCGA = 82% resilient, GMM = 67% resilient; positive affect: LCGA: 45% resilient, GMM = 26% resilient). Similar findings were observed for the data on depressive symptoms. A fewer proportion of individuals were likely to belong to the resilient trajectory and a fewer number of classes were likely to best represent the data when non-normality in the data was taken into consideration. Furthermore, when we took into consideration the count nature of the data, there was improved model fit in the one-class models (LCGA: BIC = 42,382 vs LCGA—Count: BIC = 41,618; GMM: BIC = 40,021 vs GMM—Count: BIC = 36,370).

Another important component to take into consideration is the model fit of the one-class model. When comparing the LCGA and GMM analyses in closer detail, we observed stark differences in whether the one-class model was a good fitting model (see note of Tables 1 and 2). For each of the LCGA models tested across the three outcomes, model fit was poor. For example, in the LCGA analyses for life satisfaction, positive affect, and depressive symptoms, the comparative fit index (CFI) values were 0.000 and the root mean square error of approximation (RMSEA) is above 0.200. Conversely, the CFI and RMSEA values for the single group GMM showed relatively good fit, as indicated by values close to and above 0.900 for CFI and close to and below 0.080 for RMSEA (Hu & Bentler, 1999). Typically, the LCGA model is done in SAS (PROC Traj; Nagin, 1999), where the CFI and RMSEA are not given. We find this poor model fit troubling and elaborate on this in Discussion section.

Discussion

Our goal was to evaluate two commonly held assumptions in the use of GMM for examining resilience to MLS, namely homogeneity of variance across classes and non-normality in the data. We found that across the outcomes examined, relaxing the homogeneity of variance assumption led to improved model fit (i.e., lower BIC) and substantially influenced the proportion of individuals classified into each trajectory, providing further support to a recent simulation study by Diallo and colleagues (2016) and research by Infurna and Luthar (2016a, 2016b) emphasizing the importance of relaxing this methodological assumption. When non-normality was not taken into consideration, this lead to overextraction of classes. Our findings suggest that researchers need to strongly consider the often-held assumptions of LCGA and GMM, as they greatly influence the number and proportion of individuals classified into trajectories.

Specification of GMM for Studying Resilience to MLS

The widespread use of GMM for studying resilience to MLS has necessitated an in-depth examination of GMM, in particular, the commonly held assumptions in its application. This was initially demonstrated by Infurna and Luthar (2016a, 2016b) who found that the proportion deemed resilient is dependent on data analytic choices, such as assumptions underlying the statistical model. A follow-up study by Infurna and Luthar (in press) further demonstrated that resilience is multidimensional by showing the proportion of individuals deemed resilient to spousal loss is dependent on the outcome examined, with resilience not being uniform across outcomes; resilience in one domain can co-exist with declines in other pertinent domains.

We examined the nature of how the methodological choices that we make as researchers can have tremendous implications for how they (mis)inform the conceptual models that are being tested. Using the default settings as outlined in Mplus (i.e., homogeneity of variance across classes and normally distributed data) can result in findings that signify the human capacity to be “naturally” resilient, which has been applied and done in an overwhelming number of studies. However, when applying methodological assumptions that are more in line with conceptual considerations of resilience (see Infurna & Luthar, 2016a) and more methodologically appropriate (see Diallo et al., 2016), a different picture emerges, such that recovery is more common than resilience. Similar to the findings from Diallo and colleagues (2016) who used simulated data, we found that, when using empirical data, relaxing the homogeneity of variance assumption across classes leads to an improved model fit, suggesting that this model should be favored over assuming homogeneity. This rationale is further exemplified when comparing the plots across Figures 3 and 4, with the classes identified in the LCGA models largely distinguishing themselves based on initial level differences and no within-class heterogeneity. Furthermore, based on our findings pertaining to depressive symptoms, this leads to questions regarding previous findings that have assumed normality in the data when implementing GMM (Maccallum et al., 2015). It is unclear as to whether a resilient trajectory would indeed still be modal when taking into consideration non-normality (i.e., count distribution).

Broadly speaking, our findings signify that researchers need to be mindful of the methodological assumptions applied when using LCGA and GMM, as they can have a tremendous influence on the findings that are communicated. Our findings dovetail with the “replicability crisis” in that the methodological approach can have a meaningful impact on our research findings and the importance of challenging established research findings (Aarts et al., 2015). We hope that our findings and methodological approach encourage researchers to think more deeply about the methodological assumptions applied, to focus on the importance of replication and the reexamination of established findings and that this leads to more research done across multiple labs to better inform our conceptual models.

Next Steps in the Utilization of GMM for Studying Resilience to MLS

Given the importance of how model specification can influence findings of GMM, we believe there are steps researchers can take to ensure proper implementation. First, the baseline or one-class model needs to be conceptually meaningful and provide a good fit to the data. This involves specifying the proper model for change (i.e., linear, quadratic, or multiphase), in addition to whether or not the variance parameters for levels and change are to be estimated (for discussion, see Ram & Grimm, 2009). The proper longitudinal model of change to be implemented can be decided based on the examination of the CFI and RMSEA to determine whether the model implemented provides good model fit (see Hu & Bentler, 1999) and by comparing BIC values across different models. For example, Infurna and Luthar (2016a, 2016b) showed that setting the slope variances to zero results in a poorer fitting model, when compared with relaxing this assumption, as shown by a lower RMSEA and BIC, and higher CFI. This was additionally observed in the present study when comparing the model fit for the one-class models between the LCGA and GMM analyses. If LCGA is used within the SAS PROC TRAJ procedure (Nagin, 1999), model fit statistics along these lines are not given, leaving the researcher unsure as to whether the model provides a good fit to the data. Furthermore, the statistical program R is gaining popularity and the implementation of LCGA and GMM can be done via several packages, including lcmm (Proust-Lima et al., 2015) and flexmix (Leisch, 2004), as well as through the use of OpenMx (Neale et al., 2016). In lcmm and flexmix, random-effects parameters can be specified (no random effects are the default) and when specified, the random effects parameters are constrained to be equal by default. In OpenMx, the user is responsible for defining the means and variance parameters as there is no default setting (see Grimm et al., 2017), which could potentially help with implementation.

A second consideration is whether the research questions match the use or necessity of GMM. Put differently, our empirical findings raise the issue of what is the most appropriate approach/method for examining the nature of resilience to MLS. This is along the lines suggested by Ram and Grimm (2009), where they clearly outline criteria for whether or not to use GMM. For example, what is the meaningfulness of dividing participants into distinct classes (e.g., resilient, recovery, growth, chronic low) or are researchers interested in examining model-implied change and between-person differences in change before and after MLS? The latter approach would involve the use of latent growth curve (multilevel) modeling where the goal would be to predict between-person variation in the within-person changes over time in an outcome. The focus would not as much be on the nature of change, but primarily on what are the vulnerability and protective factors that are associated with better courses of change. Conceptually, this is along the lines suggested by Rutter (2006, 2012) who discussed that resilience should be defined in terms of whether individuals exhibit relatively better levels of functioning than compared with other individuals who experienced the same adversity. Rutter (2006, 2012) additionally argued that it is a misleading implication that resilience should require superior functioning in relation to the population as a whole who did not experience the adversity, rather than relatively better functioning compared with others who experienced the same adversity. Empirically, this is shown in research by Infurna and colleagues (in press) who examined changes in life satisfaction before and after spousal loss and moderators of change (see also Lucas, Clark, Georgellis, & Diener, 2003). There are advantages and disadvantages to each approach and researchers need to be mindful of this when selecting their methodological approach. Research questions centered on GMM would be more focused on whether there are distinct trajectories or paths that individuals may follow before and after a MLS, whereas the use of latent growth curve (multilevel) modeling would focus on identifying vulnerability and protective factors that promote more positive courses of change.

At last, following the study by Infurna and Luthar (in press), we want to further emphasize the importance of the application and incorporation of a multidimensional approach to studying resilience to MLS in adulthood and old age. A large majority of studies that have used GMM to examine resilience to MLS have solely included a single outcome. We argue that multiple outcomes should and need to be considered when examining resilience because resilience is not uniform across domains, with resilience in specific domains coexisting with declines in others. For example, Luthar, Doernberger, and Zigler (1993) applied such a multidimensional approach to examining resilience in adolescents. They found that when solely considering academic competence, 74% of adolescents were deemed resilient, but when taking into consideration, symptoms of distress and social competence, far fewer, 15%, were classified as resilient (Luthar et al., 1993). We do not advocate for a kitchen sink approach, but instead feel that the outcomes to be targeted are likely adversity-specific, with in the specific case of spousal loss, depressive symptoms, grief, and loneliness may be most relevant, whereas physical and social functioning could be most relevant for onset of chronic illness.

Conclusion

Our goal was to evaluate commonly held methodological assumptions underlying the use of GMM for studying resilience to MLS. We found that relaxing the homogeneity of variance assumptions and taking into consideration non-normality in the data led to improved model fit and differences in the proportion of individuals being classified into the trajectories found (see Figures 3 and 4). Our findings and discussion should not discourage researchers from the use of GMM, but instead to more thoroughly consider the assumptions underlying the longitudinal model, as this has important ramifications for interpretation of findings. We hope our study and approach leads to increased interest in the use of GMM to examine research questions centered on the human capacity to be resilient to MLS.

Supplementary Material

Supplementary data is available at The Journals of Gerontology, Series B: Psychological Sciences and Social Sciences online.

Funding

The Health and Retirement Study (HRS) was supported by a cooperative agreement (Grant U01 AG09740) between the National Institute on Aging and the University of Michigan. The content is solely the responsibility of the authors and does not necessarily represent the official views of the funding agencies.