Abstract
We provide a comprehensive multi-aspect study of the performance of a pipeline used by the LIGO-Virgo Collaboration for estimating parameters of gravitational-wave bursts. We add simulated signals with four different morphologies (sine-Gaussians (SGs), Gaussians, white-noise bursts, and binary black hole signals) to simulated noise samples representing noise of the two Advanced LIGO detectors during their first observing run. We recover them with the BayesWave (BW) pipeline to study its accuracy in sky localization, waveform reconstruction, and estimation of model-independent waveform parameters. BW localizes sources with a level of accuracy comparable for all four morphologies, with the median separation of actual and estimated sky locations ranging from 25°.1 to 30°.3. This is a reasonable accuracy in the two-detector case, and is comparable to accuracies of other localization methods studied previously. As BW reconstructs generic transient signals with SG wavelets, it is unsurprising that BW performs best in reconstructing SG and Gaussian waveforms. The BW accuracy in waveform reconstruction increases steeply with the network signal-to-noise ratio (S/Nnet), reaching a 85% and 95% match between the reconstructed and actual waveform below S/Nnet ≈ 20 and S/Nnet ≈ 50, respectively, for all morphologies. The BW accuracy in estimating central moments of waveforms is only limited by statistical errors in the frequency domain, and is also affected by systematic errors in the time domain as BW cannot reconstruct low-amplitude parts of signals that are overwhelmed by noise. The figures of merit we introduce can be used in future characterizations of parameter estimation pipelines.
Keywords: gravitational waves – methods, data analysis
1. Introduction
The network of Advanced LIGO (aLIGO) gravitational-wave (GW) detectors (Aasi et al. 2015), consisting of aLIGO-Hanford (H1) and aLIGO-Livingston (L1), completed its first observing run (O1) in 2016 January. During O1, this network achieved the first direct detections of GWs by detecting GW150914 (Abbott et al. 2016a) and GW151226 (Abbott et al. 2016b), two signals from coalescences of binary black holes. In addition to binary black holes, other astrophysical sources of GW transients (e.g., core-collapse supernovae, magnetar flares, and cosmic string cusps) are also targeted by aLIGO (Abbott et al. 2016c). Searches for generic GW transients aim to detect weakly modeled GW signals (“bursts”) from such systems as well as from binary black holes, and also from as-yet-unknown sources (see e.g., Abbott et al. 2016d; Belczynski et al. 2016).
Detections of GW signals will be used to test and constrain models of astrophysical sources (see e.g., Abbott et al. 2016e). This usually requires reconstructing the signal waveform from the GW detector output and estimating parameters of the waveform (see e.g., Abbott et al. 2016f). For sources for which an accurate waveform model exists, such as binary black holes in circular orbits, this is done by matching the detector output with template waveforms (see e.g., Abbott et al. 2016f). In this case, the estimated parameters are astrophysical, e.g., chirp mass and spins. Parameter estimation (PE) for burst signals for which no model templates exist need a different approach. In these cases, basis functions are used to reconstruct the waveform and to estimate model-independent parameters of it, such as central time and frequency, signal duration, and bandwidth. In addition to these intrinsic parameters of the waveform, estimates can also be given on the extrinsic parameters of the source (e.g., sky location).
BayesWave (BW) is a pipeline for detecting and characterizing GW bursts that works within the framework of Bayesian statistics and uses sine-Gaussian (SG) wavelets as basis functions to reconstruct the signal (Cornish & Littenberg 2015). In O1, BW was used as a follow-up PE tool on triggers provided by the coherent Waveburst (cWB) search pipeline (Klimenko et al. 2008, 2016), which identifies coincident excess power in strain data of multiple GW detectors. We note, however, that cWB can also reconstruct the sky location of a GW source and the waveform of the GW signal, independently of BW (Klimenko et al. 2011). This provides an opportunity to compare the performances of BW and cWB in PE using the same set of triggers (for the results of this comparison, see Section 3.1). BW is effective in distinguishing GW signals from non-Gaussian noise artifacts (“glitches”), which enables the combination of the cWB and BW pipelines to achieve high-confidence detections across a range of waveform morphologies (Kanner et al. 2016; Littenberg et al. 2016). The estimates of mass parameters and sky location obtained by BW for GW150914 have been shown to be consistent with template-based PE pipelines (Abbott et al. 2016d).
In this paper we characterize the BW performance in PE by injecting a large set of simulated signals into simulated aLIGO noise, and recovering them and their parameters with BW. The main purpose of this study is to determine the accuracy of the reconstructions that can be achieved with BW. By knowing the accuracy, future studies can identify the broadest range of astrophysical models that can be tested with BW, while further improvements of BW can be guided by these results. Among the estimated parameters, we give special attention to sky location of the GW source, because of its key role in electromagnetic (EM) follow-up observations of GW events (see, e.g., Singer et al. 2014; Berry et al. 2015; Abbott et al. 2016g; Vitale et al. 2017). Sky localization of GW burst sources can also be carried out with the cWB and LALInferenceBurst (LIB) pipelines (Lynch et al. 2015; Veitch et al. 2015). An extensive analysis of the sky localization performance of cWB and LIB was published in Essick et al. (2015). Here we present a similar analysis for BW in order to characterize its performance and to allow comparisons with other burst pipelines studied in Essick et al. (2015). We note, however, that as we use a reduced set of triggers compared to Essick et al. (2015) (for an explanation, see Appendix A), our results in Figures 1–4 should not be compared directly with results in Figures 3–6 of Essick et al. (2015). Instead, to allow direct comparisons between BW, cWB, and LIB, we repeat our analysis with cWB and with LIB on the same reduced set of triggers, and present the results in Figures 1–4 (available in the online journal). We also note that new cWB sky localization results for binary black holes presented recently (see Vitale et al. 2017) show that the cWB performance has improved significantly for a three-detector network, while it has not changed significantly for the two-detector case we present here.
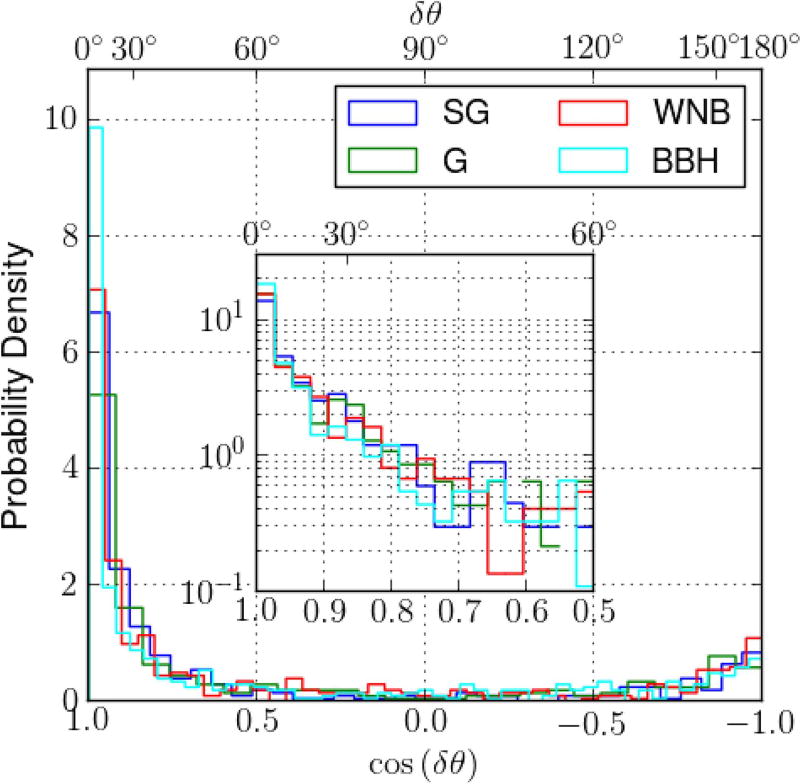
Figure 1.
Normalized histograms of angular offsets (δθ) for injections with four different morphologies (SG, G, WNB, and BBH). Most of the injected signals have cos(δθ) = 1, which indicates that BW tends to place the most probable location close to the true location. Note that the distributions for different morphologies are very similar to each other, which means that the angular offset does not depend strongly on signal morphology. The complete figure set (three figures) showing the same plot for cWB and LIB pipelines is available in the online journal.
(The complete figure set (3 images) is available.)
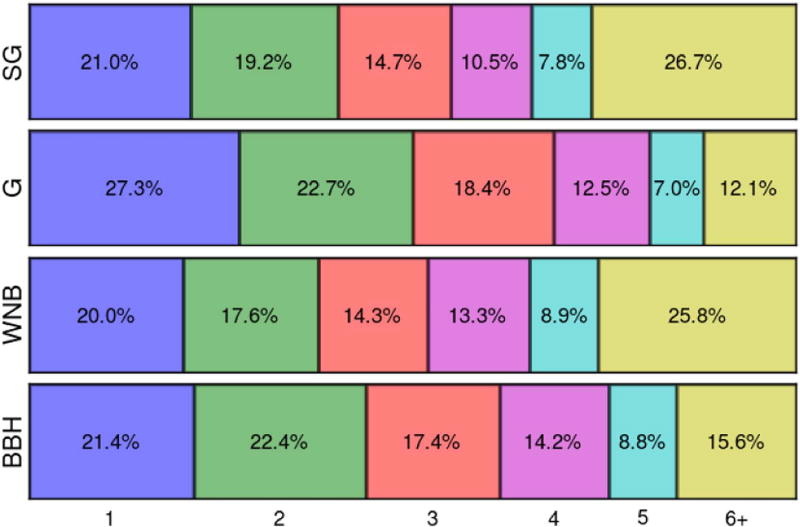
Figure 4.
Distributions of fragmentation. Each row corresponds to one of the four morphologies (SG, G, WNB, and BBH). Numbers at the bottom of the chart represent the number of disjoint regions in parts of the sky where psky ≥ p0. The number of disjoint regions is smaller than 4 for more than 50% of injected signals for all morphologies. The complete figure set (three figures) showing the same plot for cWB and LIB pipelines is available in the online journal.
(The complete figure set (3 images) is available.)
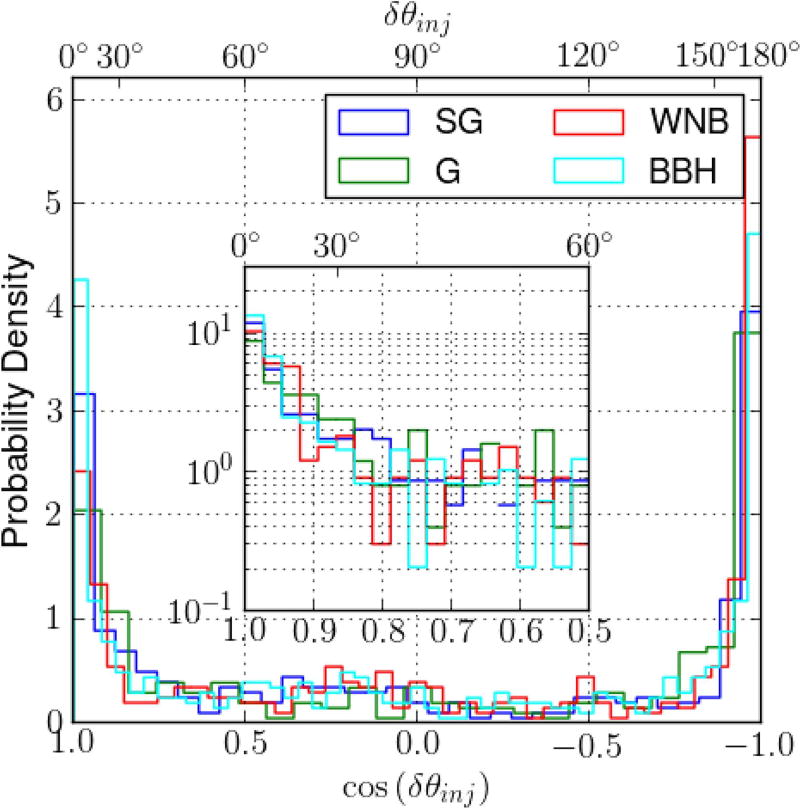
Figure 3.
Normailzed histograms of the extent (δθinj) of skymaps for the four different injection morphologies. The distributions are bimodal for all morphologies with peaks at cos(δθinj) = ±1. The complete figure set (three figures) showing the same plot for cWB and LIB pipelines is available in the online journal.
(The complete figure set (3 images) is available.)
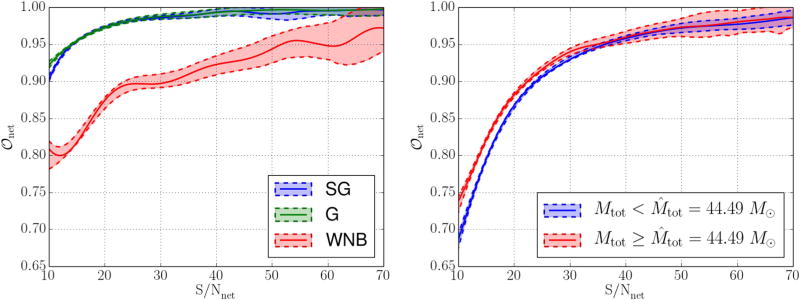
Figure 6.
Dependence of network overlaps (𝒪net) on network signal-to-noise ratios (S/Nnet) for SG, G, WNB, and BBH signals. Note that we excluded the injections with S/Nnet > 100 from the curve estimation. Shaded areas represent the 1σ uncertainty regions of the measured 𝒪net values. The left panel shows the S/Nnet dependence of 𝒪net for SG, G, and WNB signals. All three morphologies show a clear trend of increasing overlap with increasing S/Nnet. The right panel shows the S/Nnet dependence of network overlaps for BBH signals with a detector-frame total mass below and above the median total mass M̂tot = 44.49 M⊙. BW performed significantly better for signals with higher Mtot at S/Nnet ≲ 35 values.
We focus on three aspects of the BW performance: (i) sky localization, (ii) waveform reconstruction, and (iii) estimation of model-independent waveform parameters. In Section 2 we describe the methods used for creating simulated signals and noise samples, and the ones used by BW to carry out PE. In Section 3 we present the results of our analyses regarding all (i)–(iii) aspects. We summarize our findings and highlight some implications in Section 4.
2. Methods
We used software injections to test the PE performance of BW, i.e., we created mock samples of aLIGO noise and added simulated GW signals with four different morphologies to these samples. We then used these samples at trigger times provided by cWB as inputs for BW to test what it recovers from the signals embedded in the mock detector noise. In this section we discuss the characteristics of the noise samples and of the simulated signals we used (Section 2.1), as well as the methods BW uses for PE (Section 2.2).
2.1. Noise and Injections
In this section we summarize the characteristics of the injections and noise samples we used in our analyses, which are the same as those used in Essick et al. (2015). For further details on this, see Section 2, Appendix C, and Table 4 in Essick et al. (2015).
In our analysis we considered a two-detector network consisting of H1 and L1. We used stationary Gaussian mock-noise samples generated using the expected 2015 sensitivity curve of aLIGO, therefore they have slightly different characteristics than the actual noise collected during the O1 run. Projections show that the two LIGO detectors will operate in the first two months of the second observing run (O2) with sensitivity curves similar to those they operated with during O1. We therefore expect that our results are representative for this first period of O2 as well.
Our set of software injections consists of signals with four different morphologies: SG, Gaussians (G), white-noise bursts (WNBs), and binary black hole (BBH) mergers. This wide range of signal morphologies allows us to test the PE performance of BW with minimal assumptions on the GW signal. The amplitude distribution of the injected signals was chosen such as to represent a uniform distribution of GW sources in volume. Signal injections were distributed uniformly over the sky and were regularly spaced in time.
The number of signals we analyzed was determined by multiple factors (see Table 1): (i) the BW version we used runs only on triggers produced by cWB (Abbott et al. 2016d), (ii) we reduced the number of BBH triggers in order to reduce computational costs, and (iii) we only used signals that were correctly identified as signals by BW. For details on why BW identified many SG and WNB signals as glitches or Gaussian noise, and how this has been improved for O2, see Appendix A.
Table 1.
Number of Injected Signals for Each Morphology at Different Stages of the Analysis
| SG | G | WNB | BBH | |
|---|---|---|---|---|
| Triggers produced by cWB | 1112 | 256 | 769 | 2488 |
| Left out to reduce computational costs | 0 | 0 | 0 | −1988 |
|
| ||||
| Analyzed by BW | 1112 | 256 | 769 | 500 |
| Identified as glitches or Gaussian noise by BW | −779 | 0 | −355 | −1 |
|
| ||||
| Used in our analysis | 333 | 256 | 414 | 499 |
Note. For details on why BW identified many SG and WNB signals as glitches or Gaussian noise, and how this has been improved for O2, see Appendix A.
Sine-Gaussian waveforms are often used to model generic transients (e.g., Abadie et al. 2012) because they are the most localized signals in time-frequency space where generic burst searches (including cWB) operate (see Chatterji 2005). We define SG waveforms with the following two equations:
| (1a) |
| (1b) |
where α ∈ [0, π/2] is a parameter that sets the relative weights between polarizations h+ and h×, is the square of the root-sum-squared strain amplitude chosen as a free parameter in the amplitude randomization process, f0 is the central frequency, t0 is the central time, ϕ0 is the phase at time t = t0, τ is the width of the signal in the time domain (TD), and is the quality factor encoding the characteristic number of cycles within the duration of the signal.
Gaussian signals are special cases of SG signals when f0 → 0, and are defined as
| (2a) |
| (2b) |
Despite their similarity to SGs, these signals pose different challenges because they have their highest amplitude at f = 0 Hz in the frequency domain (FD), and thus they have most of their power at low frequencies where aLIGO is less sensitive.
White-noise burst waveforms are intended to model a time-localized excess power that is uniformly distributed in a given frequency band, and that satisfy
| (3) |
where w(f) values are randomly drawn from a Gaussian white noise within and chosen to be w(f) = 0 outside the band f ∈ [fmin, fmax]. We generated the right side of Equation (3) independently for the + and × polarizations, and normalized them to derive h+ and h× with the desired hrss. Unlike signals with the other three morphologies, WNB signals are not elliptically polarized because the procedure used to produce them generates h+ and h× independently.
The only astrophysical signals we used were binary black holes with spins aligned or anti-aligned with the orbital angular momentum. We only considered binaries with relatively high detector-frame total masses (Mtot ∈ [30, 50] M⊙) because their signals are more compact in time-frequency space, which makes them good targets for generic burst searches. Three different methods have been used for calculating the waveform in the three different phases of binary evolution: 3.5PN post-Newtonian expansion, numerical relativity, and analytic quasi-normal modes to calculate the inspiral, merger, and ringdown waveforms, respectively (see Hannam et al. 2010; Ajith et al. 2011 for details).
2.2. The BW Pipeline
BayesWave uses a trans-dimensional reversible-jump Markov chainMonte Carlo (RJMCMC) algorithm (Green 1995) to explore the following three competing models of the data and test them with the input data samples from each aLIGO detector: (i) Gaussian noise only, (ii) Gaussian noise with glitches, and (iii) Gaussian noise with a GW signal. This approach makes BW effective in distinguishing GW signals from glitches (Littenberg et al. 2016), but it also makes BW computationally expensive, and thus in O1, BW was used to follow-up candidate events from cWB.
BayesWave assumes that all signals are elliptically polarized, i.e., h× = εh+eiπ/2, where ε ∈ [0, 1] is the ellipticity parameter, which is 0 for linearly polarized signals and 1 for circularly polarized signals. This is a valid assumption for many expected astrophysical signals, but not for our injections with WNB morphology (see Section 2.1). However, for a LIGO-only network, it is often the case that only a single combination of the two polarizations, rather than the separate + and × components, will be detectable, making the elliptical constraint a fair approximation for many cases.
We used the BW version that had been used for the offline analysis of O1 data to attain a characterization of the BW performance during O1 and to support a fair comparison with the versions of other PE pipelines characterized in Essick et al. (2015). PE pipelines used by the LIGO-Virgo Collaboration (including BW) have undergone improvements since the beginning of O1 (some of which were motivated by this study).
3. Results
In this section we show how BW performed in different aspects of PE. These aspects are sky localization (see Section 3.1), waveform reconstruction (see Section 3.2), and point estimates of waveform central moments (see Section 3.3).
Even though the current version of BW (O2) is more efficient in identifying signals (see Appendix A), we used the version of BW used during O1 in order to characterize the BW performance during O1 and to allow a comparison of our results with those presented in Essick et al. (2015). We only analyzed signals that were properly identified as signals by BW (see Table 1). We present a reproduction of results of Essick et al. (2015) for the subset of events we used in this study to enable a fair comparison of sky localization results (see Figures 1–4).
Results presented here depend on the parameter distributions of injected signals defined in Table 4 of Essick et al. (2015) and on the corresponding detection efficiencies of the combination of cWB and BW pipelines for the different parameter sets. Results are particularly dependent on the chosen hrss distribution of injected signals, and thus on the network signal-to-noise ratio (S/Nnet) distribution of them (see inset of Figure 5). However, the hrss distribution we chose for this study is a good approximation for generic burst signals that are uniformly distributed in volume (see Appendix C in Essick et al. 2015).
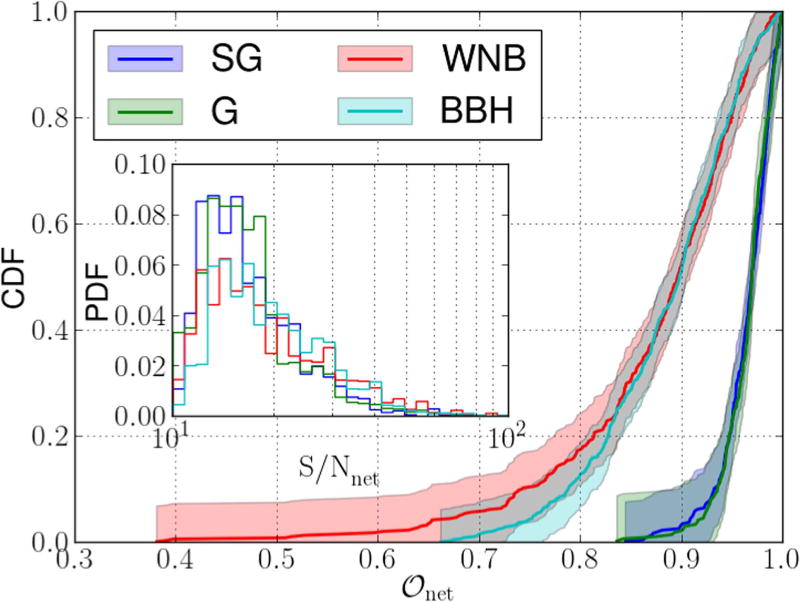
Figure 5.
Cumulative distribution function (CDF) of network overlaps (𝒪net). Shadings represent the 2σ uncertainties calculated using the Dvoretzky-Kiefer– Wolfowitz inequality (Dvoretzky et al. 1956). The lower the curves reach at a given 𝒪net value, the better the reconstruction. The inset shows the normalized histogram of the network signal-to-noise ratio (S/Nnet) for signals with four different morphologies. The curves for SG and G signals are identical within the 2σ statistical errors, and they indicate significantly better reconstructions of SG and G signals than of WNB and BBH signals.
3.1. Sky Localization
BayesWave computes a skymap defined as the posterior probability density function of the GW source location expressed as a function of celestial coordinates α (right ascension) and δ (declination), denoted by psky (α, δ). Example skymaps for each morphology are shown in Appendix B. Skymaps for all the injections can be found in the Burst First2Years sky localization Open Data release.7 There are many possible quantitative measures for the “goodness” of source localization; here we implement the measures defined in Essick et al. (2015), i.e., angular offset, searched area, extent, and fragmentation. We reproduced the results of Essick et al. (2015) for LIB and cWB using the same subset of events as we used in this study (those identified as signals by BW) to enable a direct comparison of the results (see Figures 1–4).
The first measure is the angular offset (δθ), which is the angular distance between the maximum of psky and the true location of the injected signal. Figure 1 shows normalized histograms of cos(δθ) for all injections, with the upper axis showing the corresponding δθ values. The distribution has a peak at cos(δθ) = 1, which suggests that BW tends to reconstruct the most probable location of the source close to the actual source location. There is also a smaller peak at cos(δθ) = −1, which indicates that it is more likely that BW reconstructs the opposite direction of the sky compared to the location of the injected signal than a direction perpendicular to the injected signal’s location. The reason is that opposite directions cannot be distinguished using the network antenna pattern, which has the same value at opposite directions because of the near co-alignment of H1 and L1 detectors (Singer et al. 2014). However, the peak at cos(δθ) = −1 is smaller than the peak at cos(δθ) = 1 because opposite directions are only allowed by the triangulation ring when the source is right above (or below) the detectors, and thus the triangulation ring is a great circle on the celestial sphere. We note that the distributions for different morphologies are very similar to each other, which means that the angular offset depends weakly on signal morphology. We show the summary statistics of δθ distributions for all morphologies in Table 2. It is clearly visible that BW performs best for BBH signals, while SG, G, and WNB signals show slightly higher δθ values. Statistical errors on reported values are in the order of a few percent. Figure 1 shows normalized histograms of cos(δθ) obtained with the cWB and LIB pipelines on the subset of signals identified as signals by BW.
Table 2.
Summary Statistics of 𝒜 and δθ Distributions
| Morphology | BBH | SG | G | WNB | |
|---|---|---|---|---|---|
| Fraction (in %) with searched area smaller than | 5 deg2 | 3.6 | 4.8 | 2.3 | 2.7 |
| 20 deg2 | 17.4 | 15.6 | 7.8 | 12.3 | |
| 100 deg2 | 50.1 | 46.5 | 29.3 | 41.3 | |
| 200 deg2 | 66.5 | 58.6 | 43.4 | 56.0 | |
| 500 deg2 | 87.0 | 75.4 | 67.6 | 76.1 | |
| 1000 deg2 | 94.6 | 87.7 | 84.4 | 87.4 | |
|
| |||||
| Fraction (in %) with δθ lower than | 1° | 3.0 | 1.2 | 1.6 | 1.0 |
| 5° | 15.4 | 10.5 | 12.1 | 10.1 | |
| 15° | 37.5 | 31.2 | 30.9 | 30.2 | |
| 45° | 62.7 | 69.1 | 62.9 | 61.4 | |
| 60° | 69.1 | 75.7 | 68.4 | 67.1 | |
| 90° | 76.4 | 79.9 | 75.4 | 76.1 | |
|
| |||||
| Median searched area | 99.2 deg2 | 121.3 deg2 | 252.8 deg2 | 151.0 deg2 | |
| median δδ | 25°.1 | 26°.2 | 29°.9 | 30°.3 | |
Note. Statistical errors are in the order of a few percent.
Electromagnetic follow-up observations tend to target the point of the sky with the highest psky value first, and continue with points of lower psky values. This motivates the introduction of the searched area (𝒜) as a second measure, which is the total sky area observed before aiming a hypothetical telescope at the true location of the source:
| (4) |
where H is the Heaviside step function, p0 is the value of psky at the true location of the source, and dΩ = cos δ dδ dα.
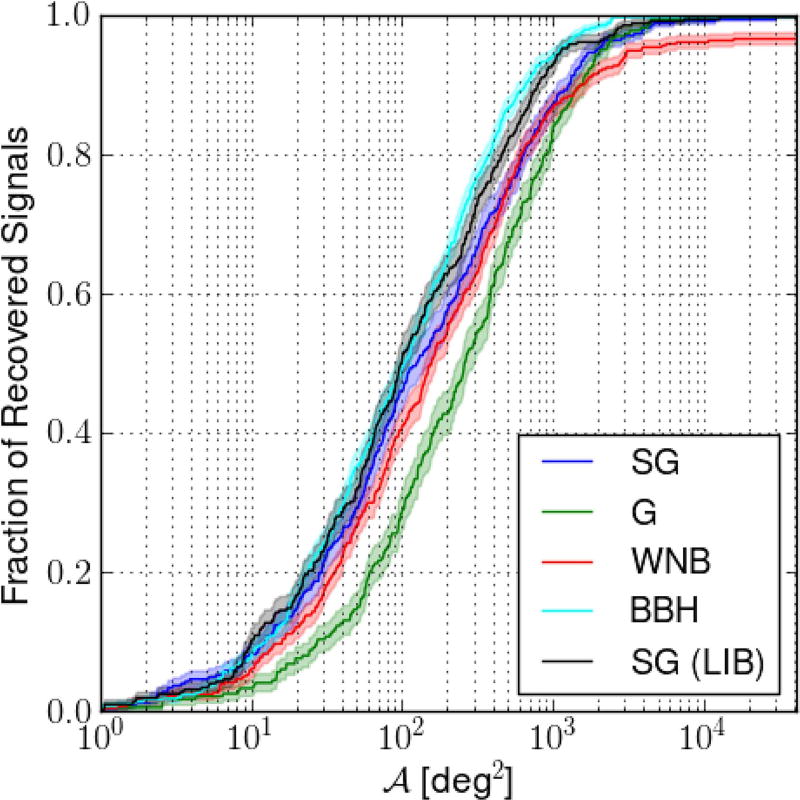
We show the cumulative histogram of 𝒜 for all injections in Figure 2. Histograms for different morphologies follow a similar trend, but the curves are shifted along the horizontal axis. This can be quantified, e.g., with median searched area, which is 252.8 deg2 for G, 151.0 deg2 for WNB, 121.3 deg2 for SG, and 99.2 deg2 for BBH signals. Another difference between the morphologies is that there is a fraction of WNB signals with a searched area equal to the whole sky (𝒜 ≃ 4 × 104 deg2). The reason is that p0 = 0 for these signals, i.e., the posterior distribution has no support at the true location of the source. There are no such signals with SG, G, and BBH morphologies. A reference curve labeled SG (LIB) shows results for the LIB pipeline of the subset of SG signals identified as signals by BW. We note that LIB uses a single SG to reconstruct the signal, so that for SG injections LIB becomes a matched-filtering analysis for which better performance is expected, while BW sometimes uses more than one SG because it favors more complex signals. This shows that LIB performed similarly, but slightly better for SG signals. We show the summary statistics of the 𝒜 distributions for all morphologies in Table 2. It is clearly visible that BW performs best for BBH signals, while SG, G, and WNB signals show significantly higher 𝒜 values. Statistical errors on the reported values are in the order of a few percent. Figure 2 shows normalized histograms of 𝒜 obtained with the cWB and LIB pipelines on the subset of signals identified as signals by BW.
Figure 2.
Cumulative histograms of the searched area (𝒜). Histograms for different morphologies follow a similar trend, except that the curves are shifted along the horizontal axis. A reference curve labeled with SG (LIB) shows results for the LIB pipeline on the subset of SG signals identified as signals by BW. The complete figure set (three figures) showing the same plot for cWB and LIB pipelines is available in the online journal.
(The complete figure set (3 images) is available.)
Even if δθ and 𝒜 are small, the favored sky positions can still be either well localized or spread out over various parts of the sky. To quantify this feature, we introduce the extent (δθinj) of a skymap as the maximum angular distance between the location of the injected signal and any other point satisfying psky (α, δ) ≥ p0. We show histograms of δθinj in Figure 3. The distributions are clearly bimodal, with peaks at cos(δθinj) = ± 1. The peak at cos(δθinj) = 1 corresponds to well-localized signals, while the peak at cos(δθinj) = −1 shows that there is a similarly large number of events with the skymap extended even to the opposite direction of the sky compared to the true location of the signal. The reason is the same effect as described previously when explaining Figure 1. We note that there are significant differences in the height of the two peaks, e.g., the histogram for the BBH signals has a peak at cos(δθinj) = 1 that is twice as high as the peak in the histogram for the G signals. Figure 3 shows histograms of δθinj obtained with the cWB and LIB pipelines on the subset of signals identified as signals by BW.
Even if previous measures indicate a well-localized source, the skymap can still be fragmented, which makes it more difficult to cover the whole with EM observations. We therefore introduce the fragmentation of a skymap as the number of disjoint regions in the union of points satisfying psky (δ, α) ≥ p0. We show the distribution of the number of disjoint regions in Figure 4. There are fewer than four disjoint regions for more than 50% of the injected signals for all morphologies. Skymaps for SG and WNB signals are significantly more fragmented than for G and BBH signals. The reason is that the skymaps of these signals are more likely to have “fringe peaks.” These are separate rings in the sky corresponding to local maxima of matches between different data streams obtained when they are shifted by half-integer multiples of the period of the signal (for details see Appendix A). Figure 4 shows distributions of the number of disjoint regions obtained with the cWB and LIB pipelines on the subset of signals identified as signals by BW.
To compare the BW performance with the performance of LIB and cWB (Essick et al. 2015), we created the equivalents of Figures 1–4 with LIB and cWB using the same subset of events as we used in this study (see Figures 1–4). We have found that all metrics show that these algorithms perform similarly in localizing the source. Histograms of 𝒜 show that 𝒜 values for BW are comparable to but systematically higher than for cWB and LIB for all morphologies, except for BBH signals, for which BW typically yields smaller searched areas than LIB. There are also more WNB skymaps with large searched areas (𝒜 ≥ 100 deg2) for LIB than for BW. This is most likely due to its ability to recover more of the signal by using multiple wavelets as opposed to a single SG template.
3.2. Waveform Reconstruction
BayesWave uses SG wavelets to reconstruct a GW signal from the detector output, which means that the recovered signal is always given as a linear combination of SG wavelets, the number of which is a parameter in the RJMCMC. To characterize the quality of waveform reconstruction, we introduce the overlap (𝒪, sometimes referred to as match), which measures the similarity of an injected (hi) and a recovered (h) waveform as
| (5) |
where (․|․) is a noise-weighted inner product, defined as
| (6) |
where Sn is the one-sided power spectral density of the detector noise, and x* denotes the complex conjugate of x.
From Equation (5) it is visible that 𝒪 ranges from −1 to 1, with 𝒪 = 1 meaning a perfect match between hi and h, 𝒪 = 0 meaning no match at all, and 𝒪 = −1 meaning a perfect anticorrelation between hi and h. With Equation (5), we can calculate the overlap using data from only one detector. To characterize the waveform reconstruction for the network of GW detectors, we introduce the network overlap (𝒪net) by changing the inner products in Equation (5) with the sum of the inner products calculated for different detectors:
| (7) |
where j denotes the jth detector in the network, and N is the number of detectors used in the analysis (note that N = 2 in this study). We note that in our analysis we only considered waveforms reconstructed from outputs of each detector (h(j)), but not the astrophysical GW polarizations (h+, h×), because the two polarizations cannot be decomposed from detections with two coaligned GW detectors, such as H1 and L1.
Figure 5 shows the cumulative distribution functions (CDFs) of 𝒪net. Shaded ranges represent the 2σ uncertainty calculated using the Dvoretzky-Kiefer-Wolfowitz inequality (Dvoretzky et al. 1956). The fraction of injected signals with 𝒪net > 0.9 is 97% for G, 96% for SG, 48% for BBH, and 47% for WNB signals after the waveform reconstruction with BW. 95% of injections have 𝒪net > 0.92 for G signals, 𝒪net > 0.91 for SG signals, 𝒪net > 0.75 for BBH signals, and 𝒪net > 0.68 for WNB signals. In Figure 5, the lower the curves reach at a given 𝒪net value, the better the reconstruction. This suggests that the BW waveform reconstruction works most effectively for SG and G signals, for which the curves are identical within the 2σ statistical error. The BW waveform reconstruction is less effective for WNB and BBH signals, and it shows similar characteristics for these morphologies at high network overlaps (≳0.8), but the distribution for WNB signals has a longer tail at low 𝒪net values. BW performs better for SG and G signals because at low S/Nnet BW tends to use fewer wavelets to avoid overfitting the data. SG and G signals can be reconstructed accurately even with only two to three SG wavelets, while this is not possible for WNB and BBH signals. This also means that the curves for SG and G signals in Figure 5 represent the highgest BW capability of reconstructing a GW signal for a given noise level, while the results for WNB and BBH signals represent the BW performance on more generic (and thus, more realistic) GW signals. We note that while 𝒪net values are lower for WNB and BBH signals, BW detects them with greater confidence because its detection statistic depends more strongly on the signal complexity than on S/Nnet (for details see Littenberg et al. 2016). The inset plot in Figure 5 shows the normalized histogram of the injected signals’ S/Nnet for the four different signal morphologies. SG and G signals have an overabundance at S/Nnet ≲ 20 relative to WNB and BBH signals. This indicates that the previously described difference in the distribution of 𝒪net is not due to the different S/Nnet distributions because BW performs better for SG and G signals, even though S/Nnet values for SG and G signals are usually lower than for WNB and BBH signals. We note that these distributions strongly depend on the parameter distributions of the injected signals as defined in Table 4 of Essick et al. (2015) and on the corresponding detection efficiencies of the combination of cWB and BW pipelines for the different parameter sets (see the S/Nnet histogram in the inset of Figure 5).
We show 𝒪net versus S/Nnet for SG, G, and WNB signals in the left panel of Figure 6. The curves were estimated with a Gaussian kernel smoother, which is a nonparametric regression method. The shaded regions between dashed lines represent the 1σ uncertainty regions calculated with the bootstrap method, in which we estimated the curve repeatedly for subsamples that were randomly drawn from the full sample. We note that we excluded the injections with S/Nnet > 100 from the estimation of these curves, and we only show the estimated curves up to S/Nnet = 70. All three morphologies show a clear trend of 𝒪net increasing with S/Nnet.
For BBH signals we calculated the 𝒪net versus S/Nnet curves in two separate bins of total mass (Mtot) of the BBH system, calculated in the detector frame. The two bins were defined with Mtot being Mtot < M̂tot and Mtot > M̂tot, where M̂tot = 44.49 M⊙ is the median of Mtot values for all BBH injections. The 𝒪net versus S/Nnet curves for BBH signals are shown in the right panel of Figure 6. Similarly to other morphologies, BBH injections also show a clear trend of increasing 𝒪net with increasing S/Nnet. At low (≲35) S/Nnet values, BW performed significantly better for signals with higher Mtot, while differences in the curves are within the level of statistical errors for higher S/Nnet values. Signals with high Mtot are recovered with better accuracy because a large portion of the signal power is in a compact region of time-frequency space and therefore can be captured with a small number of wavelets, while signals with low Mtot spend a comparatively longer amount of time in the sensitive band of the detectors, requiring more wavelets and a greater total signal strength to achieve a similar fit. This difference vanishes at high S/Nnet because BW uses more wavelets to reconstruct signals with higher S/Nnet.
Figure 6 shows (similarly to Figure 5) that BW performs very similarly on SG and G signals, and much less efficiently on WNB and BBH signals. The reason is that BW needs to use more wavelets to accurately reconstruct WNB and BBH signals. We note that despite the weaker performance on WNB and BBH signals, they also approach the reconstruction accuracy for SG and G signals at higher S/Nnet values. When we compare the two panels of Figure 6, it is visible that the curve for BBH signals is similar to the curve for WNB signals, with slightly lower overlap at low S/Nnet and slightly higher overlap at high S/Nnet values.
Our results show that BW reliably reconstructs waveforms with various morphologies. Although there are significant differences between the efficiency of reconstructions of signals with different morphologies, even for the worst case of WNB signals (which do not even match BW’s assumption that the signal is always elliptically polarized), most of them have relatively high overlaps, and there is a clear trend of 𝒪net approaching 1 as S/Nnet increases.
3.3. Point Estimates of Waveform Central Moments
For a generic burst signal, we do not have any specific astrophysical model whose parameters could be estimated. In this case, we can still give estimates of the model-independent parameters of the signal. Here we consider the central moments of the waveform as such parameters.
The first central moments are central time (t0) and central frequency (f0), and the second central moments are duration (Δt) and bandwidth (Δf), defined as
| (8a) |
| (8b) |
| (8c) |
| (8d) |
respectively, where ρTD and ρFD are the effective normalized distributions of signal energy, expressed in the time domain (TD) and in the frequency domain (FD):
| (9a) |
| (9b) |
where h(t) is the whitened (i.e., normalized with the amplitude spectral density of the detector noise) waveform for a given detector and h̃ (f) is the Fourier transform of h(t). These distributions satisfy , and .
Estimates of higher-order moments could also be given with BW, but we excluded them from our analysis because they are more strongly affected by statistical errors than estimates of the first-order moments (for a detailed discussion of this, see the end of this section).
BayesWave reconstructs the waveform and calculates the waveform moments for each sample in the Markov chain. We calculated the median value to give a point estimate of the waveform moments. To quantify the accuracy of the point estimate of waveform moment x, we define the absolute error of the estimation, ex, as
| (10) |
where x(e) is the estimated and x(r) is the real value of x. We also introduce the relative error of an estimate, ηx, as
| (11) |
We show CDFs of et0/Δt, ef0/Δf, ηΔt, and ηΔf in Figure 7, where shadings represent the 2σ uncertainties calculated using the Dvoretzky-Kiefer-Wolfowitz inequality (Dvoretzky et al. 1956). All moments were calculated for H1 detector data, but the results are also very similar for L1. We divided the absolute errors of the first-moment estimates with the real values of the corresponding second moments because we expect that the statistical error of the first-moment estimate scales with the real values of the second moments.
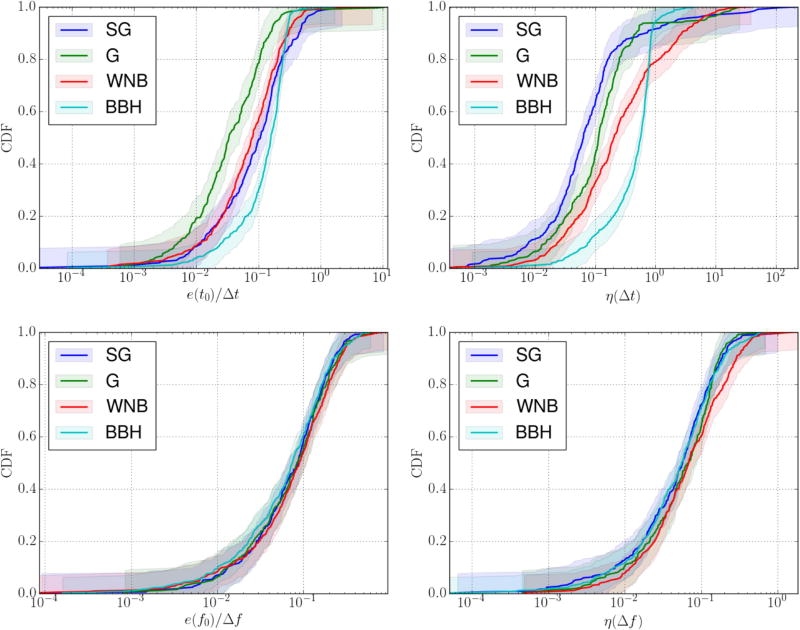
Figure 7.
Cumulative distribution functions (CDF) of waveform central moment errors: absolute errors of central time estimates divided by signal durations (et0/Δt, upper left), relative errors of duration estimates (ηΔt, upper right), absolute errors of central frequency estimates divided by signal bandwidths (ηf0/Δf, lower left), and relative errors of bandwidth estimates (ηΔf, lower right). Shadings represent the 2σ uncertainties calculated using the Dvoretzky-Kiefer-Wolfowitz inequality (Dvoretzky et al. 1956). Colors indicate CDFs for signals with sine-Gaussian (SG), Gaussian (G), white-noise burst (WNB), and binary black hole (BBH) morphologies. We list the values of the 95th percentiles and medians in Table 3.
We show CDFs of et0/Δt for different morphologies in the top left panel of Figure 7. These show that the most accurate t0 estimates with BW are obtained for G signals, while estimates for BBH signals are the least accurate. The relatively high et0 values are obtained because BW cannot reconstruct the low-amplitude parts of the signal that are overwhelmed by noise, which can cause a systematic error in the estimation of t0. For example, BW is almost insensitive to the inspiral parts of BBH signals, which make up the bulk of BBH signal durations, and this bias increases the lower the total mass of the systems is. This effect is less significant for the other three morphologies, which explains why the estimate of t0 is less accurate for BBH signals (with a median et0 value of 0.16Δt). The t0 values we obtain for H1 and for L1 are strongly correlated, which means that the error on the estimation of the difference of arrival times between H1 and L1 (determining the thickness of the sky localization triangulation ring) is typically smaller than et0.
We show CDFs of ηΔt in the top right panel of Figure 7. These curves significantly differ for different waveform morphologies. Regarding the median ηΔt, the Δt estimate is the most accurate for SG signals (with a median value of 0.06) and the least accurate for BBH signals (with a median value of 0.57). We note, however, that median values contain no information about the lengths of the tails of the ηΔt distributions. Of the four morphologies, the ηΔt distribution for the SG signals has the longest tail (see top right panel of Figure 7). For 1 ηΔt ≲ 1, CDF values for BBH signals are significantly lower than for the other three morphologies, while for 1 ηΔt ≳ 1, they are higher. The reason is the steep part of the BBH curve around 1 ηΔt = 1, which corresponds to the systematic underestimation of the duration of low-mass BBH signals (which is due to the effect explained in the previous paragraph).
We show CDFs of ef0/Δf in the bottom left panel of Figure 7. Curves for different morphologies are identical within the error bars, in contrast with CDFs of et0/Δt, where the curves are similar but not identical. This indicates that these errors are purely due to the statistical errors of the central frequency estimation, determined by the non-zero value of Δf. We note that all ef0 values are lower than Δf, and the median of ef0 is smaller than 0.1 for all morphologies (see Table 3).
Table 3.
Medians (50th Percentiles) and 95th Percentiles of Waveform Central Moment Errors for the SG, G, WNB, and BBH Signal Morphologies
| P | Signal Morphology | ||||
|---|---|---|---|---|---|
|
|
|||||
| SG | G | WNB | BBH | ||
| et0/Δt | 50th | 0.11 | 0.03 | 0.08 | 0.16 |
| 95th | 0.57 | 0.21 | 0.39 | 0.31 | |
|
| |||||
| ηΔt | 50th | 0.06 | 0.11 | 0.21 | 0.57 |
| 95th | 2.30 | 6.59 | 5.60 | 1.07 | |
|
| |||||
| ef0/Δf | 50th | 0.09 | 0.09 | 0.09 | 0.07 |
| 95th | 0.29 | 0.30 | 0.32 | 0.31 | |
|
| |||||
| ηΔf | 50th | 0.06 | 0.07 | 0.07 | 0.06 |
| 95th | 0.23 | 0.21 | 0.39 | 0.30 | |
Note. P denotes the percentile rank of values given in the corresponding table columns.
We show CDFs of ηΔf in the bottom right panel of Figure 7. The accuracies of the Δf estimate are similar for different morphologies, but not as much as for ηf0/Δf. The 95th percentiles are between 0.2 and 0.4 for the different morphologies. We note that relative errors of bandwidth estimates tend to be higher than the relative error of central frequency estimates. The reason is that estimates of second-order moments inherit errors from estimates of lower order moments (see Equations 8(c) and 8(d)) and thus have higher statistical errors. We expect that estimates of third and higher-order moments would have even larger errors, and thus we restrict our attention to examining only estimates of the first two moments. The medians and 95th percentiles of the errors for each moment and for each morphology are shown in Table 3.
As a summary, the results presented in Figure 7 show that the error distributions for f0 and Δf are very similar for different morphologies, while the error distributions for t0 and Δt show significant differences between different morphologies. This also means that while the errors of the f0 and Δf estimates are purely statistical, the errors of t0 and Δt estimates also include systematics. The latter occurs because BW cannot reconstruct low-amplitude parts of a signal that is overwhelmed by noise, which may result in a systematic error in the estimation of t0 and Δt. It is clear that the accuracy of the moment estimation is affected by how accurately the signals are reconstructed. However, we see identical CDFs of ef0/Δf for different morphologies, while they have different 𝒪net distributions, which suggests that 𝒪net is not a good indicator of the BW moment estimation accuracy.
4. Conclusion
We presented a comprehensive multi-aspect study of the performance of BW, a Bayesian GW burst PE pipeline used by the LIGO-Virgo Collaboration for reconstructing GW burst signals and their parameters. We injected a large number of simulated signals with four different morphologies (SGs, Gaussians, WNBs, and BBH signals) into simulated O1 aLIGO noise to test the BW performance in three different aspects of PE: sky localization, waveform reconstruction, and estimation of waveform central moments (for details on the methods we used, see Section 2).
BayesWave localizes sources with a level of accuracy comparable for all four morphologies, with the median separation of actual and estimated sky locations ranging from 25°.1 to 30°.3 (see Table 2), and a median searched area (𝒜, see Equation (4)) ranging from 99.2 deg2 to 252.8 deg2 (see Section 3.1). This is reasonable accuracy for a two-detector network, and is comparable to accuracies of other localization pipelines (cWB and LIB) studied previously (Essick et al. 2015). Histograms of 𝒜 (see Figure 2) show that 𝒜 values for BW are comparable to but systematically larger than for cWB and LIB for all morphologies. The exceptions are BBH signals, for which the BW 𝒜 values are systematically lower. We note that the runtime of cWB and LIB is much shorter than of BW.
BayesWave reconstructs waveforms as a linear combination of SG wavelets. To measure the goodness of reconstruction, we used the network overlap (𝒪net, see Equation (7)), which quantifies the similarity between the injected and the reconstructed signals. We have found that BW reconstructs signals with 𝒪net > 0.9 for 98% of G, 96% of SG, 45% of WNB, and 47% of BBH signals (see Section 3.2). We have also found that (see Figure 6) 𝒪net increases rapidly with increasing S/Nnet, reaching 𝒪net = 0.95 at S/Nnet ≈ 14 for SG and G, at S/Nnet ≈ 50 for WNB, and at S/Nnet ≈ 35 for BBH signals. These results suggest that we can expect very good reconstruction (𝒪net > 0.95) for almost any signal with high (≳50) S/Nnet, and reasonably good reconstruction (𝒪net > 0.85) for almost any signal with moderate (≳20) S/Nnet.
We also examined how accurately BW can estimate the central moments of a GW waveform (see Section 3.3). These are model-independent parameters of a signal, which means that by examining the estimation of them, we can characterize PE without assuming any astrophysical model for the source. We have found that errors of f0 and Δf estimations are purely statistical, while errors of t0 and Δt estimations also include some systematics. We have also found that 𝒪net is not a good indicator of the BW moment estimation accuracy. The median value of ef0/Δf is 0.09 for SG, G, and WNB signals, and 0.07 for BBH signals (see Table 3). There is no standard procedure of how the estimated moments of GW bursts can be used to test astrophysical models, but future studies can use our results to test the feasibility of particular methods using signal moments.
This paper fits into a series of studies examining PE for GW bursts (see, e.g., Klimenko et al. 2011; Essick et al. 2015). These studies can be used in comparisons with improved performances of future PE pipelines and to test the feasibility of possible astrophysical applications of future GW burst detections.
Acknowledgments
This paper was reviewed by the LIGO Scientific Collaboration under LIGO Document P1600181. We thank Marco Drago and Sergey Klimenko for their valuable comments on the manuscript. We acknowledge the Burst First2Years sky localization Open Data release.7 The authors acknowledge the support of the National Science Foundation and the LIGO Laboratory. LIGO was constructed by the California Institute of Technology and Massachusetts Institute of Technology with funding from the National Science Foundation and operates under cooperative agreement PHY-0757058. The authors would like to acknowledge the use of the LIGO Data Grid computer clusters for performing all the computation reported in the paper. Bence Bécsy was supported by the ÚNKP-16-2 New National Excellence Program of the Ministry of Human Capacities. Bence Bécsy was supported by the Hungarian Templeton Program that was made possible through the support of a grant from the Templeton World Charity Foundation, Inc. The opinions expressed in this publication are those of the authors and do not necessarily reflect the views of the Templeton World Charity Foundation, Inc. Peter Raffai is grateful for the support of the Hungarian Academy of Sciences through the “Bolyai János” Research Scholarship programme.
Appendix A
Resolving the BW O1 Version Issue with High-Q Signals
During O1, BW was prone to classifying simulated short-duration high-frequency signals that underwent many wave cycles (i.e., high-Q signals) while in the measurement band of the detector as glitches. In principle, there is no reason for the Bayesian evidence used to rank a hypothesis under consideration by BW to have strong frequency dependence.
Upon examination of the misclassified injections, it was revealed that the high-f, high-Q signals exhibit multimodal likelihood support in the (α, δ, t0, f0) parameter subspace. For these signals, the Markov chain Monte Carlo (MCMC) sampler, which serves as the central engine to the BW algorithm, was not generically sampling between the different modes and was thus prone to missing significant portions of the coherent signal and preferring the incoherent glitch model (which does not suffer the correlations between time-frequency parameters and sky location).
The cause of the multimodal likelihood function is clear. For a sinusoidal signal (Q = ∞) the waveform is perfectly degenerate when time-shifted by an integer number of wave-periods (T). For high-Q signals, a number of integer periods (or half-integer periods with a π radians phase shift), time shifts produce similarly good fits to the data. For coherent signals, these (nearly) degenerate time shifts are also present in the time delay between detectors, which, for BW, is encoded in the sky location.
To overcome the susceptibility of BW to missing modes of the likelihood when analyzing high-Q signals, we added a proposal distribution to the MCMC that explicitly suggests half-integer-period time shifts, along with half-integer-cycle phase shifts, for the wavelet parameters. Furthermore, extensive development (beyond the scope of this paper) to improve the overall capabilities of the BW MCMC to sample the complex sky-location posteriors encountered by two-detector GW networks has been completed.
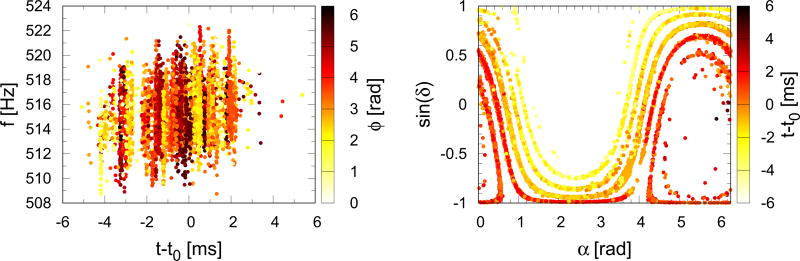
Figure 8 contains two scatter plots from the BW MCMC using the dedicated proposal distributions. The multimodal nature of the posterior is clearly displayed, as is the efficiency with which the MCMC sampler is able to move between local maxima in the likelihood. This example came from an f ~ 512 Hz, Q ~ 40 SG injection. Using the MCMC as it was during O1, we found a preference for the incoherent “glitch” model, with a Bayes factor between that and the coherent “signal” model of ~e60 in favor of the glitch model. Using the updated sampler and analyzing the same (simulated) data, we find a Bayes factor of ~e18 in favor of the signal model.
Figure 8.
Scatter plot of MCMC samples for signal model parameters of a high-Q, high-f sine-Gaussian injection. The left panel shows the time-frequency plane with points colored by the wavelet phase parameter. Multiple modes and their phase-dependence are evident. The right panel shows the same chain samples, but now projected on the sky-location plane of the parameter space and colored by the time parameter. Here again it is plainly visible how different half-integer-period time shifts correspond to different “rings” on the sky, making this a challenging distribution to sample without well-tuned proposal distributions.
Despite this upgrade to the BW MCMC engine, we elected to present results as the algorithm performed during O1 to facilitate a direct comparison with the snapshot of other burst PE techniques during the first observing run. Future studies showing how the upgraded sampler performs on similar injections are underway.
Appendix B
Example Skymaps
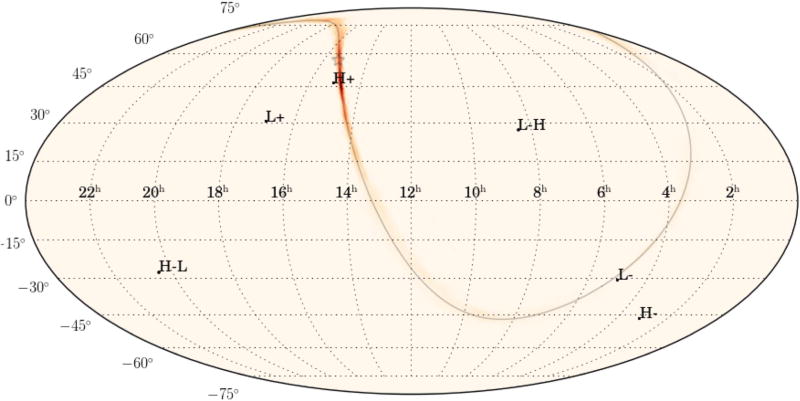
Figure 9 shows an example skymap for an injected SG signal. The injected location is marked with a star, and the corresponding triangulation ring for L1 and H1 detectors is denoted with a gray line. H–L and L–H marks the direction between the two detectors, H+ and L+ the directions above the detectors, and H- and L- the directions below the detectors. The skymap in Figure 9 is a typical map. It is consistent with the triangulation ring of the two-detector network and the constraint of the network antenna pattern, which leads to a relatively small elongated area on the sky with the maximum close to the injected location. Figure 8 shows 20 example skymaps (five for each morphology) in the online journal. Skymaps for all the signals used in this study are available in the Burst First2Years sky localization Open Data release.7
Figure 9.
Example skymap showing the reconstructed sky location for an injected SG signal. The injected location is marked with a star, and the corresponding triangulation ring for L1 and H1 detectors is denoted with a gray line. H–L and L–H marks the direction between the two detectors, H+ and L+ the directions above the detectors, and H- and L- the directions below the detectors. The complete figure set (20 figures) showing 5 example skymaps for each morphology is available in the online journal. Skymaps for all the signals used in this study are available in the Burst First2Years sky localization Open Data release (http://www.ligo.org/scientists/burst-first2years/).
(The complete figure set (20 images) is available.)
Footnotes
Supporting material: figure set
References
- Aasi J, Abbott BP, Abbott R, et al. CQGra. 2015;32:074001. [Google Scholar]
- Abadie J, Abbott BP, Abbott R, et al. PhRvD. 2012;85:122007. [Google Scholar]
- Abbott BP, Abbott R, Abbott TD, et al. PhRvL. 2016a;116:061102. [Google Scholar]
- Abbott BP, Abbott R, Abbott TD, et al. PhRvL. 2016b;116:241103. [Google Scholar]
- Abbott BP, Abbott R, Abbott TD, et al. LRR. 2016c;19:1. [Google Scholar]
- Abbott BP, Abbott R, Abbott TD, et al. PhRvD. 2016d;93:122004. [Google Scholar]
- Abbott BP, Abbott R, Abbott TD, et al. ApJL. 2016e;818:L22. [Google Scholar]
- Abbott BP, Abbott R, Abbott TD, et al. PhRvL. 2016f;116:241102. [Google Scholar]
- Abbott BP, Abbott R, Abbott TD, et al. ApJL. 2016g;826:L13. [Google Scholar]
- Ajith P, Hannam M, Husa S, et al. PhRvL. 2011;106:241101. doi: 10.1103/PhysRevLett.106.241101. [DOI] [PubMed] [Google Scholar]
- Belczynski K, Holz DE, Bulik T, O’Shaughnessy R. Natur. 2016;534:512. doi: 10.1038/nature18322. [DOI] [PubMed] [Google Scholar]
- Berry CPL, Mandel I, Middleton H, et al. ApJ. 2015;804:114. [Google Scholar]
- Chatterji S. PhD thesis. Massachusetts Institute of Technology; 2005. [Google Scholar]
- Cornish NJ, Littenberg TB. CQGra. 2015;32:135012. [Google Scholar]
- Dvoretzky A, Kiefer J, Wolfowitz J. Ann. Math. Statist. 1956;27:642. [Google Scholar]
- Essick R, Vitale S, Katsavounidis E, Vedovato G, Klimenko S. ApJ. 2015;800:81. [Google Scholar]
- Green PJ. Biometrika. 1995;82:711. [Google Scholar]
- Hannam M, Husa S, Ohme F, Müller D, Brügmann B. PhRvD. 2010;82:124008. [Google Scholar]
- Kanner JB, Littenberg TB, Cornish N, et al. PhRvD. 2016;93:022002. [Google Scholar]
- Klimenko S, Vedovato G, Drago M, et al. PhRvD. 2011;83:102001. [Google Scholar]
- Klimenko S, Vedovato G, Drago M, et al. PhRvD. 2016;93:042004. [Google Scholar]
- Klimenko S, Yakushin I, Mercer A, Mitselmakher G. CQGra. 2008;25:114029. [Google Scholar]
- Littenberg TB, Kanner JB, Cornish NJ, Millhouse M. PhRvD. 2016;94:044050. [Google Scholar]
- Lynch R, Vitale S, Essick R, Katsavounidis E, Robinet F. arXiv. 2015:1511.05955. [Google Scholar]
- Singer LP, Price LR, Farr B, et al. ApJ. 2014;795:105. [Google Scholar]
- Veitch J, Raymond V, Farr B, et al. PhRvD. 2015;91:042003. [Google Scholar]
- Vitale S, Essick R, Katsavounidis E, Klimenko S, Vedovato G. MNRAS. 2017;466:L78. [Google Scholar]