The RAPIDD Ebola Forecasting Challenge: Synthesis and Lessons Learnt

Abstract

Infectious disease forecasting is gaining traction in the public health community; however, limited systematic comparison of model performance exist. Here we present the results of a synthetic forecasting challenge inspired by the West African Ebola crisis in 2014–2015 and involving 16 international academic teams and US government agencies, and compare the predictive performance of 8 independent modeling approaches. Challenge participants were invited to predict 140 targets across 5 different time points of 4 synthetic Ebola outbreaks, each involving different levels of interventions and “fog of war”. Prediction targets included 1–4 week-ahead case incidence, outbreak size, peak timing, and several natural history parameters. With respect to weekly case incidences, ensemble predictions based on a Bayesian average of the 8 participating models outperformed any individual model and did substantially better than a null auto-regressive model. There was no relationship between model complexity and prediction accuracy; however, the top performing models for short-term weekly incidence were “light” reactive models fitted to a short and recent part of the outbreak. Individual and ensemble predictions improved with data accuracy and availability; by the second time point, just before the peak of the epidemic, estimates of final size were within 20% of the target. The 4^th challenge scenario -- mirroring an uncontrolled Ebola outbreak with substantial data reporting noise -- was poorly predicted by all modeling teams. Overall, this synthetic forecasting challenge provided a deep understanding of model performance under different data and epidemiological conditions. We recommend such “peace time” forecasting challenges as key elements to improve coordination and inspire collaboration between modeling groups ahead of the next pandemic threat, and assess model forecasting accuracy for a variety of known and hypothetical pathogens.

Introduction

The past two decades have seen rapid development and expanded use of mathematical and computational models for public health, particularly to guide intervention strategies to control emerging infectious diseases. In particular, recent health emergencies of national and international concern have been key to demonstrate how disease models can improve situational awareness in real-time and provide quantitative analysis to guide public health interventions in the midst of an outbreak. Notable examples are the 2001 foot-and-mouth disease epidemic in the UK, the SARS outbreak in 2003, the avian influenza H5N1 epizootic in 2005, the 2009 influenza pandemic, and more recently the MERS, Ebola and Zika epidemics (Lipsitch, Finelli et al. 2011, Chretien, Riley et al. 2015, Heesterbeek, Anderson et al. 2015, Bogoch, Brady et al. 2016) (Alex Perkins, Siraj et al. 2016) (Ajelli, Zhang et al. 2017). Disease models can be used to inform decision making on a range of timescales, ranging from prediction of the short-term trajectory of an epidemic (generally with a time horizon of days to weeks (Shaman, Yang et al. 2014, Medicine 2015)), projection of the benefits of different intervention strategies (also known as “scenario modeling”, with a typical horizon in the order of months, (Merler, Ajelli et al. 2015, Rainisch, Asher et al. 2015, Meltzer, Santibanez et al. 2016)) or prediction of changes in outbreak dynamics after major perturbations, such as the roll-out of new vaccination programs (typically in the order of years, (Pitzer, Viboud et al. 2009)).

The 2014–2015 West African Ebola Virus Disease (EVD) epidemic was an important testbed for the contribution of models to forecasting epidemic spread and impact, as well as for communication of the risk posed by an epidemic. Owing to weaknesses in local health infrastructure and delays in domestic and international response, the West African Ebola outbreak developed into a major crisis which rapidly devastated the region by the summer of 2014. Despite the potential for much broader international scope and major global disruption, the disease was clamped down over a year-long period of intense international response, leaving more than 28,000 cases and 11,000 deaths in its wake (Organization 2016). A variety of disease models were used in real time to generate short and long-term predictions of the expected number of cases of the unfolding outbreak and help guide the strength, timing and location of interventions (reviewed in (Chretien, Riley et al. 2015), see also (Lewnard, Ndeffo Mbah et al. 2014, Chretien, Riley et al. 2015, Rainisch, Asher et al. 2015)) and plan for vaccine trials (Merler, Ajelli et al. 2016, Camacho, Eggo et al. 2017l). Prediction efforts were in part spearheaded by an Ebola modeling coordination group led by the US HHS and by the London WHO Collaborating Center for disease modeling (Team 2014, Rainisch, Asher et al. 2015).

It is now recognized that early projections of Ebola cases and deaths made in August-September 2014 were instrumental in generating a robust public health response that ultimately ended the epidemic (Meltzer, Santibanez et al. 2016). Estimates were based on Ebola transmission model calibrated against limited epidemiological data publicly available at the time (Meltzer, Santibanez et al. 2016) (Gomes, Pastore et al. 2014). In particular, key projections put forward by the US Centers for Disease Control included 1.4 million Ebola cases in Sierra Leone and Liberia by January 2015, 4 months later, if the epidemic was left unchecked (Meltzer, Santibanez et al. 2016). Although early Ebola predictive models were useful as advocacy tools, their perceived scientific accuracy remains debated. Later in the outbreak, a variety of models were developed with increasing level of complexity, particularly with respect to demographic, spatial, and population mixing structure (Chretien, Riley et al. 2015, Ajelli, Zhang et al. 2017). After the Ebola epidemic subsided, retrospective ascertainment of model performance remained difficult, partly due to differences in the time at which the predictions were made, the epidemiological datasets used to calibrate the models, the geographic scope of the models, their assumptions, and the lack of a ‘no-intervention’ scenario available for comparison (Chretien, Riley et al. 2015).

At the tail end of the West African Ebola epidemic, in spring 2015, a workshop was organized by the RAPIDD program led by the Fogarty International Center of the National Institutes of Health (NIH) in Bethesda. The goal was to take stock of the different models used throughout the outbreak and discuss improvement in forecasting accuracy for recent and future outbreaks. The workshop convened key academic teams involved in making real-time Ebola predictions throughout the West African epidemic and US government representatives. Workshop participants concluded that a forecasting challenge relying on synthetic Ebola datasets (namely, datasets generated by a disease model) would be ideal to assess model performances in a controlled and systematic environment, and explore how prediction performances scale with epidemiological complexity and data availability. Accordingly, the RAPIDD Ebola forecasting challenge launched during September-December 2015 and convened 16 independent international academic groups and US government agencies. This effort was inspired by previous infectious disease challenges relying on empirical datasets for influenza, dengue and Chikungunya (DARPA 2015, Biggerstaff, Alper et al. 2016, NOAA 2016), and aligns with recent interest in developing stronger prediction capabilities within the US government (Chretien, Swedlow et al. 2015). To the best of our knowledge, however, the RAPIDD Ebola Challenge is the first instance of a synthetic challenge organized by the disease modeling community. Here we describe the main results of this challenge and draw key lessons to improve prediction of infectious disease outbreaks in the future.

Methods

Challenge model and epidemiological scenarios

The Ebola challenge relied on synthetic epidemiological datasets generated using a spatially structured, stochastic, agent-based model at the level of single household that integrates detailed data on Liberia demography (Merler, Ajelli et al 2015). The model was used to generate 4 plausible epidemiological scenarios, all inspired by the 2014 Liberia Ebola outbreak. A full description of the model, epidemiological scenarios, and web interface, is provided in the accompanying article by Ajelli et al (Ajelli, Zhang et al. 2017). Briefly, the model generating the synthetic data is an extension of an agent-based model originally developed for the Liberia outbreak, with realistic demographics, contact patterns, hospital information, and implementation of containment policies such as the deployment of Ebola treatment units and safe burial teams, among others (Merler, Ajelli et al 2015). The 4 synthetic outbreak scenarios represented increasing level of complexity in terms of epidemiological situation, layered interventions, data availability, and reporting noise (Table 1). While all scenarios had interventions in place, interventions were designed to be insufficient to curb the epidemic in scenario 4, leading to an uncontrolled outbreak within the timeframe of the simulations. In all other scenarios, the outbreak was controlled by the end of the simulation period.

Table 1.

Summary characteristics of the 4 Ebola scenarios considered in the Forecasting Challenge. See (Ajelli, Zhang et al. 2017) for more details.

Scenario	Outbreak dynamics	Data characteristics	Interventions
1	Controlled	Data rich; individual-level information; little noise	Safe burials ETUs Reactive behavior change
2	Controlled	Intermediate data quality and quantity	Safe burials ETUs Reactive behavior change
3	Controlled	Data poor; more noise	Safe burials ETUs Reactive behavior change
4	Uncontrolled	Data poor; more noise	Safe burials ETUs Reactive behavior change. Interventions were insufficient to curb the epidemic in the timeframe of the simulations.

The synthetic epidemiological data released to the challenge participants were subject to noise, the so-called “fog of war”, simulating incomplete reporting, missing records and other issues generally affecting data collected in real-world situations. The quality of reporting was also different in the 4 scenarios, ranging from accurate and detailed reporting in scenario 1, in which a patient line list database was made available to participants, to poor reporting in scenario 4, in which accurate information on containment policies was lacking. Participants were asked to provide disease forecasts at 5 different time points of each of the 4 scenarios, typically comprising two time points in the ascending phase, a time point near the peak, and two time points in the descending phase (Figure 1).

Figure 1.

Example of ensemble prediction graph provided to participants throughout the challenge. Here for prediction time point 5. The grey area represents the cone of incidence predictions 1–4 weeks ahead (min and max across all teams) while the red line is the mean. The black dotted line represents the synthetic epidemic curve.

Participants were asked to provide estimates for 140 targets in total, across all scenarios and time points, with each target requiring a point estimate and inter-quartile range. Prediction targets included 1 to 4-week ahead weekly incidences, final size, peak size, and peak timing. Incidence predictions were requested on a national scale and by county; however, since few participants reported county-level forecasts, we focus on national predictions here. Participants were also asked to provide estimates of natural history parameters, including case fatality rate, reproduction number, and serial interval. The release of data for each of the 5 different time points was accompanied by a situation report providing descriptive information on each scenario (Ajelli, Zhang et al. 2017).

In the summer of 2015, participants were introduced to each other and to the rules of the challenge, which stipulated that (i) any mathematical or statistical approach could be used for prediction purposes; (ii) predictions were not to be penalized by model complexity (e.g., number of parameters or equations), model type (e.g., phenomenological vs. SEIR vs. agent-based) or implementation (e.g., uncertainty estimation method); (iii) in order to avoid herd effects common in forecasting pools, the predictions of a team would remain blind to the other teams throughout the challenge, although ensemble graphs would be periodically shared; (iv) there would be a 4-week interval between any two prediction time points (which could represent a different time interval in the synthetic epidemic); and (v) noise would be added to the synthetic incidence data and situational reports.

Participants were told that all 4 synthetic outbreaks would include layered control interventions, but did not know the type, intensity or timing of interventions ahead of the challenge. Participants were aware that the synthetic outbreak datasets were generated by a published agent-based model (Merler, Ajelli et al 2015) and were provided a test dataset in August 2015 to familiarize themselves with the data structure. Participants were asked not to share the characteristics of their own forecasting models ahead of the challenge.

The challenge ran in earnest from September to December 2015. After a new batch of predictions was submitted by challenge participants, graphs displaying ensemble predictions for 1–4 week-ahead incidence were generated and shared with participants (Figure 1). A second workshop was held at the NIH in February 2016 after the conclusion of the challenge to review the structure of the different participating models, discuss performance results, and disseminate findings among policy experts and in government.

The challenge was coordinated by a team of modelers and epidemiologists from Northeastern University, Georgia State University, Copenhagen University, and FIC/NIH.

Forecasting models included in the challenge

Participants to the RAPIDD Ebola forecasting challenge self-organized in eight teams, each with a different statistical or mathematical model. Four models had been used previously during the West-African Ebola outbreak in similar versions (CDC-NIH, TOR, ASU, LSHTM; see Table 2 for details on acronyms and models), while the other four models were developed specifically for the challenge (Mc-Masters, HHS-JMA, IMP, BI of VT). Table 2 provides a brief summary of the model characteristics, which are described in full detail in the rest of the supplementary issue (Funk, Camacho et al. 2016, Pell, Kuang et al. 2016, Tuite and Fisman 2016, Ajelli, Zhang et al. 2017, Asher 2017, Champredon, Li et al. 2017, Gaffey and Viboud 2017, Nouvellet, Cori et al. 2017, Venkatramanan, Lewis et al. 2017). Four teams used semi-mechanistic models (eg, logistic growth model, renewal equation), three teams used fully mechanistic models (SIR models, cohort models, agent-based models) and one team used a hybrid approach, alternating between a SIR model and the renewal equation. Some of the models evolved throughout the challenge in response to perceived accuracy or estimation issues, as detailed in the accompanying articles. The number of parameters in participating models ranged from 2 (TOR, ASU) to 6–9 (BI of VT) (Table 2).

Table 2.

Summary characteristics of the models participating in the Ebola Forecasting Challenge.

Team	Model description	No. Parameters	Model Type	Source
ASU	Logistic growth equation	2	Semi-mechanistic	(Pell, Kuang et al. 2016)
TOR	Phenomenological model (Incidence Decay with exponential adjustment)	3	Semi-mechanistic	(Tuite and Fisman 2016)
IMP	Stochastic transmission model with a time-varying reproductive number modeled as a random walk with a drift	2	Semi-mechanistic	(Nouvellet, Cori et al. 2017)
JMA –HHS	Stochastic SEIR model with a time-varying reproductive number modeled modeled as a multiplicative normal random walk with a log-linear drift	6	Semi-mechanistic	(Asher 2017)
McMasters-1	Generalized renewal equation	> 10	Semi-mechanistic/Hybrid	(Champredon, Li et al. 2017)
McMasters-2	Compartmental SEIR model that tracks the general community and healthcare workers with hospital and funeral transmission	27	Mechanistic/Hybrid	(Champredon, Li et al. 2017)
LSHTM	Stochastic SEIR with a random walk on transmission rate	8	Mechanistic	(Funk, Camacho et al. 2016)
CDC/NIH	Deterministic SEIR model with 3 transmission risk categories	7	Mechanistic	(Gaffey and Viboud 2017)
BI of VT	Agent-based model.	6–9, varies over time	Mechanistic	(Venkatramanan, Lewis et al. 2017)
Ensemble mean	Mean of the incidence point estimates of models 1–9	N/A	Hybrid	This paper
Ensemble BMA	Bayesian average of the incidence point estimates of models 1–9	Uninformative priors	Hybrid	This paper

Ensemble predictions

Throughout the challenge, the coordination team computed ensemble prediction envelopes, based on the mean, minimum and maximum of the incidence forecasts submitted by the 8 participating teams (Figure 1). Further, after the conclusion of the challenge, a Bayesian averaging approach was introduced to calculate an alternative ensemble estimate based on the point estimates of the 8 model forecasts, in which each model forecast was weighted by prediction accuracy in the previous time points.

Performance statistics, null model, and upper bound model

Inspired by previous forecasting challenges for other diseases (DARPA 2015, Biggerstaff, Alper et al. 2016, NOAA 2016), we used a variety of performance statistics to evaluate the accuracy of incidence forecasts made by each team, including the root mean square error, the absolute and relative mean square errors, R squared (based on the equation y=ax, thus allowing negative R squared), and Pearson’s correlations between predicted and observed (synthetic) Ebola incidences. We also explored the bias of each model by fitting a linear regression to predicted and observed incidences (based on y=ax +b). In addition to the 8 participating models evaluated during the challenge, we also assessed the performances of ensemble predictions (both the mean across all model point estimates and the Bayesian averaging approach). The generic logistic-growth model (ASU team) was arguably the simplest model participating in the challenge, but we also tested a-posteriori the performances of a null model defined by an auto-regressive (AR3) process. Finally, to gauge the impact of measurement noise and intrinsic stochasticity of the epidemic and fitting processes, we refitted the agent-based model used to generate the synthetic data to its own data and evaluated prediction performances, as a performance benchmark.

Finally, for non-incidence targets such as the case fatality rate, reproduction number, serial interval, and peak timing, we compared the mean and spread of predictions (min-max) across models and over time using box plots. For incidence and non-incidence targets, the working assumption was that accuracy would improve with increasing amount of epidemic data.

Results

Here we focus on the performance of ensemble predictions and the distribution of performance statistics across all models; a detailed review of the performance of individual models as well as post-challenge analyses (e.g., model extensions) is provided in the accompanying articles.

Weekly incidence targets

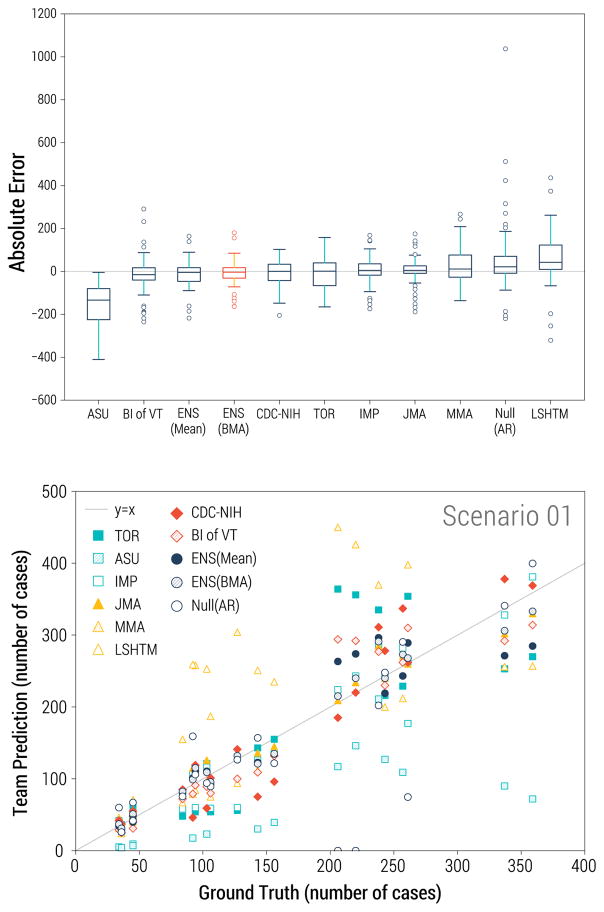
Across individual models and ensemble predictions, there was typically good agreement between all absolute error metrics for 1–4 week ahead incidence targets, with a gradient of increasing error with increasing scenario complexity (from 1 to 4, Table 3). In terms of relative errors, the median mean absolute percent (MAPE, the ratio of prediction residuals divided by the ground truth, a relative metrics which can be positive or negative) ranged from 24% to 63% across the four scenarios, with the lowest errors found in the 1^st and 4^th scenario. The median MAPE across all 4 scenarios was 40%. The ensemble prediction based on the Bayesian average consistently fared better than any individual model (MAPE range, 9–46%) and compared favorably to the data-generating agent-based model fitted to its own data (see supplementary Information). The simple mean of the point estimates of the 8 participating models was also generally better than individual model predictions but resulted in higher errors than the Bayesian average by 1–5 percentage points. The null AR(3) model resulted in good to intermediate predictions for scenarios 1 & 2, but fared particularly poorly in the more complex scenarios 3 & 4.

Table 3.

Select error metrics for Ebola incidence forecasts. Table displays values for 3 different error metrics (Mean absolute percentage error, R square, and Pearson’s correlation), by scenario and model category. Each value represents a summary error averaged over 20 incidence targets (1–4 week ahead incidence forecasts for each of 5 prediction time points). For reference, we also report the results of an auto-regressive process. Boldface values indicate a superior error metric.

Model	Scenario 1 (ideal & data rich)	Scenario 2 (intermediate complexity)	Scenario 3 (high complexity)	Scenario 4 (uncontrolled epidemic)	All scenarios combined
	Mean absolute percentage error
Individual forecasting models (median [range])*	0.24 [0.1; 0.64]	0.48 [0.27; 0.84]	0.63 [0.36; 1.56]	0.24 [0.15; 0.6]	0.4 [0.3; 0.83]
Ensemble mean *	0.13	0.39	0.51	0.16	0.30
Bayesian Modeling Average *	0.09	0.40	0.46	0.13	0.27
AR(3) model	0.31	0.37	1.24	0.35	0.57
	R squared
Individual forecasting models (median [range])*	0.7 [−2.75; 0.97]	0.69 [−2.78;0.82]	0.28 [−7.61; 0.5]	0.44 [−13.73; 0.61]	0.62 [−0.95; 0.79]
Ensemble mean *	0.88	0.69	0.45	0.54	0.76
Bayesian Modeling Average *	0.96	0.71	0.42	0.65	0.81
AR(3) model	0.27	0.18	−2.15	−3.50	−0.72
	Pearson’s correlation
Individual forecasting models (median [range])*	0.89 [0.67; 0.98]	0.86 [0.58; 0.91]	0.81 [0.54; 0.89]	0.8 [−0.24; 0.86]	0.82 [0.62; 0.89]
Ensemble mean *	0.94	0.85	0.76	0.87	0.88
Bayesian Modeling Average *	0.98	0.87	0.78	0.90	0.90
AR(3) model	0.71	0.73	0.75	0.71	0.75

^*Based on 8 teams providing incidence forecasts.

Pairwise correlation between predicted and synthetic incidences remained high across all scenarios, ranging between .8 and .89, with a mean of .82. Correlations were highest for data-rich scenario 1, and lowest for scenarios 3 and 4, including a negative correlation estimate for data-poor scenario 4. Accordingly, the R-squared metric was highest for scenarios 1 and 2 (69–70%), and lowest for scenarios 3 and 4 (28–44%). The AR(3) model predictions resulted in intermediate to poor correlations, relative to other models participating in the challenge, and even had negative R-squared values for scenarios 3–4 and overall.

Across teams and ensemble methods, the Bayesian average always outperformed individual models participating in the challenge, no matter the performance metrics, while the ensemble mean was second best for 5 of the 6 metrics. Models developed by the JMA and IMP teams had better accuracy on average across all scenarios and for scenarios 1 and 4, while the CDC model was in the next position, and the VTC team intermediate. Conversely, ASU, and to a lesser extent LSHTM, trailed in prediction accuracy, with a >2 and 3-fold larger error than any other team on average across all scenarios. In addition, the ASU and LSHTM models had negative R-squared values. The ranking of models was typically unchanged when considering Pearson’s correlation, except for a somewhat better performance of the ensemble mean relative to its ranking in other error metrics, while the Bayesian average fared relatively poorly for scenario 3 if considering Pearson’s correlation.

Teams were asked to provide inter-quartile ranges (IQR) for their weekly incidence predictions; by definition of an IQR, 50% of observations in IQRs indicates a well calibrated forecast (Supplementary Figure 1). The mean percentage of IQRs which contained the ground-truth incidence value was 38.6% (minimum and maximum of 0% and 82.5% respectively). The size of the interquartile range did not have direct impact on the percent correct (correlation between percent correct and IQR divided by mean point estimate = 0.4, P<0.05). The ASU and TOR models yielded the narrowest uncertainty measures, averaging 10% of the point estimates, while the LSHTM model provided the broadest uncertainty measures at around 160% of its point estimates. The CDC model did not provide any uncertainty measure, and hence is not part of the above statistics. If one considers that an accurate model should have only 50% of observations within its IQR, then LSHTM and IMP were the most probabilistically accurate. (Supplementary Figure 1).

Other prediction targets

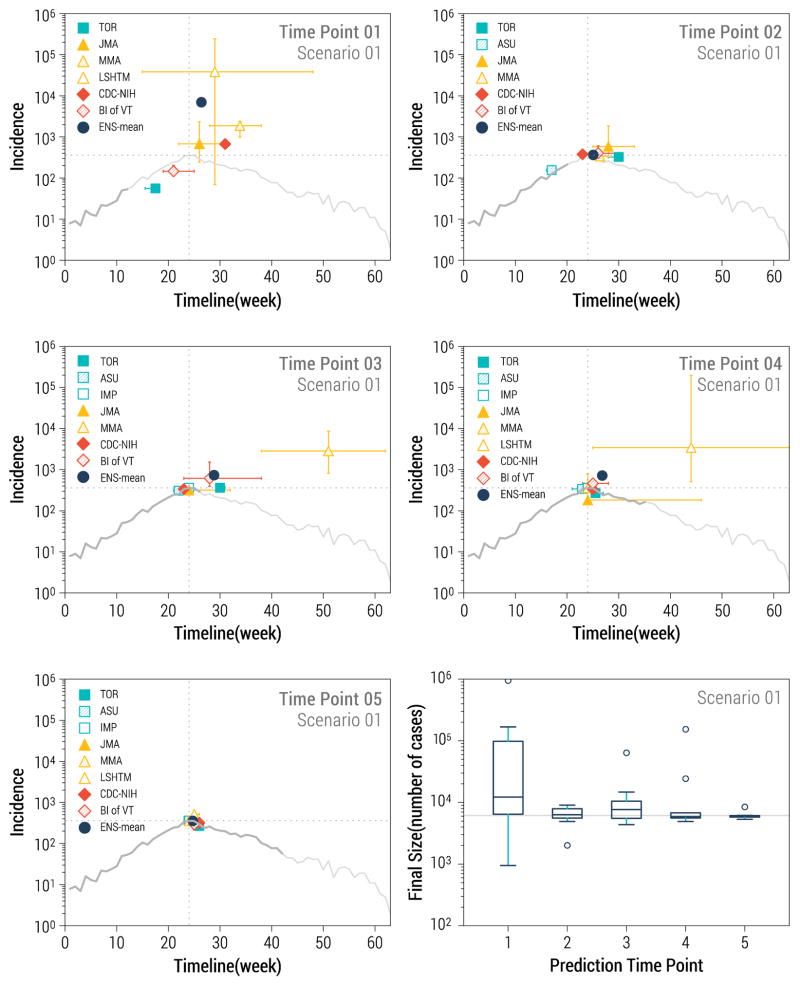
The team completion rate for forecasts of peak case incidence, peak timing and final size was excellent at 84–86%, while fewer teams provided estimates for other targets, such as CFR (29% of targets completed), serial interval (45%) or reproduction number (75%). Estimates of final sizes were highly variable for the first prediction time point (relative errors of 260 to 800%); but already by the second time point the predictions were within 10–20% of the actual values (Kruskal Wallis test for decreasing trend in errors over time, P<0.0001, Figure 3). Predictions of final size for the uncontrolled but noisy scenario 4 were over-optimistic across all models. Across all final size predictions, 33% were overestimates (the true value fell below the prediction confidence interval), 18% were underestimates (the true value was above the prediction confidence interval), and just about half of the predictions captured the true value (see also Supplementary Figures 2 to 7).

Figure 3.

Longer-term prediction targets for data-rich scenario 1. The first 5 panels represent the timing and magnitude of predicted Ebola peaks by team and prediction time point. The grey curve represents the target outbreak incidence data, with dark grey representing the amount of data available for prediction at each time point, while the light gray curve displays the full outbreak. The bottom right panel represents the distribution of final size predictions across teams by prediction time point. The solid horizontal grey line marks the true final size of the outbreak in scenario 1.

A similar pattern of declining errors with time was observed for peak size estimates (Figure 3). The median error in estimates of peak magnitude did not significantly increase from scenario 1 to 4. With regards to peak timing predictions, however, scenario 4 was associated with the poorest performance, with median error of 8 weeks over all prediction time points and teams, compared to a median of 0 week for the other scenarios (1, 2 and 3; P<0.0001).

Estimates of the reproduction number varied greatly, in part due to lack of a-priori agreement on a common estimation approach. In the first time point, R estimates varied between 1.0 and 2.7 across all teams and for all scenarios. This did not reflect actual differences among the synthetic scenarios, as all initial transmission rates were calibrated so that R would be between 1.5–1.6. All teams identified a decline in R over time for controlled scenarios 1–3, down to R <1 by the fourth time point and 0.6–0.8 by the last time point. For uncontrolled scenario 4 however, R remained higher than 1.0 throughout the 39 outbreak weeks covered by the challenge. On average, R was overestimated by .18–.22 absolute point, and the largest errors were reported at later prediction time points (P=0.04).

For scenario 1, peak forecasts were highly variable in the first prediction time point, both in terms of magnitude and location (peak predictions within 0.15 to 600-fold of true value across models and scenarios; Figure 3). In the first time point the true value of the peak fell within the confidence interval of predictions for 0–4 models, depending on the scenario, with best performances for scenario 1. Prediction stabilized after the 2nd time point (predicted peak incidences within 18–100% of true value), except for typically one outlier model.

For the uncontrolled scenario 4, most models predicted peak occurrence within the timescale of the challenge, which was too optimistic (Supplementary Figure 7). Poor performance in scenario 4 is likely due to a spurious inflection point in synthetic incidences due to the addition of stochastic noise and reporting error, which most models interpreted as a decline in transmission rates.

Discussion

Prior disease forecasting challenges focused on viral epidemic diseases are varied as influenza, dengue, and chikungunya and relied on empirical epidemic datasets collected in the outbreak area (DARPA 2015, Biggerstaff, Alper et al. 2016, NOAA 2016). To our knowledge, the 2015–16 RAPIDD Ebola Forecasting Challenge was the first infectious disease competition featuring synthetic outbreaks generated by a transmission model. It was a comprehensive and successful modeling exercise involving 16 international academic groups and US government agencies. Use of synthetic datasets was deemed essential to assess how data granularity and epidemiological complexity affect prediction performance in a controlled environment.

An important advantage of using synthetic outbreak data is to allow complete control over model assumptions, initial conditions, and time-dependent parameter values over the course of the outbreak (Ajelli, Zhang et al. 2017), while maintaining the ability to mimic realistic control scenarios. It is critical however that the transmission model used to generate synthetic data undergoes substantial testing and validation before it can be used as a realistic basis for disease forecasting. In particular, the Ebola model employed in our study had been previously calibrated using actual Ebola incidence data and had been shown to provide good agreement with the spatial-temporal evolution of the epidemic at the county level in Liberia and Guinea, making it an appealing choice for the challenge (Merler, Ajelli et al. 2015) (Ajelli, Merler et al. 2016).

A number of technical lessons were learnt during the challenge. First, with regards to short-term incidence predictions, ensemble estimates were more consistently accurate than predictions by any individual participating model. In particular, the Bayesian averaging method slightly improved accuracy over the crude mean of point estimates and had better statistical grounding. It is worth noting that the Bayesian averaging ensemble method was nearly as accurate as the data-generating fitting model fitted to its own data. In other words, overall, the Bayesian averaging ensemble method was nearly as good as the benchmark provided by the challenge model, and in some isolated instances it was even more accurate than the original model. This indicates that the set of independent models used in the challenge was sufficiently diverse and well-balanced to capture the trajectory of detailed epidemic simulations. Perhaps a subset of the 8 models included here would have done equally well in ensemble predictions, or even outperformed the full sample. While there has been considerable attention devoted to combining models and estimation procedures to improve accuracy in recent years, further work is needed to optimize the number of models and diversity of model structures to be included in successful ensemble predictions.

Second, as expected, availability of more accurate and granular epidemiological data improved forecasting accuracy, as illustrated by comparison of scenarios 1 through 4. A corollary is that the “fog of war” noise built into the incidence data, including the intentional imprecision and errors sometimes introduced in situational reports (Ajelli, Zhang et al. 2017), were highly detrimental to prediction accuracy. As a case in point, when the agent-based model used to generate the challenge data was fitted to its own “fogged” data, the prediction error averaged 24% for short-term incidences, which is substantial. It is worth remarking though, that the fitting of the agent-based model to its own data was done in conditions similar to the other models, ie blinded to model parameters and initial conditions (this sensitivity analysis was performed by a team indepandant from the team generating the data). Thus the predictions error is this analysis should be understood as the combination of “fog of war” errors with all uncertainties and choices inherent to model fitting.

In uncontrolled scenario 4, a spurious downturn was observed at prediction time point 4, primarily due to the addition of noise. No model, including the data-generating model, could capture the true trajectory of the outbreak, which resumed its incline past time point 4. For this uncontrolled scenario, unprocessed data would have revealed a monotonous increase in case incidence more clearly. In this challenge, we emphasized the importance of noise and situational uncertainty, which are expected in real-life crises situations. While we don’t necessarily believe that scenario 4 echoed the level of data uncertainty observed during the West African outbreak, considering an extreme case of “fogged data” such as scenarios drives the point that data inaccuracy entails serious loss of prediction performances. In future analyses, it would be interesting to compare prediction performance for pre-processed synthetic outbreak data, before any addition of noise, as well as “fogged data”, perhaps blinded to the teams. This would allow a careful characterization of the impact of data measurement errors on model performance.

In light of scenario 4, it would also be interesting in future work to explore which models can predict a growing incidence as part of their plausible range of outbreak trajectories, even while observations may appear to decline for a brief period. Overall, participating models were generally more likely to overestimate than underestimate incidences – perhaps stemming from a truncation of incidences at zero (eg, via the use of a log-normal transform of the beta in some models) or due to the temporal decline in R₀ due to behavior changes built into the scenarios. A related lesson is that uncertainty is important and forecasts should be provided as distributions of plausible trajectories, which ensemble approaches allow for.

To gauge the impact of measurement noise and intrinsic stochasticity of the epidemic and fitting processes, we refitted the agent-based model used to generate the synthetic challenge data to its own data and evaluated prediction performances, as a performance benchmark. To ensure independence from the team handling synthetic data generation, the fits were handled by team members not aware of the noise added to the data. These results however cannot be compared directly with the other models as the analysis was provided offline and with knowledge of the geographical structure imposed by the model. At the same time the “refitting” procedure was penalized in that it did not use any insight coming from the situation reports or ensemble analysis. For this reason, it is not possible to establish this model as a clear upper bound for the predictions, and should be considered a performance benchmark instead.

A third lesson was that availability of ‘additional’ information, including patient-level data and situational reports, is essential for situational awareness and hence better predictions, aligning with (Chowell, Viboud et al. 2017). These data were not systematically and explicitly used in model calibration, and they were sometimes amenable to interpretation; however, the teams that reported exploring these data to ‘get a feel for the outbreak dynamics’ performed better. It is possible however that increased scrutiny of patient-level information and situational reports by some teams was a proxy for increased dedication to the challenge and time spent calibrating participating models, in turn affecting prediction accuracy.

The last and perhaps most surprising lesson was that forecasting accuracy was not positively associated with a simple measure of model complexity, such as the number of model parameters. As a case in point, 2 of the 3 models with highest mean accuracy in incidence forecasts were semi-mechanistic and considered only 2 parameters. Conversely, the model with the lowest mean accuracy also had 2 parameters (the generic logistic growth model). This suggests that not only the features of the model, but also the approach that modelers employed for calibration and parameter estimation influenced predictions. For instance, a post-challenge analysis using the generalized-logistic model (instead of the simple logistic growth equation) to capture sub-exponential and exponential growth dynamics yielded significantly improved predictions with the addition of a single parameter (Pell, Kuang et al. 2016). The fact that model complexity does not appear to scale with prediction accuracy is probably one of the most important lessons from this challenge. However it must be noted that more complex mechanistic models are generally required to make predictions at finer resolution and to assess the effectiveness of possible intervention strategies. For instance, only the agent-based model BI-VT consistently provided predictions at the county level. In the future, more complex measures of model complexity, which go beyond the number of parameters, would be worth considering in relation to model performances.

A number of caveats are worth noting. First, the participating teams selected their own models without any restriction on model type or level of complexity (e.g., number of parameters, time-dependent changes in parameters, dynamical properties). Teams were also allowed to make model adjustments throughout the challenge. The challenge was entirely focused on forecasting performance and did not consider whether a model could support certain dynamical features of the Ebola epidemic including endemic states, chaos, damped or sustained oscillations, or backward bifurcations. While restrictions on the minimum or maximum level of model complexity were not imposed, this is an aspect that could be considered in future forecasting challenges.

A second caveat relates to the use of a stochastic model to generate epidemic data in this challenge (Ajelli, Zhang et al. 2017). Thus, each of the 4 synthetic outbreaks selected for the challenge corresponds to a typical but unique stochastic realization of an epidemiological scenario, rather than a deterministic solution. While this is more in line with the stochasticity expected of an actual outbreak, it focuses on a single realization. One possibility is that future forecasting challenges based on synthetic data could provide ensembles of stochastic realizations rather than a “typical” epidemic curve for each scenario, as the basis for predictions. The drawback is that it would entail a substantial amount of additional work on the participating teams making predictions.

Another caveat is that we did not evaluate the fit of the models to past incidence data (e.g., goodness of fit for the calibration period), but instead focused on assessing forecasting performance. Furthermore, some models were consistently grounded in incidence case series starting from the first reporting week (e.g., the logistic growth model) while others were only fitted piecewise to later sections of the epidemic (ie, IMP and JMA, the top performing models), an aspect of model calibration that certainly affects model performance. Future challenge exercises could incorporate basic modeling and calibration rules including consideration of goodness of fit during the calibration period as part of model performance. Indeed, the identification of systematic deviation between models and data could reveal particular trajectories not captured by specific models such as the presence of slower epidemic growth patterns indicative of spatial structure or reactive behavior (Chowell, Sattenspiel et al. 2016, Viboud, Simonsen et al. 2016) or particular dynamical properties not supported by the models (e.g., multiple waves, endemic states).

We did not fully document the number and type of adjustments that participating teams applied to their modeling frameworks throughout the challenge (e.g., number of fitted and fixed parameters). As future work, it could also be of interest to retrospectively evaluate which of the participating models can fit the entire epidemic curve based on detailed knowledge of the fog of war that was built into the incidence data. Furthermore, it would be useful to explore what would be the minimal set of models to provide ensemble predictions that are accurate 95% of the time. Key unresolved questions here are: Is there a minimal acceptable model that could realistically describe the epidemic curves for each of the transmission scenarios? How sensitive is forecasting performance to increasing prediction horizon beyond 2 generation intervals? How many different models does one need for accurate ensemble predictions of plausible epidemiological scenarios?

Lastly, the challenge was built to address technical issues around disease forecasting, rather than explore how to best translate forecasting results into policy action. We consulted with decision makers and policy-oriented modelers throughout the challenge. However, given the synthetic nature of this particular challenge, there was no immediate actionable use for the challenge outputs, in contrast to forecasts made in real-time during the 2014–2015 West African Ebola outbreak. Initial discussions with policy makers at the outset of the challenge revealed that the most useful outcomes were also typically the hardest to predict, such as prediction of the total epidemic size early in the outbreak. Further, there was also an intense and unmet need for models to answer simple logistical questions quickly (eg, how many ETU beds should I put where?). While the Ebola challenge was not designed to directly inform links between models and policy, it provided unique head-to-head comparison and evaluation of different modeling approaches – a first step towards making predictions trustworthy, and hence actionable for public health. Finally, other important questions around whether more useful predictions should focus on accuracy of point estimates vs uncertainty bounds, incidence patterns vs extinction times, are important to answer moving forward but were beyond the scope of this particular challenge.

Another important outcome of the Ebola forecasting challenge goes beyond any scientific lessons learnt about forecasting. The collaborative work, leading to effective communication and exchanges of experiences and learning are all critical elements to improve pandemic preparedness. Communication and scientific exchanges during the challenge strengthened links between participating teams. Since modelers typically research more than one infectious disease system, these exercises can be useful to build collaborative networks that are prepared to respond to the next infectious disease crisis (Chowell, Viboud et al. 2017). Further, forecasting challenges could inform the minimal requirements for epidemiological datasets to be collected in the next outbreak – in turn producing feedback for surveillance efforts about critical data elements needed to rapidly identify the type of pandemic threat and to guide the prediction modeling efforts.

Conclusions

In conclusion, the Ebola Forecasting challenge departs from previous exercises of the same kind in that it was based on synthetic data, allowing for more control of data quality and quantity and consideration of a diverse set of epidemiological situations. As with previous challenges focused on different disease systems, this research project highlights the strength of ensemble predictions over any individual mechanistic or statistical approach. Uncertainty decreased with availability of better epidemiological information; our concept of introducing ‘fog of war’ provided a realistic layer of data reporting noise but was particularly detrimental for predictions of the uncontrolled scenario. Perhaps the most surprising finding was that prediction performance was not driven by model complexity; in fact, reactive ‘light’ non-parametric models, fitted to a small but recent part of the epidemic curve, performed best for short-term predictions. On the other hand, more complex models could access finer geographical resolutions and would be in the position to answer questions concerning intervention planning and containment strategies. Longer term forecasts however such as peak size and final size were more difficult across all models, particularly for the early time points where intervention scenarios remained highly unclear – a situation reminiscent of the West African Ebola outbreak in the midst of the 2014 summer. While this study does not provide new insights on the West African outbreak, it helps understand how data aggregation and measurement error can obscure the true epidemic trajectory and highlights the importance of individual-level case data to fine tune reactive transmission models. The need for reactive predictive models is particularly important for emerging infectious crises, as public health interventions and behaviors may rapidly change over the course of an outbreak

The synthetic Ebola forecasting challenge presented here opens doors for related follow-up activities, which should contribute to perfecting infectious diseases forecasting capabilities and building resources that can be mobilized during future crises. Synthetic exercises could be particularly valuable to mimic unfolding outbreaks involving new threats, where little background information may be available. It may be useful to consider a range of challenges illustrative of a variety of pathogens characteristics and transmission routes (respiratory transmission, direct contact, diarrheal/waterborne infection, vector-borne disease), which could serve as a table top exercise for the modeling community and provide a flexible toolbox to activate in pandemic emergency. Synthetic challenges have to strike a difficult balance between providing realistic outbreak data that can be useful to train models, while not fully replicating prior outbreaks so as to keep an element of “unknown”, akin to an unfolding outbreak (Ajelli, Zhang et al. 2017). As interest in infectious disease forecasting grows (Chretien, Swedlow et al. 2015), we anticipate that forecasting challenges may become an important tool to advance the discipline.

Figure 2.

Performance statistics for incidence forecasts, displaying data for all prediction time points. Top: Box plots of the mean absolute error by team, across all scenarios. Red indicates the Bayesian ensemble mean (smallest absolute error). Bottom: Agreement between synthetic and predicted incidences by team for data-rich scenario 1.

Highlights.

• We report the results of a forecasting challenge based on synthetic, model-generated, outbreak data inspired by the Ebola epidemic in Liberia in 2014–2015.

• Eight participating teams representing 16 institutions and government agencies competed in the challenge.

• For short-term 1–4 week ahead incidences, prediction performance did not scale with model complexity.

• Prediction accuracy declined with increasing “fog of war” noise.

• Ensemble predictions consistently outperformed any individual model.

• Forecasting challenge are important tools to coordinate the modeling community in peace times

• Synthetic forecasting challenges provide a deep understanding of model accuracy and data requirements under controlled environment and could be extended to other known and unknown pathogens.