A method of gene expression data transfer from cell lines to cancer patients for machine-learning prediction of drug efficiency

ABSTRACT

Personalized medicine implies that distinct treatment methods are prescribed to individual patients according several features that may be obtained from, e.g., gene expression profile. The majority of machine learning methods suffer from the deficiency of preceding cases, i.e. the gene expression data on patients combined with the confirmed outcome of known treatment methods. At the same time, there exist thousands of various cell lines that were treated with hundreds of anti-cancer drugs in order to check the ability of these drugs to stop the cell proliferation, and all these cell line cultures were profiled in terms of their gene expression.

Here we present a new approach in machine learning, which can predict clinical efficiency of anti-cancer drugs for individual patients by transferring features obtained from the expression-based data from cell lines. The method was validated on three datasets for cancer-like diseases (chronic myeloid leukemia, as well as lung adenocarcinoma and renal carcinoma) treated with targeted drugs – kinase inhibitors, such as imatinib or sorafenib.

Introduction

The sophisticated nature of intracellular processes and events that lead to cell proliferation and cancer progression gives a hint that machine-learning methods may be applied for prediction of clinical efficiency of certain drugs and treatment methods for individual patients. This approach, sometimes termed drug scoring and/or personalized (individual) medicine, may therefore involve the analysis of expression-based features and values that describe the activation of cell signaling and metabolic pathways to distinguish the patient who will respond to suggested treatment method. Two principal approaches may be used for expression-based drug scoring. One type, say a priori scores, evaluates the abilities of a certain drug to restore the normal status of the expression-based pattern, or to terminate the physiological process that is considered pathogenic for a certain disease (e.g. cell proliferation for cancer etc.) [1]. Another possible type of drug scoring exploits precedent-based learning. These a posteriori drug scores are the result of a machine learning process on a training dataset, which contains expression-based features extracted for the patients, who were treated with a certain drug (for each patient, the clinical outcome of the treatment, whether it is a positive response or lack of it, is also known). Any machine-learning scheme may be applied to distinguish between the responder and non-responder clusters in the multi-dimensional space of expression-based features.

Usually machine learning methods require hundreds or thousands points for the training dataset to provide the adequate coverage of the phase space [2]: a condition that lies far beyond the current capacity of gene expression profiles for the cancer patients with the case histories that specify both treatment method and the clinical response. For most anti-cancer drugs it is extremely difficult (if ever possible) to find hundreds of gene expression that were obtained using the same investigation platform for the patients that were treated with the same drug with the known clinical outcome of the treatment [3–5]. From the other side, thousands of expression profiling results have been obtained for various cell lines that were used for testing the ability of hundreds of drugs to inhibit the cell proliferation [6].

Here we are proposing a novel method for the transfer of expression-based data from the more numerous cell lines to less abundant cases of real patients for subsequent application of machine-learning that predict the clinical efficiency of anti-cancer drugs (in our study, both cell lines and people were treated with kinase inhibitors, a.k.a. nibs).

According to the standard approaches [7] to validation of machine leaning methods for analysis of expression-based features, we have used the leave-one-out procedure and AUC metric with a predefined threshold as main algorithms to select appropriate predictors. To make validation tests stronger, we also did parallel analysis with using three different machine-learning methods (support vector machines [8,9], binary trees [9] and random forests [10]) to build predictor-classifiers.

Results

Data sources of cell lines and patients to design, test and validate our method

We have organized the experimental analysis based on one expression dataset of cell lines and three datasets of patients, each corresponding to specific pair of a kind of cancer-like disease together with a sort of drug used to treat this disease. The cell lines dataset of 227 elements was borrowed from the CancerRxGene study [6]. The three patients’ datasets were taken for renal carcinoma (current study), lung adenocarcinoma [3] and chronic myeloid leukemia [4] comprising 28, 38, and 28 case histories, respectively. Those datasets were treated by several preprocessing procedures for normalization and extracting informative features. The fundamental procedure to extract informative features was organized based on the OncoFinder method that transforms gene expression data into activations of particular signaling pathways [11–14].

According to the OncoFinder approach, the pathway activation score (PAS) for a given sample and a given pathway p is obtained as follows,

$$P{\rm A}{S}_p={\displaystyle \sum _{n}AR{R}_{np}\cdot \text{log}\left(CN{R}_n\right).}$$

Here the case-to-normal ratio, CNR_n, is the ratio of the expression level of gene n in the sample under investigation to the average expression level of that gene in the control, or normal, group of samples. ARR_np is the discrete value of the activator/repressor role equals the following fixed values: −1, when the gene/protein n is a repressor of molecular pathway; 1, if the gene/protein n is an activator of pathway; 0, when the gene/protein n is known to be both an activator and a repressor of the pathway; and 0.5 and −0.5, respectively, tends to be an activator or a repressor of the pathway p, respectively. A positive PAS value indicates activation of a pathway, and a negative value indicates repression. The validity of the PAS concept was confirmed [13] on the calculations according to a low-level kinetic model of EGFR pathway activation [13,15].

During the PAS calculations, we used three types of normal (control) expression values. First, it was the auto-normalization (geometric-mean normalization), where the normal expression value for each gene was calculated as a geometric mean over all cell line/disease samples for this gene. Also, we have tried the tissue-based normalization, when the normal samples were taken from the organs/tissues of healthy persons [16–18]. For CancerRxGene cell lines, as the tissue-based normalization, we have used the non-tumor glial brain tissue [19] (samples GSM362995 to GSM363004) and smooth aortic muscles [20] (samples GSM530379 and GSM530381). The overview of the data sources for the cell lines and patients is given in Table 1.

Table 1.

Data sources for the cell line and patient datasets.

Case samples	Normal samples for tissue-based normalization	Cell type	Drug	Experimental platform	# of samples
GSE68950 [6]	GSE14805 [19], GSE21212 [20]	Cancer-RxGene cell lines	Imatinib Sorafenib	Affymetrix HT Human Genome U133A mRNA array	227
Current study	GSE49972 [16]	Renal carcinoma	Sorafenib	Illumina HumanHT-12v4 Expression BeadChip and CustomArray ECD 4 × 2K/12K	28 (13 responders, 15 non-respondres)
GSE31428 [3]	GSE43458 [17]	Lung adeno-carcinoma	Sorafenib	Affymetrix Human Gene 1.0 ST Array	37 (23 responders, 14 non-responders)
GSE2535 [4]	GSE2191 [18]	Chronic myeloid leukemia	Imatinib	Affymetrix Human Genome U95 Version 2 Array	28 (16 responders, 12 non-responders)

Data transfer method: from the cell lines to patients

As was mentioned above, every cell out of 227 was treated by a given drug. The treatment result was presented by the well-known efficiency coefficient IC₅₀, the drug concentration, which allows to inhibit the cell division process by 50% [21]. To quantify drug efficiencies for cell lines for a certain drug, these lines were first sorted by the descending order according to their IC₅₀ values. After such sorting, all the lines were divided into five quintiles with equal number of members, with the first quintile contains the highest IC₅₀, and the fifth contains the lowest. Within each quintile i, the drug efficiency Y was assigned as follows, Y = (i – 1)·25, with Y = 0 for weakest responders, and Y = 100 for the strongest.

Also, every cell line was supported by gene expression profile, which was transformed, as mentioned before, into much shorter profile of activations of signaling pathways (PAS). For each drug type, only those pathways, which contain molecular targets of this drug, were taken into account. The total dataset for each cell line comprises its individual activation profile of targeted pathways and a quantilized drug efficiency (Y).

For the patients, the dataset in similar: the set of PAS for targeted pathways, and a clinical outcome of a treatment, which, as we have considered, may be either positive (responder) or negative (non-responder).

The overall datasets for the cell lines and patients for all the normalization methods used, are given in Supplementary Tables 1 and 2, respectively.

Table 2.

Performance test for data transfer form CancerRxGene data [6] to cancer/leukemia patients for regression-mode SVM with linear kernel. The AUC value was calculated for drug response prediction as a marker for observed response to the treatment.

Disease type, Drug	AUC for optimized (M, K) parameters for auto-normalization (geometric mean)	AUC for optimized (M, K) parameters for tissue-based glial [19] normalization	AUC for optimized (M, K) parameters for tissue-based aortic [20] normalization
Renal carcinoma, sorafenib (current study)	0.81	0.77	0.82
Lung adenocarcinoma, sorafenib [3]	0.72	0.77	0.78
Chromic myeloid leukemia, imatinib [4]	0.76	0.77	0.78

Using the cell line data, we determine a set of regression models, which characterize a dependency between features of the activation of signaling pathways and the drug efficiency coefficient Y. Individual regression model was calculated based on the data for a particular subset of cell lines, determined by the corresponding patient. This patient-depended subset of cell lines was defined the following procedure:

• a)on axis for every feature in the space of PAS we fix a point, associated with the chosen patient;
• b)for predefined integer M check if there exist on the axis at least M cell's points above the chosen patient's point, and also at least M cell's points below it. If this condition is satisfied, we keep the feature as relevant to the patient; all set of relevant features forms the subspace, where we determine subset of cell lines associated with the chosen patient;
• c)in the relevant subspace and for the predefined integer K we find the K nearest cell lines to the chosen patient's point [22]; that K cell line point in extracted relevant subspace is the dataset, on which the mentioned above individual regression model is constructed.

As a result of that analysis, we get for every patient two values: predicted drug score (DS), as well as prior knowledge that he (or she) gave the positive response on the treatment. Taking some threshold (τ), by which to decide the drug score is high enough to classify this patient as a responder, we are able to calculate AUC value for the whole set of patients. Taking into account that predicted drug scores for patients depend upon chosen constants M and K, we can check the AUC values over the lattice of all feasible pairs (M, K) – to find the largest connected area and the highest AUC within this area.

Validation of the data transfer procedure

The best results for the data transfer procedure described in the previous section were obtained using the support vector machine with linear kernel (Table 2, Figures 1–2, Supplementary table 3). Nine panels show different disease/drug types and normalization method for PAS calculations. Similarly to columns and rows of Table 2, columns of panels in Figures 1 and 2 stay for different normalizations, from left to right: auto-normalization (the normal expression value for each gene was calculated as a geometric mean from all cell line/disease samples for this gene over this set of samples), and tissue-based normalization with glial [19] and aortic [20] samples used as normal for CancerRxGene [6] cell lines. Rows of panels show the results for different disease/drug combinations, from top to bottom: renal cancer treated with sorafenib (current study), lung cancer treated with sorafenib [3] and chronic myelogenous leukemia treated with imatinib [4].

Figure 1.

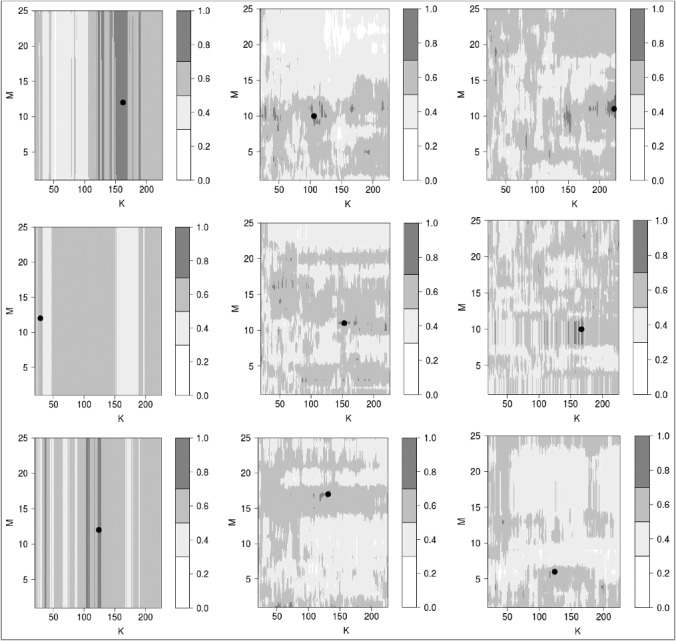
Determination of optimal setting (M_opt, K_opt) for data transfer parameters (M, K). Rows and columns of panels correspond to disease types and PAS normalizations, respectively, similarly to rows and columns of Table 2. Within each panel, the color map displays the distribution of AUC values for linear SVM predictor of drug efficiency. The darkest shade of grey shows the areas where AUC > θ for the quality threshold θ  =  0.7. The top of the biggest connected area (“island”) where AUC > θ is marked with a boldface black point.

Figure 2.

Data-transfer-assisted separation of responders from non-responders to clinical treatment of cancer-like diseases with certain drugs. Rows and columns of panels correspond to disease types and PAS normalizations, respectively, similarly to rows and columns of Table 2. Within each panel, left and right boxes represent continuous value of DS (drug score), obtained using the SVM-based regression procedure for non-responding (NonResp) and responding (Resp) patients, respectively. The central line shows the discrimination threshold value (τ) that minimizes the sum of false positive and false negative predictions; all patients with DS > τ are classified responders and vice versa.

To distinguish between clinical responders and non-responders, the threshold (τ) value is determined to minimizes the sum of false negative and false positive predictions (Figure 2): when DS > τ, a patient is classified as a drug responder, whereas the value of DS < τ indicates a non-responding case.

These optimal data transfer parameters ((M_opt, K_opt); see Figure 1), defined as the top of the biggest connected area in the map of AUC plotted as a function of M and K, when AUC exceed a threshold (θ = 0.7), appear to be stable and robust according to the leave-one-out quality assurance procedure for the patient dataset. In fact, these parameters (M_opt, K_opt) always lie within this biggest connected area (“island”), which was defined for the whole set of patients, if we perform similar optimization procedure for all but one patients (Supplementary table 4). Note also that for the auto-normalization of gene expression levels during PAS calculations for cell lines and patients makes all the points of the patient set lie in the central area of the cloud of the points of the cell line dataset. Therefore, the performance of data transfer does not depend on the parameter M (Figure 1, left column of panels).

Discussion

The clinical cases with both known treatment outcome and gene expression profile for most drugs and disease types are limited. Taking into account multi-dimensionality of expression features, it may sound attractive to involve as training datasets for machine learning the profiling results for cell line cultures treated with different drugs, since these cases are generally more numerous than the patient data with known clinical outcome. In the current work, we have used as the training set the CancerRxGene data [6] for cell lines treated with different kinase inhibitors.

In our analysis the support vector machine method [8,9] demonstrates result robustness. Another possible way to increase the robustness of such drug scoring, as we found, is the use of pathway activation strength (PAS) [11,13] for the ensembles of cell signaling pathways instead of expression levels of distinct genes.

Keeping the main goal to extract from the cell lines data essential information to transfer to patient data, and to prevent extrapolation during such data transfer, we have proposed a method that excludes from expression-based feature space any dimension, which does not provide the significant (say, M) number of points in the cell line dataset both below and above each point of the patient dataset. Such exclusion of unfit dimensions is performed using rectangular projection of all points of the cell line dataset along these unfit dimensions. Following this dimensionality reduction, we than select, similarly to the k nearest neighbor (kNN) method [22], only K points in the cell line dataset that are proximal a certain point in patient dataset, to build the SVM model. In other words, for each point of the patient dataset, our new data transfer technique filters/trims the cell line data using a floating window that surrounds every point in the patient dataset, in order to preclude extrapolation and to neglect the influence of too distant points of the cell line dataset.

This data transfer was checked on the example of three cancer-type diseases (chronic myeloid leukemia, as well as renal carcinoma and lung adenocarcinoma). For each disease type, the optimal data transfer parameters (M_opt, K_opt) allow separation of clinically responding patients from non-responding ones with AUC > 0.70. These optimal values appear to be stable according to the leave-one-out quality assurance procedure for the patient dataset. Contrary, application of our data transfer technique to the random forest machine learning method [10] did not produce a regular pattern in the AUC map over the values of M and K (data not shown). Therefore, we have concluded that random forest is not suitable for our data transfer technique, although it had produced the maximal AUC value as high as for the SVM model.

The new data transfer technique enjoys advantages of both local (like the kNN method) and global (like the SVM) machine-learning techniques. This hybrid/compromise nature of our method allows it to act successfully when purely local and global approaches fail.

Materials and methods

Transcriptome profiling for renal cancer samples

The details of experimental procedure at Illumina HumanHT-12v4 and CustomArray ECD 4 × 2K/12K platform were reported previously [14]. Raw expression data were deposited in the GEO database (http://www.ncbi.nlm.nih.gov/geo/), accession numbers GSE52519 and GSE65635.

Harmonization of Illumina and Custom Array expression profiles for renal cancer

To cross-harmonize the results for the Illunina and CustomArray gene expression profiling, all expression profiles were transformed with the XPN method [23] using the R package CONOR [24].

SVM, binary tree and random forest machine learning procedures

All the SVM calculations were performed using the R package ‘e1071’ [25] that employs the C++ library ‘libsvm’ [26]. Calculations according to binary tree [27] and random forest [10] methods were done with the R packages ‘rpart’ and ‘randomForest’, respectively.

Funding Statement

This work was supported by the National Research Center "Kurchatov Institute" [grant number 2017-1025].

Acknowledgments

The authors thank Drs. D.G. Sokov (Moscow 1st Oncological Hospital), N.M. Gaifullin (Lomonosov Moscow State University), K. Kashintsev and V. Shirokorad (Moscow Oncological Hospital 62), as well as Elena Poddubskaya (Clinical Center Vitamed), who provided renal cancer samples, together with anonymized case histories.

Disclosure of potential conflicts of interest

No potential conflicts of interest were disclosed.