A Monte Carlo Study on Dose Enhancement by Homogeneous and Inhomogeneous Distributions of Gold Nanoparticles in Radiotherapy with Low Energy X-rays

Abstract

Background:

To enhance the dose to tumor, the use of high atomic number elements has been proposed.

Objective:

The aim of this study is to investigate the effect of gold nanoparticle distribution on dose enhancement in tumor when the tumor is irradiated by typical monoenergetic X-ray beams by considering homogeneous and inhomogeneous distributions of gold nanoparticles (GNPs) in the tumor.

Methods:

MCNP-4C Monte Carlo code was utilized for the simulation of a source, a phantom containing tumor and gold nanoparticles with concentrations of 10, 30 and 70 mg Au/g tumor. A 15 cm×15 cm×15 cm cubic water phantom was irradiated with a small planar source with four monoenergetic X-ray beams of 35, 55, 75 and 95 keV energy. Furthermore, tumor depths of 2.5 cm, 4.5 cm and 6.5 cm with homogeneous and inhomogeneous distributions of nanoparticles were studied. Each concentration, photon energy, tumor depth and type of distribution was evaluated in a separate simulation.

Results:

Results have shown that dose enhancement factor (DEF) in tumor increases approximately linearly with the concentration of gold nanoparticles. While DEF has fluctuations with photon energy, 55 keV photons have the highest DEF values compared to other energies. While DEF has relatively the same values with tumor located at various depths, inhomogeneous distribution of GNP has shown different results compared with the homogeneous model. Dose enhancement can be expected with relatively deep seated tumors in radiotherapy with low energy X-rays. Inhomogeneous model is recommended for the purpose of dose enhancement study because it mimics the real distribution of GNPs in tumor.

Introduction

High atomic number materials, which are routinely used to improve contrast in X-ray diagnostic radiography, have been successfully proven to enhance radiation dose in kilovoltage X-ray radiotherapy beams [1]. The use of other high atomic number (Z) materials such as gold nanoparticles also has advantages in the form of radiation dose enhancement.

The dose delivered to a tumor during radiation therapy with photons can be enhanced by loading high atomic number (Z) materials such as gold (Au, Z=79) into the tumor, resulting in greater photoelectric absorption within the tumor than in the surrounding tissues. In the kilovoltage energy range, the high photoelectric cross-section of the high Z materials results in higher number of photoelectric interactions. Since the atomic photoelectric cross-section is approximately proportional to Z³, the absorbed dose increases with in-tumor presence of such materials.

In radiotherapy, gold nanoparticles (GNPs) are currently studied and proposed as materials to enhance the photon dose at the target [1-4]. The relatively high atomic number of gold results in a high mass energy absorption coefficient improving the treatment of the tumor target and tumor control due to the dose enhancement during radiotherapy [5-6]. In addition, GNPs are non-toxic and have good bio-compatibility when delivered to the tumor [7-8]. Gold nanoparticle enhanced radiotherapy (GNP-ERT) employs GNPs up-taken by tumor with radiation beam irradiation to enhance the delivered dose and treatment outcome. GNP-ERT was initially tested in small animals by Hainfeld, et al. [3]. He injected 1.9 nm diameter GNPs into mice bearing mammary carcinoma, and found that one-year survival rate was 86% with combination of photon beam and gold nanopatricles versus 20% with photon beam alone and 0% with gold nanoparticles alone. Hainfeld, et al. [9], as another study on small animal models, then proved that GNP-ERT was efficacious when treating highly aggressive squamous cell carcinoma. To understand the physical role of GNP dose enhancement in GNP-ERT, Monte Carlo (MC) simulation was also used for microdosimetry in other studies. Zhang, et al. [10] studied the dose enhancement with a uniform distribution of GNPs of 100 nm diameter irradiated by an ¹⁹²Ir brachytherapy source using Geant4 MC code. He found that his model, considering a GNP as a solid sphere, resulted in more accurate results than the previous model of gold-water mixture. He also concluded that GNPs’ concentration and size are factors affecting dose enhancement. Jones, et al. [11] calculated microscopic dose enhancements due to GNPs with different photon sources of ¹²⁵I, ¹⁰³Pd, ¹⁶⁹Yb, ¹⁹²Ir, 50 kVp and 6 MV. EGSnrc and NOREC MC codes were used and dose enhancement ratios of 2.0 to 20.0 were obtained when using 5 μm diameters of GNPs. For the purpose of optimization of the clinical usage of GNP based on the photon beam energy, nanoparticle size, concentration and location, Lechtman, et al. [12] used MCNP5 MC code to find the dissymmetric dependences of the above parameters using ¹⁰³Pd, ¹²⁵I, ¹⁶⁹Yb, ¹⁹²Ir brachytherapy sources and 300 kVp and 6 MV external photon beams. The microscopic dose enhancement of single GNPs with different sizes, irradiated by different photon beam energies were studied by his group [13] using Geant4 code by consideration of the Auger effect. He found that low-energy photon beams were much more efficient when interacting with GNP by two to three orders of magnitude compared to megavoltage photon beams. Moreover, the majority of energy deposition was outside the GNP, rather than self-absorbed by the nanoparticle. McMahon, et al. [2] carried out calculations on energy deposition due to the presence of GNPs using Geant4 MC code, and related the results to the biological outcome. Good agreement between the MC and experimental results in cell killing was observed, showing that MC simulation of GNPs was validated by the experiments.

In previous studies on dose enhancement by nanoparticles, it was assumed that distribution of NPs is homogeneous. However, it should be noticed that after injection of nanoparticles into the human body, they are conveyed to tumor by blood vessels. Furthermore, the number of blood vessels is higher in peripheral regions of the tumor [14-15]. With growth of the tumor, the central part becomes avascular and necrotic. For this reason, it is predicted that in a real situation, the concentration of nanoparticles inside a tumor is not homogeneous. In the present study, besides the evaluation of various parameters such as concentration, photon energy and tumor depth, an inhomogeneous distribution was considered for the concentration of gold nanoparticles inside a tumor and the effect of the inhomogeneous distribution on variation of dose enhancement inside the tumor was evaluated. Furthermore, the results of dose enhancement for homogeneous and inhomogeneous distributions were compared.

Material and Methods

Monte Carlo simulations were carried out using MCNP-4C code [16]. This code was valuable for this study because it allows investigation of dose enhancement produced by a wide range of photon energies with a broad range of gold concentrations. The code was used to produce depth dose in a phantom containing an assumed tumor. Absorbed dose calculation was performed by using *F8 tally in MCNP-4C.

The current investigation was conducted with several phantom cases that simulated typical radiation treatments using monoenergetic X-ray beams. In each case, it was assumed that gold nanoparticles were uniformly distributed throughout the tumor with 10, 30 and 70 mgAu/g tumor concentrations of gold nanoparticles. Dose enhancement for monoenergetic photons of 35, 55, 75 and 95 keV energy were investigated. GNPs distribution was defined in the atomic form with definition of weight fraction. The geometry used for the external beam included a tumor infused with homogeneous or inhomogeneous distributions of gold nanoparticles distributed within a tumor. The tumor was located in a 15×15×15 cm³ water phantom in the form of a cube. The space between the water phantom and the source included air in the simulations. In the water phantom, a soft tissue part containing 75 voxels was defined. This part was in the form of a cylinder with 15 cm height and 0.5 cm radius, including tally cells each as a voxel with 2mm height containing soft tissue material. In Figure 1 the geometry of the planar source, water phantom, tumor and the tally voxels inside the tumor is illustrated. Three groups of tally cells were used: the first group was composed of normal tissue up to the tumor region, the second one included the tumor voxels, while the third group included those cells positioned under the tumor. Tumor had 3 cm height and 0.5 cm radius and its center position was defined in three depth cases: 2.5 cm, 4.5 cm and 6.5 cm, each being studies separately. The output of *F8 tally (MeV) was divided by the cell mass to obtain the absorbed dose. It is obvious that the mass of tally cells in the presence of nanoparticles differed from that in absence of nanoparticles. The dose enhancement factor (DEF) was defined as the ratio of the point dose in a voxel of tumor region including gold nanoparticles to that of no gold nanoparticles. DEF was calculated for all cells above the tumor, inside the tumor and under the tumor on the central axis of the beam from 1mm to 100 mm.

Figure1.

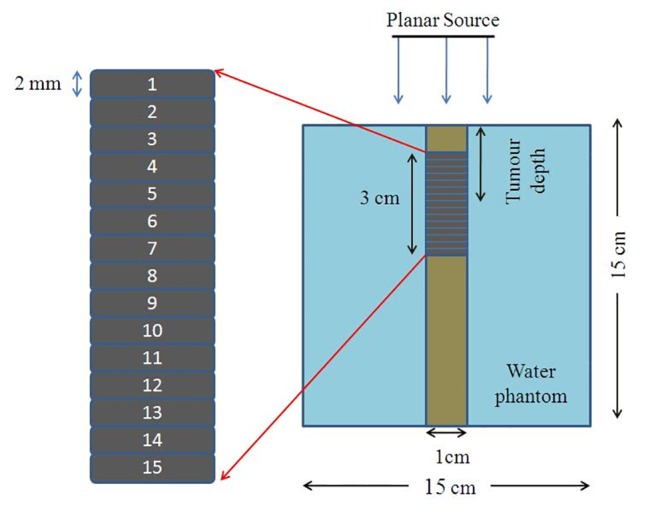
Geometric of water phantom and tumoral tissue in the simulation. Tumor devided to 15 voxels that each voxel has a number,in inhomogeneous model density of voxeles is different and voxel number 8 is the necrosis region in inhomogeneous model. This figure is not in a real scale.

The center of the tumor was located along the central axis of the beam, and a source of X-ray beam was defined at the distance of 40 cm from the surface of the phantom. The source has a 2.2×2.2 cm² plate form the photon and electron transport cut-offs were set as 10 keV in all input programs. Each concentration, photon energy, tumor depths and type of distributions were evaluated in a separate simulation.

In water phantom, the material composition of the tally cells was the same as the four-component soft tissue (tabulated in Table 1) with mass density of 1.00 g/cm³ as defined by report No. 44 by International Commission on Radiation Units and Measurements (ICRU) [17]. However, in the tumor region by adding GNPs with different concentrations, the density and material composition changed accordingly. The investigations were carried out in two cases. In the first case, GNPs were introduced into an assumed tumor inside the phantom with homogeneous concentration of nanoparticles. In the second case, GNPs were in the form of inhomogeneous concentration. Material composition and density for homogeneous model was the same for all tumor voxels; however, in the inhomogeneous model tumor was divided to three regions. The first and third regions were similar, having 7 voxels. For each voxel in these two regions, the mass densities and concentrations were calculated. The second region that included one voxel in the middle of the tumor assumed to be a necrotic region including only soft tissue. The density value of each voxel in the first and third groups of 7 voxels was calculated by assuming this hypothesis that the concentration of GNPs decreases as an exponential function of distance (e^-αx), where x (mm) is the distance from the center of the tumor to the tumor peripheral in two directions. These two directions include downward-upward and upward-downward from the center of the tumor. In this function, α is an index which was assumed to be equal to be 1.0 in this study. As a sample, the densities and compositions of the tumor voxels for 30 mgAu/g in the cases of homogeneous and inhomogeneous distributions are presented in Table 2. Nanoparticles are conveyed to the tumor volume by the tumor vasculature. In a previous study [18], an exponential diffusion function was used for the diffusion of oxygen in tumor tissue. Our selection of this descending exponential function (e^-αx) for concentration of nanoparticles was based on the previous study on modelling of diffusion of oxygen from tumor vessels [18]. It is obvious that distribution of nanoparticles in tumor is not the same as oxygen but their differences are in their indexes the exponential power. To the best of our knowledge, there is not any literature on this index for distribution of gold nanoparticles, but we have selected an index of 1.0 by comparison of several different values of indexes. It is clear that the tumor volume and the volume of necrosis portion increase with the growth of a tumor. A 2mm necrosis region (the voxel No. eight herein) mimics a tumor at early growth step. The variation of the concentration of the nanoparticles from the peripheral to central parts of the tumor was similar to variation of the number of blood vessels across the same region. The tumor was loaded using three different concentrations of 10, 30 and 70 mgAu/g tumor gold nanoparticles.

Table 1.

Composition (weight fractions) of the tumor containing gold nanoparticles and normal tissue used in this study.

Element	Tumor			Normal tissue
	10 mgAu/g	30 mgAu/g	70 mgAu/g
H	0.100160	0.098137	0.094090	0. 101170
C	0.109890	0.107670	0.103230	0.111000
N	0.025740	0.025220	0.024180	0.026000
O	0.754210	0.738973	0.708500	0.761828
Au	0.010000	0.030000	0.070000	0.000000

Table 2.

Composition (weight fractions) and density of the tumor containing gold nanoparticles for homogeneous and inhomogeneous model with 30 mgAu/g concentration.

Element	Homogeneous	Inhomogeneous
Voxel numbers	1 to 15	1 and 15	2 and 14	3 and 13	4 and 12	5 and 11	6 and 10	7 and 9	8
H	0.098137	0.095695	0.096688	0.097502	0.098166	0.098711	0.099158	0.099523	0.101172
C	0.107670	0.104992	0.10608	0.106972	0.107702	0.108300	0.108789	0.10919	0.111000
N	0.025220	0.024592	0.024848	0.025056	0.025228	0.025368	0.025482	0.025576	0.026000
O	0.738973	0.720586	0.728062	0.734183	0.739194	0.743297	0.746656	0.749406	0.761828
Au	0.030000	0.054135	0.044322	0.036287	0.02971	0.024324	0.019915	0.016305	0.000000
Density	1.029278	1.054108	1.043869	1.035634	1.028987	1.023609	1.019247	1.015701	1

As it was mentioned before in this work, DEF of both homogeneous and inhomogeneous distributions of GNPs were calculated and the obtained results were compared. The homogeneous distribution of GNPs is a simple model and it was used herein to show that how much GNPs could increase the absorbed dose in tumor as a base level for DEF in homogeneous models.

The combined error originated from statistical Monte Carlo errors was calculated as it is described here. If the error in dose calculation with *F8 tally for tumor without GNP is e1 and for tumor with GNP is e2, then the combined error (e) can be calculated from the following formula:

$e=\sqrt{e_1^2+e_2^2}$ (1)

A number of 10⁸ particle histories were followed to have an accepted level of Monte Carlo error in each tally cell. Among all situations evaluated, the maximum combined error in Monte Carlo DEF calculations for homogeneous distribution was 4.97% belonging to 35 keV energy photons with 70 mgAu/g concentration of nanoparticles. For inhomogeneous distribution, the value amounts to 3.41% which is related to 35 keV energy photons in 70 mgAu/g concentration.

Results

The average, minimum (Min.) and maximum (Max.) DEF values with 10, 30 and 70 mgAu/g concentrations of GNPs for 35, 55, 75 and 95 keV photon energies in the case of homogeneous and inhomogeneous distributions when the tumor is located at 2.5 cm depth are listed in Table 3. The corresponding values for 4.5 cm and 6.5 cm tumor locations are presented in Table 4 and Table 5, respectively. For the purpose of comparison between the homogeneous and inhomogeneous distributions, another variable which was presented in these tables is the percentage difference between the average DEFs in the homogeneous and inhomogeneous models. The average DEF values that were reported in these tables are the average of DEFs in 15 voxels in the tumor. The negative values of percentage difference in these tables are related to those cases in which the average DEF value of inhomogeneous distribution is less than that of homogeneous distribution. As summary, among all energies and depths evaluated, the highest average dose enhancement in the tumor with 10, 30 and 70 mgAu/g homogeneous concentrations of GNPs were found to be 2.34, 4.24 and 6.16, respectively. For inhomogeneous distribution, the highest values of average dose enhancement in the tumor with 10, 30 and 70 mgAu/g concentrations of GNP were found to be 2.43, 4.75, and 7.72, respectively. While the details are not reported here, the dose enhancements in the normal tissue upper to tumor were approximately equal to unity and the dose enhancements at the depths behind the tumor were below unity.

Table 3.

Calculated average, minimum and maximum DEF values in tumor with homogeneous and inhomogeneous distributions of GNPs, and the percentage difference between average DEF calculated for both models. The tumor is located at depth of 2.5 cm in the water phantom.

Concentration (mgAu/g)	Energy (keV)	Homogeneous			Inhomogeneous			Diff. (%)
		Average DEF	Min. DEF	Max. DEF	Average DEF	Min. DEF	Max. DEF
10	35	2.18	1.75	2.71	2.38	0.84	4.19	9.17
	55	2.34	2.23	2.47	2.42	0.96	3.71	3.42
	75	1.87	1.83	1.90	1.90	0.99	2.64	1.60
	95	1.96	1.81	2.05	1.93	0.96	2.83	-1.53
30	35	3.01	1.52	5.68	3.83	0.61	9.60	27.24
	55	4.24	3.63	5.13	4.72	0.87	8.73	11.32
	75	3.33	3.13	3.57	3.52	0.95	5.80	5.71
	95	3.57	2.85	4.21	3.51	0.87	6.54	-1.68
70	35	3.02	1.00	10.70	4.65	0.36	17.50	53.97
	55	6.16	4.06	9.79	7.65	0.71	17.50	24.19
	75	5.42	4.64	6.59	6.13	0.86	11.60	13.10
	95	5.76	3.41	8.64	5.77	0.71	13.90	0.17

Table 4.

Calculated average, minimum and maximum DEF values in tumor with homogeneous and inhomogeneous distributions of GNPs, and the percentage difference between average DEF calculated for both models. The tumor is located at depth of 4.5 cm in the water phantom.

Concentration (mgAu/g)	Energy (keV)	Homogeneous			Inhomogeneous			Diff. (%)
		Average DEF	Min. DEF	Max. DEF	Average DEF	Min. DEF	Max. DEF
10	35	2.17	1.76	2.70	2.38	0.85	4.17	9.68
	55	2.34	2.21	2.48	2.42	0.96	3.74	3.42
	75	1.88	1.84	1.91	1.91	0.98	2.68	1.60
	95	1.96	1.82	2.05	1.93	0.96	2.84	-1.53
30	35	2.97	1.52	5.63	3.85	0.62	9.49	29.63
	55	4.22	3.57	5.15	4.75	0.88	8.83	12.56
	75	3.35	3.16	3.61	3.58	0.95	5.90	6.87
	95	3.58	2.87	4.21	3.55	0.88	6.57	-0.84
70	35	2.95	1.00	10.50	4.71	0.38	17.20	59.66
	55	6.07	3.97	9.83	7.72	0.72	17.50	27.18
	75	5.42	4.65	6.67	6.24	0.87	11.80	15.13
	95	5.75	3.43	8.60	5.87	0.73	13.90	2.09

Table 5.

Calculated average, minimum and maximum DEF values in tumor with homogeneous and inhomogeneous distributions of GNPs, and the percentage difference between average DEF calculated for both models. The tumor is located at depth of 6.5 cm in the water phantom.

Concentration (mgAu/g)	Energy (keV)	Homogeneous			Inhomogeneous			Diff. (%)
		Average DEF	Min. DEF	Max. DEF	Average DEF	Min. DEF	Max. DEF
10	35	2.18	1.77	2.73	2.39	0.85	4.20	9.63
	55	2.34	2.22	2.49	2.43	0.97	3.77	3.85
	75	1.89	1.86	1.94	1.93	0.99	2.72	2.12
	95	1.97	1.85	2.06	1.95	0.96	2.86	-1.02
30	35	3.01	1.50	5.76	3.87	0.62	9.58	28.57
	55	4.22	3.55	5.22	4.75	0.88	8.91	12.56
	75	3.37	3.18	3.68	3.61	0.95	6.03	7.12
	95	3.60	2.91	4.20	3.57	0.89	6.60	-0.83
70	35	3.04	1.00	10.90	4.75	0.38	17.30	56.25
	55	6.10	3.89	10.10	7.72	0.72	17.70	26.56
	75	5.45	4.62	6.89	6.29	0.88	12.00	15.41
	95	5.81	3.51	8.55	5.91	0.73	14.00	1.72

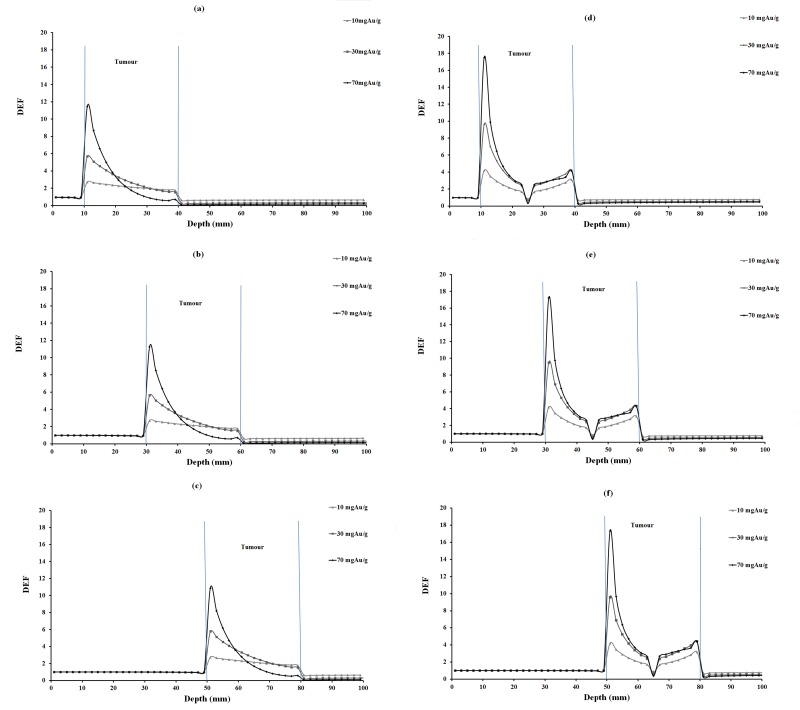
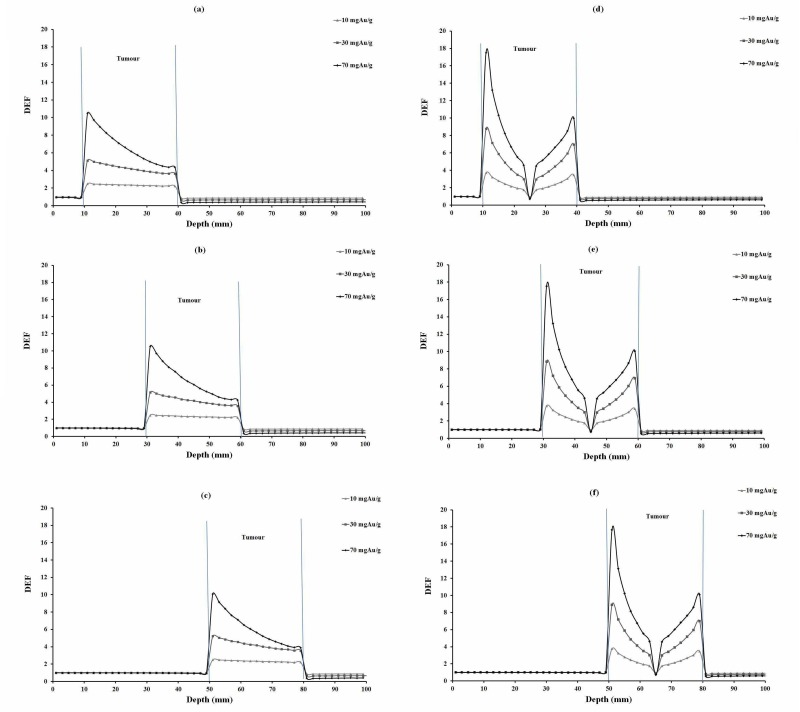
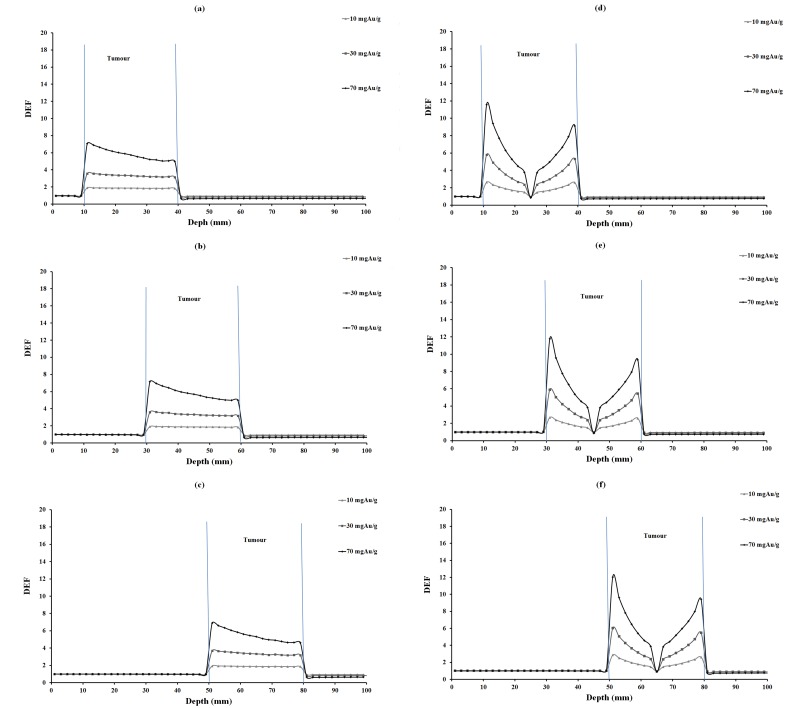
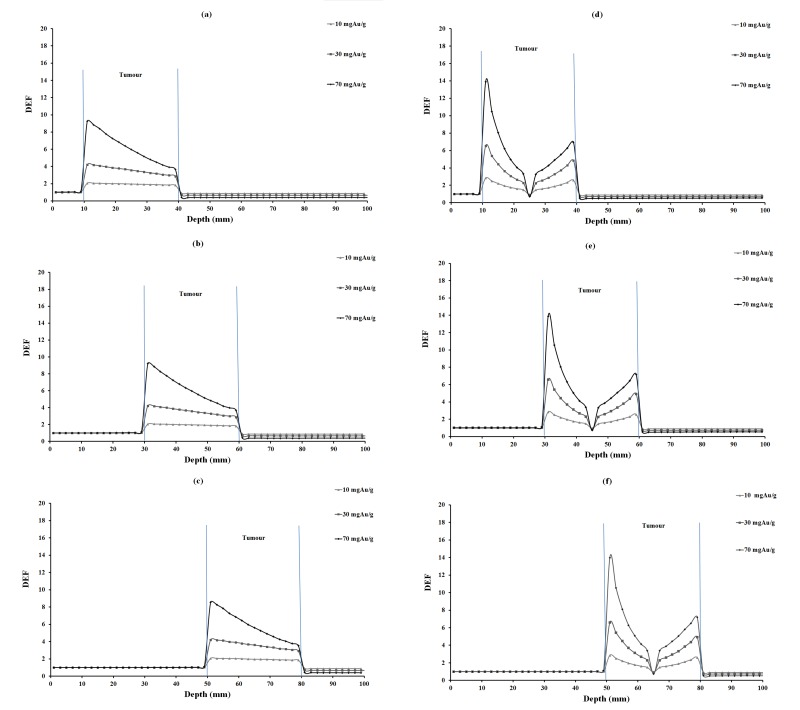
DEF versus depth for 10, 30 and 70 mgAu/g concentrations of homogeneous and inhomogeneous distributions of gold nanoparticles for 35 keV photons are plotted in Figure 2. The corresponding values for 55, 75 and 95 keV photons are illustrated in Figures 3, 4 and 5, respectively. In each figure, parts (a), (b) and (c) are related to homogeneous and parts (e), (f) and (g) are related to inhomogeneous distribution of nanoparticles.

Figure2.

DEF versus depth in the case of 35 keV monoenergetic photon beam for various tumor depths and concentrations of homogeneous and inhomogeneous distributions of GNPs. The tumor region is ranging from 10-40 mm, 30-60 mm, 50-80 mm in different parts of the figure.

Figure3.

DEF versus depth in the case of 55 keV monoenergetic photon beam for various tumor depths and concentrations of homogeneous and inhomogeneous distributions of GNPs. The tumor region is ranging from 10-40 mm, 30-60 mm, 50-80 mm in different parts of the figure.

Figure4.

DEF versus depth in the case of 75 keV monoenergetic photon beam for various tumor depths and concentrations of homogeneous and inhomogeneous distributions of GNPs. The tumor region is ranging from 10-40 mm, 30-60 mm, 50-80 mm in different parts of the figure.

Figure5.

DEF versus depth in the case of 95 keV monoenergetic photon beam for various tumor depths and concentrations of homogeneous and inhomogeneous distributions of GNPs. The tumor region is ranging from 10-40 mm, 30-60 mm, 50-80 mm in different parts of the figure.

In Figure 6, DEF and the relative dose (RD (%)) for homogeneous and inhomogeneous distributions of GNPs with 30 mgAu/g concentration in 55 keV photon energy is illustrated as a sample. The relative dose (%) was calculated as the percentage ratio of the dose in a depth to the dose at the first voxel of the phantom. For the purpose of comparisons, the relative dose in water phantom without including tumor was plotted as well.

Figure6.

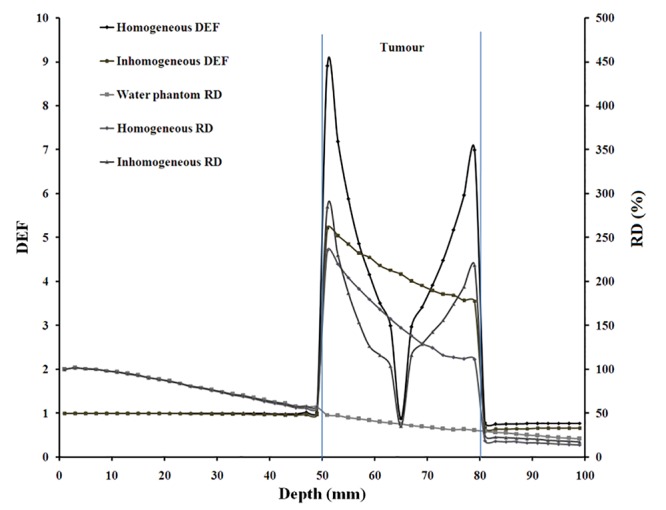
DEF and relative dose (RD (%)), as percentage of dose relative to the dose at the first voxel of the phantom, with 55 keV monoenergetic photon for 30 mgAu/g concentration of homogeneous and inhomogeneous distributions of GNPs, which were considered separately. The tumor region is ranging from 50-80 mm in the water phantom. The relative dose in water phantom was plotted as well.

Discussion and Conclusion

In this study, the DEF in tumor loaded with GNPs was evaluated for various cases of GNP concentrations, photon energy, tumor depths, homogeneous and inhomogeneous distributions of GNPs. The obtained results show that the dose enhancement is noticeable in the presence of GNPs in almost all cases. Based on the results, due to dose enhancement introduced with nanoparticles in almost all cases, it is obvious that in the presence of GNPs, treatment can be improved with low energy photons.

There are a number of parameters which affect DEF results: concentration, photon energy, tumor depth as well as homogeneous and inhomogeneous distributions. These parameters are discussed in detail herein. Concentration of GNPs has a dominant effect on DEF (Tables 3, 4 and 5; Figure 2s 2, 3, 4 and 5) in such a way that DEF increases with concentration. With the increase of concentration of gold nanoparticles, the number of photoelectric interactions would increase, and it results in higher DEF values. On the other hand, it is very important to consider the toxicity of gold nanoparticles in normal tissues. The toxicity is accounted with a limitation and in previous studies a concentration more than 30 mgAu/g has not been used. It is noTable 3 that Hainfeld et al. reported no significant toxicity for 10 mgAu/g concentration [3]. However, in our study also 70 mgAu/g concentration of GNPs was checked to show the effect of concentration better. We choose 70 mgAu/g concentration only for comparison of DEF values, and because of its toxicity it has had no use in radiotherapy. Gold nanoparticles have not been evaluated for concentrations above 20 mg/ml in animal samples, and we know that concentrations of GNPs higher than 30 mgAu/ml in normal tissue might be toxic [3]. Dose enhancement at the interface of normal tissue-tumor region (Max. DEF) increases with increase of GNP concentration. The highest dose enhancements are obtained for higher concentrations of gold nanoparticles. As a general phenomenon which is observed for all the studied photon energies, the homogeneity of DEF in the tumor volume reduces as the concentration of GNPs increases.

Photon energy is another important parameter which must be considered in the evaluation of DEF. As it can be seen from the data in Tables 3, 4 and 5, the maximum dose enhancements were found to occur for photon energies of 55keV. Figures 2, 3, 4 and 5 show that the dose is always enhanced significantly in the tumor region for all radiation energies in the range of 35-95 keV, but the highest dose enhancements are achieved for energy levels exceeding M-edge and K-edge of gold (the L-I-, L-II- and L-III- edge energies for gold atom is 14.35, 13.73, 11.92 keV an K-edge energy for gold is 80.72 keV). The maximum dose enhancement was for 55 keV and then DEF decreased in 75 keV and again increased in 95 keV energy. This effect is because of photon energy above the L-edges and K-edge of gold atom. Energies above the K-edge and also L-edges of gold are important and show more increase in DEF value. Because for superficial X-rays, photoelectric effect is the main interaction.

DEFs for tumors at 2.5 cm, 4.5 cm and 6.5 cm depths were calculated and compared (Tables 3, 4 and 5). Among tumor depths evaluated, relatively the same DEF values were observed. In this study, monoenergetic X-ray photon was considered. It is obvious that the photon intensity decreased with traverse of photons in phantom, due to inverse square law of distance and also photon absorption in the phantom material. Furthermore, a number of lower energy photons are produced with traverse of photons in the phantom material. This means that with increasing tumor depth, the photon energy would decrease, increasing the number of photoelectric interactions. On the other hand, the absorbed dose decreases due to lower intensity of photons at the steeper depths and it seems that these two effects balance each other a no significant increase or decrease in DEF with depth is seen (Figures 2-5).

When comparing DEF values for homogeneous and inhomogeneous distributions of gold nanoparticles (Figures 2, 3, 4 and 5), it is observed that DEF values are different in these two cases. The percentage differences (%) between the in-tumor average DEFs for the homogeneous and inhomogeneous distributions (Tables 3, 4 and 5) are also indicating the difference between these two situations. The negative percentage difference values are related to those data points in which the average DEF for inhomogeneous distribution is less than that in homogeneous case. In most of cases, the average DEF from homogeneous distribution is to some extent less than that from inhomogeneous one. The percentage difference is higher for lower energy photons and decreases with increasing the photon energy. This implies that the difference between the homogeneous and inhomogeneous distributions is more prominent in lower photon energies and should be taken into account in radiotherapy with lower energy photons. The concentration of GNPs near the edge of the tumor in inhomogeneous distribution is much higher than that in the middle of the tumor. This results in higher DEF at the edge of the tumor and a smaller value in the middle. Homogeneous concentration shows a relatively uniformly decreasing DEF with some difference for all points in the tumor, but inhomogeneous distribution shows more differences in tumor region. As one can notice from the DEF distributions in Figures 2-5, in both distributions the dose enhancement inside the tumor at the proximal normal tissue-tumor edge is higher than that at the distal tumor-normal tissue edge. This is as a result of shielding of photons by nanoparticles when the photons traverse inside the tumor. In the inhomogeneous model, concentrations in the peripheral regions of the tumor are higher causing more DEF values in this region, but the value decreases in the middle of the tumor in which a zero concentration (necrosis) exists. There is a limitation in the hypothesis of inhomogeneous model: blood vessels in tumor tissue are not the same in all tumor types as it was presumed here. It is obvious that when GNPs are distributed inhomogeneously, the dose uniformity in the tumor volume does not exist. Since a uniform dose distribution in the target volume is aimed in radiotherapy, this effect is accounted as a disadvantage.

In a real situation, when gold nanoparticles are injected, they are absorbed to some extent in normal tissues. In a study by Cho [5] a concentration of 2 mg/g was considered in normal tissue and this resulted in a negligible dose enhancement in the normal tissues around the tumor. In this work, introduction of gold nanoparticles in normal tissues was not performed and this effect can be a subject of further research in this field. The minimum DEF (Min. DEF) values in Tables 3-5 for homogeneous model are DEF values at the last voxel in tumor, but in inhomogeneous model the minimum DEFs are related to the necrosis region which is located in the middle of the tumor. The minimum value of DEF in the necrosis portion in the tumor results from the effect that the necrosis region does not include any nanoparticle. Also it may be interesting to see that the minimum DEF in inhomogeneous model is less than unity (Tables 3, 4 and 5). In reality, decreasing DEF in the middle of tumor could be predicted but homogeneous model could not illustrate it. Comparing the trends of change in DEF values in the tumor for homogeneous and inhomogeneous models, as presented in 2-5, implies that DEF value in inhomogeneous model does not decrease uniformly as it is in the case of homogeneous model. By reviewing the previous works on dose enhancement by nanoparticles, to the best of our knowledge, there is no similar study considering inhomogeneous model for tumor containing GNPs and unfortunately there is not any other result so that the results of this study be compared with them.

Dose enhancement in normal tissues outside the tumor is small and below unity, meaning that this will be an advantage for the normal tissues surrounding the tumor.

It is expected that photon energies which were considered in the present work are more useful for radiotherapy of the tumors located at very shallow depths. However, tumors at 2.5 cm, 4.5 cm and 6.5 cm depths have been evaluated in this study. An analysis of the effect of presence of nanoparticles on relative dose for these depths may be useful with this regard. Figure 6 illustrates DEF and relative dose values for homogeneous and inhomogeneous distributions of GNPs with 30 mgAu/g concentration in the case of 55 keV energy. The relative dose in this Figure 2 is the percentage of the dose at a voxel to the dose at the first voxel of the phantom. As it is evident from this figure, in the presence of nanoparticles, both DEF and relative dose values are high in the tumor volume while they are low in superficial normal tissues. In other words, tumor receives a higher dose value relative to the surface dose in the case of the tumor at 6.5 cm depth. Based on these results, although the photon energies evaluated herein are those used in superficial radiotherapy, the relatively deep seated tumors can also be treated with higher doses relative to the surface dose in the presence of nanoparticles with these energies. In other words, dose enhancement can be considered advantageous with relatively deep seated tumors. As a limitation, real photon sources are not monoenergetic. Furthermore, radiotherapy units which are most commonly used in radiotherapy have higher energies (higher than 4 MV) than what was considered in this study. However, energies of 35, 55, 75 and 95 keV can be achieved by modification of radiotherapy machines.

Ranjbar, et al. [19] have shown that with 10 mgAu/ml homogeneous GNPs in 85 keV photon energy for the case of a tumor located at 4.5 cm depth, DEF is 1.80 and decreases with increasing depth. Besides, an average dose enhancement factor (DEF) of 5.60 in the tumor volume with 140 keV photons for 30 mgAu/ml of gold nanoparticles was also reported by Cho, et al. [5]. While there may be differences in the conditions of these two studies compared to our study, these values are basically comparable with our results.

Other than the effects which have been evaluated in this study, there are other considerations which should be taken into account before clinical use of gold nanoparticles in radiotherapy with superficial X-rays. Some of these considerations are: toxicity of gold nanoparticles on other normal tissues, the difference between tumor angiogenesis in various tumor types under treatment, the size of the nanoparticles, the shape of the tumor, etc. As a future study, we plan to examine a spherical tumor model including vessels and necrosis, in megavoltage energy range to evaluate a situation more similar to the real geometry of tumors and photon energy involved in radiotherapy. For consideration of a real distribution of GNPs inside a tumor, it will be helpful that someone performs an experimental study by injection of GNPs in animal samples and then by imaging of the tumor to see the real distribution of the nanoparticles inside the tumor.