Diagnosis of Tempromandibular Disorders Using Local Binary Patterns

Abstract

Background:

Temporomandibular joint disorder (TMD) might be manifested as structural changes in bone through modification, adaptation or direct destruction. We propose to use Local Binary Pattern (LBP) characteristics and histogram-oriented gradients on the recorded images as a diagnostic tool in TMD assessment.

Material and Methods:

CBCT images of 66 patients (132 joints) with TMD and 66 normal cases (132 joints) were collected and 2 coronal cut prepared from each condyle, although images were limited to head of mandibular condyle. In order to extract features of images, first we use LBP and then histogram of oriented gradients. To reduce dimensionality, the linear algebra Singular Value Decomposition (SVD) is applied to the feature vectors matrix of all images. For evaluation, we used K nearest neighbor (K-NN), Support Vector Machine, Naïve Bayesian and Random Forest classifiers. We used Receiver Operating Characteristic (ROC) to evaluate the hypothesis.

Results:

K nearest neighbor classifier achieves a very good accuracy (0.9242), moreover, it has desirable sensitivity (0.9470) and specificity (0.9015) results, when other classifiers have lower accuracy, sensitivity and specificity.

Conclusion:

We proposed a fully automatic approach to detect TMD using image processing techniques based on local binary patterns and feature extraction. K-NN has been the best classifier for our experiments in detecting patients from healthy individuals, by 92.42% accuracy, 94.70% sensitivity and 90.15% specificity. The proposed method can help automatically diagnose TMD at its initial stages.

Introduction

Tempromandibular joint (TMJ) consists of mandibular condyle, glenoid fossa and articular eminence. It is one of the most complicated and active joints in human body. It can be considered to be the first joint to start functioning after birth upon suckling. Eating food continues throughout the life and the load of the joint increases gradually due to speech and other facial expressions and gestures. This joint can be involved in various types of diseases and dysfunctions throughout life, commonly called tempromandibular disorders (TMD). Various stresses and other destructive characters of modern lifestyle have resulted in noticeable increase in cases of TMD. Recent studies reported that up to 28 percent of population in different societies are involved [1]. Pain and dysfunction are the most common symptoms in different types of TMD [2]. Pain may range from a slight tenderness to a huge discomfort. Dysfunction is usually presented as mandibular movement limitations [2]. As with any other disease, on time and true diagnosis play an essential role in successful treatment of TMDs. Due to high prevalence of TMDs, it is recommended that all dental patients be screened for TMD, regardless of the apparent problem or lack of symptoms [2]. Besides taking history and clinical examinations, different radiographic techniques yield invaluable information about TMJ status. Radiographic examinations are performed to evaluate integrity of different soft and hard tissues of TMJ and the relation between them, as well as the stage and extension of the disease and assessment of treatment [3]. Pathologic changes such as decreased joint space, flattening of condyle, subcondral sclerosis, loss of cortical borders or any erosion of condylar and temporal part can be observed and detected in radiographic images [3]. Although traditional techniques such as transcranial, transpharyngial or panoramic views are widely available and inexpensive, they suffer from extensive superimpositions which degrade accuracy of diagnosis [4]. Advanced imaging techniques such as CT scanning, MR imaging, ultrasonography and CBCT are also applied to TMJ diagnosis as needed. MR imaging is the method of choice for the evaluation of soft tissue status, but bony structures are not depicted well in this modality [1]. CT scanning is useful in the evaluation of hard tissues of the joint and detection of boney changes [3]. Three dimensional and multi-planar reconstructions of the data bring brilliant images free of superimpositions. Multi-detector computed tomography (MDCT), e.g., presents high sensitivity (93%) and high specificity (100%). There are also some limitations in application of MDCT method in dental field, including higher expenses and exposure of the patients to higher doses [4]. Ultrasonography is a noninvasive, real time and radiation free technique, nonetheless the applications of this modality to TMJ imaging is practically limited to academic research. CBCT or cone beam computed tomography is the most recent imaging modality employed in dental and TMJ diagnosis. All the data needed for processing the image are gathered through a single rotation in a short time using a flat panel image receptor that imposes the patient to a relatively low radiation [5]. CBCT images depict more information about joint status compared with conventional CT images, due to higher resolution [6]. Regardless of all advantages or disadvantages of mentioned techniques, the images must finally be interpreted by a physician. This provides the probability of human error in diagnosis of joint problems; however, by increasing the knowledge and experience of operator, this probability will decrease gradually, it can never be completely ignored. Henceforth, developing methods that are less human-dependent and have high accuracy, i.e., high sensitivity and high specificity, may considerably reduce the possibility of misdiagnosis. Recently computer vision has been employed to aid in diagnosis of TMD. Sin deaux et al. tried to verify the fractal dimension of mandibular cortical bone in normal and osteoporotic men and women. They concluded that the values of fractal dimension analysis on mandibular cortical bone and mandibular cortical width were less in osteoporotic women, and recommended that cortical bone measurement be considered as an auxiliary tool to refer patients for DXA exam [7]. Gaalas et al. reported that fractal dimension of trabecular bone decreases with age in men and women [8]. Godsi et al. used the noise in the recorded image signals obtained from opening and closing of the mouth in order to diagnose TMD [9]. Local binary pattern (LBP) descriptor is a very efficient, new approach to object recognition, image segmentation, texture analysis and face analysis in computer vision field [10]. LBP possesses a low sensitivity for monotonic grayscale variations which makes it ideal for medical images processing [10]. It has been used to assess the local changes in bone structures and to correlate the changes with the severity of the diseases [10]. Trabecular and cortical compartments of bone modify occur according to environmental factors. Detection of the changes in bone structure especially trabecular compartment can lead to understanding of the nature and effect of environmental factors and possible diseases. Since TMD may be manifested as structural changes in bone through modification, adaptation or direct destruction, LBP descriptor is a good candidate technique in diagnosing the disease. In this study, we propose to use LBP characteristics augmented with oriented gradients histogram on the recorded images as a diagnostic tool in TMD assessment. The rest of the paper is organized as follows: In Section 2, we present our proposed method in detail. The experimental results are provided in Section 3. Some useful discussions are given in Section 4. Finally, Section 5 concludes the paper and summarizes our findings.

Material and Methods

The goal of this work is to aid the diagnosis of TMD by automatic processing of recoded images of the patients using an algorithm that has high enough probability of detection and simultaneously low false alarms. We propose a multi stage algorithm to achieve high sensitivity and high specificity. The following block diagram presents an overview of the stages of the proposed method. The input dataset consists of CBCT images corresponding to the right and left jaws. The training data set comprises of 264 samples of such input data sets for 132 healthy individuals and 132 patients.

Feature Extraction

Feature extraction is an important and essential step in image processing. This step extracts significant information of the image content, which maximizes intra-class similarities and minimizes inter-class similarities. The vectors obtained by feature extraction are used to train and test the data at the classification stage (Figure 1). This research aims to reveal the difference in bone structure images of healthy individuals and patients. The local binary pattern is a powerful descriptor, which represents structure and texture information of the image [11]. Therefore, in addition to pixels` gray level, we use LBP as an essential feature of the image.

Figure1.

Block diagram of automatic diagnosis of TMJ

Step 1: Local Binary Patterns

Local binary patterns are one of the best local methods representing texture [12,13]. In this method, local structures of the image are defined based on the comparison of the pixels in a neighborhood of each pixel. The LBP value of each pixel is obtained by comparing the gray value of that pixel and its neighbors according to equation [14]. In equation 1, P represents the number of neighbor pixels, R is the neighborhood radius, gi is the gray level of neighbor pixels, and gc is the central pixel gray level. In other words, the gray level values of the points in the neighborhood of a pixel are compared with that of the pixel at the center of the neighborhood from which a binary code is extracted for each pixel. The LBP value of the pixel is the weighted sum of the binary code. The procedure is illustrated in Figure 2.

Figure2.

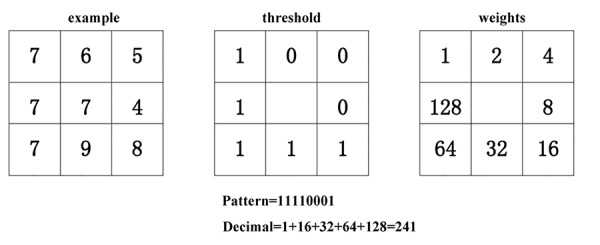
Local Binary Patterns

${\mathrm{LBP}}_{\mathrm{P,R}}={\sum }_{\mathrm{i=0}}^{\mathrm{p-1}}S(g_i-g_c)2^i,S\left(x\right)=\{\begin{array}{cc}1\hfill & \mathrm{x\ge 0}\hfill \\ 0\hfill & \mathrm{x\; <\; 0}\hfill \end{array}$ (1)

Uniform-LBP is a useful and pragmatic extension of the local binary pattern [15]. If the local binary pattern has at most two bit changes from zero to one or one to zero, it is called a uniform pattern and patterns with a larger number of bit changes are called non-uniform patterns. Uniform patterns are assigned to different labels and non-uniform patterns are all assigned to one label. It is shown that useful information of the image is hidden in uniform binary patterns. Uniform patterns have statistical robustness. Instead of all possible patterns, using uniform patterns provide better results for the produced applications. Its proved strong discriminating power and other important features, including invariability against gray-level uniform variations and computational performance, have made local binary pattern one of the most appropriate methods of image analysis. Figure 3 presents samples of healthy and patient condyle images and the processed images with LBP. This research considers eight neighbor pixels with neighborhood radius of 1. It is noted that the condylar bone area is clearly visible in local binary patterns of the healthy individuals, while some portions of the bone structure in the local binary patterns of the condylar bones are destroyed in the images of patient individuals.

Figure3.

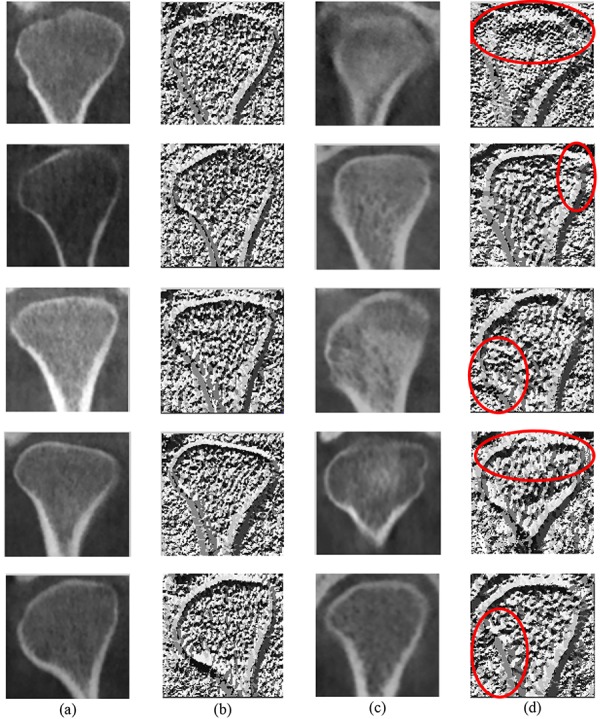
a) initial healthy condyle images, (b) healthy images after applying local binary pattern,(c) initial patient condyle images, (d) patient images after applying local binary pattern

Step 2: Histogram of Oriented Gradients

The previous step extracted the structure information of the image. The main difference between images of healthy individuals and patients is their bone edges. For a better clarity of images, the histogram of oriented gradient algorithm is applied to initial images and the images resulting from the local binary pattern. Therefore, the gradient and orientation of the edge is revealed. The histogram of oriented gradients [16,17] is a popular feature description method for object recognition in image processing. The reason for its popularity is that using the distribution of intensity gradient or edge direction, a relatively good description can be achieved from the appearance or form of the local object in an image. This approach divides the image into small square cells. The histogram of oriented gradients is computed for each cell. Subsequently, results are normalized based on the local cell groups and a descriptor is generated for each cell. In this method, the image is filtered by Sobel kernels (as Figure 4) to obtain the gradient of the image along x and y.

Figure4.

Sobel kernels

Output images are Gx and Gy, which represent the image gradient along x and y. Where, is the size of the gradient and θG shows the gradient direction. Moreover, i and j are respectively the rows and columns of images.

$\left|G\right(\mathrm{i,j}\left)\right|=\sqrt{{\left(G_x\right(\mathrm{i,j}\left)\right)}^2+{\left(G_y\right(\mathrm{i,j}\left)\right)}^2}$ (2)

${\theta }_G\left(\mathrm{i,j}\right)={\tan }^{-1}\left(\frac{G_y\left(\mathrm{i,j}\right)}{G_x\left(\mathrm{i,j}\right)}\right)$ (3)

In order to compute the histogram of gradients, in each cell, a one-dimensional histogram of gradient directions is stored for all pixels of that cell. At cell level, this one-dimensional histogram forms the basic “orientation histogram” representation. Each oriented histogram divides the gradient angle area to a fixed number, which shows the histogram bins. The pixels` gradient values of a cell are used to vote in the oriented histogram. These votes are weighted based on the gradient size in the corresponding pixel. After calculating the histogram of gradient in each cell, this histogram is assigned to the pixels of that cell [17].

Dimensionality Reduction

After feature extraction step, in order to provide better discriminability between feature vectors, as well as to reduce dimensionality, the linear algebra singular value decomposition (SVD) is applied to the feature vectors matrix of all images. Equation 4 represents matrix A and its SVD. Where, column of matrix U represents orthogonal eigenvectors AA^T and columns of matrix V represent orthogonal eigenvectors A^TA and Σ represents the eigenvalues of A^TA and AA^T.

$A=U{\mathrm{\Sigma V}}^T$ (4)

The matrix Σ is the diagonal matrix of the eigenvalues in descending order. Small eigenvalues provide no valuable information for data separation. Therefore, replacing small eigenvalues that fall below a threshold by zero can provide an estimate of matrix A that while preserving important information, it has lower rank, i.e., less dimensions. Equation 5 represents approximation of matrix A where, k is the number of non-zero eigenvalues [18].

$A_k=U{{\Sigma }_{k}V}^T$ (5)

Classification

Classification is a technique to identify the class of a new sample based on a model, which makes predictions for an observed data set. For evaluation purposes, this study uses K nearest neighbor (KNN), support vector machine, Naïve Bayesian, and random forest classifiers. These classification methods are well known and widely used in computer vision and machine learning. The k-nearest neighbor algorithm is a non-parametric method with no prior assumption about the distribution of the data. This method is a simple algorithm, which stores all the existing samples and classifies a new sample based on a similarity measure [19]. The support vector machine is based on the concept of decision planes, which define decision boundaries. SVM tries to maximize the distance between two classes by considering the problem as a quadratic planning problem [20]. Naïve Bayesian is a supervised learning algorithm, which is based on the Bayes theorem and the assumption of independence between each pair of features [21]. Random forest Is an ensemble approach. Ensemble approaches aim to combine the predictions of several learning algorithms to improve the generalizability of a learning algorithm [22].

Results

We considered a dataset consisting of CBCT images of the right and left condyles of healthy and patient individuals. These images are collected from the dentistry department of Shiraz University and include 132 images from healthy individuals and 132 images from patients. Ten-fold cross validations were used for evaluation. This method divides the data into 10 parts. For each execution, one part is considered as test data and the other nine parts are used for training. In order to include all the data in the test and training processes, this procedure is repeated 10 times and the results are averaged. Table 1 shows the specificity, sensitivity and accuracy for the evaluated subjects. Sensitivity, as defined by equation 6, refers to the ratio of positive cases, which are correctly labelled positive by the test which indicates the success rate of the test in detecting patients with disorders. Specificity, as defined by equation 7, indicates the number of healthy cases, which are correctly recognized as negative by the test [23].

Table 1.

Comparison of Specificity, sensitivity and accuracy between evaluated subjects.

Classification	Accuracy	Sensitivity	Specificity
1- NN	0.9242	0.9470	0.9015
SVM (linear)	0.8487	0.8465	0.8513
Naive Bayes	0.7562	0.7875	0.7390
Random Forest	0.7396	0.7516	0.7378

$\mathrm{Sensitivity}=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}}$ (6)

$\mathrm{Sensitivity}=\frac{\mathrm{TN}}{\mathrm{TN}+\mathrm{FN}}$ (7)

Figure 5, presents the Receiver Operating Characteristic (ROC) curve for the classifiers. ROC is used to evaluate a hypothesis testing and it is a plot of the true positive rate against the false positive rate for different possible cut-points of a diagnostic test. It is the tradeoff between sensitivity and specificity. The closer the area under the ROC curve is to its maximum value, i.e. 1, the more desirable results are achieved by the test; while the closer the surface beneath the plot is to 0.5, the less useful is the test [24]. As shown in Figure 5, the nearest neighbor classifier achieves a very good accuracy. In addition to accuracy, it also has desirable sensitivity and specificity results. Comparing the ROC curves in Figure 5 corresponding to different classifiers shows that the surface beneath ROC curve for K-NN classifier is closer to one and is the largest among that of the rest of the classifiers. Hence, K-NN has been the best classifier for our experiments in detecting patients from healthy individuals. The nearest neighbor algorithm considers the mutual distance between two actual images for labelling, while other methods exploit image to class distance as a labelling measure.

Figure5.

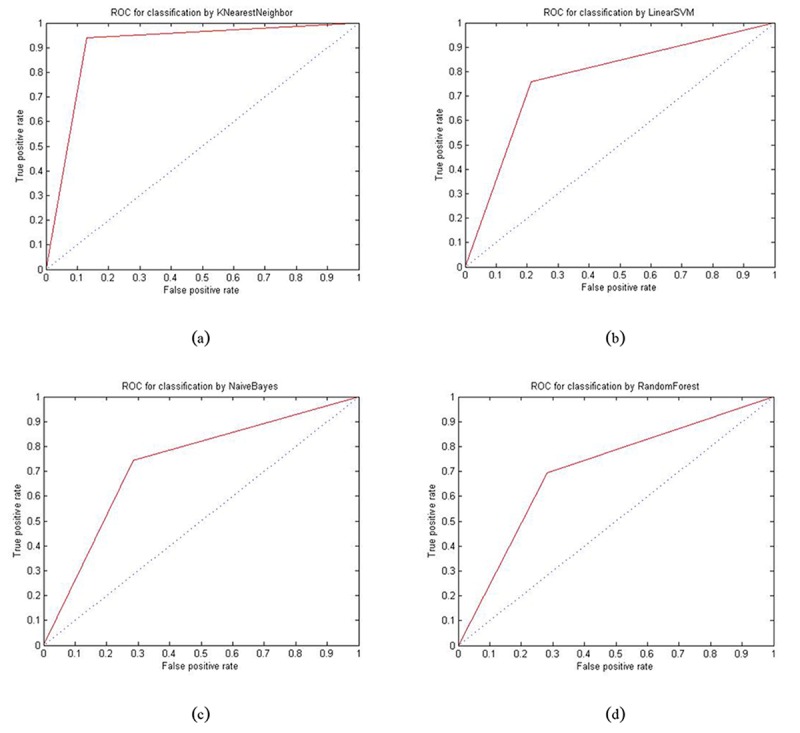
ROC curve to test the classifiers. (a) 1-nearest neighbors (b) support vector machine (c) naïve Bayes (d) random forest

Discussion

TMDs are increasing in severity and in incidence in today’s life. More and more patients refer to dental clinics seeking for TMD relief. Although great proportions of patients may be treated without imaging, especially if radiographically examined. A wide variety of techniques including conventional and advanced imaging modalities are applied to TMJ for diagnosis. Like other fields of dentistry, CBCT imaging has been proved to be reliable in TMJ diagnosis. Comparing CT scanning, CBCT falls short of osseous change detection in TMJs, due to lesser radiation exposed to the patients [4]. Unfortunately, visual diagnosis of TMJ disorders especially in its initial stages is difficult, at least for untrained eyes. On the other hand, the resolution power of CBCT imaging ranges from 100 to 150 microns which seems inadequate for cancellous bone evaluation, since the trabecular may be as thin as 40 microns [25]. Providing full automated diagnostic systems to compromise these encouraged operators and advise, has been considered by physicians and computer science engineers. Worthy of mention is the application of site specific fractal values, calculated from CBCT images, for trabecular bone analysis. Although fractal values can detect differences in the trabecular bone morphology, the clinical significance of this method is not yet identified [8]. Conventional methods of cancellous bone pattern description were also based on the analysis of rod and plate model. However, subtle changes during early bone remodelling (growth or resorption) may not be detected by these methods [25].

Regarding these weak points and resolving power of CBCT, a texture oriented approach might provide more acceptable description of bone pattern since it does not require binary segmentation of bone images [25]. The contribution of this paper is in proposing of fully automated approach to detect TMDs using image processing techniques based on local binary patterns and feature extraction. Jerome Thevenot et al., utilized local binary patterns to evaluate trabecular bone structure from micro-CT data in human osteoarthritis. They concluded that LBP method could be used to assess the changes in trabecular bone due to OA [10]. In addition to extracting the texture for different parts of an image, other features such as the edge direction and gradient size are exploited using the histogram of oriented gradients algorithm. The output from local binary patterns as well as the gray-level of the image are separately given as inputs to the second step where the histogram of oriented gradients is calculated. The histogram of oriented gradients improves the classification accuracy using edge directions and histograms of gradient. The next step improves discriminability between different classes by reducing the dimensionality using simple SVD algorithm. In this step, only the k dominant dimensions that correspond to k largest eigen-values and their corresponding eigen-vectors are considered. In the last step, i.e. the classification step, the K Nearest Neighbor (K-NN) algorithm achieves the best results among all classifiers that have been considered. K-NN has been the best classifier for our experiments in detecting patients from healthy individuals, by 92.42% accuracy, 94.70% sensitivity and 90.15% specificity. This classifier is one of the popular image classification algorithms by directly calculating image to image distances in comparison with other classifiers that need a training phase in order to calculate the distance between an image and a class. The combination of the features used as well as dimensionality reduction can be effectively used to classify healthy from unhealthy cases. The proposed method can automatically diagnose TMJ at its initial stages. Since the application of LBP for medical and dental diagnosis is novel, there are insufficient data to compare the results of different studies. Time is needed to modify the approach and to judge the benefits.