Structured Abstract
Objectives
To investigate the ploughing mechanism associated with tractional force formation on the temporomandibular joint (TMJ) disc surface.
Setting and Sample Population
Ten left TMJ discs were harvested from 6-to 8-month-old male Yorkshire pigs.
Materials and Methods
Confined compression tests characterized mechanical TMJ disc properties, which were incorporated into a biphasic finite element model (FEM). The FEM was established to investigate load carriage within the extracellular matrix (ECM) and the ploughing mechanism during tractional force formation by simulating previous in vitro plough experiments.
Results
Biphasic mechanical properties were determined in five TMJ disc regions (average±standard deviation for aggregate modulus: 0.077±0.040 MPa; hydraulic permeability: 0.88±0.37×10−3 mm4/Ns). FE simulation results demonstrated that interstitial fluid pressurization is a dominant loading support mechanism in the TMJ disc. Increased contact load and duration led to increased solid ECM strain and stress within, and increased ploughing force on the surface of the disc.
Conclusion
Sustained mechanical loading may play a role in load carriage within the ECM and ploughing force formation during stress-field translation at the condyle–disc interface. This study further elucidated the mechanism of ploughing on tractional force formation and provided a baseline for future analysis of TMJ mechanics, cartilage fatigue and early TMJ degeneration.
Keywords: biphasic theory, finite element model, fluid pressurization, temporomandibular joint, tractional force
1 | INTRODUCTION
Temporomandibular disorders (TMD) are a collective of common musculoskeletal conditions where approximately 70% of patients have TMJ disc problems1 and degenerative joint disease occurs a decade earlier compared to other synovial joints. TMJ surface incongruence has been suggested as a contributing factor.2 Understanding TMJ disc biomechanics is a first step to elucidate how TMJ cartilage develops early mechanical fatigue and degenerative joint disease.
The TMJ is a load-bearing joint consisting of the mandibular condyle, the fossa and eminence of the temporal bone, and a fibrocartilaginous disc held between the articulating surfaces. During jaw motion, the disc serves to distribute stress and lubricate surfaces. Under load, the sandwiched TMJ disc is repeatedly subjected to tangential tractional forces which are a potential source for mechanical fatigue.3,4 The tractional forces are primarily ploughing forces caused by deformation of the disc extracellular matrix (ECM) solid component, and pressurization of the fluid component, as the loaded condyle moves.3,5,6
Ploughing forces were found to be orders of magnitude larger than frictional forces.3,4,6 Previous in vitro and in vivo studies have demonstrated that tractional forces on the TMJ disc surface varied depending on stress-field velocity and geometry.7 Effects of solid matrix deformation and fluid pressurization on ploughing force formation remain unknown.
Due to the difficulties associated with measurements in vivo, computational finite element models (FEM) have been employed to simulate jaw function and predict the biomechanical environment inside the TMJ8–10 using single-phase elastic or viscoelastic material properties. However, this neglects the role of load carriage by interstitial fluid pressurization in the TMJ disc. Theoretical and experimental findings have shown that interstitial fluid plays an important role in load carriage.11–14 Previously,15 the TMJ disc was assumed to be a mixed material with solid and interstitial fluid components, and biphasic theory16 was used to predict load distribution during small jaw movements. More recently, contact loading patterns during in vitro ploughing experiments were predicted using biphasic FEM,12,13 but were based on mechanical properties from the literature.
The objective of this study was to measure TMJ disc mechanical properties and use these data in a biphasic FEM to test the hypothesis that fluid pressurization inside the TMJ disc influences load carriage between ECM solid and fluid components and is integral to the formation of ploughing forces during stress-field translation.
2 | MATERIALS AND METHODS
2.1 | Confined compression tests
To establish constitutive relations for the FEM, biphasic mechanical properties of porcine TMJ discs were measured using confined compression tests. Left TMJ discs were harvested from the heads of 6-to 8-month-old male Yorkshire pigs obtained within two hours post-mortem. Discs exhibiting fissures or bruising were discarded. Ten extracted discs were photographed, morphologically examined and wrapped in gauze soaked in a normal saline solution with protease inhibitors and stored at −80°C until mechanical tests were performed. The mechanical properties of porcine discs were reported to not significantly differ over a series of five freeze–thaw cycles.17
Cylindrical tissue plugs (N=10/region) were obtained from anterior, intermediate, lateral, medial and posterior regions of each TMJ disc (Figure 1A), using a 5-mm corneal trephine (Biomedical Research Instruments Inc., Silver Spring, MD). Thin layers from the superior and inferior surfaces were removed via sledge microtome (Model SM2400, Leica Instruments, Nussloch, Germany) with a freezing stage (Model BFS-30, Physitemp Instruments Inc., Clifton, NJ) to eliminate the biconcave shape and allow for flat surfaces during testing. The resulting specimens averaged 5 mm in diameter and 1 mm in thickness.
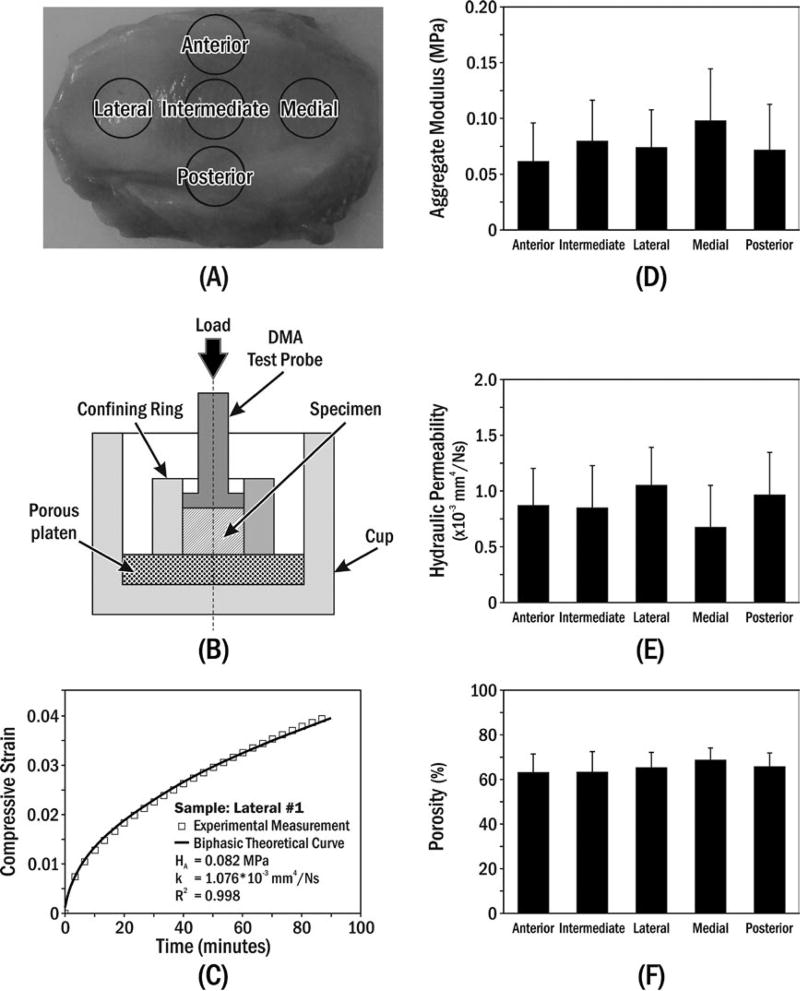
FIGURE 1.
(A) Specimen preparation. (B) Uniaxial confined compression chamber, where the polished stainless-steel confining ring prevented radial deformation and rigid permeable porous platen (20 µm average pore size) allowed water flux. (C) Typical creep behaviour of porcine TMJ disc specimen compared to biphasic theory.16 Means±standard deviations of (D) aggregate modulus, (E) hydraulic permeability and (F) porosity for specimens from five disc regions
Compression tests were performed in phosphate-buffered saline (PBS, pH 7.4, 37°C) using a mechanical tester (Dynamic Mechanical Analyzer (DMA) Q800, TA Instruments Inc., New Castle, DE) with 0.1 µm and 0.1 mN precision. The confined compression testing protocol was similar to those of previous studies18,19 (Figure 1A,B). Firstly, the specimen height was measured with a small compressive tare load (0.01 N) before injection of PBS into the testing chamber. The equilibrium swelling stress of the specimen in PBS (after ~60 minutes) was measured while probe position was held constant. Secondly, a 2-hour creep test was performed by applying a compressive stress (1.2 times equilibrium swelling stress) on top of the specimen and recording viscoelastic deformation. The equilibrium compressive aggregate modulus (HA) and hydraulic permeability (k) were then determined by curve-fitting creep data to biphasic theory.16 The load amplitude criterion for the creep test was based on linear biphasic theory assumptions made during curve fitting for small creep strain (<5%).18,19
A buoyancy method was used to determine the porosity (water volume fraction) of the disc specimens.20 The density-determination kit of an analytical balance (Sartorius Corp., Göttingen, Germany) was used to measure the specimens’ wet weights in air (Wwet) and PBS (WPBS). After the mechanical testing, specimens were lyophilized using a freeze-dry system (Labconco Corp., Kansas City, MO) for dry weight measurements (Wdry). The porosity (ϕw) was determined by
| (1) |
where ρPBS and ρw are PBS and water densities, respectively.
Aggregate moduli, hydraulic permeabilities and porosities data were tested for statistically significant differences amongst regions (SPSS 16.0, IBM, NY). One-way ANOVA and Tukey’s post hoc tests were performed with significant differences defined by P<.05.
2.2 | FEM of in vitro ploughing experiments
To simulate the in vitro ploughing experiments reported previously,3,4 a numerical model with 7242 hexahedral elements was built using open source software (FEBio.org, Salt Lake City, UT) and the confined compression test results. In the FEM, the disc material was considered biphasic, with solid and fluid components, while the indenter was assumed to be a rigid body (Table 1). The FEM simulation incorporated reported in vitro testing protocols3,4 (Figure 2A). In millimetres, the geometry of the TMJ disc strip was 24 (length)×6 (width)×2 (thickness). Static compressive loads of 1, 5 or 10 N were applied on the indenter. The stress relaxation period was either 10 or 60 seconds, after which the indenter was oscillated ±4 mm mediolaterally for four sliding cycles (3.5 Hz). Biphasic contact with an augmented Lagrangian control method was used for the sliding boundary between disc and indenter.21 Plus, a biased mesh was used on the initial contact area to decrease rapid variation of the fluid pressure.
TABLE 1.
Biphasic porcine TMJ disc properties (mean±standard deviation) obtained from the confined compression experiments and used in the FE modelling. The Poisson’s ratio (ν) for the TMJ disc was assumed to be 0.12521,24
| Location of specimen |
HA (MPa) | E (MPa) | k (10−3 mm4/Ns) | (ϕw) (%) |
|---|---|---|---|---|
| Average data | 0.077±0.040 | 0.074 | 0.88±0.37 | 65.34±7.26 |
| Anterior | 0.061±0.034 | 0.87±0.34 | 63.29±8.50 | |
| Intermediate | 0.079±0.037 | 0.84±0.38 | 63.37±9.51 | |
| Lateral | 0.073±0.034 | 1.05±0.34 | 65.46±7.02 | |
| Medial | 0.097±0.046 | 0.67±0.38 | 68.78±5.76 | |
| Posterior | 0.071±0.041 | 0.96±0.38 | 65.80±6.40 |
| (2) |
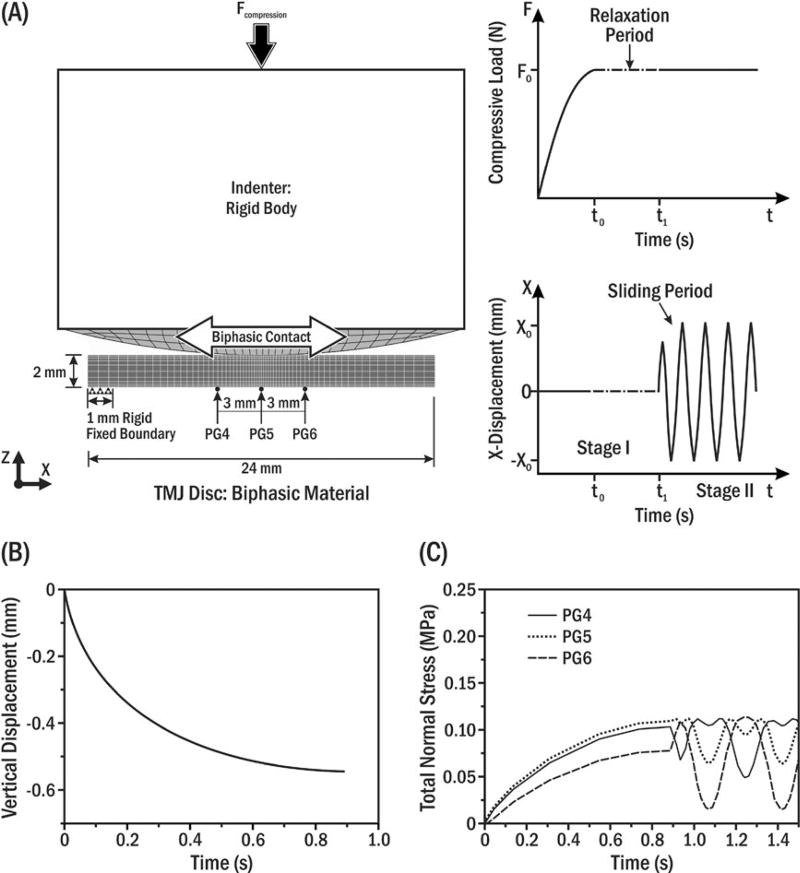
FIGURE 2.
(A) Schematic of biphasic FEM simulating in vitro ploughing experiments. Static normal compressive load (Fcompression) on the indenter was kept constant for a designated time (top right), and then, the indenter was oscillated along the disc’s mediolateral axis (bottom right). The sandpaper annulus that prevented disc translation in vitro3 was simulated in the model by fixing the far left 1 mm of the disc’s bottom surface while the remainder was allowed to slide horizontally. (B) Vertical displacement of the indenter during the initial compression period (t<t0; A top right). Note that the stress relaxation period after initial compression was neglected to be consistent with the corresponding experimental setting (t0=t1; A bottom right).3,12,13 (C) Model prediction of total normal stress during a full cycle of indenter oscillation at linearly aligned pressure gauges (PG) 4–6 separated by 3 mm. PG5 was under the disc centre
Validation of FEM output was performed by comparing computed total normal compressive stresses under the disc with reported in vitro pressure gauge data.3,4
3 | RESULTS
3.1 | Measured properties
There was good agreement of the creep data with biphasic theory as evidenced by average R2=0.99 for all specimens (eg Figure 1C). Creep data were used to determine aggregate modulus (HA) and hydraulic permeability (k) for each specimen (Figure 1C). No significant regional differences (Table 1) were found for aggregate moduli (P=.231, Figure 1D); hydraulic permeability (P=.195, Figure 1E); or porosity (P=.940, Figure 1F). Overall averages (±SD), by combining results from all regions, for aggregate modulus, hydraulic permeability and porosity, were 0.077±0.040 MPa, 0.88±0.37×10−3 mm4/Ns and 65.34±7.26%, respectively (Table 1).
3.2 | FEM simulation
The loading configuration (7.6 N compressive load; 3.5 Hz sliding frequency; Figure 2A) from the in vitro ploughing experiments was applied3,4 and FEM output validated by comparing indenter vertical displacement profile and magnitude (Figure 2B) and predicted total normal stresses at pressure gauges (PG) 4–6 (Figure 2C), with measured experimental data.3,4
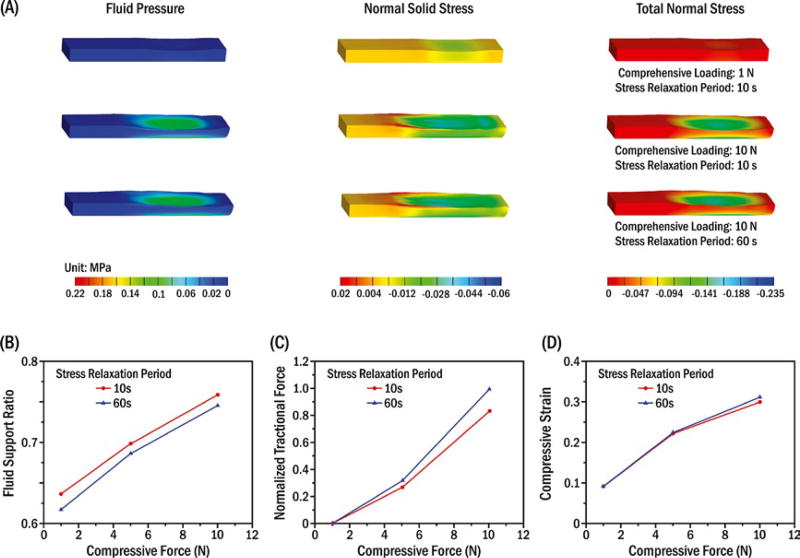
Fluid pressure (σfluid pressure), normal solid stress (σsolid stress) and total tissue normal compressive stress (σtotal stress) inside the porcine TMJ discs during stress-field translation were simultaneously obtained from the biphasic FEM (Figure 3A). Peak fluid pressure and total tissue normal compressive stress were one order of magnitude higher than the normal solid stress. Peak normal solid stress and fluid pressure markedly increased to one order of magnitude higher after compressive loads were increased from 1 to 10 N. In contrast, biomechanical response changes inside the disc were relatively smaller after load duration was increased from 10 to 60 seconds. Correspondingly, the fluid support ratio (fluid pressure/total tissue normal stress) increased 11% and 20% after compressive loads increased from 1 to 5 and 10 N, respectively, whereas it dropped approximately 2% after load duration was increased from 10 to 60 seconds (Figure 3B). Compared to 1 N compressive load effects, tractional forces on the indenter increased by 57 and 173 times while compressive strain increased 140% and 224% under 5 and 10 N compressive loads, respectively. After load duration was increased from 10 to 60 seconds, tractional force and compressive strain showed maximum increases of 19% (Figure 3C) and 4% (Figure 3D), respectively, under a 10 N compressive load.
FIGURE 3.
Model results for multiple compressive loads (1 N, 10 N) and stress relaxation periods (10 s, 60 s) when the indenter reached the lateral end of the oscillation. (A) Biphasic estimated three-dimensional distributions of fluid pressure (σfluid pressure), normal solid stress (σsolid stress) and total tissue normal stress (σtotal stress) inside the porcine TMJ discs, where16 −σfluid pressure+σsolid stress=σtotal stress negative and positive values indicate compressive and tensile stresses, respectively. Relationships of compressive load and (B) fluid support ratio; (C) normalized tractional force, where 10 N compressive load and 60 s stress relaxation period were used for normalization; and (D) compressive strain (defined by vertical displacement of the indenter/disc thickness)
4 | DISCUSSION
This study created and tested a new biphasic FEM to investigate ECM load carriage and ploughing. The loading parameters were consistent with in vivo data where average nocturnal TMJ forces of ≤10 N22 and peak TMJ stress-field translation velocities of <40 mm/s23 were reported. The biomechanical responses determined by the new FEM were in the same range as those from previous in vitro ploughing experiments3,4 and simulation studies.12,13 The disc’s fluid component sustained >80% of the compressive load during ploughing. These data further validated the hypothesis that interstitial fluid pressurization is a dominant element concerning TMJ disc load bearing, stress distribution and lubrication.11–14,24,25
The FEM also showed that increased magnitude and duration of the compressive load produced increased solid matrix deformation and increased ploughing-related tractional force due to loss of interstitial fluid pressurization. Although fluid pressurization played a protective role by increased fluid support with increased load, the consequences of increased duration of load resulted in fluid pressure dissipation and larger solid matrix stress and ploughing force. Hence, one possible mechanism for disc fatigue could be chronic TMJ loading, which leads to elevated solid matrix strain and larger ploughing forces.
The use of confined compression tests to obtain appropriate TMJ disc material properties for the current FEM is supported by the excellent fit (average R2=0.99) of creep data with biphasic theory. Compared to results from previous indentation compression studies,14,26 current results showed the average aggregate modulus (0.077 MPa) was approximately 2–3 times greater, and the average hydraulic permeability (0.88×10−3 mm4/Ns) was one order of magnitude lower, possibly due to differences in testing configurations.
In contrast to the inhomogeneous properties of human TMJ discs,18 the porcine TMJ discs used had homogenous compressive moduli, which may be due to the young age of the pigs. Also, the disc superficial layers were removed. Future research should consider if there are age and surface effects on the biphasic properties of TMJ discs.
The current FEM did not include strain rate-dependent non-linear tensile behaviour of the TMJ disc. This likely created errors in estimated tractional forces during rapid stress-field translation. The in vitro non-linear ploughing forces produced during rapid sliding speeds3 were not achieved in the current study. Appropriate constitutive properties are required to study the effects of rapid stress-field translation conditions.
5 | CONCLUSIONS
Fluid pressurization plays a dominant role in supporting TMJ disc loads during movement. The magnitude and duration of loads markedly affected the tractional force formation due to the time-dependent loss of fluid pressurization. These results suggest that chronic jaw-loading activities may promote mechanical fatigue of the TMJ disc.
Acknowledgments
This project was supported by NIH grants R03DE018741 and R01DE021134 to HY, R01DE016417 to JCN and NSF Graduate Research Fellowship to SEC.
Footnotes
The authors declare no potential conflicts of interest with respect to the authorship and/or publication of this article.
CONFLICT OF INTERESTS
The authors have no conflict of interests to report.
References
- 1.Farrar WB, McCarty WL., Jr Inferior joint space arthrography and characteristics of condylar paths in internal derangements of the TMJ. J Prosthet Dent. 1979;41:548–555. doi: 10.1016/0022-3913(79)90092-1. [DOI] [PubMed] [Google Scholar]
- 2.Nickel JC, McLachlan KR. An analysis of surface congruity in the growing human temporomandibular joint. Arch Oral Biol. 1994;39:315–321. doi: 10.1016/0003-9969(94)90123-6. [DOI] [PubMed] [Google Scholar]
- 3.Nickel JC, Iwasaki LR, Beatty MW, Marx DB. Laboratory stresses and tractional forces on the TMJ disc surface. J Dent Res. 2004;83:650–654. doi: 10.1177/154405910408300813. [DOI] [PubMed] [Google Scholar]
- 4.Nickel JC, Iwasaki LR, Beatty MW, Moss MA, Marx DB. Static and dynamic loading effects on temporomandibular joint disc tractional forces. J Dent Res. 2006;85:809–813. doi: 10.1177/154405910608500906. [DOI] [PubMed] [Google Scholar]
- 5.Mow VC, Ateshian GA, Spilker RL. Biomechanics of diarthrodial joints: a review of twenty years of progress. J Biomech Eng. 1993;115:460–467. doi: 10.1115/1.2895525. [DOI] [PubMed] [Google Scholar]
- 6.Nickel JC, McLachlan KR. In vitro measurement of the frictional properties of the temporomandibular joint disc. Arch Oral Biol. 1994;39:323–331. doi: 10.1016/0003-9969(94)90124-4. [DOI] [PubMed] [Google Scholar]
- 7.Nickel J, Spilker R, Iwasaki L, et al. Static and dynamic mechanics of the temporomandibular joint: plowing forces, joint load and tissue stress. Orthod Craniofac Res. 2009;12:159–167. doi: 10.1111/j.1601-6343.2009.01449.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Beek M, Koolstra JH, van Ruijven LJ, van Eijden TM. Three-dimensional finite element analysis of the human temporomandibular joint disc. J Biomech. 2000;33:307–316. doi: 10.1016/s0021-9290(99)00168-2. [DOI] [PubMed] [Google Scholar]
- 9.del Palomar AP, Santana-Penin U, Mora-Bermudez MJ, Doblare M. Clenching TMJs-loads increases in partial edentates: a 3D finite element study. Ann Biomed Eng. 2008;36:1014–1023. doi: 10.1007/s10439-008-9487-y. [DOI] [PubMed] [Google Scholar]
- 10.Tanaka E, Hirose M, Inubushi T, et al. Effect of hyperactivity of the lateral pterygoid muscle on the temporomandibular joint disk. J Biomech Eng. 2007;129:890–897. doi: 10.1115/1.2800825. [DOI] [PubMed] [Google Scholar]
- 11.Ateshian GA. The role of interstitial fluid pressurization in articular cartilage lubrication. J Biomech. 2009;42:1163–1176. doi: 10.1016/j.jbiomech.2009.04.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Guo H, Nickel JC, Iwasaki LR, Spilker RL. An augmented Lagrangian method for sliding contact of soft tissue. J Biomech Eng. 2012;134:084503. doi: 10.1115/1.4007177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Spilker RL, Nickel JC, Iwasaki LR. A biphasic finite element model of in vitro plowing tests of the temporomandibular joint disc. Ann Biomed Eng. 2009;37:1152–1164. doi: 10.1007/s10439-009-9685-2. [DOI] [PubMed] [Google Scholar]
- 14.Zimmerman BK, Bonnevie ED, Park M, et al. Role of interstitial fluid pressurization in TMJ lubrication. J Dent Res. 2015;94:85–92. doi: 10.1177/0022034514553626. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Donzelli PS, Gallo LM, Spilker RL, Palla S. Biphasic finite element simulation of the TMJ disc from in vivo kinematic and geometric measurements. J Biomech. 2004;37:1787–1791. doi: 10.1016/j.jbiomech.2004.01.029. [DOI] [PubMed] [Google Scholar]
- 16.Mow VC, Kuei SC, Lai WM, Armstrong CG. Biphasic creep and stress relaxation of articular cartilage in compression? Theory and experiments. J Biomech Eng. 1980;102:73–84. doi: 10.1115/1.3138202. [DOI] [PubMed] [Google Scholar]
- 17.Allen KD, Athanasiou KA. A surface-regional and freeze-thaw characterization of the porcine temporomandibular joint disc. Ann Biomed Eng. 2005;33:951–962. doi: 10.1007/s10439-005-3872-6. [DOI] [PubMed] [Google Scholar]
- 18.Kuo J, Zhang L, Bacro T, Yao H. The region-dependent biphasic viscoelastic properties of human temporomandibular joint discs under confined compression. J Biomech. 2010;43:1316–1321. doi: 10.1016/j.jbiomech.2010.01.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Yao H, Justiz MA, Flagler D, Gu WY. Effects of swelling pressure and hydraulic permeability on dynamic compressive behavior of lumbar annulus fibrosus. Ann Biomed Eng. 2002;30:1234–1241. doi: 10.1114/1.1523920. [DOI] [PubMed] [Google Scholar]
- 20.Gu WY, Yao H. Effects of hydration and fixed charge density on fluid transport in charged hydrated soft tissues. Ann Biomed Eng. 2003;31:1162–1170. doi: 10.1114/1.1615576. [DOI] [PubMed] [Google Scholar]
- 21.Ateshian GA, Maas S, Weiss JA. Finite element algorithm for frictionless contact of porous permeable media under finite deformation and sliding. J Biomech Eng. 2010;132:061006. doi: 10.1115/1.4001034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Iwasaki LR, Gonzalez YM, Liu H, Marx DB, Gallo LM, Nickel JC. A pilot study of ambulatory masticatory muscle activities in temporomandibular joint disorders diagnostic groups. Orthod Craniofac Res. 2015;18(Suppl 1):146–155. doi: 10.1111/ocr.12085. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Gallo LM, Nickel JC, Iwasaki LR, Palla S. Stress-field translation in the healthy human temporomandibular joint. J Dent Res. 2000;79:1740–1746. doi: 10.1177/00220345000790100201. [DOI] [PubMed] [Google Scholar]
- 24.Moore AC, Burris DL. An analytical model to predict interstitial lubrication of cartilage in migrating contact areas. J Biomech. 2014;47:148–153. doi: 10.1016/j.jbiomech.2013.09.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Soltz MA, Ateshian GA. Experimental verification and theoretical prediction of cartilage interstitial fluid pressurization at an impermeable contact interface in confined compression. J Biomech. 1998;31:927–934. doi: 10.1016/s0021-9290(98)00105-5. [DOI] [PubMed] [Google Scholar]
- 26.Kim KW, Wong ME, Helfrick JF, Thomas JB, Athanasiou KA. Biomechanical tissue characterization of the superior joint space of the porcine temporomandibular joint. Ann Biomed Eng. 2003;31:924–930. doi: 10.1114/1.1591190. [DOI] [PubMed] [Google Scholar]