A comparison between block and smooth modeling in finite element simulations of tDCS

Abstract

Current density distributions in five selected structures, namely, anterior superior temporal gyrus (ASTG), hippocampus (HIP), inferior frontal gyrus (IFG), occipital lobe (OCC) and pre-central gyrus (PRC) were investigated as part of a comparison between electrostatic finite element models constructed directly from MRI-resolution data (block models), and smoothed tetrahedral finite element models (smooth models). Three electrode configurations were applied, mimicking different tDCS therapies. Smooth model simulations were found to require three times longer to complete. The percentage differences between mean and median current densities of each model type in arbitrarily chosen brain structures ranged from −33.33–48.08%. No clear relationship was found between structure volumes and current density differences between the two model types. Tissue regions nearby the electrodes demonstrated the least percentage differences between block and smooth models. Therefore, block models may be adequate to predict current density values in cortical regions presumed targeted by tDCS.

I. Introduction

Finite element (FE) simulation is a popular tool to predict current flows related to a neuromodulation therapy, such as transcranial direct current stimulation (tDCS) [1,2,3,4]. The process of constructing a detailed mesh of each structure inside the head is a time-consuming step in formulation of the FE model [1,4], particularly where large numbers of tissues are involved. Reducing the number of elements by creating a coarser mesh can help modeling to be more efficient; however, in commercial software e.g., COMSOL (COMSOL, Inc., MA), segmented data requires pre-meshing steps to allow coarser mesh assignment, such as tissue boundary smoothing, small island elimination, etc. These pre-processing steps can take extra time and make modeling less efficient. Converting MRI images directly to a hexahedral finite element model is more efficient, but considered less accurate than creating smooth tissue boundaries [5]. However, there is presently no ground truth of accuracy in tDCS simulation. Given the averaging nature of electrical current flow, as represented in tDCS simulations, we hypothesize that creating a smooth mesh may not be necessary. In this paper, we compare current density distributions formed mimicking tDCS therapy using two types of model workflow: first, by assigning conductivity values directly to the MRI data voxel size and shape (block model) and by assigning conductivity values to the MRI data after completing pre-meshing processes (smooth model).

II. Methods

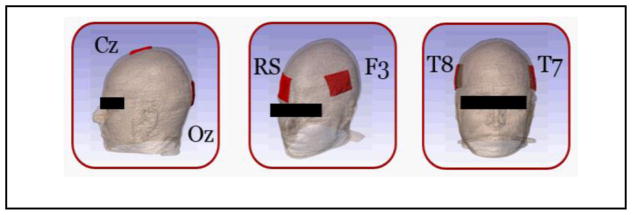
A segmented human head model derived from a T1-weighted data set was processed and current density predictions were simulated using two modeling pipelines: block and smooth model-based. Three electrode montages were created in MATLAB (Mathworks, MA) applied between: F3 and right supraorbital (RS) locations; between T7 and T8; and between Cz and Oz locations. The first-named electrode location in each montage was chosen as the anode, as shown in Fig 1. A total current of 1 mA was injected at the anode, and the cathode was set to ground. C code software [4] was used to simulate results in block models, while ScanFE, Simpleware (Exeter, UK) and COMSOL were used to formulate the smooth meshes and simulate solutions to the electrostatic problem, respectively. Further details of the modeling pipeline are described in the following subsections.

Figure 1.

Electrode montages. (from left to right: Cz-Oz, F3-RS and T7-T8)

A. Model construction

A T1-weighted MRI data set of a healthy human head was obtained using a 3T Achieva Phillips MR machine located at the McKnight Brain Institute, University of Florida. The dataset was resampled to have 256×256×256 isotropic resolution (1 mm³ voxels) using Freesurfer v5.0 (Cambridge, MA). A combination of automatic and manual segmentation (following a human cross-sectional atlas [6]) was used to segment head data set into eleven tissue types: white matter, gray matter, CSF, skin, fat, muscle, blood, air, eyes, cancellous and cortical bone. All segmented masks were combined to form a final model using ScanIP, Simpleware (Exeter, UK). Isotropic conductivity values were assigned to each tissue type as shown in Table I.

TABLE I.

Tissue conductivity values for each tissue for frequency less than 1 kHz.

Tissue types	Conductivity values (S/m)	Reference
Air	0	-
Blood	6.7×10−1	Geddes and Baker (1967)
Cancellous Bone	21.5×10−3	Akhtari et al. (2002)
Cortical bone	5.52×10−3	Akthari et al. (2002)
Cerebrospinal fluid	1.8	Baumann et al. (1997)
Fat	2.5×10−2	Gabriel et al. (1996)
Gray matter	1.0×10−1	Gabriel et al. (1996)
Muscle	1.6×10−1	Geddes and Baker (1967)
Sclera, lens	5.0×10−1	Gabriel et al. (1996)
Skin	4.3×10−1	Holdefer et al. (2006)
White matter	3.835×10−1	Geddes and Baker (1967)

B. Block model simulation

Segmented masks from ScanIP were imported into MATLAB to check for tissue mask overlap and assign tissue conductivities. Individual masks were combined into one conductivity volume and meshed into linear tetrahedral elements (6 tetrahedra per cube). The total number of elements was approximately 4 million. Conductivity values were assigned per voxel cube, where one voxel was composed of six tetrahedral elements. Stiffness and boundary condition matrices were formulated specific to solution of the Laplace equation with mixed boundary conditions, and stored. Voltage values at each node were solved for from the matrices by using the preconditioned conjugate gradient (pcg) method in MATLAB. The current density at each node was calculated based on the solved voltage gradient and block conductivity values.

C. Smooth model simulation

Individual masks created by using the ScanIP module were translated to an active model in ScanFE module, Simpleware. The model was meshed into linear tetrahedral elements totaling of approximately 4.3 millions then exported to COMSOL 5.0 where tissue conductivities as shown in Table I were assigned [4]. The electric currents (ec) module in COMSOL was selected where the normal current density was injected to the anode electrode and the cathode electrode was set to ground. Current density values were extracted using the command mphinterp and exported to a 256×256×216 meshgrid using the COMSOL MATLAB Livelink interface (MLI).

D. Selected structure calculations

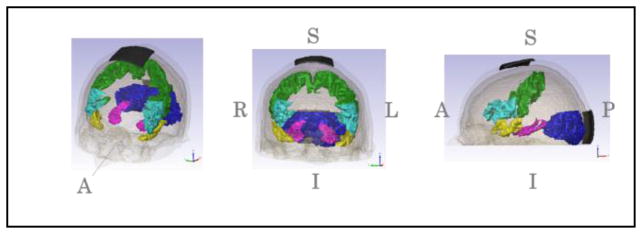
Five structures were selected for the block-smooth comparison. They were the anterior superior temporal gyrus (ASTG), hippocampus (HIP), inferior frontal gyrus (IFG), occipital lobes (OCC) and pre-central gyrus (PRC) as shown in Fig. 2. Mean and median values of current density magnitudes in each structure for each current montage considered were computed in MATLAB using each approach. Voxel based volumes for each structure were also computed in ScanIP. Differences between current density values were computed by subtracting smooth model results from block model results.

Figure 2.

Five selected structures. (ASTG (yellow), HIP (magenta), IFG (cyan), OCC (blue), PRC(green))

III. Results

A summary of the results in terms of structure volumes, and mean and median current densities are shown in Tables II, III and IV, respectively. Negative values in Table III and IV indicated larger values were observed in block models compared to smooth models. Percentage differences in volumes were less than 2% in all cases. Percentage differences calculated between mean and median current densities ranged from −27.77–48.08% and −33.33–36.00%, respectively.

TABLE II.

Total volumes for each of the selected structures.

Structure name	Volume (mm3)
	Block model	Smooth model
ASTG	7.18×103	7.29×103
HIP	8.24×103	8.26×103
IFG	1.35×104	1.33×104
OCC	5.54×104	5.63×104
PRC	3.00×104	3.04×104

TABLE III.

Percentage differences in mean current density for the selected structures comparing block and smooth models.

Structure name	Percent Difference (%)
	F3-RS	Cz-Oz	T7-T8
ASTG	27.91	10.35	38.76
HIP	−27.77	−23.60	−7.06
IFG	3.88	−11.62	34.48
OCC	16.69	11.08	36.62
PRC	25.01	28.98	44.08

TABLE IV.

Percentage differences in median current density for the selected structures comparing block and smooth models.

Structure name	Percent Difference (%)
	F3-RS	Cz-Oz	T7-T8
ASTG	−4.76	28.57	15.52
HIP	−33.33	36.00	−8.77
IFG	−14.47	30.77	24.00
OCC	−5.88	2.60	14.47
PRC	−11.76	20.00	11.59

A. Mean current density in selected structures

Mean current densities for block and smooth models are shown in Table V, VI and VII for F3-RS, Cz-Oz and T7-T8 montages, respectively. Of the structures considered, the maximum mean current density for the F3-RS montage occurred in the IFG for block model, and PRC for smooth model. For Cz-Oz and T7-T8 montages, OCC had the largest mean current density for both block and smooth models. The minimum mean current density for F3-RS and Cz-Oz were observed in HIP and ASTG, respectively. For the T7-T8 montage, minimum mean current density was observed in ASTG for the block model and HIP for the smooth model.

TABLE V.

Mean current density in selected structures with F3-RS montage for block and smooth models.

Structure name	Mean current density (A/m2)
	Block model	Smooth model
ASTG	9.52×10−6	1.32×10−5
HIP	9.29×10−6	7.2710−6
IFG	4.61×10−5	4.80×10−5
OCC	3.32×10−5	3.98×10−5
PRC	4.20×10−5	5.60×10−5

TABLE VI.

Mean current density in selected structures with Cz-Oz montage for block and smooth models.

Structure name	Mean current density (A/m2)
	Block model	Smooth model
ASTG	6.27×10−6	7.00×10−6
HIP	9.51×10−6	7.69×10−6
IFG	1.79×10−5	1.60×10−5
OCC	1.68×10−4	1.89×10−4
PRC	5.35×10−5	7.53×10−5

TABLE VII.

Mean current density in selected structures with T7-T8 montage for block and smooth models.

Structure name	Mean current density (A/m2)
	Block model	Smooth model
ASTG	1.10×10−5	1.79×10−5
HIP	1.66×10−5	1.55×10−5
IFG	2.07×10−5	3.16×10−5
OCC	1.21×10−4	1.90×10−4
PRC	6.09×10−5	1.09×10−4

B. Median current density in selected structures

Table VIII, IX and X show median current densities calculated in the selected structures. The absolute largest and smallest median current density values were observed in the same structures for both block and smooth model. The IFG had the maximum median current density for F3-RS montage while the largest median current density for Cz-Oz and T7-T8 montages was observed in OCC.

TABLE VIII.

Median current density in selected structures with F3-RS montage for block and smooth models.

Structure name	Median current density (A/m2)
	Block model	Smooth model
ASTG	1.76×10−2	1.68×10−2
HIP	1.44×10−2	1.08×10−2
IFG	3.48×10−2	3.04×10−2
OCC	7.20×10−3	6.80×10−3
PRC	1.52×10−2	1.36×10−2

TABLE IX.

Median current density in selected structures with Cz-Oz montage for block and smooth models.

Structure name	Median current density (A/m2)
	Block model	Smooth model
ASTG	1.08×10−2	8.40×10−3
HIP	1.36×10−2	1.00×10−2
IFG	1.36×10−2	1.04×10−2
OCC	3.16×10−2	3.08×10−2
PRC	2.16×10−2	1.80×10−2

TABLE X.

Median current density in selected structures with T7-T8 montage for block and smooth models.

Structure name	Median current density (A/m2)
	Block model	Smooth model
ASTG	1.96×10−2	2.32×10−2
HIP	2.48×10−2	2.28×10−2
IFG	1.52×10−2	2.00×10−2
OCC	2.6010−2	3.04×10−2
PRC	2.44×10−2	2.76×10−2

The minimum median current density was observed in OCC and ASTG for F3-RS and Cz-Oz, respectively. For T7-T8 montage, the lowest median current density was observed in IFG.

C. Modeling efficiency

The separate block and smooth modeling workflows proceeded after a common segmentation process that took approximately three days to complete. A typical block model simulation for a single electrode montage, spanning from model meshing to current density calculation completed in approximately 2×10³ seconds (~33 minutes). Simulation of the same problem using the smooth model required pre-meshing steps that took about 30–60 minutes, plus a simulation and meshing time of approximately 4×10³ seconds (~66 minutes). The smooth modeling workflow thus required ~96–126 minutes to execute. Therefore, smooth modeling pipeline required around two to three times longer to complete than the identical phase of the block modeling pipeline.

IV. Discussion

There was no distinct trend that linked the volume size of the structures with percentage differences for both mean and median current density calculations. However, there was a relationship between the structures’ proximity to the electrodes and the percentage differences in either measure. The structures that were located between the pair of electrodes and were presumed targeted by the anode-cathode configurations had the smallest percentage differences. For example, OCC was a structure targeted by the Cz-Oz montage and had the least percentage difference among the other structures for the same electrode configuration. Similarly, IFG was a target structure for F3-RS and had the least percentage difference between block and smooth median current densities. HIP showed the least percentage differences in T7-T8 montages compared to the other two montages. Even though HIP was not a primary target structure for T7-T8, it was located in between these electrodes. The observed relationship between target/nearby structures and percentage differences suggested that regions with high current flow located in between the anode-cathode electrodes were the least affected by the difference in modeling techniques i.e., block versus smooth. Furthermore, there was no preference of which pipeline was more accurate due to lack of a gold standard in tDCS simulation. However, smooth modeling required up to three times longer than block modeling to execute. Therefore, even though either pipeline could potentially be more correct than the other, the block modeling pipeline offered shorter simulation time and was thus considered more efficient.

V. Conclusion

We have presented a comparison between block versus smooth modeling simulation in five selected structures. Current density mean and median were calculated and found to be greater than most smooth model results. The block model workflow took up to three times faster to complete than smooth modeling. Overall, direct conversion from MRI to linear tetrahedral FE model (block) did not necessarily involve much change in structural volume (less than 2%) and current density simulation results (less than 15%) compared to results generated using the longer smooth modeling pipeline, for tissue regions that were located nearby the electrode pairs. Therefore, we have demonstrated that block model pipeline was adequate to carry on an isotropic current density FE simulation related to tDCS, in forward calculations relating to lead field calculations in brain source localization or in electrical impedance tomography; and potentially to other types of neurostimulation or neuromodulation FE simulation e.g., TMS and DBS.