Low-Rank Graph-Regularized Structured Sparse Regression for Identifying Genetic Biomarkers

Abstract

In this paper, we propose a novel sparse regression method for Brain-Wide and Genome-Wide association study. Specifically, we impose a low-rank constraint on the weight coefficient matrix and then decompose it into two low-rank matrices, which find relationships in genetic features and in brain imaging features, respectively. We also introduce a sparse acyclic digraph with sparsity-inducing penalty to take further into account the correlations among the genetic variables, by which it can be possible to identify the representative SNPs that are highly associated with the brain imaging features. We optimize our objective function by jointly tackling low-rank regression and variable selection in a framework. In our method, the low-rank constraint allows us to conduct variable selection with the low-rank representations of the data; the learned low-sparsity weight coefficients allow discarding unimportant variables at the end. The experimental results on the Alzheimer’s Disease Neuroimaging Initiative (ADNI) dataset showed that the proposed method could select the important SNPs to more accurately estimate the brain imaging features than the state-of-the-art methods.

1 Introduction

With a myriad of brain imaging data and genome sequence data around the world, there has been an effort to associate the genetic sequence with the structural and/or functional brain imaging for Alzheimer’s Disease (AD) study [1], [2], [3]. For example, brain imaging data have been regarded as quantitative phenotypes to investigate the genetic variants in brain structure and function as it has a potential promise to understand complex neurobiological systems, from genetic determinants to cellular processes and further to the complex interplay of brain structure. On the other hand, the genotypes (e.g., the APOEε4 allele) have been suspected to associate with the development of early and late-onset AD as the genetic variants may reflect the variability of neuroimaging phenotypes [4], [5], [6].

The main challenge in current imaging-genetic association study comes from the large number of variables from both brain imaging data and genetic data, thus requiring appropriate statistical techniques such as regression, variable selection and sparsity constraint. In the literature, pairwise univariate analysis (e.g., Pearson correlation coefficient) measures the correlation between individual phenotype and an isolated genotype without considering the potential correlations on the phenotypes and the genotypes. Regularized ridge regression (e.g., [7], [8], [9], [10], [11], [12]) conducts the imaging-genetic association study via ordinary least square estimation, which considers the correlations among the variables (e.g., the genotypes in this work) and but ignore the correlations among the corresponding responses. Earlier, Wang et al. [13] proposed to consider the interlinked structures among Single Nucleotide Polymorphisms (SNPs) to output interpretable results. Batmanghelich et al. [14] uses a sparse Gaussian model to conduct the imaging genetic analysis. The studies in [15], [16], [17], [18] also considered the correlations among the responses to implicitly output interpretable results. In a nutshell, the state-of-the-art methods have individually manifested that all kinds of correlations (e.g., between the responses and the variables, among the variables, and among the responses) are useful and necessary for imaging-genetic analysis. Furthermore, techniques for use of correlations inherent in the data may result in more reliable models [13], [19], [20], [21]. However, to our best knowledge, the previous studies were limited in the sense that they didn’t jointly consider the relational information in a unified framework.

In this paper, we propose a novel low-rank variable selection method in a regularization-based linear regression framework by taking correlations inherent in phenotypes and genotypes into account and also avoiding the adverse effect of noise and redundancy. We use the genotype data (i.e., variables) to regress the phenotype data (i.e., responses) with a least square regression to consider the correlations between the variables and the responses. We further devise new regularization terms to exploit the inherent information in both brain imaging data and genetic data for better understanding their associations. Specifically, we employ a low-rank regression model with the hypothesis of the low-rank property in both brain imaging data and genetic data to consider the correlations among the responses. Then, we devise a novel acyclic digraph regularization along with a structured sparsity regularization (i.e., ℓ_2,1-norm regularization) to consider the potential relations among the variables. The rationales of our method are: 1) the high-dimensional data have low-rank representation and redundant variables due to noise or dependency in the data; 2) graph learning has been successfully used for AD study by considering the similarity among the data; and 3) the structured sparsity constraint can effectively select highly informative SNPs in predicting brain imaging features. Finally, we conduct the biomarker selection for the brain imaging features using the Alzheimer’s Disease Neuroimaging Initiative (ADNI) data. The important SNPs selected by our new method can more accurately predict the brain imaging features than the biomarkers selected by other state-of-the-art approaches.

Compared to the state-of-the-art methods, the proposed model has the following contributions. First, this work uses the low-rank assumption to take the advantages of the correlations among both the neuroimaging features (i.e., Region-Of-Interests (ROIs)-based features in this paper) and the SNPs to improve accuracy of selecting genetic biomarkers related to AD. Our motivation is that noise and redundancy may induce the low-rank of the data [22] and there exist correlations among both the SNPs and the ROIs [3], [14], [23]. For example, multiple SNPs derive from one gene, while brain regions (e.g., ROIs or voxels) are anatomically connected. In addition, the low-rank regression, which makes a constraint on the rank of the coefficient matrix to convert the high-dimensional data to their low-rank representation [24], [25], [26], [27], has been widely used in statistics and is significantly different from subspace learning [28], [29], [30], [31], [32], [33], which learns the low-dimensional representation of the data by only considering the correlations among the variables.

Second, inspired by the popular application of the self-representation property of the samples, where each sample is represented by a small subset of other samples, in machine learning and computer vision [34], [35], [36], [37], this work devises a novel self-representation property of variables to represent each variable by other variables excluding itself. Their difference is obviously: 1) the exiting methods take each subjects as a node to build a undirected graph while our method regards each variable as a node to build a digraph, where the out-degree has different meaning from the in-degree of the digraph; 2) the exiting methods represent each sample by other samples including itself, thus easily leading to a trivial solution, while our method avoids this issue by excluding each variable to represent itself.

Lastly, we integrate the low-rank assumption and the sparsity in a framework to achieve their optimal results with the motivation that while different forms of constraints help construct reliable models, it can introduce unexpected redundancies and noises. In our model, variable selection causes to discard unimportant variables by satisfying the low-rank constraint, while the low-rank constraint makes it possible for variable selection in the low-rank representations of the data. In this way, the proposed method avoids the adverse influences of noise and redundancy to achieve optimal results of both low-rank regression and variable selection. In a statistical learning context, the propose model has the effects of: 1) feature embedding on both genetic data and brain imaging data via a low-rank constraint, and 2) variable selection on genetic data via the proposed sparse digraph and the structured sparsity regularization, simultaneously.

2 Materials and Data Preprocessing

We obtained the SNP and structural Magnetic Resonance Imaging (MRI) data of 737 non-Hispanic Caucasian participants from the Alzheimers Disease Neuroimaging Initiative database (adni.loni.usc.edu) for performance evaluation. The ADNI was launched in 2003 by the national institute on aging, the national institute of biomedical imaging and bio-engineering, the food and drug administration, private pharmaceutical companies, and non-profit organizations. The main goal of ADNI was designed to test if the serial of MRI, positron emission tomography, other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of Mild Cognitive Impairment (MCI) and early AD. As a consequence, ADNI recruited over 800 adults (aged 55 to 90) to participate in the research. More specifically, approximately 200 cognitively normal older individuals were followed for 3 years, 400 people with MCI were followed for 3 years, and 200 people with early AD were followed for 2 years. Please refer to ‘www.adni-info.org’ for up-to-date information.

2.1 Phenotype Extraction

In this paper, we regard the gray matter tissue volume of the Regions Of Interest (ROIs) as a phenotype by assuming their high relations to AD. We obtained raw Digital Imaging and Communications in Medicine (DICOM) MRI scans from the public ADNI website, where these MRI scans have been reviewed for quality, and automatically corrected for spatial distortion caused by gradient nonlinearity and B1 field inhomogeneity. We then processed all MR images following the same procedures in [38], [39] as detailed below:

• We used the MIPAV software¹ on all images to conduct anterior commissure-posterior commissure correction, and then corrected the intensity inhomogeneity using the N3 algorithm [40].

• A robust skull-stripping method [41] was applied to extract only a brain on all structural MR images. The manual edition and intensity inhomogeneity correction were followed for better quality.

• After repeating N3 algorithm three times to remove the cerebellum based on registration and intensity inhomogeneity correction, we used FAST algorithm in [42] to segment the structural MR images into three different tissues, i.e., gray matter, white matter, and cerebrospinal fluid.

• We used HAMMER [43] to conduct registration and obtained the ROI-labeled images, for which we used the Jacob template [44] to dissect a brain into 93 ROIs.

• For each of the 93 ROIs in a labeled image, we computed the gray matter tissue volume. Thus, for each MR image, we extracted a feature vector of 93 gray matter tissue volumes.

By following the previous work [13], [19], in this paper, we considered 16 ROIs, which were identified as highly related to AD in different studies [13], [45], [46], as the informative phenotypes. The selected ROIs, marked in Fig. 1 (left) are parahippocampal gyrus left, uncus right, hippocampal formation right, uncus left, middle temporal gyrus left, perirhinal cortex left, temporal pole left, entorhinal cortex left, lateral occipitotemporal gyrus right, hippocampal formation left, amygdala left, parahippocampal gyrus right, middle temporal gyrus right, amygdala right, inferior temporal gyrus right, and lateral occipitotemporal gyrus left.

Fig. 1.

Illustration of phenotype data (i.e., 16 brain regions) (left) and the top 26 AD genes (excluding the APOE gene) and the corresponding numbers of their SNPs used in the ‘Small’ dataset (right).

2.2 Genotype Extraction

After sequentially pre-processing by the standard quality control (QC) step and the imputation step, we selected the SNPs, within the boundary of 20 K base pairs of the 153 AD candidate genes listed on the AlzGene database (www.alzgene.org) as of 4/18/2011 [47], to be used in this work.

The QC criteria for the SNP data include: 1) call rate check per subject and per SNP marker; 2) gender check; 3) sibling pair identification; 4) the Hardy-Weinberg equilibrium test; 5) marker removal by the minor allele frequency; and 6) population stratification. In this paper, we used the MaCH software to impute the missing SNPs satisfied the QC step.

As a consequence, we obtained 2,098 SNPs extracted from 153 genes (boundary: 20 KB) using the ANNOVAR annotation.² In this paper, we used these 2,098 genotype data to form two datasets for performance evaluation. First, we regarded the dataset with 2,098 SNPs as the ‘Large’ dataset. Second, by following [13], [19], we further selected the SNPs, overlapping with the top 40 AD candidate genes reported in the AlzGene database from 2,098 SNPs, to form the ‘Small’ dataset, which consisted of 304 SNPs on 27 genes. The illustration of the selected 303 genes (excluding the APOE gene) and their corresponding SNPs can be found in the right subfigure of Fig. 1.

3 Proposed Method

In this section, we describe the proposed method for the imaging-genetic analysis between the SNPs and the neuroimaging phenotypes.

3.1 Low-Rank Constrained Variable Selection

Given n samples of p SNPs X ∈ ℝ^n×p and q neuroimaging phenotypes, i.e., volume of ROIs, Y ∈ ℝ^n×q, we assume that there exists a linear association between SNPs and neuroimaging phenotypes. Hereafter, we regard X and Y as the variable matrix and the response matrix, respectively. In order to identify the potential correlations between the SNPs and the volume of ROIs, we formulate their association via a linear regression as follows:

$${\mathbf{y}}^i={\mathbf{x}}^i\mathbf{W}+\mathbf{b},$$ (1)

where W ∈ ℝ^p×q denotes a weight coefficient matrix and b ∈ ℝ^q×1 is a bias term. In the least-square sense, our objective is to find the optimal coefficient matrix W and bias term b, which can be formulated as follows:

$$\underset{\mathbf{W},\mathbf{b}}{min}{\Vert \mathbf{Y}-\mathbf{XW}-\mathbf{e}{\mathbf{b}}^{\top }\Vert }_F^2,$$ (2)

where e ∈ ℝ^n×1 denotes a column vector with all ones. The ordinary least square estimation [48] can give a closed form solution to Eq. (2), i.e., Ŵ = (X^⊤X)⁻¹X^⊤Y, which does not consider possible correlations among the responses.

It is, however, noteworthy that recent studies of brain imaging analysis witnessed high correlations among different brain regions [18], [49]. Moreover, X^⊤X is invertible only when it has full rank, which does not always hold due to noises, outliers, and potential correlations inherent in the data, especially, in imaging-genetic analysis [18]. In addition, given a large number of SNPs, some of them may not be related to neuroimaging phenotypes. These observations motivate us to seek a subset of low-rank variables in SNPs. On the other hand, the previous studies (e.g., [18], [21], [50], [51]) have manifested that the low-rank assumption in data representation helps make the resulting regression model more accurate.

In these regards, we first impose a low-rank constraint on W (i.e., rank(W) ≤ min(p, q) or rank(W) ≤ min(n, p, q) [48]) to seek the low-rank representations of SNPs and neuroimaging phenotypes. With the low-rank constraint on W, it is possible to decompose it into the product of two low-rank matrices, e.g., W = UV^⊤, where U ∈ ℝ^p×r and V ∈ ℝ^q×r by assuming r = rank(W). Meanwhile, based on the hypothesis that not all the SNPs are associated with neuroimaging phenotypes, it is desirable to find or select the phenotype-related SNPs in the regression framework. In order for this, we further introduce an ℓ_2,1-norm sparse regularization on U into our objective function. By considering the low-rank constraint and the sparse regularization together, we formulate our objective function as follows:

$$\underset{\mathbf{U},\mathbf{V},\mathbf{b}}{min}{\Vert \mathbf{Y}-\mathbf{XU}{\mathbf{V}}^{\top }-\mathbf{e}{\mathbf{b}}^{\top }\Vert }_F^2+\alpha {\Vert \mathbf{U}\Vert }_{2,1},\text{subject}\text{to}{\mathbf{V}}^{\top }\mathbf{V}=\mathbf{I}.$$ (3)

where I ∈ ℝ^r×r is an identity matrix and α is a control parameter for regularization term. In Eq. (3), the orthogonality constraint on V, i.e., V^⊤V = I, encourages the column vectors in V uncorrelated and shrinks the heterogeneity between X and Y, i.e., the relation between X and Y are more homogeneous. Actually, Eq. (3) conducts feature selection by a sparse reduced-rank regression [52].

Clearly, the low-rank of U and V via the low-rank constraint on W implies that the variable and response matrices of X and Y can be represented by a linear combination of r low-dimensional latent variables and latent responses, each of which can be obtained from XU and YV. From a machine learning context, this can be interpreted as low-rank regression on both X and Y by considering the correlations among the responses, i.e., regarding q responses as a group. It is noteworthy that, subspace learning, popularly used in machine learning and computer vision, also converts the high-dimensional data into their low-dimensional representation. However, most of subspace learning methods consider the correlations among the variables which is also taken into account in our proposed method by designing a sparse acyclic digraph detailed in Section 3.2. Moreover, low-rank regression has been seldom used in imaging-genetic analysis.

The ℓ_2,1-norm regularization penalizes U in a row-wise manner by considering the correlations among the variables to output important variables. Specifically, Eq. (3) first conducts variable selection and low-rank regression to convert X to yield its low-dimensional representation XU, and then applies an orthogonal transformation to yield XUV^⊤, by which we can estimate the latent associations between X and Y. These sequential transformations allow to conduct heterogeneous data associations, i.e., molecular-level genetic data and tissue-level brain imaging data in our work.

3.2 Sparse Graph Representation in SNPs

As a gene sequence includes a number of SNPs, there may be high correlation among SNPs [21], [51]. Moreover, while there are thousands of SNPs, some of them may not be associated with neuroimaging phenotypes. In this work, we further hypothesize that the internal correlations among SNPs can give additional information to make better association between SNPs and neuroimaging phenotypes. Thus, we utilize such potential correlations in our regression method in the form of regularization.

The correlations between each pair of the SNPs are often measured by Pearson correlation, with no consideration of high order relations. To better reflect the complex relations among SNPs, we exploit a graphical representation, where we explicitly denote the relational characteristics among variables such that if a variable (i.e., target) can be represented by a linear combination of a subset of other variables (i.e., sources), then there are directed arcs from the sources to the target. To be precise, we design a sparse acyclic digraph by denoting each variable as a node and representing relations among variables with directed arcs. By the acyclic property, we confine that each variable can be represented by the other variables to avoid obtaining a trivial solution. In addition, by the digraph, the out-arcs and the in-arcs are differentiated with different meanings. Lastly, we hypothesize that there are some representative variables with which all the variables can be represented effectively.

Let 𝒢 = (𝒩, ℰ) denote a graph with a set of 𝒩 nodes (i.e., p nodes (or variables) in this paper) and a set of ℰ edges. An arc x_i → x_j denotes that x_i is involved in representing x_j and the contribution of x_i is specified by s_ij. The larger the value of s_ij, the more x_i is involved in representing x_j. The number of out-arcs of a node x_i, called as ‘out-degree’ and denoted by deg⁺(x_i), means its contribution to represent other variables. The number of in-arcs of a node x_j, called as ‘in-degree’ and denoted by deg⁻(x_j), indicates the contribution of x_j in representing x_j. Obviously, the outdegrees of the representative variables and the outdegrees of the non-representative³ variables are, respectively, at most (p − 1) and zero. By assuming d′ as the number of representative variables, their corresponding indegrees are at most (d′ − 1) (excluding itself) and at most d′, i.e., a non-representative variable is presented by all d′ representative variables.

By denoting the set of edges in a matrix S ∈ ℝ^p×p, where s_ij denotes an edge from a node x_i to a node x_j, we can derive a sparse graph representation problem as follows:

$$\underset{\mathbf{S},\mathbf{p}}{min}{\Vert \mathbf{X}-\mathbf{XS}-\mathbf{e}{\mathbf{p}}^{\top }\Vert }_F^2+\alpha {\Vert \mathbf{S}\Vert }_{2,1}+\beta {\Vert \mathbf{S}\Vert }_1,\text{subject}\text{to}\mathit{diag}(\mathbf{S})=0.$$ (4)

where p ∈ ℝ^p×1 is a bias term, α and β are the control parameters, and diag(S) denotes the diagonal values of a matrix S. The ℓ_2,1-norm regularization imposes unimportant rows of S to be zeros, while the ℓ₁-norm regularization pushes unimportant elements of S to be zeros. Note that 1) the ℓ_2,1-norm regularization in Eq. (4) determines the set of variables, which are involved in representing at least one of all the variables; 2) the ℓ₁-norm regularization selects a sub-set of the variables, which are chosen by ℓ_2,1-norm regularization, useful in representing each variable independently, e.g., x_k and x_l, respectively, are represented by two representative variables (i.e., x_i and x_j) and three representative variables; and 3) diag(S) = 0 pushes the diagonal elements of S to be zeros for avoiding the trivial solution of S.

3.3 Low-Rank Graph-Regularized Variable Selection Model

Eq. (3) conducts a low-rank variable selection between Y and X to output informative variables, while Eq. (4) conducts a sparse graph representation on variables. We can integrate these two objective functions in a unified framework to obtain our final objective function as follows:

$$\underset{\mathbf{S},\mathbf{U},\mathbf{V},\mathbf{b},\mathbf{p}}{min}{\Vert \mathbf{Y}-\mathbf{XU}{\mathbf{V}}^{\top }-\mathbf{e}{\mathbf{b}}^{\top }\Vert }_F^2+\gamma {\Vert \mathbf{S}\Vert }_1+\alpha {\Vert \mathbf{X}-\mathbf{XS}-\mathbf{e}{\mathbf{p}}^{\top }\Vert }_F^2+\beta {\Vert [\mathbf{U},\mathbf{S}]\Vert }_{2,1}\text{subject}\text{to}{\mathbf{V}}^{\top }\mathbf{V}=\mathbf{I}\text{and}\mathit{diag}(\mathbf{S})=0.$$ (5)

Note that the regularization of ||[U, S]||_2,1 plays the role of finding informative variables (i.e., SNPs) by jointly solving these two regression problems of ${\Vert \mathbf{Y}-\mathbf{XU}{\mathbf{V}}^{\top }-\mathbf{e}{\mathbf{b}}^{\top }\Vert }_F^2$ and ${\Vert \mathbf{X}-\mathbf{US}-\mathbf{e}{\mathbf{b}}^{\top }\Vert }_F^2$, where [U, S] ∈ ℝ^p×(p+q) implies that Eq. (5) selects the variables (i.e., SNPs) be jointly satisfying the constraints of two variable selection models. This makes the selected SNPs more confident. As integrating it with the low-rank constraint on V, both variable selection and low-rank regression may further be strengthened. More specifically, the low-rank constraint outputs the low-rank (i.e., low-dimensional) representations of X and Y so that the sequential variable selection is conducted by avoiding the impact of the noise of the data, hence improving its performance. In contrast, by simultaneously considering the correlations between the responses and the variables as well as the correlations among the variables, the structured sparsity constraints ensure the low-rank constraint to explore the low-rank representations of data on the ‘purified data’ by removing uninformative SNPs.

After optimizing Eq. (5) with the framework of Iteratively Reweighted Least Square (IRLS) [53], the variables with non-zero rows on both U and S are regarded as the representative variables.

4 Experiments

4.1 Competing Methods

To evaluate the proposed method, we compared it with the following state-of-the-art methods in imaging-genetic analysis, including regularized Ridge Regression (RR) [48], Multi-Task Feature Learning (MTFL) [54], group MultiTask Feature Learning (gMTFL) [13], and sparse Reduced-Rank Regression (sRRR) [18]. We listed the detail of the competing methods as follows:

• RR imposes an ℓ₂-norm penalty regularization to shrink the regression coefficients. This minimizes a penalized residual sum of squares for analyzing multiple regression data. Since the variances of least square estimation may be large, the estimation of RR could be far from the true values while multi-collinearity occurs, i.e., variables used in a regression are highly correlated.

• MTFL employs a least square loss function plus a structured sparse regularizer (e.g., an ℓ_2,1-norm regularization as in our method) to learn sparse representations shared across multiple responses. This method only considers the correlations between the variables and the responses and is able to control the number of learned common variables across the responses using the structured sparse regularization. MTFL has been widely used in AD study, such as [46], but does not consider the correlations among the responses.

• gMTFL considers the interlinked relationship among the genotypes (i.e., the variables) to select informative genotypes by considering each SNP as a variable and each neuroimaging feature as a responses (i.e., a learning task) in a multi-task regression framework. gMTFL does not take the correlations among the responses into account.

• sRRR conducts low-rank regression on both the neuroimaging phenotypes and the genotypes and implicitly enforces the sparsity in the regression coefficients. However, sRRR does not consider the correlations among the variables.

4.2 Experimental Setting

By following the previous work [19], we considered the K ∈ {20, 40, …, 200} number of SNPs, selected by different methods. Specifically, we first sorted SNPs based on the magnitude of the corresponding coefficients and then selected the top K number of SNPs for prediction. For performance comparison, we exploited the Root Mean Squared Error (RMSE) as a metric.

We used 5-fold cross-validation to compare all methods. Specifically, we first randomly partitioned the whole dataset into 5 subsets. We then selected one subset for testing and used the remaining 4 subsets for training. We repeated the whole process 10 times to avoid the possible bias during dataset partitioning for cross-validation. The final performance was obtained by averaging results from all experiments. We further employed a nested 5-fold cross-validation for model selection by setting parameters in the range of {10⁻³, …, 10³} for all methods and varying the values of r in {1, 2, …, 10} for our method.

4.3 Experimental Analysis

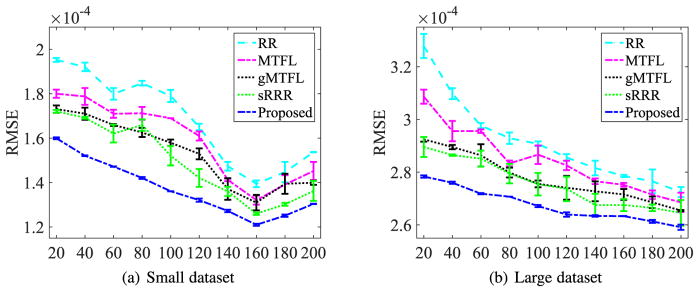
The RMSE performances (including mean and standard deviation) in Fig. 2 implied the observations as follows.

Fig. 2.

Changes of the RMSE of the competing methods according to the different numbers of the selected SNPs. The horizontal axis indicates the numbers of the selected SNPs.

• The proposed method achieved the best performance by improving on average 9.97 percent over the competing methods. This manifested that our method accurately estimated the imaging features thanks to the constraints of (1) low-rank and (2) acyclic digraph with sparse penalty in a unified framework. The paired t-tests at 95 percent significance level between our method and each of the competing methods showed that the respective p-values were less than 0.001 on both Small and Large datasets.

• The more the selected SNPs in the regression model, the better performance the method achieved, i.e., smaller RMSE. That is because more SNPs enabled to build reliable models. However, the values of RMSE of all methods first decreased to their minima (i.e., about 160 selected SNPs out of 304 SNPs) and then began to increase on Small dataset. This indicated that too many SNPs may add noise or redundancy, thus it is essential to conduct SNP selection on high-dimensional data for imaging-genetic analysis.

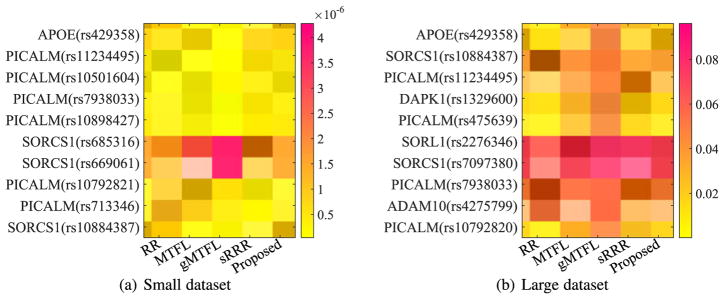
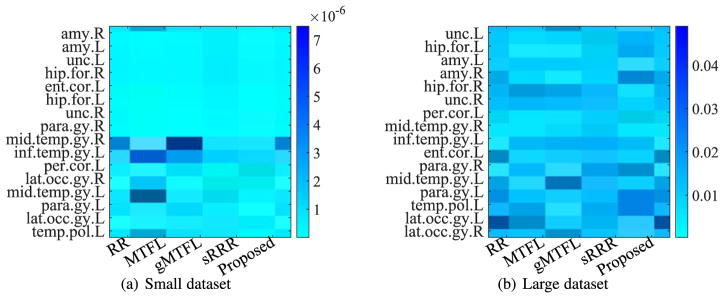
In our experiments, we averaged the absolute value of UV^⊤ in Eq. (5) from all 50 experiments to sort the resulting matrix in a descending order along the rows (or the columns) to select the top 10 SNPs (or to obtain the orders of all ROIs) of our proposed method. We then reported the heatmaps of the regression coefficients of the selected top 10 SNPs and the ordered ROIs, respectively, of all methods, in Fig. 3 and Fig. 5. In particular, from Fig. 3, we have the following observations:

Fig. 3.

Heatmaps of regression coefficients of the top 10 SNPs selected by the proposed method, whose vertical axis denotes the name of SNPs and their corresponding names of genes.

Fig. 5.

Heatmaps of regression coefficients of the ROIs, whose vertical axis denotes the name of ROIs, i.e., uncus left (unc.L), hippocampal formation left (hip.for.L), amygdala left (amy.L), amygdala right (amy.R), hippocampal formation right (hip.for.R), uncus right (unc.R), perirhinal cortex left (per. cor.L), middle temporal gyrus right (mid.temp.gy.R), inferior temporal gyrus right (inf.temp.gy.L), entorhinal cortex left (ent.cor.L), parahippocampal gyrus right (para.gy.R), middle temporal gyrus left (mid.temp.gy.L), parahippocampal gyrus left (para.gy.L), temporal pole left (temp.pol.L), lateral occipitotemporal gyrus left (lat.occ.gy.L), and lateral occipitotemporal gyrus right (lat.occ.gy.R), respectively.

• The top 10 selected SNPs were from six genes, i.e., PICALM, SORCS1, APOE, DAPK1, ADAM10, and SORL1, each of which has been reported as one of the top 40 genes at AlzGene database. Specifically, our proposed method selected the APOE gene on two datasets. In addition, our method selected six SNPs from PICALM gene and three SNPs from SORCS1gene, on Small dataset, and selected four SNPs, two SNPs, one SNP, one SNP, and one SNP, respectively, from gene PICALM, SORCS1, DAPK1, ADAM10 and SORL1, on Large dataset. It is noteworthy that the selected top 10 SNPs from two datasets with our method only have four overlappings, i.e., APOE (rs429358), PICALM (rs11234495), PICALM (rs7938033), and SORCS1 (rs10884387), even though Small dataset is the subset of Large dataset. That is, the top SNPs selected in Small dataset (i.e., PICALM (rs10501604), PICALM (rs10898427), SORCS1 (rs685316), SORCS1 (rs669061), PICALM (rs10792821), and PICALM (rs713346)) weren’t overlapped with the top 10 SNPs selected in Large dataset. Actually, their corresponding ranks were top 32, 45, 22, 24, 12, and 20, out of 2,098 SNPs in the experiments of Large dataset. The reason may be that there are more noisy SNPs in Large dataset, compared to Small datast.

• Our experimental results on two datasets selected top 10 SNPs from three common genes, such as PICALM, SORCS1, and APOE. A number of literature have indicated that they are in relation to AD. Specifically, first, PICLAM, a new Aβ toxicity modifier gene, has been frequently reported to significantly associate with a risk of late-onset AD [1], [4], [49]. For example, the SNPs such as ‘rs7938033’ and ‘rs11234495’, which were selected on two datasets, have been reported in relation to heritable neuro-developmental disorders [6]. In particular, the SNPs ‘rs11234495’ was experimentally indicated to strongly associate with both the left formation and the right hippocampal formation [19]. Second, the APOE-ε4 variant of the APOE gene has been reported to be responsible for the production of apolipoprotein E [6]. In our experiments, all methods selected its SNP ‘rs429358’ as one of top SNPs and our method indicated its strongest association with phenotypes. Lastly, as [55], [56] presented, the temporal cortex of gene SORCS1 influences Amyloid Precursor Protein (APP) processing to play an important role in the regulation of Aβ production in AD.

• Even though these three genes (such as SORL1, ADAM10, and DAPK1) were only selected as top 10 SNPs on the experiments of Large dataset, they have been reported in relation to AD. For example, the genetic variants in the gene SORL1 have been shown to associate with the age at onset of AD [57], [58], while ADAM10 gene encodes the major a-secretase responsible for cleaving APP in families with late-onset AD [59], [60]. In addition, DAPK1 plays an important role in neuronal apoptosis and could affect the pathology of late-onset AD [61], [62].

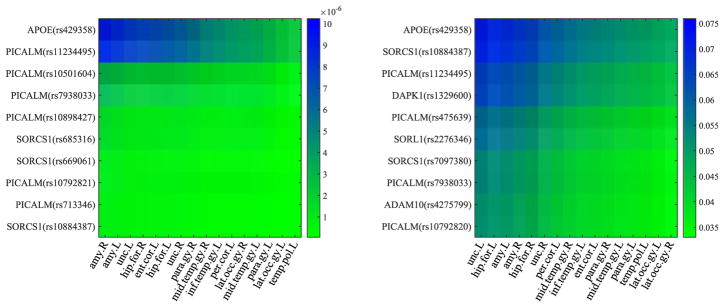
Fig. 4 manifested that the top 10 SNPs selected by our proposed method are highly related to the ROIs known in relation to AD. This verified the reasonability of our proposed method. Fig. 4 verified again that there is strong relationship between the top ranked SNPs (such as APOE gene) and the top ranked ROIs, which have been demonstrated in both Figs. 3 and 5.

Fig. 4.

The relationship of regression coefficients between the ROIs and the top 10 SNPs selected by the proposed method in terms of the absolute value of UV^⊤ on Small dataset (left) and Large dataset (right).

Fig. 5 implies that different brain regions have different contributions for image-genetic analysis even though all of these 16 ROIs have been verified in relation to AD. For example, the amygdala right and the uncus left, respectively, were reported to have the highest contribution, by the methods (such as MTFL, sRRR and our proposed method) on Small dataset and the methods (such as RR, gMTFL, sRRR, and our proposed method) on Large dataset. In addition, each of brain regions showed different contributions in different methods. This may result in different performance of different methods for imaging-genetic analysis.

4.4 Discussion

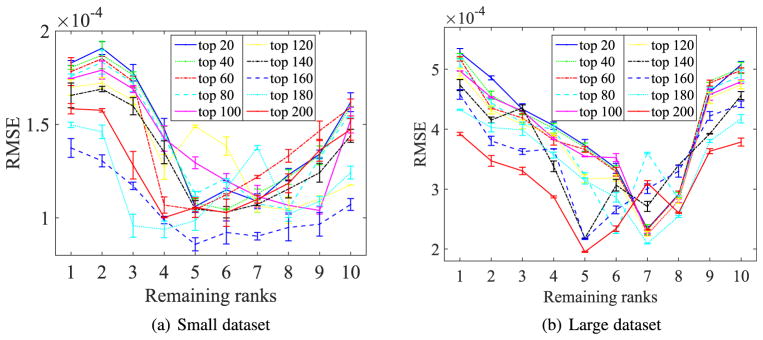
In this section, we investigate the sensitivity of the numbers of ranks (i.e., r) of our proposed method, by reporting the RMSE of different numbers of the ranks with different numbers of SNPs to predict the test data in Eq. (5). Fig. 6 visualized the change of RMSE according to different values of the rank, i.e., r ∈ {1, 2, …, 10}, where the mean and the standard deviation of the RMSE were obtained from all 50 experiments and each curve represents the change of RMSE with a fixed number of SNPs to predict the test data, e.g., ‘top 100’ denotes the change of RMSE using top 100 SNPs to predict the test ROIs.

Fig. 6.

RMSE of the proposed method with different numbers of ranks using different numbers of SNPs to predict test data.

Fig. 6 indicated that the best ranges for our method to predict test data are [4, …, 8] and [5, …, 8] on Small dataset and Large dataset, respectively. This clearly manifested that it was reasonable to make a low-rank assumption, which helps find the low-rank structure of high-dimensional SNP data via considering the correlations among the responses.

5 Conclusion

In this paper, we proposed a novel low-rank graph-regularized sparse regression model to find the associations between SNPs and brain imaging features. The proposed low-rank constraint and sparse graph representation regularization in SNPs along with a structured sparsity constraint in a linear regression framework helped to effectively utilize the inherent information in genetic data and brain imaging data, and thus finding informative associations. The experimental results indicated that our proposed method achieved the best performance of imaging-genetic analysis, compared to the competing methods.

Although the proposed method has been demonstrated to outperform all the competing methods in our experiments, the performance of our proposed framework can be further improved for SNP selection. First, we assume there is a linear relationship between SNPs and ROIs, but the data are often found to have complex nonlinear relationship. In this case, even though a number of literature have reported that the sparsity-inducing regularization may implicitly result in nonlinear relationship, an explicit assumption of nonlinear relationship (e.g., mapping the original data into kernel space by kernel functions) could be tried in our further work. Second, we only selected 16 ROIs related to AD to conduct SNP selection in this work. It should have other ROIs which are also in relation to SNPs in imaging-genetic analysis. For example, Vounou et al. focused on the association analysis between the whole brain (i.e., 93 ROIs in our work) and the entire genome [18]. Hence, SNP selection with the whole brain imaging features should be very interesting for image-genetic analysis as the current focus can be taken as one of its special cases. Third, in this work, we considered only a single brain imaging modality, it would be also important to extend our model to SNP selection with variables of multiple brain imaging modalities, which have been demonstrated to provide complementary information to each other in AD diagnosis [38]

Biographies

Xiaofeng Zhu is with Guangxi Normal University, China. His research interests include data mining and machine learning.

Heung-Il Suk (S08M12) received the BS and MS degrees in computer engineering from Pukyong National University, Busan, Korea, in 2004 and 2007, respectively, and the PhD degree in computer science and engineering, Korea University, Seoul, Republic of Korea, in 2012. From 2012 to 2014, he was a Postdoctoral Research Associate at the University of North Carolina, Chapel Hill, NC, USA. Since March 2015, he is an Assistant Professor at the Department of Brain and Cognitive Engineering, Korea University, Seoul. His current research interests include machine learning, medical image analysis, brain-computer interface, and computer vision.

Heng Huang received both BS and MS degrees from Shanghai Jiao Tong University, Shanghai, China, in 1997 and 2001, respectively. He received the PhD degree in Computer Science from Dartmouth College in 2006. He started working as an assistant professor in Computer Science and Engineering Department at University of Texas at Arlington in 2007, and became a tenured associate professor at the same department in 2013. He has been a full professor at the same department since 2015 and became the Distinguished University Professor. At 2017, his joined the Electrical and Computer Engineering department at the University of Pittsburgh as the John A. Jurenko Endowed Professor in Computer Engineering. His research interests include machine learning, data mining, bioinformatics, medical image computing, neuroinformatics, and health informatics.

Dinggang Shen is Jeffrey Houpt Distinguished Investigator, and a Professor of Radiology, Biomedical Research Imaging Center (BRIC), Computer Science, and Biomedical Engineering in the University of North Carolina at Chapel Hill (UNC-CH). He is currently directing the Center for Image Analysis and Informatics, the Image Display, Enhancement, and Analysis (IDEA) Lab in the Department of Radiology, and also the medical image analysis core in the BRIC. He was a tenure-track assistant professor in the University of Pennsylvanian (UPenn), and a faculty member in the Johns Hopkins University. He’s research interests include medical image analysis, computer vision, and pattern recognition. He has published more than 800 papers in the international journals and conference proceedings. He serves as an editorial board member for eight international journals. He has also served in the Board of Directors, The Medical Image Computing and Computer Assisted Intervention (MICCAI) Society, in 2012–2015. He is Fellow of The American Institute for Medical and Biological Engineering (AIMBE).