Redesigning existing transcranial magnetic stimulation coils to reduce energy: application to low field magnetic stimulation

Abstract

Objective

To present a systematic framework and exemplar for the development of a compact and energy-efficient coil that replicates the electric field (E-field) distribution induced by an existing transcranial magnetic stimulation coil.

Approach

The E-field generated by a conventional low field magnetic stimulation (LFMS) coil was measured for a spherical head model and simulated in both spherical and realistic head models. Then, using a spherical head model and spatial harmonic decomposition, a spherical-shaped cap coil was synthesized such that its windings conformed to a spherical surface and replicated the E-field on the cortical surface while requiring less energy. A prototype coil was built and electrically characterized. The effect of constraining the windings to the upper half of the head was also explored via an alternative coil design.

Main results

The LFMS E-field distribution resembled that of a large double-cone coil, with a peak field strength around 350 mV/m in the cortex. The E-field distributions of the cap coil designs were validated against the original coil, with mean errors of 1%–3%. The cap coil required as little as 2% of the original coil energy and was significantly smaller in size.

Significance

The redesigned LFMS coil is substantially smaller and more energy-efficient than the original, improving cost, power consumption, and portability. These improvements could facilitate deployment of LFMS in the clinic and potentially at home. This coil redesign approach can also be applied to other magnetic stimulation paradigms. Finally, the anatomically-accurate E-field simulation of LFMS can be used to interpret clinical LFMS data.

1. Introduction

Transcranial magnetic stimulation (TMS) is a technique for noninvasive brain stimulation that uses brief magnetic pulses to induce an electric field (E-field) in the brain which in turn elicits or modulates neural activity. Conventional TMS induces E-field strengths near the threshold for generating action potentials in the brain. It is widely used in the neurosciences as a tool for probing brain function connectivity [1]. Presently, TMS is FDA-approved for the treatment of depression and migraine as well as for pre-surgical cortical mapping and is under study for many other psychiatric and neurological disorders [2,3].

Low field magnetic stimulation (LFMS) is a subthreshold form of TMS that is being studied as a treatment for depression and sleep disorders [4–7]. LFMS is distinct from conventional repetitive TMS in that LFMS (1) uses low E-field strengths that do not evoke action potentials, (2) exposes the brain to a spatially more diffuse field, and (3) comprises pulse trains with a different shape and temporal pattern. Currently, LFMS is administered using coils based on MRI gradient coils, which has several disadvantages for both energy efficiency and clinical usability. The standard LFMS coil is much larger than the human head and inevitably some of its windings reside a large distance from the brain. As a result, it requires orders-of-magnitude more energy during operation than the energy delivered to the subject’s head. In addition to the energy inefficiency, the large size and weight of the coil hinder portability and result in a high material cost for manufacturing.

Addressing these technological limitations, this paper presents the design and implementation of a small, energy-efficient LFMS coil that induces an E-field in the brain with strength and distribution matching those of the standard LFMS coil. This design approach is based on the work of Koponen et al. who presented a method for designing coils with windings that conform to a spherical surface and produce fields with desired physical characteristics (e.g., focality and depth criteria) and minimized energy [8]. We adapt their approach to design energy-efficient, spherical-shaped cap coils with E-field distributions matching those generated by existing TMS and LFMS coils. Moreover, we introduce a complementary optimization scheme that constrains the location of the coil windings without significantly affecting the E-field characteristics in the brain. This enables design constraints on implementation and tolerability such as excluding windings from the neck and the face. Finally, we compare the E-fields of the original coil and the designed cap coil in an anatomically realistic head model to determine how successful the optimization process is.

2. Methods

2.1. Overview

The coil redesign process consisted of four stages. First, the E-field distribution of the standard LFMS coil was characterized in a spherical head model with both experimental measurements and simulations using the finite element method. The standard coil E-field was simulated in an anatomically realistic head model as well. Second, an energy-efficient cap coil that achieves the same field distribution as the standard coil was designed by the algorithm with or without additional spatial constraints on the windings. Third, the cap coil design was validated in the spherical head model via E-field simulations and measurements of a physical prototype. The measurements of the E-field distribution and other electrical characteristics were compared with the standard coil, simulations, and theoretical calculations. Fourth, simulations in an anatomically realistic head model were performed to verify the replication of the E-field distribution in clinical use, and the cap coil’s current was adjusted (calibrated) to minimize the cortical E-field error between the cap coil and the standard LFMS coil.

2.2. Cap coil design

An analytical expression for the E-field generated inside a spherical conductor (modeling the human head and brain) by an arbitrary divergence-free current distribution residing outside of the conductor was given by Koponen et al. [8]. They demonstrated that the current distribution with the minimum energy required to generate a prescribed E-field distribution within the conductor must reside on a spherical shell that is a minimal distance exterior to the conductor’s surface. Charge accumulation on the air-conductor interface generates a secondary field that cancels out the contribution of radial current distributions and, hence, the minimum energy current distribution must be tangential to the conductive sphere. These principles indicate that energy-optimal coils have windings that are both near and tangential to the head, i.e., with no winding elements directed away from the scalp. The standard LFMS coil (see figure 1) has windings that both reside a large distance from the head and are not tangential to the scalp, making it a particularly good candidate for redesign.

Figure 1.

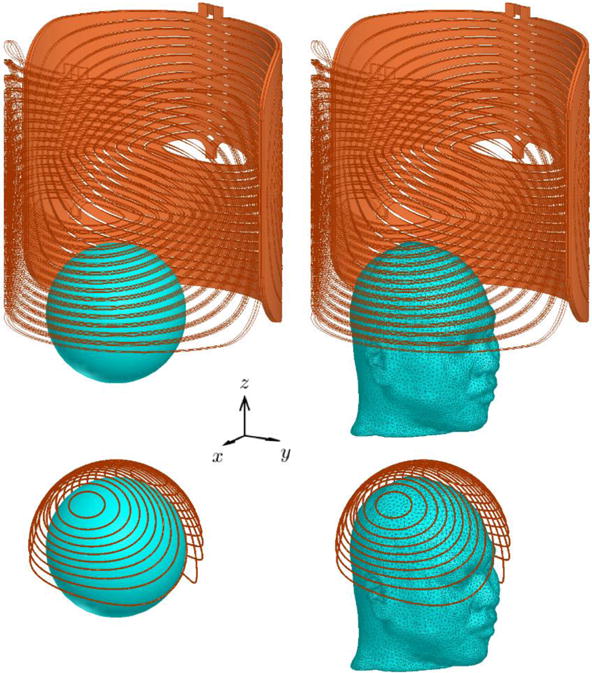
The four combinations of coil and head models on the same scale. For consistency, the standard LFMS coil (top row) is shown placed vertically, not horizontally as it is normally positioned in clinical use. The right half is only shown as outlines for clarity. The two layers of each winding are connected at the center and at the opposite end (where current is fed by a current source) to form a closed loop. The cap coil (bottom row) consists of isolated windings on a spherical surface of 10.5 cm radius. The 8.5 cm spherical head model is shown positioned on the x-y plane with a shift of −3.78 cm in the y direction in the standard LFMS coil and centered within the cap coil. The realistic head model is positioned to match the position of the spherical head.

The necessary mathematical background as given by Koponen et al. are first summarized in sections 2.2.1 and 2.2.2 and the procedures that generate the equivalent minimum-energy spherical (cap) coil are then described in sections 2.2.3 to 2.2.5. MATLAB (The MathWorks, Natick, MA) was used to perform the mathematical analysis and computation.

2.2.1. Spherical surface current density and its induced E-field and energy

A surface current density $\overrightarrow{J}(\theta ,\varphi ,t)$ on a spherical shell of radius R with separable time and spatial variation can be decomposed into orthonormal solenoidal (i.e., divergence-free) vector bases

$$\overrightarrow{J}(\theta ,\varphi ,t)=\frac{f(t)}{R}{\displaystyle \sum _{l=1}^{\mathrm{\infty }}{\displaystyle \sum _{m=-l}^l{j}_{lm}{\overrightarrow{\Phi }}_{lm}(\theta ,\varphi )}}.$$ (1)

Here f(t) is the normalized temporal waveform of the current, j_lm are the coefficients of the decomposition, the bases functions ${\overrightarrow{\Phi }}_{lm}$ are the normalized solenoidal component of real vector spherical harmonics with degree l and order m (denoted ${\mathbf{Y}}_{l,l}^m$ by Koponen et al. [8]), and θ and ϕ are the polar and azimuthal angles of spherical coordinates. The real vector spherical harmonics are defined by real scalar spherical harmonics Y_lm(θ, ϕ) as

$${\overrightarrow{\Phi }}_{lm}=\frac{\widehat{r}}{\sqrt{l(l+1)}}\times \nabla Y_{lm}(\theta ,\varphi ),$$ (2)

where $\widehat{r}$ is the unit radial vector. The real vector spherical harmonics are orthonormal, i.e.,

$$\langle {\overrightarrow{\Phi }}_{lm},{\overrightarrow{\Phi }}_{l^{\prime }{m}^{\prime }}\rangle ={\displaystyle {\int }_0^{\pi }{\displaystyle {\int }_0^{2\pi }{\overrightarrow{\Phi }}_{lm}\cdot {\overrightarrow{\Phi }}_{l^{\prime }{m}^{\prime }}\mathrm{d}\varphi \sin \theta \mathrm{d}\theta }}={\delta }_{l{l}^{\prime }}{\delta }_{m{m}^{\prime }}.$$ (3)

The E-field induced by $\overrightarrow{J}$ inside a spherical homogenous conductor of radius R₀ is

$$\overrightarrow{E}(r,\theta ,\varphi ,t)=\dot{f}(t){\displaystyle \sum _{l=1}^{\mathrm{\infty }}{\displaystyle \sum _{m=-l}^l{E}_{lm}{\left(\frac{r}{R}\right)}^l{\overrightarrow{\Phi }}_{lm}(\theta ,\varphi )},}$$ (4)

where r is the radial coordinate (r ≤ R₀ ≤ R) and the dot notation represents the time derivative. The coefficients E_lm are related to those of $\overrightarrow{J}$ by

$$E_{lm}=-\frac{{\mu }_0}{2l+1}{j}_{lm},$$ (5)

in which μ₀ is the vacuum permeability.

The total energy of the surface current density, U, is given by summation of the contribution of each harmonic component

$$U={\displaystyle \sum _{l=1}^{\mathrm{\infty }}{\displaystyle \sum _{m=-l}^l{U}_{lm}}}=\frac{{\mu }_{0}R}{2}{\displaystyle \sum _{l=1}^{\mathrm{\infty }}{\displaystyle \sum _{m=-l}^l\frac{j_{lm}^2}{2l+1}}}.$$ (6)

Equations (4) to (6) show that higher degree terms have faster radial decay for the induced E-field and therefore require more energy to generate a given field strength within the conductor. The high degree spherical harmonics correspond to rapidly varying spatial frequencies, which only shape fine spatial details and contribute little to the global field distribution; therefore, they typically have small amplitudes, as the fields generated by conventional magnetic stimulation devices in the cortex are relatively diffuse.

2.2.2. Equivalent coil windings and electrical parameters

By “bundling” the continuous current density into discrete loops of current, a magnetic stimulation coil can be formed that approximates the surface current density and its induced E-field distribution. Mathematically, this is performed by approximating isolines of the stream function associated with the surface current density [9]

$$\overrightarrow{J}=\nabla \psi \times \widehat{n},$$ (7)

where the normal unit vector of the surface $\widehat{n}$ coincides with the unit radial vector $\widehat{r}$ for spherical geometry. The stream function, ψ, is a scalar function and its time-independent component can be decomposed by real scalar spherical harmonics

$$\psi (\theta ,\varphi ,t)=f(t){\displaystyle \sum _{l=1}^{\mathrm{\infty }}{\displaystyle \sum _{m=-1}^l{\psi }_{lm}{Y}_{lm}(\theta ,\varphi )},}$$ (8)

with coefficients related to those of the surface current density by

$${\psi }_{lm}=-\frac{j_{lm}}{\sqrt{l(l+1)}.}$$ (9)

To form a coil with N windings, the stream function is discretized with a step size of

$$I=\frac{max\psi -min\psi }{N},$$ (10)

which for sufficiently large N gives a good estimate of the required coil current to generate the same E-field. The coil loops are then formed as isolines of ψ at the center of the N levels

$${\psi }_n=min\psi +(n-1/2)In=1,\dots ,N.$$ (11)

For a symmetric surface current density, it can be shown that the stream function is antisymmetric and the isoline with ψ = 0 coincides with the great circle of symmetry. Therefore, N should be an even number to avoid forming a coil winding that bisects the head in the sagittal plane.

Besides the coil current, in this study we further consider the inductance of the coil. With the energy and current of the coil given by equations (6) and (10), respectively, the inductance is

$$L=2U/I^2.$$ (12)

2.2.3. Harmonic decomposition of E-field and quantification of errors

Reversing the above derivation, any desired E-field distribution ${\overrightarrow{E}}_0$ on a spherical surface of radius r₀ centered inside the spherical volume conductor can be induced by surface currents residing on a spherical shell with radius R larger than that of the conductor. More specifically, the coefficients for the E-field are obtained by calculating the inner product of equation (4) and the real vector spherical harmonics bases at any given time t₀

$$E_{lm}=\langle {\overrightarrow{E}}_0(r_0,\theta ,\varphi ,t_0),{\overrightarrow{\Phi }}_{lm}\rangle \frac{1}{\dot{f}(t_0)}{\left(\frac{R}{r_0}\right)}^l.$$ (13)

The appropriate driving currents are then determined from equations (5) and (1).

For the LFMS coil, the E-field on the cortical surface of the spherical model with r₀ of 7 cm was obtained via both measurement and simulation, and validated against each other (see section 2.3 for LFMS coil configuration and head positioning, and sections 2.4 and 2.5 for measurement and simulation setup). The E-field was sampled from the simulation for the spherical harmonic decomposition with maximum degree and order of 15. Due to the left-right symmetry of the LFMS E-field, coefficients of spherical harmonics of odd sine (negative odd m) and even cosine (non-negative even m) types should be zero. These spherical harmonics were excluded to reduce computation, approximately halving the number of terms (120 out of 255 for 0 ≤ |m| ≤ l ≤ 15). As expected, the spherical harmonic decomposition revealed that most of the high degree coefficients had absolute values orders-of-magnitude smaller than the low degree terms. This was in agreement with the diffuse nature of the E-field generated by the large LFMS coil, and is true in general for realistic coil designs because complex field patterns with high spatial frequencies require relatively high energy to be induced inside the head.

Ideally, the decomposition coefficients preserve all the original information of the E-field. In reality, many factors introduce numerical errors, such as calculating a summation instead of integration due to limited spatial sampling of the E-field (discretization error) and truncation of the spherical harmonic series in the calculation (truncation error). Discretization of the stream function further increases the error. To evaluate how well the spherical-harmonic-defined E-field ( ${\overrightarrow{E}}_{\mathrm{SH}}$) matched the original distribution ( ${\overrightarrow{E}}_{\text{LFMS}}$), the E-field was reconstructed from spherical harmonics at each step of the design process and the absolute (Δ_E) and relative (δ_E) errors were calculated

$$\begin{gathered} {\mathrm{\Delta }}_E=\Vert {\overrightarrow{E}}_{\mathrm{SH}}-{\overrightarrow{E}}_{\text{LFMS}}\Vert , \\ {\delta }_E={\mathrm{\Delta }}_E/\Vert {\overrightarrow{E}}_{\text{LFMS}}\Vert . \end{gathered}$$ (14)

In TMS, the coil current from the stimulator can be easily adjusted to scale the E-field and is typically performed to calibrate for the subject variability in motor threshold. Therefore, the normalized E-field distribution was considered to define another error metric for the field replication. To exclude potential outliers of the simulated E-field due to numerical inaccuracies, especially at conductivity boundaries in the realistic head model, we considered the peak E-field amplitude to be the 99.9th percentile of the sampled distribution [10]. Thus, the normalized distribution, $\overrightarrow{g}$, and the distribution error, δ_g, are defined respectively as

$$\begin{gathered} \overrightarrow{g}=\overrightarrow{E}/{\Vert \overrightarrow{E}\Vert }_{99.9\mathrm{\%}}, \\ {\delta }_g=\Vert {\overrightarrow{g}}_{\mathrm{SH}}-{\overrightarrow{g}}_{\text{LFMS}}\Vert . \end{gathered}$$ (15)

Although the cortical surface in the spherical head model is a full sphere, in reality the brain is approximately a hemisphere located above the equator, i.e., eyebrow level. Therefore, the calculated error statistics and the E-field measurements (see section 2.4) were confined to the upper hemisphere.

2.2.4. Unconstrained cap coil design

With the decomposition coefficients of the E-field, the surface current density at a given radius and its energy can then be calculated using equations (5) and (6), respectively. The radius of the surface current density and subsequent coil implementation was chosen as 10.5 cm for this study. This was larger than the typical spherical head model radius of 8.5 cm [11] to accommodate the oval shape and size of average human heads, as well as to leave space for the coil casing.

The energy of the spherical surface current density is lower compared to the standard LFMS coil according to the minimum-energy principles by Koponen et al. [8]. As demonstrated by the analysis in section 2.2.1, higher degree terms in the spherical harmonic representation have proportionally larger contribution to the energy compared to their contribution to the E-field. Additionally, higher degree terms are prone to numeric errors due to the limited accuracy of the simulated (or measured) E-field (further discussed in section 4.2.2). Therefore, an unconstrained design method is proposed to truncate the higher degree terms in order to further reduce the energy of the surface current density and generate smoother coil windings without significantly affecting the overall field distribution in the cortex. The coefficients E_lm were iteratively set to zero starting with the higher degree and order (i.e., l = 15, m = 15, −14, …, then l = 14, m = −14, 13, … etc.) until any of the error metrics would exceed preset criteria, which were chosen as 1% of maximum E-field for the absolute error and 2% for the relative error and distribution error.

The remaining non-zero coefficients were then used to generate the stream function, which was discretized with N = 20 to obtain a coil with practical winding density and inductance. Isolines were generated by applying the MATLAB function contour on the stream function in spherical coordinates and were then transformed into coil windings described in Cartesian coordinates.

2.2.5. Constrained cap coil design

The unconstrained design process yielded a coil with windings extending somewhat below the equator of the sphere (see figure 4, center column). Although the windings did not reach very low regions (θ < 118°), they covered areas around the eyes, nose, and ears. A cap coil covering the eyes of the user can cause claustrophobia and obstruct the field of vision. If the design method yields cap coils extending much lower for other applications, implementation and placement on the head can be difficult. Therefore, an optimization algorithm was implemented on the spherical harmonic coefficients to restrict the corresponding cap coil to the upper hemisphere while minimizing the coil energy and limiting the distortion of the E-field distribution within preset criteria.

Figure 4.

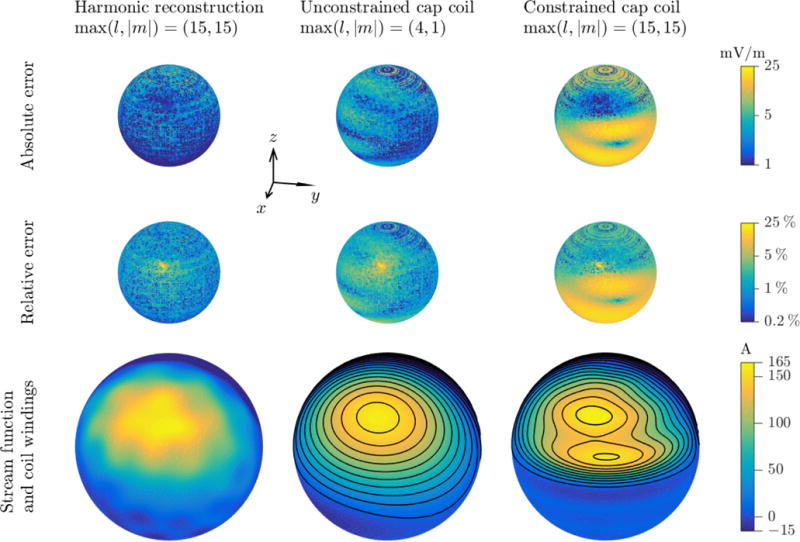
LFMS cap coil designs. From left to right: spherical harmonics representation of the standard LFMS coil simulation, unconstrained cap coil design, and constrained cap coil design. Top and middle rows: distributions of E-field absolute and relative errors compared to the simulation on the cortical surface of the spherical model. Bottom row: stream function and coil windings for the two coil designs. Color scale for each row is shown to the right; note logarithmic scale in top and middle rows, and asymmetric scale in bottom row, covering only the range of stream function values on the shown right hemisphere.

The cost function of the optimization problem was the coil energy. The constraints of the optimization problem were imposed on the stream function which determines the coil shape. As the LFMS E-field had left-right symmetry with zeros in the upper hemisphere, the stream function was anti-symmetric and reached its global maximum and minimum on the upper hemisphere. Therefore, the coil windings that extended to the lower hemisphere were formed by level-sets of the smallest absolute values (ψ_n = ±I/2, ±3I/2, …). By constraining the stream function in the lower hemisphere with |ψ| ≤ I/2 = max ψ/2N, isolines defined by equation (11) would not be located in the lower hemisphere. Additional constraints were imposed on the E-field to limit its error compared to the original distribution. The error constraints were relaxed (doubled) compared to the unconstrained design (see Table 1) to allow convergence of the solution under the stream function constraints. The MATLAB function fmincon was used to solve the nonlinear optimization problem (Table 1) with the coefficients of spherical harmonic decomposition as the initial point.

Table 1.

Summary of constrained optimization problem for the cap coil design.

Optimization variables	Elm	E-field coefficients for 0 < |m| ≤ l ≤ 15
Cost function	U	Coil energy
Constraints	|ψ| ≤ I/2 = max ψ/2N	Stream function in lower hemisphere
	${\mathrm{\Delta }}_E\le 2\mathrm{\%}max\Vert {\overrightarrow{E}}_{\text{LFMS}}\Vert$	Error metrics of E-field in upper hemisphere
	δE ≤ 4%
	δg ≤ 4%

2.3. LFMS description

The primary component of the tabletop LFMS device (Tal Medical, Boston, MA) is a cylindrical magnetic coil with a horizontal longitudinal axis and symmetric, dual-layer windings similar to the transverse gradient coil of an MRI machine (figure 1) [5]. The radius of the coil is 17 cm [5], its length is approximately 34 cm, and its measured inductance is 376 μH. The current waveform produced by the corresponding pulse generator is a train of alternating trapezoids with 256 μs ramp times and peak dwell times of 768 μs, which yields an E-field with 256 μs rectangular pulses of polarity alternating every 1024 μs [5]. When the current amplitude is set to 28.5 A, corresponding to the standard clinical protocol, the peak energy stored in the coil is approximately 153 mJ. During treatment, the subject lies supine with the superior part of the head inside the cylindrical coil cavity and the eyebrow ridge aligned with its front end.

For consistency, we defined a global Cartesian coordinates system (figure 1). The origin was coincident with the front end of the standard LFMS coil and at the center of the coil’s cross section. The z-axis was oriented into the coil along its longitudinal dimension, the x-axis pointed from the subject’s left to right, and the y-axis pointed anteriorly. The center of the head was offset from the origin by approximately −3.78 cm in the y-direction, matching the standard clinical LFMS protocol used by Tal Medical (Boston, MA) and McLean Hospital (Belmont, MA). For sampling the cortical E-field data, a local spherical coordinate system was used with its origin centered in the head and reference axes parallel to the global coordinates.

2.4. E-field measurement

A robotic probe [12] was used to measure the E-field vector distribution on a 7 cm hemispherical surface corresponding to the cortex in a 8.5 cm conductive spherical head model [11]. Briefly, the probe was comprised of two small isosceles triangular coils fixed in orthogonal planes and wrapped around a polylactic acid former, which was 3D-printed with an approximate resolution of 0.2 mm. The two equal sides of the triangular coils had a length of 7 cm and the base had a length of 6.5 mm. The vertex opposite the base of each coil was placed at the center of the spherical head. Each coil had 10 turns of 36 AWG magnet wire, and stacking was minimized to achieve a consistent loop size. The probe was itself mounted on a pair of circular platforms, each with an angular position controlled by a servo motor (Parallax Inc., Rocklin, CA). The E-field measurement probe was programmed to scan 1000 points along a distance-optimized path [12] on its 7 cm radius spherical surface (i.e., 3.25 points/cm²). The voltages induced in the probe coils by the LFMS magnetic field were filtered and then digitized using a 2-channel oscilloscope (DS1052, Rigol Technologies, Beaverton, OR).

2.5. Finite element simulations

The E-field was numerically determined using ANSYS Maxwell 16.2 (ANSYS, Canonsburg, PA), a low-frequency electromagnetics solver using the finite element method. Specifically, the ANSYS Maxwell eddy-current differential equation formulation module was used. Models of the LFMS coil, cap coil equivalent, and spherical and realistic head models were obtained by the procedures outlined below. For each simulation, the coordinate system described in section 2.3 was used and the magnetic field was assumed to have decayed completely at a radius of 0.5 m; correspondingly, the computational domain comprised a sphere with 0.5 m radius and Neumann boundary condition of zero normal magnetic field. For all models, the meshes were constructed with surface length constraints and a maximum element size of 5 mm. The total number of tetrahedral elements were approximately 800,000 and 500,000 for the LFMS coil and cap coils respectively, and 50,000 and 800,000 for the spherical and realistic head models, respectively. All regions had a relative permittivity of one and the air region had zero conductivity. A frequency domain solver was used with tolerance specified as 0.1%. Under the quasi-static assumption for magnetic stimulation [13,14], the amplitude of the E-field solution is proportional to the frequency of the magnetic field. The frequency of the harmonic solver was therefore set to 1.24 kHz according to the 256 μs duration of the slope of the LFMS current waveform, matching the E-field amplitude between the frequency domain and the time domain. For other TMS pulse waveforms, the simulation frequency can be similarly set according to its temporal characteristics. Simulation was performed on a desktop computer with an Intel Core i7 CPU and 64 GB RAM. Simulation time varied between 12 to 48 hours depending on the complexity of the model. Coil energy was calculated by integrating the magnetic field energy over the simulation space and coil inductance was estimated using the calculated energy and specified coil current.

2.5.1. Standard LFMS coil

The metal windings of the LFMS coil were modeled according to design drawings provided by Tal Medical (figure 1, top row). Each coil layer consisted of a spiral winding pattern on a 3.175-mm-thick sheet of copper (conductivity set to 5.8×10⁷ S/m) that formed a half-cylindrical shell. The two winding layers were connected not only at the spiral center, as in the actual device, but also at the terminals located on the end opposite to the head, creating a closed loop. The latter connection reduced the size of the simulation space by eliminating the need to simulate the leads that would connect to the pulse generator, which had minimal impact on the field applied to the head. The injection of current in the coil was modeled by applying current sources at the cross-sections of the coil where the stimulator cable normally connects to the coil. The current amplitude was set to 28.5 A, the same peak current amplitude as the LFMS coil. The boundary condition of the coil surface was set to insulation.

2.5.2. LFMS cap coil

The unconstrained cap coil winding design was imported into a 3D computer aided design software package (SolidWorks, Waltham, MA), where a circular wire profile with a 1.65 mm radius was assigned (figure 1, bottom row). The wire conductivity was set to that of copper, and the driving current value provided in each winding was set to 15.8 A, according to equation (10) (see Table 2, row 4).

Table 2.

E-field and electrical characteristics of the standard LFMS coil and the two cap coil designs in the spherical and realistic head models.

Head model	Coil	Data type	E-fielda (peak, mean ± SD) $\Vert \overrightarrow{E}\Vert$ (mV/m)	ΔE (mV/m)	Errorb (mean ± SD) δE(%)	δg (%)	Energy U (mJ)	Current I (A)	Inductance L (μΗ)
Spherical head	Standard coil	Simulation	343, 192 ± 72		0 (reference)		151	28.5	372
		Measurements	361, 208 ± 76	22.1 ± 8.6	13.4 ± 8.9	4.6 ± 2.2	153	28.5	376
		Harmonic Reconstruction	339, 192 ± 72	2.2 ± 1.6	1.3 ± 1.6	0.8 ± 0.8	3.28	16.1c	25.3c
	Unconstrained cap coil	Design	343, 191 ± 73	3.0 ± 1.8	1.9 ± 1.9	0.9 ± 0.5	3.12	15.8	24.9
		Simulation	353, 194 ± 74	4.2 ± 2.9	2.6 ± 5.1	1.3 ± 0.7	3.27	15.8	26.2
		Measurements	403, 227 ± 84	36.5 ± 14.0	20.7 ± 36.4	2.8 ± 1.3	3.31	15.8	26.5
			”	22.5 ± 10.6d	12.5 ± 13.4d	3.3 ± 1.8d	”	”	”
	Constrained cap coil	Design	332, 190 ± 68	6.6 ± 4.9	4.0 ± 3.9	1.9 ± 1.8	3.70	16.1	28.5
Realistic head	Standard coil	Simulation	359, 116 ± 58		0 (reference)		151	28.5	26.2
			362, 110 ± 57f		”		”	”	”
	Unconstrained cap coil	Simulation	386, 125 ± 63	11.8 ± 6.8	11.3 ± 7.9	1.9 ± 1.4	3.27	15.8	26.2
			357, 116 ± 58e	6.9 ± 5.0e	7.2 ± 7.3e	”	2.79e	14.6e	”
			359, 110 ± 56e,f	7.1 ± 4.8e,f	8.1 ± 8.7e,f	2.0 ± 1.3f	”	”	”

^aThe E-field’s peak amplitude is defined as the 99.9th percentile of the distribution. Statistics are calculated on 1000 sampling points for the measurements; 32400 points on the upper hemisphere of the spherical model for the simulations, spherical harmonic reconstruction, and designs; and 4 million points within the grey matter volume of the realistic model, unless otherwise noted.

^bThe E-field errors are calculated against the respective simulations of the standard coil (first and eighth row), unless otherwise noted. Statistics involving measurement data are calculated on the 1000 measurement sampling points and otherwise the same as the E-field.

^cThe spherical harmonic reconstruction are given current and inductance values calculated for 20 coil windings, matching the cap coil prototype.

^dComparison with the standard coil measurements (second row).

^eAfter calibrating the coil current in the realistic head model.

^fFor the whole brain volume (grey matter and white matter).

2.5.3. Spherical head model

For simulations with the spherical head model, we followed an approach similar to Deng et al. [11]. The head was assumed to consist of a sphere of 8.5 cm radius with a uniform conductivity of 0.33 S/m and an insulating boundary condition. The center of the sphere was located at coordinate (0, 0, −3.78 cm) of the standard LFMS coil and at the origin of the cap coil shell (figure 1, left column). The E-field was sampled on a spherical shell of 7 cm radius, corresponding to the cortical surface, in one degree intervals for both angular directions (64800 points).

2.5.4. Realistic head model

LFMS was simulated in an MRI-derived realistic head model of a healthy male subject developed in a previous study [15]. The 3D model generation was performed using Simpleware ScanIP (Synopsys, Mountain View, CA). The tissue boundaries were imported into ANSYS and a head model was generated from their enclosing volumes. The five homogenous isotropic conductive layers were assigned as follows [15]: 0.33 S/m for scalp, 0.0083 S/m for skull, 1.79 S/m for cerebrospinal fluid, 0.33 S/m for gray matter, and 0.14 S/m for white matter. The head above the eyebrow level was approximately half of an oblate ellipsoid with semi-principal axes approximately 8.5 cm in the x dimension and 9.5 cm in the y and z dimensions, respectively. The head size of this subject was within the normal range but slightly larger than the mean value on which the spherical head model was based [16]. Consequently, using the head model directly would have required redesigning the cap coil to be larger, which would also increase the coil energy. Therefore, for a direct comparison with the spherical model using the same coil design, the size of the realistic head model was isotropically scaled by about −10% to match the dimensions of the spherical model. This also allowed more practical head placement inside the cap coil to account for space of the casing and other support structures of the cap coil that were not modeled in the simulations. The implications of coil and head size are further discussed in section 4.2.1. The head was placed within the coils to match the respective positions of the spherical head model (figure 1, right column). The E-field was sampled with a spatial resolution of 1 mm and 0.5 mm within the entire head and the brain, respectively (available as supplementary data online). Besides statistics of the E-field, we also analyzed several regions of interest (see figure 3) selected to include nodes in a network dysregulated in depression [15,17].

Figure 3.

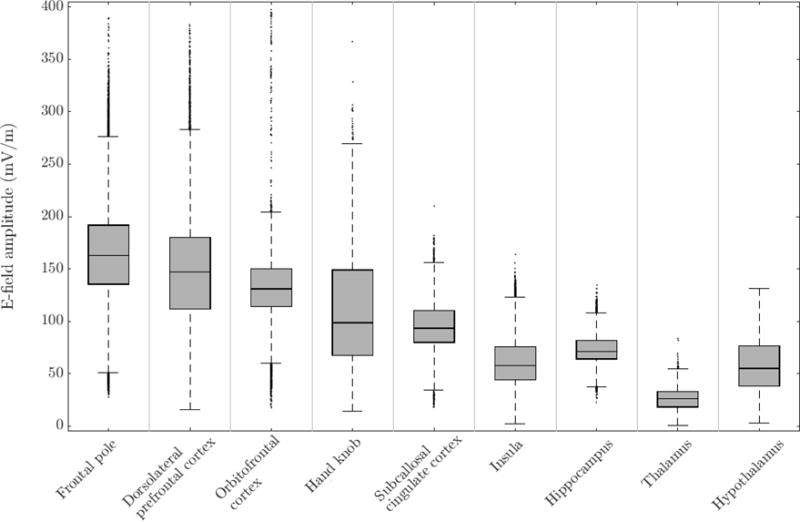
Descriptive statistics of the E-field generated by the standard LFMS coil in several regions of interest in the realistic head model. The box shows the interquartile range (25^th to 75^th percentiles) with median marked as horizontal line within the box. The whiskers lengths are 1.5 times the interquartile range, covering the central 99.3 percentile assuming normal distribution. Outliers are shown as dots.

2.6. Cap coil implementation and experimental validation

A computer aided design software package (Autodesk Inventor Professional 2016, Autodesk, San Rafael, CA) was used to design a spherical shell former with inner and outer radii of 10 cm and 10.5 cm, respectively. Grooves with semicircular cross section of 2 mm radius were added on the outer surface according to the winding pattern generated by the unconstrained cap coil design (figure 4, center column) to guide the placement of the wires. Two wider grooves were cut perpendicular to the windings on their lower portion to accommodate the wires connecting adjacent turns (see figure 5(a)).

Figure 5.

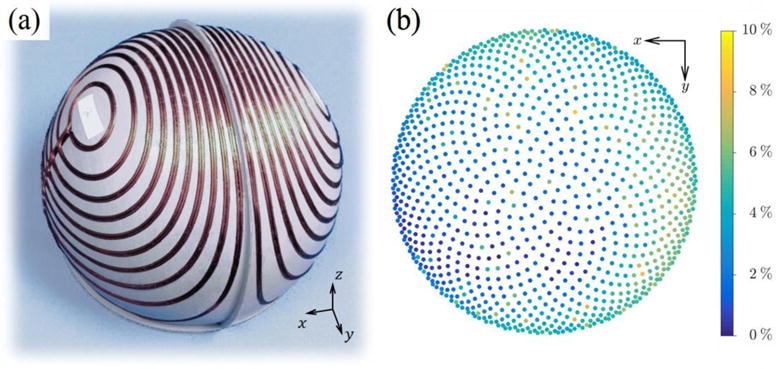
(a) LFMS cap coil prototype on a 3D printed former without the connecting cable. (b) E-field distribution error δ_g between measurements of the cap coil and the standard LFMS coil.

The former was 3D printed using a polylactic acid filament. Two spatially parallel strands of 14 AWG magnet wire (EIS, Charlotte, NC) were first bent and then set in the former grooves using a quick-setting epoxy (Loctite, Düsseldorf, Germany), with the cross-sectional center of the wires aligned with the outer surface. When these two sets of turns were connected electrically in series, the doubling of the turns resulted in a quadrupling of the coil inductance. This configuration was used during the experimental measurements for compatibility with the LFMS pulse generator. However, for direct comparison with the simulations which used a single set of turns, the reported inductance and coil current were scaled by 0.25 and 2, respectively, from their measured values. In addition, a 246 μH air-core inductor was added in series for impedance matching with the LFMS pulse generator; this does not affect the LFMS coil current, since the pulse generator has current controlled output. Inductances were measured with an LCR meter (889A, BK Precision, Yorba Linda, CA).

The E-field was measured with the probe described in section 2.4, with the cap coil placed over the measurement probe so that the sampling points of the spherical head model were concentric with the coil. The current waveform delivered by the LFMS pulse generator to the cap coil was the same as for the standard coil, but the amplitude was set at 7.9 A, half of the value determined in the design phase, to account for the doubling of turns.

We did not manufacture the constrained cap coil design (figure 4, right column) since the high level of agreement between theory, simulation, and prototype measurements for the unconstrained coil indicated that the simulations represent the performance of real coils very accurately.

3. Results

3.1. Characterization of standard LFMS coil

The spherical model simulation and measurements of the E-field distribution of the standard LFMS coil are shown in figure 2 and statistics are given in Table 2 (rows 1 and 2). The laterally symmetric E-field featured bilateral zeros and was strongest in an elliptical region centered near the vertex, with larger spread in the anterior–posterior direction than in the lateromedial direction. The experimental measurements resulted in a peak field strength 5.2% higher than predicted by the spherical model simulation, which can be attributed to several factors like small errors in the measurement probe’s location and rotation with respect to the coil and are further discussed in section 4.1. Despite these experimental uncertainties that could produce a systematic scaling in the measured E-field amplitude and therefore large absolute and relative errors, the normalized field distributions matched well between the experimental data and simulations (Table 2, row 2). The coil energy and inductance were also in good agreement, and the slightly higher measurement values were likely due to contribution of stray inductance from external connections.

Figure 2.

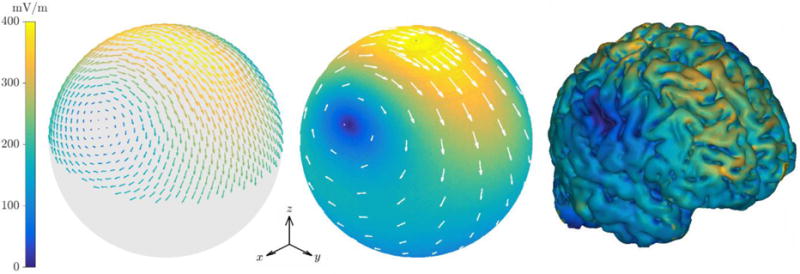
E-field of the standard LFMS coil for current amplitude of 28.5 A. From left to right: measurements on a 7 cm radius hemisphere; simulation results on a 7 cm radius sphere with the surface color showing the field magnitude and white arrows showing the field vectors; simulated field magnitude on the cortical surface of the realistic head model.

The global spatial features of the spherical model E-field were preserved in the anatomically realistic simulation (figure 2, right, and figure 6, top row), even though the E-field had more local variation because of the cortical folds. The zeros of the E-field distribution were located in the lateral parietal lobes. Consistent with previous observations in the literature [18,19], inhomogeneity of conductivity and the orientation of the gyri and sulci produced E-field “hot spots” on the cortical folds. The cortical E-field (Table 2, row 8) presented a smaller mean magnitude compared to the spherical head, reflecting the field’s decay in the sulci. The peak E-field strength in the realistic head agreed well with the spherical model (top hemisphere). The E-field magnitude in specific regions of interest (figure 3) showed that, as expected, superficial cortical areas (frontal pole, dorsolateral prefrontal cortex, orbitofrontal cortex, and hand knob) received stronger stimulation than deeper regions (subcallosal cingulate cortex, insula, hippocampus, thalamus, hypothalamus).

Figure 6.

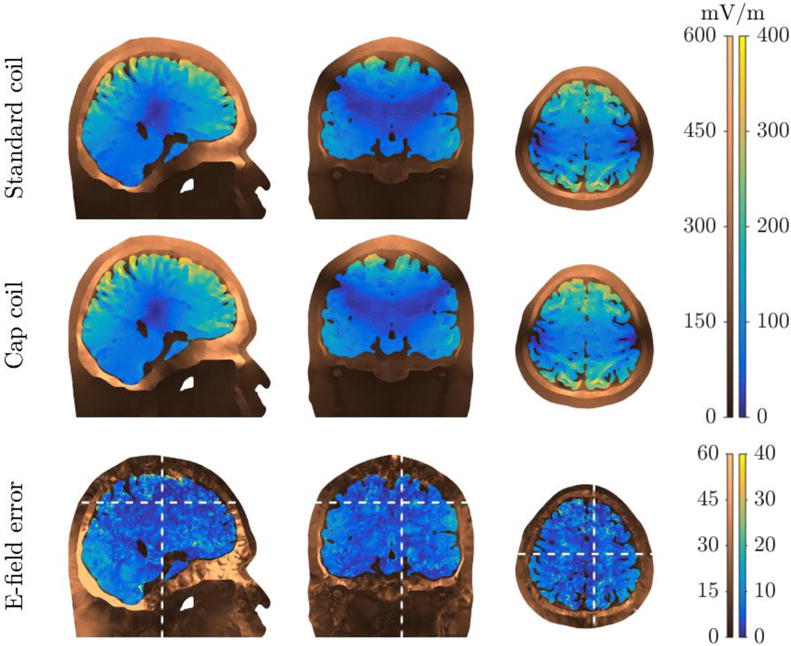
Cross-sectional view of the E-field magnitude from the standard LFMS coil and unconstrained cap coil simulations (top and middle rows) and the magnitude of the vector difference between them (bottom row) in the realistic head model. The locations of the slices are indicated by the white dashed lines in the bottom row. The E-field is shown with different color maps and scales for the brain and the other head tissues.

3.2. Cap coil designs

The simulated E-field of the standard LFMS coil in the spherical head model was used for the coil redesign procedure because it had higher resolution than the measurements and included the lower hemisphere. A small radial component (approximately 0.2% of local field magnitude on average) due to numerical inaccuracy in the finite element method was removed. The small errors of the field reconstruction with spherical harmonic terms up to a degree and order of (l, |m|) = (15,15) are shown in figure 4 (left column) and summarized in Table 2 (row 3). The surface current density residing on a 10.5 cm radius spherical shell matched the field generated by the LFMS coil in the cortex, while having significantly smaller energy than that of the LFMS coil (3.28 mJ versus 151 mJ), demonstrating the energy savings associated with making the coil smaller. However, the numeric noise of the simulated LFMS E-field was amplified by the higher degree harmonics and manifested as local variations in the stream function.

For the unconstrained design (figure 4, center column; Table 2, row 4), the higher degree harmonics were eliminated to further reduce energy and remove the numeric noise. The maximum degree and order of the retained spherical harmonics were (l, |m|) = (4,1). The E-field reconstructed with the remaining non-zero coefficients had only a slight increase in the errors, whereas the energy was further reduced by 5% to 48 times less than the standard LFMS coil and the stream function became smoother. The unconstrained cap coil design had an almost hemispherical shape, rotated slightly towards the anterior of the head, with the center of each side approximately aligned with the E-field zeros. The coil windings extended below the equator, especially on the front side, covering the regions corresponding to the eyes and ears but not the nose.

The constrained design generated spherical harmonic coefficients that restricted the amplitude of the stream function in the lower hemisphere, so that coil windings were only generated in the upper hemisphere (figure 4, right column; Table 2, row 7). Among the three constraints on the E-field error metrics, only the one for the mean relative error was active for the obtained solution. The most significant change compared to the unconstrained coil was that the constrained stream function had additional local extrema—two in the upper hemisphere on each side, breaking locally the winding into two smaller ones. Therefore, the total number of winding turns was larger than the discretization levels of the stream function (24 versus 20). The E-field distribution of the constrained design had large errors in the lower hemisphere, especially in the regions near the equator where the coil windings of the unconstrained design were removed. However, these errors were irrelevant to brain stimulation and were excluded from the cost function for the optimization. The energy increased by about 20% compared to the unconstrained designed, and was still 40 times less than the standard coil.

3.3. Validation of cap coil design in spherical head model

Computational validation of the unconstrained cap coil design was performed on the spherical head model in ANSYS. The E-field and its errors (Table 2, row 5) were slightly larger than their values calculated in the design process (Table 2, row 4) due to the discretization of the continuous stream function, with a slight increase in the coil energy and inductance.

The cap coil prototype described in section 2.6 (figure 5(a)) further provided the experimental validation (Table 2, row 6), with electrical characteristics matching the concomitant simulations. The normalized E-field distribution (figure 5(b)) had only small errors, which indicated success in replicating the field distribution of the standard coil. The cap coil registered a maximum field strength at the vertex that was 11.6% larger than the measurement for the standard LFMS coil (Table 2, row 2); this discrepancy and possible sources of uncertainty are explored in section 4.3, but it should be noted that this error can be trivially compensated by adjusting the coil current.

3.4. Verification and calibration of E-field in realistic head model

The simulated field distribution of the cap coil was similar to that of the standard LFMS coil in the realistic head model (figure 6, middle row). The location of the zeros on the lateral parietal lobe were shifted slightly downward compared to those of the standard coil. The field strength (Table 2, row 9) in the cortex was stronger by about 8% compared to the standard coil (Table 2, row 8), which was likely due to the proximity of the cap coil to the cortex and its morphological complexity. However, since the current amplitude for the cap coil was derived using a spherical head model, the realistic head model required calibration for the cap coil to match the standard coil’s E-field. By decreasing the cap coil current to 14.6 A (a −7.6% change), the mean error of the cortical field distribution was minimized and the energy of the cap coil was further reduced by 14.7% (Table 2, row 9) to 54 times less than the standard coil. After adjustment, the cap coil also matched the E-field distribution in deeper brain regions, with the E-field errors within the whole brain volume only slightly larger than those in the cortex (figure 6, bottom row; Table 2, row 9).

4. Discussion

4.1. Characterization of standard LFMS coil

We characterized the E-field of the standard LFMS coil via measurements corresponding to the spherical head model as well as through simulations in both spherical and realistic head models. Overall, the E-field pattern was similar in shape to that of a large double-cone coil [11,20]. The peak E-field magnitudes in both the spherical and realistic head models (around 350 mV/m) were larger than previously reported (250 mV/m) by Rohan et al. [5]. The most likely explanation for this discrepancy is the shift of the head off the coil’s axis in our model to reflect clinical use, which placed the head closer to the coil windings. Many other differences in modeling approach could contribute as well. For example, Rohan et al. used a two-step approach, in which the primary E-field was first solved in free space with the coil represented as a continuous current density distribution and then used to calculate the secondary E-field from the shielding charge of the head. In contrast, we used a realistic 3D model of the coil and computed the total E-field in a single step with the adaptive solver in ANSYS. Also, our head model was segmented into fewer tissue compartments, i.e., lumping muscle and fat with skin, and used different conductivity values and relative permittivity of one.

Our experimental measurements of the E-field confirmed our spherical model simulations and the field distributions matched well according to a variety of metrics. The small discrepancy (4.7%) in E-field amplitude could be attributed to experimental factors of the probe, including the inaccuracy of and uncertainties in its placement and orientation with regard to the coils and a slight rotational imbalance during measurements due to uneven structural loads. The probe’s design and manufacturing tolerance also affected the measurements. For example, the probe’s triangular windings were stacked where the two bases crossed, which resulted in slight arcing. Further, the two sides of the isosceles loops were slightly shorter at the apex due to limitations of 3D-printing of acute angles. Therefore, the normalized distributions served as the primary metric for comparisons that involved the measured E-field to address a potential systematic scaling in the field amplitude.

Compared to the measurements, the finite element simulations had a significantly higher sampling density of the field, including the lower hemisphere, and therefore provided the design procedure with sufficient data to reduce the numeric error for the harmonic decomposition. The spatial sampling could be improved further if its relationship with numeric accuracy is explored and enhanced numerical methods are used for the integration in the spherical harmonics decomposition. However, the simulation errors and concomitant assumptions also need to be considered. For example, the wiring between the turns and the cable to the current generator were neglected since their contribution to the field should be small. Numeric errors also existed, such as a small radial component of the simulated E-field that ideally should not exist in the spherical head model.

4.2. Design considerations

4.2.1. Cap coil size and number of windings

A number of parameters need to be chosen for the coil design to meet the specifications. The radius of the spherical surface on which the current density is, and therefore the coil windings are, defined has to be large enough to fit around the subject’s head. The spherical head model used in our simulations adhered to previous studies, with a radius based on measurements of female adults. Previous simulations of the E-field induced by TMS coils showed that, within the assumptions of the spherical model, the intracranial E-field is quantitatively and qualitatively similar for the head sizes across the two sexes [21]. Unlike flat coils, however, the cap coil needs to be large enough to accommodate the relevant range of head size, or, alternatively, a range of coil sizes can be made to fit different subjects. The cap radius affects the coil energy and other electrical characteristics: For the unconstrained design, a 1% increase in coil radius within the range of 9.5 cm to 11 cm approximately increases the energy, current, and inductance linearly by 4.1%, 1.7%, and 0.9%, respectively. For example, compared the 10.5 cm coil demonstrated in this study, an 11 cm radius coil would increase the coil energy by about 20%, decreasing the energy improvement over the standard LFMS coil from around 50-fold to 40-fold, which is still highly significant.

Increasing the number of winding turns N increases the coil inductance and peak voltage, and reduces the required peak current; this affects the requirements for the pulse generator design. Further, increasing N theoretically improves the quality of field replication, as it increases the number of quantization levels of the stream function, producing a better approximation of the surface current density. However, increasing N also increases the density of the windings; and as a result, designs with large N could be difficult or impossible to implement because of physical wire spacing constraints. Furthermore, a large N can form coil windings associated with small fluctuation of the stream function near zero, for example in the lower hemisphere, which have a minor contribution to the E-field and need to be discarded for a practical implementation.

4.2.2. Numerical accuracy of harmonic decomposition and truncation of high degree terms

The spherical harmonic decomposition of the measured or simulated E-field distribution (the reference field) is key to the design method, and its numerical accuracy should be evaluated, especially for the higher degree terms. Eliminating some harmonic terms from the design process given a priori knowledge of the reference field reduces errors. We halved the number of spherical harmonics to exclude coefficients that should theoretically be zero due to the left–right symmetry. The number of harmonics could be further halved for a reference field with anterior–posterior symmetry (e.g., for a head aligned with the cylindrical axis of the standard coil).

For the remaining terms, the error of the reference field’s projection onto the orthonormal vector bases, i.e., the inner product in equation (13), are amplified by a factor of (R/r₀)^l for the coefficients E_lm. The errors of E_lm are doubled for the stream function coefficients ψ_lm (i.e., $(2l+1)/\sqrt{l(l+1)}\approx 2$), whereas for the energy terms U_lm, the errors of E_lm are squared and further amplified by a factor of (2l + 1). Thus, the inaccuracy of the terms grows significantly with increasing degree, especially for the energy. For example, the energy of the spherical harmonic reconstruction calculated with the highest degree of 20 would be 17 times larger (55.3 mJ, versus 3.3 mJ with highest degree of 15) due to large errors in the additional energy terms.

This numeric instability, however, was not inherent to the decomposition itself. It rather stemmed from the limited accuracy of the reference field, which was computed to an accuracy of 0.1% in the simulations. Theoretically, the projection terms should decay exponentially to zero with increasing degree. However, additional analysis revealed that their amplitude approached approximately a level of 10⁻⁴ when normalized to the largest term with (l, m) = (1,1), reflecting spectral noise due to numerical inaccuracy of the field distribution. Therefore, the accuracy of the reference field is the limiting factor, and the highest degree of the harmonics should be set appropriately for the available accuracy. For the unconstrained design, our approach was to iteratively exclude higher degree terms. This method could be further improved by estimating the minimal degree necessary, given the accuracy of the reference field. For example, by using a simple thresholding on the projection terms with a normalized threshold of 10⁻³, the spherical harmonic representation of the LFMS field has only three additional non-zero terms with highest degree of 6 compared to our coil prototype, showing that a maximum degree of 6 would likely be sufficient to begin with. And to limit the error amplification for the stream function and energy, the radius of the coil should not differ too much from the radius of the sampling surface for the reference field. Alternatively, the matching of the tangential components of the E-field between the original coil and the harmonic reconstruction could be performed on the surface of the coil, therefore removing the error amplification altogether; the E-field within the brain would be matched by equation (4), with errors compressed when converting harmonic terms from a larger radius to a smaller one.

4.2.3. Unconstrained and constrained designs

The unconstrained coil design obtained a surface current density with significantly lower energy compared to the standard LFMS coil by utilizing the minimal energy principle of Koponen et al. [8] and truncating the high degree terms in the spherical harmonic decomposition to further reduce energy and avoid the aforementioned accuracy issues. Aside from the slight forward rotation due to the anterior-posterior asymmetry of the head in the standard LFMS coil, our unconstrained cap coil design resembles the hemispherical coil recently designed by Sánchez et al. using inverse boundary element method with criteria of minimum inductance and optimized E-field [22] as well as the minimum-energy coil of Koponen et al. [8]. This resemblance is due to the similar energy minimization and the LFMS coil’s maximum E-field coinciding with their E-field optimization location at the vertex. While coils of arbitrary shapes could be designed with many additional requirements and performance constraints utilizing discretized numeric methods [22,23], the similarity in coil shape indicates that energy minimization of coil designs converges to spatial patterns consisting of low degree spatial harmonics regardless of the approach details.

An exploratory constrained optimization was performed to improve the practicality of the cap coil by restricting the coil windings to the upper hemisphere, away from the eyes, ears, and neck. The optimization was conducted with the coil energy as the cost function and the E-field error metrics as additional constraints. In general, increasing the maximum degree of spatial harmonics in this optimization problem would yield lower energy solutions. However, increasing the number of harmonics could result in numerical accuracy issues, difficulties solving the nonlinear optimization problem, and higher computational costs. The choice of the constraints and the cost function can also affect the performance of the optimization and E-field replication. For example, using the root-mean-square for the E-field error metrics instead of the mean could make the optimization faster and more robust because the former is a convex function. If the constraints on errors were chosen more strictly, or if the absolute or relative error metrics were assigned to be the cost function, the constrained cap coil design could have better E-field replication but higher coil energy and more complex coil windings (results not shown). Generally, the optimization approach could be modified to accommodate specific design requirements.

4.2.4. Application to other stimulation paradigms

Our methodology for matching the induced E-field while minimizing the coil energy is applicable to optimization of any existing TMS coil design, including for clinical applications of suprathreshold TMS. For example, the H1 coil, which is part of a TMS system approved by the US Food and Drug Administration for the treatment of depression, features winding elements perpendicular to the surface of the head [24] which reduce its energy efficiency and increase its size [8,20]. By eliminating the wire elements extending radially from the head, the design optimization approach presented here can be used to generate an equivalent and more compact coil with increased energy efficiency and hence reduced power supply and cooling needs. Energy-optimized winding patterns that induce the same E-field can be similarly derived for other conventional coils without significant radial winding components, such as circular, figure-8, and double-cone coils; however, the proposed energy optimization may result in either a decrease or an increase in coil size.

4.3. LFMS cap coil

The energy of the two cap coil designs is 30 to 50 times less than the standard LFMS coil, potentially reducing the power requirements from over a hundred watts to several watts. Consequently, the bulky, desktop-sized current generator for the standard LFMS system could be supplanted by a portable, battery-powered one. The E-field distribution of the standard LFMS coil was accurately replicated by the cap coil, both on the cortical surface of the spherical head model and within the entire brain volume in the realistic head models. For the simulations with the spherical head model, the cap coil’s E-field on the cortical surface had a 4.2 mV/m difference on average (2.6% relative error) compared to the standard LFMS coil, reflecting additional errors introduced by the discretization of the stream function to those of the design process (3.2 mV/m and 2.0%). Comparing the measurements, the cap coil’s peak field strengths was larger (404 mV/m versus 361 mV/m, an 11% difference), although the distributions also had good agreement when normalized (3.3% error on average). The cap coil’s measurement was more sensitive to the aforementioned experimental factors due to the proximity between the windings and the probe and was likely augmented by ringing in the pulse waveform that was introduced by the inductance mismatch described in section 2.6. Even if the amplitude difference were substantive, it would not be of any practical consequence since the driving current could simply be scaled to account for the disparity, especially considering that the current required adjustment to match the field in the realistic head model.

The theoretical aspect of the design method was entirely based on matching the E-field on the cortical surface in the spherical head model, in which equation (4) explicitly connects the E-field distributions at various depths within the head [8]. The simulations in the realistic head model (Table 2 and figure 6) revealed that this fundamental depth-dependence of the E-field proved beneficial when replicating the field distribution using a cap coil. Due to the dominance of the slowly-decaying low degree spatial harmonic components, the overall spatial distributions of the E-field matched well within the entire brain, including several deeper regions of interest. After appropriate adjustment of the coil current, the E-field errors in the cortex and entire brain were only slightly larger than the error introduced by the design process in the spherical head model (6.9 mV/m and 7.2 mV/m versus 4.2 mV/m). The realistic head simulation therefore provided a mechanism for calibrating the cap coil current amplitude to match both the distribution and strength of the E-field in actual use. This could be helpful for subthreshold neuromodulation applications such as LFMS, which, unlike suprathreshold TMS, cannot use motor threshold to calibrate the current amplitude for each coil. The field errors in the skull and scalp of the upper head were also small and comparable to the errors inside the brain. On the other hand, the lower portion of the head deviated from the spherical model significantly and had the greatest difference in proximity to the two coils. However, since the low amplitude of the E-field in these regions situated below the brain (base of cranium and posterior neck) likely has negligible therapeutic influence, the larger E-field error there would be unlikely to impact the stimulation effects in the brain. Simulations using subject-specific head models can also address inter-subject variability, which is sometimes performed in TMS studies. However, given its spatially-diffuse nature, the LFMS E-field distribution is less sensitive to inter-subject variation of the head geometry than focal TMS, and a sufficiently large cap coil preserves the global features with only small local variations in different subjects.

5. Conclusion

This paper developed a design pipeline to produce spherical-shaped cap coils that can reliably replicate the E-field distribution on the cortex generated by existing TMS or LFMS coils while significantly reducing energy and, in some cases, size. We demonstrated this method for LFMS using improved measurements and models of standard LFMS. A prototype was implemented for one of the designs, achieving a remarkable 50-fold reduction in the requisite energy. Simulations in a realistic head model demonstrated that the E-field matched in both superficial and deep brain regions. These findings establish a basis for the development of portable and/or head-worn LFMS coils for potential home use (provided safety and efficacy of LFMS for relevant therapeutic indications is established). This approach can also be applied to optimization of other existing TMS coil designs.