Design and Analysis of Group-Randomized Trials in Cancer: A Review of Current Practices

Abstract

The purpose of this paper is to summarize current practices for the design and analysis of group-randomized trials involving cancer-related risk factors or outcomes and to offer recommendations to improve future trials.

We searched for group-randomized trials involving cancer-related risk factors or outcomes that were published or online in peer-reviewed journals in 2011–15. During 2016–17, in Bethesda MD, we reviewed 123 articles from 76 journals to characterize their design and their methods for sample size estimation and data analysis.

Only 66 (53.7%) of the articles reported appropriate methods for sample size estimation. Only 63 (51.2%) reported exclusively appropriate methods for analysis.

These findings suggest that many investigators do not adequately attend to the methodological challenges inherent in group-randomized trials. These practices can lead to underpowered studies, to an inflated type 1 error rate, and to inferences that mislead readers. Investigators should work with biostatisticians or other methodologists familiar with these issues. Funders and editors should ensure careful methodological review of applications and manuscripts. Reviewers should ensure that studies are properly planned and analyzed. These steps are needed to improve the rigor and reproducibility of group-randomized trials.

The Office of Disease Prevention (ODP) at the National Institutes of Health (NIH) has taken several steps to address these issues. ODP offers an online course on the design and analysis of group-randomized trials. ODP is working to increase the number of methodologists who serve on grant review panels. ODP has developed standard language for the Application Guide and the Review Criteria to draw investigators’ attention to these issues. Finally, ODP has created a new Research Methods Resources website to help investigators, reviewers, and NIH staff better understand these issues.

Group-randomized trials, also called cluster-randomized trials, are comparative studies in which investigators randomize groups to study conditions, usually intervention and control, and observe members of those groups to assess the effects of the intervention (Campbell and Walters, 2014; Donner and Klar, 2000; Eldridge and Kerry, 2012; Hayes and Moulton, 2009; Murray, 1998). In this context, a group refers to any group that is not constituted at random, so that there is some connection among its members. For example, if worksites are randomized to study conditions and workers within those worksites are observed to assess the effects of an intervention, the worksites are the groups and the workers are the members.

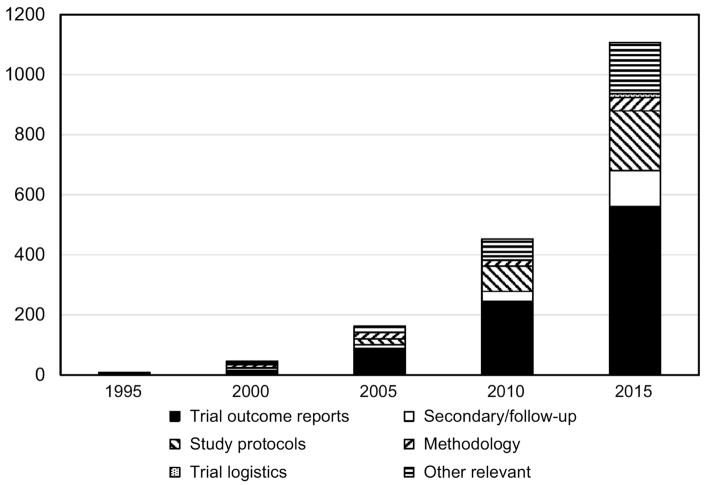
Just as the randomized clinical trial is the gold standard in public health and medicine when allocation of individuals is possible, the group-randomized trial is the gold standard when allocation of groups is required (Murray, 1998). That will occur whenever investigators evaluate an intervention that operates at a group level, manipulates the social or physical environment, or cannot be delivered to individuals without substantial risk of contamination. These trials have become increasingly common over the last 20 years (Figure 1); our search suggested a 280-fold increase in the number of group-randomized trials published in 2015 compared to 1995.

Figure 1.

Turner et al. (Turner et al., 2017a; Turner et al., 2017b) and Crespi (Crespi, 2016) recently reviewed the design and analytic challenges inherent in group-randomized trials. They note that the connections among group members create an expectation for positive intraclass correlation in observations taken on members of the same group (Kish, 1965); such correlation invalidates the independence assumption underlying the usual analytic methods and use of those methods will yield a Type I error rate that is inflated, often badly (Campbell and Walters, 2014; Cornfield, 1978; Donner and Klar, 2000; Eldridge and Kerry, 2012; Hayes and Moulton, 2009; Murray et al., 1998; Zucker, 1990). When only a few groups are randomized to each condition, the degrees of freedom (df) and power available for a valid test of the intervention effect will be limited. Finally, random assignment of only a few groups to each condition may jeopardize the internal validity of the trial by failing to distribute potential confounders evenly (Campbell and Walters, 2014; Donner and Klar, 2000; Eldridge and Kerry, 2012; Hayes and Moulton, 2009; Murray, 1998). Consideration must be given to these challenges as trials are planned and analyzed to support valid inference. Clear reporting is also important (Campbell et al., 2004).

Previous reviews have documented design and analytic problems in these trials (Brown et al., 2015; Crespi et al., 2011; Diaz-Ordaz et al., 2013; Diaz-Ordaz et al., 2014; Donner et al., 1990; Eldridge et al., 2008; Ivers et al., 2011; Murray et al., 2008; Rutterford et al., 2015; Simpson et al., 1995; Varnell et al., 2004). The most recent comprehensive review by Ivers et al. suggested that the methods had improved in trials published between 2000 and 2008; in particular, they reported that 61% and 70% of trials used appropriate methods for sample size and analysis, respectively (Ivers et al., 2011). In an earlier 2008 review focusing on cancer-related trials and covering much of the same time period, Murray et al. reported that only 24% and 45% of trials used appropriate methods for sample size and analysis, respectively (Murray et al., 2008). As a result, we have mixed evidence on whether the state of the practice with regard to the design and analysis of group-randomized trials has improved after 2000.

To the extent these problems continue, they contribute to the reproducibility challenges facing biomedical research (Collins and Tabak, 2014). To improve that situation, it is important to monitor the quality of the methods used and to encourage use of the best methods. This article assesses the state of the practice for group-randomized trials in studies published during 2011–2015 involving cancer-related risk factors and outcomes and offers recommendations for improvement.

Methods

The methods used for this review were based on those used in an earlier review by some of the same authors (Murray et al., 2008). We developed a list of groups used in these trials: (clinics, clusters, churches, colleges, communities, groups, hospitals, neighborhoods, physicians, practices, schools, units, wards, workplaces, worksites), hereafter represented as {groups}. We searched titles and abstracts in MEDLINE for human studies containing the following search term combinations: [cancer AND {groups}] AND [((community, cluster, group)(−, )(random*, rct)) OR ({groups}(were, were then, to be, are)(random*)) OR ((randomly assigned the {groups}) OR ({groups}(−based random*))]. We excluded articles based on the following key words in titles and abstracts: [(parallel)(−, )(group random*)] OR [(2-, 3-)(group random*)] OR [(two-, three- )(group random*)] OR [cluster random sampl*, rand* survey]. We also excluded articles based on key words in titles [protocol, review, metaanalysis, meta-analysis] and in publication types [review, meta-analysis]. The search identified 1451 candidate articles.

These articles were then annually inspected for the exclusion criteria and articles that met any of those criteria were excluded; some articles met more than one exclusion criteria. Articles reporting the results of studies in which groups were not randomly assigned to study conditions were excluded, as were studies that did not analyze observations taken on individual participants, and studies that lacked a clear statement that all groups were randomized to conditions. We excluded pilot studies because their goal is usually to evaluate intervention feasibility rather than efficacy. We excluded non-inferiority and equivalence trials because they are uncommon among group-randomized trials (Turner et al., 2017a) and cross-over and stepped-wedge designs because the impact of the intraclass correlation is reduced (Murray et al., 2010; Rhoda et al., 2011).

After these exclusions, we reviewed 123 primary articles (cf. Table A1) and 39 additional articles cited as background articles (cf. Table A2); these background articles were reviewed solely to inform the evaluation of methods for sample size estimation. Each article was reviewed independently by the first or second author and by two of the other six authors for design characteristics and methods used for sample size estimation and analysis of intervention effects.

For sample size estimation, we reviewed articles to determine whether authors reported evidence of taking group randomization into account a priori in establishing the size of the trial. Alternatives judged to be acceptable included reporting the expected intraclass correlation (Kish, 1987), coefficient of variation (Hayes and Moulton, 2009), or variance inflation factor (Donner et al., 1981), also known as the design effect (Kish, 1987).

For analysis of intervention effects, Table 1 (adapted from Murray et al. (Murray et al., 2008)) presents the criteria used to judge whether methods were appropriate. Methods considered appropriate included mixed-model regression such as mixed model analysis of variance or covariance (ANOVA/ANCOVA) and linear and non-linear random coefficients models (Murray, 1998, 2001; Murray et al., 2004; Turner et al., 2017b); generalized estimating equations (GEE) (Liang and Zeger, 1986; Murray et al., 2004; Turner et al., 2017b; Zeger and Liang, 1986); Cox regression; and two-stage analyses (Austin, 2007; Braun and Feng, 2001; Gail et al., 1996; Murray, 1998; Murray et al., 2006; Raab and Butcher, 2005; Turner et al., 2017b), including randomization tests (Edgington, 1995; Good, 1994).

Table 1.

Analytic methods frequently used in group-randomized trials and the conditions under which their use is appropriate.

Method	Appropriate Application
Mixed-model methods
ANOVA/ANCOVAa	One time point in the analysis
Repeated measures ANOVA/ANCOVA	Two time points in the analysis
Random coefficients approach	Three or more time points in the analysis
Generalized Estimating Equations
With correction for limited dfb	< 38 df for the analysis
With no correction for limited df	≥38 df for the analysis
Cox regression
With shared frailty	Time-to-event outcome
Without shared frailty	Not appropriate
Two-stage Methods (analysis on group means or other summary statistic)	At the level of the unit of assignment
Post-hoc correction based on external estimates of intraclass correlation	Validity depends on validity of external estimates of intraclass correlation
Analysis at subgroup levelc, ignoring group-level intraclass correlation	Not appropriate
Analysis at individual level, ignoring group-level intraclass correlation	Not appropriate
Analysis at individual level, modeling group as a fixed effect	Not appropriate

^aANOVA: analysis of variance; ANCOVA: analysis of covariance

^bdf: degrees of freedom

^cSubgroup level: a lower level in the group hierarchy, e.g., classrooms in a trial that randomized schools

This work was performed in Bethesda Maryland during 2016–17.

Because each of these methods can be applied incorrectly, we established additional criteria. Mixed-model ANOVA/ANCOVA was considered appropriate if variation at the condition level was assessed against variation at the group level, with df based on the number of groups, and with one or two time-points included in the analysis. If more than two time points are included in the analysis, a random coefficients analysis preserves the nominal Type I error rate whether the data satisfy the assumptions of the random coefficients analysis or the mixed-model repeated measures ANOVA/ANCOVA, while the mixed-model repeated measures ANOVA/ANCOVA will do so only if the data satisfy the assumptions of the repeated measures analysis. Unfortunately the mixed-model repeated measures ANOVA/ANCOVA does not provide a test of that assumption (Murray et al., 1998); as a result, random coefficient analyses were considered appropriate while mixed-model repeated measures ANOVA/ANCOVA were not. Analysis based on GEE was considered appropriate if there were 38 or more df for the test of the intervention effect, or if special steps were taken to correct the downward bias in the empirical sandwich estimator when there are fewer than 38 df (Bellamy et al., 2000; Feng et al., 1996; Ford and Westgate, 2017; Huang et al., 2016; Kahan et al., 2016; Li and Redden, 2015; McNeish and Stapleton, 2016; Murray et al., 1998; Murray et al., 2004; Preisser et al., 2003; Scott et al., 2014; Westgate, 2013). Cox regression was considered appropriate if the analysis included a shared frailty to reflect group randomization (Clayton and Cuzick, 1985; Jahn-Eimermacher et al., 2013; Vaupel et al., 1979). Two-stage approaches were considered appropriate if the second stage was conducted at the group level with df based on the number of groups. Several articles reported less common methods and we reviewed those methods to judge if they were suitable. Disagreements on any coding decisions were resolved through discussion.

Several approaches were considered inappropriate (Table 1). We cited several above -- repeated measures with >2 time points, GEE with <38 df and no small-sample correction, Cox regression without shared frailty. We note three other approaches that were considered inappropriate here. Analysis at a subgroup level, e.g., at the level of the classroom in a study that randomized schools, will have an inflated type 1 error rate unless the subunit captures all the variability attributable to the unit of assignment (Murray et al., 1996). Analysis at an individual level, ignoring the group altogether, will have an inflated type I error rate unless the intraclass correlation is zero (Campbell and Walters, 2014; Donner and Klar, 2000; Eldridge and Kerry, 2012; Hayes and Moulton, 2009; Murray, 1998); this is the classic error in the analysis of data from a group- or cluster-randomized trial. Analysis at an individual level, modeling group as a fixed effect is also inappropriate, and will result in an even higher type 1 error rate unless the intraclass correlation is zero (Zucker, 1990).

In addition, we coded articles on whether they reported an observed ICC for their primary outcome, whether they included a CONSORT flow diagram, and whether they had been registered in a national or international trial registry.

Once the articles were coded, we generated cross-tabulations to summarize the results. In addition, we fit bivariate logistic regression models to screen study characteristics for inclusion in a subsequent multiple logistic regression model to predict exclusive use of methods judged to be appropriate, with the inclusion criterion set at a two-sided p<0.25.

Results

The Studies

Table A3 lists the journals that published the studies reviewed for this paper. Nine (7.3%) of the 123 articles were published in Preventive Medicine; five (4.1%) were published in the American Journal of Preventive Medicine, four (3.3%) were published in Lancet, the Journal of Clinical Oncology, and in Annals of Family Medicine; three (2.4%) were published in the American Journal of Public Health, the Journal of General Internal Medicine, and Psycho-oncology. The remaining articles were spread across variety of other journals, with no more than two (1.6%) in any single journal.

Design Characteristics

Table 2 presents the design characteristics for the 123 articles. Most (88.6%) employed a design with just two study conditions, usually intervention vs. control, a value that reflects the complexity and cost often involved in these trials. Most (76.4%) employed a nested cohort design, wherein the same members are observed over time to assess the impact of the intervention (Murray, 1998). Most (54.5%) employed restricted randomization (e.g., a priori matching, stratification, or constrained randomization) in their design, consistent with current recommendations (Donner and Klar, 2000; Murray, 1998; Murray et al., 2004). Most (76.4%) included a single time point in their analysis and many (21.1%) used two time points (a baseline and follow-up measure). Most were primary (36.6%) or secondary prevention trials (43.9).

Table 2.

Characteristics of 123 articles reporting results of group-randomized trials in cancer research in peer-reviewed journals during the period 2011–2015, inclusive.

Characteristic	N	%
Number of Study Conditions
Two	109	88.6
Three	9	7.3
Four or more	5	4.1
Design
Cohort	94	76.4
Cross-sectional	26	21.1
Combination of Cohort and Cross-sectional	3	2.4
Type of Randomization
Restricted Randomization	67	54.5%
Matching only	16	13.0
Stratification only	46	37.4
Constrained Randomization only	2	1.6
Matching and Stratification	3	2.4
Simple or Unrestricted Randomization	56	45.5
Type of Group
Churches	6	4.9
Communities, Neighborhoods or Community Groups	15	12.2
Families	4	3.3
Housing Projects or Apartment Buildings	1	0.8
Clinicians, Provider Groups, Hospitals	65	52.8
Schools, Classes, Day Care Centers	24	19.5
Time perioda	4	3.3
Worksites	4	3.3
Average Number of Groups per Condition in the Analysis
1 Group	0	0.0
2–5 Groups	3	2.4
6–8 Groups	9	7.3
9–12 Groups	16	13.0
13–24 Groups	31	25.2
≥ 25 Groups	58	47.2
Variable	1	0.8
not reported	5	4.1
Average Number of Members per Group in the Analysis
<10 Members	30	24.4
10–49 Members	44	35.8
50–99 Members	19	15.4
≥100 Members	25	20.3
not reported	5	4.1
Number of Time Points in the Analysis
1 Time point	94	76.4
2 Time points	21	17.1
3–9 Time points	8	6.5
Focus of Study
Primary Prevention	45	36.6
Secondary Prevention	54	43.9
Tertiary Prevention	24	19.5
Target Population
Individuals with no personal history of the target cancer	33	26.8
Cancer survivors during primary treatment	11	8.9
Cancer survivors after primary treatment	5	4.1
Unknown or mixed cancer survivorship	74	60.2
Primary Outcome Variables
Alcohol Use	3	2.4
Delivery of Health Services	22	17.9
Dietary Variables	9	7.3
Fatigue	0	0.0
Incidence of Cancer	4	3.3
Knowledge of Cancer or Attitudes Regarding Cancer	10	8.1
Lymphedema	0	0.0
Mortality from Cancer	1	0.8
Neuropathy	0	0.0
Pain	3	2.4
Physical Activity	5	4.1
Quality of Life	6	4.9
Screening	33	26.8
Sun Protection	3	2.4
Tobacco Use	10	8.1
Weight	1	0.8
Other	13	10.6

^aSome studies randomized time periods. For example, some clinic-based studies randomized blocks of six weeks to study conditions, so that patients who saw their provider were given the treatment randomly assigned to their time block. This work was performed in Bethesda Maryland during 2016–17.

Relatively few trials (9.8%) included an average of eight or fewer groups per condition and many (47.2%) included an average of 25 or more. The average number of members per group ranged from an just over one to almost 15,000.

Many trials randomized providers or hospitals (52.8%) or schools (19.5%). There was a broad variety of outcomes reported, with screening (26.8%) and delivery of health services (17.9%) the most common outcomes.

Sample Size Methods

Thirty (24.4%) articles made no mention of sample size estimation. Eight (6.5%) reported a power analysis but provided no details as to the methods used. Two (1.6%) reported that variance had been inflated to account for the group randomization, but provided no further detail. Sixty-six (53.7%) reported appropriate methods for sample size calculations and reported an intraclass correlation, coefficient of variation, variance inflation factor, or design effect.

Analytic Methods

For 63 (51.2%) of the 123 articles, all analyses reporting intervention effects were judged to be appropriate given the design of the study (Table 3), indicating that they accounted for the expected correlation in the data and used degrees of freedom based on the number of groups or clusters. Mixed model regression methods were used most often, though GEE and two-stage methods were used in several studies.

Table 3.

Distribution of analytic methods in 123 articles reporting on group-randomized trials in cancer research published in peer-reviewed journals during the period 2011–2015, inclusive.

Criteria	N	%	N	%
Articles reporting only appropriate methods	63	51.2
Mixed-model ANOVA or ANCOVA with 1 time point			39	56.5
Mixed-model repeated measures with 2 time points			7	10.1
Random coefficients model with >2 time points			2	2.9
Generalized estimating equations with ≥38 degrees of freedom			9	13.0
Cox regression with adjustment for the unit of assignment			4	5.8
Two-stage analysis			6	8.7
Other			2	2.9
Articles reporting both appropriate and inappropriate methods	17	13.8
Appropriate Methods
Mixed-model ANOVA or ANCOVA with 1 time point			11	64.7
Mixed-model repeated measures with 2 time points			1	5.9
Random coefficients model with >2 time points			0	0.0
Generalized estimating equations with ≥38 degrees of freedom			2	11.8
Cox regression with shared frailty for the unit of assignment			3	17.6
Two-stage analysis			0	0.0
Other			0	0.0
Inappropriate Methods
Analysis at an individual level, ignoring groups			16	94.1
Analysis at a subgroup level, ignoring groups			0	0.0
Analysis with group as a fixed effect			0	0.0
Mixed-model repeated measures, > 2 time points			0	0.0
GEE with ≤38 df and no small sample correction			1	5.9
Individual-level analysis with post-hoc correction			0	0.0
Other			0	0.0
Articles reporting only inappropriate methods	37	30.1
Analysis at an individual level, ignoring groups			18	45.0
Analysis at a subgroup level, ignoring groups			7	17.5
Analysis with group as a fixed effect			2	5.0
Mixed-model repeated measures, > 2 time points			3	7.5
GEE with ≤38 df and no small sample correction			8	20.0
Individual-level analysis with post-hoc correction			1	2.5
Other			1	2.5
Not enough information provided	6	4.9

This work was performed in Bethesda Maryland during 2016–17.

Seventeen (13.8%) articles reported some analyses that were judged to be appropriate and some that were not. The most commonly used approach judged to be inappropriate was an analysis at an individual level that ignored the groups altogether.

Thirty-seven (30.1%) articles reported only analyses that were judged to be inappropriate. The most commonly used approach was again an analysis at the individual level that ignored the groups altogether. There were also several articles that employed analyses based on GEE with fewer than 38 df when the otherwise beneficial asymptotic properties are less likely to hold; none reported use of any of the correction methods suggested in the literature to address this problem (Bellamy et al., 2000; Feng et al., 1996; Ford and Westgate, 2017; Huang et al., 2016; Kahan et al., 2016; Li and Redden, 2015; McNeish and Stapleton, 2016; Murray et al., 1998; Murray et al., 2004; Preisser et al., 2003; Scott et al., 2014; Westgate, 2013).

Six articles (4.9%) did not provide sufficient information to judge whether their analytic methods were appropriate. Often these articles referenced an acceptable method but did not provide enough detail to determine whether the method had been used appropriately.

One-hundred and two (82.9%) of the studies reported one or more statistically significant intervention effects. Of that number, 51.0% reported only analyses judged to be appropriate, 27.4% reported only analyses judged to be inappropriate, 13.7% reported a combination, and 7.8% did not provide enough information.

Financial Support

Forty-three of the studies were supported by the National Institutes of Health (NIH). Of that number, 25 (58.1%) reported only analyses judged to be appropriate, which was not significantly higher than the overall proportion of 51.2%.

Registration and Reporting

Of the 123 studies, 70 (56.9%) were registered in a national or international trials database, 31 (25.2%) reported an ICC for their primary outcome, and 97 (78.9%) included a CONSORT flow diagram.

Regression Analysis

In the bivariate logistic regression models to screen study characteristics for inclusion in a subsequent multiple logistic regression model to predict exclusive use of methods judged to be appropriate, only two variables met the criterion of p<0.25: whether the manuscript reported any foreign source of funding, and whether any cohort analyses were included. Neither variable was statistically significant in the multiple logistic regression model (both p-values >0.10).

Discussion

Our review identified 123 articles published in 76 journals that reported intervention results based on a group-randomized trial related to cancer or cancer risk factors during the period 2011–15. The number of articles and their distribution across so many journals underscore just how widespread the use of interventions requiring group-randomized trials for their evaluation has become in cancer research. That is also reflected in Figure 1, which shows a 280-fold increase in the number of published outcome reports from 1995 to 2015.

Of the two most recent reviews of the state of the practice for design, analysis, and sample size in group-randomized trials, Murray et al. (Murray et al., 2008), published in 2008 and covering papers published 2002–2006, is most comparable to the current study, as they used the same eligibility criteria and almost the same evaluation criteria. There were three notable improvements in the findings from the current review compared to that 2008 review. First, there was a substantial increase in the proportion of studies that reported enough information to demonstrate that their sample size calculations had been done properly (53.7%, up from 24%). Second, there was a substantial increase (47.2%, up from 16%) in the proportion that included 25 or more groups per condition. Third, there was a modest improvement in the number of articles that reported only analytic methods judged to be appropriate to assess intervention effects (51.2%, up from 45%) and a modest improvement in the number of articles reporting at least some analytic methods judged to be appropriate to assess intervention effects (65%, up from 49.4%). These comparisons suggest that the state of the practice with regard to design, analysis, and sample size methods has improved comparing 2011–15 to 2002–06.

The other recent review, published by Ivers et al. in 2011 and covering papers published 2000–2008, reported that 61% and 70% of trials used appropriate methods for sample size and analysis, respectively (Ivers et al., 2011). Ivers et al. placed no limits on the content areas of the trials, where we limited our review to trials involving cancer-related risk factors and outcomes. Perhaps more importantly, we required both evidence that a generally acceptable analysis method had been applied correctly, and that no inappropriate methods had been reported, where Ivers et al. did not. Had we ignored the application of inappropriate methods, the proportion that we would have judged to have used appropriate analytic methods would have risen to 65.0%, and if we had also allowed the incorrect application of appropriate methods, the proportion would have risen to 74.0%. As a result, the explanation for the difference between our current findings and those of Ivers et al. may be a function of the criteria used to judge whether analytic methods were appropriate.

Our review also identified areas where improvement was lacking. First, all of the articles that reported only methods judged to be inappropriate used methods that have been widely discredited for more than a decade, such as ignoring the group entirely in the analysis (Murray et al., 2004). Given that 27 (73.0%) of these articles also reported statistically significant intervention effects, many of those reported effects may be Type I errors. Second, this review gave full credit for an appropriate analysis if the authors indicated that they had used mixed models as specified in Table 1. We looked more closely and found that only 23 of 39 articles that reported using a mixed-model ANOVA or ANCOVA reported that group had been included in the model as a random effect. Of the eight articles that reported using a repeated measures ANOVA or ANCOVA or a random coefficients analysis, only two reported that both group and time x group had been included in the model as random effects. Failure to include these random effects would mean that the analyst was assuming that the component of variance associated with time x group was zero, and if that assumption was wrong, the mixed model would have been mis-specified, and the type I error rate would be unknown. We have generally advised against testing variance components for significance, and discarding them if they are not significant, as standard errors for variance components are not well estimated when the component is close to zero, and the df available for those tests are usually limited (Murray, 1998). Had we required an explicit statement that the analysis had included the time x group term, the proportion of articles that reported only methods judged to be appropriate would have dropped from 51.2% to 32.5%. Better reporting of analytic details will clarify this situation in the future, and in the meantime, we emphasize the need for that information.

The regression analysis did not identify any design or analytic features considered in this paper that predicted use of inappropriate methods, suggesting that the problems we identified were not specific to a particular subset of the papers, but instead were found quite broadly in the literature.

Given that the CONSORT guidance for group-randomized trials was published in 2004 (Campbell et al., 2004), one would expect a high level of compliance with their key recommendations. We did observe high compliance for inclusion of a CONSORT flow diagram (78.9%) but poor compliance for reporting an observed ICC for the primary outcome (25.2%). We found that 56.9% had registered their trial in a national or international trials database, such as clinicaltrial.gov.

Although we tried to identify all group-randomized trials in cancer research published from 2011 through 2015, our review may be incomplete. In addition, we limited the review to the design and analytic features that were specific to these trials and did not critique the articles for more general design and analytic issues. We did not critique the studies in terms of their intervention programs and of course the results of any trial will depend on the quality of the intervention as well as on the quality of the design and analytic methods.

It is clear that additional effort is needed to take full advantage of the information that is readily available regarding the proper design and analysis of group-randomized trials. Recognizing that there is a role for funding agencies, the NIH Office of Disease Prevention (ODP) is taking several steps to address this problem.

ODP has recently released a 7-part, self-paced online course on the Design and Analysis of Pragmatic and Group-Randomized Trials in Public Health and Medicine. The course is designed for investigators who have prior training in introductory research design and regression methods. Each part has a 25–35 minute video and both the slide sets and a transcript are available to download. ODP provides a suggested activity and answer key for each segment, an e-mail address for questions about the material, and a reference list. ODP created the course after determining that such a course was not readily available either online or on many College or University campuses.

ODP is working to increase the number of methodologists who serve on grant review panels. Without enough methods experts, applications may score well in spite of serious methodological problems, and that will not advance the science. ODP is partnering with the Center for Scientific Review to provide a new web-based tool to their Scientific Review Officers to help them identify methods experts for possible service on the panels. Methodologists are often not Principal Investigators, and most of the existing tools available to Scientific Review Officers are focused on Principal Investigators. The ODP tool draws on data from extramural researchers who complete the Prevention Research Expertise Survey on the ODP website. One of the methods included on the survey is the design and analysis of group- or cluster-randomized trials, so this tool will help reviewers identify experts in those methods.

ODP has worked with the NIH Office of Extramural Research (OER) to develop standard language that is now included in the Application Guide and in Funding Opportunity Announcements that may support future clinical trials. The language alerts investigators to the special issues that accompany group-randomization and refers them to a website where they can get more information. ODP has created a website, ResearchMethodsGuidance.nih.gov, that provides additional information and a sample size calculator to help investigators plan new trials.

Group-randomized trials remain the gold standard for studies designed to evaluate an intervention that operates at a group level, manipulates the social or physical environment, or cannot be delivered to individuals. The issue is not whether to employ these trials, or even how to employ them, but rather to ensure that they are planned and analyzed using appropriate methods so that we can have confidence in their published results. NIH is taking steps to draw attention to these issues, and we encourage investigators, journal reviewers, and other funding agencies to do the same.

Highlights.

• We summarize design and analytic practices for group-randomized trials in cancer.

• Only 66% reported appropriate methods for sample size estimation.

• Only 51.2% reported exclusively appropriate methods for analysis.

• Many investigators still do not attend to the methods challenges in these trials.

• The NIH Office of Disease Prevention has taken steps to address this situation.