Microfocus X-ray data collection from 18 non-overlapping regions of a single protein crystal revealed unit-cell non-isomorphism and subtle protein dynamics across the crystal specimen.
Keywords: protein dynamics, microfocus X-ray diffraction, non-isomorphism, principal component analysis, crystal disorder
Abstract
Real macromolecular crystals can be non-ideal in a myriad of ways. This often creates challenges for structure determination, while also offering opportunities for greater insight into the crystalline state and the dynamic behavior of macromolecules. To evaluate whether different parts of a single crystal of a dynamic protein, EutL, might be informative about crystal and protein polymorphism, a microfocus X-ray synchrotron beam was used to collect a series of 18 separate data sets from non-overlapping regions of the same crystal specimen. A principal component analysis (PCA) approach was employed to compare the structure factors and unit cells across the data sets, and it was found that the 18 data sets separated into two distinct groups, with large R values (in the 40% range) and significant unit-cell variations between the members of the two groups. This categorization mapped the different data-set types to distinct regions of the crystal specimen. Atomic models of EutL were then refined against two different data sets obtained by separately merging data from the two distinct groups. A comparison of the two resulting models revealed minor but discernable differences in certain segments of the protein structure, and regions of higher deviation were found to correlate with regions where larger dynamic motions were predicted to occur by normal-mode molecular-dynamics simulations. The findings emphasize that large spatially dependent variations may be present across individual macromolecular crystals. This information can be uncovered by simultaneous analysis of multiple partial data sets and can be exploited to reveal new insights about protein dynamics, while also improving the accuracy of the structure-factor data ultimately obtained in X-ray diffraction experiments.
1. Introduction
Interconversion of protein conformational states is critical for diverse biological phenomena such as enzymatic turnover, allosteric signal transduction and mechanical force generation. Consequently, understanding protein function often requires the characterization of multiple structural states and their interconversions (Karplus & Kuriyan, 2005 ▸; Frauenfelder et al., 1991 ▸; Koshland, 1998 ▸; Hilser et al., 2006 ▸; Fersht, 1998 ▸). Traditional crystallographic studies are generally not well suited to describe conformational heterogeneity, and elucidating the atomic details of structural variations in protein molecules remains a major challenge (van den Bedem & Fraser, 2015 ▸).
Models derived from crystallography typically represent the single, lowest-energy conformation of the crystallized molecules. However, increasing efforts are being directed towards identifying alternative conformations of protein molecules, and researchers have explored diverse strategies to achieve this goal. Some studies have used various ‘trapping’ strategies, which rely on the introduction of mutations (Fanning et al., 2016 ▸; Schultz-Heienbrok et al., 2004 ▸), ligands (Śliwiak et al., 2016 ▸; Zimmermann et al., 2017 ▸; Fieulaine et al., 2011 ▸) or varied physical conditions (Moffat & Henderson, 1995 ▸; Schlichting & Chu, 2000 ▸) to capture different structural states of a molecule. This is a laborious task that involves obtaining multiple different crystals and solving an independent structure from each of them (Nolen et al., 2004 ▸). In contrast, others have used computational methods to identify alternative conformations from a single electron-density map (Fraser et al., 2011 ▸; van den Bedem et al., 2009 ▸; Keedy et al., 2015 ▸; Lang et al., 2010 ▸, 2014 ▸). This approach can be applied using just one data set from a single crystal, although it often requires high-resolution diffraction, and the observable conformational states are limited to those that are well populated within the crystal lattice.
Here, we describe a method for characterizing conformational and crystal-packing heterogeneity in proteins that is complementary to previously developed strategies. We demonstrate that a crystal pathology, which initially impeded structure determination of the EutL bacterial microcompartment (BMC) shell protein, could be exploited to identify distinct alternative conformations of the molecule in different regions of a single crystal specimen. Specifically, we used microfocus X-ray diffraction to collect 18 spatially independent data sets from a plate-like crystal that suffered from mild long-range disorder. To analyze and visualize the relationships between many data sets simultaneously, we employed a principal component analysis, similar to but somewhat simplified compared with recent methods developed by Diederichs and coworkers for multi-dimensional analysis (Brehm & Diederichs, 2014 ▸; Diederichs, 2017 ▸). This approach illuminated a surprising variation in internal structure within the crystal. It also facilitated the collection of internally consistent merged data sets and ultimately revealed subtle protein dynamics and conformational polymorphism across a single crystal.
2. Materials and methods
2.1. Protein preparation and crystallization
We prepared highly pure EutL (Clostridium perfringens) protein for crystallization following a protocol that has been described previously (Thompson et al., 2014 ▸, 2015 ▸). Briefly, recombinant hexahistidine-tagged protein was expressed in Escherichia coli BL21 (DE3) cells. The cells were subsequently harvested and lysed. The lysate was clarified by centrifugation and applied onto an immobilized metal-affinity column charged with nickel ions. The protein was eluted using an imidazole gradient, and a second purification step consisting of gel filtration was performed to remove residual contaminants and to exchange the protein into crystallization buffer (20 mM Tris pH 8.0, 100 mM NaCl). The protein was concentrated to 20 mg ml−1, mixed in a 1:1 ratio with mother liquor [0.1 M sodium/potassium phosphate buffer pH 6.6, 0.25 M sodium chloride, 10%(w/v) PEG 8000] and crystallized by vapor diffusion in hanging-drop format.
2.2. X-ray data collection and reduction
Prior to X-ray data collection, we harvested individual plate-like crystals from crystallization drops and cryoprotected them using 50% mother liquor with 2 M trimethylamine-N-oxide before plunge-cooling them in liquid nitrogen.
Two distinct crystallographic experiments were conducted to produce the results described here. In both cases, X-ray diffraction data were collected at the Advanced Photon Source while maintaining the crystals at cryogenic temperature (100 K).
In the first experiment, we used a robust, high-quality crystal to collect a single reference data set on beamline 24-ID-C equipped with a 70 × 30 µm beam aperture and an ADSC Quantum 315 CCD detector. The total diffraction-weighted X-ray dose required to obtain this data set was 5.2 MGy, as determined using RADDOSE-3D (Zeldin et al., 2013 ▸).
In a second experiment, we used a relatively thin crystal (approximately 150 × 100 × 5 µm) and collected 18 separate data sets from spatially independent regions of the crystal specimen on beamline 24-ID-E, which was equipped with an ADSC Quantum 315 CCD detector. A microdiffraction beam-shaping aperture allowed us to collect these data sets using a 5 µm microbeam, which facilitated the collection of many data sets from minimal, non-overlapping volumes of the crystal. During this multiple-collection experiment, each data set was obtained using the same strategy, which measured a 75° wedge of reciprocal space centered on a vector normal to the flat facet of the plate-like crystal, giving 90% theoretical completeness for space group C2. This minimal wedge of data was selected to give near-completeness of the data sets while maintaining their spatial independence. X-ray exposure times for individual data sets were chosen empirically to balance the need for strong diffraction across a long exposure period with the desire to limit decay. The diffraction-weighted X-ray dose used for each of these 18 data sets was 57.5 MGy, again determined using RADDOSE-3D (Zeldin et al., 2013 ▸). Owing to the particular experimental requirements here, the X-ray dosages for individual data sets were higher than usually deemed optimal for typical diffraction experiments (Owen et al., 2006 ▸; Holton, 2009 ▸). We note that despite this relatively large dose, diffraction remained strong throughout the duration of the X-ray exposure.
All X-ray data were indexed, integrated, scaled and merged using XDS and XSCALE, and intensities were then converted to structure factors with XDSCONV (Kabsch, 2010 ▸). To aid in the analyses described below, multiple data sets collected from a single crystal were all indexed and scaled relative to the same reference data set. Assignment of the free set of reflections was performed using PHENIX (Adams et al., 2010 ▸). The same set of free reflections for each of the data sets was used for atomic refinement, in order to prevent cross-contamination of free and working reflections when refining models against various different sets of reflections.
2.3. Pairwise comparison of data sets in reciprocal space and real space
After collecting 18 independent data sets from spatially non-overlapping regions of a single crystal and reducing the data to structure factors, we calculated a separate R factor (R iso) between every pairwise combination of data sets according to (1),
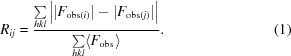 |
Next, we sought to compare unit-cell geometries in order to check for potential non-isomorphism between the data sets. We based these calculations on the unit-cell metric tensor: an orientation-independent description of the (squared) size of a unit cell. If matrix A contains the Cartesian coordinates of a set of unit-cell axes as columns, then the unit-cell metric tensor is G = A T A, with T indicating the transpose. We calculated G for each data set, and we then calculated a 3 × 3 distortion matrix D for each pairwise combination of metric tensors. The distortion matrix D operates by multiplication on the second metric tensor, G 2, to yield the first metric tensor, G 1, according to (2),
Therefore, D is given by (3),
We note that when the unit cells are perfectly isomorphous their metric tensors are necessarily equivalent (G 1 = G 2), and the distortion matrix becomes the identity matrix (D = I).
In order to capture the unit-cell non-isomorphism between each pair of data sets in the form of a single scalar quantity, we calculated a ‘pairwise distortion index’ by comparing a given distortion matrix with the identity matrix and computing the sum described by (4), where dij and iij represent corresponding elements in the distortion matrix and the identity matrix, respectively,
The metric described by (4) was found to be a useful estimator of the fractional difference between two unit cells, and is similar to the metrics used by data-processing algorithms to decide whether measured Bragg positions match a given lattice system (Otwinowski & Minor, 1997 ▸).
2.4. Identification of related data sets by principal component analysis
Particularly in the context of serial crystallography, sophisticated mathematical treatments have recently been developed for the multi-dimensional analysis of many partial data sets (Diederichs, 2017 ▸). Here, we opted for a simplified variation based on principal component analysis of R factors. From N individual data sets (and subsets thereof), we constructed a square symmetric, N × N matrix R, the elements rij of which are given by the pairwise R factors between the corresponding data sets i and j; the diagonal elements are zero (see equation 1). In the present study, the number of data sets was N = 18.
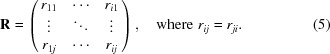 |
This matrix contains sufficient information to cast the N data sets as points in an N-dimensional space such that the distances between them correspond to their pairwise R factors, using distance-geometry equations. To perform this, the elements of the R-factor matrix are first mean-centered using the law of cosines to give a new N × N matrix X T X, known in some contexts as a Gram or second-moment matrix, with each element (X T X)ij describing the dot product of x i with x j, where in the present application x i represents the high-dimensional coordinates of data set i. The elements of X T X are obtained from the elements of the R-factor matrix as follows,
with d ij values having the same meaning as r ij and the values of d 0i first being calculated according to
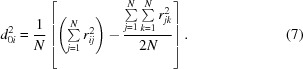 |
To describe the spread of the constellation of data sets in their high-dimensional coordinate space, the matrix X T X is then factored by eigenvalue decomposition to yield X. This is a common procedure for principal component analysis. The resulting matrix X contains the coordinates x i of each data set projected onto the principal directions, and the eigenvalues of X T X quantify how much of the variation between the data points as a whole is captured by each principal component. After obtaining X, we visualized the 18 points representing our X-ray data sets projected onto the first two principal components.
Recently, Diederichs (2017 ▸) introduced a similar algebraic method of projecting related data sets onto a low-dimensional space that is somewhat more complex than our method, but is better suited to handle situations where the level of random noise in the data sets is large.
2.5. Structure determination and model refinement
For reference, we initially solved the conventional, single-data-set structure of EutL by molecular replacement with Phaser, using a different EutL structure (PDB entry 4edi; Thompson et al., 2015 ▸) as a search model. A solution was found in space group C2. After placing the search model in the unit cell, we performed iterative model building and refinement with Coot (Emsley et al., 2010 ▸) and phenix.refine (Afonine et al., 2012 ▸). Automated refinement of atomic coordinates and B factors was performed using TLS parameters, a riding hydrogen model and automatic weight optimization. The final structure was deposited in the Protein Data Bank (PDB; http://www.rcsb.org; Berman et al., 2000 ▸) under accession code 4tlh. The same structure-determination protocol was used for the two structures that were later solved from two separately merged data sets (described subsequently), which were also deposited in the PDB under accession codes 6arc and 6ard.
2.6. Normal-mode analysis of EutL
Normal-mode analysis of a EutL trimer was performed using the WebNMA server (Tiwari et al., 2014 ▸) using a previously determined EutL structure (PDB entry 4edi) as the input model. R.m.s.d. calculations between static X-ray structures were calculated with ProDy (Bakan et al., 2011 ▸, 2014 ▸).
3. Results
3.1. Plate-like crystals of EutL are prone to translocation disorder
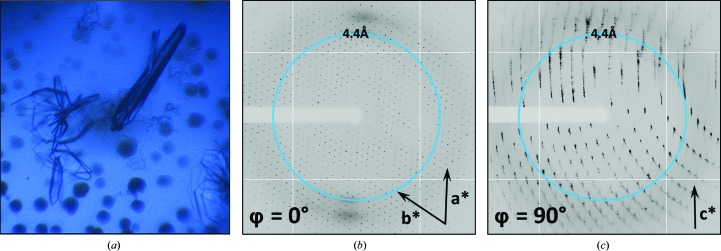
EutL is a 24 kDa protein that forms trimers in the context of its structural and molecular-transport roles in the shell of the ethanolamine-utilization (Eut) bacterial microcompartment (Thompson et al., 2015 ▸). The EutL crystals used for this study grew with a thin, plate-like morphology. The formation of plate-like crystals is common for BMC family proteins, as their natural predisposition to form hexagonally packed molecular layers favors lateral growth. Crystal formation was relatively inconsistent, however, and the crystal morphology was highly variable even within a single drop (Fig. 1 ▸ a). Plate-like crystals tended to be tens to hundreds of micrometres in their largest dimensions, but only about 5 µm in their smallest dimension. Occasionally, crystals approached 20 µm in thickness. Crystals typically grew in clusters, and among the crystals there were also spherical aggregates of protein.
Figure 1.
The occurrence of pathological diffraction from crystals of the EutL protein. (a) Crystals grew as plate clusters in drops that also contained spherulite structures. (b, c) Diffraction images from some specimens displayed strong indications of disordered hexagonal layers. The images shown are separated by 90° in reciprocal space and the directions of the presumptive a*, b* and c* axes are shown.
Initial X-ray diffraction screening of the plate-like EutL crystals revealed diffraction features indicative of varying levels of lattice-translocation disorder. We observed that many of the crystals diffracted well when the incident X-ray beam was normal to the face of a plate-like crystal, but poorly when the beam was incident upon the edge of the same crystal (Figs. 1 ▸ b and 1 ▸ c). Specifically, when the crystals were illuminated along their edges the resulting Bragg peaks were streaky and suffered from splitting, which prevented successful indexing and integration of the diffraction intensities. For diffraction images in which the X-rays were normal to the large faces of the crystals, measuring the distances and angles between the Bragg positions in these images suggested the presence of hexagonal layers in the crystal (a = b = 65.9 Å, γ = 120°). These lattice dimensions are consistent with the anticipated two-dimensional biological assembly of EutL. Unfortunately, the pathological diffraction observed for these crystals prevented structure determination for some time.
3.2. Determination of a EutL reference structure from a high-quality monoclinic crystal
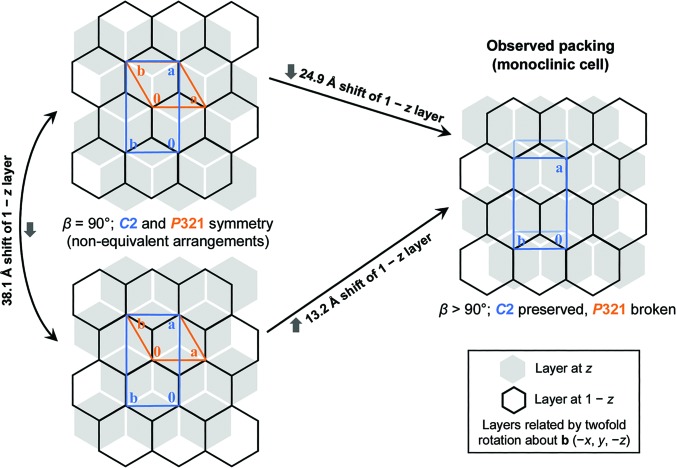
After screening numerous crystals that suffered from varying levels of translocation disorder, we eventually identified a crystal specimen that lacked obvious indications of pathology, making it suitable for structure determination. This particular crystal was among the thickest that we obtained, at approximately 20 µm in its thinnest dimension. Using this crystal, we collected X-ray diffraction data and processed them to a resolution of 1.7 Å in space group C2 (Table 1 ▸). We solved the structure by molecular replacement. Using another EutL structure (PDB entry 4edi; tetragonal crystal form) as the search model, we placed a trimer in the asymmetric unit. The model was iteratively rebuilt and refined to convergence (Table 1 ▸), revealing a structure that was highly similar to related tandem BMC-domain proteins for which structures have been determined, including a EutL ortholog from E. coli (Tanaka et al., 2010 ▸) and PduB (Pang et al., 2012 ▸), a shell protein from the Pdu-type bacterial microcompartment. Interestingly, while the crystal is composed of oppositely facing layers of EutL trimers, each with P3 symmetry, the crystal cannot be described by a hexagonal lattice system. Instead, an offset of the rotational symmetry elements in one layer relative to the next breaks the potential P321 symmetry, resulting in a monoclinic lattice belonging to space group C2 (Fig. 2 ▸). Oppositely facing layers of hexagonally packed trimers can obtain P321 symmetry by aligning their threefold symmetry elements in two distinct ways. These unique possibilities are related to one another: one arrangement can be converted to the other by the translocation of one layer of trimers. The vector describing this translocation is perpendicular to the hexagonal a axis and has length (a/31/2). The observed monoclinic lattice has its second layer offset relative to the first in a position that is intermediate between the two unique P321 arrangements (Fig. 2 ▸).
Table 1. X-ray diffraction data-reduction and atomic refinement statistics for the structures reported here and deposited in the Protein Data Bank.
Values in parentheses are for the highest resolution shell.
| Reference data set | Group 1 merged | Group 2 merged | |
|---|---|---|---|
| Wavelength (Å) | 0.9792 | 0.9791 | 0.9791 |
| Resolution range (Å) | 33.43–1.70 (1.74–1.70) | 19.80–1.90 (1.95–1.90) | 20.11–2.00 (2.05–2.00) |
| Unit-cell parameters (Å, °) | a = 118.4, b = 66.0, c = 79.4, α = 90, β = 108.3, γ = 90 | a = 118.7, b = 66.1, c = 80.1, α = 90, β = 108.5, γ = 90 | a = 118.7, b = 66.1, c = 78.6, α = 90, β = 111.2, γ = 90 |
| Space group | C2 | C2 | C2 |
| Unique reflections | 63737 (4382) | 43719 (3317) | 35264 (2652) |
| Multiplicity | 3.7 (3.7) | 17.4 (4.8) | 4.6 (1.7) |
| Completeness (%) | 99.5 (99.5) | 94 (96) | 92 (94) |
| 〈I/σ(I)〉 | 11.02 (1.6) | 20.96 (4.4) | 8.66 (1.7) |
| Wilson B factor (Å2) | 16.9 | 15.4 | 17.6 |
| R meas (%) | 9.4 (99.3) | 13.5 (39.7) | 14.9 (57.7) |
| CC1/2 | 99.8 (58.7) | 99.8 (89.7) | 99.2 (71.8) |
| R work | 0.163 | 0.137 | 0.180 |
| R free | 0.195 | 0.181 | 0.217 |
| No. of atoms | 5380 | 5616 | 5118 |
| Protein residues | 653 | 653 | 653 |
| Solvent molecules | 504 | 676 | 322 |
| Ions | 2 | 2 | 1 |
| Average B factor (Å2) | 24.1 | 20.5 | 22.3 |
| R.m.s.d., bonds (Å) | 0.009 | 0.010 | 0.003 |
| R.m.s.d., angles (°) | 1.15 | 0.99 | 0.53 |
| Ramachandran plot | |||
| Favored | 98.4 | 98.6 | 97.5 |
| Allowed | 1.6 | 1.1 | 2.5 |
| Outliers | 0.0 | 0.3 | 0.0 |
| MolProbity clashscore | 1.34 | 3.15 | 1.15 |
| PDB code | 4tlh | 6arc | 6ard |
Figure 2.
Staggered packings of trigonal protein layers in EutL crystals. Left: two unique, but related, packing arrangements obeying P321 symmetry in a crystal composed of oppositely facing layers of trimers (orange cells). Right: partial offset of the threefold symmetry axes in successive layers of the crystal (perpendicular to the hexagonal axis; the a axis here) leads to breakage of trigonal symmetry while preserving monoclinic symmetry (C2, blue cell).
3.3. Microdiffraction facilitates the collection of many data sets from a single crystal specimen
Knowing that our crystals tended to exhibit varying levels of lattice disorder, we sought to determine whether this property of the crystals might allow us to identify alternative protein conformations. We selected a single crystal that was relatively large (>100 µm) in two dimensions but very thin (∼5 µm) in the third dimension. Using a very small X-ray beam (5 µm cross-sectional diameter), we collected 18 spatially independent data sets from this crystal (Fig. 3 ▸). The specific regions of the crystal used for data collection were chosen to allow sufficient distance between them so that the irradiated volumes would not overlap, but the chosen regions were otherwise irregularly arranged. Additional care was taken to select an initial crystal orientation and rotation range that would maximize the data completeness while minimizing the irradiated volume and avoiding physical overlap between the exposed regions. The thinness of the crystal aided in achieving this objective. The X-ray data were collected and processed as described in §2, and the variation in the quality of the 18 data sets is summarized in Table 2 ▸. The individual data sets were all processed to comparable resolutions (1.9–2.5 Å), all in space group C2, and were of reasonable quality as judged by signal-to-noise ratios (and by correlation between random half-data sets; CC1/2). In the present study we did not push the limits of resolution to low CC1/2 values, as we wished to avoid confounding the measurement of differences between data sets with high noise. We also note that two specific regions of the crystal that were sampled did not diffract well enough to produce useful data (these regions are denoted by the letter X in Fig. 3 ▸).
Figure 3.
Images of the crystal specimen that formed the basis for the multi-data-set study. A single, plate-like crystal (a) was used to collect 18 spatially independent data sets using a 5 µm X-ray beam. An enlarged view (b) shows the non-overlapping locations from which the data sets were collected, with the boundary of the crystal highlighted in false color (cyan). The numbers correspond to the data-set numbers described in the text, and the red dots denote the approximate size and location of the X-ray beam used to collect each data set. Areas of the crystal that were tested but did not diffract are denoted by a letter X.
Table 2. Summary of the variation in data quality for 18 spatially independent data sets collected from a single EutL crystal.
| Worst | Best | |
|---|---|---|
| Maximum resolution (Å) | 2.5 | 1.9 |
| Completeness (%) | 83.3 | 90.8 |
| 〈I/σ(I)〉, overall | 7.4 | 10.5 |
| 〈I/σ(I)〉, highest resolution shell | 2.0 | 3.1 |
| R meas, overall (%) | 15.7 | 7.6 |
| R meas, highest resolution shell (%) | 54.4 | 32.2 |
| CC1/2, overall | 92.2 | 99.6 |
| CC1/2, highest resolution shell | 71.9 | 87.9 |
3.4. Pairwise comparison of data sets reveals non-isomorphism
In order to test whether our independent data sets might contain unique structural information, we first calculated all possible pairwise R factors between them. Many of the R values between data sets were considerably higher than expected given the relatively conservative resolution limits chosen for the collection of the individual data sets. This provided an early indication of variability and a conclusion that a structure-determination study based on an attempt to merge all the data together would be imprudent. We noticed that the R factors calculated on structure factors tended to be either small (<20%) or rather large (∼40%), with virtually no intermediate values. Because large crystallographic R factors can be the result of differing molecular structures existing within the same lattice (conformational differences), or of the same molecular structure existing within a different lattice (unit-cell non-isomorphism), this observation prompted us to explore more carefully the relationship between pairwise R factors and unit-cell non-isomorphism for our 18 data sets.
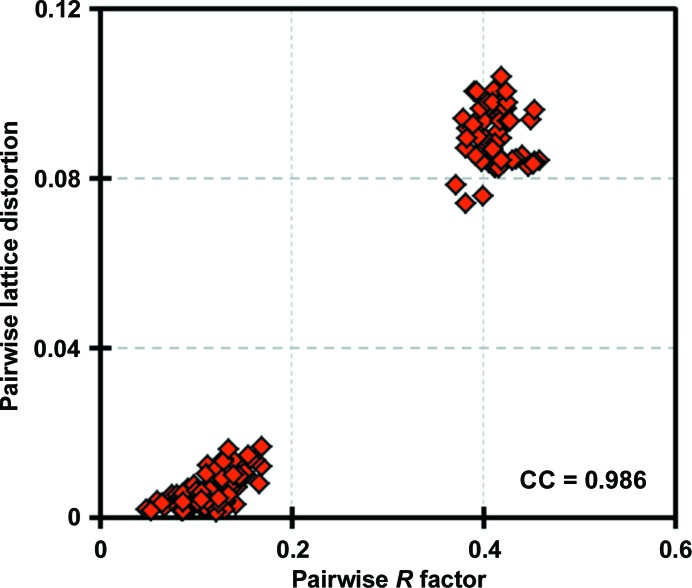
To evaluate unit-cell polymorphism, we calculated a pairwise ‘lattice-distortion index’, which was intended to serve as a single scalar metric describing the fractional deviations between two unit cells (see §2). The largest deviations between unit cells were as high as 0.1, reported on a fractional unit-cell scale. By plotting the pairwise R factors and the pairwise distortion indices against one another, we discovered that the R factors and distortion indices were highly correlated (ρ = 0.99), confirming that the largest differences in structure-factor magnitudes between data sets did indeed result from unit-cell non-isomorphism (Fig. 4 ▸). While this analysis clearly demonstrated the presence of non-isomorphism in the crystal, it did not indicate how many different unit cells were present.
Figure 4.
Correlation of R values and unit-cell variations between pairs of diffraction data sets. 18 data sets collected from different regions of a single crystal were compared pairwise using lattice-distortion indices and R factors calculated between structure-factor magnitudes for equivalent reflections that had been integrated and reduced within separate data sets. The correlation coefficient of these two values across the 153 (18 × 17/2) pairwise comparisons was 0.986. Two separable clusters are evident.
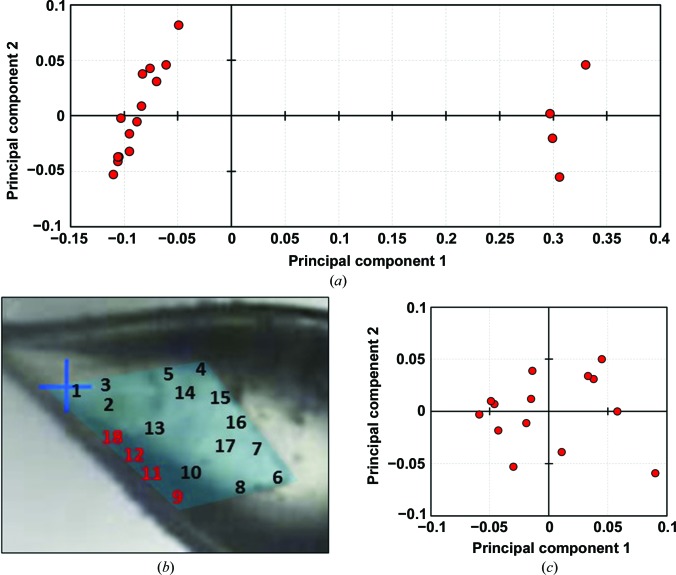
3.5. Principal component analysis reveals two major groups of non-isomorphous data sets
In order to determine how many unique structures were represented by our 18 data sets, we used the pairwise R factors to formulate a square, symmetric, 18 × 18 matrix that could be analyzed by principal component analysis (see §2), after which points representing the 18 data sets could be projected onto the (first two) principal components (Fig. 5 ▸ a). The resulting eigenvalues indicate that the first two principal components capture 86% of the variation between the X-ray data sets, with the first principal component alone capturing 81% of the variation. A visual analysis revealed that the 18 data sets could be readily clustered into two main subgroups: a major subgroup of 14 members (data sets 1–8, 10 and 13–17) and a minor subgroup of four members (data sets 9, 11–12 and 18). Interestingly, the four data sets belonging to the minor subgroup were all collected from neighboring regions located along a single side of the plate-like crystal (Fig. 5 ▸ b). The co-localization of data sets comprising the minor group along a single edge of the crystal leads to several hypotheses about the cause of the observed non-isomorphism. Possible explanations include differences in dehydration or cryocooling along this edge of the crystal (which lies at the edge of the loop; Fig. 3 ▸) or a growth defect that might be related to the tendency of these plate-like crystals to attach to one another (Fig. 1 ▸). Additional experiments comparing spatially resolved structural measurements of multiple crystals would be required to test these ideas.
Figure 5.
Principal component analysis based on pairwise R-factor comparisons between multiple data sets. The R values were cast as distances between data sets, allowing them to be embedded in a high-dimensional space and then projected onto their two principal components for display. (a) A comparison of all 18 data sets collected from a single crystal reveals two clear groups (consistent with Fig. 4 ▸). A major group of 14 data sets and a minor group of four data sets are apparent. (b) Interestingly, the minor group of data sets were all collected from the same edge of the crystal specimen. (c) Further attempts to cluster the major group of 14 data sets using the same PCA approach did not reveal any finer groupings.
We repeated our principal component analysis on the major subgroup of 14 data sets (data sets 1–8, 10 and 13–17) to see if we could identify finer data-set subgroupings. This time, we began with a 14 × 14 pairwise R-factor matrix and again projected the points corresponding to data sets onto the first two principal components (Fig. 5 ▸ c). In this case, while the eigenvalues show that the first two principal components capture 56% of the variation between data sets, clear partitions within the major subgroup were not evident.
3.6. Structure determination from the two major groups of data sets
After clustering our data sets, we separately merged together the 14 data sets of the major subgroup (group 1) and the four data sets of the minor subgroup (group 2), yielding two ‘average’ data sets, each of acceptable quality and both better than possible if joined together. To illustrate this point, we also calculated statistics for the blind merging of all 18 data sets with no PCA-based sorting. Notably, the overall R meas value for this blindly merged data set (32.6%) was much worse than for the individual group 1 and 2 data sets (13.5 and 14.9%, respectively; see Table 1 ▸). Additionally, while the blindly merged data had a higher overall multiplicity than the group 1 data set alone (21.3 versus 17.4), it has a lower overall signal-to-noise ratio 〈I/σ(I)〉 (18.2 versus 21.0). In contrast, the overall CC1/2 values for the blindly merged data set are not significantly different than for the group 1 and group 2 data sets (99.7 versus 99.8 and 99.2, respectively). The findings made it clear that the individual group 1 and group 2 data sets had significantly different unit-cell parameters, revealing long-range non-isomorphism in the single crystal used for our data collection. The unit-cell deviations between data sets belonging to the same subgroup were less than 0.02 (expressed on a fractional scale), while the deviations between data sets from different subgroups were in the range 0.07–0.11. This observation confirmed the existence of two effectively distinct unit cells across the 18 data sets. These two averaged unit cells were a = 118.7, b = 66.1, c = 80.1 Å, α = 90, β = 108.5, γ = 90° and a = 118.7, b = 66.1, c = 78.6 Å, α = 90, β = 111.2, γ = 90°. We refined separate atomic structures against each of the average merged data sets representing the two subgroups by first performing molecular replacement, followed by iterative model building and refinement of individual atomic coordinates and B factors, until the models reached convergence. We note that the free set of reflections was kept consistent throughout all structures described here. Data-reduction and refinement statistics for each of the two merged data sets and structures are provided in Table 1 ▸.
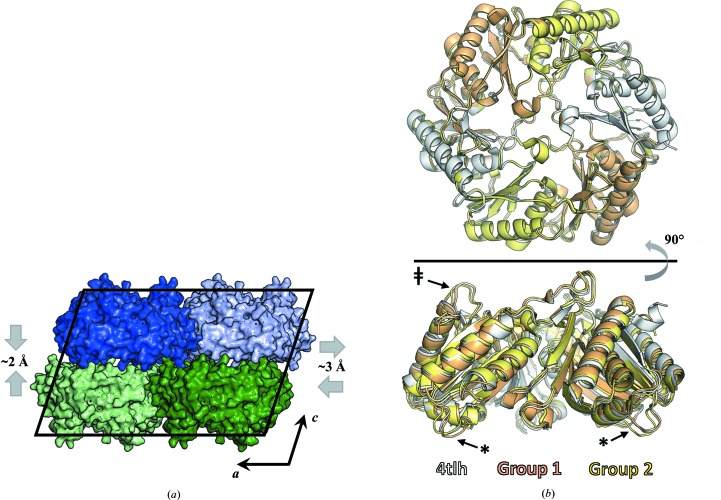
The differences between the two average structures consist of significant unit-cell deformations, as well as subtle conformational differences between the molecules in their respective lattices. Comparing the unit-cell parameters for the two data sets (Table 1 ▸) reveals that the lattice of the minor group has undergone shearing and compression relative to the lattice of the major group (Fig. 6 ▸ a). The combined effects of changes in unit-cell lengths and angles correspond to relative movements between molecules of about 5 Å. Parallel ab planes slide 3.0 Å relative to their neighbors and become 2.0 Å closer to one another. The differences between the two observed lattices suggests that the translocation disorder observed for some crystal specimens might result from stochastic displacements of adjacent layers of crystallized molecules along the monoclinic a axis. Additionally, overlaying the EutL trimers that comprise the asymmetric unit in each of the two structures reveals the conformational differences that accompany the alterations in the crystal packing. Subtle but significant differences between the two structures are observed for two regions of the molecule. The first is a short helical segment flanked by two small loops, spanning residues 16–35 on the concave side of the EutL trimer (Fig. 6 ▸ b; denoted with asterisks), near a putative protein–protein interaction site (Jorda et al., 2015 ▸). The second is a surface loop that includes residues 114–122 on the convex side of the trimer (Fig. 6 ▸ b; denoted by a double dagger), which points toward the trimeric symmetry axis in direct contact with a second key loop whose conformation dictates the functional state of the central pore (Tanaka et al., 2010 ▸; Thompson et al., 2015 ▸).
Figure 6.
A comparison of structures refined against the two major data-set groups. Significant differences exist between the group 1 and group 2 crystal structures. (a) Two specific unit-cell distortions differentiate the group 1 and group 2 structures. The group 2 cell has a wider β angle owing to a lateral shift of one layer relative to another along the a axis and a reduction in the distance between layers. (b) Coincident with the lattice distortions are subtle conformational differences in the EutL protein. The most significant differences between the two structures occur in regions spanning residues 16–35 on the concave side of the trimer (denoted with an asterisk) and residues 114–122 on the convex side of the trimer (denoted with a double dagger). The structure derived from the high-quality, single-crystal data set (PDB entry 4tlh) is shown for additional comparison.
3.7. Local differences between structures correlate with other calculations of protein flexibility
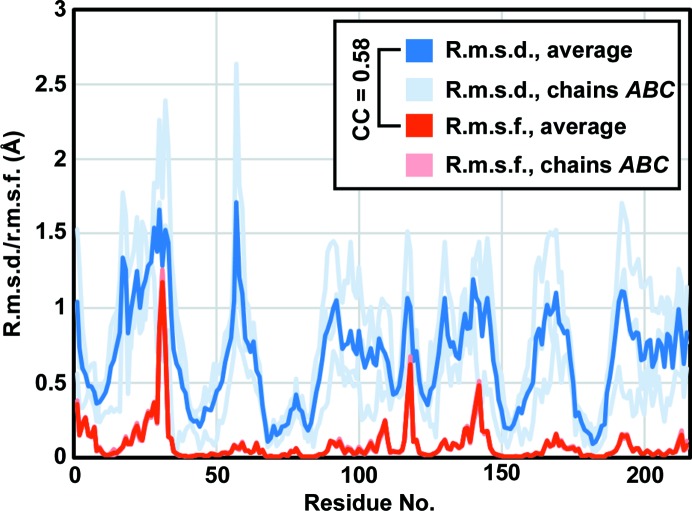
After observing small conformational differences between the two average structures, we wanted to ascertain whether these differences were merely consequences of the different packing arrangements, or whether they might be relevant to the intrinsic motions of the protein molecule. We compared the observed root-mean-square deviation (r.m.s.d.) between the positions of Cα atoms in our two crystal structures with the root-mean-square fluctuation (r.m.s.f.) of Cα atoms predicted from normal-mode analysis (NMA), and found a significant correlation (CC = 0.58; Fig. 7 ▸).
Figure 7.
Differences between the group 1 and group 2 structures correlate with normal-mode calculations of protein flexibility. The plot shows Cα r.m.s.d. values for comparison of the group 1 and group 2 structures, along with Cα r.m.s.f. calculations from normal-mode analysis of a EutL trimer. The values for individual chains in a trimer are shown (light lines), as are the average values (dark lines). The correlation coefficient between the average r.m.s.d. and average r.m.s.f. is 0.58.
4. Discussion
The present study emphasizes that significant crystallographic differences can exist in a spatially dependent fashion within a single protein crystal. To the extent that such differences exist, large numbers of spatially separated data sets (even if they are individually incomplete) could provide richer and ultimately more interpretable structural findings on complex molecules. We identified a crystal form of the EutL microcompartment shell protein that suffered from long-range disorder, harvested a single crystal specimen and probed its spatially dependent features using microdiffraction. We collected a total of 18 unique data sets from small, non-overlapping volumes of the crystal. With these multiple data sets in hand, we utilized an algebraic framework, similar in intent to that used by Diederichs and coworkers (Brehm & Diederichs, 2014 ▸; Diederichs, 2017 ▸), but simpler in execution, to analyze their differences in reciprocal space in order to group them according to systematic similarities and differences that might represent distinct underlying structures. We found that although all of the data sets were collected from a single macroscopic crystal, they could be separated into two strongly non-isomorphous groups. From these, independent structure determinations revealed a minor loop movement that, while small, is consistent with other analyses of the structural flexibility of the protein. Specifically, the average Cα r.m.s.d. between the two non-isomorphous structures we determined agreed well with the average Cα r.m.s.f. calculated from a normal-mode analysis of the EutL trimer. Interestingly, Harata and Akiba previously reported that for both triclinic and monoclinic lysozyme crystals dehydration leads to lattice perturbations that preserve the space-group symmetry and overall packing arrangement, but cause unit-cell non-isomorphism. In their experiments, the changes in the lattice were likewise coincident with changes in protein conformation and/or flexibility, as judged by changes in TLS parameters and by the shift of a specific sodium-binding loop that could be modeled from the electron density (Harata & Akiba, 2004 ▸, 2006 ▸).
Characterization of conformational heterogeneity and overcoming long-range disorder in crystals are both significant, yet seemingly disparate, challenges in protein crystallography. The work that we present here, however, suggests that these two issues may be intertwined and can be addressed simultaneously for favorable cases in which perturbations to the crystal lattice are coupled to conformational rearrangements. In such cases, a particular conformational rearrangement may be restricted by crystal-packing constraints imposed by a given unit cell, and therefore only possible when accompanied by changes to the lattice. Our study leaves open the question of what behavior might be revealed by similar experiments conducted at room temperature rather than under cryogenic conditions. In the present study clear non-isomorphism was detected, but only minor protein structural variations were evident. Further studies of other systems could reveal more dramatic cases of structural heterogeneity within crystals, or cases where the unit cell remains roughly isomorphous throughout the crystal, but where local regions of molecular structure might nonetheless exhibit conformational differences. Even where major conformational differences are absent, circumventing non-isomorphism problems lowers errors in structure-factor measurements, and clustering data sets could provide a valuable means for identifying systematic errors (Diederichs, 2017 ▸). The general importance of redundancy in data collection is increasingly being recognized, and serial crystallography experiments are becoming routine (Mueller et al., 2012 ▸; Assmann et al., 2016 ▸; Dods et al., 2017 ▸; Weinert et al., 2017 ▸; Mathews et al., 2017 ▸; Standfuss & Spence, 2017 ▸), but averaging measurements of potentially non-equivalent physical entities (for example structure factors from different regions of a crystal) may be detrimental. The improvement in data quality that can be gained by clustering multiple related data sets into isomorphous groups during data reduction has been explored previously in several contexts (Liu et al., 2011 ▸; Giordano et al., 2012 ▸; Foadi et al., 2013 ▸; Zander et al., 2016 ▸; Assmann et al., 2016 ▸; Diederichs, 2017 ▸; Yamamoto et al., 2017 ▸), although previous work has generally focused on non-isomorphism resulting from changes to crystal-packing interactions, rather than emphasizing the potential to use this feature of protein crystals as a means to explore conformational heterogeneity. With continuing advances in the throughput of traditional data collection (Svensson et al., 2017 ▸; Broecker et al., 2018 ▸) and in serial crystallography (Standfuss & Spence, 2017 ▸), there is a growing opportunity to parse conformational space by carefully analyzing large quantities of diffraction data. In this regard, serial crystallography experiments may hold great potential, as they typically involve measuring diffraction snapshots from thousands of unique crystals.
Our work here parallels other recent studies analyzing multiple X-ray diffraction data sets in search of alternative protein conformations. One example is the experiment conducted by Horrell and coworkers, who used a ‘multiple structures one crystal’ (MSOX) experiment to collect a series of X-ray data sets sequentially from the same crystal volume following X-ray-induced reduction of a metalloenzyme (Horrell et al., 2016 ▸). This MSOX approach explores changes over time while assuming spatial homogeneity, and in that sense is orthogonal to our work, which exploits spatial heterogeneity rather than time-dependent heterogeneity to identify alternative protein conformations. Another example is the work of Moffat and coworkers, who have analyzed various types of ‘dynamic crystallography’ experiments and identified different structural states by performing singular value decomposition on sets of electron-density maps derived from different crystal specimens or individual specimens under different conditions (Schmidt et al., 2003 ▸; Rajagopal, Kostov et al., 2004 ▸; Rajagopal, Schmidt et al., 2004 ▸; Ren et al., 2013 ▸). These methods are particularly elegant for analyzing experiments in which a specific electromagnetic or chemical perturbation has been introduced. These analyses have generally been applied as comparisons in real space (i.e. between electron-density maps); such point-by-point comparisons between density maps effectively imply unit-cell isomorphism across specimens and data sets. Our work takes a different approach, both by analyzing different parts of a single crystal and by performing analyses in reciprocal space to enable early consideration of non-isomorphism. The results presented here emphasize that in addition to offering important possibilities for improving structure-factor data quality in a range of experimental scenarios, algebraic clustering of related data sets according to their reciprocal-space similarity can be a powerful tool for elucidating the details of protein conformational heterogeneity.
Supplementary Material
PDB reference: EutL, 4tlh
PDB reference: 6arc
PDB reference: 6ard
Acknowledgments
The authors thank Dr Michael Sawaya for a critical reading of the manuscript, as well as Dr James Holton, Dr Malcom Capel, Dr Kanagalaghatta Rajashankar and Dr Jon Schuermann for information related to X-ray dose calculations.
Funding Statement
This work was funded by U.S. Department of Energy, Office of Science grant DE-FC03-02ER63421. W. M. Keck Foundation grant 2843398.
References
- Adams, P. D. et al. (2010). Acta Cryst. D66, 213–221.
- Afonine, P. V., Grosse-Kunstleve, R. W., Echols, N., Headd, J. J., Moriarty, N. W., Mustyakimov, M., Terwilliger, T. C., Urzhumtsev, A., Zwart, P. H. & Adams, P. D. (2012). Acta Cryst. D68, 352–367. [DOI] [PMC free article] [PubMed]
- Assmann, G., Brehm, W. & Diederichs, K. (2016). J. Appl. Cryst. 49, 1021–1028. [DOI] [PMC free article] [PubMed]
- Bakan, A., Dutta, A., Mao, W., Liu, Y., Chennubhotla, C., Lezon, T. R. & Bahar, I. (2014). Bioinformatics, 30, 2681–2683. [DOI] [PMC free article] [PubMed]
- Bakan, A., Meireles, L. M. & Bahar, I. (2011). Bioinformatics, 27, 1575–1577. [DOI] [PMC free article] [PubMed]
- Bedem, H. van den, Dhanik, A., Latombe, J.-C. & Deacon, A. M. (2009). Acta Cryst. D65, 1107–1117. [DOI] [PMC free article] [PubMed]
- Bedem, H. van den & Fraser, J. S. (2015). Nature Methods, 12, 307–318. [DOI] [PMC free article] [PubMed]
- Berman, H. M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T. N., Weissig, H., Shindyalov, I. N. & Bourne, P. E. (2000). Nucleic Acids Res. 28, 235–242. [DOI] [PMC free article] [PubMed]
- Brehm, W. & Diederichs, K. (2014). Acta Cryst. D70, 101–109. [DOI] [PubMed]
- Broecker, J., Morizumi, T., Ou, W.-L., Klingel, V., Kuo, A., Kissick, D. J., Ishchenko, A., Lee, M.-Y., Xu, S., Makarov, O., Cherezov, V., Ogata, C. M. & Ernst, O. P. (2018). Nature Protoc. 13, 260–292. [DOI] [PubMed]
- Diederichs, K. (2017). Acta Cryst. D73, 286–293. [DOI] [PMC free article] [PubMed]
- Dods, R. et al. (2017). Structure, 25, 1461–1468. [DOI] [PubMed]
- Emsley, P., Lohkamp, B., Scott, W. G. & Cowtan, K. (2010). Acta Cryst. D66, 486–501. [DOI] [PMC free article] [PubMed]
- Fanning, S. W. et al. (2016). Elife, 5, e12792.
- Fersht, A. (1998). Structure and Mechanism in Protein Science: A Guide to Enzyme Catalysis and Protein Folding. New York: W. H. Freeman & Co.
- Fieulaine, S., Boularot, A., Artaud, I., Desmadril, M., Dardel, F., Meinnel, T. & Giglione, C. (2011). PLoS Biol. 9, e1001066. [DOI] [PMC free article] [PubMed]
- Foadi, J., Aller, P., Alguel, Y., Cameron, A., Axford, D., Owen, R. L., Armour, W., Waterman, D. G., Iwata, S. & Evans, G. (2013). Acta Cryst. D69, 1617–1632. [DOI] [PMC free article] [PubMed]
- Fraser, J. S., van den Bedem, H., Samelson, A. J., Lang, P. T., Holton, J. M., Echols, N. & Alber, T. (2011). Proc. Natl Acad. Sci. USA, 108, 16247–16252. [DOI] [PMC free article] [PubMed]
- Frauenfelder, H., Sligar, S. G. & Wolynes, P. G. (1991). Science, 254, 1598–1603. [DOI] [PubMed]
- Giordano, R., Leal, R. M. F., Bourenkov, G. P., McSweeney, S. & Popov, A. N. (2012). Acta Cryst. D68, 649–658. [DOI] [PubMed]
- Harata, K. & Akiba, T. (2004). Acta Cryst. D60, 630–637. [DOI] [PubMed]
- Harata, K. & Akiba, T. (2006). Acta Cryst. D62, 375–382. [DOI] [PubMed]
- Hilser, V. J., García-Moreno, E. B., Oas, T. G., Kapp, G. & Whitten, S. T. (2006). Chem. Rev. 106, 1545–1558. [DOI] [PubMed]
- Holton, J. M. (2009). J. Synchrotron Rad. 16, 133–142.
- Horrell, S., Antonyuk, S. V., Eady, R. R., Hasnain, S. S., Hough, M. A. & Strange, R. W. (2016). IUCrJ, 3, 271–281. [DOI] [PMC free article] [PubMed]
- Jorda, J., Liu, Y., Bobik, T. A. & Yeates, T. O. (2015). PLOS Comput. Biol. 11, e1004067. [DOI] [PMC free article] [PubMed]
- Kabsch, W. (2010). Acta Cryst. D66, 125–132. [DOI] [PMC free article] [PubMed]
- Karplus, M. & Kuriyan, J. (2005). Proc. Natl Acad. Sci. USA, 102, 6679–6685. [DOI] [PMC free article] [PubMed]
- Keedy, D. A., Fraser, J. S. & van den Bedem, H. (2015). PLOS Comput. Biol. 11, e1004507. [DOI] [PMC free article] [PubMed]
- Koshland, D. E. Jr (1998). Nature Med. 4, 1112–1114. [DOI] [PubMed]
- Lang, P. T., Holton, J. M., Fraser, J. S. & Alber, T. (2014). Proc. Natl Acad. Sci. USA, 111, 237–242.
- Lang, P. T., Ng, H.-L., Fraser, J. S., Corn, J. E., Echols, N., Sales, M., Holton, J. M. & Alber, T. (2010). Protein Sci. 19, 1420–1431. [DOI] [PMC free article] [PubMed]
- Liu, Q., Zhang, Z. & Hendrickson, W. A. (2011). Acta Cryst. D67, 45–59. [DOI] [PMC free article] [PubMed]
- Mathews, I. I., Allison, K., Robbins, T., Lyubimov, A. Y., Uervirojnangkoorn, M., Brunger, A. T., Khosla, C., DeMirci, H., McPhillips, S. E., Hollenbeck, M., Soltis, M. & Cohen, A. E. (2017). Biochemistry, 56, 4751–4756. [DOI] [PMC free article] [PubMed]
- Moffat, K. & Henderson, R. (1995). Curr. Opin. Struct. Biol. 5, 656–663. [DOI] [PubMed]
- Mueller, M., Wang, M. & Schulze-Briese, C. (2012). Acta Cryst. D68, 42–56. [DOI] [PMC free article] [PubMed]
- Nolen, B., Taylor, S. & Ghosh, G. (2004). Mol. Cell, 15, 661–675. [DOI] [PubMed]
- Otwinowski, Z. & Minor, W. (1997). Methods Enzymol. 276, 307–326. [DOI] [PubMed]
- Owen, R. L., Rudiño-Piñera, E. & Garman, E. F. (2006). Proc. Natl Acad. Sci. USA, 103, 4912–4917. [DOI] [PMC free article] [PubMed]
- Pang, A., Liang, M., Prentice, M. B. & Pickersgill, R. W. (2012). Acta Cryst. D68, 1642–1652. [DOI] [PubMed]
- Rajagopal, S., Kostov, K. S. & Moffat, K. (2004). J. Struct. Biol. 147, 211–222. [DOI] [PubMed]
- Rajagopal, S., Schmidt, M., Anderson, S., Ihee, H. & Moffat, K. (2004). Acta Cryst. D60, 860–871. [DOI] [PubMed]
- Ren, Z., Chan, P. W. Y., Moffat, K., Pai, E. F., Royer, W. E., Šrajer, V. & Yang, X. (2013). Acta Cryst. D69, 946–959. [DOI] [PMC free article] [PubMed]
- Schlichting, I. & Chu, K. (2000). Curr. Opin. Struct. Biol. 10, 744–752. [DOI] [PubMed]
- Schmidt, M., Rajagopal, S., Ren, Z. & Moffat, K. (2003). Biophys. J. 84, 2112–2129. [DOI] [PMC free article] [PubMed]
- Schultz-Heienbrok, R., Maier, T. & Sträter, N. (2004). Protein Sci. 13, 1811–1822. [DOI] [PMC free article] [PubMed]
- Śliwiak, J., Dolot, R., Michalska, K., Szpotkowski, K., Bujacz, G., Sikorski, M. & Jaskolski, M. (2016). J. Struct. Biol. 193, 55–66. [DOI] [PubMed]
- Standfuss, J. & Spence, J. (2017). IUCrJ, 4, 100–101. [DOI] [PMC free article] [PubMed]
- Svensson, O., Gilski, M., Nurizzo, D. & Bowler, M. W. (2017). BioRxiv, 236596.
- Tanaka, S., Sawaya, M. R. & Yeates, T. O. (2010). Science, 327, 81–84. [DOI] [PubMed]
- Thompson, M. C., Cascio, D., Leibly, D. J. & Yeates, T. O. (2015). Protein Sci. 24, 956–975. [DOI] [PMC free article] [PubMed]
- Thompson, M. C., Crowley, C. S., Kopstein, J., Bobik, T. A. & Yeates, T. O. (2014). Acta Cryst. F70, 1584–1590. [DOI] [PMC free article] [PubMed]
- Tiwari, S. P., Fuglebakk, E., Hollup, S. M., Skjærven, L., Cragnolini, T., Grindhaug, S. H., Tekle, K. M. & Reuter, N. (2014). BMC Bioinformatics, 15, 427. [DOI] [PMC free article] [PubMed]
- Weinert, T. et al. (2017). Nature Commun. 8, 542. [DOI] [PMC free article] [PubMed]
- Yamamoto, M., Hirata, K., Yamashita, K., Hasegawa, K., Ueno, G., Ago, H. & Kumasaka, T. (2017). IUCrJ, 4, 529–539. [DOI] [PMC free article] [PubMed]
- Zander, U., Cianci, M., Foos, N., Silva, C. S., Mazzei, L., Zubieta, C., de Maria, A. & Nanao, M. H. (2016). Acta Cryst. D72, 1026–1035. [DOI] [PMC free article] [PubMed]
- Zeldin, O. B., Gerstel, M. & Garman, E. F. (2013). J. Appl. Cryst. 46, 1225–1230.
- Zimmermann, I., Egloff, P., Hutter, C., Stohler, P., Bocquet, N., Hug, M., Siegrist, M., Svacha, L., Gera, J., Gmuer, S., Spies, P., Gygax, D., Geertsma, E. R., Dawson, R. J. P. & Seeger, M. A. (2017). BioRxiv, https://doi.org/10.1101/168559.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
PDB reference: EutL, 4tlh
PDB reference: 6arc
PDB reference: 6ard