Polaritons reach the quantum limit, providing a new and promising platform of strongly coherent and interacting particles.
Abstract
Polaritons are quasi-particles that originate from the coupling of light with matter and that demonstrate quantum phenomena at the many-particle mesoscopic level, such as Bose-Einstein condensation and superfluidity. A highly sought and long-time missing feature of polaritons is a genuine quantum manifestation of their dynamics at the single-particle level. Although they are conceptually perceived as entangled states and theoretical proposals abound for an explicit manifestation of their single-particle properties, so far their behavior has remained fully accounted for by classical and mean-field theories. We report the first experimental demonstration of a genuinely quantum state of the microcavity polariton field, by swapping a photon for a polariton in a two-photon entangled state generated by parametric downconversion. When bringing this single-polariton quantum state in contact with a polariton condensate, we observe a disentangling with the external photon. This manifestation of a polariton quantum state involving a single quantum unlocks new possibilities for quantum information processing with interacting bosons.
INTRODUCTION
Light would be the perfect component for future quantum information processing devices if not for its too-feeble interaction (1). A remedy is to rely on hybrid systems that involve a matter component, bringing in strong interactions (2, 3). In the regime of strong coupling that binds together light and matter, the resulting polaritons appear as candidates of choice to deliver the strongly interacting photons required in tomorrow’s quantum technology (4), and researchers have recently demonstrated a photon-photon gate relying on these ideas a single atom in a cavity (5–7). At a theoretical level, the polariton is itself an entangled superposition of light with a dipole-carrying medium, of the form |U/L〉 = α|0a1b〉 ± β|1a0b〉, with |1a〉 a photon and, depending on the system, |1b〉 a phonon, a plasmon, an exciton, or even a full atom. The exciton-polariton, which lives in semiconductors (8), has already shown itself to be on par with cold atom physics, with reports that include Bose-Einstein condensation (9), superfluidity (10, 11) [up to room temperature (12)], topological physics (13), and an ever-growing list of other exotic quantum macroscopic phases (14). This two-dimensional (2D) quasi-particle combines as it propagates the antagonist properties of light (lightweight and highly coherent) and matter (heavy and strongly interacting) (15). It also holds great promise for the future of classical technology because it could allow the shift from electronic to optical devices (16) and the emergence of the future generation of lasers (17, 18). Given their ease of control in 2D geometries in scalable and versatile semiconductor platforms, one of the major prospects of exciton-polaritons is to power quantum-based technologies, as particles akin to photons but with much stronger nonlinearities.
However, even in configurations that are expected to provide strong quantum correlations (19), exciton-polaritons have so far remained obstinately classically correlated. However useful their description as a quantum superposition of excitons and photons, with α and β complex probability amplitudes, the actual state typically realized in the laboratory is instead a thermal or coherent distribution of these particles that yield, in the case of coherent excitation, product states |α〉a|β〉b (20). The variables α and β obey the same equations of motion and evolve identically to quantum probability amplitudes, but they describe instead classical amplitudes of coherent fields for the photon (a) and exciton (b), with no trace of purely quantum effect such as entanglement or nonlocality. This does not invalidate the interest in and importance of reaching the genuinely quantum-correlated regime of polaritons (from now on, we will use polariton for exciton-polariton) (21–23). Following decades of sustained efforts in this direction, the state of the art is the recently reported unambiguous squeezing of the polariton field (24). This remains, however, a weak demonstration of nonclassicality (a classical field can be squeezed in all its directions). What is instead required for a full exploitation of quantum properties is a stronger class CQ of quantum states that are nonconvex mixtures of Gaussian states, that is, akin to Fock states and suitable for performing full quantum information processing (25).
The polariton blockade (26) that relies on nonlinearities to produce antibunching has, so far, remained unsuccessful. Much hope was rekindled by the unconventional polariton blockade (27, 28) based on destructive interference of the paths leading to two-excitation states, predicting much stronger antibunching in theoretical calculations (29), although not in the sought class CQ (30). The race for quantum polaritonics is, thus, still in its starting blocks, and several questions remain pending to justify polaritons as strong contenders for quantum information processing. One of the main uncertainties is whether polaritons are robust against pure dephasing. Because they are partly composed of interacting particles—excitons—they could be strongly affected by the environment in a way that is harmful for their quantum coherence. Furthermore, even assuming that one could generate a polariton qubit, another desirable quality of polaritons remains to be established: Can interactions with other polaritons substantially affect a single polariton? This would allow the use of flying polaritons to build nonlinear quantum gates in complex patterned circuits (31).
RESULTS AND DISCUSSION
Exciting with quantum light
We answer these two outstanding questions in the affirmative: Can polaritons break the classical barrier and do interactions affect their quantum state? We do so by turning to a new paradigm for creating quantum polaritons. Instead of realizing a quantum state from within, for example, on the basis of its strong nonlinearities, we imprint it from outside (32). The resonant excitation by a classical field that drives the harmonic part of the polariton (the cavity) used in most experiments so far is the main reason why polaritons are hampered in reaching the quantum regime (33). Because photonics is, so far, leading in the generation, transfer, and manipulation of quantum states and because photons couple well to polaritons, this opens an opportunity to realize and explore quantum effects with polaritons. To ensure the quantum nature of the polariton field, we use entangled photon pairs: One photon goes to the microcavity, and the other is later used to check that quantum correlations are still present and, therefore, have been transferred to the polaritons. The source of entangled photon pairs is a continuous wave (cw) laser at λ = 405 nm, downconverted from a periodically poled KTP crystal (PPKTP) (34) to generate pairs of photons with a bandwidth narrow enough to couple to our microcavity. The latter is described in Materials and Methods. The PPKTP is introduced inside a Sagnac interferometer (see sketch in Fig. 1) (34) that allows us to create polarization-entangled photons in a state of the form , where |H〉 stands for a horizontally polarized photon and |V〉 stands for a vertically polarized one. The phase can be controlled to create a Bell state by placing a liquid crystal in one arm of the interferometer, at the end of which a pair of nondegenerate polarization-entangled photons is emitted in different directions: the idler at the wavelength of the polariton resonances (λ ~ 830 nm) and the signal at higher energies (λ ~ 790 nm). The high-energy photon is then directed to a standard polarization tomography stage, consisting of a quarter waveplate (QWP) followed by a half waveplate (HWP), a polarizing beamsplitter (PBS), and an avalanche photodetector (APD). We instead direct the low-energy photon toward the microcavity, where it excites a single polariton; it is stored there until its eventual re-emission, where it is retrieved and finally directed to a second tomography stage, similar to the one for the first photon. We used a homemade coincidence unit to measure the coincidence counts from the two APDs in 4-ns windows. By taking these measurements for all the combinations of polarizations on each detector (that makes 6 × 6 possibilities for the three polarization bases: circular, vertical, and diagonal) (35), we are able to determine whether the photon that transformed into a polariton and back retained the nonlocal quantum correlations of a Bell state. If this is the case, then this proves that the polariton state that inherited and later passed on this information was itself in a genuine one-particle quantum state and was furthermore entangled with the external photon propagating on the other side of the setup. Namely, we have created the state , where pH and pV are the boson annihilation operators for the horizontally and vertically polarized polaritons and aH and aV for the signal photon. Although this could be expected from a standard linear theory of light propagating through resonant dielectrics, the failure of polaritons to demonstrate other expected quantum correlations, such as in optical parametric oscillator scattering, shows that it is not obvious whether polaritons are proper carriers of quantum features. In particular, their composite nature and large exciton component could lead to fast decoherence (for example, via phonon scattering). The spectral shape of the idler state is shown in Fig. 2A. Using single-mode laser excitation of the PPKTP crystal, the bandwidth of the entangled photon pairs is reduced to 0.46 nm, which is only 35% wider than the polariton state. Using temperature tuning on the nonlinear crystal, we could move the idler resonance from 825 to 831 nm. To check that the entangled idler is transferred into the polariton state and not merely passing through the cavity mode, we performed transmission measurements while scanning the energy of the idler from below the lower polariton branch (LPB) to above the upper polariton branch (UPB). In Fig. 2B, the effect of the microcavity on the idler state shows that no light is transmitted when the idler is out of resonance with the polaritons. This means that every photon that passes through the sample has been converted into a polariton. If this were not the case, then we would have observed a finite signal at the cavity mode (between the LPB and UPB) which is completely absent even in logarithmic scale.
Fig. 1. Scheme and principle of the experiment.
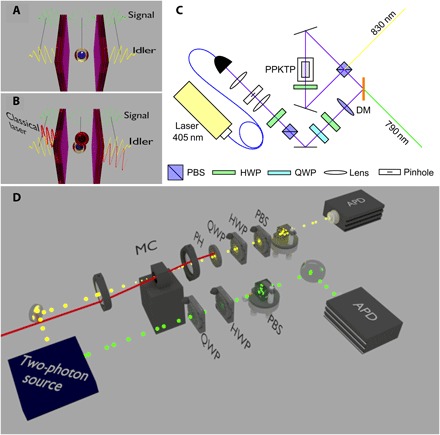
(A) Linear regime: A single photon (yellow, idler) gets into the microcavity, where it becomes a polariton, which is later reconverted into an external photon. When this photon is entangled with another (green, signal), we show that the entanglement is preserved throughout. (B) Interacting regime: A single photon (yellow, idler) enters the microcavity along with photons from a classical laser (red). The polaritons in the microcavity interact. This affects the entanglement of the single polariton in a way that allows measurement of the polariton-polariton interaction. (C) Sketch of the Sagnac interferometric source. DM, dichronic mirror. (D) Sketch of the setup implementing these configurations. PH, pinhole.
Fig. 2. Photon-polariton conversion.
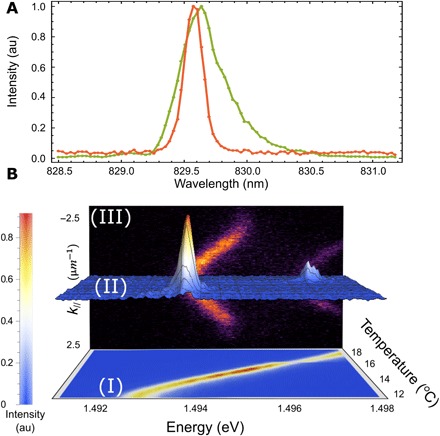
(A) Green, normalized emission of the PPKTP crystal; orange, normalized transmission of the emission of the PPKTP crystal through the LPB. au, arbitrary units. (B) Changes on the resonance as a function of the temperature of the two-photon source. I, 2D map of the emission of the crystal outside of the microcavity. II, Transmitted intensity as a function of the energy as the temperature varies. Two peaks can be identified that correspond to the resonances with one of the two polariton branches. The color bar corresponds to both I and II. III, Far field of the emission under noncoherent pumping.
Measuring the entanglement and nonlocality
For a bipartite system such as our photon pair, we can quantify entanglement through the concurrence, as defined in Materials and Methods, which is zero for classically correlated or uncorrelated states and gets closer to one the higher the quantum entanglement. To study the transfer of entanglement into the polariton field, we compare the concurrence of the two photons without the microcavity (corresponding to the maximally entangled state) to that in which the photon is emitted by the microcavity after the idler photon has been converted into a polariton of the LPB with zero momentum (kp = 0). As can be seen in Fig. 3, the concurrence diminishes from 0.826 in the case of two freely propagating photons to 0.806 when one of the photons is converted into a polariton. The maximum concurrence of the PPKTP source is limited to 0.826 because the entangled state could not be optimized at the operation wavelengths needed to interface photons with polaritons. Nevertheless, the concurrence is large and remains so when the photon passes through the microcavity. This result is proof that we have generated a single polariton within the microcavity and that it existed there as a quantum state with no classical counterpart. If the single photon were lost in the polariton thermal noise or coupled to a collection of other polariton states, then we would observe no entanglement. The transfer of the photon to and from a polariton state conserves the original degree of entanglement almost entirely. This result is encouraging for a future exploitation of quantum polaritonics.
Fig. 3. Tomography measured between the signal and idler photons.
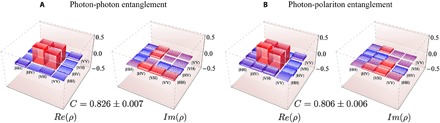
The signal is sent directly toward the detector, whereas the idler photon becomes a polariton when entering the sample. (A) Real (Re; left) and imaginary (Im; right) components of the density matrix for the source of photon pairs without the sample. The concurrence is not one because the operation wavelength is not optimal for the source. (B) Real (left) and imaginary (right) components of the density matrix when passing through the microcavity. The concurrence of 0.806 shows that polaritons retain the entanglement.
Beyond the preservation of concurrence, we also demonstrated the nonlocality between the signal photon and the polariton created by the idler photon. We did so by probing the classical Clauser-Horne-Shimony-Holt (CHSH) inequality (36) S ≤ 2 where
| (1) |
with
| (2) |
a function of the coincident counts Cpq(x, y) between the two measurement ports of our tomography setup for the photons with polarization p, q ∈ {−,+} in the bases x = a, a′ and y = b, b′, where , , b = 0, and are the combinations of polarization angles that maximize the Bell’s inequality violation. This can be obtained by rotating the tomography HWPs in a/2, a′/2, b/2, and b′/2. Figure 4 shows the measured Bell curves, which show the photon coincidences associated with these bipartite polarization measurements, along with the continuous correlated oscillations predicted by the theory. In the optimum configuration, we obtain a value of S = 2.463 ± 0.007, which unambiguously violates the CHSH inequality and proves the nonlocal character of the photon-polariton system.
Fig. 4. Coincidences between the external photons and the polaritons as a function of the polarization.
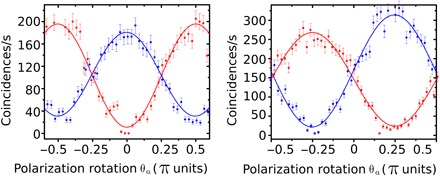
Left, Bell curves for a polarization angle b = 0. Right, Bell curves for b = − π/4. Red squares and blue circles denote the ++ and +− coincidences, respectively.
The above experimental results demonstrate that, although polaritons are quasi-particles in a solid-state system with complex and yet-to-be-fully-characterized interactions with their matrix and other polaritons (37), they can be used as quantum bits which maintain their quantum state almost unvaried and can transfer it back and forth to an external photon. In particular, this shows that several effects, such as pure dephasing, coupling to phonons, radiative lifetime, etc., are not detrimental to quantum coherence.
Nonlinearity at the single polariton level
To answer the second important question on the possibility of affecting and ultimately controlling the quantum state that we have created, we need to go into the nonlinear regime and study the effect of polariton interactions. To observe these nonlinearities within our available equipment, we repeat the experiment in a non–polariton-vacuum configuration. Namely, instead of exciting the sample with one photon of the PPKTP source only, we add the excitation of a classical laser, which is the most common way to excite a microcavity (see sketch in Fig. 1). In this case, the entangled photon is sent on resonance with the UPB and the classical laser with the LPB. We have chosen this configuration to avert the effects of relaxation of the classical source into lower energy states while, at the same time, keeping the quantum state clearly distinguishable from the other polaritons. Note, however, that polariton-phonon interaction and Auger processes, although minimized at low temperature and low power of excitation, cannot be completely avoided.
The classical pumping power changes from having only the vacuum state up to an average estimated at 380 polaritons at any given time, with a density still below 1 polariton/μm2. The calibration of the population is explained in Materials and Methods. In the conditions of our experiment, the full interacting polariton Hamiltonian can be reduced to the simple form (see the Supplementary Material)
| (3) |
where qσ are quantized operators for the upper polariton at k = 0 with polarization σ = ↑, ↓ and the lower polariton condensate has been absorbed in the coefficients through a mean-field approximation for the coherent state |α↑/↓〉 with polarization ↑/↓
| (4a) |
| (4b) |
where and ω0 are constants linked to the Hopfield coefficients that arise due to the geometry of the experiment (see the Supplementary Materials) and V(1,2) corresponding to same (1) or opposite (2) spin polariton-polariton interactions. The nonlinear crystal emits pairs of polarization-entangled photons of the form
| (5) |
where cξ is the quantum operator for the signal photon that goes straight to the detector. The qξ photon becomes a polariton and evolves according to the Hamiltonian (3). Even for the free propagation , the possible asymmetry for the ξ = H and V polarizations results in different phase shifts, which alter the wave function as a whole. The rightmost term in Eq. 3, on the other hand, results in a change of the state of polarization. By analyzing the quantum correlations between the signal and idler after passing through the cavity, one can thus gain information on the microscopic parameters ω↑/↓ and g↑↓.
Loss of concurrence
At the level of the concurrence, our observation demonstrates a decay with increasing polariton density (after increasing laser pumping), as shown in Fig. 5 (data points). Although the evolution of the wave function is expected, the loss of concurrence seems to suggest a decoherence of the single polariton when affected by interactions with the condensate. The loss of concurrence is due to several factors: The presence of the condensate in the LPB induces a coupling between the upper polaritons with opposite spins, which breaks the quantum superposition into a (disentangled) product state. Furthermore, because the lower polariton condensate has Poissonian fluctuations (38), each pair of entangled photons sees the microcavity in an instantaneous different state in which their wave function evolves in a different way. Averaging over many of these individual realizations, the entanglement, as measured through the signal/idler correlations in polarization, is spoiled, and the state of the pair of entangled photons becomes mixed. Implementing these effects in the model allows us to convert our experimental findings into a theoretical pattern that corresponds to them very closely (solid blue line). It is assumed for the model that the quantum state of the LPB is in a coherent state at a finite k of the single-mode ground state of the system, with a finite extension in a space of A = 706 μm2, imposed by the laser, whereas the spot in which the single photon impinges on the sample has a radius three times smaller. Furthermore, the time that each polariton stays inside the cavity is assumed to follow a Poisson distribution with a mean value of 3 ps. In addition to these factors that spoil the concurrence due to polariton interactions, we should also take into account effects from the condensate that would likewise spoil the concurrence for noninteracting polaritons. There is a complex redistribution of polaritons on their branch and scattering from the condensate to the state to which the single photon arrives, which are also detrimental to the concurrence regardless of the interaction strengths. However, as shown in the Supplementary Materials, the noise induced by the scattered polaritons is small enough to allow us to resolve the effect of interactions. With these conditions, we fit the observation with a same-spin interaction between excitons of V(1) = 73.9 μeV·μm2 and with opposite spin of V(2) = −0.1V(1), which, although larger than the estimate given by microscopic theories (39), are consistent with other recent observations (40) that attribute these high values to the presence of an exciton reservoir. This reservoir undoubtedly could be excited by thermal processes and Auger effects that, in addition to the background noise, would also be detrimental to the concurrence. Although the magnitude of this interaction remains to be confirmed and further studied, our calculation shows that the wave function of a single-polariton Fock state is affected by its interactions with the condensate in the LPB, albeit in a random way as ruled by fluctuations currently beyond our control.
Fig. 5. Concurrence between the external photons and the polaritons as a function of the power of the classical laser impinging onto the sample.
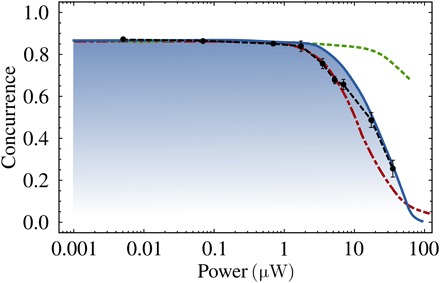
Each data point (black bullet) is obtained from the 36 measurements of coincidences in all the combinations of polarization (the dotted line serves as a guide). The solid blue line is a theoretical simulation of a model of fluctuating polarized lower polaritons that interact with the single upper polariton injected by the quantum source with an interaction strength of 0.9% of the radiative broadening, which is in quantitative agreement with the observation. The dashed-dotted red line shows the theoretical simulation of a model of a condensate assuming thermal fluctuations, which gives the worst fit for the experimental observation and suggests that, as expected, the condensate has Poissonian fluctuations. The dashed green line shows the loss of concurrence without polariton interactions, due only to the polaritons scattered to the state at which the single photon arrives (cf. Supplementary Material), confirming that the amount of noise in the experiment is small enough to observe the effects of interactions on a single polariton.
Quantum spectroscopy
This technique of excitation by quantum light provides new methods of gaining information on the condensate itself, methods able to affect quantum correlations of two particles in a measurable way without producing any sizable output in single-photon observables such as luminescence. For instance, one can go further in characterizing the underlying Hamiltonian by mapping its effect on all possible polarized qubit states—that is, how it transforms the Poincaré sphere. When in possession of entangled states, as in our case, this can be achieved with a single input state only, thanks to a technique (further detailed in Materials and Methods) known as ancilla-assisted quantum process tomography (AAQPT) (41). In essence, the sphere rotates under unitary transformation and shrinks under the effect of decoherence. Our joint experimental/theoretical analysis, as presented in Fig. 6, shows that the sphere does not rotate, although it experiences some wobbling until, with greater pumping, it shrinks into a spindle. The experimental tomography is a direct postprocessing of the data. The theory applies the same procedure to input states (5) undergoing the evolution of Hamiltonian (3). We find that the shrinking into a spindle, also due to the fluctuating condensate that causes the loss of concurrence, can be obtained with no rotation of the sphere with increasing pumping when ω↑ − ω↓ and g↑↓ remain constant on average. In these conditions, both polarization states at the extremities of the spindle have a constant energy shift, and there is no admixture of polarization. This results in decohering all polarization states except for the eigenstates ↑, ↓, while not producing a unitary rotation.
Fig. 6. Ancilla-assisted quantum process tomography.
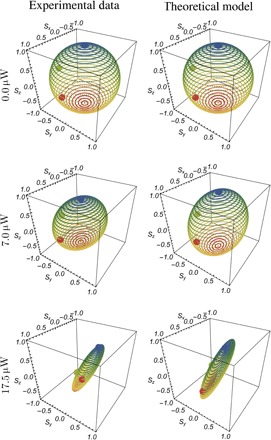
Our technique allows us to observe the effect of the lower polariton condensate on the polarization of an upper polariton qubit, as a function of increasing pumping (left column). The shrinking of the Poincaré sphere into a spindle confirms that the qubit is affected by its interaction with the lower condensate, whose fluctuations lead to an effective decoherence when averaging. The theoretical model leads to agreement with the observed phenomenology (right column) and points towards future methods for characterizing also the condensate itself.
CONCLUSIONS
In conclusion, we have observed and confirmed a genuinely quantum state of the polariton field, able to interact with other polaritons. Our experiments also bring an implementation of quantum spectroscopy to semiconductors (32, 42–44) by using quantum-correlated light to access phenomena and information out of reach with a classical laser, as illustrated by our estimation of interactions in the presence of a polariton condensate. Further and systematic investigations using these techniques will allow placements of stricter boundaries around the strengths that we have reported and clarify the nature of the strongly correlated gas that is formed at high densities. Our current results have obvious implications for the design and implementation of a new generation of quantum gates, routing interacting polaritons in predetermined landscapes. Polaritons thus appear to be the precursors of the long-sought strongly interacting photons needed for the realization of scalable and efficient quantum computers.
MATERIALS AND METHODS
Theoretical model
The theory models the experiment by feeding Hamiltonian (3) (see the Supplementary Materials for its derivation from the full polariton Hamiltonian) with the initial state in Eq. 5 and acquiring statistics over repetitions of this scenario with coefficients (4) fluctuating with Poissonian distributions with a mean |α↑↓|2, modeling a polariton condensate beyond mean field. The entanglement for bipartite systems can be quantified unambiguously with the concurrence, which extracts the number of nonclassical correlations from the density matrix
| (6) |
where N is a constant put here so that Tr(ρ) = 1 and, for example, VHHV stands for
| (7) |
where the states |ψj〉 are those computed from the fluctuating Hamiltonian, as explained in the Supplementary Materials. This corresponds to the experimental configuration where every element of the density matrix is reconstructed through a tomographic process that requires up to 36 measurements detecting every possible combination of polarization. From the density matrix in Eq. 6, we computed the concurrence as C[ρ] ≡ max(0, λ1 − λ2 − λ3 − λ4), where the λi are the eigenvalues in decreasing order of the matrix . Here, and σy is a Pauli spin matrix.
The AAQPT characterizes the action of an unknown map (black box) acting on one of two entangled qubits, by using only one input and one output state to recreate the associated map. This is thanks to the intrinsic correlations of the bipartite state that dispense with the need to consider the transformation of a large collection of input states. Because any qubit |ψ〉 encoded in the polarization degree of freedom has a Stokes decomposition of its associated density matrix , where is the Stokes vector and is the vector of Pauli matrices (35), AAQPT allows one to obtain the black box (the microcavity with a lower polariton condensate in our case) map χ from the expression , where and are the Stokes parameterization of the state of the single photon before and after it goes through the cavity, respectively. The numerical calculation of χ is obtained by the linear decomposition χ = (A−1B)T, with A and B obtained from the state of the pair of entangled photons before and after one of the photons has gone though the cavity and defined as Ai,j = Tr[(σi ⊗ σj)ρout] and Bi,j = Tr[(σi ⊗ σj)ρin]. In the experiment, where errors and noise could lead to a nonphysical result, the map is best estimated by a maximum likelihood process over χ. This technique minimizes the statistical dispersion of the expectation values between χraw and its trace-preserving and completely positive version χphysical. An intuitive representation of the map χ that facilitates its interpretation is given through the Poincaré sphere, where any qubit is mapped as a point on the surface, using (r1, r2, r3) as (x, y, z) coordinates (Fig. 6). There, r0 represents the intensity of the field, r1 is the degree of linear polarization, r2 is that of diagonal polarization, and r3 is that of circular polarization.
Sample and setup
The microcavity sample was composed of front and back distributed Bragg reflectors with 20 pairs each, confining light, and one In0.05Ga0.95As quantum well (QW), confining excitons. The QW was placed at the antinode of the cavity to maximize their interaction and enter the strong-coupling regime (45). The experiment consisted of four different parts: photon generation, signal-photon tomography stage, polariton source, and polariton tomography stage. The first part consisted of a Sagnac interferometer excited with a single-mode diode laser at 405 nm, a pumping power of 6.5 mW, and bandwidth of full width at half maximum <5 pm. Its power selection was achieved by fixing an HWP before a PBS, and the horizontal output polarization was again rotated in a desired arbitrary polarization before a dichronic mirror. To increase the efficiency of the PPKTP, we introduced a lens to focalize the diode right on the crystal. The second and fourth sections of the setup were used for the tomography measurement. The idler photon went through the polariton source, which consisted of a cryostat at 20 K and a pressure of 100 mbar. The single photon was focused on the surface of the microcavity, and the emitted photons were recollected with a second lens sending them directly to the fourth stage (the idler’s tomography stage). In the experiment measuring nonlinear effects, an additional laser was sent to the microcavity at a particular angle. The transmitted photons given by the laser were covered with a diaphragm (pinhole) at the Fourier plane of the recollection lens. The entanglement measurement took place in the tomography analysis (46). In our case, we applied a hypercomplete tomography by projecting the bipartite state onto a combination set of three bases: logical (|H〉 and |V〉), diagonal [ and ], and circular [ and ]. Each local projection was performed by applying a rotation in a QWP and a HWP, followed by a PBS as polarization filter (see Fig. 1). Finally, the remaining photons belonging to the qubit of both the signal and the idler were coupled to a single-mode optical fiber, connected to an avalanche photodetector (APD). The reconstruction of the state saw the relative coincident count events among all the mentioned projections during the desired integration time. In that way, we measured the state by projecting many copies of the same. The measurements corresponding to the results reported in Fig. 5 were unavoidably affected by the presence of the classical cw laser, which was minimized by momentum selection of the polariton signal (as shown in Fig. 1D). The contribution of this noise, however, was subtracted from the raw data by performing desynchronized tomography for each power of the external laser. The calibration of the population and density in the presence of the classical laser was obtained by means of four different parameters: the pumping power, the photon energy, the polariton lifetime, and the laser spot size. The numbere of photons per second delivered by the laser to the microcavity was calculated as the power/energy ratio. Given the transmission of the microcavity and assuming the same number of photons to be emitted on both sides of the sample, only 0.5% of the photons became polaritons. Multiplying this rate of polaritons per second by the lifetime of a polariton (measured as 3 ps) gives a maximum of 380 polaritons for the highest power used. The polariton density was obtained by dividing by the spot area of the driving laser A = 706 μm2.
Supplementary Material
Acknowledgments
Funding: This work was supported by the European Research Council Starting Grants (i) POLAFLOW (grant agreement no. 308136, http://polaritonics.nanotec.cnr.it) and (ii) 3D-QUEST (3D–Quantum Integrated Optical Simulation; grant agreement no. 307783, http://www.3dquest.eu). This work was also partially supported by “Becas Chile Program” of Ph.D. Scholarships from Comisión Nacional de Investigación Científica y Tecnológica (CONICYT); the Spanish Ministry of Economy and Competitiveness (MINECO) under contract FIS2015-64951-R [Classical and Quantum Electrodynamics of light-matter coupling (CLAQUE)]; and the Ministry of Science and Education of the Russian Federation under project no. RFMEFI61617X0085. Author contributions: D.S. and F.P.L. conceived the idea. A.C., B.S., M.D.G., F.C., and D.G.S.-F. prepared the setup and performed the experiments with help from D.B. and L.D. V.T. and G.B. grew the sample, and A.F. prepared the sample for transmission measurements. J.C.L.C., C.S.M., and E.d.V. developed the theory under the supervision of F.P.L. L.M., P.M., and F.S. supervised the experiments on photon-photon and photon-polariton concurrence. D.S. coordinated and supervised the project. All authors contributed to the analysis and interpretation of the data as well as the editing of the manuscript. Competing interests: The authors declare that they have no competing interests. Data and materials availability: All data needed to evaluate the conclusions in the paper are present in the paper and/or the Supplementary Materials. Additional data related to this paper may be requested from the corresponding authors.
SUPPLEMENTARY MATERIALS
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/4/eaao6814/DC1
section S1. Interaction Hamiltonian
section S2. Dynamics of the entangled photons
section S3. Effect of noise on the measurement
fig. S1. Luminescence of the sample at the wave vector at which the single photon impinges normalized to the intensity of the single polariton.
fig. S2. Counting photon coincidences as a function of pumping power.
Reference (47)
REFERENCES AND NOTES
- 1.O’Brien J. L., Optical quantum computing. Science 318, 1567–1570 (2007). [DOI] [PubMed] [Google Scholar]
- 2.Cirac J. I., Zoller P., Kimble H. J., Mabuchi H., Quantum state transfer and entanglement distribution among distant nodes in a quantum network. Phys. Rev. Lett. 78, 3221–3224 (1997). [Google Scholar]
- 3.Reiserer A., Kalb N., Rempe G., Ritter S., A quantum gate between a flying optical photon and a single trapped atom. Nature 508, 237–240 (2014). [DOI] [PubMed] [Google Scholar]
- 4.Reiserer A., Rempe G., Cavity-based quantum networks with single atoms and optical photons. Rev. Mod. Phys. 87, 1379–1418 (2015). [Google Scholar]
- 5.Volz J., Scheucher M., Junge C., Rauschenbeutel A., Nonlinear π phase shift for single fibre-guided photons interacting with a single resonator-enhanced atom. Nat. Photonics 8, 965–970 (2014). [Google Scholar]
- 6.Hacker B., Welte S., Rempe G., Ritter S., A photon-photon quantum gate based on a single atom in an optical resonator. Nature 536, 193–196 (2016). [DOI] [PubMed] [Google Scholar]
- 7.Tiarks D., Schmidt S., Rempe G., Dürr S., Optical π phase shift created with a single-photon pulse. Sci. Adv. 2, e1600036 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.A. Kavokin, J. J. Baumberg, G. Malpuech, F. P. Laussy, Microcavities (Oxford Univ. Press, ed. 2, 2017). [Google Scholar]
- 9.Kasprzak J., Richard M., Kundermann S., Baas A., Jeambrun P., Keeling J. M. J., Marchetti F. M., Szymańska M. H., André R., Staehli J. L., Savona V., Littlewood P. B., Deveaud B., Dang L. S., Bose–Einstein condensation of exciton polaritons. Nature 443, 409–414 (2006). [DOI] [PubMed] [Google Scholar]
- 10.Amo A., Sanvitto D., Laussy F. P., Ballarini D., del Valle E., Martin M. D., Lemaître A., Bloch J., Krizhanovskii D. N., Skolnick M. S., Tejedor C., Viña L., Collective fluid dynamics of a polariton condensate in a semiconductor microcavity. Nature 457, 291–295 (2009). [DOI] [PubMed] [Google Scholar]
- 11.Amo A., Lefrère J., Pigeon S., Adrados C., Ciuti C., Carusotto I., Houdré R., Giacobino E., Bramati A., Superfluidity of polaritons in semiconductor microcavities. Nat. Phys. 5, 805–810 (2009). [Google Scholar]
- 12.Lerario G., Fieramosca A., Barachati F., Ballarini D., Daskalakis K. S., Dominici L., De Giorgi M., Maier S. A., Gigli G., Kéna-Cohen S., Sanvitto D., Room-temperature superfluidity in a polariton condensate. Nat. Phys. 13, 837–841 (2017). [Google Scholar]
- 13.Karzig T., Bardyn C.-E., Lindner N. H., Refael G., Topological polaritons. Phys. Rev. X 5, 031001 (2015). [Google Scholar]
- 14.Carusotto I., Ciuti C., Quantum fluids of light. Rev. Mod. Phys. 85, 299–366 (2013). [Google Scholar]
- 15.Venema L., Verberck B., Georgescu I., Prando G., Couderc E., Milana S., Maragkou M., Persechini L., Pacchioni G., Fleet L., The quasiparticle zoo. Nat. Phys. 12, 1085–1089 (2016). [Google Scholar]
- 16.Ballarini D., De Giorgi M., Cancellieri E., Houdré R., Giacobino E., Cingolani R., Bramati A., Gigli G., Sanvitto D., All-optical polariton transistor. Nat. Commun. 4, 1778 (2013). [DOI] [PubMed] [Google Scholar]
- 17.Schneider C., Rahimi-Iman A., Kim N. Y., Fischer J., Savenko I. G., Amthor M., Lermer M., Wolf A., Worschech L., Kulakovskii V. D., Shelykh I. A., Kamp M., Reitzenstein S., Forchel A., Yamamoto Y., Höfling S., An electrically pumped polariton laser. Nature 497, 348–352 (2013). [DOI] [PubMed] [Google Scholar]
- 18.Kim S., Zhang B., Wang Z., Fischer J., Brodbeck S., Kamp M., Schneider C., Höfling S., Deng H., Coherent polariton laser. Phys. Rev. X 6, 011026 (2016). [Google Scholar]
- 19.Ardizzone V., Abbarchi M., Lemaître A., Sagnes I., Senellart P., Bloch J., Delalande C., Tignon J., Roussignol P., Bunching visibility of optical parametric emission in a semiconductor microcavity. Phys. Rev. B 86, 041301 (2012). [Google Scholar]
- 20.Dominici L., Colas D., Donati S., Restrepo Cuartas J. P., De Giorgi M., Ballarini D., Guirales G., López Carreño J. C., Bramati A., Gigli G., del Valle E., Laussy F. P., Sanvitto D., Ultrafast control and Rabi oscillations of polaritons. Phys. Rev. Lett. 113, 226401 (2014). [DOI] [PubMed] [Google Scholar]
- 21.Ciuti C., Branch-entangled polariton pairs in planar microcavities and photonic wires. Phys. Rev. B 69, 245304 (2004). [Google Scholar]
- 22.Savasta S., Stefano O. D., Savona V., Langbein W., Quantum complementarity of microcavity polaritons. Phys. Rev. Lett. 94, 246401 (2005). [Google Scholar]
- 23.Demirchyan S. S., Chestnov I. Y., Alodjants A. P., Glazov M. M., Kavokin A. V., Qubits based on polariton rabi oscillators. Phys. Rev. Lett. 112, 196403 (2014). [DOI] [PubMed] [Google Scholar]
- 24.Boulier T., Bamba M., Amo A., Adrados C., Lemaître A., Galopin E., Sagnes I., Bloch J., Ciuti C., Giacobino E., Bramati A., Polariton-generated intensity squeezing in semiconductor micropillars. Nat. Commun. 5, 3260 (2014). [DOI] [PubMed] [Google Scholar]
- 25.Filip R., Mišta J. L. Jr, Detecting quantum states with a positive Wigner function beyond mixtures of Gaussian states. Phys. Rev. Lett. 106, 200401 (2011). [DOI] [PubMed] [Google Scholar]
- 26.Verger A., Ciuti C., Carusotto I., Polariton quantum blockade in a photonic dot. Phys. Rev. B 73, 193306 (2006). [Google Scholar]
- 27.Liew T. C. H., Savona V., Single photons from coupled quantum modes. Phys. Rev. Lett. 104, 183601 (2010). [DOI] [PubMed] [Google Scholar]
- 28.Bamba M., Imamoğlu A., Carusotto I., Ciuti C., Origin of strong photon antibunching in weakly nonlinear photonic molecules. Phys. Rev. A 83, 021802 (2011). [Google Scholar]
- 29.Flayac H., Savona V., Nonclassical statistics from a polaritonic Josephson junction. Phys. Rev. A 95, 043838 (2017). [Google Scholar]
- 30.Lemonde M.-A., Didier N., Clerk A. A., Antibunching and unconventional photon blockade with Gaussian squeezed states. Phys. Rev. A 90, 063824 (2014). [Google Scholar]
- 31.Schneider C., Winkler K., Fraser M. D., Kamp M., Yamamoto Y., Ostrovskaya E. A., Höfling S., Exciton-polariton trapping and potential landscape engineering. Rep. Prog. Phys. 80, 016503 (2017). [DOI] [PubMed] [Google Scholar]
- 32.López Carreño J. C., Sánchez Muñoz C., Sanvitto D., del Valle E., Laussy F., Exciting polaritons with quantum light. Phys. Rev. Lett. 115, 196402 (2015). [DOI] [PubMed] [Google Scholar]
- 33.Laussy F. P., del Valle E., Schrapp M., Laucht A., Finley J. J., Climbing the Jaynes–Cummings ladder by photon counting. J. Nanophotonics 6, 061803 (2012). [Google Scholar]
- 34.Fedrizzi A., Herbst T., Poppe A., Jennewein T., Zeilinger A., A wavelength-tunable fiber-coupled source of narrowband entangled photons. Opt. Express 15, 15377–15386 (2007). [DOI] [PubMed] [Google Scholar]
- 35.James D. F. V., Kwiat P. G., Munro W. J., White A. G., Measurement of qubits. Phys. Rev. A 64, 052312 (2001). [Google Scholar]
- 36.Clauser J. F., Horne M. A., Shimony A., Holt R. A., Proposed experiment to test local hidden-variable theories. Phys. Rev. Lett. 23, 880–884 (1969). [Google Scholar]
- 37.Deveaud B., Polariton interactions in semiconductor microcavities. C. R. Phys. 17, 874–892 (2016). [Google Scholar]
- 38.Love A. P. D., Krizhanovskii D. N., Whittaker D. M., Bouchekioua R., Sanvitto D., Al Rizeiqi S., Bradley R., Skolnick M. S., Eastham P. R., André R., Dang L. S., Intrinsic decoherence mechanisms in the microcavity polariton condensate. Phys. Rev. Lett. 101, 067404 (2008). [DOI] [PubMed] [Google Scholar]
- 39.Tassone F., Yamamoto Y., Exciton-exciton scattering dynamics in a semiconductor microcavity and stimulated scattering into polaritons. Phys. Rev. B 59, 10830–10842 (1999). [Google Scholar]
- 40.Walker P. M., Tinkler L. and Skryabin D. V., Farrer I., Ritchie D. A., Skolnick M. S., Krizhanovskii D. N., Dark solitons in high velocity waveguide polariton fluids. Phys. Rev. Lett. 119, 097403 (2017). [DOI] [PubMed] [Google Scholar]
- 41.Altepeter J. B., Branning D., Jeffrey E., Wei T. C., Kwiat P. G., Thew R. T., O’Brien J. L., Nielsen M. A., White A. G., Ancilla-assisted quantum process tomography. Phys. Rev. Lett. 90, 193601 (2003). [DOI] [PubMed] [Google Scholar]
- 42.Kira M., Koch S. W., Quantum-optical spectroscopy of semiconductors. Phys. Rev. A 73, 013813 (2006). [Google Scholar]
- 43.Aßmann M., Bayer M., Nonlinearity sensing via photon-statistics excitation spectroscopy. Phys. Rev. A 84, 053806 (2011). [Google Scholar]
- 44.Mukamel S., Dorfman K. E., Nonlinear fluctuations and dissipation in matter revealed by quantum light. Phys. Rev. A 91, 053844 (2015). [Google Scholar]
- 45.Weisbuch C., Nishioka M., Ishikawa A., Arakawa Y., Observation of the coupled exciton-photon mode splitting in a semiconductor quantum microcavity. Phys. Rev. Lett. 69, 3314–3317 (1992). [DOI] [PubMed] [Google Scholar]
- 46.Altepeter J. B., Jeffrey E. R., Kwiat P. G., Photonic state tomography. Adv. At., Mol., Opt. Phys. 52, 105–159 (2005). [Google Scholar]
- 47.Mølmer K., Castin Y., Dalibard J., Monte Carlo wave-function method in quantum optics. J. Opt. Soc. Am. B 10, 524–538 (1993). [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/4/eaao6814/DC1
section S1. Interaction Hamiltonian
section S2. Dynamics of the entangled photons
section S3. Effect of noise on the measurement
fig. S1. Luminescence of the sample at the wave vector at which the single photon impinges normalized to the intensity of the single polariton.
fig. S2. Counting photon coincidences as a function of pumping power.
Reference (47)


