Machine Learning Force Field Parameters from Ab Initio Data

Abstract

Machine learning (ML) techniques with the genetic algorithm (GA) have been applied to explore a polarizable force field parameters using only ab initio data from quantum mechanics (QM) calculations of molecular clusters at the MP2/6-31G(d,p), DFMP2(fc)/jul-cc-pVDZ, and DFMP2(fc)/jul-cc-pVTZ levels to predict experimental condensed phase properties (i.e., density and heat of vaporization). The performance of this ML/GA approach is demonstrated on 4,943 dimers electrostatic potentials and 1,250 clusters interaction energies for methanol. Excellent agreement between the training dataset from QM calculations and the optimized force field model can be achieved. Better results are achieved by introducing an offset factor during the machine learning process to compensate for the discrepancy of the QM calculated energy and the energy reproduced by optimized force field, where the offset factor maintain the local “shape” of the QM energy surface. Throughout the machine learning process, experimental observables were not involved in the objective function, but were only used for model validation. The best model, optimized from the QM data at the DFMP2(fc)/jul-cc-pVTZ level, appears to perform even better than the original AMOEBA force field (amoeba09.prm), which was optimized empirically to match liquid properties. The present effort shows the possibility of using machine learning techniques to develop descriptive polarizable force field using only QM data. The ML/GA strategy to optimize force field parameters described here could easily be extended to other molecular systems.

TOC image

INTRODUCTION

Classical simulations based on detailed atomic models and molecular mechanical (MM) potential functions are increasingly playing an important role in physics, chemistry, biochemistry, and materials science. To obtain meaningful results, the accuracy of the potential function, or force field, underlying such molecular dynamics (MD) simulations is of critical importance.^1–8 The simple force fields that are widely used for biomolecular simulations, in particular, are empirically optimized to reproduce a number of calculated quantum mechanics (QM) and experimental properties.⁴ While such an empirical approach can provide atomic models of useful accuracy, they can do so only if the simulated system of interest is built from the set of previously parameterized chemical functionalities. This has a critical impact on the predictive power of MD simulations in general. For instance, in the absence of any prior knowledge from experiment, it is unclear if the properties of a neat liquid of a compound comprising previously untreated atom types could be reliably predicted. A force field that requires an empirical calibration against experimental data is expected to be inherently more limited when applied to systems that depart from a pre-defined set of chemical functionalities.⁸

The primary objective of the present study is to test the ability of machine learning (ML) techniques with the genetic algorithm (GA) to parameterize a polarizable force field by relying exclusively on ab initio QM data. A central question that we are trying to answer with the present effort is whether the resulting model can accurately predict neat liquid properties of a compound over a range of temperatures from only QM data, without any a priori information from experiment. The general idea that one could develop molecular potential functions from first principles QM data rests on ideas from early efforts by Clementi and co-workers in the 1970’s.⁹ They constructed an additive force field model by fitting the potential energies for the water dimer in various geometrical configurations calculated using the QM configuration-interaction method. However, the resulting MCY model did not accurately simulate liquid water. In retrospect, a serious limitation was the total neglect of many-body (MB) effects. To test our ML/GA strategy, it is important to choose a functional form that incorporates a correct physical representation of many-body effects and that provides an accurate description of physicochemical properties of the condensed phase. Force fields that explicitly account for induced electronic polarization offer a step in the right direction.^10–16 While non-polarizable additive force fields used in biomolecular simulations, which represent polarization in an average manner with effective fixed partial charges, can achieve a reasonably accurate representation of the condensed phase, they do so as the result of numerous empirical compromises.^{4, 17} Consequently, it is possible that the functional form of non-polarizable additive force fields might be too limited to achieve the desired physical accuracy over a range of thermodynamic states.

Different functional forms of polarizable force fields have been proposed for simulating chemical and biomolecular systems. Those polarizable force fields include models based on classical Drude oscillators,^{16, 18–19} the CHARMM charge equilibration (CHEQ) model based on fluctuating partial charges,¹⁵ the AMBER ff02 based on inducible dipoles,²⁰ and the Atomic Multipole Optimized Energetics for Biomolecular Applications (AMOEBA) force field.^21–22 While most models remain at the level of atomic point charges, the AMOEBA force field further incorporates static field contributions from atomic dipoles and quadrupoles. More recently, there has been considerable progress in the design of potential energy functions to simulate water by building upon rigorous representations of the many-body expansion of the interaction energies.^23–25 Schmidt and collaborators have advanced a strategy on the basis of the symmetry-adapted perturbation theory (SAPT) methodology,^26–27 yielding models with relatively good properties for dense liquid systems. Similarly, the latest SAPT models may need to incorporate Axilrod−Teller three-body dispersion and exchange to yield accurate models of dense systems.²⁸ Similarly, the MB-pol model developed by Paesani and co-workers has demonstrated that it is possible to achieve high accuracy across all phases of water through a quantitative and physically correct representation of both short- and long-range many-body contributions.²⁵ Of particular importance, the MB-pol model incorporates many-body van der Waals interactions. Considerations of explicit multi-body van der Waals terms go back to early work by Mezei²⁹ and Clementi.^30–31 However, it is not yet clear whether such a rigorous treatment of many-body effects could be routinely implemented with more complicated molecules. The present effort, we have chosen to work with the AMOEBA functional form because of its relative mathematical simplicity and flexibility.

We have chosen the methanol molecule to explore the feasibility of our ML/GA parameterization strategy. This choice is motivated by the observation that methanol represents a molecule of sufficient complexity comprising both a hydroxyl polar group, able to form hydrogen bonds, as well as a bulky non-polar alkyl group.³² The competing nature of these interactions makes methanol an excellent test case to explore the feasibility of our ML/GA strategy to generate force field parameters that relies exclusively on QM data.

METHODS

The complete functional form of the AMOEBA force field has been described in detail elsewhere.^{21, 33} The present focus is mainly on the non-bonded electrostatic and van der Waals (vdW) interaction parameters. Because the internal covalent interaction (bond, angle, dihedral and torsional parameters) are not expected to greatly affect the properties of the condensed liquid phase, they remained unchanged from the original AMOEBA force field (amoeba09.prm).²² To compute the electrostatic energy (E_elec) between methanol molecules, the AMOEBA force field requires 44 independent parameters. Those parameters are monopole (q), dipole (μ_x, μ_y, μ_z), quadrupole expressed as a traceless symmetric matrix with five independent elements (Q_xx, Q_yx, Q_yy, Q_zx, Q_zy), atomic polarizability (α) for the four methanol atom types (O, C, H_C, and H_O). A unique Thole damping factor (a) was used for all atoms, following the AMOEBA convention. The AMOEBA force field represents the vdW interactions as a buffered 14-7 potential.³⁴ To compute the vdW energy (E_vdW) between methanol molecules, the functional form requires 10 parameters. Eight of those parameters are the R_min, and ε_min for the four atoms types of methanol. Finally, two additional parameters (the so-called reduction factor λ) are required to scale the position of the two hydrogen atoms interaction site along their corresponding covalent bond.¹⁴

Force field parameterization, i.e. the determination of the optimal parameters associated with a complex functional form, is a challenging optimization problem in a space of high dimensionality. Local optimization approaches generally carry out this task by attempting to minimize an objective function using a simple gradient-based algorithm (e.g., steepest descent, conjugate gradient method),^35–36 and are only effective if the starting point is sufficiently close to a satisfactory solution. However, even with pre-existing knowledge about the objective function and the parameter space, a number of problems can arise. For example, the convergence to optimal parameters is not guaranteed when the objective function is rugged, non-differentiable, or when the initial value deviates significantly from the global minimum. Ultimately, the range of parameter values that must be explored grows dramatically as the complexity of the force field functional form increases. Here, to overcome the challenge encountered with force field parameterization using ML techniques, we have used the genetic algorithm (GA), which is an evolutionary algorithm that mimics the process of natural selection.³⁷ Previous successful applications of the genetic algorithm in similar contexts include the determination of the parameters for the ReaxFF reactive force field,^{2–3, 5} and various force fields including Morse+QEq charge transfer ionic potential (CTIP),⁶ and a new hybrid bond-order potential (HyBOP) for materials system.^{2–3, 5–6, 38–39}

In the present work, electrostatic parameters were determined in a first stage, and vdW parameters were optimized in a second stage (i.e., the electrostatic parameters were kept unchanged while the vdW parameters are optimized on the second stage). The optimization of the electrostatic parameters of methanol was carried out in two steps. In a first step, the value of the atomic multipoles was obtained from the QM electrostatic potential on the Connolly surface of a single isolated methanol molecule. The QM electrostatic potential of a methanol monomer, ϕ^QM, was calculated at the MP2 level of theory with various basis sets including Pople-style⁴⁰ and correlation consistent⁴¹ basis sets. The results are given in Table 1. A Distributed Multipole Analysis (DMA)^42–44 was carried out using the Gaussian Distributed Multipole Analysis (GDMA 2.2) program^{42, 45–46} for the electronic density results from different MP2 basis sets. The multipole parameters of each atomic site were identified using the Tinker^{21, 47–51} package (the Poledit and Potential program). In a second step, all 44 electrostatic parameters were refined from the QM electrostatic potential calculated from an extensive training dataset of 4,943 methanol dimers using the genetic algorithm. This second step differs from the standard protocol used to determine the electrostatic parameters for the AMOEBA polarizable force field from QM calculations,^{22, 33} which relies on the unperturbed monomer. By considering dimers in this situation, the mutual induced polarization of the two molecules is explicitly taken into account, allowing a direct determination of the atomic polarizabilities. The methanol dimer configurations were sampled through placing two methanol molecules, where one methanol was sampled over shell radius (1- 4 Å) on another methanol’s Connolly surface. In total, 4,943 methanol dimer configurations were sampled. These 4,943 configurations of methanol dimers were relaxed through MP2 geometry optimization via Gaussian09 program,⁵² while fixing the position of the carbon atoms. The optimization of electrostatic parameters seeks to minimize the objective function Δ as the averaged root mean square deviation (ARMSD) between the QM result and the parameterized force field calculation, shown in equation (1):

$$\begin{gathered} \mathrm{\Delta }=\frac{1}{N_{\text{cluster}}}{\displaystyle \sum _{j=1}^{N_{\text{cluster}}}\sqrt{{\chi }^2(p_1,p_2,\dots p_m)}} \\ =\frac{1}{N_{\text{cluster}}}{\displaystyle \sum _{j=1}^{N_{\text{cluster}}}\left(\sqrt{\frac{1}{n^{\text{grid}}}{\displaystyle \sum _{k=1}^{n^{\text{grid}}}{({\varphi }_k^{\mathrm{QM}}-{\varphi }_k^{\mathrm{FF}}(p_1,p_2,\dots p_m\left)\right)}^2}}\right)} \end{gathered}$$ (1)

where $\left(p_1,p_2,\dots p_m\right)$ represent the electrostatic parameters of the force field and $N_{\mathit{cluster}}=4,943$. It is noteworthy that the static monopole, dipoles and quadrpoles remained essentially unchanged during this second step, which primarily affected the optimization of the atomic polarizabilies.

Table 1.

The electrostatic potential energy (E_ESP) for methanol monomer from MP2 calculations using different basis sets and from the corresponding fitted multipole parameters, with the corresponding root mean square deviation and relative error.

Basis	ESP from MP2 (kcal/mol)	ESP from fitted multipole (kcal/mol)	RMSD (kcal/mol)	Relative Error (%)
6-31G(d, p)	4.878	4.865	0.165	0.267
6-31+G*	5.675	5.649	0.172	0.458
6-31G*	5.059	5.046	0.170	0.257
6-311G(d, p)	5.947	5.935	0.172	0.202
6-311G(2df, 2pd)	4.462	4.447	0.154	0.336
6-311G*	5.187	5.172	0.156	0.289
6-311+G*	5.648	5.626	0.167	0.390
6-311++G**	5.307	5.282	0.165	0.471
6-311+G**	5.309	5.285	0.166	0.452
Aug-CC-pvDz	4.758	4.729	0.177	0.609
Aug-CC-pvTz	4.748	4.723	0.165	0.527
Aug-CC-pvQz	4.745	4.720	0.165	0.527

In a second stage, the parameters for the vdW interactions were optimized to best-match the interaction between a central methanol molecule and its nearest neighbors via supermolecular QM computations for a large number of clusters extracted from classical MD simulations of liquid methanol using the original amoeba09.prm.²² The idea of exploiting simulation-derived ensemble to optimize force field parameters was first suggested by. Mezei,.⁵³ The electrostatic parameters optimized in the previous step are kept unchanged at this stage. Second-order Møller–Plesset perturbation theory⁵⁴ (MP2) was employed as the QM method to calculate the interaction energy, with basis sets superposition error (BSSE) counterpoise correction.⁵⁵ This level of theory and basis sets has been widely verified by previous studies to predict energetics and structural properties.⁵⁶ One set of QM calculations was carried out at the MP2/6-31G(d,p) with BSSE level using the Gaussian09 program.⁵² Two additional sets density-fitted MP2 and frozen core approximation QM calculations were carried out at the DFMP2(fc)/jul-cc-pVDZ and DFMP2(fc)/jul-cc-pVTZ level with BSSE counterpoise corrections using the Psi4 quantum chemistry package.⁵⁷ A total of 1,250 clusters were included in the training set (999 clusters of 9 molecules, 157 clusters of 11 molecules, and 94 clusters of 13 molecules). The MD simulation system used to generate the snapshots from which the clusters were extracted comprises 344 methanol molecules. The MD trajectory was generated under periodic boundary conditions (PBC) in the NpT ensemble at constant pressure and temperature using the original AMOEBA force field (amoeba09.prm).²² To acquire a wide range of clusters configurations, NpT ensemble simulations were performed on the system at various temperatures and pressures, from T = 193.15 K, p = 1.0 atm, T = 293.15 K, p = 1.2 atm, to T = 393.15 K, p = 6.293 atm, with final stable density of the system as ρ = 0.933, 0.794 and 0.627 g/ml, respectively. These MD simulations were generated with an integration time step of 1 fs using the GPU dynamics program in the Tinker-OpenMM suite (http://biomol.bme.utexas.edu/tinker-openmm). Table 3 provides further details about the clusters extracted from the different MD simulation systems. The optimization of the vdW parameters seeks to minimize the objective function F given by,

$$F(p_1,p_2,\dots p_m)={\displaystyle \sum _j{\left(\mathrm{\Delta }{E}_j^{\mathrm{QM}}-\delta -\mathrm{\Delta }{E}_j^{\mathrm{MM}}(p_1,p_2,\dots p_m)\right)}^2}$$ (2)

where δ is an offset factor and $\mathrm{\Delta }{E}_j^{\mathrm{QM}}$ and $\mathrm{\Delta }{E}_j^{\mathrm{MM}}$ are the interaction energies between the central molecule and the surrounding molecules for the j-th cluster in the training set calculated from the QM and MM force field, respectively. The vdW parameters in the force field were optimized using the interaction energy from 1,250 methanol clusters by employing the developed ML/GA framework.^{6–7, 38}

Table 3.

Number distribution of the extracted clusters (9 molecules, 11 molecules and 13 molecules) from different liquid MD systems.

MD simulations	9 methanol	11 methanol	13 methanol
ρ = 0.933 g/ml, T = 193.15 K, p = 1.000 atm	372	157	94
ρ = 0.794 g/ml, T = 293.15 K, p = 1.200 atm	502	N/A	N/A
ρ = 0.627 g/ml, T = 393.15 K, p = 6.293 atm	125	N/A	N/A

A flowchart of the ML/GA optimization protocol is depicted in Figure 1. Briefly, the optimization starts with a set of parent parameters, which is defined as the population. For parameters optimization of the force field, the parents may have different ranges of settings. Some of the individuals in this population present a better fit, which in the context of parameters optimization means lower value in the objective function, e.g., Δ and F in Eqs (1) and (2). Fit parents survive and are allowed to mate, which is accomplished by crossing patterns with other fit individuals. During crossover, random mutations in the genes are also allowed to a certain degree to avoid a stagnant gene pool and a better sampling of the parameters space. The offspring individuals form the next generation of parents and this process continues until some pre-defined criteria are met. For the ML/GA optimization of electrostatic parameters, the process was initiated by generating a population of sets of parameters randomly, such that their values lie within physically allowable limits, which are ±1.5 times of value from Tinker Poledit and Potential programs for methanol monomer at MP2/6-311G(d,p) level of QM calculations. The searching range of the 44 independent electrostatic parameters over which the ML/GA optimization was is given in Table 2.

Figure 1.

Flowchart of the machine learning with genetic algorithm (ML/GA) strategy describing the sequence of steps employed in this work.

Table 2.

Range of the 44 independent electrostatic parameters over which the ML/GA was performed.

	Parameters	Atom types
		O	H (−O)	C	H (−C)
EESP	Monopole (q)	−1.0 ~ 0	0 ~ 0.4	0 ~ 0.3	0 ~ 0.06
	Dipole (μx,μy,μz)	(0 ~ 0.5, 0.0, 0 ~ 0.4)	(−0.14 ~ 0, 0.0, −0.4 ~ 0)	(−0.4 ~ 0, 0.0, 0 ~ 0.9)	(−0.1 ~ 0, 0.0, −0.1 ~ 0)
	Quadrupole $\left[\begin{array}{ccc}{Q}_{xx}& \ast & \ast \\ Q_{yx}& Q_{yy}& \ast \\ Q_{zx}& Q_{zy}& \ast \end{array}\right]$	$\left[\begin{array}{ccc}0~0.6& \ast & \ast \\ 0.0& -0.8~0& \ast \\ 0~0.6& 0.0& \ast \end{array}\right]$	$\left[\begin{array}{ccc}0~0.28& \ast & \ast \\ 0.0& 0~0.06& \ast \\ -0.2~0& 0.0& \ast \end{array}\right]$	$\left[\begin{array}{ccc}0~0.06& \ast & \ast \\ 0.0& -0.11~0& \ast \\ -0.6~0& 0.0& \ast \end{array}\right]$	$\left[\begin{array}{ccc}0~0.15& \ast & \ast \\ 0.0& -0.17~0& \ast \\ -0.08~0& 0.0& \ast \end{array}\right]$
	Polarizability (α)	0.5 ~ 1.0	0.2 ~ 0.7	1.0 ~ 1.6	0.2 ~ 0.7
	Thole’s factor (a)	0.3 ~ 0.5	0.3 ~ 0.5	0.3 ~ 0.5	0.3 ~ 0.5

For the ML/GA optimization of the vdW parameters, the process was initiated by generating a population a population of N_p = 120 parameters sets randomly, such that their values lie within physically allowable limits. The searching range of the 11 independent vdW parameters over which the ML/GA optimization was performed is given in Table 4. For each set of parameters, we compute the interaction energies for all structures in the training dataset using Tinker and evaluate the objective function F given by Eq. (2). Sets of parameters were then ranked in ascending order. After the ranking, non-linear roulette wheel selection^58–59 was performed to select the best 60% members, i.e., the ones with lowest values of F, which were then subjected to genetic operations: mutation and crossover with crossover-rate 3%. These mutations introduce sufficient diversity into the population, and the non-linear selection scheme helps to avoid premature convergence of the ML/GA run. After the genetic operations, both the parent and offspring sets of parameters are ranked by their value of F. The best N_p parameters sets are then chosen to constitute the next generation. Such an optimization routine ensures that only satisfactory parameters sets survive after each generation; upon repeating this workflow for sufficient generations and sampling viable regions in the parameters space, we performed three separate ML/GA runs starting with different random populations. From each of the converged ML/GA run, we chose the final parameters set corresponding the lowest value of F. Monitoring the evolution of the parameters during the iterations of the GA algorithm shows that they initially vary rapidly until they settle down and undergo very small variations (< 0.0001%) around final values. The calculated correlation coefficients between the vdW parameters from the GA after the initial variations show that some of the vdW parameters are coupled. For example, the parameters ε_min for H_O and H_C are anti-correlated, which is expected because the decrease in one interaction must be compensated by an increase in the other to match the target energy during the GA optimization. This code is freely available for download at https://github.com/AmYingLi/GA4AMOEBA.

Table 4.

Range of the 11 independent vdW parameter over which the ML/GA optimization were performed.

Parameters		Atom types
		O	H (-O)	C	H (-C)
EvdW	Minimum energy depth (εmin)	3.5 ~ 4.0	2.5 ~ 3.0	2.2 ~ 2.8	3.5 ~ 4.0
	Minimum energy distance (Rmin)	0.12 ~ 0.15	0.001 ~ 0.0015	0.4 ~ 0.6	0.001 ~ 0.009
	H reduction factor (λ)	N/A	0.9 ~ 0.95	N/A	0.9 ~ 0.95
	Energy offset (δ)	0.05 ~ 8.0

RESULTS AND DISCUSSION

We successfully generated electrostatic and vdW parameters for the methanol molecule consistent with the functional form of the AMOEBA force field by exclusively taking QM data of molecular clusters as training datasets and using machine learning techniques. For the sake of clarity, we emphasize that the intended objective of the present effort is not to offer a re-calibration of the original AMOEBA force field for methanol that could be transferable to other systems. Our central goal is to test whether it is practically feasible to get parameters for a force field of a physically reasonable functional form without any prior experimental data, and to be sufficiently accurate for liquid simulations. For this reason, we refer to these results as “optimized force field models”, and reserve the acronym AMOEBA only for the original force field: amoeba09.prm.

In the following, we present the results for the electrostatic parameters and the vdW parameters from the genetic algorithm optimization by calibrating the electrostatic potential and the interaction energy for methanol molecules. Finally, a number of additional classical MD simulations were carried out using the set of optimized parameters to calculate the density (ρ) and heat of vaporization (ΔH_vap) of liquid methanol to verify the accuracy of the ML/GA strategy to generate force field parameters. The condensed liquid phase system consists of 344 methanol molecules simulated with periodic boundary conditions (PBC) in the NpT ensemble at a constant pressure of 1 atm as temperature varies from −5°C to 60°C. The density and heat of vaporization were averaged from three different simulations up to 2.5 ns initiated with different random velocities.

One important methodological question for a machine learning strategy is whether the number of clusters included in the training set is sufficiently large to yield a statistically meaningful sampling for parameters determination. As a control, to ascertain the validity of the ML/GA strategy, we first attempted to recover the vdW parameters using interaction energy generated directly from the original amoeba09.prm force field (the original electrostatic parameters from amoeba09.prm were kept unchanged for this test). If the ML/GA strategy is functioning properly, then the generated parameters should be very close to the original vdW parameters amoeba09.prm. In practice, it was found that a minimum dataset of 600 clusters of 9 methanol molecules was necessary to accurately recover the amoeba09.prm parameters, where 300 clusters were extracted from MD trajectories generated at atmospheric pressure and corresponding density, and 300 clusters were extracted from MD trajectories generated at high pressure. The resulting liquid properties from MD simulations using the ML/GA generated vdW parameters were essentially identical to those of the original amoeba09.prm. This test confirmed that our ML/GA protocol was effective, as long as the training set was sufficiently large (more than several hundred configurations).

The electrostatic parameters were determined by training the atomic multipoles (q, $\overrightarrow{\mu }$, $\overleftrightarrow{Q}$), atomic polarizabilities (α) and Thole’s factor (a) from the QM electrostatic potential on the Connolly surface of a methanol molecule using the Gaussian Distributed Multipole Analysis (GDMA 2.2) tool^{42, 45} and the Tinker package.^{47, 49–50} We then refined the atomic polarizabilities and Thole’s factor with a set of methanol dimers using the ML/GA. The ML/GA generated electrostatic parameters from the MP2/6-311G(d,p) level are given in Table 5. Because the AMOEBA force field adopts a universal Thole’s damping factor, during the refinement step, the only varying parameter for each atom type is the polarizability. From table 5, we can see what are the change of the polarizability (α) and Thole’s factor (a) through learning the electrostatic potential from a monomer to 4,943 dimers (denoted as →). As shown in Table 6, the electrostatic potential calculated from this ML/GA generated force field model closely matches the QM at the MP2/6-311G(d,p) level for 4,943 methanol dimers. In fact, the deviations are smaller than those given by the original parameterization of the AMOEBA force field (amoeba09.prm).²² The new optimized force fields were cross-validated by comparing the MM and QM electrostatic potential for 502 clusters of 9 methanol molecules, which were not used in the training process. The results, given in Table 6, show that the deviations between the force field with ML/GA generated parameters and the QM calculations are smaller than those obtained with amoeba09.prm.²² It is important to note that such comparisons with AMOEBA are meaningful because essentially the same QM methods [MP2/6-311G(d,p) and MP2/aug-cc-pVTZ] were originally used to determine the amoeba09.prm electrostatic parameters.²² Therefore, the discrepancies of the resulting parameters is likely due to sampling differences. Because the operational purpose of the permanent electrostatic multipoles determined here is to reproduce interaction energies and forces between molecules, they may differ slightly from the multipoles determined via a spatial partitioning, scheme, such as based on localized Wannier functions.^60–62

Table 5.

ML/GA generated the electrostatic parameters.

	Parameters	Atom types
		O	H (−O)	C	H (−C)
EESP	Monopole (q)	−0.45883	0.21357	0.15811	0.02905
	Dipole (μx,μy,μz)	(0.23922, 0.0, 0.16079)	(−0.06982, 0.0, −0.20347)	(−0.19328, 0.0, 0.45462)	(−0.04887, 0.0, −0.04808)
	Quadrupole $\left[\begin{array}{ccc}{Q}_{xx}& \ast & \ast \\ Q_{yx}& Q_{yy}& \ast \\ Q_{zx}& Q_{zy}& \ast \end{array}\right]$	$[\begin{array}{ccc}0.31570& 0.0& 0.03229\\ 0.0& -0.40859& 0.0\\ 0.03229& 0.0& 0.09289\end{array}$	$[\begin{array}{ccc}0.14001& 0.0& -0.10133\\ 0.0& 0.03002& 0.0\\ -0.10133& 0.0& -0.17003\end{array}$	$[\begin{array}{ccc}0.02941& 0.0& -0.30849\\ 0.0& -0.05306& 0.0\\ -0.30849& 0.0& 0.02365\end{array}$	$[\begin{array}{ccc}0.07423& 0.0& -0.04155\\ 0.0& -0.08433& 0.0\\ -0.04155& 0.0& 0.01010\end{array}$
	Polarizability (α)	0.986➔0.852	0.573➔0.438	1.240➔1.351	0.573➔0.438
	Thole’s factor (a)	0.3908➔0.390	0.3908➔0.390	0.3908➔0.390	0.3908➔0.390

Table 6.

Root mean square deviation (RMSD) of electrostatic potential between different force field models and the QM calculations at the MP2/6-311G(d,p) level. The force fields include the new optimized electrostatic parameters and the original AMOEBA force field (amoeba09.prm). The methanol clusters include 4943 dimers and 502 nonamers (9 molecules cluster).

RMSD of Eelec (kcal/mol)	AMOEBA	Optimized force field model
4,943 dimers	0.723	0.305
502 nonamers	0.718	0.495

The current procedure used to determine the electrostatic parameters, which considers the mutual induced polarization of the two molecules in methanol dimers, differs from the standard AMOEBA protocol.^{22, 33} In the latter, one commonly fits the permanent electrostatic multipoles from a QM electrostatic potential (ESP) map at a series of point around the molecule of interest. However, while considering an isolated molecule certainly provides the necessary information to fit the static atomic electrostatic multipoles of the unperturbed molecule, it also makes it difficult to determine the optimal set of atomic polarizabilities that are needed. To overcome this challenge, we exploited the mutually perturbed ESP map for homodimers in the determination of atomic polarizabilites (while accounting explicitly for the mutual induced polarization of the molecules from one another). In practice, all sets of electrostatic parameters, determined either from the monomer of homodimer QM data, remain fairly similar to one another. This overall consistency reflects the fact that the electrostatic features of a small molecule like methanol are accurately constrained by the QM calculations. In contrast, the determination of the vdW parameters without any experimental data is much more challenging. The vdW parameters in the AMOEBA force field (amoeba09.prm) were empirically adjusted to yield accurate liquid properties. A key question is whether a strategy exclusively based on QM calculations has the ability to yield force field models of equivalent accuracy.

The vdW parameters were optimized to best match the interaction between a central methanol molecule and the finite polarization response to its nearest neighbors via supermolecular QM computations for a large number of clusters representative of the liquid phase. This approach is different than formal perturbative approaches that seek to estimate intermolecular interactions from the wave function of an isolated monomer such as symmetry-adapted perturbation theory (SAPT).^{26–28, 63–64} In principle, SAPT could be used as an alternative route to generate the target data for the ML/GA optimization. A total of 1,250 methanol clusters of 9, 11 and 13 molecules were considered in the supermolecular QM cluster computations. Typical cluster configurations from the training set are depicted in Figure 2. The interactions were characterized by considering three different levels of QM calculations: MP2/6-31G(d,p), DFMP2(fc)/jul-cc-pVDZ, and DFMP2(fc)/jul-cc-pVTZ. The distribution of the interaction energy for 1,250 methanol clusters calculated at the MP2/6-31G(d,p) is shown in Figure 2(d). The distribution converging to a Gaussian-like shape suggests that the number of the configurations is adequate to provide a sufficient sampling of these systems. The ML/GA generated vdW parameters for all force field models are given in Table 7.

Figure 2.

Illustration of the methanol cluster configurations used for the force field parameterization. Typical configurations of the (a) 9 molecules, (b) 11 molecules, and (c) 13 molecules of methanol are shown (the H atom is displayed in white, C atom in cyan and O atom in red). The interaction energy between the central molecule (circled by a dashed line) and the surrounding molecules is used in the optimization of the vdw parameters. (d) Distribution of interaction energies from MP2/6-31G(d,p) of 1,250 methanol clusters (999 clusters of 9 molecules, 157 clusters of 11 molecules, and 94 clusters of 13 molecules).

Table 7.

ML/GA generated van der Waals parameters.

vdW parameters		Amoeba09	MP2/6-31G(d,p)		MP2/jul-cc-pVDZ		MP2/jul-cc-pVTZ		CCSD(T)*
Atom Type			δ = 0	δ ≠ 0	δ = 0	δ ≠ 0	δ = 0	δ ≠ 0	δ = 0
O	εmin	3.4050	3.7132	3.4745	3.6377	3.4687	3.5617	3.4372	3.6165
	Rmin	0.1100	0.1274	0.1484	0.1505	0.1483	0.2037	0.1484	0.1026
HO	εmin	2.6550	3.1559	2.1463	2.4495	2.3580	2.9640	2.2861	2.0481
	Rmin	0.0135	0.0026	0.0100	0.0045	0.0100	0.0026	0.0103	0.0100
	λ	0.910	0.9131	0.9049	0.9198	0.9001	0.9399	0.9014	0.9090
C	εmin	3.7600	2.8536	3.9092	3.1137	3.8046	3.4887	3.8005	3.8744
	Rmin	0.1010	0.2803	0.1018	0.1373	0.1185	0.1920	0.1198	0.1051
HC	εmin	2.8700	3.8178	2.9984	3.3133	2.9583	3.3784	2.7496	2.0066
	Rmin	0.0240	0.0048	0.0200	0.0118	0.0215	0.0068	0.0212	0.0203
	λ	0.910	0.9120	0.9333	0.9077	0.9085	0.9312	0.9490	0.9357

ε_min is the minimum energy depth; R_min is the minimum energy distance; λ is the hydrogen reduction factor

^*Parameters optimized only from QM data on methanol dimer

First we discuss the results from force field models optimized without the offset factor δ in Eq. (2). This means that the parameters are generated to match the absolute value of the QM interaction energies for the training set. The optimized force field models generated from the different QM calculations, MP2/6-31G(d,p), DFMP2(fc)/jul-cc-pVDZ, and DFMP2(fc)/jul-cc-pVTZ, converge reasonably well, with correlation coefficients of 0.974, 0.977 and 0.979, respectively. This is confirmed by observing Figure 3 (a), (b), and (c), where the interaction energies from QM and the force field models are strongly correlated. However, the ultimate test is to verify the ability of the optimized force field model to accurately predict condensed phase properties of liquid methanol. Table 8 shows the result of density and heat of vaporization from polarizable force fields optimized from QM data at the MP2/6-31G(d,p), DFMP2(fc)/jul-cc-pVDZ and DFMP2(fc)/jul-cc-pVTZ levels. Results from the original AMOEBA force field (amoeba09.prm)²² are included for comparison. The performance of the force field models optimized to match the absolute value of the QM interaction energies (offset factor δ set to zero) is disappointing. The liquid density from the model based on MP2/6-31G(d,p) is 0.401 g/ml, and the density from the model based on DFMP2(fc)/jul-cc-pVDZ is 0.568 g/ml, which are in poor agreement with experiment (0.786 g/ml). The heat of vaporization from these two models is also too small. The model based on DFMP2(fc)/jul-cc-pVTZ performs slightly better, with a density of 0.686 g/ml and a heat of vaporization of 8.58 kcal/mol.

Figure 3.

Comparison of the interaction energy (_ΔE) for 1,250 methanol clusters, including 999 clusters of 9 molecules, 157 clusters of 11 molecules, and 94 clusters of 13 molecules, computed from (a) MP2/6-31G(d,p) (b) DFMP2(fc)/jul-cc-pVDZ, and (c) DFMP2(fc)/jul-cc-pVTZ and the optimized force field model fitted without the offset parameter δ in Eq. (2). (d), (e) and (f) are the optimized force field model fitted with the offset parameter δ in Eq. (2).

Table 8.

Density (ρ) and heat of vaporization (ΔH_vap) of liquid methanol calculated from MD simulations (T = 25 °C and p = 1 atm) using different optimized polarizable force fields. The optimized vdW parameters were determined from according to the Eq (1) without δ and with δ offset. For comparison, the results from the AMOEBA force field (amoeba09.prm) are given. The MD results were averaged from 3 simulations of 2.5 ns.

Property	Exp.	MD
		MP2/6-31G(d,p)		DFMP2(fc)/jul-cc-pVDZ		DFMP2(fc)/jul-cc-pVTZ		AMOEBA
		δ = 0	δ ≠ 0	δ = 0	δ ≠ 0	δ = 0	δ ≠ 0
ρ (g/ml)	0.786	0.401	0.759	0.568	0.763	0.686	0.781	0.774
ΔHvap (kcal/mol)	8.95	6.54	9.44	7.23	9.43	8.58	8.98	9.17

To address this shortcoming, an offset factor δ was introduced in Eq. (2). The purpose of the offset factor is to free the parameter optimization from the absolute magnitude of the QM interaction energies.^65–67 It should be noted that the offset factor δ is not directly used in the force field functional form, but only acting as a hyper-parameter for the GA. In essence, when δ is included in Eq. (2), the force field parameters are generated to reproduce the local “shape” of the energy surface of the cluster as a function of the atomic coordinates, while releasing the requirement to match the absolute magnitude of the QM interaction energies. This strategy has some similarities with force-matching methodologies, where a force field is optimized on the basis of the local first derivative of the energy function,⁶⁸ though here the emphasis is put on relative interactions energies rather than on trying to match local forces. With a non-zero offset factor (δ ≠ 0), the force field parameters generated from ML/GA based on the different QM training datasets, MP2/6-31G(d,p), DFMP2(fc)/jul-cc-pVDZ, and DFMP2(fc)/jul-cc-pVTZ, converges similarly well, with correlation coefficients of 0.955, 0.971, and 0.975, respectively. The effect of the offset factor between the interaction energies from QM and the force field models is noticeable in Figure 3 (d), (e), and (f). However, as observed in Table 8, these force field models clearly produced liquid properties that are closer to experiment. While the inaccuracy of force field optimized without the offset δ becomes less important with better QM data, the trend in Table 8 suggests that meaningful information about the overall shape of the energy surface and the relative interaction energies is already contained within lower level QM calculations. The best parameter set, obtained from the QM data at the DFMP2(fc)/jul-cc-pVTZ level, appears to perform even better than the original AMOEBA force field (amoeba09.prm),²² which was optimized empirically to match liquid properties. This force field model is also able to reproduce the radial distribution functions of liquid methanol determined from neutron scattering,⁶⁹ as shown in Figure 4.

Figure 4.

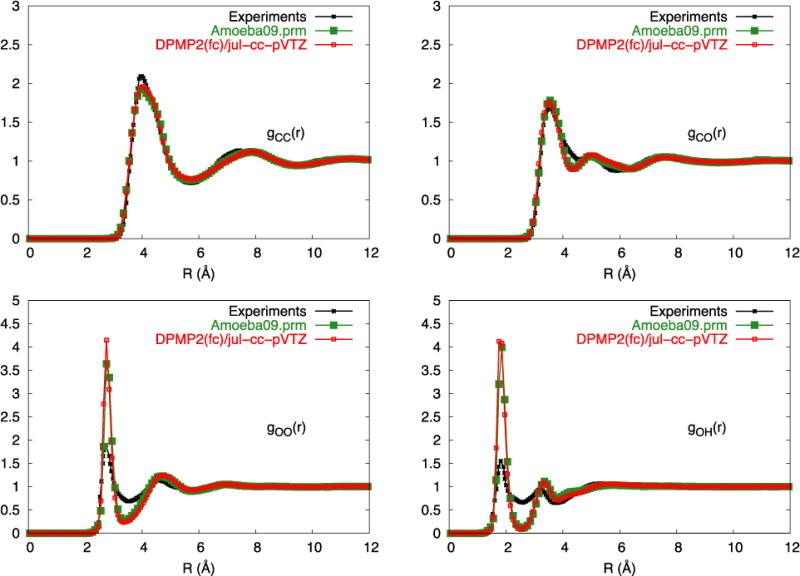
Liquid structure of methanol. The radial distribution function of methanol determined from neutron scattering⁶⁹ compares favorably with the present force field model.⁷³ The O-H hydrogen bonding peak is, however, higher than the experiment. This may reflect the neglect of quantum effects of the nuclei in the simulations,²⁵ as well as inaccuracies in the experimentally determined pair correlation functions.

Figures 3g, 3h, and 3i compare the interaction energies from QM and the original AMOEBA force field (amoeba09.prm),²² which signifies that different basis sets of the MP2 method give out different accuracy. The original AMOEBA force field (amoeba09.prm)²² is directly compared with the QM data in Figure 3 (g, h and i). This comparison leads to an interesting observation; there appears to be a shift between AMOEBA and the QM calculations that closely reflects the offset factor δ used in the force field models optimization. While the vdW parameters of the AMOEBA force field (amoeba09.prm)²² field are empirically adjusted to yield accurate liquid properties, the shifts observed in Figures 3g, 3h, and 3i essentially mirror the offset factor δ used in the force field models optimization very consistently. This observation reinforces the conclusion that seeking to match the absolute interaction energies based on MP2/6-31G(d,p) and DFMP2(fc)/jul-cc-pVDZ levels leads to inaccurate force field models.

A comparison of the interaction energy from the QM calculations and from the force field with the optimized parameters is shown in Figure 3 for the 1,250 clusters. Considering Figure 3, one can see that the ML/GA generated hyper-parameters, offset factor δ, decreases with increasingly accurate QM method, equal to 4.4 kcal/mol for MP2/6-31G(d,p), 2.5 kcal/mol for DFMP2(fc)/jul-cc-pVDZ, and 1.2 kcal/mol for DFMP2(fc)/jul-cc-pVTZ). This is also consistent with the observation that DFMP2(fc)/jul-cc-pVTZ is the QM data leading to the best force field model optimized to match the absolute value of the QM interaction energies (offset factor δ set to zero). By introducing a hyper-parameter in GA, an offset factor δ in Eq. (2), we relieve the parameter optimization from the constraint of matching the absolute value of the interaction energy. ML in the presence of the offset factor yields force field models that try to reproduce the “shape” of the potential energy surface in the multi-dimensional space of the cluster coordinates. The relative accuracy of the different parameters generated by ML/GA for the AMOEBA force field model in Table 8 suggests that the relative “shape” of the potential energy surface is more important than matching the absolute value of the interaction energies. Ultimately, discrepancies (the offset factor δ) of interaction energy calculated from MP2 and the ML/GA generated parameters for AMOEBA force field model are likely due to the incompleteness of the basis sets for the particular level of QM (MP2) theory and the insufficiency sampling of configurations in parameterization of force field.^{56, 65–67} This might be the reason that higher level QM data is able to elucidate some details that are difficult to capture at the lower level. The obvious lesson from this is that the QM level must be sufficiently high.

As a final test of the accuracy of the polarizable force field optimized from QM data, additional sets of MD simulations were generated to examine the density and heat of vaporization of liquid methanol as a function of temperature. For this test, we used the vdW parameters optimized from the QM data at the DFMP2(fc)/jul-cc-pVDZ and DFMP2(fc)/jul-cc-pVTZ levels. Figure 5 shows ρ and ΔH_vap as temperature varies from −5°C to 60°C calculated from NpT MD simulations. We observe that the polarizable force field optimized from QM data accurately predicts the density and heat of vaporization, in excellent accord with experiments, over the range of temperatures.

Figure 5.

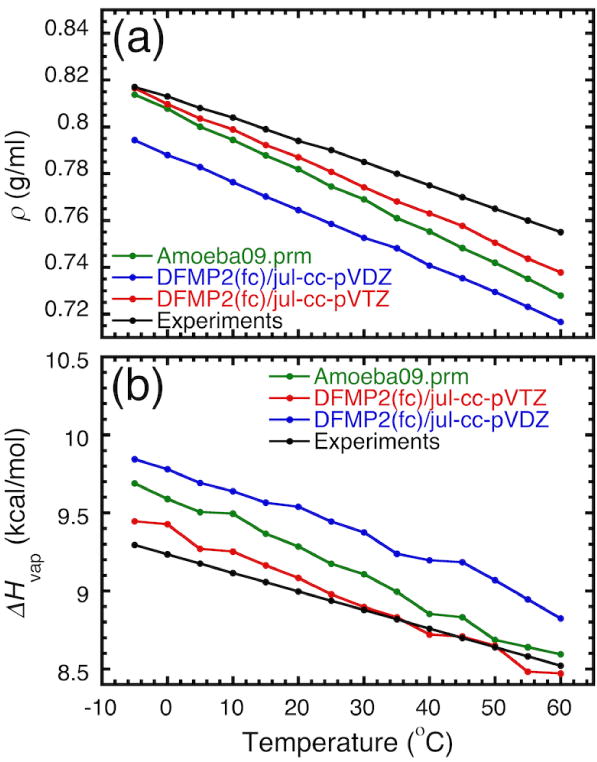
Density (ρ) and heat of vaporization (ΔH_vap) of methanol as a function of temperature from MD simulations using the optimized polizable force field optimized from the DFMP2(fc)/jul-cc-pVDZ and DFMP2(fc)/jul-cc-pVTZ data. For comparison the results from experiments and the original AMOEBA force field (amoeba09.prm) are also shown.

Finally, it is important to emphasize that consideration of many-body dispersion effects, even with pair-wise long-range vdW interactions, appears to be crucial to generate accurate force field models. For instance, attempts to use ML of the vdW parameters based on the training dataset from the interaction energy calculated at the MP2/6-31G(d,p) level for a large set of methanol dimers spanning a wide range of carbon-carbon (2 to 10 Å) distance failed to yield an accurate ML/GA generated parameters for AMOEBA force field. While the force field model with ML/GA generated parameters succeeds in accurately reproducing the dimer QM training data, the resulting force field model fails to provide an accurate representation of the bulk liquid system. MD simulations (at 25°C and 1 atmosphere) showed that such a force field model, with machine learning of vdW parameters only from dimers, severely underestimates the liquid density (0.572 g/ml) and heat of vaporization (7.32 kcal/mol) compared to experiment. We also used CCSD(T)^70–72 to calculate the interaction energies of methanol dimers. While a good correlation between the QM target data and the interaction energy from the force field model was obtained (R= 0.998), the model did not yield accurate condensed matter properties when used in MD simulations. This shows that using training data from sufficiently large cluster for the parameterization is important. The lesson here is that machine learning of the vdW parameters using QM data on clusters larger than simple dimers was essential to incorporate many-body dispersion effects into the force field model. This observation is consistent with previous results from McDaniels and Schmidt, who showed that Axilrod-Teller three-body dispersion and exchange terms needed to be incorporated in their SAPT force field of methanol to obtain a satisfactory model of the liquid phase.²⁸ In force field optimization, it is often tempting to put more emphasis on training data obtained from the highest possible level of QM. The challenge is that, to remain computationally tractable, one is typically limited to smaller systems of a few molecules that are not able to capture all the pertinent information to represent the features of a condensed phase system. This example shows that the training data must include QM calculations on sufficiently large cluster sizes. Even though the functional form for the vdW interactions comprises only pair-wise terms, it appears that many-body dispersion effects are “effectively” incorporated during the optimization of the vdW parameters based on the cluster QM data. While this may appear surprising, the situation is analogous to the fixed charges in an additive non-polarizable force field, which are empirically optimized to account for polarization in an effective manner.

CONCLUSIONS

The present study demonstrates the feasibility of predicting the condensed phase properties (i.e., density and heat of vaporization) of a substance by optimizing the parameters of a polarizable force field using QM data exclusively—without any a priori information from experiment. Experimental data was only used for validating the final force field models. This idea was tested on methanol, a small yet challenging molecule containing both polar and nonpolar moieties. A genetic algorithm was utilized to overcome the challenges of parameter optimization in a high dimensional space. For the electrostatic component of the force field, we optimized all the multipoles, polarizabilities, and Thole damping factors of methanol. The ML/GA based on dimers was able to nearly reproduce the canonical AMOEBA electrostatic parameters, the optimized parameters displaying smaller deviations relative to the QM electrostatic potential than the AMOEBA original parameters.

The vdW parameters were optimized by attempting to match the interaction energy between a central molecule and the surrounding molecules for a large number of methanol clusters. These clusters were extracted from snapshots of condensed phase MD simulations to be as representative as possible of the liquid phase. Following this protocol, excellent agreement between the optimized force field model and the QM calculations could be achieved. However, only the QM calculation from fairly high level provides sufficiently accurate vdW parameters for MD simulation to get proper condensed phase properties of methanol. Consistently better results were obtained by a using a parameterization strategy allowing for an offset factor δ between the force field and the QM target data. Through this strategy, which bears some similarities with force-matching methodologies,⁶⁸ the force field is optimized to reproduce the local “shape” of the QM energy surface without matching its absolute value. Without the offset factor δ, the absolute magnitude of the QM interactions is incorporated into the MM force field via the optimized vdW parameters, yielding models that appear to be less accurate in simulations of dense liquids.

One of the main difficulties of parameterizing a force field without any experimental input stems from the reliability of the QM calculations. Here, we consider three QM methods: MP2/6-31G(d,p), DFMP2(fc)/jul-cc-pVDZ and DFMP2(fc)/jul-cc-pVTZ. It is well known that MP2 with different basis sets can lead to different accuracy. Furthermore, there appears to be an additional issue with the overestimation of interaction energy from MP2 calculations, when using a small basis set.^{56, 65–67} The present results show that QM calculations relying on more extensive basis sets lead to a more accurate determination of the interaction energies. In principle, sampling of larger molecular clusters would also be expected to increase accuracy. Nevertheless, the current strategy was able to leverage moderate computation resource to tune the force field parameters for reasonable agreement between the MD simulated data and experimental values.