ASYMPTOTIC DISTRIBUTION OF ΔAUC, NRIs, AND IDI BASED ON THEORY OF U-STATISTICS

Abstract

The change in AUC (ΔAUC), the IDI, and NRI are commonly used measures of risk prediction model performance. Some authors have reported good validity of associated methods of estimating their standard errors (SE) and construction of confidence intervals, whereas others have questioned their performance. To address these issues we unite the ΔAUC, IDI, and three versions of the NRI under the umbrella of the U-statistics family. We rigorously show that the asymptotic behavior of ΔAUC, NRIs, and IDI fits the asymptotic distribution theory developed for U-statistics. We prove that the ΔAUC, NRIs, and IDI are asymptotically normal, unless they compare nested models under the null hypothesis. In the latter case, asymptotic normality and existing SE estimates cannot be applied to ΔAUC, NRIs, or IDI. In the former case SE formulas proposed in the literature are equivalent to SE formulas obtained from U-statistics theory if we ignore adjustment for estimated parameters. We use Sukhatme-Randles-deWet condition to determine when adjustment for estimated parameters is necessary. We show that adjustment is not necessary for SEs of the ΔAUC and two versions of the NRI when added predictor variables are significant and normally distributed. The SEs of the IDI and three-category NRI should always be adjusted for estimated parameters. These results allow us to define when existing formulas for SE estimates can be used and when resampling methods such as the bootstrap should be used instead when comparing nested models. We also use the U-statistic theory to develop a new SE estimate of ΔAUC.

AN INTRODUCTION AND A MOTIVATING EXAMPLE

In current medical research, risk prediction is viewed as an objective way to assess the risk of a patient to develop a disease and is often used by clinicians in making treatment decisions. The Framingham [1] and ATP III models for 10-year risk of cardiovascular outcomes[2], and the Gail model for 5-year risk of breast cancer[3] are among the first widely used risk prediction models. Moreover, in recent years risk-prediction models have played an increasingly important role in medical decision making and have been directly incorporated into updates of existing treatment guidelines. For instance, the U.S. Preventive Services Task Force recently issued updated guidelines on aspirin use in prevention of cardiovascular events[4], based on the results of a microsimulation model, that used the ACC/AHA risk equations for 10-year CVD risk[5]. Therefore, the quality of the performance of a risk prediction model is often crucial for assigning the most beneficial treatment and making correct policy decisions.

Risk prediction models are often evaluated in terms of calibration and discrimination. Discrimination measures how well a given model separates events from non-events; calibration measures the closeness of the model-based and observed risks of the outcome. The area under the receiver operating characteristics curve (AUC of ROC)[6–7] is a widely used measure of discrimination. In 2008 several new intuitively-appealing measures of discrimination were introduced such as the Net Reclassification Index (NRI) and Integrated Discrimination Improvement (IDI)[8–9]. They rapidly gained popularity and at the time of writing this paper had been referenced more than 2800 times. Simple estimators for variance and asymptotic distributional behavior were proposed to allow construction of confidence intervals.

While some papers reported good validity of the methods for confidence intervals and variance estimators of ΔAUC, NRIs, and IDI[8, 10–11], others questioned their performance[10, 12–14]. To illustrate these conflicting views, we ran some simulations and summarize the results in Table 1. For two nested models with binary outcome and multivariate normal predictor variables, we compare observed and theoretical standard errors of ΔAUC, three types of NRIs (continuous (NRI_>0), 2-category NRI at event rate threshold (NRI(r)) and 3-category NRI (3cNRI), and IDI. AUC is a measure of discrimination. It is equal to the probability that the risk of a randomly picked event is greater than for randomly picked non-event[6–7]. ΔAUC measures improvement in quality of discrimination between events and non-event by the new model relative to the old one[11]. NRI_>0, another measure of discrimination, calculates the difference between fractions of correct and incorrect movements of predicted probabilities among events and adds to it a similar quantity calculated for non-events[9]. Categorical NRIs are similar to NRI_>0 but consider only movements across categories. NRI(r) uses two categories defined by event rate threshold[15]. 3cNRI uses three categories defined by any thresholds[16]. IDI combines average change in probabilities among events and among non-events[8]. For comparison we included the regression coefficient (β) for the new predictor variable x₂. The relative bias of standard error estimate is calculated as $\frac{(\text{theoretical se}-\text{obsercved se})}{\text{obsercved se}}100\%$. Shaded areas in Table 1 indicate scenarios in which the relative bias is 5% or more in our simulations, while white areas indicate when standard errors have very low bias (<5%). Asymptotic theory developed for three of the five statistics performed very well in most situations, while the bias of the 3-category NRI is comparable to that of the standard error estimator of the Kaplan-Meier survival probability (when sample size is small)[17], and the se estimator of the IDI has the strongest bias of the five statistics.

Table 1. Relative bias (%) of standard errors of ΔAUC, NRI_>0, 3-category NRI, and IDI.

Relative bias of standard error estimates of ΔAUC, IDI and three types of NRI $(\mathit{\text{rel}}.\mathit{\text{bias}}=\frac{{\mathit{\text{se}}}_{\mathit{\text{formula}}.\mathit{\text{based}}}-{\mathit{\text{se}}}_{\mathit{\text{bootstrap}}}}{{\mathit{\text{se}}}_{\mathit{\text{bootstrap}}}}\times 100\%)$. We evaluated the performance of two nested risk prediction models: a logistic regression model with two multivariate normally distributed predictor variables (x₁ and x₂) and a baseline logistic regression model with only one of the predictors (x₁). We considered several simulations scenarios: effect size by the new predictor (x₂) of 0, .2 and .7, effect size by commonly used predictor variable (x₁) is .7, sample sizes of 30,000, 2,000 and 500 observations, 0.1 event rate, B=1,000 simulated datasets. 2% and 10% cutoffs were used for 3cNRI calculation.

		Relative Bias (%) of the Standard Error Estimate of
effect size	ssize	βx2	ΔAUC	NRI>0	NRI(r)	3cNRI	IDI
0	30,000	3	7	29	−7	−7	−31
0	2,000	0	8	26	−12	−13	−37
0	500	0	8	26	−12	−13	−37
0.2	30,000	3	1	−3	1	−5	−42
0.2	2,000	1	−1	−3	−1	−10	−45
0.2	500	1	−1	−3	−1	−10	−45
0.7	30,000	2	0	−1	0	−26	−38
0.7	2,000	1	3	−2	1	−26	−39
0.7	500	1	3	−2	1	−26	−39

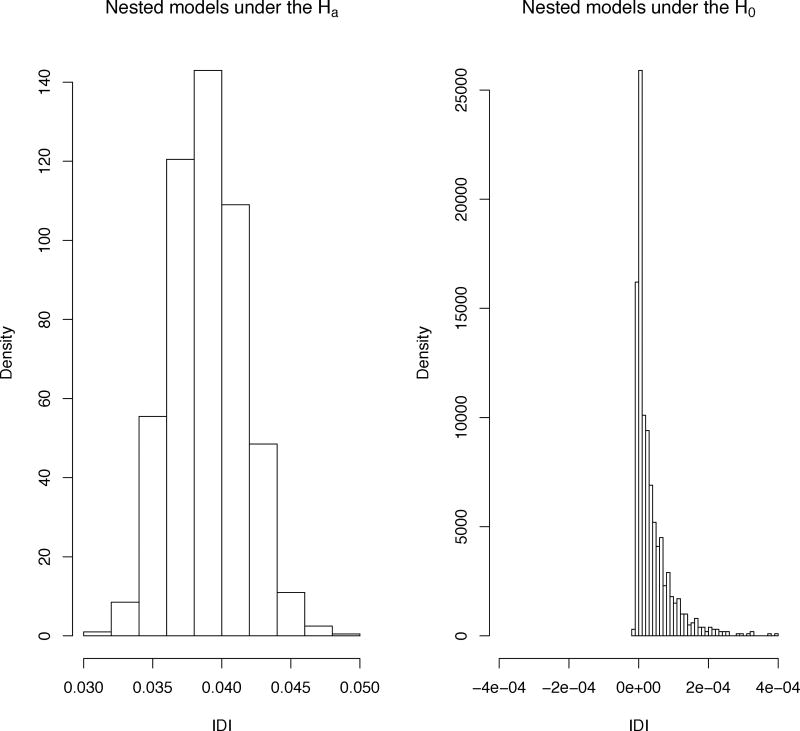
Confidence intervals for ΔAUC, NRI_>0, categorical NRIs, and IDI proposed to date rely on asymptotic normality [8–9, 11, 18–19]. In Figure 1 we show an example in which the IDI is asymptotically normally distributed under the alternative hypothesis of meaningful effect (left panel) and right-skewed under the null hypothesis of no meaningful effect (right panel) [20].

Figure 1.

Histograms of IDI when comparing nested models under the alternative (left panel), and under the null (right panel). x₁, x₂ are predictors from the full model; x₁ is the predictor from the reduced model. Left panel: simulated nested models under the alternative x₁,), x₂ |D=1~N(μ, Σ) and x₁, x₂ |D=0~N(0, Σ). Right panel: simulated nested models under the null x₁ |D=1~N(μ, σ²), x₁ |D=0~N(0, σ²) and x₂~N(0, σ²). x₂ is an uninformative predictor.

This paper is a validity study of previously proposed asymptotic distribution results of ΔAUC, IDI and three types of NRIs (continuous (NRI_>0), 2-category NRI at event rate threshold (NRI(r)) and 3-category NRI (3cNRI)[8–9, 11, 18–19] when comparing two nested models. Using U-statistics theory we explicitly specify conditions when asymptotic results are valid and when resampling methods such as the bootstrap should be used instead. These results help us disentangle several reports of the asymptotic distribution and performance of variance estimators of ΔAUC, IDI, and three types of the NRI. The paper is structured as follows: notation is introduced in Section 1; the main result is stated and proved in Section 2; in Section 3 we apply theoretical findings to the Framingham Heart Study Data; and the implications of these findings are discussed in Section 4.

1. NOTATION

Let D be an outcome of interest, with D=1 for events and D=0 for non-events. Our goal is to predict the event status using p predictor variables. Conditioning on the event status, predictor variables follow two (potentially different) distribution functions: x|D=0~F(․), y|D=1~G(․). Assume that for each of N patients, their disease status D and vector of predictor variables are available. There are n₀ non-events and n₁ events. The prediction based on the full set of p predictor variables is to be compared with that based on a reduced number of predictor variables, p−1. We assume that the linear model is true and that one of the linear models for binary outcome is employed (logistic regression, linear discriminant analysis (LDA), etc). We use this model to estimate linear coefficients in order to combine multiple predictor variables into one metric, the risk score. Unless otherwise specified, we assume that the models are nested, so the new model adds k new predictors to the old model. The regression technique of choice produces coefficients estimates ${\mathit{a}}^{\ast \prime }=(a_1^{\ast },\dots ,a_{p-k}^{\ast },0,\dots ,0)$ (reduced model) and a′ = (a₁ …, a_p) (full model). Corresponding risk scores are calculated as a′x and a*′x for non-events and a′y and a*′y for events, with the symbol * always denoting the reduced model. We sought to test whether the risk prediction model with p predictors performs better than the model with only the first p−k predictors. We will consider ΔAUC, three varieties of the NRI and the IDI as measures of model performance. They are often used in current medical research on risk prediction. Analysis of their performance, advantages and disadvantages is an active area of methodological research on risk prediction. Below we review standard formulas[8–9, 11] for ΔAUC, continuous NRI (NRI_>0), 3cNRI, NRI(r), and IDI.

ΔAUC

The Area under ROC curve (AUC) can be interpreted as the probability that the risk score of a randomly picked event is higher than a randomly picked non-event. The AUC is estimated by the Mann-Whitney statistic[6–7] - a non-parametric unbiased estimator, often referred to as the c-statistic[21–22] and can be written as: $\mathit{\text{AUC}}=\frac{1}{n_0{n}_1}{\sum }_{i=1}^{n_0}{\sum }_{j=1}^{n_1}I[\mathit{a}\prime {\mathit{x}}_{\mathit{i}}<\mathit{a}\prime {\mathit{y}}_{\mathit{j}}]$, where I[․] is the indicator function.

The AUC for the reduced model is: ${\mathit{\text{AUC}}}^{\ast }=\frac{1}{n_0{n}_1}{\sum }_{i=1}^{n_0}{\sum }_{j=1}^{n_1}I[{\mathit{a}}^{\ast \prime }{\mathit{x}}_{\mathit{i}}<{\mathit{a}}^{\ast \prime }{\mathit{y}}_{\mathit{j}}]$

Then ΔAUC is:

$$\mathrm{\Delta }\mathit{\text{AUC}}=\frac{1}{n_0{n}_1}\sum _{i=1}^{n_0}\sum _{j=1}^{n_1}I[\mathit{a}\prime {\mathit{x}}_{\mathit{i}}<\mathit{a}\prime {\mathit{y}}_{\mathit{j}}]-\frac{1}{n_0{n}_1}\sum _{i=1}^{n_0}\sum _{j=1}^{n_1}I[{\mathit{a}}^{\ast \prime }{\mathit{x}}_{\mathit{i}}<{\mathit{a}}^{\ast \prime }{\mathit{y}}_{\mathit{j}}]$$

ΔAUC is one of the most widely used measures of discrimination.

Continuous NRI (NRI_>0)

NRI_>0[9] is the difference of proportions of individuals with events and non-events whose predicted probabilities moved up:

$${\mathit{\text{NRI}}}_{>0}=\frac{{\sum }_{i=1}^{n_1}\mathit{\text{Sign}}[p_{\mathit{\text{new ev}}}-p_{\mathit{\text{old ev}}}]}{n_1}-\frac{{\sum }_{i=1}^{n_0}\mathit{\text{Sign}}[p_{\mathit{\text{new nonev}}}-p_{\mathit{\text{old nonev}}}]}{n_0}=\frac{\#\mathit{\text{events up}}}{n_1}-\frac{\#\mathit{\text{nonevents up}}}{n_0}$$

3-category NRI

3-category NRI[16] is very close to the original definition of categorical NRI[9] but takes into account the size of the jump from category to category (number of categories moved). It is defined as:

$$3\mathit{\text{cNRI}}=\frac{1}{n_1}\sum _{i=1}^{n_1}\#{\mathit{\text{categories up}}}_i-\#{\mathit{\text{categories down}}}_i-\frac{1}{n_0}\sum _{j=1}^{n_0}\#{\mathit{\text{categories up}}}_j-\#{\mathit{\text{categories down}}}_j$$

This definition of categorical NRI is preferable over its original 2008 version[8], due to several attractive properties[16], including the fact that 3cNRI=0 if marginal cells of the reclassification table stay the same for the two models. By using weights it treats jumps across one versus two categories differently, and the event rate has a limited impact on the magnitude of the 3cNRI. Therefore it successfully resolves several criticisms of the original definition of categorical NRI[23–24].

NRI at the event rate (NRI(r))

In their 2016 paper, Pencina, Steyerberg and D’Agostino[15] investigate the properties of a two-category NRI with categories defined by the proportion of cases in the sample (r) and show that it has several advantages: like ΔAUC, it is invariant to the event rate and has intuitive interpretation as the proportion of correct reclassifications.

IDI

IDI[8] is defined as:

$$\mathit{\text{IDI}}=\frac{{\sum }_{i=1}^{n_1}{p}_{\mathit{\text{new ev }}i}-p_{\mathit{\text{old ev }}i}}{n_1}-\frac{{\sum }_{i=1}^{n_0}[p_{\mathit{\text{new nonev }}i}-p_{\mathit{\text{old nonev }}i}]}{n_0}$$

IDI is related asymptotically to the rescaled Brier score and to the difference in discrimination slope[25]. We mentioned some criticisms of IDI above and below we address some of them.

Now we can formulate the following null hypotheses for the six statistics defined above:

$$H_0^{\mathit{\text{AUC}}}:\mathrm{\Delta }\text{AUC}=0\text{ vs }{H}_a^{\mathit{\text{AUC}}}:\mathrm{\Delta }\text{AUC}\ne 0$$

$$H_0^{\mathit{\text{NRI}}}:{\text{NRI}}_{>0}=0\text{ vs }{H}_a^{\mathit{\text{NRI}}}:{\text{NRI}}_{>0}\ne 0$$

$$H_0^{\mathit{\text{NRI}}}:\text{ NRI}(\mathrm{r})=0\text{ vs }{H}_a^{\mathit{\text{NRI}}}:\text{ NRI}(\mathrm{r})\ne 0$$ (1)

$$H_0^{3\mathit{\text{cNRI}}}:3\text{cNRI}=0\text{ vs }{H}_a^{3\mathit{\text{cNRI}}}:3\text{cNRI}\ne 0$$

$$H_0^{\mathit{\text{IDI}}}:\text{ IDI}=0\text{ vs }{H}_a^{\mathit{\text{IDI}}}:\text{ IDI}\ne 0$$

Pepe et al[26–27] showed that each of the five hypotheses in (1) are equivalent to testing the significance of the set of the new predictors in the new regression model (2).

$$H_0:{\mathrm{a}}_{p-k+1},\dots ,{\mathrm{a}}_p=\mathbf{0}\text{ vs }{H}_a:{\mathrm{a}}_{p-k+1},\dots ,{\mathrm{a}}_p\ne \mathbf{0}$$ (2)

Therefore when we consider data under the null we can without loss of generality assume that the null is formulated in terms of non-significance of the linear coefficient by the new predictor variable, that is the hypothesis in (2).

2. MAIN RESULT

We formulate our main results as follows.

ΔAUC, NRI_>0, NRI(r), 3cNRI and IDI:

• STATEMENT 1. are generalized U statistics with estimated parameters.

• STATEMENT 2. belong to non-degenerate subclass if and only if they compare any non-nested models or nested models under the alternative hypothesis in (2). As non-degenerate U-statistics

  1. They follow normal distribution asymptotically.
  2. Available variance formulas are algebraically equal to the variance estimators provided by U-statistics theory if we ignore adjustment for estimated parameters.
  3. Variance of ΔAUC, NRI_>0, and NRI(r) does not need to be adjusted for estimated parameters if predictor variables are normally distributed.
  4. Variance of IDI and 3-category NRI should always be adjusted for estimated parameters.

• STATEMENT 3. ΔAUC, NRI_>0, NRI(r), 3cNRI and IDI belong to the degenerate subclass if and only if they compare nested models under the null hypothesis in (2). As degenerate U-statistics they do not follow normal distribution and available variance estimators do not apply for them.

2.1 ΔAUC, NRI_>0, NRI(R), 3CNRI AND IDI BELONG TO THE U-STATISTICS FAMILY

In Appendix A2 we prove Statement 1 showing that statistics considered in this paper belong to a U-statistics family[28]. Rigorous asymptotic distribution theory of U-statistics has been developed by Hoeffding[29], Lehman[30], Sukhatme[31] and others. The form of the U-statistics’ distribution depends on whether the U-statistics are degenerate. Non-degenerate U-statistics are normally distributed and formulas for their standard errors are available. Degenerate U-statistics are distributed as an infinite sum of weighted Chi-square random variables and derivation of their standard error is challenging.

In Appendix A2 we show that ΔAUC, NRI_>0, NRI(r), 3cNRI and IDI are degenerate if and only if they compare nested models under the null. In all other situations they belong to the non-degenerate class of U-statistics. Degeneracy and non-degeneracy conditions are listed in Table 2.

Table 2.

Non-degeneracy conditions of ΔAUC, NRI_>0, NRI(r), 3cNRI, and IDI

	Models are under the null	Models are under the alternative
Nested Models	Degenerate*	Non-degenerate
Non-nested Models	Always non-degenerate

^*Null is defined as in (2) in the previous section. H₀: a_p−k+1, …, a_p = 0

Degenerate and non-degenerate U-statistics form very different classes in terms of their asymptotic behavior. In the following sections we will consider these two situations separately.

2.2 NON-DEGENERATE CASE

ΔAUC, NRIs and IDI are non-degenerate if they evaluate the performance of two non-nested models or of nested models under the alternative. This is the most practically interesting case because only in this situation we need to construct confidence intervals for ΔAUC, NRIs and IDI. Hoeffding[29] and Lehman[30] showed that non-degenerate U-statistics are asymptotically normally distributed. U-statistics theory also provides their variance formulas[28] but notes that variances should be adjusted for estimated parameters. Adjustment has been studied by Sukhatme[32], Randles[33] and de Wet[34] and is summarized in[28].

Available variance estimators are identical to U-statistics theory-based variance estimators if we ignore an adjustment for estimated parameters

In the Appendix we derived variances of ΔAUC, NRIs and IDI based on U-statistics theory, ignoring adjustment for estimated parameters and presented them in Table 3. The standard errors of NRI_>0 and NRI(r) based on the U-statistics theory are exactly the same as the ones derived by Pencina et al in [10][11]. The standard error formula for ΔAUC is new. It is equal to the variance of the change in ranks. This representation is more intuitive but it assumes no tied ranks.

Table 3.

Variance formulas in non-degenerate case, unadjusted for estimated parameters.

	$\widehat{{\sigma }^2}$, ignoring the adjustment for estimated parameters	Requires Adjustment?
${\hat{\sigma }}_{\mathrm{\Delta }\mathit{\text{AUC}}}^2$ no tied ranks	$\frac{\mathit{\text{Var }}({\mathit{\text{rank}}}_e^{\ast }({\mathit{\alpha }}^{\ast \mathit{T}}{\mathit{x}}_{\mathit{i}})-{\mathit{\text{rank}}}_e({\mathit{\alpha }}^{\mathit{T}}{\mathit{x}}_{\mathit{i}}))}{n_0}+\frac{\mathit{\text{Var }}({\mathit{\text{rank}}}_{\mathit{\text{ne}}}^{\ast }({\mathit{\alpha }}^{\ast \mathit{T}}{\mathit{y}}_{\mathit{j}})-{\mathit{\text{rank}}}_{\mathit{\text{ne}}}({\mathit{\alpha }}^{\mathit{T}}{\mathit{y}}_{\mathit{j}}))}{n_1}$	No
${\hat{\sigma }}_{\mathrm{\Delta }\mathit{\text{AUC}}}^2$ tied ranks	Use DeLong formula[11]	No
${\hat{\sigma }}_{{\mathit{\text{NRI}}}_{>0}}^2$	$\frac{{\hat{p}}_{\mathit{\text{ne}}}^{\mathit{\text{up}}}(1-{\hat{p}}_{\mathit{\text{ne}}}^{\mathit{\text{up}}})}{n_0}+\frac{{\hat{p}}_e^{\mathit{\text{up}}}(1-{\hat{p}}_e^{\mathit{\text{up}}})}{n_1}$	No
${\hat{\sigma }}_{\mathit{\text{NRI}}(r)}^2$	$\frac{{\hat{p}}_{\mathit{\text{ne}}}^{\mathit{\text{up}}}+{\hat{p}}_{\mathit{\text{ne}}}^{\mathit{\text{down}}}-{({\hat{p}}_{\mathit{\text{ne}}}^{\mathit{\text{up}}}-{\hat{p}}_{\mathit{\text{ne}}}^{\mathit{\text{down}}})}^2}{n_0}+\frac{{\hat{p}}_{\mathit{\text{ev}}}^{\mathit{\text{up}}}+{\hat{p}}_{\mathit{\text{ev}}}^{\mathit{\text{down}}}-{({\hat{p}}_{\mathit{\text{ev}}}^{\mathit{\text{up}}}-{\hat{p}}_{\mathit{\text{ev}}}^{\mathit{\text{down}}})}^2}{n_1}$	No
${\hat{\sigma }}_{3c\mathit{\text{NRI}}}^2$	$\frac{4({\hat{p}}_{\mathit{\text{ne}}}^{2\mathit{\text{up}}}+{\hat{p}}_{\mathit{\text{ne}}}^{2\mathit{\text{down}}})+{\hat{p}}_{\mathit{\text{ne}}}^{1\mathit{\text{up}}}+{\hat{p}}_{\mathit{\text{ne}}}^{1\mathit{\text{down}}}-{(2({\hat{p}}_{\mathit{\text{ne}}}^{2\mathit{\text{up}}}-{\hat{p}}_{\mathit{\text{ne}}}^{2\mathit{\text{down}}})+{\hat{p}}_{\mathit{\text{ne}}}^{1\mathit{\text{up}}}-{\hat{p}}_{\mathit{\text{ne}}}^{1\mathit{\text{down}}})}^2}{n_0}+\frac{4({\hat{p}}_{\mathit{\text{ev}}}^{2\mathit{\text{up}}}+{\hat{p}}_{\mathit{\text{ev}}}^{2\mathit{\text{down}}})+{\hat{p}}_{\mathit{\text{ev}}}^{1\mathit{\text{up}}}+{\hat{p}}_{\mathit{\text{ev}}}^{1\mathit{\text{down}}}-{(2({\hat{p}}_{\mathit{\text{ev}}}^{2\mathit{\text{up}}}-{\hat{p}}_{\mathit{\text{ev}}}^{2\mathit{\text{down}}})+{\hat{p}}_{\mathit{\text{ev}}}^{1\mathit{\text{up}}}-{\hat{p}}_{\mathit{\text{ev}}}^{1\mathit{\text{down}}})}^2}{n_1}$	Yes
${\hat{\sigma }}_{\mathit{\text{IDI}}}^2$	$\frac{\mathit{\text{Var}}(\mathrm{\Delta }\mathit{\text{predp}}({\mathit{x}}_{\mathit{i}}))}{n_0}+\frac{\mathit{\text{Var}}(\mathrm{\Delta }\mathit{\text{predp}}({\mathit{y}}_{\mathit{j}}))}{n_1}$	Yes

U-statistics theory adds one more layer to variance calculations, namely that when U-statistic relies on estimated parameters, its variance in general should be adjusted for estimated parameters. In many cases ΔAUC, NRIs and IDI rely on estimated parameters (linear coefficients of regression models), their variances may need to be adjusted for estimated parameters or we need to show that such adjustment is not necessary. In the following section we prove that for some of the statistics under certain assumptions, adjustment for estimated parameters is unnecessary.

Variances of ΔAUC, NRI_>0, and NRI(r) do not need to be adjusted for estimated parameters if predictor variables are normally distributed

Sometimes adjustment for estimated parameters can be avoided. Sukhatme[32], Randles[33] and de Wet[34] showed that adjustment for estimated parameters is unnecessary if and only if a certain condition is met[28]. Below we check this condition and show that under normality of predictor variables, standard error estimates of ΔAUC, continuous NRI and NRI(r) do not need to be adjusted for estimated parameters.

STATEMENT 2.C

If ΔAUC, NRI_>0, and NRI(r) when comparing nested models are non-degenerate (therefore according to Table 2 they are under the alternative) and if predictor variables are normally distributed, then standard errors of ΔAUC, continuous NRI and NRI(r) do not need to be adjusted for estimated parameters.

Proof

We restate here the condition for adjustment for estimated parameters:

Suhkatme-Randles-de Wet Condition:

• Standard errors for a U-statistic with estimated parameters does not need to be adjusted for estimated parameters if and only if the derivative of the expected value of the U-statistic with respect to parameters is zero.

For example for ΔAUC this condition is written as $\frac{\partial }{\partial a}E[\mathrm{\Delta }\mathit{\text{AUC}}]=0$.

In our assumptions predictors are normally distributed, therefore linear discriminant analysis (LDA) is the most efficient way to estimate regression coefficients[35]. Su and Liu[36] also showed that under these assumptions LDA coefficients maximize Mahalanobis distance[37] (M²) between risk scores of events and non-events. Therefore the gradient of Mahalanobis distance with respect to parameters is zero. For nested models ΔAUC is a function of the Mahalanobis distances $(\mathrm{\Delta }\mathit{\text{AUC}}=\mathrm{\Phi }(\sqrt{\frac{M_p^2}{2}})-\mathrm{\Phi }(\sqrt{\frac{M_{p-k}^2}{2}}))$[36], where p is the number of predictor variables in a model and Φ is the standard normal c.d.f. Hence the gradient of ΔAUC with respect to parameters is zero as well. Therefore the standard error of ΔAUC under the assumption of normality of predictor variables does not need to be adjusted for estimated parameters.

Similarly we can use a closed-form formula for NRI_>0[38] for nested models: ${\text{NRI}}_{>0}=4\mathrm{\Phi }\left(\frac{\sqrt{M_p^2-M_{p-k}^2}}{2}\right)-2$ to show that gradient of NRI_>0 is also zero at the LDA coefficients. Therefore the standard error of NRI_>0 also does not need to be adjusted for estimated parameters.

Pencina, Steyerberg and D’Agostino[15] showed that NRI(r) under normality assumptions when comparing nested models can be written as: $\mathit{\text{NRI}}(r)=2·\left(\mathrm{\Phi }\right(\sqrt{\frac{M_p^2}{2}})-\mathrm{\Phi }(\sqrt{\frac{M_{p-k}^2}{2}}\left)\right)$. The same reasoning can be applied to NRI(r) to show that $\frac{\partial }{\partial a}\mathit{\text{NRI}}(r)=0$. Therefore NRI(r) does not need to be adjusted for estimated parameters under the assumptions of this statement.

q.e.d.

STATEMENT 2.D

Variances of IDI and 3-category NRI should always be adjusted for estimated parameters

Note that the IDI and 3cNRI also can be expressed in closed form under normality of predictor variables [16, 38] (please see the Appendix), but their closed form expression does not rely exclusively on the Mahalanobis distance. It also depends on the estimated rate of events r, which becomes one of the parameters. Under normality of predictor variables LDA solution maximizes Mahalanobis distance, and therefore the derivative of $M_p^2$ with respect to regression parameters is zero. However there is no such result for partial derivative of the closed form formulas of IDI and 3cNRI with respect to event rate. Derivatives of closed-form formulas of 3cNRI and IDI with respect to event rate were calculated in the Appendix A4. Both derivatives are non-linear in r and both are in general non-zero. For example derivatives of 3cNRI and IDI are 2.02 and 1.04 correspondingly for event rate observed in FHS of 7.65%, when comparing models with Mahalanobis distances of 0.7 and 0.8 and using 5% and 7.5% cutoffs to calculate 3cNRI. Therefore the Sukhatme-Randles-deWet condition is not satisfied for IDI and 3cNRI, and standard errors of IDI and 3cNRI should be adjusted for estimated parameters.

Our empirical results in Table 1 support the main theoretical results proven in this paper. Variances of ΔAUC, NRI_>0, and NRI(r) calculated from unadjusted formulas have on average very small relative bias compared to those of the IDI and 3-category NRI whose variances must be adjusted for estimated parameters.

Also the top three rows of Table 1 are calculated for the degenerate case (when comparing two nested models under the null). All five statistics are degenerate and theoretical formulas for their variance estimator are not applicable: existing variance formulas have strong bias for all five statistics when comparing nested models under the null.

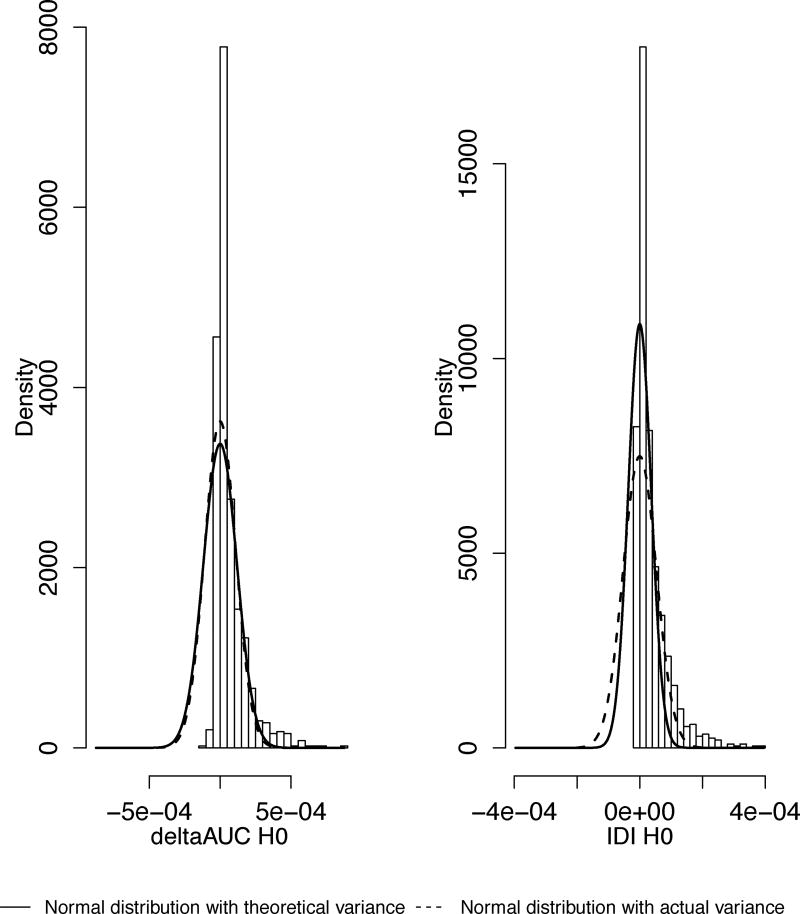
To illustrate further the main theoretical findings of this paper, we simulated a binary model with normally distributed predictor variables. In Figure 2 we plot histograms of ΔAUC, NRIs and IDI calculated for nested models under the alternative and overlay two normal distribution curves with empirical (dotted line) and theoretical (solid) variances. In the top row are ΔAUC, NRI_>0, and NRI(r). They do not need to be adjusted for estimated parameters and the dotted and solid curves almost completely overlap. In the bottom row are IDI and 3cNRI. They require adjustment for estimated parameters, and the two curves do not overlap because the theoretical variance is an incorrect estimate of the actual variance of 3cNRI and IDI.

Figure 2.

Two normal density curves with empirical (dotted line) and theoretical from Table 2 (solid line) variances overlaid on the histograms of the five statistics calculated for nested models under the alternative (non-degenerate case). Simulated two predictor variables and binary outcomes: x₁, x₂ |D=1~N(μ, Σ) and x₁, x₂ |D=0~N(0, Σ). x₁, x₂ are predictors from the full model; x₁ is the predictor from the reduced model.

Statement 2.C and 2.D for logistic regression and non-normal data

We showed in the proof of Statement2.C that by estimating parameters with LDA we ensured that Sukhatme-Randles-deWet condition holds true. What would happen if we had used logistic regression to estimate parameters instead of the LDA? To use theoretical variance formulas we need to show that adjustment for parameters estimated by logistic regression is not required. Therefore we need to satisfy the Sukhatme-Randles-deWet condition. Parameter estimates produced by logistic regression and the LDA are both consistent under assumption of normality[35]; therefore, when sample size is sufficiently large the two estimates are very close. In Table 1 we used logistic regression to estimate parameters for simulated normal data. Table 1 supports the theoretical findings of Statement 2.C and 2.D despite the use of logistic regression.

The proof of Statement 2.C and the discussion above rely on normality of predictor variables. An important question is how sensitive these results are to the normality assumption. In Section 3 we apply the results of this section to real-life non-normal data using logistic regression and discuss the implications.

2.3 DEGENERATE CASE

In the Appendix we show that when comparing nested models under the null ΔAUC, NRIs and IDI belong to a degenerate class of U-statistics. They are distributed as an infinite sum of weighted Chi-square distributions. Histograms in Figure 3 demonstrate why any test that assumes normality is invalid for ΔAUC and IDI.

Figure 3.

Histograms of ΔAUC and IDI when comparing nested models under the null. Two normal density curves with empirical (dotted line) and theoretical (solid line) variances overlaid on the histograms of ΔAUC and IDI calculated for nested models under the null (degenerate case). Simulated two predictor variables and binary outcome: x₁ |D=1~N(μ, σ²), x₁ |D=0~N(0, σ²) and x₂~N(0, σ²). x₂ is an uninformative predictor. x₁, x₂ are predictors from the full model; x₁ is the predictor from the reduced model.

Injecting random noise to remedy degeneracy

In previous sections we discussed problems induced by the degenerate state of ΔAUC, NRIs and IDI when they compare nested models under the null. Their asymptotic distribution and variance estimators become practically intractable. In their non-degenerate state ΔAUC, NRIs and IDI follow a normal distribution asymptotically, and variance formulas are available. In this section we show how degeneracy is at the root of the problem. We will artificially move ΔAUC, NRIs and IDI away from degeneracy and show that their distribution functions shift to normal distribution. This will shed some light on other aspects of NRI behavior that we will discuss later in the section. In the Appendix the degeneracy condition is formulated in mathematical terms and it follows that the nested models under the null are the fundamental reason for the degeneracy of ΔAUC, NRI_>0, IDI, and all categorical versions of the NRI. So let us consider two nested models under the null. ΔAUC, NRIs and IDI calculated for these two models will be in a degenerate state. To force them to move away from the degeneracy we need to violate the degeneracy condition: one way is to force the models away from the null, and an alternative way is to un-nest them. In practical situations we have no control over a model being under the null or under the alternative. However we can try to un-nest the two models by injecting random noise, i.e., add a weak predictor to the smaller model and another independent weak predictor of the same strength to the other model. Histograms of these statistics for the same models but with injected noise are in the right column of the Figure 4. Their distributions shift to asymptotic normality. Results for variance estimators hold in this example too: variance estimate of ΔAUC is still satisfactory and the variance of the IDI is underestimated by existing formulas. Our simulations indicate that de-degenerating these two U-statistics comes at the price of a substantial increase of variance and leads to a loss of power. However this exercise helps to explain why the distribution of NRI_>0, NRI(r) and 3cNRI appear more Gaussian for the degenerate state in our simulations (Figure 5). The IDI can be written as: $\mathit{\text{IDI}}=\frac{{\sum }_{i=1}^{n_1}{p}_{\mathit{\text{new ev}}}-p_{\mathit{\text{old ev}}}}{n_1}-\frac{{\sum }_{i=1}^{n_0}{p}_{\mathit{\text{new nonev}}}-p_{\mathit{\text{old nonev}}}}{n_0}$. The NRI_>0 uses the same definition as IDI but dichotomizes the change in predictive probability:

$${\mathit{\text{NRI}}}_{>0}=\frac{{\sum }_{i=1}^{n_1}\mathit{\text{Sign}}[p_{\mathit{\text{new ev}}}-p_{\mathit{\text{old ev}}}]}{n_1}-\frac{{\sum }_{i=1}^{n_0}\mathit{\text{Sign}}[p_{\mathit{\text{new nonev}}}-p_{\mathit{\text{old nonev}}}]}{n_0}$$

Figure 4.

Left column: two nested models under the H₀; right column: the two models after un-nesting, preserving the H₀. Left panel models: x₁, x₂ are predictors from the full model; x₁ is predictor from the reduced model. x₁ |D=1~N(μ, σ²), x₁ |D=0~N(0, σ²) and x₂~N(0, σ²). x₂ is an uninformative predictor.

Right panel models: x₁, x₂, x₃ are predictors from the full model; x₁, x₄ are predictors from the reduced model. x₁ |D=1~N(μ, σ²), x₁ |D=0~N(0, σ²) and x₂~N(0, σ²). x_3,4|D=1~N(ε, Iσ²) and x_3,4|D=0~N(0, Iσ²). x₂ is an uninformative predictor, x₃, x₄ are added “noise” – simulated weak independent predictors.

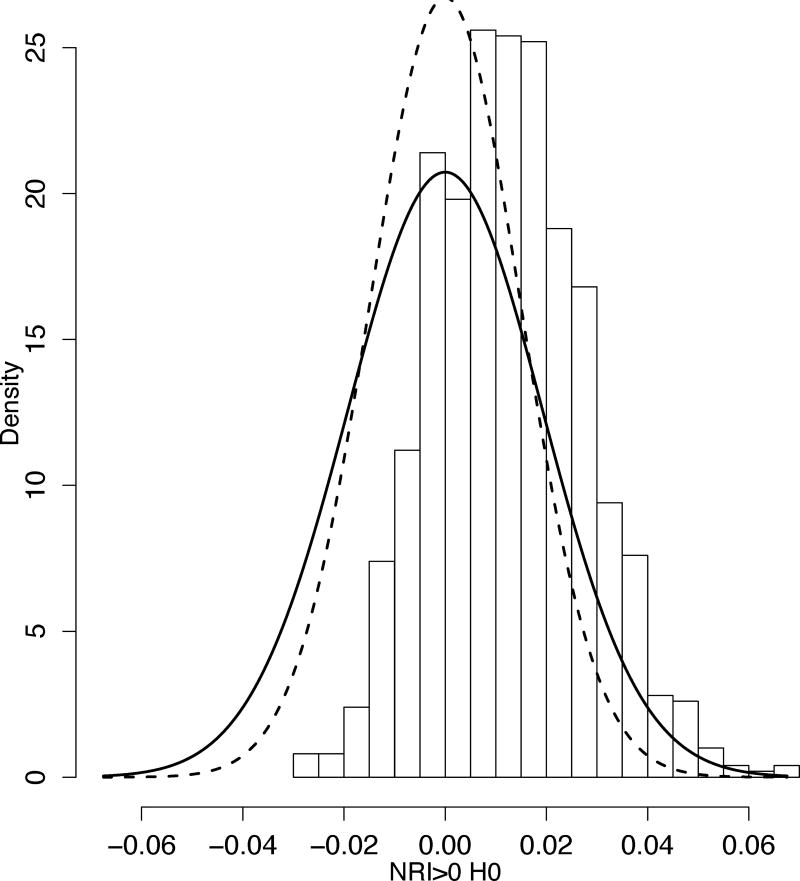
Figure 5.

Histogram of NRI>0 under H₀. Simulated two predictor variables and a binary outcome: x₁|D=1~N(μ, σ^2), x₁ |D=0~N(0, σ²) and x₂~N(0, σ²). x₂ is an uninformative predictor. x₁, x₂ are predictors from the full model; x₁ is the predictor from the reduced model.

Therefore we can view the NRI_>0 as an IDI that adds to each summand a random component that complements it to the nearest of the values of 1 or −1. This random component operates as injected noise in the Figure 4. It adds enough noise so that NRI_>0 transitions to non-degeneracy and its histogram looks Gaussian, even though a predictor variable of interest (x₂) does not improve the performance of the model (Figure 5). Note that NRI_>0 remains biased. Its bias is studied in [39].

3. PRACTICAL EXAMPLE

We apply our results to Framingham Heart Study (FHS)[1, 40] data. Full information about this data set and the study including the enrollment criteria is reported in[40]. Briefly, 8365 people free of cardiovascular disease at baseline examination were followed for 12 years. The outcome of interest was coronary heart disease (CHD), and 640 people developed CHD during followup (7.7%). Predictor variables in this example include age, total (TCL) and high-density lipoprotein (HDL) cholesterol, systolic (SBP) and diastolic blood pressure (DBP), baseline diabetes status and current smoking. All continuous variables are log-transformed. We use logistic regression to run the full model with all the predictors. We also ran a series of smaller nested models, which we obtained by omitting from the full model one of the predictor variables.

The bootstrap estimator of the standard error is consistent for a wide range of statistics under mild regularity conditions[41–43]. Therefore we can use the bootstrap estimate of the standard error of ΔAUC, NRI_>0 and IDI as a proxy for the gold standard, i.e. as an estimator with established consistency. For this reason we define the relative bias of the formula-based standard error as the difference between the average of a formula-based and bootstrap-based variance estimates divided by the bootstrap-based variance estimate.

In this practical example all predictors are statistically significant; therefore according to results of this paper ΔAUC, NRI_>0 and IDI are non-degenerate U-statistics, and according to Statement 2C we would expect low bias of the theoretical standard error formulas for ΔAUC, NRI_>0 and NRI(r) and high bias for those that require adjustment for estimated parameters: 3-category NRI and IDI.

Results

Relative bias of the standard error was calculated for FHS data using bootstrap as described in the previous section. Results are presented in Table 4.

Table 4.

Relative bias (bottom table) $(\text{rel}.\text{bias}=\frac{{\mathit{\text{se}}}_{\mathit{\text{formula}}.\mathit{\text{based}}}-{\mathit{\text{se}}}_{\mathit{\text{bootstrap}}}}{{\mathit{\text{se}}}_{\mathit{\text{bootstrap}}}}\times 100\%)$ and averaged bootstrap estimates were calculated by bootstrapping FHS dataset by simple random sampling with replacement. The full model included baseline values of age, TCL, HDL, SBP,DBP, diabetes status and current smoking. The first row compares the full model to the same model without SBP as a predictor. The row “AGE” compares the full model to the same model but with age omitted from the list of predictors.

	Parameter Estimates
	β1	ΔAUC	NRI>0	NRI(r)	3cNRI3	IDI
SBP	1.39	0.00	0.03	0.01	0.00	0.00
HDL	−1.65	0.03	0.44	0.06	0.12	0.02
TCL	1.57	0.01	0.25	0.02	0.06	0.01
AGE	2.73	0.02	0.46	0.06	0.16	0.01
DBP	1.05	0.00	0.20	0.01	0.01	0.00
SMOKING	0.50	0.01	0.16	0.02	0.05	0.00
DIABETES	0.55	0.00	−0.10	0.00	0.00	0.00
		Relative Bias (%) of Standard Error Estimate of
	zscore(β)2	ΔAUC	NRI>0	NRI(r)	3cNRI3	IDI
SBP	3.05	−23	−3	−24	−24	−45
HDL	−10.93	−2	−6	−8	−28	−38
TOT	6.70	−2	−4	−13	−26	−29
AGE	10.41	9	−5	−6	−34	−36
DBP	2.16	20	−36	−19	−36	−16
SMOKING	5.62	−13	−1	−16	−29	−27
DIABETES	3.61	−3	−56	−16	−19	−43

¹β is the linear coefficient by added predictor variable (larger model). Continuous predictors were log-transformed but not standardized.

²z-scores of β coefficients (β/se(β)).

³2% and 10% cutoffs were used to calculate 3cNRI.

As we anticipate, the two statistics that require adjustment for estimated parameters (IDI and 3cNRI) have a stable strong bias in Table 3. However contrary to our expectations, bias of the theoretical standard error estimates of the three statistics that should not require adjustment for estimated parameters (ΔAUC, NRI_>0 and NRI(r)) varies greatly. For example the DeLong formula for standard error of ΔAUC often underestimates it by as much as 23% and the formula for NRI_>0 by as much as 56%. Statement 2 is proved under assumption of normally distributed predictors and this result is consistent with empirical simulations in Table 1. But some of the simulations with real-life data in Table 4 still show substantial bias. To further explore this phenomenon, first, we check the stability of our results in Table 3. We replicate bootstrap analysis several times with the FHS data set but with different random seed. Relative bias is still present across replications. Second, we use the result obtained by Harrell et al[21] that is, that tests of c-index (a survival analysis version of AUC) have very low power. We hypothesize that ΔAUC, NRI_>0 and NRI(r) experience similar loss of power. We observed in our simulations that transition to non-degeneracy is gradual (see Appendix Figure A1), so lack of power may be explained by degenerate behavior of the ΔAUC, NRIs, and IDI even for moderately strong predictor variables; therefore, we cannot use standard error formulas developed under the assumption of non-degeneracy. This reasoning implies that if we artificially inflate the strength of the added predictor variable, ΔAUC, NRI_>0 and NRI(r) should move further away from the null and the relative bias of standard error estimates of ΔAUC, NRI_>0 and NRI(r) will go down. Standard error estimates of 3-category NRI, and IDI have another problem: they require adjustment for estimated parameters. This problem cannot be solved by artificial inflation of effect size so we expect bias of their standard error estimates to stay strong. Table 5 shows the results of the bootstrap for the same data as in Table 4, but with artificially inflated effect sizes of added predictor variables.

Table 5.

Analysis presented in Table 3 was repeated but effect size of each added predictor variable was artificially inflated. $\text{rel}.\text{bias}=\frac{{\mathit{\text{se}}}_{\mathit{\text{formula}}.\mathit{\text{based}}}-{\mathit{\text{se}}}_{\mathit{\text{bootstrap}}}}{{\mathit{\text{se}}}_{\mathit{\text{bootstrap}}}}\times 100\%$. Effect size of dichotomous variables was inflated by artificially increasing their prevalence among events.

	Parameters Estimates
	β	ΔAUC	NRI>0	NRI(r)	3cNRI	IDI
SBP	21.70	0.20	1.50	0.44	0.95	0.43
HDL	5.63	0.17	1.16	0.34	0.70	0.26
TCL	14.35	0.21	1.63	0.48	1.08	0.55
AGE	2.72	0.02	0.46	0.06	0.16	0.01
DBP	36.90	0.22	1.83	0.55	1.23	0.77
SMOKING	1.34	0.04	0.56	0.09	0.18	0.04
DIABETES	2.32	0.06	0.62	0.06	0.12	0.11
		Relative Bias (%) of Standard Error Estimate of
	zscore (β)	ΔAUC	NRI>0	NRI(r)	3cNRI	IDI
SBP	29.46	−2	−12	0	−36	−26
HDL	27.46	2	−7	−2	−37	−25
TCL	27.90	0	−7	−7	−38	−22
AGE	10.41	7	−4	−8	−35	−35
DBP	22.58	1	−9	−2	−40	−27
SMOKING	14.63	−2	−2	−3	−24	−39
DIABETES	21.34	0.02	−0.23	0.08	−0.11	−0.38

Since we have artificially forced predictor variables away from the null, results presented in Table 5 now support Statement 2. As expected, formula-based standard error estimates of ΔAUC, NRI_>0 and NRI(r) have low bias and 3-category NRI and IDI have high bias because the latter group requires adjustment for estimated parameters.

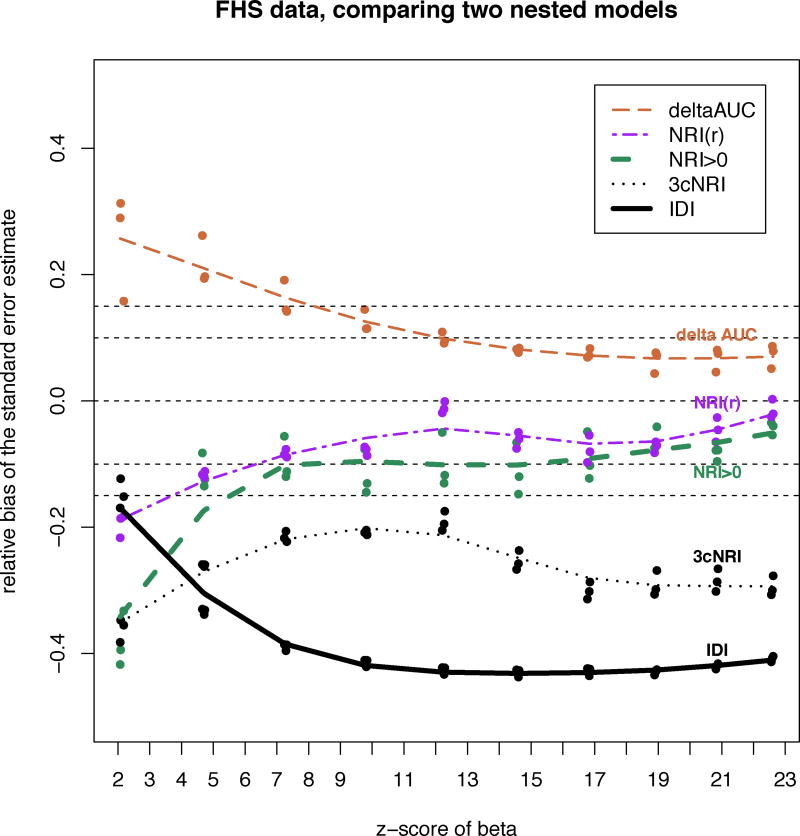
In Figure 6 we illustrate the relationship between relative bias of formula-based standard error and effect size of the added predictor.

Figure 6.

Relative bias of standard error estimate as a function of strength of the added predictor variable (z-score of β_DBP) using Framingham Heart Study data. Reduced model included predictor variables: age, HDL and total cholesterol, systolic blood pressure, smoking and diabetes status. Full model = reduced model+diastolic blood pressure (DBP). We artificially varied the strength of added DBP variable and calculated relative bias of variance estimate using theoretical formula relative to its bootstrapped value. zscore(β_DBP) = β_DBP /se(β_DBP). rel.bias=(se_{formula.based}−se_bootstrap)/se_bootstrap.

Results of this bootstrap analysis using real-life data suggest that Statement 2 is sensitive to the assumption of non-degeneracy. Statistical significance at the 0.05 level of added predictor variable is not sufficient to guarantee non-degeneracy and associations with stronger effect sizes are required for asymptotic formulas to become consistent. In our example when p-values of added predictor variables are weaker than 10⁻⁵, ΔAUC, NRI_>0 and NRI(r) are too close to degeneracy. Figure A1 in the Appendix illustrates very slow gradual transition away from degeneracy of ΔAUC as the added predictor variable gets stronger. I.e. the distribution of ΔAUC is still non-normal when the z-score of the added predictor variable is less than 4.0 (p-value≤6·10⁻⁵). Much stronger effect sizes are needed to achieve non-degeneracy. This observation explains why formula-based standard error estimators of NRI_>0, NRI(r) and ΔAUC are biased in Table 4 when p-values of the added predictor variable are less than .05 but greater than 10⁻⁵.

Figure 6 illustrates that in FHS data as the added predictor variable gets stronger, bias of se estimates of ΔAUC, NRI_>0, and NRI(r) decreases. With z-scores of beta coefficient ≥ 4.0 relative bias of formula-based standard error estimates of NRI_>0, NRI(r) falls below 15% while standard error of ΔAUC is still overestimated by the asymptotic formula and requires an even stronger predictor to lower its relative bias below 15%. When the z-score of the added predictor in nested models framework is less than 4.0 (p-value > 10⁻⁵) standard errors of ΔAUC, NRI_>0,and NRI(r) should be estimated using resampling methods. Electronic Health Records, pooled genetic cohorts, social networks data, etc. can result in very large sample sizes and potentially very low p-values. For such large sample sizes traditional resampling technique can become time consuming. Our results show that in this situation formula-based standard error estimates of ΔAUC, NRI_>0, and NRI(r) may have low bias, and may be estimated by using the formulas presented in Table 2. Table 5 implies that bias of added dichotomous predictors may remain strong in all scenarios. Standard errors of 3-category NRI and IDI always require adjustment for estimated parameters. As illustrated in Figure 6, their bias stays strong. For these reasons resampling methods should be preferred in all situations to estimate standard errors of 3-category NRI and IDI. We recommend similar strategies in estimating confidence intervals for ΔAUC, NRI_>0, NRI(r), 3-category NRI and IDI.

4. DISCUSSION

This validation study shows that the behavior of ΔAUC, NRI_>0, NRI(r), 3-category NRI, and IDI is affected by the interplay of several factors including the shift to degeneracy (non-normality) when comparing two nested models under the null, and the lack of adjustment for estimated parameters for 3-category NRI and IDI.

Our results explicitly specify conditions under which normal distribution theory can and cannot be applied to ΔAUC, NRI_>0, IDI and categorical versions of the NRI when comparing two nested models. A few tests of these statistics have been proposed and all with the exception of[20] rely on asymptotic normality. Our results imply that tests that rely on asymptotic normality are invalid for nested models and should not be used. Fortunately testing is unnecessary: Pepe et al[26] proved that testing of several measures of model performance is redundant because improvement in most of these statistics is equivalent to the significance of the new predictor variable. Therefore the recommended strategy is to establish the significance of the regression coefficient first and then evaluate improvement in model performance by producing confidence intervals for measures of performance such as ΔAUC, NRIs, and IDI.

Using U-statistics theory we proved that when the added predictor variable is significant, the distribution of ΔAUC, NRI_>0, NRI(r), 3-category NRI, and IDI is normal, therefore asymptotic confidence intervals can rely on the normal distribution. We considered their variance estimators and showed in Statement 2 that theoretical standard error estimates of ΔAUC, NRI_>0 and NRI(r) are valid when predictor variables are normally distributed. Our practical example using Framingham Heart Study data demonstrated that when the added predictor is significant but the p-value is not particularly low, the variance of NRI_>0, NRI(r) is still underestimated by the formula and the variance of ΔAUC is overestimated. Our simulations demonstrated that a stronger added predictor variable is required to reach non-degeneracy, a necessary condition for validity of the formulas. We offer an example in which the p-value of added predictor variable <10⁻⁵ is needed for ΔAUC, NRI_>0, and NRI(r) to fully transition to non-degeneracy, and for the relative bias of the standard error of NRI_>0 and NRI(r) to drop to below 15% (Figure 6). Such high effect sizes and significance levels might be common in Big Data studies.

While formula-based standard errors of ΔAUC, NRI_>0 and NRI(r) are valid in the situations described above, formula-based standard error estimators of 3-category NRI and IDI are not. Unless they are adjusted for estimated parameters, they underestimate actual variance. Therefore existing standard errors formulas for 3-category NRI and IDI should not be used and bootstrap or other resampling technique should be employed instead.

Additionally, using U-statistics theory we showed that the standard error estimator of ΔAUC can be calculated as the variance of the change in ranks of predicted probabilities (Table 3). In our numerical simulations the new variance estimator was identical to the one produced by DeLong et al[11] and the two are likely algebraically equivalent when there are no ties in predicted probabilities. However, rigorous proof of this result is beyond the scope of this paper.

In summary, when comparing two nested models after establishing the significance of the regression coefficient of an added predictor variable, we recommend estimating formula-based standard errors and confidence intervals of ΔAUC, NRI_>0 and NRI(r) when the significance of predictor variables is strong enough (p-value<10⁻⁵, z-score>4.0 in our FHS data example). In other situations the CIs of ΔAUC are too conservative; while CIs for all other statistics are too narrow therefore resampling techniques (such as bootstrap) should be used to estimate these. Standard errors of IDI and 3-calegory NRI should always be estimated by the bootstrap or other resampling technique.