Molecular Dynamics Simulation of the Oil Sequestration Properties of a Nonionic Rhamnolipid

Abstract

A detailed molecular dynamics simulation study is presented on the behavior of aggregates composed of the nonionic monorhamnolipid α-rhamnopyranosyl-β-hydroxydecanoyl-β-hydroxydecanoate (Rha-C10-C10) and decane in bulk water. A graph theoretical approach was utilized to characterize the size and composition of the many aggregates generated in our simulations. Overall, we observe that the formation of oil in Rha-C10-C10 aggregates is a favorable process. Detailed analysis on the surfactant/oil aggregate shows that larger aggregates are stable. The shape and size of the aggregates are widely distributed, with the majority of the aggregates preferring ellipsoidal or cylindrical structures. Irrespective of the decane concentration in the system, we did not observe free decane in any of the simulations. Further insights into the binding energy of decane were carried out using free-energy perturbation calculations. The results showed that the trapped decane molecules provide stability to the Rha-C10-C10 aggregates of size N = 50 which are shown to be unstable in our previous study and allow for the growth of larger aggregates than pure Rha-C10-C10 in water. The density profile plots show that decane molecules encapsulated inside the aggregate preferred to remain closer to the center of mass. This study points to the feasibility of using this biosurfactant as an environmental remediation agent.

Graphical abstract

1. INTRODUCTION

Surfactants are a class of amphiphilic molecules which aggregate at the interface between two phases and lower the interfacial tension. As a result, surfactants reduce repulsive forces between dissimilar phases, allowing immiscible phases to mix more easily.¹ It is this behavior that results in the formation of aggregates in which nonpolar molecules are trapped in the interior of a micelle strongly interacting with the tail groups of surfactant molecules, whereas the polar head groups of the surfactant interact with water. The structure of surfactants also results in a rich diversity of spontaneously formed structures in aqueous solution including micelles, vesicles, and bilayers. Because of these unique properties, surfactants have found applications in a variety of processes and products. Some applications include detergents, cosmetics, emulsifiers, pharmaceuticals, wetting agents, agricultural and industrial processes, paints, and enhanced oil recovery. The vast majority of surfactants are synthetic in origin, and because of the ubiquity of surfactants in daily life, questions regarding the long-term effects of these compounds on the environment are a growing concern. To meet this challenge, interest in industrial applications of biosurfactants, surfactants of biological origin, has grown in recent years.

Biosurfactants are a type of surface-active molecule produced by microorganisms to aid the uptake and oxidation of insoluble hydrocarbon substrates.² Biosurfactants are also utilized for various biological activities including antibiotic, antifungal, insecticidal, antiviral, immunomodulator, and antitumoral activities.^3–5 One of the more common types of biosurfactants of current research interest is rhamnolipid produced predominantly by the bacteria Pseudomonas aeruginosa. Other genera have been observed to produce different types of surfactants,⁶ including Rhodococcus, Nocardia, Flavobacterium, Corynebacterium, Clostridium, Acinetobacter, Thiobacillus, Bacillus, and Alcanivorax. Rhamnolipids are named such because they contain either a mono- or dirhamnose head group connected to a β-hydroxyalkanoyl-β-hydroxyalkanoic acid tail.⁷ Despite their lack of similarity to more conventional surfactants, such as sodium dodecyl sulfate, rhamnolipids work remarkably well at lowering surface tension and exhibit low critical micelle concentrations.⁸ Because of their strong surfactant properties, rhamnolipids have also been a focus for environmental recovery operations, most notably heavy-metal chelation in contaminated soil⁹ and oil spill remediation, the latter of which being the inspiration for our current work.

Oil dispersants function in principle by partitioning large oil slicks into microscopic droplets which can be readily degraded by microorganisms.^10,11 Although this method lessens the exposure of coastal areas to crude oil, it vastly increases the exposure to aquatic organisms. The Deepwater Horizon oil spill of 2010 is the second largest oil spill in history with 780 million liters of crude oil released and saw the subsequent deployment of Corexit 9500 as a dispersant,¹² raising numerous questions about long-term environmental effects. Rico-Martínez et al.¹³ simulated the conditions in the Gulf of Mexico during the spill to investigate the impact on the marine rotifer Brachionus plicatilis. Their findings indicated that while crude oil and Corexit alone had toxicity similar to rotifer, the mixture of the two substances had a synergistic effect, increasing the overall toxicity (specifically to the species Brachionus manjavacas) by up to a factor of 52. Additional studies^14–16 have investigated health effects from Corexit exposure to humans as well as animal species. Because of the widespread use of conventional dispersants to treat oil spills and questions surrounding the safety of these products, more environmentally friendly surfactants such as rhamnolipids make for attractive alternatives.

The interfacial properties of oil/water interfaces are topics of considerable research interest for a number of industries as evidenced by the large number of publications on the subject. Molecular dynamics (MD) simulation of surfactant behavior at interfaces is a topic of ongoing interest.^17–20 Numerous experiments have also investigated oil recovery specifically using rhamnolipid surfactants.^21–23 However, to our knowledge, there have been no investigations utilizing MD to study oil/water interactions with rhamnolipid surfactants. MD has a potential additional advantage of screening the multitude of rhamnolipid derivatives that are available.²⁴

In the present study, MD simulations were performed on systems containing different concentrations of surfactant and oil in water. We have considered decane as a representative nonpolar molecule. The (R, R) diastereomer of two different anomeric forms of α-rhamnopyranosyl-β-hydroxydecanoyl-β-hydroxydecanoate (Rha-C10-C10), the α and the β, was considered for the study, and a representative structure of the α anomer is presented in Figure 1. The structural properties of oil-in-water emulsions formed were characterized to understand the change in Rha-C10-C10 aggregates upon the addition of nonpolar molecules. Further insights into the stability of the oil molecules trapped inside the surfactant aggregate were analyzed using free-energy perturbation (FEP) calculations.

Figure 1.

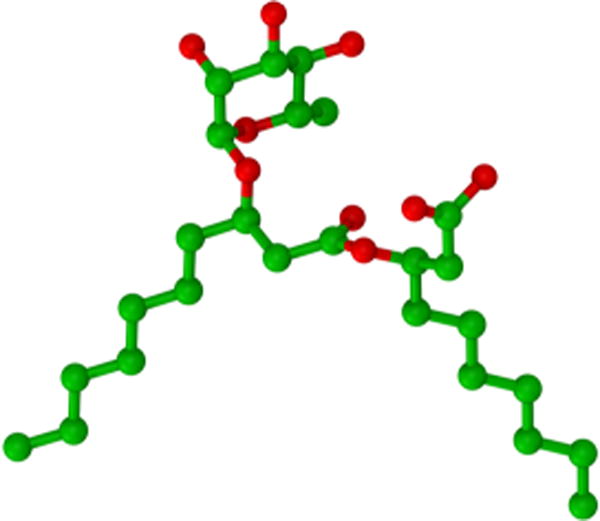
Chemical structure of the monorhamnolipid investigated, carbon atoms are in green, whereas oxygen atoms are red, and hydrogen atoms have been removed for clarity.

2. SIMULATION METHODS

2.1. Classical MD Simulation

Force field parameters for nonionic Rha-C10-C10 and decane were generated from the CHARMM general force field.²⁵ It has been experimentally determined that these rhamnolipid aggregates have a pK_a of 5.5 which is around neutral, meaning that the nonionic form is useful for a variety of applications.²⁶ These parameters are the same used in previous work²⁷ and have been experimentally validated. Table 1 presents an overview of the systems considered in this study. An initial system was prepared with varying concentrations of decane and Rha-C10-C10 surfactant. Each starting configuration was generated by randomly placing surfactant and decane molecules in a 100 × 100 × 100 ų cubical box using PACKMOL²⁸ software. The starting configuration was then solvated with TIP3 water²⁹ molecules, ensuring at least 2.8 Å separation from heavy atoms of both the surfactant and the decane. All of the simulations were carried out in the isobaric−isothermal ensemble (NPT) with periodic boundary conditions. A cutoff for nonbonded interactions was set at 10 Å, and a switch function starting at 8 Å was used for van der Waals interactions. The temperature was controlled by a Langevin thermostat,³⁰ whereas the constant pressure was enforced with the Nosé−Hoover Langevin barostat.³¹ All bonds involving hydrogen atoms were constrained with the SHAKE algorithm,³² and a timestep of 1 fs was employed for MD integration. Initial configurations were first energy-minimized and then heated to 300 K and equilibrated at 1 atm pressure. To avoid the long relaxation times of micelle formation, a modified simulated annealing³³ procedure was employed with the following schedule: (i) the temperature is increased from 300 to 400 K in 200 ps, (ii) the system is equilibrated at constant pressure at 400 K for 800 ps, (iii) the system is slowly cooled to 300 K, (iv) replicas are saved starting at 360 K and descending in 10 K increments, (v) replicas are energy minimized and reinitialized at 300 K in an effort to generate greater polydispersity, (vi) simulations are equilibrated for 10 ns, and (vii) a final 5 ns trajectory is generated for dynamic analysis. All simulations were performed using NAMD 2.9 with the CHARMM 36 force field.^34,35

Table 1.

Overview of Systems Studied in this Work

Rha-C10-C10 molecules	decane molecules	water molecules	mole fraction χrhammnolipid (%)	effective Rha-C10-C10 concn (mM)	effective decane concn (mM)
100	10	28 222	0.353	166	16.6
100	20	28 028	0.355	166	33.2
100	30	27 896	0.357	166	49.8
100	40	27 855	0.357	166	66.4
100	50	27 559	0.361	166	83.0
210	90	23 690	0.875	349	149.4
225	75	23 246	0.956	374	124.5
240	60	23 082	1.026	398	99.6
255	45	22 556	1.116	423	74.7
270	30	22 318	1.194	448	49.8
285	15	22 220	1.266	473	24.9

2.2. Free-Energy Perturbation

Additional model systems were prepared using PACKMOL where decane molecules were placed inside a prearranged surfactant aggregate. These systems were energy-minimized before heating to 300 K and equilibrated for 15 ns. The final coordinates from this simulation were used as a starting point for free-energy calculations.

FEP calculations were employed to study the binding free energy of the decane molecules trapped inside. Scheme 1 presents the thermodynamic cycle used to calculate the binding free energy. A single decane molecule was first reversibly annihilated in bulk water to determine the free energy of hydration. A single decane molecule was then selected from the interior of a micellar structure, and a harmonic force constraint of 5 kcal/mol was applied to keep the decane within 5 Å of the micelle center of mass (COM). The target decane was then reversibly annihilated to determine the free energy of binding for a micelle of given size. The entire process represents a thermodynamic cycle of transferring decane from the gas phase to the interior of a micelle and vice versa. All free-energy calculations were performed in both the forward and backward directions corresponding to annihilation and creation of solute. Both forward and backward calculations were stratified into 100 λ windows, and a soft core potential was used with a van der Waals radius shifting coefficient of 5.0. Electrostatic interactions were scaled to zero from λ = 0.0 to λ = 0.5 to avoid numerical instabilities when λ approaches either end point. Each λ window was equilibrated in an NPT ensemble for 50 ps followed by 100 ps of simulation. The creation and annihilation simulations were combined using the Bennett acceptance ratio method³⁶ as implemented in the ParseFEP plugin in VMD.³⁷

Scheme 1.

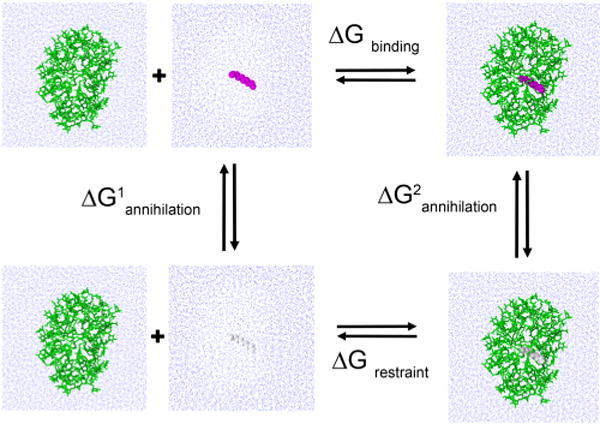
Thermodynamic Cycle Used to Determine the Free Energy of Binding a Decane Molecule to a Micelle

3. RESULTS AND DISCUSSION

3.1. Simulation of Surfactant and Decane in Water

The oil sequestration properties of Rha-C10-C10 were studied by simulating a system containing Rha-C10-C10 molecules and decane in water. An initial system was prepared using PACKMOL software and solvated using TIP3 water molecules. An equilibrium NPT simulation was performed on the system for analysis. Figure 2 presents the representative picture of a starting system and the simulated system. As shown in Table 1, different concentrations of Rha-C10-C10 and decane were considered for the MD simulation. All of the surfactant and decane systems in this study are partitioned into two groups: a low surfactant concentration regime (systems of 166 mM surfactant) and a high surfactant concentration regime (systems of 349 mM surfactant and above).

Figure 2.

Overview of the system preparation and final result. Decane molecules are shown as magenta spheres, whereas Rha-C10-C10 are displayed as green tubes and water molecules are represented as blue dots. Hydrogen atoms are removed for visual clarity.

A wide range of aggregate compositions were observed ranging from single Rha-C10-C10 monomers in solution to aggregates composed of 68 surfactant monomers and 33 decane molecules. The low surfactant concentration systems produced smaller, polydispersed aggregates, whereas the high-concentration systems resulted in large monodisperse aggregates. Figure 3 shows a representative example for the low- and high-concentration simulated systems.

Figure 3.

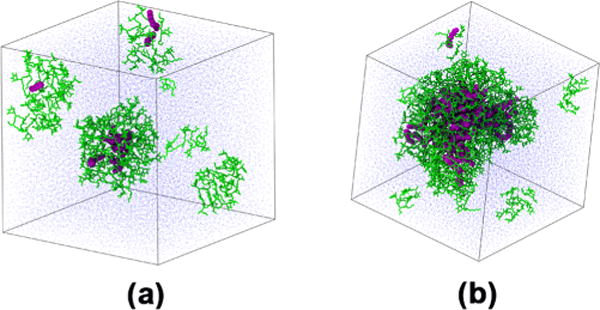
Representative figures for both the low (a) and high (b) concentration regimes. Both boxes are 100 × 100 × 100 ų.

3.1.1. Connectedness

Because of the high polydispersity observed and large number of aggregates observed in our simulations, a graph theory-based approach was used to identify micellar aggregates. This was necessary for both analysis and identification of stable aggregates. This data structure was implemented such that each surfactant was a node and interacting monomers were the edges. An interaction was defined as followed: the middle carbon atom of each tail group and the terminal carbon of each tail group (four carbons total) were chosen and tested with all of the other surfactant molecules in the system to see if the distance between target atoms was <5 Å. This cutoff was chosen because this distance from each target carbon covers the entire length of the tail group for Rha-C10-C10. Thus, monomers that were within the 5 Å cutoff were connected by an edge in the graph representation. The average degree of connectedness is a useful parameter to characterize a graph and is given by

$$\langle k\rangle =\frac{2E}{N}$$ (1)

where E is the number of edges and N is the number of nodes. The graph representation and degree of connectedness were constructed with the aid of the NetworkX software package.³⁸ Interestingly, this representation of our surfactant/oil system is characterized by the degree of connectedness. We see that the connectedness decreases linearly with the mole fraction of decane in solution. This holds for both the low surfactant concentration and high surfactant concentration regimes and is presented in Figure 4.

Figure 4.

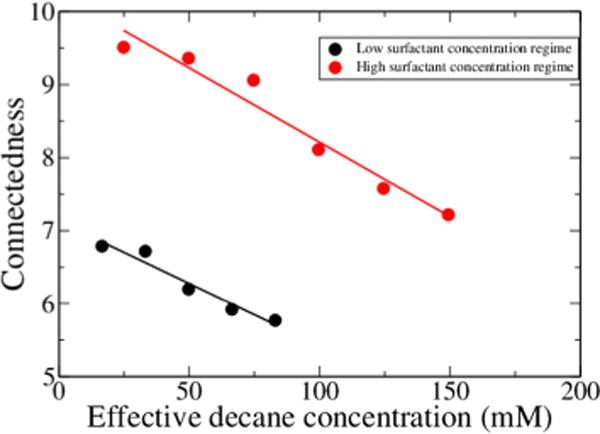
Average degree of connectedness is plotted as a function of decane concentration for both high- and low-concentration surfactant systems.

3.1.2. Eccentricity

Detailed analysis was carried out on the structure and fluxionality of the aggregates observed in the simulation employing various parameters. The fluxionality of the aggregates were estimated by monitoring each aggregates eccentricity (e) defined as the following

$$e=1-\frac{I_{min}}{I_{\text{avg}}}$$ (2)

where I_min is the principal moment of inertia with the smallest magnitude and I_avg is the average of all three principal moments of inertia. The parameter e is useful for characterizing the anisometry of a given aggregate where an e value of zero corresponds to an aggregate with three degenerate principal moments of inertia and thus a spherical shape. As the eccentricity value approaches unity, it is indicative of deviation from a spherical shape and an elongation along a principal axis, that is, an aggregate shape closer to an ellipsoid. As stated in the aim of the study, we have examined both α and β anomers of Rha-C10-C10 and the results are shown in Figure 5. It is observed from the figure that there is no significant difference in the stability of the aggregates between the two anomeric forms. The plot reveals that high oil/surfactant aggregates show a characteristically wider eccentricity distribution (red circles), implying that these aggregates are highly dynamic. It is observed that smaller premicellar aggregates show a wide range in eccentricity because these structures are unable to segregate hydrophobic regions from water, whereas less fluxional structures have a characteristically sharper distribution of eccentricity values. Larger aggregates (found in the upper right corner) tend to be less fluxional. Smaller premicellar aggregates encapsulating decane molecules are observed to be much more eccentric than the larger aggregates. Irrespective of the number of decane molecules trapped inside, larger aggregates are less fluxional structures.

Figure 5.

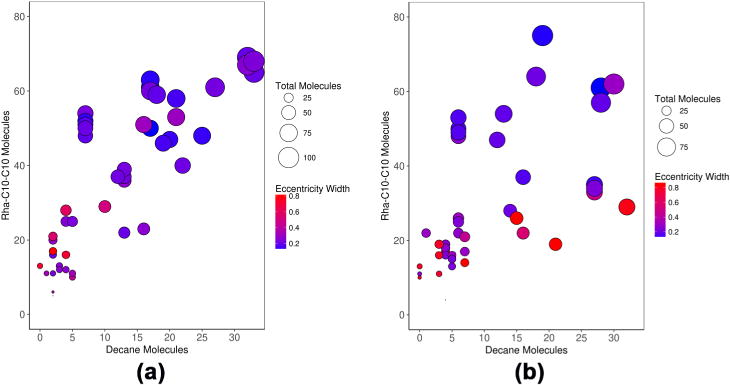
Plots of system composition for α-Rha-C10-C10 anomer (a) and β-Rha-C10-C10 anomer (b). The radii of the circles are proportional to the overall size of the aggregate (the sum of decane and Rha-C10-C10), and the circles are colored based on the width of the eccentricity values.

3.1.3. Radius of Gyration

Further insight into the relative size and shape of the aggregates was obtained from the radius of gyration tensor. A detailed discussion on this scheme is presented in the Supporting Information. It was observed that in general as the overall shape of a given aggregate increased, it adopted a more cylindrical-type shape. Figure 6 shows the results of the analysis of the radius of gyration for four representative aggregates: N11(D2), N48(D7), N52(D7), and N61(D27) where N is the number of Rha-C10-C10 molecules and D is the number of decane molecules. It is evident from the figure that as the overall size of the aggregate increases, the peak shifts toward the lower left of the contour map, which corresponds to a cylindrical shape. The smaller aggregate N11(D2) (a) briefly samples disklike conformations, whereas the largest structure N61(D27) (d) is strictly cylindrical. The majority of the structures sampled were in the cylindrical region. Smaller, premicellar aggregates (total size < 20) are highly eccentric and sample larger regions of conformations.

Figure 6.

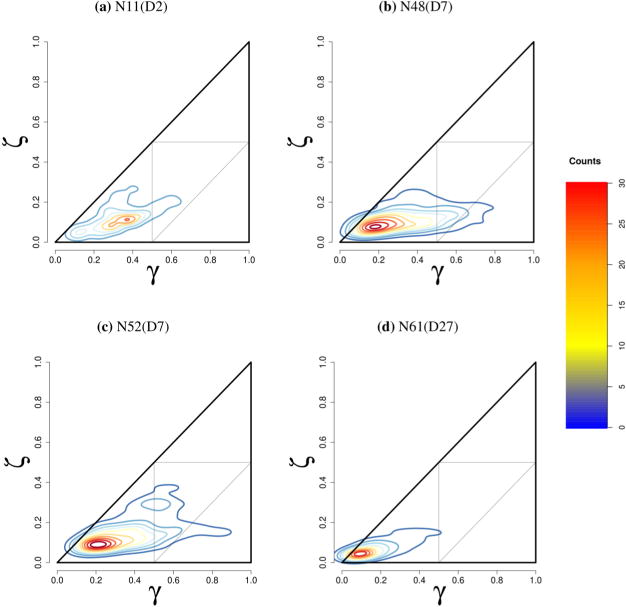
Plot of given aggregates shape conformations as a function of γ and ζ parameters over the course of a given trajectory. Note that no samples should exceed the triangular boundaries because both γ and ζ are the squares of the ratios of the principle moments, but that this is an artifact of kernel density estimation.

The principle moments of the radius of gyration tensor are indicative of the overall size of a given aggregate. Finding the magnitude of the radius of gyration,

$$R_g=\sqrt{{R_1}^2+{R_2}^2+{R_3}^2}$$ (3)

we may estimate the size of the aggregates which can be compared to light-scattering experiments. Figure 7 gives an overview of the scaling of the radius of gyration as a function of the number of molecules (sum of surfactants and decanes) in the microemulsion. We find good agreement with our previous results for the scaling of the radius of gyration for nonionic Rha-C10-C10. Once again, we note that there is little difference between the two anomers.

Figure 7.

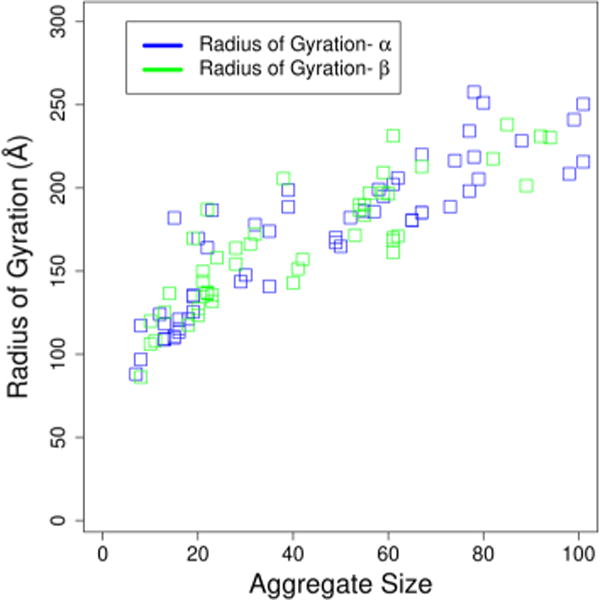
Overview of the scaling of the radius of gyration averaged over 5 ns for all aggregates. Aggregate size refers the sum of surfactants and decane molecules. Similar results were obtained in our previous work for Rha-C10-C10 micelles in pure water.

3.1.4. Accessible Surface Area

The accessible surface area (ASA) was measured to gain insight into the ability of a Rha-C10-C10 aggregate to trap nonpolar molecules. Irrespective of the amount of oil trapped inside, the extent of hydrophobic region exposed to water is an indication of instability. Using the method of Lee and Richards,³⁹ solvent ASAs were calculated for both the nonpolar and polar components of the aggregate. This technique removes all of the water molecules from the system and rolls a probe molecule across the surface of the target cluster. A 1.6 Å probe was used because this size closely mimics a water molecule. The results are presented for both α and β anomers in Figure 8. It can be seen from the plot that there is no difference in behavior between the two anomers. The rate of change of the ASA scales differently for the individual components of the emulsion. Smaller aggregates have relatively little difference in the ASA between the trapped decane, hydrophobic tails, and hydrophilic head groups. However, as the overall size of the emulsions grow, the scaling of the ASA for hydrophobic components grows more slowly than the ASA for the head groups and the scaling for the ASA of the decane molecules is even slower. Oil molecules are well-protected from bulk water in larger aggregates by both the hydrophilic head groups and hydrophobic tail groups of the Rha-C10-C10. We also observe that the ASA rapidly decreases for trapped decanes as the ratio of surfactant to decane increases.

Figure 8.

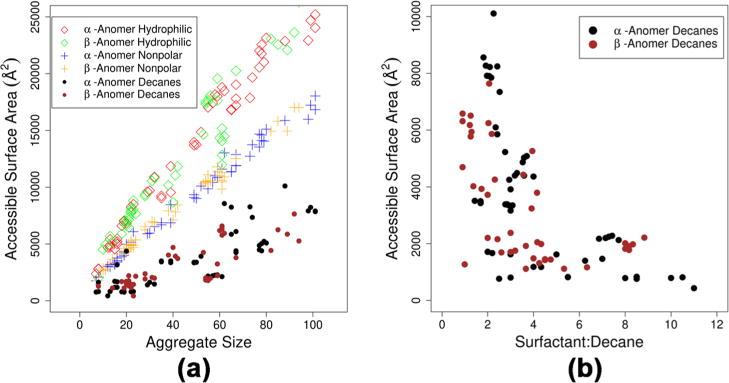
Plot of the ASA for hydrophobic and hydrophilic (head groups) components of the microemulsions (left) and plot of the ASA for trapped decane molecules as a function of surfactant to decane ratio (right).

3.2. Free-Energy Calculations

To better understand the stability of Rha-C10-C10/oil emulsions, we prepared model systems where decane molecules were encapsulated in Rha-C10-C10 aggregates. Table 2 lists all of the model systems considered for this investigation. These model systems were chosen such that they could accommodate a range of decane molecules that would provide insights into the oil sequestration ability of Rha-C10-C10. We studied a small aggregate (30 monomer) and big aggregate (50 monomer) micelle. The motivation for the selection of these model systems stems from the results of our previous work.⁴⁰ We found that the most stable micellar aggregate of nonionic Rha-C10-C10 in water was ≤N40. By choosing an aggregate of sizes N30 and N50, we have chosen micellar structures that fall on either side of the observed aggregate size. The number of decane molecules encapsulated in these aggregates range from 1 to 30 decanes. The result presented in Table 2 shows that the binding free energy calculated in all cases is negative, indicating that the formation of a surfactant/decane aggregate is a favorable process. A single decane trapped inside N50 aggregate is twice as stable as single decane trapped in N30. An increase in the amount of decane trapped inside N50 results in a less negative free-energy value. There is no significant change in the binding free energy of decane in the aggregate N50 containing decane in the range of 10−20. As seen from these results, smaller aggregates provide less stability to decane compared to that of larger aggregates. We examine a variety of decane quantities trapped in a 50 and 30 monomer micelle and observe that a single decane molecule is more strongly bound in both cases than a decane molecule trapped with other decane molecules. The results for these simulations are presented in Table 2 with the harmonic force constant and free energy of solvation included in the calculation.

Table 2.

Resulting Free Energy of Binding for a Large (50 Monomers) and Small (30 Monomers) Micelle. ΔG_binding Is Given as a Result of $\mathbf{\Delta }{\mathbf{G}}_{\mathbf{a}\mathbf{n}\mathbf{n}\mathbf{i}\mathbf{h}\mathbf{i}\mathbf{l}\mathbf{a}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}}^{\mathbf{1}}-\mathbf{\Delta }{\mathbf{G}}_{\mathbf{a}\mathbf{n}\mathbf{n}\mathbf{i}\mathbf{h}\mathbf{i}\mathbf{l}\mathbf{a}\mathbf{t}\mathbf{i}\mathbf{o}\mathbf{n}}^{\mathbf{2}}+\mathbf{\Delta }{\mathbf{G}}_{\mathbf{r}\mathbf{e}\mathbf{s}\mathbf{t}\mathbf{r}\mathbf{a}\mathbf{i}\mathbf{n}\mathbf{t}}$

Rha-C10-C10	decanes	ΔG (kcal/mol)
30	1	−3.939
30	8	−3.653
50	1	−8.916
50	11	−4.293
50	13	−4.496
50	15	−4.354
50	17	−4.344
50	19	−4.280

Our previous work⁴⁰ found that the same rhamnolipid congener formed aggregates of N ≤ 40. We hypothesize that an aggregate of 50 monomers is unfavorable and that trapped decane works to stabilize this structure and as a result, the free energy to bind a single decane inside N50 is more negative than any of our other results. This hypothesis is supported by the radial density plots constructed for the model systems under investigation. The plot for N50(D1) shows a large distribution of hydrophilic head group components as well as water near the COM. This indicates that N50(D1) is not considered a stable micelle because it does not properly segregate nonpolar components from polar components. This is observed over the course of the trajectory as N50(D1) forms a disklike structure with high eccentricity. Conversely, the N30(D1) aggregate shows a proper distribution of components. A direct comparison of the eccentricity for the N30(D1) and N50(D1) aggregates, as seen in Figure 9, shows that the smaller aggregate is sharply peaked, whereas the larger aggregate produces a more bimodal distribution.

Figure 9.

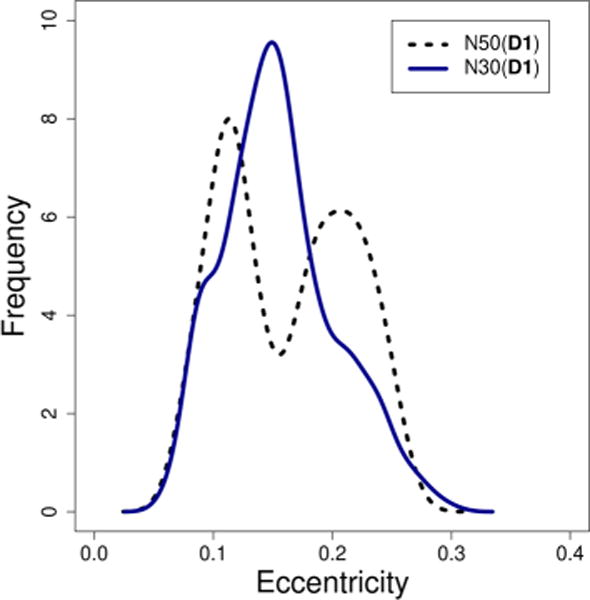
Comparison of the eccentricity for the N30(D1) and N50(D1) system shows that the larger cluster fluctuates between conformations, whereas the smaller has a sharper distribution.

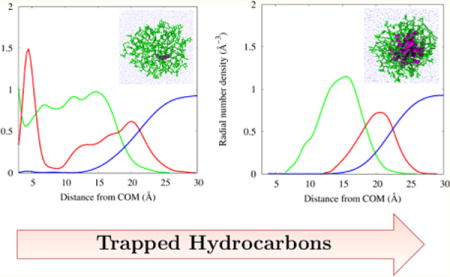
Radial number density plots help to illustrate the distribution of components in an aggregate. Figure 10 gives an overview on the effect of added decane to a micellar core. The system with only a single decane does not separate hydrophilic from hydrophobic components because it is such a highly fluxional structure. A micelle of size N > 40 is unlikely to form, and it takes an increase in the amount of hydrophobic components to form aggregates of this size. As we increase the amount of trapped decane, the radial plots show a characteristic segregation of micellar components at a cost of increased overlap between both the decane and surfactant tails with bulk water.

Figure 10.

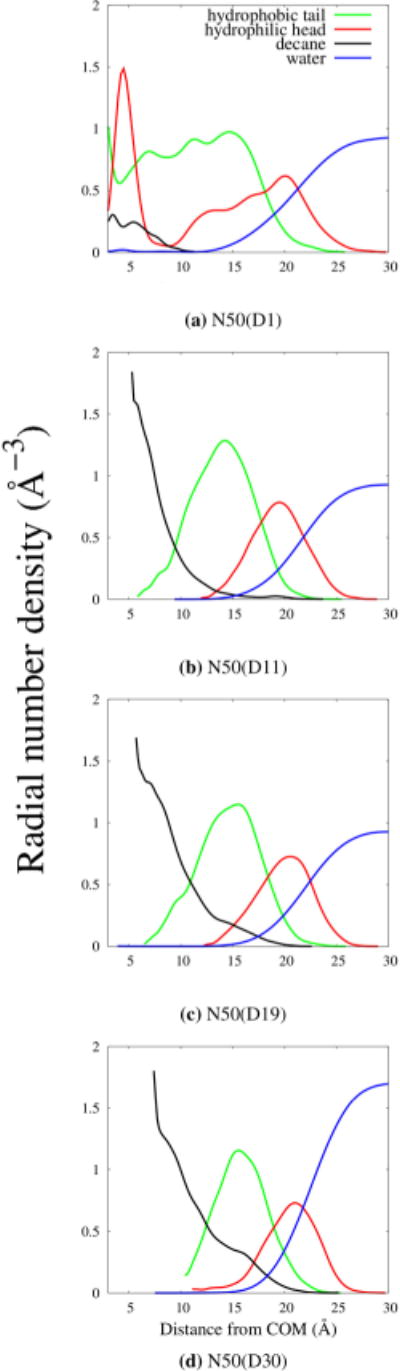
Radial density plots for given model systems. N50(D1) is not a true micellar system because it has not effectively separated hydrophobic components from hydrophilic components.

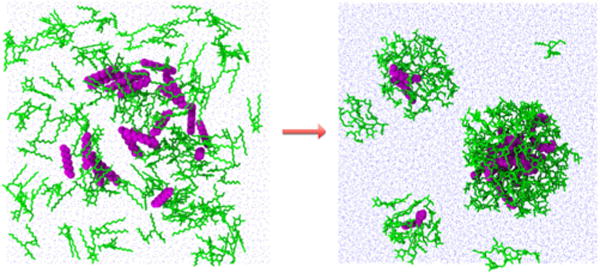
The free energy of binding rapidly decreases for the N50 aggregate upon the trapping of additional decane. This is due to the decane molecules stabilizing the hydrophobic core of the micelle. For low concentrations of oil, the trapped decane is highly mobile in the interior of the micelle. As the concentration of decane increases, the decane becomes more centrally located, as indicated by Figure 11, which shows the distance between the surfactant molecules COM and the trapped decane molecules COM. This indicates that for larger, unfavorable aggregates, the presence of trapped oil provides structure to stabilize the overall micellar structure, as illustrated by Figure 12.

Figure 11.

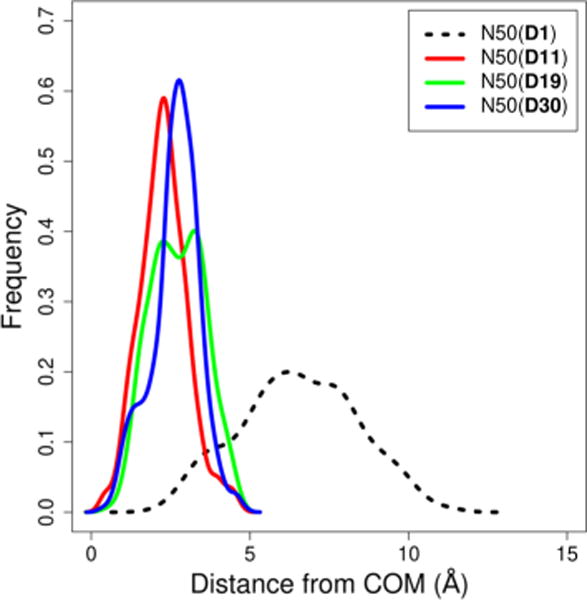
Distance between the surfactant monomers COM and trapped decane molecules COM. Increasing decane concentration moves the COM of the decane toward the COM of the aggregate, leading to a more structured aggregate.

Figure 12.

Illustration of the structural differences between aggregates of fixed surfactants N = 50 with small and large amounts of decane. N50(D1) has a flattened more eccentric dynamics, whereas N50(D19) is stabilized by its trapped hydrocarbon molecules.

3.2.1. Hydrogen-Bonding Interaction

Hydrogen bond interactions are important in the stability of the Rha-C10-C10 aggregates. The head group contains numerous hydrogen-bonding sites that can interact with both other head groups as well as bulk water. The previous section showed that trapping decane is a favorable process and we are interested to see if the trapped decane influences the formation of new hydrogen bonds within the aggregate and with bulk water. We found that the hydrogen-bonding interactions within the aggregate as well as with bulk water do not vary upon the addition of decane molecules. It is interesting to see that as many as 30 decanes trapped inside N50 do not disrupt the hydrogen bonds. Although they do not contribute to new hydrogen-bonding interactions, they do not disturb the hydrogen bonds already present (see Figure S1).

The present study was an attempt to understand the oil sequestration properties of nonionic Rha-C10-C10. The results discussed above imply that nonionic Rha-C10-C10 is a good choice for trapping decane molecules. Rhamnolipid aggregates of size N > 40 are not stable in bulk water because of the lack of a strong hydrophobic core and a lack of hydrogen-bonding interactions between monomers of the aggregate. Decane molecules provide the much needed hydrophobic core upon solubilization in the micellar aggregate. Stabilization of larger aggregates (>40) is also possible by incorporating strong hydrogen-bonding donor/acceptor regions in the monomer, whereas increasing the length of the alkyl chains is another possible way to strengthen the hydrophobic density.

Our previous study utilized the potential of mean force calculations to determine the barrier of removing a single monomer from a micelle of sizes N30 and N40 and found it to be 8 and 6 kcal/mol, respectively. Although we did not try this approach for a trapped decane molecule, it should be noted that the barrier to extract a monomer should be much lower in magnitude because the head group of a monomer is located at the micellar surface, whereas decane is buried deep within the core of the aggregate. This would indicate that it is much harder to remove a trapped decane molecule than a single monomer from a stable micellar aggregate.

4. CONCLUSIONS

We utilized MD simulation to probe both the ability of a particular biosurfactant, Rha-C10-C10, to trap hydrocarbons and the effect of hydrocarbons on the stability of Rha-C10-C10 surfactant micelles. A graph theoretical approach was a useful tool to characterize both the size and components of a large amount of aggregates formed in each system. Both the ability to form larger aggregates of surfactant and encapsulated decane and the results of the calculated binding free energy of decane show that nonionic Rha-C10-C10 favorably traps nonpolar molecules. We also found that there is no significant change in the hydrogen-bonding interactions between surfactants of the aggregates upon the addition of trapped decane molecules. The absence of free decane molecules in our simulations further demonstrates the effectiveness of the rhamnolipid congener for oil sequestration applications.