Abstract
Creep, the time dependent deformation of a structure under load, is an important viscoelastic property of bone and may play a role in the development of permanent deformity of the vertebrae in vivo leading to clinically observable spinal fractures. To date, creep properties and their relationship to geometric, microstructural, and material properties have not been described in isolated human vertebral bodies. In this study, a range of image-based measures of vertebral bone geometry, bone mass, microarchitecture and mineralization were examined in multiple regression models in an effort to understand their contribution to creep behavior. Several variables, such as measures of mineralization heterogeneity, average bone density, and connectivity density persistently appeared as significant effects in multiple regression models (adjusted r2: 0.17–0.56). Although further work is needed to identify additional tissue properties to fully describe the portion of variability not explained by these models, these data are expected to help understand mechanisms underlying creep and improve prediction of vertebral deformities that eventually progress to a clinically observable fracture.
Keywords: Creep, vertebral body, material properties, geometry, microstructure
INTRODUCTION
Creep, the time-dependent deformation of a structure under prolonged load, is understood to play an important role in deformity of vertebral bone due to progressive accumulation of residual strain (Pollintine et al., 2009). To date, aspects of creep have been studied in animal trabecular bone (Bowman et al., 1998; Bowman et al., 1994; Manda et al., 2016; Rimnac et al., 1993; Shepherd et al., 2011; Xie et al., 2017), animal vertebrae and motion segments (Bailey et al., 2014; Kim et al., 2012; van der Veen et al., 2008), and demineralized bone (Bowman et al., 1999; Summitt and Reisinger, 2003). Creep properties have also been studied in isolated human cancellous (Kim et al., 2011; Novitskaya et al., 2014; Yamamoto et al., 2006; Zilch et al., 1980) and cortical bone (Caler and Carter, 1989; Fondrk et al., 1988), and vertebral motion segments (Busscher et al., 2011; Kazarian, 1975; Keller et al., 1987; Luo et al., 2012; Pollintine et al., 2009). It has been shown that creep behavior is sensitive to mechanical damage to the bone (Fondrk et al., 1988), disc health (Adams et al., 2006) and is suggested to play a role in fracture healing (Goodship et al., 1998). It has also been suggested that permanent deformation resulting from creep may develop at physiological load levels and contribute to the fatigue behavior of vertebral bone (Yamamoto et al., 2006), resulting in progressive loss of strength and ultimate failure of the bone tissue (Bowman et al., 1998; Bowman et al., 1994).
Despite the importance of creep in bone, no previous study has specifically examined creep behavior and addressed the relationship between microstructural organization and creep in human vertebral bodies. Engineering theories suggest that the viscoelastic behavior of cellular materials such as cancellous bone is affected by the distribution of material densities and voids (Ajdari et al., 2009; Andrews and Gibson, 2001; Huang and Gibson, 2003). Correspondingly, previous studies demonstrated that creep is associated with microstructural properties in human and bovine cancellous bone (Kim et al., 2011; Manda et al., 2016). In addition, significant relationships have been demonstrated between uniaxial compressive creep rate and both average and variability of grey values within the bone phase of segmented μCT images (a measure of bone tissue mineralization), in human vertebral cancellous cores (Kim et al., 2011). However, no such relationship was found between bone tissue mineralization and nanoindentation creep rate in femoral cortical bone (Wu et al., 2012).
With results varying between anatomical site, species, and outcomes from different measurement methods, the extent to which the abovementioned findings can be directly applied to isolated human vertebrae remains unknown. Therefore, the current study aims to establish relationships between creep of human cadaveric vertebral bodies and clinically available measures of vertebral geometry and bone mineral density as well as microstructural and hard tissue properties measured using microcomputed tomography.
METHODS
Human cadaveric thoraco-lumbar spines were acquired from tissue banks under local IRB approval and T12 vertebrae were harvested from 23 donors. Donors with a history of HIV, hepatitis, diabetes, renal failure, metastatic cancer, osteomalacia, hyperparathyroidism, Paget’s disease of bone, spine surgery, cause of death involving trauma, and corticosteroid, anticonvulsant or bisphosphonate use were not included. Vertebral bodies were dissected, soft tissue and posterior elements were removed, and specimens were stored wrapped in saline-soaked gauze at −20 °C until imaging and testing were performed. The donor set consisted of 13 men and 10 women between the ages of 41 and 97.
The prepared specimens were scanned using a custom-built μCT system and reconstructed at an isotropic voxel size of 40 micrometers (Kim et al., 2015). Specimens were wrapped in saline-soaked gauze throughout scanning to maintain hydration. The largest possible cubical volume of interest (VOI) consisting of only cancellous bone was cropped from the center of the reconstructed bone volume and the VOI was segmented using global thresholding within Microview (GE Healthcare, Illinois, USA). Grey values were preserved during segmentation for calculation of average (μCT.GV.Av), standard deviation (μCT.GV.SD) and coefficient of variation (μCT.GV.CV= μCT.GV.SD/μCT.GV.Av) of grey values as mineralization parameters (Figure 1). Scan-to-scan consistency was assured by normalizing grey values using a material density phantom present in each scan. Images were then binarized and processed using CT-Analyzer (v1.12.0.0; Bruker, Kontich, Belgium) to obtain 3D measures of bone volume fraction (BV/TV), trabecular thickness (Tb.Th), trabecular number (Tb.N), trabecular spacing (Tb.Sp), degree of anisotropy (DA), connectivity density (Conn.Dn), and structure model index (SMI). Standard deviation (SD) of BV/TV (BV/TV.SD), Tb.Th (Tb.Th.SD), Tb.N (Tb.N.SD) and Tb.Sp (Tb.Sp.SD) were calculated as measures of microstructural heterogeneity from the distribution of 2D stereology results from axial slices, indicating a slice to slice variation of the corresponding variable in the superior-inferior direction (Yeni et al., 2011).
Figure 1.
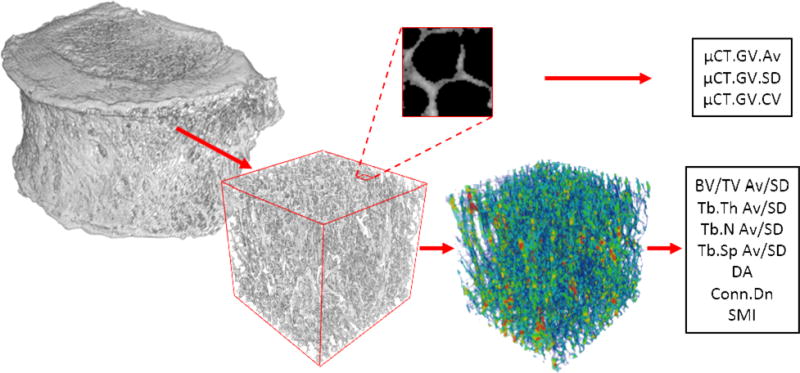
Cubic volumes of interest were extracted from the cancellous centrum of microcomputed tomography images to calculate stereological parameters (bottom; trabecular thickness map presented). Average, standard deviation, and coefficient of variation of the grey values were calculated using the entire cube (top; exploded 2mm axial view demonstrating trabecular bone grey value distribution).
In order to measure volumetric BMD, the same specimens were scanned using high resolution computed tomography (HRCT) and reconstructed at 0.7 mm axial pixel spacing with 0.75 mm slice thickness (Siemens Sensation 64). The vertebrae were mounted and consistently aligned via a custom, radiolucent clamping tray in the center of a scanning tank filled with 0.9% saline to simulate surrounding soft tissue. A single, unique threshold value that delineates bone from soft tissue was determined for each vertebral body and applied within a custom segmentation algorithm to produce a closed surface gray value mask of the vertebral body (Zauel et al., 2005). Volume masks representing cancellous and cortical bone were prepared from HRCT images using a previously described semiautomatic segmentation method (Buie et al., 2007; Oravec et al., 2015). The segmented volume masks were multiplied with the original gray value images, from which integral cancellous+cortical (iBMD), volumetric cancellous (cBMD), and shell (shBMD) bone mineral density (BMD) were calculated (Figure 2a). Integral cancellous+cortical volume (CT-Vol), area of anterior-posterior (AP) and lateral-medial (LM) projections (Area.AP, Area.LM), height and width in AP (Height.AP, Width.AP) and LM (Height.LM, Width.LM) were also recorded using the prepared binary masks (Figure 2b).
Figure 2.

(a) HRCT images were segmented to produce cancellous, shell, and cancellous+shell binary masks which were multiplied with source CT volumes to produce volumetric BMDs for each region (cBMD, shBMD, and iBMD, respectively). (b) The anterior-posterior and lateral-medial projections of the integral cancellous+cortical mask were used to calculate in each orientation area (Area.AP, Area.LM), height (Height.AP, Height.LM) and width (Width.AP, Width.LM).
The vertebral bodies were then scanned using dual x-ray absorptiometry (DXA) in AP and LM orientations using a fast array lumbar spine protocol (Hologic Discovery-A). Specimens were again aligned to imaging axes using a radiolucent tray immersed in 0.9% saline. BMD and bone mineral content (BMC) were measured for two views of each vertebra (BMD.AP, BMC.AP, BMD.LM, BMC.LM) within Hologic Discovery software using standard clinical analysis techniques. Area in AP (DXA-Area.AP) and LM (DXA-Area.LM) directions were also recorded.
Following imaging studies, creep tests were conducted in a materials test machine (Model 8850; Instron, Canton, MA) with specimens fully submerged in saline at 37°C. Vertebral endplates were left intact (i.e., not cut) and potted using a parallel plate jig using dental stone to ensure flat and parallel boundary conditions. The vertebra-endcap construct was constrained in metal platens. The specimens were loaded to 1000 N in uniaxial compression (Point A, Figure 3) in order to apply a physiologic load level representative of that experienced during standing (Ignasiak et al., 2017; Iyer et al., 2010; Pollintine et al., 2009; Sato et al., 1999) and kept at that level for 2 hours. After 2 hours (Point C, Figure 3), specimens were unloaded to a finite minimum load of 100 N and displacement was recorded during recovery for another 2 hours. Loading and unloading was performed under force control at 10 N/second. Elastic displacement before creep (De), creep displacement (Dcr), total displacement (Dtot), elastic recovery (Rel), creep recovery (Rcr) and residual displacement (Dres), and residual displacement from creep alone (Dres-cr) were calculated using load vs. time data (Figure 3). In order to examine creep independently from its association with stiffness, creep displacements corrected for their dependence on elastic displacements were also calculated by normalizing with De (e.g., Dcr-norm, Rcrnorm, and Dres-norm). In order to characterize the time dependence of the creep behavior, a modified Kohlrausch-Williams-Watts (KWW) function of the form “Dcr = a(1-EXP(−(t/τcr)n) + Ct” was fit to the creep portion of the displacement vs. time data (points A–C in Figure 3), and τcr (the time constant, a measure of viscoelasticity and fast response to a load), n (the stretch exponent, a measure of the rate of change of the decay function), and C (added to the KWW function as the steady state creep rate) were recorded as outcome variables (Iyo et al., 2004; Sasaki et al., 1993). Displacement values were normalized to a range of 0–1 using the maxima and minima of creep data prior to curve fitting. If tertiary creep or failure occurred, the creep function was fit until the steady state portion of the creep curve became nonlinear. Curve fitting was performed in TableCurve 2D (Systat Software Inc., Chicago, IL, USA).
Figure 3.
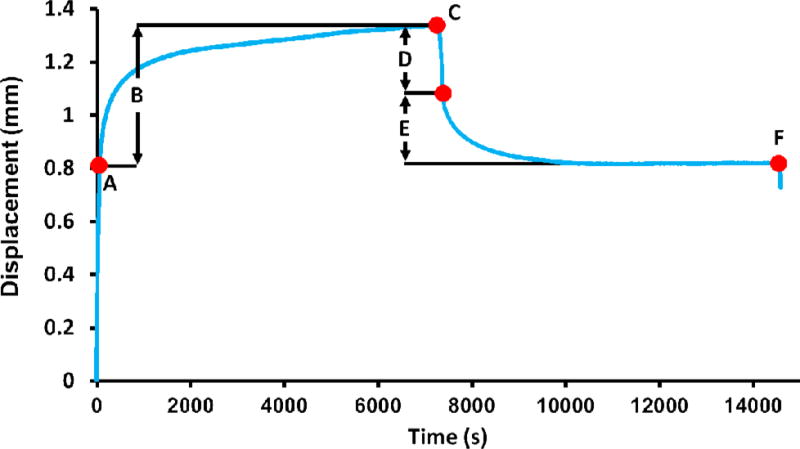
A representative creep curve (74 year old male). Displacement parameters that define the creep behavior were calculated as: (A) elastic displacement before creep (De), (B) creep displacement (Dcr), (C) total displacement (Dtot), (D) elastic recovery (Rel), (E) creep recovery (Rcr), and (F) residual displacement (Dres). Residual from creep alone (Dres-cr) was calculated as Dcr-Rcr. Quasistatic loading and unloading occurred over 100 seconds. Curve fitting was performed on the region between A–C.
Within each variable type (i.e., μCT, HRCT and DXA-derived geometric, microstructural, and material parameters), candidate parameters causing high multicollinearity (as determined by a variance inflation factor>5) were eliminated (Table 1). Multiple regression models were constructed using a stepwise procedure to examine relationships between measures of creep and parameters which passed the multicollinearity test. Pearson product-moment correlations were evaluated between creep and BMD variables. For all models, if BMD variables were found to be significantly correlated to a creep variable, the most significant BMD variable was introduced first and forced to stay in the model. Significance in multiple regression models and pairwise correlations was considered as P<0.05. All analyses were performed in JMP (v10.0, SAS Institute, Inc., Cary, NC).
Table 1.
Measured parameters causing high multicollinearity within each variable type were introduced in the presented order and those with variance inflation factor (VIF) >5 were eliminated from subsequent multiple regression models. The subset that passed the VIF test (indicated by ✓) were included in multiple regression models.
| Type | Variable | VIF < 5 |
|---|---|---|
| Geometric | CT-Vol | ✓ |
| Area.AP | ✓ | |
| Height.AP | ||
| Width.AP | ||
| Area.LM | ||
| Height.LM | ||
| Width.LM | ||
| DXA-Area.AP | ||
| DXA-Area.LM | ||
| Microstructural | BV/TV | ✓ |
| Tb.Th | ✓ | |
| Tb.N | ||
| Tb.Sp | ||
| DA | ✓ | |
| Conn.Dn | ✓ | |
| SMI | ||
| BV/TV.SD | ||
| Tb.Th.SD | ||
| Tb.N.SD | ||
| Tb.Sp.SD | ||
| Material | μCT.GV.Av | ✓ |
| μCT.GV.SD | ✓ | |
| μCT.GV.CV |
RESULTS
Three of 23 specimens experienced catastrophic failure during the test. Creep deformations were not calculated for these three specimens. The three failed specimens constituted the three lowest bone densities (BMD from anterior-posterior DXA was 0.176–0.196 g/cm2 for the three specimens, vs. 0.265–0.786 g/cm2 for the remaining specimens). Average and standard deviation of measured parameters, as well as normalized displacement values, are presented in Table 2.
Table 2.
Average (Av) and standard deviation (SD) of measured creep deformations and curve fit parameters.
| Variable | Description (see Figure 2) | n | Av | SD |
|---|---|---|---|---|
| De | Elastic displacement before creep (mm) | 20 | 0.617 | 0.288 |
| Dcr | Creep displacement (mm) | 20 | 0.341 | 0.269 |
| Rcr | Creep recovery (mm) | 20 | 0.171 | 0.100 |
| Dres | Residual displacement (mm) | 20 | 0.528 | 0.356 |
| Dres-cr | Residual displacement from creep (mm) | 20 | 0.170 | 0.214 |
| Dcr-norm | Normalized creep displacement | 20 | 0.545 | 0.358 |
| Rcr-norm | Normalized creep recovery | 20 | 0.290 | 0.172 |
| Dres-norm | Normalized residual displacement | 20 | 0.256 | 0.246 |
| Rel | Elastic Recovery (mm) | 20 | 0.191 | 0.059 |
| Dtot | Total Displacement (mm) | 20 | 0.958 | 0.487 |
| τcr | Creep time constant (s) | 22 | 345.728 | 139.664 |
| n | Stretch exponent | 22 | 0.657 | 0.109 |
| C | Creep rate (mm/s) | 22 | 0.000043 | 0.000095 |
| r2adj for curve fit | 22 | 0.998 | 0.002 |
Among the creep variables, Dres-cr and Dres-cr-norm were positively associated with age (p<0.03 and p<0.04, respectively) but none were associated with sex (p=0.06–0.88). Among the predictors that passed the VIF test, only Area.AP was associated with sex, with greater values for males than for females (p<0.05) but none were associated with age (p=0.06–0.98). Therefore, age and sex were not considered further in multiple regression models.
Significant positive correlations were found between creep displacement and recovery (r2=0.68, p<0.002) and residual displacements (r2=0.80–0.96, p<0.0001), as well as creep rate (r2=0.46, p<0.05) (Table 3). In addition, creep rate had significant positive correlations with residual displacements (r2=0.55–0.56, p<0.02) and the stretch exponent (r2=0.52, p<0.02). Finally, a significant positive correlation was found between the stretch exponent and recovery displacement (r2=0.46, p<0.05). All other correlations between measured creep parameters were nonsignificant.
Table 3.
Correlations between all creep parameters used in multiple regression models. r2 value is presented followed by p value in parentheses. All significant correlations were positive, and nonsignificant correlations are indicated by NS.
| Creep (Dcr) | Recovery (Rcr) | Residual (Dres) | Residual from Creep (Dres-cr) | Time constant (τcr) | Stretch exponent (n) | Creep rate (C) | |
|---|---|---|---|---|---|---|---|
| Creep (Dcr) | 1 | 0.68(<0.002) | 0.80 (<0.0001) | 0.94(<0.0001) | NS | NS | 0.46 (<0.05) |
| Recovery (Rcr) | 1 | NS | NS | NS | 0.46 (<0.05) | NS | |
| Residual (Dres) | 1 | 0.84 (<0.0001) | NS | NS | 0.56 (<0.02) | ||
| Residual from Creep (Dres-cr) | 1 | NS | NS | 0.55 (<0.02) | |||
| Time constant (τcr) | 1 | NS | NS | ||||
| Stretch exponent (n) | 1 | 0.52 (<0.02) | |||||
| Creep rate (C) | 1 |
Measures of bone mass and size (BMD.LM, BMD.AP, and Area.AP) were the most significant contributors among candidate variables in the most explanatory multiple regression models of Dcr (r2adj=0.56, Figure 4), Dres-cr (r2adj=0.56), and C (r2adj=0.45) (Table 4). Rcr (r2adj=0.17) and n (r2adj=0.27) had only single BMD terms in their models.
Figure 4.
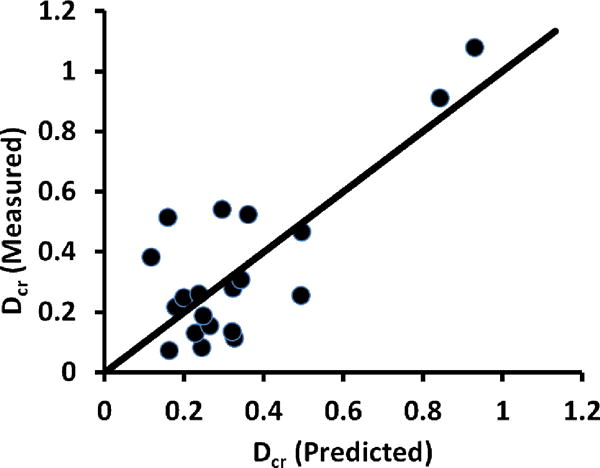
Measured vs. predicted creep displacements for Dcr. The multiple regression model for Dcr contained BMD.LM, GV.SD, and Conn.Dn (r2adj=0.56).
Table 4.
Summary of the most explanatory multiple regression models of creep measurements. Each cell shows r2adj followed by the predictor(s) in the model (sign of estimate, parameter name, p-value in each row). If a BMD variable was found to be significantly correlated to a creep variable, the BMD variable was introduced first and forced to stay in the model. NS indicates no significant models.
| Creep variable | Displacement | Normalized Displacement |
|---|---|---|
| Creep (Dcr) | 0.56: (−) BMD.LM (<0.0009) (+) GV.SD (<0.003) (+) Conn.Dn (<0.01) |
NS |
| Recovery (Rcr) | 0.17: (−) BMD.AP (<0.05) |
0.17: (−) BV/TV (<0.04) |
| Residual (Dres) | 0.17: (+) GV.SD (<0.04) |
0.32: (−) Area.AP (<0.04) (+) GV.SD (<0.05) |
| Residual from Creep (Dres-cr) | 0.56: (−) Area.AP (<0.002) (+) GV.SD (<0.003) (+) Conn.Dn (<0.03) |
0.33: (−) Area.AP (<0.04) (+) GV.SD (<0.04) |
| Time constant (τcr) | NS | |
| Stretch exponent (n) | 0.27: (−) BMD.LM (<0.007) |
|
| Creep rate (C) | 0.45: (−) iBMD (<0.0005), (−) Conn.Dn (<0.05) |
|
GV.SD significantly contributed to models for Dcr, Dres, and Dres-cr, independently from the DXA-based BMD or area variables. In fact, Dres (r2adj=0.17) had only variability of tissue mineral density (GV.SD) as a significant effect. Connectivity density also significantly contributed to models of creep, residual from creep, and creep rate, independently from BMD or area variables, and for Dcr and Dres-cr, independently from GV.SD.
When normalized for stiffness to account for the contribution of elastic displacement, GV.SD was persistent in the most significant models for both stiffness-normalized residual displacement and residual displacement from creep alone (Dres-norm and Dres-cr-norm, respectively). No significant model was calculated for Dcr-norm. BV/TV, rather than BMD.AP, was present in the most significant model for Rcr-norm (r2adj=0.17).
DISCUSSION
This study examined relationships between image-based measures of geometric, microstructural and material properties and creep behavior of human vertebral bodies. Measures of bone mineral density, size, variability of tissue mineral density, and connectivity density presented as persistent effects in multiple regression models of creep deformations. Most measured creep parameters contained density or size as covariates in their models as expected. Relationships for residual displacements included connectivity density and variability of tissue mineral density but not bone mineral density.
To our knowledge, this is the first report on the creep behavior of isolated human vertebral bodies. As such, direct numerical comparison of descriptive data (Table 2) to literature values is difficult due to the difference in specimen type as well as considerable experimental differences including load level, duration, and methodological details such as strain measurement techniques, specimen preparation, hydration and temperature regulation during testing. Characteristics of measured load-deformation curves were generally consistent with published data from human trabecular bone and motion segments (Kim et al., 2011; Pollintine et al., 2009; Yamamoto et al., 2006). That is, following initial elastic loading, a gradual, time-dependent height loss characteristic of creep was observed until load was removed, at which point immediate height recovery was followed by gradual, time-dependent height recovery.
Models of creep deformations including a size or density term demonstrated inverse relationships with measures of BMD and vertebral area, consistent with findings of previous work in which creep deformation was negatively correlated with BMD in human vertebral motion segments (Luo et al., 2012). As such, bones that are larger and denser, not surprisingly, deform and recover less in the creep process. However, BMD variables were not significant in models of displacements normalized by stiffness (Table 4), suggesting that the ability of BMDs to predict creep behavior may be limited by the strength of the relationship between creep and elastic behavior. Therefore, identification of clinically measurable predictors of creep behavior could enhance the assessment of vertebral fracture risk above that can be done using BMD alone if, as laboratory evidence supports, creep is a distinct contributor to deformities observable as clinical fractures.
Consistent with earlier work, heterogeneity of a gray value based measure of mineralization, but not its average, presented as a common variable in models of several creep parameters. In previous correlational studies, μCT.GV.CV has been shown to be associated with creep behavior of human vertebral cancellous bone (Kim et al., 2011) and rat vertebral bodies (Kim et al., 2012). Kim et al. (2011) observed that creep rate (calculated using a power law fit to the creep data) of cancellous vertebral bone cores, but not creep deformations, was significantly correlated with both μCT.GV.SD and μCT.GV.CV. Results from the current study indicate significant, positive correlations between the variability of gray values (GV.SD), but not their average, and creep deformation parameters (i.e., Dcr, Dres, Dres-cr, Dres-norm, and Dres-cr-norm) but not creep displacement rate (calculated as the linear coefficient C added to the stretched exponential function). It is important to note the differences that may lead to this discrepancy. The rate calculated using power law is the slope of the log-log plot of strain vs. time, while the rate calculated in this study is the coefficient of the linear term added to the stretched exponential fit. Power law, therefore, models both the “fast” creep and quasi-steady state creep with a single term, whereas the stretched exponential plus linear function separates the types of creep to explicitly calculate a steady state rate. As a result, it is difficult to comment on differences between whole bone and cores in terms of creep rate. However, the differences between creep in cored and intact vertebral bodies, in regard to the relationship of creep displacements and gray value variability (which were calculated the same way between the two studies), suggest that excised tissue may not fully reflect the creep behavior of the whole vertebra. The portions of the vertebra excluded by coring (i.e., the relative contribution of mineralization distributions in the cancellous, shell, and endplate components) may thus be important in both the development and recovery of deformations in bone during physiological creep. Similarly, although the focus of the current work was creep behavior of isolated vertebral bodies under uniaxial compression, creep may be modulated by different load distributions facilitated by other structures of the vertebral column such as the posterior elements. Although inclusion of posterior elements is understood to contribute little to the compressive properties of vertebrae (Hutton and Cyron, 1978), they are suggested to play a role in the development and spatial distribution of creep deformations in the vertebral body, with anterior creep strain more than twice that of the posterior aspect in vertebral motion segments (Pollintine et al., 2009). In addition, while the current study finds density variability to be associated with creep deformations, the spatial relationships of densities with creep were not specifically addressed.
Increased mineralization heterogeneity may lead to an increased potential for the presence of “point defects” on the trabecular lattice which could provide a mechanism for increased creep and residual deformation, such that dislocation occurs at the cement line in trabeculae, similar to that demonstrated in cortical bone during prolonged creep loading (Lakes and Saha, 1979). This phenomenon is analogous to grain boundary migration which is well described in slip creep of engineering materials (Herring, 1950; Nabarro, 2002). In addition, as the range of tissue mineral density is increased, a larger portion of trabecular structure with high mineralization may stifle defect diffusion, in essence reaching a percolation threshold (Sasaki et al., 1986). In bone, defect diffusion is understood to be affected by changes in mineralization variability due to, for example, mineral inclusions in the collagen matrix (Sasaki et al., 1993). In the current study, all measured deformations except recovery deformations (Rcr and Rcr-norm) showed significant positive correlations with GV.SD and residual displacements did not contain average BMD in their models (Table 4). Increased creep and residual deformation may be attributed to the modification of defect dynamics within the bone tissue related to increased mineralization heterogeneity, for example due to a state of rapid turnover (Ciarelli et al., 2009). Recovery deformations were only correlated with measures of average bone mass, suggesting that the processes of creep and recovery after creep are likely governed by different mechanisms in human vertebrae, possibly arising from multiple levels of bone’s hierarchal structure.
In addition to GV.SD, both creep and residual from creep had trabecular connectivity (Conn.Dn) in their most significant models. After taking into account BMD and tissue mineral heterogeneity, Conn.Dn was positively correlated with creep deformation and residual from creep, suggesting that, all things being equal, decreased connectivity results in more desirable creep characteristics (i.e., less creep with lower residual deformation). This finding seems counterintuitive but not entirely unfounded, as previous studies have demonstrated negative correlations between stiffness and Conn.Dn (Ding et al., 2002; Yeni et al., 2011). The negative correlation found between creep rate and Conn.Dn and the positive correlation found between C and n (Table 3) suggest that this effect is due to a faster response to load in vertebrae with higher connectivity, and creep displacement may eventually get higher for vertebrae with less connectivity. In the case of high connectivity, the majority of creep deformation would take place earlier (i.e., increasing n is related to a faster rate of primary creep), while deformation in vertebrae with lower connectivity would continue to increase at a higher rate. However, the time required for creep deformation in low connectivity bone to surpass that of high connectivity bone may be longer than a day-night cycle (Yamamoto et al., 2006). When the dependence of creep on elastic displacement is minimized by normalization, Conn.Dn was no longer present in the models, suggesting that the association of Conn.Dn with Dcr and Dres-cr is not independent from its association with stiffness.
A relatively slow ramp (10 N/sec) was applied to avoid overshoot under load control. At low loading rates the instantaneous response may be biased by contribution of the viscous component (Wu et al., 2011). Despite this, curve fitting of the “hold” portion of the creep experiment is understood to be unaffected by initial loading rate (Oyen and Ko, 2007) and deformations subsequent to the initial elastic loading used in multiple regression models were calculated relative to the starting displacement of the creep hold period (De). The target load level of 1000 N was based on that used effectively in Pollintine et al., 2009, which is the closest specimen construct in the vertebral creep literature. In the Pollintine at al. study, in several cases these load levels yielded high creep and elastic deformations (>5% strain), which was attributed to pre-existing damage. Despite being in line with theoretical estimates of load levels encountered during physiological tasks (Ignasiak et al., 2017; Iyer et al., 2010), this load level was too high for the lowest density specimens. The current findings are expected to help inform loading protocols for future creep studies of vertebral bodies.
Although we found statistically demonstrable effects of vertebral geometry and mineralization heterogeneity on vertebral creep, the explained variation is relatively low. While the use of a solid phantom in normalizing μCT-derived grey values allows for highly precise measurement of tissue mineral density (Kazakia et al., 2008), future studies more directly measuring composition of the hard tissue and organization of the collagenous matrix may identify additional determinants of vertebral creep. Most measured parameters could have potentially been derived from microcomputed tomography alone, however we chose to use a combination of readily available clinical imaging approaches where available and appropriate, especially for geometric measurements. In other words, laboratory imaging was used to identify features of microstructure and mineralization additional to those that can be measured using clinical imaging modalities. The T12 level was selected for use in this study as vertebral fractures are commonly observed at this level. While this is considered a strength of the current study, examination of additional levels in future studies could provide further insight into the mechanisms that uniquely affect fracture-critical vertebral levels. Finally, uniaxial compression was simulated in this cadaver study and the extent to which the current findings apply to creep of vertebrae under in vivo loading needs further elucidation.
In this work, we described relationships between creep properties of human vertebral bone and vertebral geometry, bone mass, microarchitecture and mineralization distributions. Several variables, such as mineralization heterogeneity, average bone density, and connectivity density persistently appeared as significant effects in multiple regression models, however many of the parameters are limited in their direct clinical translation as they are measured using laboratory imaging techniques. As such, future work will aim to establish relationships between creep properties and measurements from clinically available imaging modalities. The image variables selected for this study represented a range of geometric, microstructural and hard tissue properties and these data are expected help understand mechanisms underlying creep and improve prediction of vertebral deformities that eventually progress to a clinically observable fracture.
Acknowledgments
This project was supported, in part, by the National Institutes of Health under NIH grants AR059329 and AR070363. Its contents are solely the responsibility of the authors and do not necessarily represent the official views of NIH. We thank Nicole Ramo for her help in specimen dissection, Angela Xiao for her work in CT analysis, and Doris Moneace in DXA imaging. Human tissue used in the presented work was provided, in part, by National Disease Research Interchange (NDRI).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Conflict of interest statement
There are no financial or personal relationships with other people or organizations that could inappropriately bias the content of this paper.
References
- Adams MA, Pollintine P, Tobias JH, Wakley GK, Dolan P. Intervertebral Disc Degeneration Can Predispose to Anterior Vertebral Fractures in the Thoracolumbar Spine. Journal of Bone and Mineral Research. 2006;21:1409–1416. doi: 10.1359/jbmr.060609. [DOI] [PubMed] [Google Scholar]
- Ajdari A, Canavan P, Nayeb-Hashemi H, Warner G. Mechanical properties of functionally graded 2-D cellular structures: A finite element simulation. Materials Science and Engineering: A. 2009;499:434–439. [Google Scholar]
- Andrews EW, Gibson LJ. The role of cellular structure in creep of two-dimensional cellular solids. Materials Science and Engineering: A. 2001;303:120–126. [Google Scholar]
- Bailey JF, Hargens AR, Cheng KK, Lotz JC. Effect of microgravity on the biomechanical properties of lumbar and caudal intervertebral discs in mice. J Biomech. 2014;47:2983–2988. doi: 10.1016/j.jbiomech.2014.07.005. [DOI] [PubMed] [Google Scholar]
- Bowman S, Gibson L, Hayes W, McMahon T. Results from demineralized bone creep tests suggest that collagen is responsible for the creep behavior of bone. Journal of biomechanical engineering. 1999;121:253–258. doi: 10.1115/1.2835112. [DOI] [PubMed] [Google Scholar]
- Bowman SM, Guo XE, Cheng DW, Keaveny TM, Gibson LJ, Hayes WC, McMahon TA. Creep contributes to the fatigue behavior of bovine trabecular bone. Journal of biomechanical engineering. 1998;120:647–654. doi: 10.1115/1.2834757. [DOI] [PubMed] [Google Scholar]
- Bowman SM, Keaveny TM, Gibson LJ, Hayes WC, McMahon TA. Compressive creep behavior of bovine trabecular bone. J Biomech. 1994;27:301–310. doi: 10.1016/0021-9290(94)90006-x. [DOI] [PubMed] [Google Scholar]
- Buie HR, Campbell GM, Klinck RJ, MacNeil JA, Boyd SK. Automatic segmentation of cortical and trabecular compartments based on a dual threshold technique for in vivo micro-CT bone analysis. Bone. 2007;41:505–515. doi: 10.1016/j.bone.2007.07.007. [DOI] [PubMed] [Google Scholar]
- Busscher I, van Dieen JH, van der Veen AJ, Kingma I, Meijer GJ, Verkerke GJ, Veldhuizen AG. The effects of creep and recovery on the in vitro biomechanical characteristics of human multi-level thoracolumbar spinal segments. Clinical biomechanics. 2011;26:438–444. doi: 10.1016/j.clinbiomech.2010.12.012. [DOI] [PubMed] [Google Scholar]
- Caler WE, Carter DR. Bone creep-fatigue damage accumulation. J Biomech. 1989;22:625–635. doi: 10.1016/0021-9290(89)90013-4. [DOI] [PubMed] [Google Scholar]
- Ciarelli TE, Tjhia C, Rao DS, Qiu S, Parfitt AM, Fyhrie DP. Trabecular packet-level lamellar density patterns differ by fracture status and bone formation rate in white females. Bone. 2009;45:903–908. doi: 10.1016/j.bone.2009.07.002. [DOI] [PubMed] [Google Scholar]
- Ding M, Odgaard A, Danielsen CC, Hvid I. Mutual associations among microstructural, physical and mechanical properties of human cancellous bone. Journal of Bone & Joint Surgery. 2002:900–907. doi: 10.1302/0301-620x.84b6.11994. British Volume 84-B. [DOI] [PubMed] [Google Scholar]
- Fondrk M, Bahniuk E, Davy D, Michaels C. Some viscoplastic characteristics of bovine and human cortical bone. J Biomech. 1988;21:623–630. doi: 10.1016/0021-9290(88)90200-x. [DOI] [PubMed] [Google Scholar]
- Goodship AE, Cunningham JL, Kenwright J. Strain rate and timing of stimulation in mechanical modulation of fracture healing. Clinical orthopaedics and related research. 1998:S105–115. doi: 10.1097/00003086-199810001-00012. [DOI] [PubMed] [Google Scholar]
- Herring C. Diffusional Viscosity of a Polycrystalline Solid. Journal of Applied Physics. 1950;21:437–445. [Google Scholar]
- Huang JS, Gibson LJ. Creep of open-cell Voronoi foams. Materials Science and Engineering: A. 2003;339:220–226. [Google Scholar]
- Hutton W, Cyron B. Spondylolysis: The role of the posterior elements in resisting the intervertebral compressive force. Acta orthopaedica Scandinavica. 1978;49:604–609. doi: 10.3109/17453677808993246. [DOI] [PubMed] [Google Scholar]
- Ignasiak D, Rüeger A, Sperr R, Ferguson SJ. Thoracolumbar spine loading associated with kinematics of the young and the elderly during activities of daily living. J Biomech. 2017 doi: 10.1016/j.jbiomech.2017.11.033. In Press. [DOI] [PubMed] [Google Scholar]
- Iyer S, Christiansen BA, Roberts BJ, Valentine MJ, Manoharan RK, Bouxsein ML. A biomechanical model for estimating loads on thoracic and lumbar vertebrae. Clinical biomechanics. 2010;25:853–858. doi: 10.1016/j.clinbiomech.2010.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Iyo T, Maki Y, Sasaki N, Nakata M. Anisotropic viscoelastic properties of cortical bone. J Biomech. 2004;37:1433–1437. doi: 10.1016/j.jbiomech.2003.12.023. [DOI] [PubMed] [Google Scholar]
- Kazakia G, Burghardt A, Cheung S, Majumdar S. Assessment of bone tissue mineralization by conventional x‐ray microcomputed tomography: Comparison with synchrotron radiation microcomputed tomography and ash measurements. Medical physics. 2008;35:3170–3179. doi: 10.1118/1.2924210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kazarian L. Creep characteristics of the human spinal column. The Orthopedic clinics of North America. 1975;6:3–18. [PubMed] [Google Scholar]
- Keller T, Spengler D, Hansson T. Mechanical behavior of the human lumbar spine. I. Creep analysis during static compressive loading. J Orthopaed Res. 1987;5:467–478. doi: 10.1002/jor.1100050402. [DOI] [PubMed] [Google Scholar]
- Kim DG, Navalgund AR, Tee BC, Noble GJ, Hart RT, Lee HR. Increased variability of bone tissue mineral density resulting from estrogen deficiency influences creep behavior in a rat vertebral body. Bone. 2012;51:868–875. doi: 10.1016/j.bone.2012.08.124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim DG, Shertok D, Ching Tee B, Yeni YN. Variability of tissue mineral density can determine physiological creep of human vertebral cancellous bone. J Biomech. 2011;44:1660–1665. doi: 10.1016/j.jbiomech.2011.03.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim W, Oravec D, Nekkanty S, Yerramshetty J, Sander EA, Divine GW, Flynn MJ, Yeni YN. Digital tomosynthesis (DTS) for quantitative assessment of trabecular microstructure in human vertebral bone. Medical engineering & physics. 2015;37:109–120. doi: 10.1016/j.medengphy.2014.11.005. [DOI] [PubMed] [Google Scholar]
- Lakes R, Saha S. Cement line motion in bone. Science. 1979;204:501–503. doi: 10.1126/science.432653. [DOI] [PubMed] [Google Scholar]
- Luo J, Pollintine P, Gomm E, Dolan P, Adams MA. Vertebral deformity arising from an accelerated “creep” mechanism. Eur Spine J. 2012;21:1684–1691. doi: 10.1007/s00586-012-2279-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Manda K, Xie S, Wallace RJ, Levrero-Florencio F, Pankaj P. Linear viscoelasticity - bone volume fraction relationships of bovine trabecular bone. Biomechanics and modeling in mechanobiology. 2016 doi: 10.1007/s10237-016-0787-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nabarro FRN. Creep at very low rates. Metallurgical and Materials Transactions A. 2002;33:213–218. [Google Scholar]
- Novitskaya E, Zin C, Chang N, Cory E, Chen P, D’Lima D, Sah RL, McKittrick J. Creep of trabecular bone from the human proximal tibia. Materials Science and Engineering: C. 2014;40:219–227. doi: 10.1016/j.msec.2014.03.057. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oravec D, Quazi A, Xiao A, Yang E, Zauel R, Flynn MJ, Yeni YN. Digital tomosynthesis and high resolution computed tomography as clinical tools for vertebral endplate topography measurements: Comparison with microcomputed tomography. Bone. 2015;81:300–305. doi: 10.1016/j.bone.2015.07.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oyen ML, Ko CC. Examination of local variations in viscous, elastic, and plastic indentation responses in healing bone. Journal of Materials Science: Materials in Medicine. 2007;18:623–628. doi: 10.1007/s10856-007-2311-7. [DOI] [PubMed] [Google Scholar]
- Pollintine P, Luo J, Offa-Jones B, Dolan P, Adams MA. Bone creep can cause progressive vertebral deformity. Bone. 2009;45:466–472. doi: 10.1016/j.bone.2009.05.015. [DOI] [PubMed] [Google Scholar]
- Rimnac C, Petko A, Santner T, Wright T. The effect of temperature, stress and microstructure on the creep of compact bovine bone. J Biomech. 1993;26:219223–221228. doi: 10.1016/0021-9290(93)90360-q. [DOI] [PubMed] [Google Scholar]
- Sasaki N, Nakayama Y, Yoshikawa M, Enyo A. Stress relaxation function of bone and bone collagen. J Biomech. 1993;26:1369–1376. doi: 10.1016/0021-9290(93)90088-v. [DOI] [PubMed] [Google Scholar]
- Sasaki N, Yamamura H, Matsushima N. Is there a relation between bone strength and percolation? Journal of Theoretical Biology. 1986;122:25–31. doi: 10.1016/s0022-5193(86)80223-5. [DOI] [PubMed] [Google Scholar]
- Sato K, Kikuchi S, Yonezawa T. In vivo intradiscal pressure measurement in healthy individuals and in patients with ongoing back problems. Spine. 1999;24:2468. doi: 10.1097/00007632-199912010-00008. [DOI] [PubMed] [Google Scholar]
- Shepherd TN, Zhang J, Ovaert TC, Roeder RK, Niebur GL. Direct comparison of nanoindentation and macroscopic measurements of bone viscoelasticity. Journal of the mechanical behavior of biomedical materials. 2011;4:2055–2062. doi: 10.1016/j.jmbbm.2011.07.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Summitt MC, Reisinger KD. Characterization of the mechanical properties of demineralized bone. Journal of Biomedical Materials Research Part A. 2003;67:742–750. doi: 10.1002/jbm.a.10123. [DOI] [PubMed] [Google Scholar]
- van der Veen AJ, Mullender MG, Kingma I, van JH, Smit TH. Contribution of verftebral bodies, endplates, and intervertebral discs to the compression creep of spinal motion segments. J Biomech. 2008;41:1260–1268. doi: 10.1016/j.jbiomech.2008.01.010. [DOI] [PubMed] [Google Scholar]
- Wu Z, Baker TA, Ovaert TC, Niebur GL. The effect of holding time on nanoindentation measurements of creep in bone. J Biomech. 2011;44:1066–1072. doi: 10.1016/j.jbiomech.2011.01.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Z, Ovaert TC, Niebur GL. Viscoelastic properties of human cortical bone tissue depend on gender and elastic modulus. Journal of orthopaedic research: official publication of the Orthopaedic Research Society. 2012;30:693–699. doi: 10.1002/jor.22001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xie S, Manda K, Wallace RJ, Levrero-Florencio F, Simpson AHRW, Pankaj P. Time Dependent Behaviour of Trabecular Bone at Multiple Load Levels. Ann Biomed Eng. 2017:1–8. doi: 10.1007/s10439-017-1800-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yamamoto E, Paul Crawford R, Chan DD, Keaveny TM. Development of residual strains in human vertebral trabecular bone after prolonged static and cyclic loading at low load levels. J Biomech. 2006;39:1812–1818. doi: 10.1016/j.jbiomech.2005.05.017. [DOI] [PubMed] [Google Scholar]
- Yeni YN, Zinno MJ, Yerramshetty JS, Zauel R, Fyhrie DP. Variability of trabecular microstructure is age-, gender-, race- and anatomic site-dependent and affects stiffness and stress distribution properties of human vertebral cancellous bone. Bone. 2011;49:886–894. doi: 10.1016/j.bone.2011.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zauel R, Fyhrie DP, Yeni YN. Segmentation Algorithm With Improved Connectivity For Accurate 3D Representation Of Microcomputed Tomographic Images Of Human Vertebral Bodies. 51st Annual Meeting of the Orthopaedic Research Society; Washington, D.C.. 2005. p. 1260. [Google Scholar]
- Zilch H, Rohlmann A, Bergmann G, Kölbel R. Material properties of femoral cancellous bone in axial loading. Archives of orthopaedic and traumatic surgery. 1980;97:257–262. doi: 10.1007/BF00380706. [DOI] [PubMed] [Google Scholar]


