Prediction Model and Risk Stratification Tool for Survival in Patients With CKD

Abstract

Introduction

Because chronic kidney disease (CKD) adversely affects survival, prediction of mortality risk should help to identify individuals requiring therapeutic intervention. The goal of this project was to construct and to validate a risk scoring system and prediction model of the probability of 2-year mortality in a CKD population.

Methods

We applied the Woodpecker approach to develop prediction equations using linear, exponential, and combined models. A risk indicator R on a scale of 0 to 10 was calculated as follows: starting with 0, add 0.048 for each year of age above 20, 0.45 for male sex, 0.49 for each stage of CKD over stage 2, 1.04 for proteinuria, 0.72 for smoking history, and 0.49 for each significant comorbidity up to 5.

Results

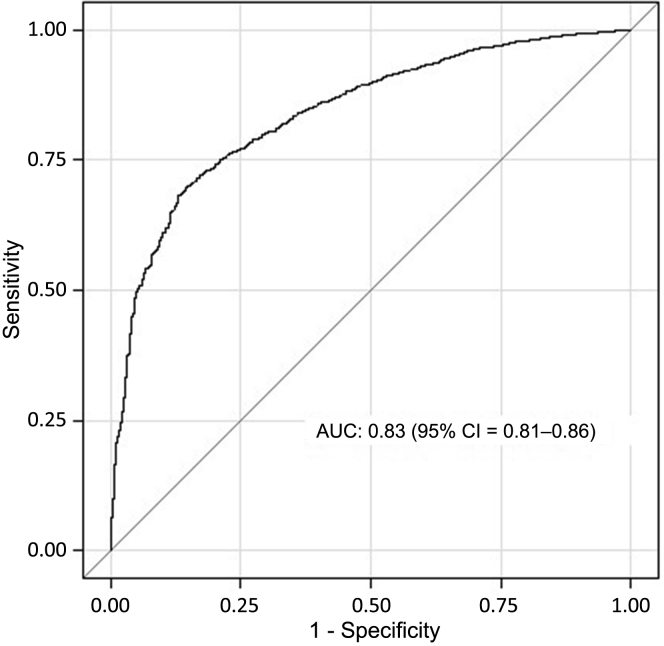
Using R to predict 2-year mortality, the model yielded an area under the receiver operating characterisic curve of 0.83 (95% confidence interval = 0.81−0.86) with 5062 subjects with CKD ≥stage 2 from a National Health and Nutrition Examination Survey cohort (1999−2004) having a 3.2% 2-year mortality. The combined expression offered results closest to most actual outcomes for the entire population and for each CKD stage. For those patients with higher risk (R ≥ 4−5, >5−6, and >6), the predicted 2-year mortality rates were 3.8%, 6.4%, and 13.0%, respectively, compared to observed mortality rates of 2.7%, 4.5%, and 13.3%.

Conclusion

The risk stratification tool and prediction model of 2-year mortality demonstrated good performance and may be used in clinical practice to quantify the risk of death for individual patients with CKD.

Chronic kidney disease (CKD) affects an estimated 13% of the population in the United States,¹ and has an even higher prevalence in elderly persons.² An important goal of treatment is to prevent the progression of CKD to end-stage renal disease (ESRD) and the need for dialysis or kidney transplantation. Equally important, CKD bestows a very significant mortality risk,3, 4 similar to that of cardiovascular disease.⁵ It increases patient risk of mortality by 36% independent of other cardiovascular risk factors.⁶ Furthermore, even relatively mild decreases in kidney function are associated with significantly increased risk of mortality.7, 8 In the era of personalized medicine, it is helpful to predict the risk of an individual patient to direct intervention of preventive measures in individuals at highest risk for progression and death. Identifying a high-risk group of individuals is also important for other reasons, for example, to select the population of interest for clinical trials or for health care policy research. Furthermore, developing prediction models and risk stratification tools may help to counsel patients in a more evidence-based manner.

Factors associated with mortality in the CKD population are similar to those in the general population, including age, male sex, and comorbidities. However, there are some differences; for example, hypertension does not seem to predict greater mortality according to some authors7, 8, 9 but is a good predictor according to others.¹⁰ The role of race/ethnicity is unclear,9, 11 and some additional risk factors play a significant role, namely, elevated phosphate level,¹¹ degree of kidney dysfunction,7, 8 and hemoglobin level.7, 12

Prediction models of CKD patient survival have been developed but with only a fair degree of accuracy (c-stat 0.72 in the validation dataset and 0.69 in external validation).¹³ In general, developing prediction models and their validation requires careful analysis and statistical use of data.¹⁴ Recently, we developed the Woodpecker approach to streamline construction of a model from existing data in the literature that allows generation of a risk indicator and prediction formulae15, 16 that were used to predict 2-year mortality risk in the general population.¹⁷

The goal of this project was to apply the Woodpecker approach to construct and to validate a risk scoring system and prediction model of the probability of 2-year mortality in patients with CKD of stage 2 and greater. We developed and compared the results of various prediction equations based on linear, logistic regression, and Cox regression models to actual mortality.

Methods

Selection of Variables for the Prediction Formula

Several studies describing factors predicting CKD patients’ survival were selected as a source of our prediction model. The selection of the studies was based first on those reports in which multiple variables are included in the model adjusting for each other. That type of study is different from a hypothesis-driven design, in which a particular primary variable is evaluated and the selection of covariates is based on potential confounding effects.¹⁸ Furthermore, we were looking for a well-designed study with a relatively large sample size using the same outcome definition as in our model. The selection of the specific variables in the model was determined by choosing the best predictors of the outcome, but was also driven by criteria of practicality (e.g., variables difficult to obtain are not practical), parsimony, and physiologic plausibility.

Using PubMed, we searched for papers with key words “chronic kidney disease” and “mortality,” limiting the search to studies in humans, papers with full text available, and published in the last 10 years in the “core clinical journals.” That search returned 525 items. In addition, we reviewed papers generated by the CKD Prognosis Consortium.19, 20, 21, 22, 23 We carefully reviewed selected reports, paying careful attention to study design, sample size, generalizability of the study population, and availability of information necessary for our prediction model construction. That selection left us with 10 final papers7, 8, 9, 11, 12, 24, 25, 26, 27, 28, 29; from those we selected the 4 most relevant reports for our final model.7, 8, 11, 29 The analysis in 1 reference²⁸ was not included, as it presented risk factors that were reported elsewhere, and the quantified impact of some (gender, comorbidities) was very close to that in other reports,8, 29 whereas age and CKD stage had a higher impact than reported elsewhere.8, 11

Our initial prediction model was based on a previously published study of 6541 subjects with CKD, defined as <60 ml/min per 1.73 m² (i.e., stage 3 CKD or above), who were 20 years of age or older and followed for up to 5 years.⁸ Using the Cox model, Johnson et al.⁸ identified the variables associated with mortality in 2678 cases (11.4 deaths/100 person-years). Two variables were selected from this model for our analysis, namely, sex and stage of CKD. Some other potential risk factors (e.g., proteinuria) were not included in our study from that report, because of a large amount of missing data. Several variables were added to the model from other reports of similar populations described elsewhere.¹⁶ Combining predictors from different studies in the same model is based on specific assumptions: (i) homogeneity,³⁰ the assumption that the populations are similar between the studies (that can be demonstrated by comparing baseline statistics); and (ii) independence of the predictors, lack of interaction, and lack of collinearity. We note that meta-analysis and meta-regression methods30, 31 present more elaborate ways to combine results rather than simply combining the regression coefficients in a linear way. However, for the practical purpose of developing a prediction algorithm, the latter should be adequate.¹⁶

Specifically, using the initial model, we added age,¹¹ proteinuria, smoking history,⁷ and a number of important comorbidities.²⁹ The approach to comorbidities was based on a report by Tonelli et al.,²⁹ in which the authors studied the number of comorbidities in association with mortality. As done in that report and to make our model the most practical, we also assigned 1 point to each of the comorbidities. The following conditions that were also available in the National Health and Nutrition Examination Survey (NHANES) dataset were included in our calculation of the comorbidities: diabetes mellitus, hypertension, coronary artery disease, stroke, congestive heart failure, chronic obstructive pulmonary disease/asthma, anemia, cancer, liver disease, osteoporosis, arthritis, thyroid disease, and hyperphosphatemia.

Regression coefficients for continuous variables were derived from reported hazard ratios. The number of comorbidities was reported as a categorical variable,²⁹ and to quantify the risk of comorbidity, we assumed a linear relationship between the number of comorbidities and the hazard ratio of mortality. The linear coefficient of a fitted line with intercept being close to 0 is 1.33, meaning that each new comorbidity up to 5 adds 1.33 on average to the hazard ratio. Therefore, the regression coefficient associated with each additional comorbidity (up to 5), the natural logarithm of 1.33, is 0.285.

Our final model therefore included age (regression coefficient [β] = 0.039), male sex (β = 0.365), stage of CKD (β = 0.4 over stage 2), presence of proteinuria, defined as albumin-to-creatinine ratio of ≥300 mg/g³² (β = 0.85), positive smoking history (β = 0.588), and number of serious comorbidities (each β = 0.4). The risk indicator, R, was then calculated by factoring these coefficients to a scale from 0 to 10 as follows: starting with 0, add 0.048 for each year of age above 20, 0.45 for male sex, 0.49 for each stage of CKD over stage 2, 1.04 for proteinuria, 0.72 for smoking history, and 0.49 for each significant comorbidity up to 5 (as described more fully in the Supplementary Material).

We used the stage of CKD rather than eGFR for the following 2 reasons: (i) CKD stage rather than eGFR was used as a predictor in the original paper that was used for model generation; and (ii) from a practical standpoint, although the most recent eGFR is not always available, the stage of CKD is usually well documented in the patient records. The stage of CKD might have been somewhat overestimated for 2 potential reasons: (i) The Modification of Diet in Renal Disease Study (MDRD) equation,³³ which was used for estimated glomerular filtration rate (eGFR), calculation tends to classify more people as having CKD compared to the Chronic Kidney Disease−Epidemiology Collaboration (CKD-EPI) equation²²; and (ii) we used non−isotope dilution mass spectrometry−calibrated Jaffe assay serum creatinine values that were reported in NHANES dataset.³⁴ The presence and stage of CKD in our validation dataset was defined based on estimated GFR calculated using the expression derived by Levey et al.³³: eGFR = 186 × [serum creatinine^(−1.154)] × [age in years^(−0.203)] × 0.742 if female × 1.212 if black. This original MDRD equation is used for creatinine values that are not calibrated to an isotope dilution mass spectrometry. With the effort to standardize reported creatinine values, a new equation was developed in which the coefficient of 173 is used instead of 186. NHANES reported isotope dilution mass spectrometry–adjusted creatinine values starting in 2008, whereas before that, unadjusted values were reported, and therefore, the original equation was used in this study.

Calculating the Probability of Event

We estimated the probability of the outcome (P) as a function of the risk indicator (R) and the outcome rate in the population at 2 years. We used a simplified linear expression and 2 more complex exponential expressions to predict the probability of outcome¹⁵:

• 1.Linear expression: Probability of 2-year mortality, $P\left(R\right)=\frac{R\text{·}r}{\hat{\text{R}}}$, where r is the outcome rate in the target population (2-year mortality, 3.18%) and $\hat{\text{R}}$ scaled from 0 to 10 is the value of risk indicator for the “average” person in the target population ($\hat{\text{R}}$ = 3.402), so the final expression is $P\left(R\right)=R·0.009347$
• 2.Exponential expression based on logistic regression: $P\left(R\right)=\frac{1}{1+{\left(e^{a+R/1.229}\right)}^{-1}}$ where a is the intercept: a $=ln\frac{r}{1-r}-\frac{\hat{\text{R}}}{1.229}$. Using $\hat{\text{R}}$ and r of our target population a = −6.81814 and $P\left(R\right)=\frac{1}{1+{\left(e^{R/1.229-6.81814}\right)}^{-1}}$
• 3.Exponential expression based on Cox model: P(R) $=1-e^{-q_T\text{·}\left(e^{R/1.229}\right)}$, where $q_T$ is baseline hazard: $q_T=-\frac{\text{ln}(1-r)}{e^{\hat{\text{R}}/1.229}}$. Using target population data, $q_T=0.001076$ and $P\left(R\right)=1-e^{-0.001076\text{ ·}\left(e^{R/1.229}\right)}$
• 4.Finally, we considered a combined expression, averaging the predictions generated by the linear model and the exponential expression based on logistic regression. We previously demonstrated that predictions of exponential models are similar to those of linear model in the lower risk subjects, although in higher risk groups, linear models tend to underestimate the risk whereas exponential models tend to overestimate it.15, 16 We hypothesized that the characteristics of the target population (described by $\frac{r}{\hat{\text{R}}}$) would determine which model better estimates the actual outcome. Specifically, in a population with higher $\frac{r}{\hat{\text{R}}}$ (population with higher mortality despite lower average risk) exponential curves become more flat and closer to linear models. On the other hand, in a population with lower $\frac{r}{\hat{R}}$ (low outcome rate despite higher average risk) exponential curves are sharper and the discrepancy between linear and exponential predictions is greater.¹⁵ We propose that the true outcome is in the area between the predictions of these 2 models.

Validation Dataset

For our target (validation) dataset, we used the NHANES cohort, which initially included 29,402 subjects enrolled in the survey between 1999 and 2004 with mortality information available through 31 December 2006. Data collection for NHANES was based on a substantial oversampling of young children, females, older persons, African American/black persons, and Mexican Americans so as to identify those most at risk for poor nutrition for the purpose of the NHANES study. Only adults (≥18 years old) were included in our analysis. Files covering 1999 to 2000 (n = 9965), 2001 to 2002 (n = 11,039), and 2003 to 2004 (n=10,122) were merged, and variable name inconsistencies were corrected in the merged dataset. Records with missing eGFR values or missing mortality information were deleted. Subjects with CKD stage 2 or above were included in the study; thus, the dataset consisted of 5062 records. Information for prediction modeling was extracted from several NHANES files, including demographics, physical examination and body measurements, questionnaire, and laboratory files (Table 1).

Table 1.

NHANES variables used as the source of information for independent predictors used in the model

Predictor	NHANES variable(s)
Age, yr	HSAGEIR
Sex	RIAGENDR Gender
Urine albumin-to-creatinine	URXUMASI Urine albumin concentration; URXUCR Urine creatinine concentration
Creatinine level	LBXSCR Creatinine (mg/dl)
Phosphate level	LBXSPH Phosphorus (mg/dl)
Hypertension	BPQ020 Ever told you had high blood pressure; BPQ030 Told had high blood pressure 2+ times; BP040A Taking prescription for hypertension
Diabetes mellitus	DIQ010 Doctor told you have diabetes; DIQ050 Taking insulin now
Coronary artery disease	MCQ160C Ever told you had coronary heart disease; MCQ160D Ever told you had angina/angina pectoris; MCQ160E Ever told you had heart attack
Stroke	MCQ160F Ever told you had a stroke
CHF	MCQ160B Ever told you had congestive heart failure
COPD/asthma	MCQ010: Ever told you had asthma; MCQ160G: Ever told you had emphysema; MCQ160K Ever told you had chronic bronchitis; RDQ133 Doctor prescribe wheezing medication
Anemia	MCQ053 Taking treatment for anemia past 3 mo; LBXHCT Hematocrit; LBXHGB Hemoglobin
Cancer	MCQ220 Ever told you had cancer or malignancy
Arthritis	MCQ160A Doctor ever said you have arthritis
Thyroid disease	MCQ160I Ever told you had thyroid disease
Liver disease	MCQ160L Ever told you had any liver condition
Osteoporosis	OSQ060 Ever told had osteoporosis/brittle bones; OSQ070 Ever treated for osteoporosis
Smoking	BPQ043A Told to stop smoking for hypertension; SMD070 Number cigarettes smoked per day now; SMQ040 Do you now smoke cigarettes

CHF, congestive heart failure; COPD, chronic obstructive pulmonary disease; NHANES, National Health and Nutrition Examination Survey.

Outcome Variable

The outcome in this study is 2-year mortality. The mortality information was obtained from the Centers for Disease Control and Prevention (CDC) website and linked to the NHANES data using the unique subject ID. The National Center for Health Statistics has conducted a mortality linkage of NHANES to death certificate data found in the National Death Index. The NHANES Linked Mortality Files include the continuous NHANES years (1999−2004) and provide mortality follow-up data from the date of survey participation through 31 December 2006.

Validation and Statistical Analysis

Means and SDs were used to summarize continuous variables with normal distribution. Categorical variables were summarized as percent of total. The data collected were analyzed using the SAS software version 9.3 (SAS Institute, Cary, NC). To quantify goodness of fit of our prediction models, we used area under the receiver operating characteristic (ROC) curve and calibration. The ROC curve was used to validate the risk indicator comparing predicted risk to the actual outcome. After the probability for each individual subject was computed, the subjects were divided into 6 groups based on R value (0−2, >2−3, >3−4, >4−5, >5−6, and >6). For each category, we calculated the actual mortality rate and compared that to the prediction based on R.

Results

Baseline Characteristics of the Study Population

The final study population consisted of 5062 subjects with CKD stage 2 or above with mean age of 59.1 years, 51.1% male, 65.3% non-Hispanic white, 13.3% non-Hispanic black, and 15.6% Mexican American. Of the study population 13.3% had diabetes mellitus. Stage 2 CKD was present in 84.2% of the subjects; the remainder had more advanced CKD. The 2-year mortality was 3.18% in this target population. Other baseline characteristics of the study population are presented in Table 2.

Table 2.

Baseline characteristics of the NHANES study population (validation population, n = 5062)

Variable	Mean (SD) or % of total for categorical variables	Range: minimum–maximum	95% CI for mean	Number with missing data
Age, yr	59.1 (17.0)	18.0–84.9	58.6–59.6	0
Sex
Male	51.1%
Female	48.9%
Race
Non-Hispanic white	65.3%
Non-Hispanic black	13.3%
Mexican American	15.6%
Other Hispanic	3.3%
Other	2.6%
Systolic blood pressure, mm Hg	130.3 (22.0)	72.0–237.0	129.7–131.0	225
Diastolic blood pressure, mm Hg	71.5 (12.7)	8.0–122.0	71.2–71.9	274
Presence of diabetes	13.3%
Smoking history	15.0%
Stage of chronic kidney disease
2	84.2%
3	14.0%
4	1.0%
5	0.7%
Hemoglobin, g/dl	14.4 (1.5)	5.9–19.7	14.3–14.4	1
Albumin, g/dl	4.2 (0.3)	2.2–5.5	4.2–4.3	0
Blood urea nitrogen, mg/dl	16.1 (7.3)	2.0–122.0	15.9–16.3	0
Creatinine, mg/dl	1.08 (0.7)	0.7–13.7	1.06–1.1	0
Calcium, total, mg/dl	9.5 (0.4)	6.7–12.5	9.49–9.51	0
Phosphorus, mg/dl	3.7 (0.6)	1.8–8.1	3.69–3.72	0
eGFR, ml/min per 1.73 m2	73.8 (14.8)	3.5–91.0	73.4–74.2	0
Urine albumin-to-creatinine ratio, mg/g	80.1 (548.8)	0.15–15637.7	64.8–95.4	111
Prevalence of proteinuria and microalbuminuria (defined by urine albumin-to-creatinine ratio)	3.5% >300 mg/g 15.9% >30 mg/g
Number of comorbidities	1.77 (1.52)	0 - 5	1.73 - 1.81	0
2-yr Survival	96.8%

eGFR, estimated glomerular filtration rate.

Risk Stratification Tool

The risk indicator (R) was based upon adding regression coefficients rounded to 2 decimal points (except for age) for practicality, as noted in the Methods. It should be noted also that the risk stratification tool, R, is an artificial score on a scale of 0 to 10 that indicates a relative risk of the outcome compared to other members of the study population. Therefore, the score of 0 does not mean the probability of death is nonexistent, and 10 does not mean that the chance of mortality is 100%. A higher or lower R score simply indicates that a particular subject belongs to higher or lower risk group within the particular population.

Prediction models based on the risk indicator R demonstrated a strong degree of discrimination when compared with the actual 2-year mortality in the NHANES population sample, with an area under the ROC curve (AUC) of 0.83 (95% confidence interval [CI] = 0.81−0.86) (Figure 1). In comparison, the model based only on age yielded an AUC of 0.79 (95% CI = 0.76−0.82), and that based only on the number of comorbidities yielded an AUC of 0.73 (95% CI = 0.69−0.76).

Figure 1.

Receiver operating characteristic curve for the predicted risk of mortality in the National Health and Nutrition Examination Survey (NHANES) population based on the risk indicator R. Area under the curve = 0.83 (95% confidence interval = 0.81−0.86).

Predicting Probability of Outcome

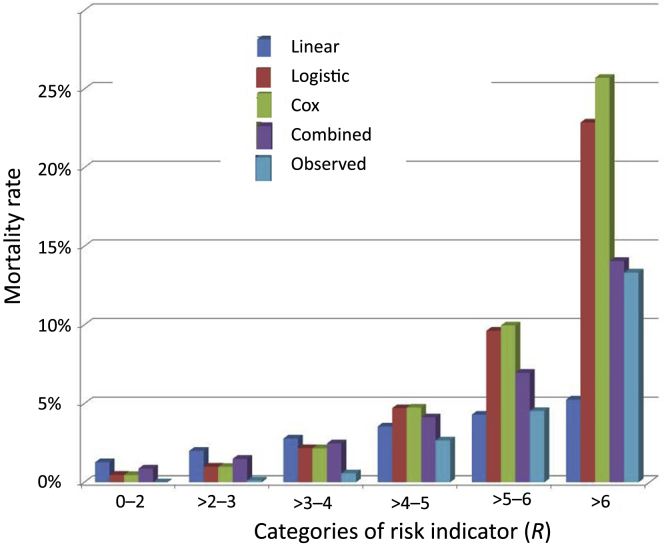
We used the 4 different expressions to predict actual probability of the outcome (i.e., mortality) as described in the Methods: namely, linear expression; exponential expression based on logistic regression; exponential expression based on Cox model; and the combined expression averaging the predictions generated by the linear model and the exponential expression based on logistic regression. When the subjects were combined into 6 groups of increasing risk, the actual mortality rate compared to the predicted probability of death based on R using each of the formulae is as shown in Table 3 and Figure 2. Analysis was then repeated for each stage of CKD separately (because of small sample sizes, stages 4 and 5 were combined into a single group). As noted in Table 3, the combined expression offered predictive results closest to the actual outcomes, particularly in the higher-risk groups. For those with R > 4 to 5, >5 to 6, and >6, the observed 2-year mortality rates were 2.7%, 4.5%, and 13.3%, respectively, compared to predicted mortality rates of 3.8%, 6.4%, and 13.0%.

Table 3.

Observed mortality (%) and predicted probability of death (%) by the logistic, linear, and combined models in the entire study population divided by risk indicator R

Risk indicator	Observed mortality %	Predicted percent mortality (96% confidence interval)
		Logistic	Linear	Combined
CKD entire group (n = 5062)
R = 0–2 (n = 343)	0	0.42 (0.41–0.42)	1.22 (1.21–1.25)	0.82 (0.81–0.84)
R > 2–3 (n = 869)	0.12	0.88 (0.86–0.89)	1.93 (1.92–1.94)	1.40 (1.39–1.42)
R > 3–4 (n = 1060)	0.57	1.93 (1.91–1.96)	2.68 (2.66–2.69)	2.31 (2.29–2.32)
R > 4–5 (n = 1276)	2.66	4.20 (4.15–4.25)	3.43 (3.42–3.44)	3.81 (3.78–3.84)
R > 5–6 (n = 928)	4.53	8.64 (8.52–8.75)	4.14 (4.13–4.16)	6.39 (6.33–6.46)
R > 6–9 (n = 585)	13.33	20.91 (20.24–21.57)	5.08 (5.04–5.11)	12.99 (12.64–13.34)
CKD stage 2 (n = 4263)
R = 0–2 (n = 342)	0	0.42 (0.41–0.42)	1.23 (1.21–1.25)	0.82 (0.81–0.84)
R > 2–3 (n = 859)	0.12	0.88 (0.86–0.89)	1.93 (1.92–1.94)	1.40 (1.39–1.42)
R > 3–4 (n = 1030)	0.58	1.93 (1.90–1.96)	2.68 (2.66–2.69)	2.30 (2.28–2.32)
R > 4–5 (n = 1146)	2.36	4.17 (4.12–4.23)	3.42 (3.41–3.43)	3.80 (3.76–3.83)
R > 5–6 (n = 658)	3.8	8.47 (8.33–8.60)	4.13 (4.11–4.14)	6.30 (6.22–6.37)
R > 6–9 (n = 228)	8.33	17.42 (16.74–18.1)	4.89 (4.85–4.93)	11.15 (10.8–11.51)
CKD stage 3 (n = 710)
R = 0–2 (n = 1)	0	0.37	1.13	0.74
R > 2–3 (n = 10)	0	0.93 (0.80–1.06)	1.99 (1.86–2.12)	1.46 (1.33–1.59)
R > 3–4 (n = 27)	0	2.05 (1.86–2.24)	2.73 (2.64–2.83)	2.39 (2.25–2.54)
R > 4–5 (n = 129)	5.43	4.43 (4.27–4.59)	3.48 (3.44–3.52)	3.96 (3.86–4.05)
R > 5–6 (n = 254)	5.91	9.0 (8.78–9.23)	4.19 (4.17–4.22)	6.60 (6.47–6.72)
R > 6–9 (n = 289)	14.53	21.68 (20.79–22.57)	5.13 (5.08–5.17)	13.40 (12.94–13.87)
CKD stages 4–5 (n = 89)
R = 0–2 (n = 0)	NA	NA
R > 2–3 (n = 0)	NA	NA
R > 3–4 (n = 3)	0	2.28 (1.18–3.37)	2.85 (2.38–3.32)	2.56 (1.78–3.34)
R > 4–5 (n = 1)	0	4.36	3.49	3.93
R > 5–6 (n = 16)	12.5	9.91 (8.82–11.01)	4.29 (4.17–4.41)	7.10 (6.49–7.71)
R > 6–9 (n = 68)	25.0	29.31 (26.57–32.06)	5.13 (5.37–5.62)	17.40 (15.97–18.84)

CI, confidence interval.

Analysis was performed in the entire study population and in subgroups based on stage of chronic kidney disease (CKD). The Cox model was omitted, as the results were essentially identical to the logistic model.

Figure 2.

Predicted probability of mortality in comparison to observed mortality rate using the linear, exponential logistic expression, exponential Cox expression, and combined expression formulae in the groups, divided by the risk indicator R.

Discussion

Patients with CKD represent a very significant fraction of the population and diminished GFR makes a negative impact on survival in different patient populations.9, 35, 36, 37 Although therapy is driven by a desire to avoid dialysis, it is actually more likely for most CKD patients to die than to end up on dialysis.²⁴ In this project, we developed a prediction algorithm to quantify the individual mortality risk based on a few clinical and demographic factors.

Predictors of mortality in the CKD population have been evaluated in the past, specifically renal function level,25, 38 calcium-phosphate metabolism,³⁹ and demographic characteristics⁴⁰ were found to be associated with the outcome. However, actual practical risk stratification tools or other predictive analytics are less well represented in the literature. Several risk scores have been developed for death13, 41, 42 and progression to end-stage renal disease⁴³ in this population. As in this report, risk scores represent linear combination of regression coefficients of the multivariate models. Independent variables used for prediction are similar in these scores and largely overlap with those used by us (e.g., proteinuria, degree of renal dysfunction, serum phosphate level).41, 42 Traditional prediction models use large datasets to generate a prediction equation, which is then further validated on the fraction of the same dataset. That approach is prone to shortfalls: specifically, overfitting and inability to generalize. The degree of accuracy of the existing models is also somewhat variable from somewhat limited¹³ to reasonably high.²⁵

Compared to existing predictive analytics, our approach15, 16, 17 has several important advantages. The distinctive feature of this method is that predictive analytics are developed based on existing literature by combining several groups of predictors from different published reports and are then adjusted to the target population by using descriptive statistics of the group. As opposed to the usual prediction modeling in which the prediction equation is developed once and is not modified based on a new population or new information available, the Woodpecker approach allows us to make changes to the model for the distinctive features of the new populations by incorporating simple descriptive statistics. Furthermore, as current literature results can be easily added to the model, the model remains flexible and up to date with the existing literature. That in turn translates into a short implementation time of the emerging clinical outcome research and the ability to bring current literature to the bedside. Also, from a validation point of view, it is important to mention that there is very little chance of overfitting, because the model is developed externally to the validation dataset. Indeed, prediction models are more practical when they are intuitive and easy to understand. Associations that do not make much sense to clinicians will not make a trusted model. The components of our prediction model have been shown to be associated with mortality outcome in other published analyses.4, 7, 8, 11 This association might be causative (e.g., age, comorbidities). Alternatively, the risk predictors might be markers of severity of illness (e.g., hemoglobin level, stage of CKD).¹² We went through an elaborate selection of our predictors, trying to keep the balance between developing a comprehensive model and, at the same time, keeping it practical and parsimonious. We reviewed a number of outcome studies in the CKD population and selected predictors from 4 of them.7, 8, 11, 29 The final model was based on age, sex, stage of CKD, presence of proteinuria, smoking, and the number of comorbidities that we chose to include. We decided to use the number of comorbidities rather than the presence of specific comorbid conditions, such as diabetes, based on a recently published report quantifying the risk based on the number of comorbidities present.²⁹ To quantify the role of age, we selected a study with a conservative estimate for its hazard ratio.¹¹ Of note, the c-statistic was 0.7 for prediction of mortality in the study⁸ that we used for development of our model, whereas the area under the ROC curve was 0.83 for validation in an external dataset in our study.

We demonstrated that although the model was developed using different sets of data, it performed well in the validation dataset (NHANES cohort of 1991−2004). This was particularly true for the high-risk categories of patients who would be of most interest to clinicians. For example, we assume that a predicted 2-year mortality rate of 13.0% (vs. the actual mortality of 13.3%) in those at highest risk would engender changes in medical management that might reduce risk. Although overall performance of the model is acceptable, there are some subcategories in regard to which the performance was somewhat diminished: specifically, the model overestimated the probability of mortality in lower-risk groups in patients with CKD stage 2.

In reporting our results, we used the “Transparent Reporting of a multivariable prediction model for Individual Prognosis or Diagnosis” as a guide to ensure that the paper reflects the TRIPOD statement.⁴⁴

Limitations

There are potential fundamental limitations of prediction modeling, for example, using variables derived from historical data to predict future outcomes. In this study, the algorithm was developed and validated on data from the early 2000s. Although the assumption is that it will perform reasonably well now, the algorithm has not been tested in a more recent group of CKD patients. The quality of any retrospective data may pose a limitation; however, in our experience, NHANES data seem to be reasonably complete and accurate. Furthermore, it should be noted that there is a potential limitation that has to do with data selection: NHANES specifically oversampled the enrollment of minority individuals so that an epidemiologic analysis that is extrapolated to a dissimilar population might have to use weighted data. However, the relatively good performance of the algorithm to an external target population indicates the robustness of the model.

The reader should keep in mind that the performance of predictions drawn from statistical inference using the Woodpecker technique is based on the validity of several assumptions. There are generic assumptions applicable to multivariate models that could not be tested by us without access to the raw data. Because we developed our prediction model based on results of reported data, we trust that those authors tested their assumptions. Specifically, multivariate models are based on the assumptions of linearity, independence (lack of collinearity), and lack of interactions between the predictors. Additional distribution assumption regarding normality in the data might be important for certain steps of the technique (for example, calculating average risk indicator for the target population and using it in deriving probability of outcome).

Furthermore, we tested our regression model that was fitted into NHANES data for comparison of performance. We added interaction terms to the model (the product of phosphate level and GFR, the product of age and number of comorbidities, the product of comorbidities and proteinuria). We noted that the relationship between other independent variables and outcome did not change in a major way and that the interaction terms were nonsignificant in the model. We also checked the NHANES dataset for correlation between independent variables to test for multicollinerarity in bivariate analysis and found multiple significant correlations. The highest degree of correlation is between age and CKD stage (r = 0.34), age and comorbidities (r = 0.48), and CKD stage and comorbidities (r = 0.34). With this degree of correlation, we deemed that it was still appropriate to include these variables in the same regression model. Finally, it is noted that other authors used the combination of seemingly collinear (nonindependent) factors in their models: renal function and phosphate,²⁵ age and GFR level,¹³ proteinuria and serum albumin level,41, 43 and GFR and anemia level.⁴¹

In addition, because we used published reports as a source of information for the prediction model, there is a potential issue of selection. We addressed that by selecting 1 report that would be the best match the target population, and we populated the model with predictors and corresponding regression coefficients from it, rather than averaging regression coefficient values reported in different studies.

In conclusion, we have developed a risk stratification tool and prediction model of 2-year mortality rates that demonstrated good performance and may be used in clinical practice to quantify the approximate risks of death for individual patients with CKD, especially those at higher risk for death.

Disclosure

All the authors declared no competing interests.