The Interplay of Rogue and Clustered Ryanodine Receptors Regulates Ca²⁺ Waves in Cardiac Myocytes

Abstract

Ca²⁺ waves in cardiac myocytes can lead to arrhythmias owing to delayed after-depolarisations. Based on Ca²⁺ regulation from the junctional sarcoplasmic reticulum (JSR), a mathematical model was developed to investigate the interplay of clustered and rogue RyRs on Ca²⁺ waves. The model successfully reproduces Ca²⁺ waves in cardiac myocytes, which are in agreement with experimental results. A new wave propagation mode of “spark-diffusion-quark-spark” is put forward. It is found that rogue RyRs greatly increase the initiation of Ca²⁺ sparks, further contribute to the formation and propagation of Ca²⁺ waves when the free Ca²⁺ concentration in JSR lumen ([Ca²⁺]_lumen) is higher than a threshold value of 0.7 mM. Computational results show an exponential increase in the velocity of Ca²⁺ waves with [Ca²⁺]_lumen. In addition, more CRUs of rogue RyRs and Ca²⁺ release from rogue RyRs result in higher velocity and amplitude of Ca²⁺ waves. Distance between CRUs significantly affects the velocity of Ca²⁺ waves, but not the amplitude. This work could improve understanding the mechanism of Ca²⁺ waves in cardiac myocytes.

Introduction

Ca²⁺ sparks due to the opening of clustered RyRs are the elementary Ca²⁺ release events in normal cardiac myocytes (Cheng et al., 1993; Cheng and Lederer, 2008), which could occur in self-propagating succession along the length, and contribute to waves of elevated Ca²⁺ concentration under some pathological conditions (López-López et al., 1995). Ca²⁺ waves have been observed in a diversity of cells (Ridgway et al., 1977; Fabiato, 1983; Cornellbell and Finkbeiner, 1991) and studied experimentally and theoretically (Fabiato and Fabiato, 1972; Fabiato, 1985; Backx et al., 1989; Swietach et al., 2010). Generating Ca²⁺ waves in myocytes is associated with RyRs gating and sarcoplasmic reticulum Ca²⁺ overload (Petrovic et al., 2015; Williams et al., 2017). Quarky Ca²⁺ release (QCR or Ca²⁺ quark) with a small amplitude and a long duration arising from rogue RyRs is another significant Ca²⁺ release mechanism (Wang et al., 2001; Cheng and Wang, 2002; Brochet et al., 2011; Shang et al., 2014). Hence, Ca²⁺ waves are a natural consequence of regenerative Ca²⁺ releases of both Ca²⁺ sparks and quarks. There is, however, lack of studies to relate Ca²⁺ waves to the interplay of Ca²⁺ sparks and quarks from the junctional sarcoplasmic reticulum (JSR). Based on the Fickian diffusion of cytoplasmic Ca²⁺, a computational model was developed to show the effects of rogue RyRs on Ca²⁺ waves under heart failure (Lu et al., 2010). Given the spark-width paradox from the Fickian diffusion models (Walker et al., 2014), the anomalous diffusion model can solve the problem and look more deeply into the mechanism of diffusion (Sato and Bers, 2011).

On the other hand, one of the challenges in developing models for Ca²⁺ waves is the inconsistence between computational and experimental free Ca²⁺ concentration in the cytoplasm ([Ca²⁺]_cyto) (Izu et al., 2013). The computational results of [Ca²⁺]_cyto were ~20 μM (Chen et al., 2013) under physiological conditions or even as high as ~100 μM (Izu et al., 2001; Chen et al., 2014) under pathological conditions, which disagrees with the measured [Ca²⁺]_cyto of ~1 μM (Williams et al., 1985; Takamatsu and Wier, 1990). Although a “wave front sensitization” model showed [Ca²⁺]_cyto of ~1 μM (Keller et al., 2007), Sobie et al. indicated that elevated JSR Ca²⁺ level is a critical factor to raise RyRs open probability (Sobie et al., 2017). Hence, JSR Ca²⁺ regulation should be incorporated into the computational models of Ca²⁺ waves to show the decrease of Ca²⁺ flux through rogue and clustered RyRs as the JSR depletes (Sobie et al., 2004; Picht et al., 2011; Izu et al., 2013).

The objective of the study is to quantify the interplay of rogue and clustered RyRs on regulating Ca²⁺ waves in cardiac myocytes. A two-dimensional (2D) model of Ca²⁺ waves in the cytoplasm was proposed with considering the distribution of clustered and rogue RyRs on the JSR membrane. The anomalous subdiffusion of Ca²⁺ in the cytoplasm and JSR Ca²⁺ regulation were also included. The stochastic opening Ca²⁺ release units (CRUs) of rogue and clustered RyRs was regulated by free Ca²⁺ concentrations in both cytoplasm and JSR lumen. With these features, we showed the importance of rogue RyRs on the initiation and propagation of Ca²⁺ waves.

Materials and methods

Geometrical model

Considering the quasi-isotropic diffusion of Ca²⁺ in the cytoplasm (Izu et al., 2001), we adopted a 2D model to mimic Ca²⁺ waves. Figure 1A shows the geometrical model of a cardiac myocyte, the x- and y-directions of which refer to the longitudinal axis and z-line, respectively. Baddeley et al. have experimentally observed the RyR distribution on the JSR membrane (Baddeley et al., 2010). Most RyR channels form regular arrays, defined as “clustered RyRs.” Others are rogue RyRs uncoupled from the clustered RyRs. Clustered and rogue RyRs are randomly distributed. Figure 1B shows schematic representative of the CRU distribution on JSRs, which includes CRUs of clustered RyRs (~22 RyR channels in a CRU) and CRUs of rogue RyRs (~3 RyR channels in a CRU). CRUs of clustered RyRs (~2 CRUs in a JSR) are surrounded by randomly distributed CRUs of rogue RyRs (~8 CRUs in a JSR).

Figure 1.

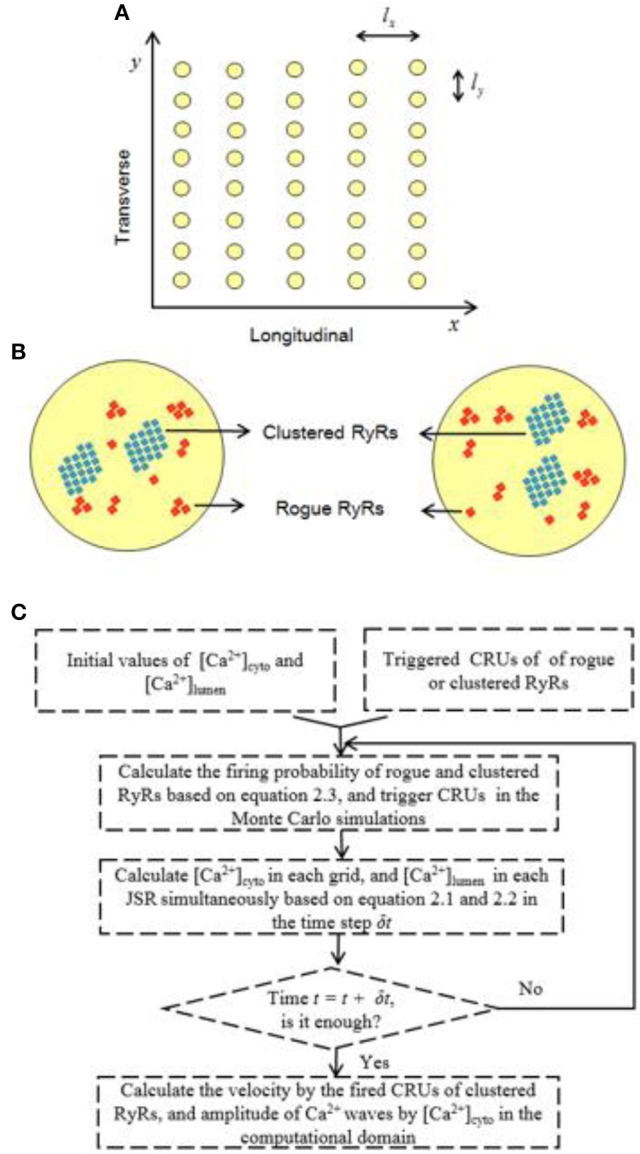
Schematic illustration of the 2D model for Ca²⁺ waves. (A) Schematic representative of the 2D geometrical model of a cardiac myocyte. The yellow circles denote JSRs. The spacing intervals between JSRs: l_x = 2 μm and l_y = 0.8 μm. (B) Schematic representative of two JSRs, which include randomly distributed clustered and rogue RyRs (l = 0.1 μm). (C) A flow diagram for the Monte Carlo simulations.

Governing equations

Ca²⁺ release events are simulated synchronously by a hybrid model, which consists of two parts: a model of Ca²⁺ waves in the cytoplasm and a model of Ca²⁺ blinks in JSRs. The reaction-diffusion system for Ca²⁺ waves in the cytoplasm based on the anomalous subdiffusion model, including the distribution of clustered and rogue RyRs, is described as follows:

$$\begin{array}{l}\frac{\partial {[{\text{Ca}}^{2+}]}_{\text{cyto}}}{\partial t}=D_x\frac{{\partial }^{\beta }{[{\text{Ca}}^{2+}]}_{\text{cyto}}}{\partial x^{\beta }}+D_y\frac{{\partial }^{\beta }{[{\text{Ca}}^{2+}]}_{\text{cyto}}}{\partial y^{\beta }}+J_{\text{dye}}\\ +J_{\text{buffer-cyto}}+J_{\text{pump}}+J_{\text{clustered}}+J_{\text{rogue}},\end{array}$$ (1)

where [Ca²⁺]_cyto is the free Ca²⁺ concentration in the cytoplasm, t is time, x and y are the spatial coordinates, D_x(= 300 μm²s⁻¹) and D_y (= 150 μm²s⁻¹) denote the Ca²⁺ diffusion coefficients for anisotropic diffusion. The anomalous subdiffusion order β is 2.25. J_dye is the flux due to the Ca²⁺ fluorescent indicator dye, Fluo-4-AM, in the cytoplasm. J_{buffer−cyto} is the flux due to the endogenous stationary buffers. J_pump is the pumping rate of SR Ca²⁺-ATPase. SR pumps will be started when ${\left[{\text{Ca}}^{2+}\right]}_{\text{cyto}}$ exceeds the resting Ca²⁺ concentration level (0.1 μM). The detailed description is in the Appendix A in Supplementary Material. On the other hand, the balance equation for Ca²⁺ blinks in each JSR is written as:

$$\frac{\partial {[{\text{Ca}}^{2+}]}_{\text{lumen}}}{\partial t}=J_{\text{release}-\text{lumen}}+J_{\text{buffer}-\text{lumen}}+J_{\text{refill}},$$ (2)

where [Ca²⁺]_lumen is the free Ca²⁺ concentration in the lumen of a JSR. J_{release−lumen} denotes the Ca²⁺ release flux caused by opening of clustered RyRs (J_clustered) and rogue RyRs (J_rogue). J_{buffer−lumen} is the Ca²⁺ flux due to the buffer, calsequestrin, in the JSR. J_refill is the refilled Ca²⁺ flux to the JSR. The detailed description is in the Appendix B in Supplementary Material. Various parameters of the dye and buffers in the cytoplasm and JSR lumen are listed in Table 1, similar to previous studies (Chen et al., 2013; Kong et al., 2013).

Table 1.

Standard parameter values for the dye and buffers.

Dye or buffers	[F]T or [Bn]T (μM)	$k_F^{+}$or $k_n^{+}$ (μM−1s−1)	$k_F^{-}$or$k_n^{-}$ (s−1)
PARAMETERS IN CYTOPLASM
Fluo-4-AM	50	80	90
Calmodulin	24	100	38
Troponin	70	39	20
SR	47	115	100
SL	1,124	115	1,000
PARAMETERS IN JSR LUMEN
Calsequestrin	14,000	100	60,000

Firing probability of rogue and clustered RyRs

The firing probability per unit time for CRUs of rogue or clustered RyRs is determined by Ca²⁺ concentrations in the cytoplasm and JSR (Györke and Gyorke, 1998; Qin et al., 2008, 2009), which can be expressed as:

$$P_{\text{firing}}=P_{\text{cyto}}·{\Phi }_{\text{lumen}},$$ (3)

where P_cyto and Φ_lumen refer to the firing probability per unit time of Ca²⁺ release events controlled by ${\left[\text{C}{\text{a}}^{2+}\right]}_{\text{cyto}}$ and [Ca²⁺]_lumen, respectively. The detailed description is in the Appendix C in Supplementary Material.

Numerical solutions

The 2D computational domain of a cardiac cytoplasm (20 × 20 μm²) was meshed with squares of 0.1 × 0.1 μm to simulate Ca²⁺ release events from multiple JSRs. JSRs (i.e., yellow circles with radius of 0.3 μm in Figure 1A) are uniformly distributed in the computational domain with l_x (2 μm) along x-axis and l_y (0.8 μm) along y-axis. Moreover, CRUs are stochastically distributed at nodes within each JSR, which includes 8 CRUs of rogue RyRs (N_rogue = 8) and 2 CRUs of clustered RyRs (N_clustered = 2). As shown in Figure 1C, Equations (1–3) were solved using a FORTRAN-developed program similar to a recent study (Chen et al., 2018). The shifted Grünwald formula of center difference (Tadjeran and Meerschaert, 2007) was used to discretize the fractional differential term in Equation (1) as:

$$\frac{{\partial }^{\alpha }{[{\text{Ca}}^{2+}]}_{\text{cyto}}(x,y,t)}{\partial x^{\alpha }}=\frac{1}{h^{\alpha }}\underset{M\to \infty }{\lim }{\displaystyle \sum _{k=0}^M{g}_k{[{\text{Ca}}^{2+}]}_{\text{cyto}}(x-(k-1)h,y,t)}$$ (4)

$$\frac{{\partial }^{\alpha }{[{\text{Ca}}^{2+}]}_{\text{cyto}}(x,y,t)}{\partial y^{\alpha }}=\frac{1}{h^{\alpha }}\underset{M\to \infty }{\lim }{\displaystyle \sum _{k=0}^M{g}_k{[{\text{Ca}}^{2+}]}_{\text{cyto}}}(x,y-(k-1)h,t),$$ (5)

where $g_k=\frac{\Gamma (k-\alpha )}{\Gamma (k+1)}$, Γ denotes the Gamma function. α = β−1 = 1.25, k is an integer with α < k < α+1, and h is the mesh size. Free Ca²⁺ concentrations in the cytoplasm and JSR were calculated simultaneously. The variable time step algorithm was used. The zero-flux boundary condition was set to the 2D computational domain of a cardiac cytoplasm for the Monte Carlo simulations.

Results and discussion

Interplay of rogue and clustered RyRs in neighbor JSRs

We have recently studied the effects of rogue RyRs on single Ca²⁺ sparks and quarks using the model in Equations (1–5), which was validated against the experimental measurements in rat cardiac myocytes (Chen et al., 2018). Here, we used the experimentally-validated numerical model to investigate whether a Ca²⁺ spark could trigger rogue and clustered RyRs in neighbor JSRs or not. Snapshots of Ca²⁺ release events in a computational domain of 20 × 20 μm² were taken at 10, 20, and 40 ms when a CRU of clustered RyRs was fired. Figures 2A,B show rogue RyRs at point (11.9, 9.6) and clustered RyRs at point (12.0, 9.6), respectively, activated by the Ca²⁺ spark at point (10.0, 9.6). Moreover, the release of clustered RyRs could trigger other CRUs of clustered RyRs in neighbor JSRs with the help of rogue RyRs, as shown in Figure 2C. The results demonstrate that Ca²⁺ sparks from the opening CRUs of clustered RyRs could activate CRUs of clustered RyRs and rogue RyRs in neighbor JSRs to increase [Ca²⁺]_cyto.

Figure 2.

Interplay of rogue and clustered RyRs in neighbor JSRs. Snapshots of Ca²⁺ release events in a computational region of 20 × 20 μm² were taken at 10, 20, and 40 ms from left to right when a CRU of clustered RyRs was fired. (A) Rogue RyRs in a neighbor JSR are activated. (B) Clustered RyRs in a neighbor JSR are initiated by a Ca²⁺ spark directly. (C) Clustered RyRs are triggered with the help of rogue RyRs.

Initiation of Ca²⁺ waves

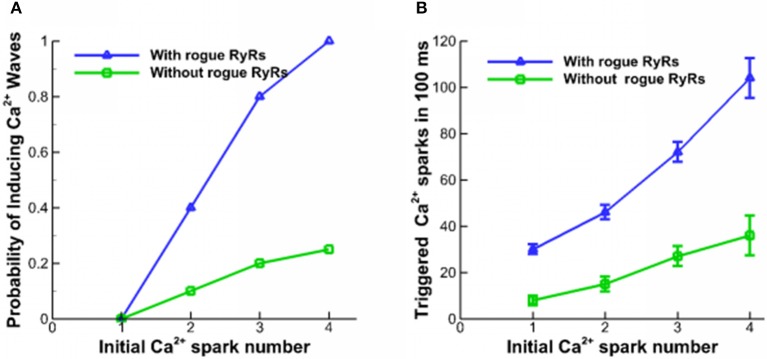
Ca²⁺ waves could be triggered in a domain where [Ca²⁺]_cyto is higher than the resting Ca²⁺ concentration level (Lu et al., 2010; Izu et al., 2013). A Ca²⁺ spark with a large current or several neighbor Ca²⁺ sparks could also trigger Ca²⁺ waves (Chen et al., 2014). Here, several neighbor Ca²⁺ sparks are used to activate Ca²⁺ waves in the simulation. The lowest propagation velocity of Ca²⁺ waves was detected in the range of 40–110 μm/s (Cheng et al., 1996). Since the disappearance of Ca²⁺ waves is related to a progressive decline of the wave propagation velocity, the longitudinal velocity is assumed to be higher than 40 μm/s. Figure 3A shows the probability of inducing Ca²⁺ waves as a function of the number of Ca²⁺ sparks initiating from a corner in a square of 20 × 20 μm² for 100 ms. The beginning level of [Ca²⁺]_lumen is 1.0 mM. The initial Ca²⁺ sparks arise from one CRU of clustered RyRs. Since Ca²⁺ quarks increase Ca²⁺ concentration in the cytoplasm, they enhance the probability of inducing Ca²⁺ waves in myocytes. Accordingly, Figure 3B shows the number of triggered Ca²⁺ sparks in 100 ms. A single Ca²⁺ spark could not form Ca²⁺ waves while four neighbor Ca²⁺ sparks with the help of rogue RyRs guarantee the formation of Ca²⁺ waves.

Figure 3.

Properties of Ca²⁺ waves. (A) The probability of inducing Ca²⁺ waves triggered by different numbers of Ca²⁺ sparks. (B) The number of triggered Ca²⁺ sparks in 100 ms.

Propagation of Ca²⁺ waves

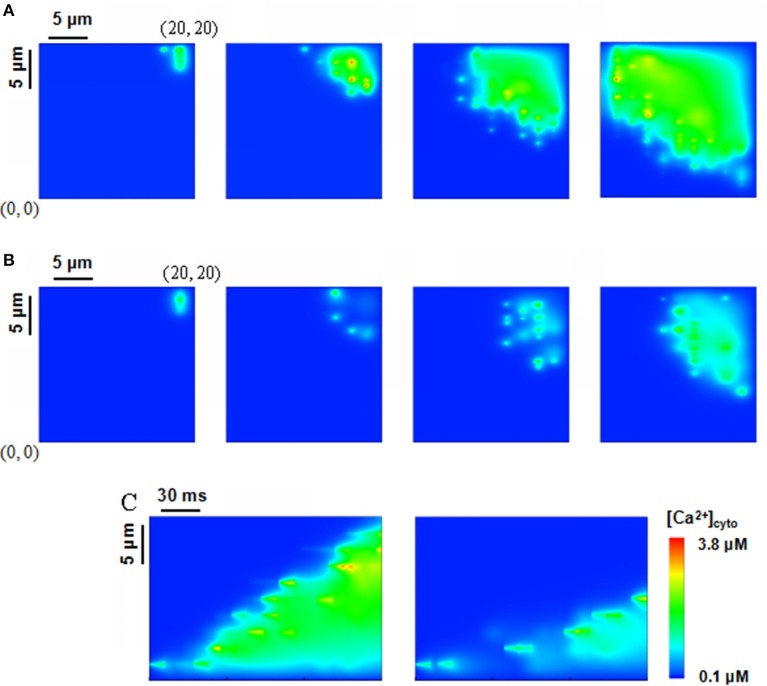
Ca²⁺ waves in Figure 4 were generated in a computational domain of 20 × 20 μm² and recorded at 10, 50, 100, and 150 ms from left to right when the beginning level of [Ca²⁺]_lumen is 1.0 mM. Four Ca²⁺ sparks were initiated at points (18, 19.2), (18, 18.4), (18, 17.6), and (18, 16.8) with considering rogue RyRs. A comparison of Figures 4A,B indicates much faster Ca²⁺ waves and higher amplitude when the effects of rogue RyRs are included in the computational model. Moreover, we found the “spark-diffusion-quark-spark” mode. Ca²⁺ released from clustered RyRs diffuses to a neighbor JSR, rogue RyRs are firstly activated in a stochastic manner to form Ca²⁺ quarks, and subsequently they make activation of clustered RyRs to produce a Ca²⁺ spark. The CRUs on the next z-line repeat the process to release Ca²⁺ in the cytoplasm.

Figure 4.

Ca²⁺ waves triggered by four sparks at the corner of a computational domain, i.e., (18, 19.2), (18, 18.4), (18, 17.6), (18, 16.8) in the region of 20 × 20 μm². The beginning level of [Ca²⁺]_lumen is 1.0 mM. (A,B) Snapshots of Ca²⁺ waves initially triggered by Ca²⁺ sparks with rogue RyRs (A) and without considering rogue RyRs (B) at 10, 50, 100, 150 ms from left to right. (C) Computational results for line-scan images of [Ca²⁺]_cyto with and without rogue RyRs at the line of y = 16.8.

Figure 4C shows the computational results for line-scan images of Ca²⁺ concentration with and without considering rogue RyRs at the line of y = 16.8. The results reveal that rogue RyRs accelerate the propagation of waves by triggering more Ca²⁺ sparks. The longitudinal propagating velocity has mean ± SD value of 95.9 ± 8.0 μm/s, which agrees with the experimental records (typically 100 μm/s) (Takamatsu and Wier, 1990; Wier and Blatter, 1991). Furthermore, Ca²⁺ concentration in the simulation is in the range of 0.1–3.8 μM. The computational predictions are close to the experimental measurements (0.5–1.2 μM; Williams et al., 1985), and less than previous simulations (Izu et al., 2001; Chen et al., 2013).

Importance of [Ca²⁺]_lumen-dependent regulation

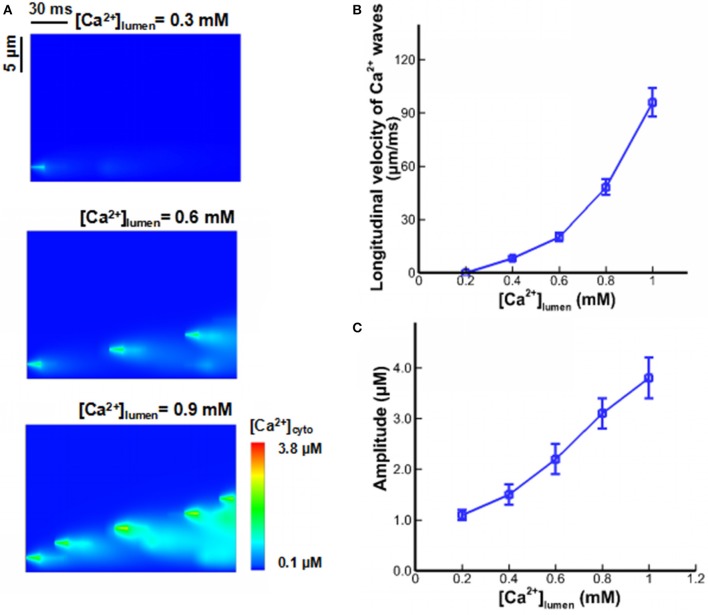
In previous mathematical models of Ca²⁺ waves, [Ca²⁺]_lumen-dependent regulation was not considered, and Ca²⁺ fluxes from CRUs were related to the current and duration of Ca²⁺ sparks and quarks only. We determined the effects of [Ca²⁺]_lumen-dependent regulation on properties of Ca²⁺ waves when the beginning level of [Ca²⁺]_lumen was set to 0.3, 0.6, and 0.9 mM. Local variation in the waves is shown in Figure 5A. Ca²⁺ waves are very sensitive to [Ca²⁺]_lumen. There is an exponential increase in the velocity of Ca²⁺ waves with the increase of [Ca²⁺]_lumen, as shown in Figure 5B. Moreover, a threshold value of [Ca²⁺]_lumen (i.e., >0.7 mM) exists for generation of steady Ca²⁺ waves. Figure 5C shows the amplitude of Ca²⁺ waves linearly increase with [Ca²⁺]_lumen because of the large driving force ([Ca²⁺]_lumen-[Ca²⁺]_cyto) of Ca²⁺ sparks and quarks.

Figure 5.

Ca²⁺ waves under different [Ca²⁺]_lumen. (A) Computational results for line-scan images of [Ca²⁺]_cyto at the line of y = 16.8 when [Ca²⁺]_lumen = 0.3, 0.6, and 0.9 mM. (B) The longitudinal velocity of Ca²⁺ waves affected by [Ca²⁺]_lumen. (C) The amplitude of Ca²⁺ waves affected by [Ca²⁺]_lumen.

Effects of parameters of rogue RyRs

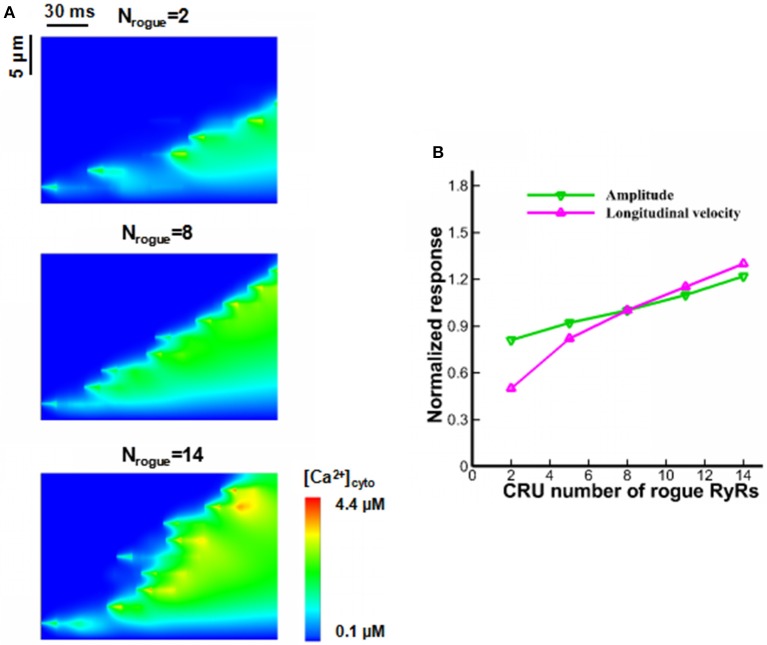
There are a large number of randomly-distributed rogue RyRs near clustered RyRs. Sensitivity analysis on Ca²⁺ waves was performed with respect to the changes in CRU number of rogue RyRs in a JSR (N_rogue). Figure 6A shows computational results for line-scan images of [Ca²⁺]_cyto at the line of y = 16.8 when CRU number of rogue RyRs in a JSR are 2, 8, and 14. As shown in Figure 6B, the amplitude and velocity increase with the increased CRU number of rogue RyRs because of high Ca²⁺ quarks and Ca²⁺ sparks.

Figure 6.

Effects of CRU number of rogue RyRs in a JSR on wave propagation. (A) Computational results for line-scan images of [Ca²⁺]_cyto at the line of y = 16.8 when CRU number of rogue RyRs has values of 2, 8, and 14. (B) The amplitude and longitudinal velocity of Ca²⁺ waves when N_rogue varies from 2 to 14.

The Ca²⁺ release per CRU of rogue RyRs is mainly determined by the current through rogue RyRs (I_rogue) and the duration of current flow (T_rogue). The current and duration of rogue RyRs are 0.15 pA and 20 ms in Figures 2–6. Table 2 presents properties of Ca²⁺ waves for different values of (I_rogue × T_rogue). There is a strong correlation between Ca²⁺ release through rogue RyRs and wave properties. When the release time of rogue RyRs decreases by half to 10 ms with the current of 0.15 pA, the longitudinal velocity and amplitude of waves decrease. When the current increases from 0.15 to 0.3 pA with the duration of 20 ms, Ca²⁺ waves have higher values of amplitude and longitudinal velocity. Hence, the release amount of rogue RyRs characterized by (I_rogue × T_rogue) is a significant parameter to affect wave properties.

Table 2.

Effects of Ca²⁺ release per CRU of rogue RyRs on properties of Ca²⁺ waves.

Irogue × Trogue	0.15 × 10	0.15 × 20	0.3 × 20
Longitudinal velocity (μm/s)	76.2	95.9	154.0
SEM	6.4	8.0	14.4
Amplitude (μM)	3.4	3.8	4.5
SEM	0.3	0.3	0.4

Lu et al. pointed out that rogue RyRs were scattered over the 2D plane randomly (Lu et al., 2010). However, fluorescent imaging showed that QCR events were detected almost at the same site as Ca²⁺ sparks (Brochet et al., 2011). The stochastic gating of a cluster contains 10–100 RyRs in a JSR and the mean number of RyRs is ~21.6 (Soeller et al., 2007; Baddeley et al., 2009). Figure 7 shows that the distance between CRUs in the range of 0.05–0.2 μm has slight effects on the amplitude of Ca²⁺ waves. However, the longitudinal velocities are 144.3 ± 13.1 and 63.6 ± 7.8 μm/s, respectively with respect to the distance of 0.05 and 0.2 μm. Therefore, the distance between CRUs of rogue RyRs and clustered RyRs should be taken into consideration in the propagation of Ca²⁺ waves.

Figure 7.

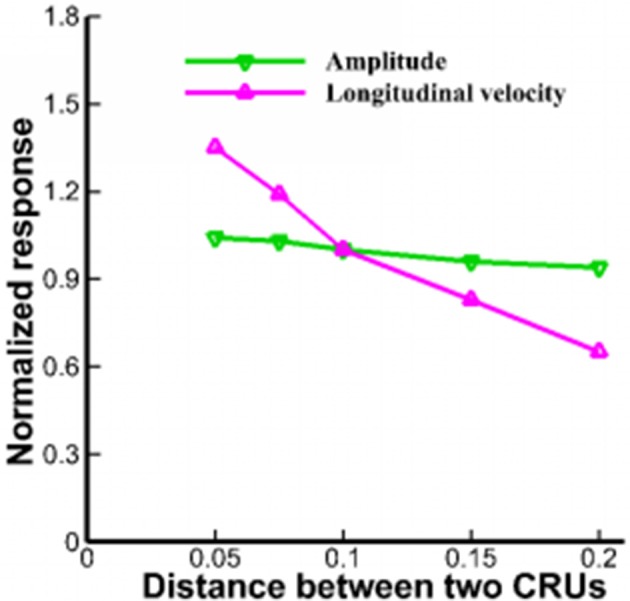
The amplitude and longitudinal velocity of Ca²⁺ waves when l varies from 0.05 to 0.2 μm.

Effects on activities from subcellular to cellar levels

When a myocyte is under paced, several spontaneous Ca²⁺ sparks or quarks can occur in the cytoplasm. It is, however, difficult to induce Ca²⁺ waves that require abundant currents to trigger cardiac action potentials (Izu et al., 2013). In some pathological conditions (e.g., arrhythmias), Ca²⁺ waves occur in cardiac myocytes and affect the heart's normal function (Lakatta and Guarnieri, 1993). Ten Tusscher and Panfilov developed a ventricular cell model including subspace calcium dynamics that controls L-type calcium current and calcium-induced calcium release (CICR) (ten Tusscher and Panfilov, 2006). The model was used to study the effects of I_Na recovery dynamics in combination with action potential duration (ADP) restitution on alternans and spiral breakup. On the other hand, the present results suggest that Ca²⁺ release from JSRs is prone to be initiated to cause Ca²⁺ waves with the help of rogue RyRs when [Ca²⁺]_lumen is large enough. Moreover, when the CRU number of rogue RyRs in a JSR or Ca²⁺ release per CRU of rogue RyRs is large enough, or the distance between CRUs is small, the membrane potential would be elevated significantly to trigger action potential in single myocytes.

Potential implications

This study shows some implications to heart diseases relevant to Ca²⁺ waves in cardiac myocytes. According to our simulations, JSR Ca²⁺ overload could increase RyR opening probability and generate Ca²⁺ waves in heart (Williams et al., 2017). Mutation in RyRs could trigger ventricular tachycardia and sudden cardiac death (Lehnart et al., 2006). Moreover, the amplitude and velocity of Ca²⁺ waves are significantly affected by the parameters of rogue RyRs, which may contribute to the formation of fibrillation (Macquaide et al., 2015) and arrhythmias (Ter Keurs and Boyden, 2007). A reduction of CRU number, the averaged current and releasing time of rogue RyRs resulted in an inhibition of Ca²⁺ waves or dyssynchronous Ca²⁺ transients in myocytes of congestive heart failure (Louch et al., 2013). Therefore, inhibition of Ca²⁺ quarks through rogue RyRs may be a promising therapeutic target to prevent fibrillation in congestive heart failure.

Critique of the study

The present study showed Ca²⁺ waves relevant to the interplay of rogue and clustered RyRs. It addressed the importance of rogue RyRs to increase the initiation of Ca²⁺ sparks, the incidence and propagation of Ca²⁺ waves when [Ca²⁺]_lumen is large. The amplitude and velocity of Ca²⁺ waves are in agreement with the experimental measurements. However, the model should be improved such that more parameters are added to investigate the mechanisms of Ca²⁺ waves. This study used the fixed release time of rogue and clustered RyRs. It should be a random variable depending on JSR regulation. The detailed structure of clustered RyRs should be taken into consideration because it can influence the frequency of Ca²⁺ sparks (Walker et al., 2014). Moreover, the present study comes from the assumption of a 2D model in healthy myocytes. A 3D model should be developed to investigate Ca²⁺ waves in future studies.

Conclusion

We developed a mathematical model to investigate the interplay of rogue and clustered RyRs on regulating Ca²⁺ waves in the cytoplasm. The computational results on Ca²⁺ waves agree with experimental measurements in cardiac myocytes. It shows that four neighbor Ca²⁺ sparks at the corner of a cardiac myocyte could induce Ca²⁺ waves. Ca²⁺ quarks increase the probabilities of triggering Ca²⁺ sparks and speed up the propagation of Ca²⁺ waves at high [Ca²⁺]_lumen. A new wave propagation mode of “spark-diffusion-quark-spark” is put forward. Particularly, Ca²⁺ waves could occur only when [Ca²⁺]_lumen is higher than a threshold value of 0.7 mM. More rogue RyRs in a JSR result in more opening CRUs of rogue and clustered RyRs. Besides, Ca²⁺ release from CRUs of rogue RyRs is a strong factor of wave properties. The velocity of Ca²⁺ waves is affected significantly by the distance between CRUs. This study helps to understand basic mechanisms of Ca²⁺ waves in cardiac myocytes.

Author contributions

XC, YH, and WT designed and performed the numerical calculation; YF analyzed and interpreted data; XC, YH, and WT wrote the manuscript.

Conflict of interest statement

The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.

Supplementary material

The Supplementary Material for this article can be found online at: https://www.frontiersin.org/articles/10.3389/fphys.2018.00393/full#supplementary-material