The Bioenergetics of Exercise

Abstract

Animals possess a remarkable ability to perform physical activity over a wide range of workloads and durations, reflecting both the inherent efficiency and large reserve capacity of energy transfer systems. Deciphering how different organ/physiological systems respond to the acute and chronic demands of exercise depends on a foundational understanding of the redox and bioenergetic principles that underlie the flow of electrons in living systems and its coupling to ATP synthesis. The purpose of this review is to set the stage to cover (1) the thermodynamic driving forces responsible for generating and maintaining the energy charge that establishes and sustains life for cells, and (2) how cellular energy transfer systems respond to changes in energy demand to ensure energy charge is preserved.

All organisms require an input of energy to generate and sustain life. The ultimate source of that energy is sunlight, which is captured by plants, algae, and photosynthetic bacteria to synthesize complex organic compounds that are ingested and broken down by nonphotosynthetic organisms. Basic science texts often refer to the energetics of life as emanating from the transformation of energy from food into useful work, focusing on the biochemical pathways responsible for the catabolism of organic compounds in cells, ending with the mitochondrial oxidative phosphorylation system (OXPHOS). This approach, although accurate, often fails to convey the thermodynamic driving forces that actually bring a cell to life energetically. For example, how is the energy transformation that is necessary to establish cellular life generated in the first place? Is it driven by the breakdown of ingested organic molecules, or are there other driving forces? What are the normal driving forces for flux through catabolic pathways? How is cellular energy charge maintained in the face of increased energy demand? The next section covers the basic principles of bioenergetics—the free energy forces and conversions that are used to establish and maintain energy homeostasis for all cells. That is followed by a section on how energy charge is maintained in cells during periods of increased energy demand, as occurs during exercise, through the integration of energy transfer systems.

SETTING THE CHARGE

Oxygen’s Electronegativity as the Primary Driving Force

In the 1780s, Luigi Galvani discovered that the legs of a frog hemicorpus could be stimulated to contract by applying an electrical current. To fans of the occult, this gave birth to the idea that electricity could be used to bring inanimate biological material to life, as popularized by Mary Shelley’s novel Frankenstein published early the next century. “Galvanism”—the application of an electric current to stimulate a muscle to contract—gave birth to the modern study of electrophysiology. In physics and chemistry, however, “galvanism” refers to the conduction of electrical current between two molecules with differing electronegativities (i.e., the tendency to attract electrons).

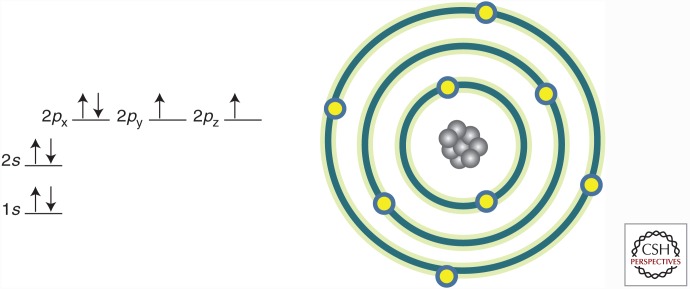
The oxygen atom has the second highest electronegativity of all elements (fluorine is the most electronegative), a property that serves as the primary driving force of bioenergetics. Electronegativity is a function of the nuclear charge of the atom relative to the number and location of electrons in the atomic shells. The oxygen atom contains eight protons in its nucleus and eight electrons within its orbitals in the configuration shown in Figure 1.

Figure 1.

Electron configuration of the oxygen atom. Depicted is the configuration of electrons in the orbitals surrounding the oxygen atom. Arrows represent electrons with a specific spin resonance.

Moving out from the nucleus, electrons with opposite spin resonances (direction of arrow) pair, filling each successive orbital. For the oxygen atom, the 2p orbital contains two unpaired electrons with the same spin resonance, making it two electrons short of filling the 2p orbital and thus accounting for its high electronegativity (Fig. 1). In fact, the oxygen atom does not exist in nature, stabilizing its outer shell by sharing unpaired electrons with another oxygen atom to form an oxygen molecule (O₂), or by combining with two hydrogen atoms to form a water molecule (H₂O). The electronegativity of the oxygen atom is also much greater than hydrogen. Thus, it is this difference in electron affinity—the strength of oxygen as a molecular electron magnet—that strongly favors the conversion of O₂ to H₂O. This simple chemistry serves as the primary thermodynamic driving force for aerobic metabolism.

Reduction Potential

The electron affinity of atoms in more complex chemical species is influenced by the surrounding environment and as such cannot be deduced simply from an atom’s electronegativity. Proteins contain two common amino acids with reversible affinity for electrons, cysteine, and methionine, each of which contain sulfur. Similar to oxygen, the sulfur atom contains two unpaired electrons in its outer shell (3p), accounting for its high electronegativity. However, the electron affinity of sulfur containing amino acids in proteins is influenced by the surrounding molecular environment, and thus is characterized by a different but related property known as reduction potential (redox potential or oxidation/reduction potential). Similar to electronegativity, reduction potential is defined as the tendency of a chemical species to gain an electron(s)—to become more negatively charged or “reduced.” A chemical species that loses an electron(s) is said to become “oxidized,” because O₂ is typically the final electron acceptor in biology.

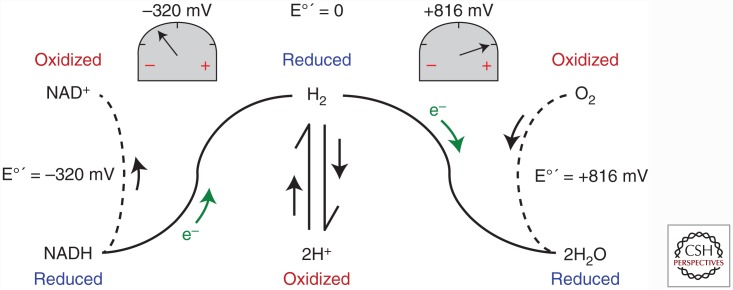
Reduction potentials are measured in relative terms by a technique known as a half-cell reaction. Under standard temperature and pressure conditions, two solutions, one containing the simplest redox couple 2H⁺/H₂ at equilibrium (reference solution) and the second containing equal concentrations (usually 1 m) of the oxidized and reduced forms of the redox couple of interest (test solution), are connected by an electron conduit and a voltmeter. By convention, the reduction potential of the standard hydrogen electrode is set to zero. If the test solution contains, for example, the O₂/2H₂O redox couple, electrons will flow from the hydrogen half-cell to reduce oxygen to water because the reduction potential of O₂ is greater than that of H⁺, generating a positive reading on the voltmeter. On the other hand, if the test solution contains the NAD⁺/NADH redox couple, then electrons will flow in the other direction from the test solution to reduce 2H⁺, generating a negative reading on the voltmeter (i.e., the reduction potential of NAD⁺ is less than that of H⁺) (Fig. 2). It is important to emphasize that reduction potential refers to the tendency of the oxidized form of a redox couple to attract an electron(s) (i.e., an electron magnet), not the tendency of the reduced form to give up an electron(s) (the latter is referred to as the oxidation potential, but is less frequently used to avoid confusion).

Figure 2.

Schematic of half-cell reaction system for determining reduction potential of redox couples. See text for explanation.

Therefore, the reduction potential of O₂ is greater than that of H⁺, which in turn is greater than that of NAD⁺. In fact, the standard reduction potential at pH = 7, 37°C, designated E°^′ for the O₂/2H₂O redox couple is ∼816 mV and for the NAD⁺/NADH redox couple is ∼–320 mV, a difference of more than 1 volt! At the molecular level, this difference in reduction potential between these two particular redox couples represents a tremendous amount of potential energy (i.e., Gibbs free energy difference, ΔG) and, as we shall see, is the primary bioenergetic driving force.

Metabolic Accounting

Before covering how that potential energy is used, consider first the complete catabolism of one molecule of glucose through glycolysis and the tricarboxylic acid (TCA) cycle. All six carbon atoms in glucose are converted to CO₂, yielding a little bit of energy in the form of ATP plus 16 hydrogens. The easiest thing for nature to have performed is to simply allow the hydrogens to combine with oxygen to produce water. Instead, those hydrogens, and more specifically the electrons they carry, are captured by electron carrier proteins (NAD⁺, FAD⁺) during each reaction in glycolysis and the TCA cycle in which hydrogen is liberated, effectively shielding the electrons from oxygen. Once those electrons from glycolysis are shuttled into the mitochondria, the stage is set to make use of that >1-volt difference in reduction potential between NAD⁺ and O₂.

Using Reduction Potential to Generate Membrane Potential

The mitochondrial electron transport system (ETS) is a wonder of nature, a molecular engine that capitalizes on the potential energy difference between a strong (O₂) and weak (NAD⁺) electron magnet to increase the yield of ATP by ninefold. The ETS consists of a series of >20 redox couples contained within several multiprotein complexes embedded in the mitochondrial inner membrane. There are two features of the ETS that are essential to understanding how the engine works. The first is, similar to a conventional electrical circuit, electron flow through the ETS occurs by default, as long as there is a continuous draw on the circuit (i.e., O₂→2H₂O) and a source of electrons (e.g., NADH). The second is that three of the complexes (I, III, and IV) in the ETS couple electron flow to proton pumping, such that neither can occur without the other. Both of these features are considered in detail below.

Although typically described as beginning with the transfer of electrons from NADH to complex I, it is functionally more useful to think of the ETS as beginning with O₂ because it is the high reduction potential of the O₂/2H₂O redox couple that is drawing electrons; that is, setting the “pull” on the system. O₂ (E°^′ = ∼816 mV) initially draws electrons from a redox couple with a lower E°^′, the cytochrome a₃ electron carrier in complex IV (E°^′ = ∼600 mV), which in turn draws electrons from a redox couple just upstream (E°^′ = ∼300 mV) and so on back through each of the complexes. Although an oversimplification, the reduction potential of each electron carrier is less than the next carrier downstream (i.e., toward O₂), and higher than the carrier upstream, creating a draw of electrons through the entire redox potential span back to the NAD⁺/NADH redox couple (E°^′ = −320 mV). It is important to appreciate that this is an open electric circuit, meaning that as long as O₂ and NADH are not rate limiting and a regulator is not applied, electron flow is wide open.

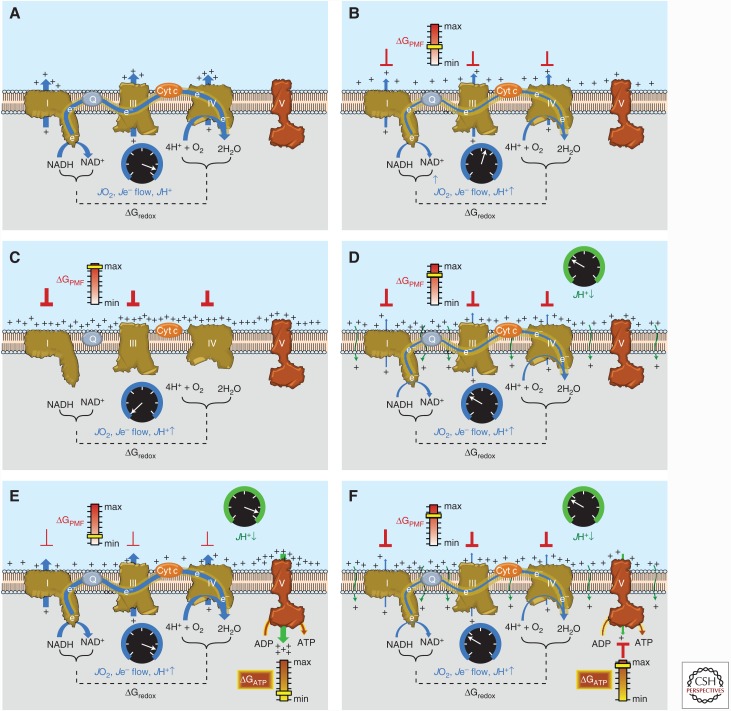
Despite the constant draw of electrons by O₂, mitochondrial oxygen consumption of course is very dynamic and responsive to demand—a function of the second feature of the system. The simplest way to grasp this is to do a thought experiment. Imagine starting from scratch with the ETS embedded in an artificial membrane vesicle and a constant supply of O₂. As soon as a source of electrons (i.e., NADH generating substrate) is introduced, electrons will start flowing, O₂ will start being consumed, and H⁺ will start being pumped out of the matrix at complexes I, III, and IV (Fig. 3A). Initially, the rate at which all three are occurring will essentially be wide open, as described in the previous paragraph. As protons accumulate along the outer surface of the inner membrane, however, a positive charge and H⁺ concentration difference begin to develop across the membrane, known as the proton motive force (Δp or PMF) (Fig. 3B). Because the capacitance (i.e., ability to separate an electrical charge when a voltage is applied) of biological membranes is high, even a small difference in ion concentration generates a significant electrical potential across the membrane. Thus, although possessing both an electrical (i.e., charge difference) and chemical (i.e., concentration difference) component, it is the membrane potential (ΔΨ) that accounts for the vast majority of the PMF. Recognize that the Gibbs free energy difference in reduction potential between the O₂/2H₂O and NAD⁺/NADH redox couples (ΔG_redox) is being used to drive the generation of a different form of free energy across the membrane, the ΔG_PMF. As the process continues, however, the accumulation of H⁺ on the outer surface of the membrane, and therefore the increasing ΔG_PMF, begins to create a backpressure on the proton pumps, gradually slowing the rate of electron flow and respiration (Fig. 3B). Eventually, ΔG_PMF builds until the backpressure counterbalances the driving pressure (ΔG_redox) of the proton pumps. At this point, ΔG_PMF = ΔG_redox and the rates of electron flow, proton pumping, and O₂ consumption slow to zero. The ETS reaches a standstill (i.e., static head), not because it is defective, but because opposing free energy forces reach a balance point against each other (Fig. 3C).

Figure 3.

Sequential schematic detailing the driving forces governing the control of mitochondrial oxidative phosphorylation. The reader is encouraged to refer to the text for additional details. (A) Conceptual representation of an electron transport system (ETS) embedded within an artificial membrane vesicle. Addition of reducing equivalents (NADH) generates immediate and rapid rates of O₂ consumption (JO₂), electron flow (Je⁻ flow), and proton pumping (JH⁺↑) at complexes I, III, and IV driven by the high ΔG_redox between the O₂/H₂O and NAD⁺/NADH redox couples. (B) As protons accumulate on the outer surface of the membrane, an electrochemical gradient or proton motive force (PMF) begins to build, creating a free energy backpressure (ΔG_PMF) against the pumps, gradually slowing JO₂, Je⁻ flow, and JH⁺↑. (C) Eventually, the backpressure increases to the point that it counterbalances the proton pumps, at which point JO₂, Je⁻ flow, and JH⁺↑ decrease to zero. (D) In mitochondria, basal proton conductance back into the matrix (JH⁺ ↓) prevents the ΔG_PMF from reaching max, thereby allowing JO₂, Je⁻ flow, and JH⁺↑ to proceed at a rate equivalent to the rate of JH⁺↓. (E) Activation of ATP synthase (complex V) by addition of ADP accelerates proton conductance, thereby lowering ΔG_PMF and thus increasing JO₂, Je⁻ flow, and JH⁺↑ accordingly. (F) As [ATP]/[ADP]+[P_i] increases, the free energy associated with ATP hydrolysis (ΔG_ATP) increases and creates back pressure on the ATP synthase, gradually slowing the rate of ATP synthesis, causing ΔG_redox to climb and JO₂, Je⁻ flow, and JH⁺↑ to slow accordingly back to the rate driven by basal proton conductance. Cyt c, Cytochrome c.

If ΔG_redox sets the current and ΔG_PMF functions as a brake on electron flow, then it should be apparent that getting respiration going again will require easing off on ΔG_PMF. In reality, functioning mitochondria never reach a static head because the mitochondrial inner membrane is slightly leaky to protons. This means that ΔG_PMF never reaches the level necessary to completely oppose ΔG_redox (i.e., the brake is never fully depressed), but is at some lower level that is determined by the rate at which protons are conducting back into the matrix (Fig. 3D). What accounts for the proton leak is not entirely clear, although a significant portion is thought to be mediated by the adenine nucleotide translocase (Brand et al. 2005; Divakaruni and Brand 2011). Regardless of the mechanism, this “idling” of mitochondria is analogous to the idling of an engine, occurs in every mitochondrion in every cell, and accounts for as much as 25% of basal energy expenditure (Rolfe et al. 1999).

Using Membrane Potential to Generate Energy Charge

Having generated a steady-state ΔG_PMF from the ΔG_redox for the O₂/2H₂O to NAD⁺/NADH span, the system is now poised to use the ΔG_PMF to drive other reactions, the most prominent of which is the synthesis of ATP. Again, to understand the different free energy forces at play, it is most useful to continue the thought experiment and to imagine a cell that lacks mitochondria and thus, energetically, has yet to be brought to life. At pH = 7.0 and an approximate physiological Mg²⁺ concentration of 10⁻² M, the apparent equilibrium constant for the hydrolysis of ATP is 10⁵ m—meaning that the reaction is favored to the right with much greater [ADP] than [ATP] at equilibrium. Using typical cytoplasmic concentrations of 10⁻³ m ADP and 10⁻² m P_i, the concentration of ATP at equilibrium will only be 10⁻¹⁰ m (Nicholls and Ferguson 2013). To shift the reaction away from equilibrium in favor of ATP therefore requires an input of energy. Enter the newly charged mitochondria and the ATP synthase enzyme. By providing another path for protons to conduct back into the mitochondrial matrix, the F_o/F₁ ATP synthase uses the ΔG_PMF to drive the phosphorylation of ADP (Stock et al. 1999), accelerating rates of proton conductance, electron transport, and O₂ consumption accordingly. Again, starting from scratch (i.e., very low [ATP]/[ADP]+[P_i]), the initial rate of proton conductance through the ATP synthase, and thus drop in ΔΨ (i.e., release of brake), will be a function of the maximal activity of the ATP synthase enzyme. However, as the ratio of [ATP]/[ADP]+[P_i] increases, the departure from equilibrium generates a new chemical Gibbs free energy for ATP hydrolysis (ΔG_ATP) (Fig. 3E), which will gradually build, creating product feedback pressure on the ATP synthase and the ΔG_PMF driving it. Proton conductance therefore begins to slow, causing ΔG_PMF to again gradually increase and respiration to gradually slow until the maximal [ATP]/[ADP]+[P_i] that can be generated by the OXPHOS system is achieved (i.e., when ΔG_ATP = ΔG_PMF) (Fig. 3F). At this point, proton conductance is minimal through the ATP synthase and the mitochondria are therefore back to their idling rate of respiration determined by the rate of proton leak.

To summarize, the high reduction potential of the O₂/H₂O redox couple generates the biological electrical current that powers the mitochondria. The free energy difference across the O₂/H₂O and NAD⁺/NADH redox span (ΔG_redox) is used to generate a Δp across the mitochondrial inner membrane, which in turn is used by the ATP synthase to drive ADP phosphorylation. Two regulators on the system prevent the wide open flow of electrons: (1) Δp (primarily the ΔΨ component), which regulates proton pumping and thus electron flow; and (2) [ATP]/[ADP]+[P_i], which regulates proton conductance through the ATP synthase and therefore ΔΨ. Recognize that the rate of mitochondrial respiration in response to an increase in [ADP] increases, not in an attempt to restore ΔΨ, but precisely because ΔΨ decreases as an outcome of the increased H⁺ conductance through ATP synthase. Thus, the mitochondrial ETS is a continuously operating “charged battery,” poised to respond instantaneously to any change in proton conductance. As ATP synthase accounts for most of the dynamic range of proton conductance, it should therefore be apparent that the mitochondrial ETS is a demand-based system largely regulated by the rate of ATP usage.

UTILIZING THE CHARGE

As mentioned above, under standard conditions and pH = 7, the hydrolysis of ATP is heavily favored with an apparent equilibrium constant of 10⁵ m. To give some context to the magnitude of energy conversion by the mitochondria, the OXPHOS system is capable of maintaining a mass action ratio for the ATP hydrolysis reaction of as low as 10⁻⁵ m, or a full ten orders of magnitude away from the equilibrium constant. It is the free energy associated with this displacement from equilibrium, given by the Gibbs energy equation (for derivation, see Nicholls and Ferguson 2013), which allows ATP hydrolysis to drive otherwise thermodynamically unfavorable processes (e.g., >10,000-fold Ca²⁺ gradient between sarcoplasmic reticulum [SR] and cytosol generated by SR Ca²⁺-ATPase, 20-fold Na⁺ gradient at plasma membrane–generated Na⁺/K⁺ ATPase, etc.). OXPHOS, therefore, energetically “brings the cell to life” by providing the ΔG_ATP necessary to establish and maintain the displacement from equilibrium for hundreds, if not thousands, of reactions.

At this juncture, there are three important points to emphasize. The first has already been alluded to; the magnitude of displacement from equilibrium for any chemical process (A→B) coupled to the hydrolysis of ATP is a function of the magnitude of Gibbs energy (ΔG_ATP) available to drive that displacement. This is because as A is converted to B and the reaction displaced from equilibrium, the Gibbs energy arising from that displacement (i.e., -ΔG favoring B→A) builds until it counterbalances the positive Gibbs energy available from ATP hydrolysis, creating a static head (analogous to that mentioned earlier). In living cells, however, virtually all reactions or processes displaced from equilibrium will spontaneously re-equilibrate at a slow rate. Maintaining the displacement from equilibrium of any reaction coupled to ATP therefore requires a constant input of Gibbs energy, or ΔG_ATP. The net result, rather than a static head, is a steady-state homeostasis in which the rate of loss of product draws an equal rate of replacement at the expense of ATP usage. Maintaining homeostasis undoubtedly accounts for a significant portion of basal mitochondrial respiratory activity and overall metabolic rate, the second point to emphasize. Third, any stimulus that dissipates a disequilibrium created and maintained by ATP will correspondingly accelerate the rate of ATP usage until the disequilibrium is re-established, further emphasizing how the respiratory system is governed by and continuously adjusting to energy demand.

ATP Use during Exercise

The transition from rest to exercise imposes an energetic challenge that is unique to skeletal muscle cells compared with most other cell types, owing to the heavy increase in myosin ATPase and SR Ca²⁺ ATPase activities that occur with contractile activity. Although difficult to directly measure, relative steady-state rates of ATP usage are estimated to increase to ∼1.5 µmol · g muscle⁻¹ · s⁻¹, a 50- to 100-fold increase over baseline, in well-trained humans during heavy cycling exercise (i.e., ∼3.5 L · min⁻¹ VO₂). ATP concentration of mammalian muscle is ∼7-8 µmol · g muscle⁻¹, enough to last only a few seconds. Muscle ATP concentration, however, rarely declines during exercise except under heavy workloads at or near exhaustion, illustrating the remarkable capacity of the ATP synthesis pathways to keep pace with demand in muscle (Meyer and Wiseman 2012).

The importance of maintaining ATP concentration is further emphasized by considering the free energy thresholds required to maintain cell function. For example, during incremental exercise to exhaustion in humans, muscle ΔG_ATP declines from ∼64 kJ · mole⁻¹ to ∼50 kJ · mole⁻¹ (Jeneson and Bruggeman 2004). A drop of only 2 kJ · mole⁻¹ more would limit the ability of the SR Ca²⁺-ATPase to resequester Ca²⁺ after contraction against the gradient normally still present between the SR and cytosol, and the ability of the Na⁺/K⁺ ATPase pump to reestablish the sodium gradient across the sarcolemma membrane (Chen et al. 1998; Meyer and Wiseman 2012). Thus, in a sense, fatigue is necessary to prevent muscle cells from committing energetic suicide.

Pathways for ATP Production

How then is [ATP] and ΔG_ATP maintained in muscle during exercise? Given the emphasis of this review, the seemingly obvious answer is from the increase in mitochondrial OXPHOS activity reacting automatically to the increase in ATPase rate. Indeed, in isolated mitochondria at 37°C, O₂ consumption increases to a new steady-state rate within just a few seconds after a stepwise addition of ADP. However, the response time to achieve a steady-state rate of O₂ consumption in muscle during a rest to submaximal exercise transition in humans can be 30 sec or longer (Rossiter et al. 1999), implying that the energy coupling pathways are more complicated in vivo. This is likely by necessity as mitochondrial volume is estimated to be ∼12% and 8% of the cytoplasmic volume in type I and type II muscle fibers from humans (Dahl et al. 2015), making it spatially challenging to directly couple sites of ATP usage to ATP resynthesis (i.e., referred to as mitochondrial resistance to energy transfer). In 1988, Meyer (1988) proposed that this problem is overcome by the presence of the creatine shuttle. In striated muscle, creatine kinase (CK) catalyzes the reversible reaction:

$$\text{ADP}+\text{PCr}\rightleftarrows \text{Cr}+\text{ATP},$$

with a standard equilibrium constant (K_CK) of ∼150 (Golding et al. 1995). Total CK activity is high in the cytosol, indicating that the reaction is likely near equilibrium under most circumstances. In the cytosol of a resting myofiber, the concentration of creatine is over 100-fold higher than ADP, meaning any small increase in [ADP] will generate a much larger increase in [Cr], effectively amplifying and distributing the signal. Once reaching the mitochondria, the increase in [Cr] is converted back to an increase in [ADP] by CK localized in the mitochondrial intermembrane space (Wallimann et al. 2011), increasing the sensitivity of OXPHOS to cytosolic changes in [ADP] (Perry et al. 2011). Thus, similar to a capacitor in an electrical circuit, the creatine shuttle serves as a metabolic capacitor—an immediately available source of stored energy that is discharged in parallel with the activation of the OXPHOS system. In contrast to the CK system, the mitochondrial OXPHOS system has little metabolic capacitance (i.e., stored ATP), instead relying on the regulation of proton conductance to generate energy. Because the two systems are intimately connected through the exchange of adenine nucleotides, the net effect is that any stepwise increase ATPase activity will elicit an increase in flux through both the CK (i.e., decrease in [PCr]) and mitochondrial OXPHOS (i.e., measured as O₂ consumption) systems, both of which will occur over equal but opposite exponential time courses until a steady-state balance of flux is achieved. The model predicts that the time required to achieve a new steady state varies linearly with the total creatine pool (i.e., the size of the capacitor) and inversely with mitochondrial density (i.e., the resistance to energy transfer) (Meyer and Wiseman 2012), predictions that have been confirmed experimentally (Glancy et al. 2008). Therefore, the integration between the two systems ensures that the response to any increase in ATPase rate is both rapid and sustained, insuring the maintenance of ΔG_ATP.

It is essential to recognize from the preceding that all pathways of ATP synthesis are integrated with one another in real time. For example, imagine a cell devoid of mitochondria that is relying exclusively on glycolysis for ATP production. At rest, steady-state basal rates of ATPase activity and flux through glycolysis will be balanced, generating steady-state concentrations of CK shuttle components. If fully functioning mitochondria are then introduced, the force of the OXPHOS system will drive the ATP/ADP ratio higher and distribute the increase in energy charge throughout the cell via the CK shuttle according to K_CK (↓[ADP], ↑[PCR], ↓[Cr], ↑[ATP]), providing additional charge to the capacitor. ATPase and ATP synthesis rates will still be balanced (i.e., demand not changed), but the source of ATP synthesis will now be distributed between glycolysis and OXPHOS. If the ATPase rate is increased, as occurs with the onset of exercise, flux through the CK shuttle, glycolysis, and OXPHOS pathways will increase simultaneously until a new integrated steady-state balance of fluxes is achieved, again on an exponential time course determined by the size of the creatine pool and the mitochondrial density. Last, exercise physiology texts tend to present the activation of ATP synthesis pathways in response to exercise in a sequential order from the most rapidly activated/shortest lasting (i.e., ATP/PCr) to intermediately activated/lasting (i.e., glycolysis) to the most slowly activated/longest lasting (i.e., OXPHOS). This approach, unfortunately, fails to capture the integrated nature of the distribution and maintenance of energy charge that occurs in cells in response to exercise.

FACTORS AFFECTING MITOCHONDRIAL BIOENERGETIC EFFICIENCY

Evolution undoubtedly favored maximizing the efficiency of OXPHOS to protect against fuel reserves becoming depleted while hunting for the next meal, or for that matter to prevent from becoming the next meal. It should be apparent from the previous sections, however, that the ETS, by its very nature, is not 100% efficient. Basal proton conductance represents a partial loss of the potential maximum ΔG_PMF available to drive ΔG_ATP, energy that is instead released as heat. The JO₂ that results from proton leak, known as state 4 respiration, is known as “uncoupled” respiration because it represents the rate of proton conductance not directly coupled to ATP synthesis (state 3 respiration). An increase in state 4 respiration, or a lower respiratory coupling ratio (i.e., state 3 JO₂/state 4 JO₂), is often interpreted as indicative of a decrease in OXPHOS efficiency. However, proton leak across the mitochondrial inner membrane is driven by ΔΨ, increasing nonlinearly with increasing ΔΨ, but decreasing to near zero as ADP-stimulated respiration increases (i.e., as ΔΨ decreases) (Korshunov et al. 1997). This insures that OXPHOS is most efficient when mitochondria are synthesizing ATP and conversely that more of the potential energy is diverted to heat production at rest when ATP demand is low (Lark et al. 2016).

Nevertheless, with the emergence of obesity and related diseases in Western societies, there is great interest in the potential therapeutic efficacy of targeting uncoupling in mitochondria to increase nonproductive energy expenditure. Hibernating animals use uncoupling to their advantage, increasing proton conductance in brown adipose tissue (BAT) mitochondria by inducing and activating uncoupling protein 1 (UCP1) to generate heat during the winter (Nicholls 2001; Cannon and Nedergaard 2004). Humans have on average only 50–80 g of BAT, which theoretically could increase energy expenditure by ∼20% if fully activated (Cypess et al. 2009), although recent studies have failed to support this contention (Blondin et al. 2015; Jensen 2015). Beige (or brite) cells are another type of UCP1-positive thermogenic adipocyte induced within subcutaneous white adipose tissue in response to a variety of factors, including cold exposure and exercise (Wu et al. 2012; Stanford and Goodyear 2016). Whether beiging can increase energy expenditure in humans sufficient to induce weight loss is also as yet unclear (Kusminski et al. 2016). UCP2 and UCP3, two related uncoupling proteins expressed in a variety of cell types, also catalyze an increase in proton conductance, but their role appears to be in protecting against oxidative stress rather than adaptive thermogenesis (Divakaruni and Brand 2011). Chemically uncoupling mitochondria with a protonophore, such as 2,4-dinitrophenol (DNP), has long been known to be an effective weight-loss treatment. DNP, however, was banned in the late 1930s because of its narrow margin between therapeutic efficacy and fatal hyperthermia (Colman 2007). The recent development of chemical uncouplers with broader pharmacodynamic ranges offer some therapeutic promise (Lou et al. 2007; Perry et al. 2013), but must be balanced against the potential negative impact on ΔG_ATP and downstream bioenergetic and thermal regulation. Proton “slip” (electron transport without proton pumping) (Brand et al. 1994) and fatty acid flip–flop (Garlid et al. 1996) are other potential means of uncoupling, but these mechanisms remain controversial (Brand and Nicholls 2011). Finally, it appears that cells have their own mechanism for naturally balancing energy supply and energy demand. The ETS, as well as other dehydrogenase enzymes (e.g., pyruvate dehydrogenase complex), leak electrons and produce H₂O₂ when under-elevated “reducing pressure” (i.e., as a release valve when substrate supply outpaces demand). The H₂O₂ is, in turn, enzymatically reduced to water via redox-buffering circuits that ultimately draw electrons from NADPH. In the mitochondria, the regeneration of NADPH from NADP⁺ is catalyzed largely by nicotinamide nucleotide transhydrogenase (NNT), a mitochondrial inner membrane protein that uses the membrane potential to generate and maintain a high NADPH/NADP⁺ ratio, analogous to ATP synthase maintaining a high ATP/ADP ratio. Continuous cycling of such redox circuits and, therefore, proton flux through NNT appears to represent a significant source of energy expenditure and a natural means by which cells balance energy supply with energy demand (Fisher-Wellman et al. 2015).

CONCLUDING REMARKS

Thermodynamics and bioenergetics are not the easiest concepts to grasp. This review uses the approach of considering how energy charge is first established and distributed to bring cells to life. The overriding principle is nonequilibrium thermodynamics, that is, how the natural driving force of reduction potential of the O₂/H₂O redox couple is transformed to other electrochemical (ΔG_PMF) and chemical (ΔG_ATP) driving forces that are used to create and sustain the displacement from equilibrium that constitutes life for cells. Willis et al. (2016) have recently proposed a hydraulic analog model of OXPHOS to help conceptualize the interaction of the various driving forces that the reader may find helpful. For more in-depth coverage of bioenergetics, the reader is referred to Bioenergetics IV by Nicholls and Ferguson (2013).

Mitochondrial and cellular bioenergetics are foundational to understanding how cells sense and respond to the energetic challenges imposed by exercise. Viewing cellular responses and adaptations to stressors related to health and disease in the context of the nonequilibrium thermodynamics and energetic driving forces is critical to guiding experimental design and data interpretation.