Parietal-Occipital Interactions Underlying Control- and Representation-Related Processes in Working Memory for Nonspatial Visual Features

Abstract

Although the manipulation of load is popular in visual working memory research, many studies confound general attentional demands with context binding by drawing memoranda from the same stimulus category. In this fMRI study of human observers (both sexes), we created high- versus low-binding conditions, while holding load constant, by comparing trials requiring memory for the direction of motion of one random dot kinematogram (RDK; 1M trials) versus for three RDKs (3M), or versus one RDK and two color patches (1M2C). Memory precision was highest for 1M trials and comparable for 3M and 1M2C trials. And although delay-period activity in occipital cortex did not differ between the three conditions, returning to baseline for all three, multivariate pattern analysis decoding of a remembered RDK from occipital cortex was also highest for 1M trials and comparable for 3M and 1M2C trials. Delay-period activity in intraparietal sulcus (IPS), although elevated for all three conditions, displayed more sensitivity to demands on context binding than to load per se. The 1M-to-3M increase in IPS signal predicted the 1M-to-3M declines in both behavioral and neural estimates of working memory precision. These effects strengthened along a caudal-to-rostral gradient, from IPS0 to IPS5. Context binding-independent load sensitivity was observed when analyses were lateralized and extended into PFC, with trend-level effects evident in left IPS and strong effects in left lateral PFC. These findings illustrate how visual working memory capacity limitations arise from multiple factors that each recruit dissociable brain systems.

SIGNIFICANCE STATEMENT Visual working memory capacity predicts performance on a wide array of cognitive and real-world outcomes. At least two theoretically distinct factors are proposed to influence visual working memory capacity limitations: an amodal attentional resource that must be shared across remembered items; and the demands on context binding. We unconfounded these two factors by varying load with items drawn from the same stimulus category (“high demands on context binding”) versus items drawn from different stimulus categories (“low demands on context binding”). The results provide evidence for the dissociability, and the neural bases, of these two theorized factors, and they specify that the functions of intraparietal sulcus may relate more strongly to the control of representations than to the general allocation of attention.

Introduction

Visual working memory (VWM) research has seen a convergence in recent years between cognitive models emphasizing the role of attention to knowledge structures (Cowan, 1988, 1995, 1999) and neurophysiological evidence for the sustained engagement of circuits in posterior cortex involved in the perception of the remembered information (Supèr et al., 2001; Pasternak and Greenlee, 2005; Serences et al., 2009; Sprague et al., 2014; Foster et al., 2016; van Kerkoerle et al., 2017). Among the outstanding questions about the precise mechanisms and boundary conditions of this principle of “sensorimotor recruitment” in working memory (e.g., D'Esposito and Postle, 2015) is understanding the contributions to VWM of the territory of the intraparietal suclus (IPS) vis-a-vis classically defined visual circuits of occipital cortex.

A role for IPS in the short-term retention of egocentrically encodable spatial information is well established (Chafee and Goldman-Rakic, 1998; Schluppeck et al., 2006; Hamidi et al., 2008; Jerde et al., 2012). For nonspatial stimuli, however, the literature is more complicated. Delay-period fMRI signal intensity is elevated in IPS for even simple stimuli: for example, motion directions (Riggall and Postle, 2012) or color patches (Todd and Marois, 2004), and varies with working memory load in a manner that can predict individual differences in VWM capacity (Todd and Marois, 2004, 2005; Xu and Chun, 2006), as do the dynamics of cross-frequency oscillatory synchrony localized to IPS (Palva et al., 2010). Such load sensitivity could be consistent with a role in storage (Xu and Chun, 2006; Xu, 2017) or in attentional control (Fukuda et al., 2015), or both. It is well established that IPS contributes to the attentional control of visual perception (Anderson et al., 2010; Scolari et al., 2015), as well as to the control of mnemonic stimulus representation, during both stimulus encoding (Mitchell and Cusack, 2008, 2011; Galeano Weber et al., 2016) and retention (Nelissen et al., 2013). Finally, efforts to decode stimulus identity from delay-period signal in IPS has been uneven, with some successful (Christophel et al., 2012; Ester et al., 2015; Bettencourt and Xu, 2016; Yu and Shim, 2017), some successful only under certain task instructions (Sarma et al., 2016), and some unsuccessful (Linden et al., 2012; Riggall and Postle, 2012; Emrich et al., 2013; Lee et al., 2013).

Theoretical models of an amodal attentional resource hypothesized to constrain the number of units or objects that have to be maintained in working memory (Cowan, 1995) have drawn support from observations from the IPS. Common patterns of delay-period load sensitivity in IPS are observed for multiple stimulus modalities (Brahmbhatt et al., 2008; Majerus et al., 2010; Chein et al., 2011; Cowan et al., 2011), and multivariate pattern analysis (MVPA) classifiers trained to discriminate high- from low-load conditions of VWM for colored squares can successfully discriminate comparable conditions during working memory for visually presented letters, and vice versa (Majerus et al., 2016). To date, however, many studies using load manipulations have used items drawn from the same category. This may confound the effects of load, per se, with the possibly more specific control requirements of managing the retention of multiple items drawn from the same category. Same-category memory could entail more competition between items, leading to loss of precision, and can increase the demands on context binding as proposed by many computational models (Oberauer and Lin, 2017; Schneegans and Bays, 2017) and generate “misbinding” (or “swap”) errors (Bays et al., 2011).

The present study compared load manipulations for category-homogeneous (1 vs 3 random dot kinematograms [RDKs]) versus category-heterogeneous (1 RDK and 2 colors) memory sets, to address two interrelated questions. First, can the general attentional demands of a load manipulation be dissociated from the putatively more specific demands of the control of context binding? Second, does load-sensitive activity in the IPS relate more closely to one or the other of these two hypothetically dissociable types of top-down control?

Materials and Methods

Subjects.

Twelve individuals (3 female; mean age 25 years, SD 4 years), who reported normal or corrected-to-normal vision, no history of neurological or psychiatric illness, and no contraindications for fMRI were recruited from the local community. Recruitment and experimental methods were approved by the University of Wisconsin–Madison Health Sciences Institutional Review Board, all subjects provided written informed consent and were monetarily compensated for their participation.

Stimuli and procedure.

After training, subjects performed the delayed-recall task in the MRI scanner. Six blocks of 30 trials (13 min each) were performed during concurrent fMRI, and an additional three blocks of 24 trials (10 min 4 s each) were performed during the same session while the subject was in the scanner, but without concurrent fMRI acquisition (more detail below).

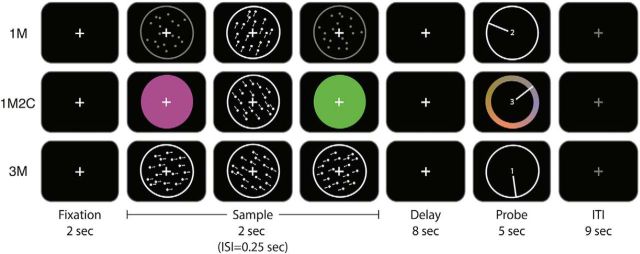
The background of the projected image was black throughout each scanning session, and each trial began with the onset of a white fixation mark (2 s), which remained on the screen until the trial-ending memory probe. Initial fixation was followed by the serial presentation of three sample-display events. Each sample-display event comprised the 500 ms presentation of a circular aperture subtending ∼11° of visual angle, centered on fixation, and, depending on the condition, filled with one of three types of stimulus: (1) a field of stationary, low-contrast gray dots (dot diameter ∼0.13°; dot density ∼0.07 dots/square degree); (2) a field of high-contrast white dots moving with 100% coherence at 2.75°/s; or (3) a uniform patch of color. Although dots could move in any of the possible 360° of motion, on 90% of trials one was drawn from the closed set of 7°, 127°, and 247° (to afford MVPA, as described below). During postscan debriefing, no subject reported noticing the recurring presentation of a small number of directions, and the other two were selected at random. Colors were drawn at random, with replacement, from a circular CIE L*a*b* color space, with the constraint that no two sample items presented on the same trial could be closer on the color wheel than 50°. The circle was centered in the color space at (L = 70, a = 20, b = 38) with a radius of 60. Thus, colors had equal luminance and varied in hue and saturation. Inter-stimulus interval (ISI) between sample-display events was 250 ms. The 2 s of sample presentation was followed by an 8 s delay period (white cross), then a recall period of 5 s, and finally 9 s of inter-trial interval (ITI) (total trial length of 26 s).

There were three trial types: remember 1 direction of motion (1M); remember 3 directions of motion (3M); and remember 1 direction of motion and 2 colors (1M2C). On 1M and 1M2C trials, stimulus order across the three sample-display events was equiprobable and unpredictable. For all three trial types, the recall stimulus was a dial of the same diameter and location as the stimulus aperture, with a digit appearing in the center and a needle extending from the digit to the circular edge of the dial. The digit (1, 2, or 3) corresponded to the sample-display event that was to be recalled (the first, second, or third, respectively). For trials requiring recall of the direction of motion, the circular edge of the dial acted as a “direction-of-motion wheel,” and subjects adjusted the direction of the needle (via a trackball) to indicate their memory of the direction of the probed sample and pressed a button to register their response. For trials requiring color recall, a color wheel appeared superimposed on the edge of the dial, and subjects adjusted the needle to indicate their memory of the probed color (Fig. 1). On all trials, the starting position of the needle was randomly determined. On 3M and 1M2C trials, each stimulus had an equal probability of being probed. An equal number of trials of each type occurred, in an unpredictable order, during each of six 30-trial runs. This design allowed us to compare the effects of a manipulation of load on VWM for motion, when the two additional items on load-of-3 trials were drawn from the same or different stimulus domains.

Figure 1.

Experimental procedure. Participants fixated at the center of the screen and remembered 1M, 1M2C, or 3M on different trials. After a long delay of 8 s, participants rotated the needle to indicate the probed motion direction or color.

Because memory for each item on 1M2C trials was probed an equal number of times, those performed during fMRI scanning yielded only one-third as many instances of recall of motion as did the other two trial types. To acquire a sufficient number of motion-probed 1M2C trials to fit to a mixture model (described in Behavioral analyses), an additional 24-trial block was performed by each subject before the first and fourth scanned block, and immediately after the sixth one. Each block of these supplementary behavioral trials contained 24 1M2C trials (randomly ordered), and half of these 1M2C trials probed the RDK and half probed a color. This yielded an additional 36 motion recall trials that were combined with the 18 from the fMRI session to yield a total of 54 1M2C trials that were entered into the mixture model.

The behavioral experiment was administered via the Psychophysics Toolbox (http://psychtoolbox.org) running in MATLAB (The MathWorks), presented using a 60 Hz projector (Avotec Silent Vision 6011), and viewed through a coil-mounted mirror in the MRI scanner. An fMRI-compatible trackball fiber optic response pad (Current Designs, HHSC-TRK-2) was used to record the behavioral responses.

Behavioral analyses.

As with Emrich et al. (2013), we used this delayed-recall (also known as “delayed estimation”) procedure to estimate the precision of mnemonic representations by fitting response error to a three-factor mixture model. The model (Bays et al., 2009), implemented with code available from http://www.bayslab.com, uses maximum likelihood estimation to generate estimates of the following: (1) the proportion of responses based on a working memory representation of the probed item (“responses to target”); (2) the proportion of responses incorrectly based on a representation of an unprobed item (i.e., “misbinding” or “swap” errors); (3) the proportion of responses that were guesses not based on any working memory representation; and (4) a “concentration” parameter that estimates the precision of target responses (i.e., based on the distance between the true target position and the subject's response, for the set of responses estimated to have come from categories 1 and 2). Conceptually, the concentration parameter is similar to a model-free measure of the precision of responses that is computed as the inverse of the SD of the distribution of responses. It is taken as a proxy for the fidelity of the working memory representation. Reaction time (RT) of the response-ending button press was also collected, although this measure was necessarily noisy because it included the time to adjust the response dial with a trackball positioned adjacent to the thigh of the supine subject.

fMRI data acquisition.

Subjects were in a comfortable supine position and wore earplugs and headphones. Whole-brain images were acquired using a 3 Tesla GE MR scanner (Discovery MR750; GE Healthcare) at the Lane Neuroimaging Laboratory at the University of Wisconsin–Madison HealthEmotions Research Institute (Department of Psychiatry). BOLD data were acquired with a gradient-echo planar sequence (2 s TR, 25 ms TE, 60° flip angle) within a 64 × 64 matrix (39 sagittal slices, 3.5 mm isotropic). Each of the six fMRI scans generated 390 volumes. A high-resolution T1 image was also acquired for all subjects for coregistration to the functional data with a fast-spoiled, gradient-recalled-echo sequence (8.2 ms TR, 3.2 ms TE, 12° flip angle, 160 axial slices, 256 × 256 in plane, 1.0 mm isotropic).

fMRI data preprocessing.

We preprocessed the functional data using the Analysis of Functional NeuroImages (AFNI) software package (http://afni.nimh.nih.gov) (Cox, 1996). For each subject's data, all volumes were spatially aligned to the final volume of the last functional run, then to the structural volume. The preprocessing steps were slice-timing correction, detrending, conversion to percentage signal change, and spatial smoothing with a 4 mm FWHM Gaussian kernel.

Univariate analyses.

We calculated the percentage signal change in BOLD activity relative to baseline for each time point during the working memory task; baseline was chosen as the average BOLD activity of the first TR of each trial. A conventional mass-univariate GLM analysis was implemented in AFNI, with sample, delay, and probe periods of the task modeled with boxcars (2 s, 8 s, and 5 s in length, respectively) that were convolved with a canonical hemodynamic response function.

ROI definition.

Much of the motivation for the present study came from the fact that we have previously observed different patterns of activity, consistent with the operation of distinct cognitive operations, in different parts of the brain. In particular, in a task requiring VWM for 1 versus 2 versus 3 RDKs, successful MVPA decoding of delay-period stimulus information, consistent with a storage function, was primarily observed in occipital cortex, whereas load-sensitive variation in BOLD signal intensity, perhaps reflecting a control operation, was observed in IPS, as well as in regions of PFC (Emrich et al., 2013). Therefore, our a priori hypotheses were tested in functionally defined, anatomically constrained ROIs based theoretically on past work. These ROIs allow the most powerful examination of the hypotheses, given individual differences in brain anatomy. However, given that functional ROIs are necessarily biased by the voxel selection procedure, we also developed anatomical ROIs, motivated by past work, to ask more general, nomothetic questions about areas of the cortex.

The principal hypothesis tests were performed in two anatomically constrained functional ROIs: an occipital sample ROI intended to capture regions previously associated with the delay-period retention of stimulus representations; and a parietal delay ROI intended to capture regions of IPS previously shown to demonstrate delay-period load sensitivity of BOLD signal intensity (Emrich et al., 2013). The occipital sample ROI was defined as the 2000 voxels displaying the strongest loading on the contrast (sample − baseline) from the GLM, collapsed across the three conditions, and located within an anatomically defined occipital ROI (see below). The parietal delay ROI was defined as the 2000 voxels displaying the strongest loading on the contrast (delay − baseline), also collapsed across the three conditions, and located within an anatomically defined IPS ROI. In effect, the [sample − baseline] and [delay − baseline] contrasts served as the basis for feature selection for the MVPA that we planned to carry out in the occipital cortex and IPS, respectively.

Occipital and parietal anatomical ROIs were created by extracting masks for V1-V4, V3a, V3b, and LO, and for IPS0-IPS5, respectively, from the probabilistic atlas of Wang et al. (2015), and warping them to each subject's native space. Based on the results from occipital and parietal ROIs, we followed-up with additional analyses performed in the left hemisphere half and the right hemisphere half of the parietal delay ROI, and in the PFC with a lateral PFC delay ROI comprising the 2000 voxels with the strongest loading on the contrast (delay − baseline), collapsed across the three conditions, and located anatomically within a region defined by the union of masks of the superior, middle, and inferior frontal gyri supplied by AFNI. This lateral PFC delay ROI was also divided into a left hemisphere half and the right hemisphere half.

Pattern classification.

Multivariate pattern classification was performed using the Princeton MultiVoxel Pattern Analysis toolbox (www.pni.princeton.edu/mvpa/). The 10% of trials that did not include one of the three critical directions of motion, as well as the first and last trials of each run, were discarded from further analysis. We used L2-regularized logistic regression with a penalty term of 25 to classify the three critical motion directions. Specifically, the classifier was trained and tested on the three motion directions at each time point through a leave-one-trial-out k-fold cross-validation procedure. The training dataset was collapsed across all three trial types. For each iteration, an estimate (ranged from 0 to 1) of the similarity between the pattern on the test trial and the training pattern (also known as MVPA “evidence”) (compare Lewis-Peacock and Postle, 2012) was generated for each of the three motion directions. Classification performance was characterized by the difference between the evidence for the target motion direction relative to the mean of the evidences for the two nontarget motion directions and averaged across trials within each condition. Classifier performance values >0 indicated higher sensitivity for the correct motion direction, compared with the incorrect motion directions.

Of primary theoretical interest was the item-level classification of stimulus motion direction (7° vs 127° vs 247°). Additionally, however, we also planned to perform category-level MVPA to assess the discriminability of activity related to the trial type (1M vs 3M vs 1M2C).

Task-related patterns of covariation.

Following our previous work (Emrich et al., 2013), we used ANCOVA to evaluate evidence for correlated sensitivity to trial type (e.g., 1M vs 3M) across pairs of dependent variables (i.e., permutations of BOLD loading on covariates from the GLM analyses [also known as “beta values”] vs classification performance vs behavioral precision). Unlike simple correlations, ANCOVA accommodates the fact that each subject contributes a value for each level of the factor of trial type. It removes between-subject differences and assesses evidence for “within-subject correlation”: the extent to which remaining variation in one dependent variable can be explained by variation in a second (Bland and Altman, 1995).

Instead of modeling trial epochs across trials, as we did when defining the sample and delay ROIs, we modeled the sample, delay, and probe periods on a trial-by-trial basis (still using boxcar regressors of 2, 8, and 5 s, respectively) to better capture the fluctuation in BOLD activity between trials. Classification performance for these analyses was calculated across the average signal from 10 to 14 s after trial onset; behavioral precision was defined as the concentration parameter in the mixture model. First, to test for replication of the finding that load-related changes in MVPA predict load-related changes in behavioral precision (Emrich et al., 2013), we performed an ANCOVA of classification performance in the occipital sample ROI versus behavioral precision, across 1M and 3M trial types. Next, assuming successful replication, to assess whether this effect is related to memory load, per se, or, rather, to the additional control demands imposed by stimulus homogeneity, we repeated this analysis, but across the trial types 1M and 1M2C. All subsequent analyses were also performed separately for 1M versus 3M and for 1M versus 1M2C. A second set of ANCOVAs was planned to examine, at each ROI, whether load-sensitive patterns of delay-period BOLD activity related to load-sensitive patterns of behavioral precision. Finally, to further investigate evidence for parietal control of working memory representation (Mitchell and Cusack, 2008, 2011; Nelissen et al., 2013; Galeano Weber et al., 2016), a third set of ANCOVAs, one at each IPS ROI, was planned to assay relations between parietal BOLD activity and occipital MVPA performance.

Experimental design and statistical analysis.

The experiment was a within-subject design of three trial types: 1M, 3M, and 1M2C. Tests of changes across three trial types, and across ROIs, were performed using one-way repeated-measures ANOVA. Tests of difference between two conditions were performed using paired two-tailed t tests. Tests of difference between one condition and 0 were performed using one-sample two-tailed t tests. Bonferroni correction was applied to all pairwise comparisons, unless specified otherwise. Evaluation of within-subject correlations (ANCOVAs) was described in the section above.

In addition to this frequentist statistical reporting, we also estimated Bayes factors for each of the comparisons. The Bayes factor can be understood as the ratio of the likelihood of the alternate hypothesis compared with the null hypothesis. For the Bayes factors, values >1 indicate greater evidence in favor of the alternative hypothesis (i.e., that decoding was successful), and values < 1 indicate greater evidence in favor the null hypothesis (i.e., that decoding was unsuccessful, implying that there is no stimulus information in that ROI). Bayes factors allow for the quantitative assessment, for each effect in each ROI, of the strength of evidence in favor of the null versus the alternative hypothesis. In this analysis, we chose the simplest possible prior distribution for the Bayes factor analysis, which is a uniform distribution from 0 to the maximum possible classification performance value (which we set to 0.35, a value 0.01 higher than the highest classification performance achieved in any subject's data, in the occipital sample ROI).

Results

Behavior

The (model-free) descriptive statistics suggested that task difficulty increased from 1M to 1M2C to 3M, as reflected in the distribution of response error (converted to “precision” as 1/SD of error, F_(2,22) = 7.07, p = 0.004; and as reflected in RT, F_(2,22) = 16.05, p = 5 × 10⁻⁵; Table 1).

Table 1.

Behavioral responses to direction-of-motion probes^a

Trial type	Descriptive data		Three-factor mixture model (parameter estimates)
	Distribution of response error (converted to 1/SD)	RT (s)	Probability of response to target	Probability of response to nontarget	Probability of guess response	Concentration
1M	2.97 (0.47)	2.42 (0.47)	0.932 (0.26)	NA	0.068 (0.003)	30.2 (0.47)
3M	1.84 (0.31)	2.66 (0.09)	0.867 (0.40)	0.002 (0.002)	0.131 (0.039)	20.1 (3.1)
1M2C	2.36 (0.37)	2.55 (0.09)	0.901 (0.41)	NA	0.098 (0.004)	20.4 (2.5)

^aValues are mean (SEM).

Results from mixture modeling indicated no differences across trial types in the probabilities of target responses, of nontarget responses, or of guesses (all p values >0.148; Table 1). The concentration parameter, which provides an estimate of the precision of mnemonic representations, was significantly higher for 1M trials than for both 3M trials (t₍₁₁₎ = 10.56, p = 0.021) and 1M2C trials (t₍₁₁₎ = 11.83, p = 0.046), but did not differ between 3M trials and 1M2C trials (t₍₁₁₎ = 0.13, p > 0.999).

Univariate delay-period activity

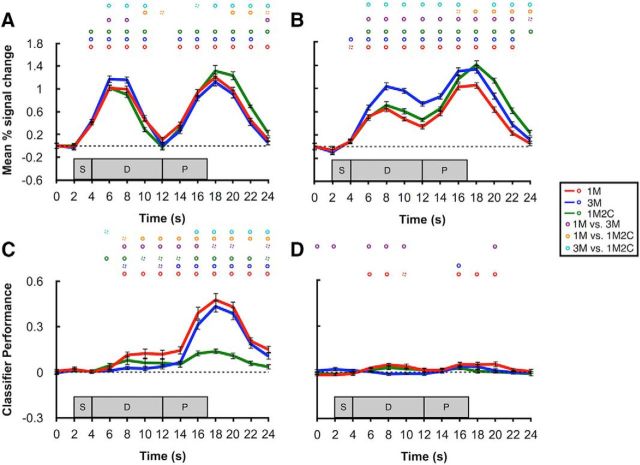
BOLD activity in the occipital sample ROI decreased steadily after the stimulus-evoked response, dropping to baseline by time 12 s. Moreover, activity in the 3M condition was higher than the other two conditions during the very early delay period, but it did not differ at later delay time points across any of the three conditions (Fig. 2A). Comparisons between average delay-period activity (10–14 s) further confirmed no difference between any two of the conditions (all p > 0.132).

Figure 2.

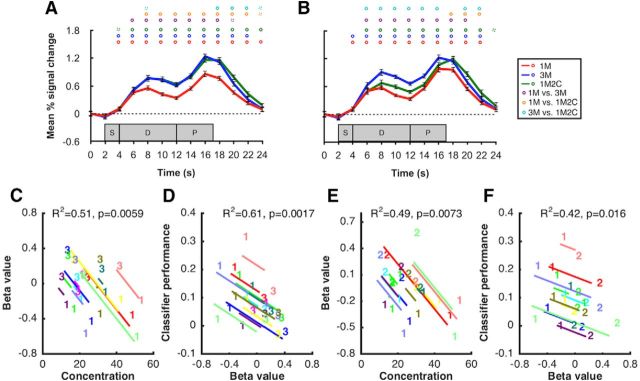
BOLD activity and classification performance in sample and delay ROIs. A, Time course of BOLD activity in occipital sample ROI. B, Time course of BOLD activity in parietal delay ROI. C, Time course of classifier performance in occipital sample ROI. D, Time course of classifier performance in parietal delay ROI. Red, blue, and green lines indicate the 1M, 3M, and 1M2C conditions, respectively. Circles on top of each plot represent significance of each time point. Purple, orange, and cyan circles represent the comparisons of 1M versus 3M, 1M versus 1M2C, and 3M versus 1M2C, respectively. Solid circles represent p < 0.05. Dashed circles represent p < 0.10. All p values were corrected with false discovery rate. Shaded gray areas represent the timing of the sample (S), delay (D), and probe (P) epochs of each trial. Error bars indicate ±1 SEM.

In the parietal delay ROI, in contrast, one-sample t tests against 0 at each time point confirmed that delay-period activity was elevated in a sustained manner for all the three conditions. Furthermore, although delay-period activity in the 3M condition was significantly higher than in the two other conditions, it did not differ between the 1M and the 1M2C conditions (Fig. 2B). Average delay-period activity (10–14 s) in the 3M condition was also significantly higher than the other two conditions (t₍₁₁₎ = 7.95 and 4.63, p = 7.0 × 10⁻⁶ and 7.2 × 10⁻⁴, respectively).

Pattern classification

Item-level decoding

In the occipital sample ROI, the remembered direction of motion could be successfully decoded from the delay period on a time point-by-time point basis for the 1M condition, and from the delay period of all three conditions when signal was collapsed across all delay time points (10–14 s, all p values <0.05; Fig. 2C). Comparison between conditions indicated that delay-period decoding performance was significantly superior for the 1M condition relative to 3M and 1M2C (t₍₁₁₎ = 4.19, p = 0.005; t₍₁₁₎ = 3.84, p = 0.008, respectively), but that it did not differ between 3M and 1M2C (t₍₁₁₎ = 1.00, p > 0.999).

In contrast to the occipital sample ROI, decoding performance in the parietal delay ROI was much weaker and much more variable. Time point-by-time point classification was only significant in early portions of the delay in the 1M condition. Likewise, difference between 1M and 3M conditions was also observed only during the early delay period.

Category-level decoding

In both the occipital sample ROI and the parietal delay ROI, MVPA successfully discriminated 1M from 3M from 1M2C trial types at p values <0.001 for all pairwise comparisons.

Task-related patterns of covariation in BOLD activity, MVPA, and behavioral precision

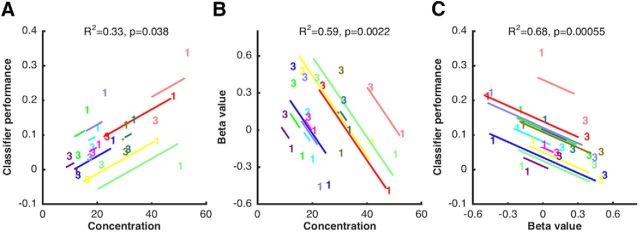
In the occipital sample ROI, and replicating a previous finding (Emrich et al., 2013), ANCOVA of data from 1M and 3M revealed a significant within-subject correlation relating the load-related decline in MVPA to the load-related decline in behavioral precision (r² = 0.33, p = 0.038; Fig. 3A).

Figure 3.

Within-subject correlations between behavioral precision, BOLD activity, and classification sensitivity, as a function of memory load (1M vs 3M). A. Results from ANCOVA relating behavioral precision (concentration parameter from mixture model) and classification performance in occipital sample ROI. B, Results from ANCOVA relating behavioral precision and delay-period BOLD activity (beta value from GLM) in parietal delay ROI. C, Results from ANCOVA relating delay-period BOLD activity in parietal delay ROI and classification sensitivity in occipital sample ROI. In each plot, data from each subject are portrayed in a different color. The “1” and “3” symbols indicate individual values in the 1M and 3M conditions, respectively. Lines indicate the best fit of the group-level linear trend (i.e., the within-subject correlation) in relation to each individual subject's data.

Next, and of primary theoretical interest for the present study, we performed a series of ANCOVAs intended to elucidate functional correlates of the elevated delay-period activity in the parietal delay ROI. Beginning with the 1M versus 3M comparison, a significant within-subject correlation indicated that the load-related increase in delay-period signal in the parietal delay ROI was negatively related to the load-related decrease in behavioral precision (r² = 0.59, p = 0.002; Fig. 3B). This is the opposite pattern from what was observed in the occipital sample ROI. Furthermore, a second ANCOVA indicated that the 1M-to-3M load-related increase in delay-period signal was also significantly negatively related to the load-related decrease in classification performance in the occipital sample ROI (r² = 0.68, p = 0.00055; Fig. 3C). Interestingly, neither of these effects was significant in comparable analyses comparing the load manipulation of 1M versus 1M2C (r² = 0.14, p = 0.206; r² = 0.09, p = 0.312).

Anatomically defined ROIs

Although our primary theoretical interest was in the functions of delay-period activity in the parietal delay ROI, the results from this ROI were necessarily biased by our voxel selection procedure. Therefore, to address more general questions about the organization VWM functions in posterior parietal cortex, we repeated all the aforementioned analyses in the anatomical ROIs covering the IPS. To anticipate our findings in summary, the results revealed a gradient along the IPS, with the delay-period signals and analytically derived effects in the caudal-most portions of IPS generally weak or not detectable, and progressively taking on the characteristics of the parietal delay ROI at progressively more rostral subregions along the IPS.

Group-average effects

Beginning with delay-period BOLD activity, inspection of the time series data revealed that it decreased to baseline by the end of the delay in IPS0 but became progressively more elevated in more rostrally located ROI (data not shown). An F test of parameter estimates from GLM delay covariates, collapsing across 1M, 3M, and 1M2C conditions, indicated a highly significant caudal-to-rostral increase (F_(5,66) = 19.08, p = 1.1 × 10⁻¹¹; Fig. 4A). Similarly, the 1M versus 3M effect of load also increased progressively from IPS0 to IPS5 (F_(5,66) = 3.11, p = 0.014; Fig. 4B).

Figure 4.

Delay-period BOLD activity and classification sensitivity in each IPS anatomical ROI. A, Delay-period BOLD activity, collapsing across 1M, 3M, and 1M2C conditions. B, Load effect: 3M − 1M. C, Mean classification of averaged delay-period signal for the 1M condition in the functionally defined occipital sample and parietal delay ROIs, and in anatomically defined IPS0-IPS5. Error bars indicate ±1 SEM.

An F test of average delay-period MVPA performance failed to find evidence for a similar gradient (F_(5,66) = 0.10, p = 0.992). We further examined the MVPA performance for each condition separately and performed t tests to evaluate the significance of classifier performance in each subregion. Consistent with the results in the parietal delay ROI, only the 1M condition showed a trend of successful decoding of motion direction (Fig. 3C; for statistical results, see Table 2).

Table 2.

Statistical results of MVPA performance for 1M, 3M, and 1M2C conditions separately

	t value			p value (FDR corrected in each condition, for anatomically defined ROIs)			Bayes factor
	1M	3M	1M2C	1M	3M	1M2C	1M	3M	1M2C
Parietal delay ROI	1.83	0.58	1.58	0.094	0.576	0.142	0.57	0.02	0.25
IPS0	2.37	0.32	0.92	0.075	0.752	0.378	2.64	0.75	0.10
IPS1	2.45	0.48	1.94	0.075	0.752	0.122	2.23	0.02	0.47
IPS2	2.57	0.65	1.75	0.075	0.752	0.131	4.29	0.02	0.01
IPS3	1.91	0.79	1.92	0.100	0.752	0.122	0.65	0.02	0.66
IPS4	2.05	0.82	2.01	0.098	0.752	0.122	0.80	0.02	0.74
IPS5	0.93	0.84	2.18	0.370	0.752	0.122	0.11	0.02	1.03

To better interpret the marginally significant decoding results in IPS, we calculated Bayes factor for each of the comparisons. The Bayes factor analysis showed a gradient of the amount of evidence in favor of the alternative hypothesis along IPS. For the 1M condition, the alternative hypothesis (decoding performance >0) was more likely than the null hypothesis (decoding performance not different from 0) in caudal parts of IPS (IPS0-2) for the 1M condition, and vice versa in IPS3-5. For the 3M and 1M2C conditions, in contrast, the Bayes factors in all parietal ROIs (with the exception of IPS5 in the 1M2C condition) revealed greater evidence in the data for the null hypothesis (Table 2).

Patterns of covariation

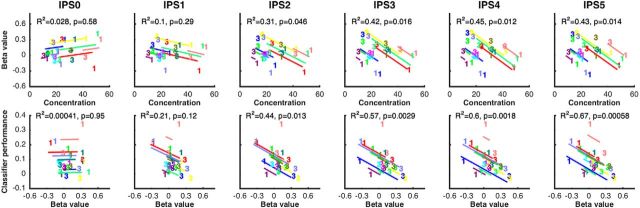
In the parietal delay ROI, the level of BOLD signal in the 1M versus the 3M condition predicted the effects of this manipulation on behavioral precision. At a finer grain of anatomical resolution, this relation was not observed in IPS0 and IPS1 (r² = 0.028 and r² = 0.10, respectively), began to emerge in IPS2 (r² = 0.31), and was uniformly robust for IPS3-IPS5 (r² values > 0.40; Fig. 5). In the parietal delay ROI, the level of BOLD signal in the 1M versus the 3M condition also predicted the effects of this manipulation on MVPA performance in the occipital sample ROI. In the anatomically defined ROIs, this effect was not significant in IPS0 and IPS1 (r² = 0.0004 and r² = 0.21, respectively) but was robust and progressively stronger from IPS2-IPS5 (r² values >0.40; Fig. 5).

Figure 5.

Within-subject correlation between behavioral precision, BOLD activity, and classification sensitivity, as a function of memory load (1M vs 3M), in each IPS anatomical ROI. Top row, results from ANCOVAs relating behavioral precision and BOLD activity. Bottom row, results from ANCOVAs relating BOLD activity in each IPS anatomical ROI and classification performance in the occipital sample ROI.

Exploratory analyses by hemisphere, and of lateral PFC

All of the analyses of IPS ROIs that have been reported up to this point suggest a much more prominent role for IPS activity, whether assessed as aggregated BOLD signal intensity or with MVPA, in the delay-period control of working memory for three items drawn from the same category than for three items drawn from two different stimulus categories. Furthermore, BOLD signal intensity of IPS delay-period activity was comparable in the 1M and 1M2C conditions, and the 1M to 1M2C load effect in IPS failed to show within-subject correlation with either neural or behavioral precision. Although these findings provided clear answers to the two principal questions that motivated this experiment, they left unanswered how our data might explain the general effects of memory load: the fact that behavioral precision was comparably lower for both 3M and 1M2C trials relative to 1M; and the fact that delay-period stimulus decoding from occipital cortex was comparably lower for both 3M and 1M2C trials relative to 1M. To address this question, we returned to the theoretical proposition that an amodal attentional resource underlies VWM capacity limitations. Because previous studies performed within this framework have primarily identified load-sensitive modality-independent effects in left-hemisphere regions of IPS and frontal cortex (Cowan et al., 2011; Li et al., 2014; Majerus et al., 2016), we performed these additional analyses in the left-hemisphere and right-hemisphere parietal delay ROIs, and in the left-hemisphere and right-hemisphere lateral PFC delay ROIs (as described in Materials and Methods).

In a unilateral left-hemisphere parietal delay ROI, 1M2C delay-period activity (averaged across 10–14 s) was significantly higher than was 1M delay-period activity (t₍₁₁₎ = 2.28, p = 0.043), and the ANCOVA relating load-related change in delay-period activity to behavioral precision also approached significance (r² = 0.24; p = 0.09); no such trends were in evidence in the right hemisphere. Importantly, in the left-hemisphere lateral PFC delay ROI, delay-period activity was elevated for both the 1M2C and 3M conditions relative to 1M and did not differ between 1M2C and 3M (Fig. 6A). Furthermore, for both of these conditions, the ANCOVAs relating BOLD signal intensity in the left-hemisphere lateral PFC delay ROI to behavioral precision and to occipital MVPA, as a function of memory load, revealed reliable within-subject correlations (r² values >0.3; p values <0.05; Fig. 6C–F); such trends became a lot weaker in the right-hemisphere lateral PFC delay (r² values = 0.29 and 0.03, p values = 0.06 and 0.55), where delay-period activity for the 1M2C condition was reduced (Fig. 6B).

Figure 6.

BOLD activity and within-subject correlation in the lateral PFC ROIs. A, Time course of BOLD activity in left hemisphere lateral PFC ROI. B, Time course of BOLD activity in right hemisphere lateral PFC ROI. Red, blue, and green lines indicate the 1M, 3M, and 1M2C conditions, respectively. Circles on top of each plot represent significance of each time point for 1M versus 3M (purple), 1M versus 1M2C (orange), and 1M2C versus 3M (cyan). Solid circles represent p < 0.05. Dashed circles represent p < 0.10. Shaded gray areas represent the timing of the sample (S), delay (D), and probe (P) epochs of each trial. Error bars indicate ±1 SEM. Results from ANCOVAs relating variation as a function of the 1M versus 3M manipulation (C) between BOLD activity in the left hemisphere lateral prefrontal ROI and behavioral precision and (D) between BOLD activity in the left hemisphere lateral prefrontal ROI and classifier performance from occipital sample ROI. Results from ANCOVAs relating variation as a function of the 1M versus 1M2C manipulation (E) between BOLD activity in the left hemisphere lateral prefrontal ROI and behavioral precision and (F) between BOLD activity in the left hemisphere lateral prefrontal ROI and classifier performance from occipital sample ROI. In each plot, data from each subject are portrayed in a different color. The “1,” “2,” and “3” symbols indicate individual values in the 1M, 1M2C, and 3M conditions, respectively.

Discussion

Although delay-period activity in the IPS increases monotonically with memory load (Emrich et al., 2013), and in a manner that saturates with VWM capacity (Todd and Marois, 2004, 2005), the functions that this activity supports remain unclear. Many studies to date have confounded memory load with the potential for elevated demands on context binding. It is well established, both at behavioral (Wickens et al., 1963; Wickens, 1973) and neural (Postle et al., 2004; Cohen et al., 2014) levels, that mnemonic representations of same-category items interfere to a greater extent than heterogeneous items. Furthermore, our serial presentation and single-item probing procedure required subjects to retain not just the physical properties of each stimulus, but also the order in which it had been presented. The 3M trials were expected to place greater demands on context binding (Oberauer and Lin, 2017), for the reason that the ordinal context of each item could be confused with those of two other items, whereas on 1M2C trials such confusion was only possible for the two colors, but not for the single RDK. Despite these considerations, however, the fact that VWM for heterogeneous items is also capacity limited left open at least two possibilities for our study. First, neural operations recruited by 3M and 1M2C may have differed only quantitatively, in which case capacity limitations in VWM might be understood as deriving from limitations inherent in the operations summarized here. Second, and more consistent with our findings, 3M and 1M2C trials may differentially tap into two discrete sets of mental operations: one engaged to address demands of context binding and one more generally associated with capacity limitations, regardless of stimulus category or modality. Additionally, and mutually compatible with the context-binding account, the two load-of-three-items conditions also afforded different strategies for chunking by category, a possibility that cannot be disambiguated with the present design.

IPS and the control of demands on context binding

Delay-period activity in IPS was much more strongly implicated in controlling the effects of stimulus homogeneity than in the effects of varying memory load. Spatially aggregated delay-period BOLD activity was greater for 3M than for 1M and 1M2C and did not differ between the latter two. Furthermore, IPS BOLD sensitivity to the 1M-to-3M manipulation predicted the 1M-to-3M drop in VWM fidelity, both as estimated in behavioral performance and in delay-period decoding of occipital stimulus representation. No such relations were observed in 1M versus 1M2C comparisons. This means that factors other than load, per se, drove these within-subject correlations. Although our results do suggest a possible alternative explanation for the load-sensitive activity reported in the earlier work by Todd and Marois (2004, 2005), our study used a different method to define the functionally activated ROI. Therefore, we cannot rule out the possibility that there are two discrete sources of load-sensitive activity: one putatively related to context binding and the other to memory storage.

Our findings are broadly consistent with the operation of a salience map (Colby and Goldberg, 1999; Knops et al., 2014) under conditions in which the most behaviorally relevant stimulus dimension to be tracked is order of presentation, rather than the more traditionally studied spatial location (Jerde et al., 2012). The representation of temporal order information engages PPC and lateral PFC (Marshuetz et al., 2000). Interestingly, many current computational models also emphasize that context binding is fundamental to VWM function, and that the critical context can often be temporal (Oberauer and Lin, 2017; Schneegans and Bays, 2017). Because only temporal order served as context in the present study, it remains to be examined whether this “context binding” hypothesis generalizes to other domains, such as space.

Despite the marked differences of processing requirements between the 3M and 1M2C conditions, data from these two conditions were also similar in many respects. Behaviorally, the two conditions did not differ statistically in terms of precision, probability of target responses, or guessing. Neurally, decoding of the critical motion direction from the occipital sample ROI did not differ between these two. Furthermore, swap errors for RDK stimuli, which were only possible in the 3M condition, were nonexistent. The most parsimonious explanation for these outcomes is that the additional demands of the 3M condition, relative to 1M2C, were overcome by the recruitment of IPS-based control. The absence of swap errors may be explained by the effective implementation of context binding, which is reflected in the greater delay-period activity in IPS in the 3M condition.

Constraints on working memory capacity

The patterns of IPS activity that we have emphasized up to this point have not shown strong evidence for activity related to category-independent capacity limitations on VWM. One would expect a region whose activity reflected more general capacity limitations to show greater delay-period activity for 1M2C than 1M. Consistent with previous studies (Cowan et al., 2011; Li et al., 2014; Majerus et al., 2016), our data suggest that such activity is strongly left lateralized, trending in IPS, and robust in lateral PFC. Indeed, our data are consistent with a model of at least partial independence between a left-lateralized amodal attentional resource that most prominently draws on lateral PFC (Cowan, 1995), and an IPS-supported salience map that can perform the function of context binding. This pattern is also consistent with computational models that posit distinct explanations for binding errors versus the effects of load, the latter being attributed to changes in signal-to-noise (Oberauer and Lin, 2017; Schneegans and Bays, 2017), as would be expected in a system operating under a normalization regime (Carandini and Heeger, 2011).

Functional distinction between occipital and parietal cortex, and a gradient of function along the IPS

Together with evidence for the dissociability of two kinds of control, our data also confirmed a clear distinction between patterns of activity in occipital cortex versus IPS, suggesting different contributions to VWM. This dissociation is highly robust and replicable, in that three previous studies (Riggall and Postle, 2012; Emrich et al., 2013; LaRocque et al., 2017) have demonstrated similar patterns of results. Whereas aggregated delay-period BOLD signal intensity in the occipital sample ROI did not differ between the three conditions, nor from baseline levels; in the parietal delay ROI, it was elevated in all three conditions, and markedly more so for 3M than 1M2C and 1M. This IPS activity is associated with a control function, as it is correlated with both behavioral and neural estimates of VWM fidelity. In contrast, delay-period MVPA decoding, which suggests a role in information storage, was markedly superior in the occipital sample ROI. Specifically, decoding of mnemonic representations was successful in the occipital sample ROI regardless of memory load, whereas successful decoding in the parietal ROIs was only possible, or trending, when only one item was held in memory.

The contribution of the parietal cortex to VWM storage, per se, is controversial and remains to be fully understood. Task-specific delay-period selectivity for motion direction was not observed in single neurons in the lateral intraparietal area of monkeys (Sarma et al., 2016). However, delay-period motion direction can be decoded from local field potentials regardless of task (Masse et al., 2017). Another study has demonstrated that lateral intraparietal area neurons encode the magnitude of the difference in shape between a target and a nonmatching foil rather than shape identity (Ong et al., 2017). Human fMRI studies also produced mixed findings, with some successful (Christophel et al., 2012; Ester et al., 2015; Bettencourt and Xu, 2016; Yu and Shim, 2017) and some unsuccessful (Linden et al., 2012; Riggall and Postle, 2012; Emrich et al., 2013; Lee et al., 2013) when decoding stimulus identity from delay-period activity in the parietal cortex.

Along the length of the IPS, differences in function were graded, rather than categorical. The 1M-to-3M load sensitivity of delay-period activity was lowest for IPS0 and became progressively greater for each more rostrally located ROI. This gradient was mirrored in the results of analyses indexing control-related patterns of activity. The evidence for functional interactions between parietal signals and occipital mnemonic representations, as well as the evidence for a relation between parietal signals and behavior, were nonexistent for the more caudal part of IPS and became progressively larger for more rostral parts. Thus, rather than being highly localized, the working-memory-related control functions of the IPS may emerge and strengthen along a caudal-to-rostral gradient. This observation is broadly consistent with longstanding views suggesting a functional distinction between caudal and rostral IPS (Xu and Chun, 2006; Cole et al., 2013; Freud et al., 2016).

The neural bases of working memory capacity limitations

Empirical observation has demonstrated that VWM is capacity limited (Luck and Vogel, 1997; Cowan, 2001), with individual differences stable and trait-like (Fukuda et al., 2015), and predictive of many other cognitive measures (Cowan, 2014). Although this characteristic of human cognition undoubtedly derives from many sources, two that have received considerable attention are an amodal resource that must be allocated across all to-be-held items in memory, and processes to control interactions among mnemonic representations. Our results provide evidence that these two are mutually compatible and supported by at least partially dissociable systems in the brain.