Deconvolution of Voltage Sensor Time Series and Electro-diffusion Modeling Reveal the Role of Spine Geometry in Controlling Synaptic Strength

SUMMARY

Most synaptic excitatory connections are made on dendritic spines. But how the voltage in spines is modulated by its geometry remains unclear. To investigate the electrical properties of spines, we combine voltage imaging data with electro-diffusion modeling. We first present a temporal deconvolution procedure for the genetically encoded voltage sensor expressed in hippocampal cultured neurons and then use electro-diffusion theory to compute the electric field and the current-voltage conversion. We extract a range for the neck resistances of 〈R〉 = 100 ± 35MΩ. When a significant current is injected in a spine, the neck resistance can be inversely proportional to its radius, but not to the radius square, as predicted by Ohm’s law. We conclude that the postsynaptic voltage cannot only be modulated by changing the number of receptors, but also by the spine geometry. Thus, spine morphology could be a key component in determining synaptic transduction and plasticity.

In Brief

Based on fluorescence recordings, Cartailler et al. recover the voltage dynamics in dendritic spines by deconvolution. They investigate electricity at a nanometric scale using electro-diffusion modeling and concluded that spine geometry and electrolyte shape the current-voltage conversion and electrical resistance.

INTRODUCTION

Neurons communicate via synaptic microdomains, where an input current generates a voltage change in the post-synaptic neuron. This voltage change, induced by excitatory current, reflects the strength of the synaptic connection between two interacting neurons (Jack et al., 1975; Holmes et al., 1992; Koch and Segev, 1998, Chapter 2), (Qian and Sejnowski, 1989; Yuste, 2010) and depends on two components: the first is the number of glutamatergic receptors for excitatory neurons and the second is the geometry of the post-synaptic terminal. However the relative contribution between these two factors is still unclear. For example, the post-synaptic structure is often a dendritic spine, the geometry of which is involved in modulating the time-scale of diffusion (Svoboda et al., 1997; Korkotian et al., 2004; Bloodgood and Sabatini, 2005; Tønnesen et al., 2014; Holcman and Schuss, 2013). In parallel, increasing the number of receptors on that terminal leads to a larger synaptic current (Huganir and Nicoll, 2013; Elias and Nicoll, 2007; Kessels and Malinow, 2009). But diffusion alone is not sufficient to interpret the synaptic response because it is driven by electro-diffusion involving an electric field and diffusing ions. Electro-diffusion has been applied successfully for studying ionic fluxes and gating of voltage channels (McLaughlin and Poo, 1981; Bezanilla, 2008; Eisenberg, 2007). Those studies were all based on the fact that at the nanometer scale, the cylindrical symmetry of a channel model reduces to a one-dimensional segment, allowing the study of the electric field and charge densities in the channel pore (Eisenberg, 1999; Eisenberg et al., 1995). Moreover, recent studies have clearly shown that the current in the synaptic cleft reflects the coupling between moving ions and the local electrical field (Sylantyev et al., 2013; Savtchenko et al., 2004).

In a dendritic spine, voltage changes during the synaptic response are generated by the interactions between the ionic flow and the spine geometry. Dendritic spines are heterogenous microdomains at the limit of optical resolution and for that reason, voltage changes were estimated for many years using modeling and numerical simulations of passive cable equations, the basis for the Hodgkin-Huxley model (Koch and Segev, 1998). This approach is however not appropriate for spines because their micro-geometry composed of a bulby head connected to a thin neck is significantly different from that of a cable. In addition, cable theories break down when applied to small neuronal compartments, such as dendritic spines, because they assume spatial and ionic homogeneity. Linear approximations of electro-diffusion that couples the electric field with the ionic flow have been used to improve the estimation of the voltage changes in spines, approximated as cylinders of various sizes, but assuming local electroneutrality (Qian and Sejnowski, 1989). This method was later on generalized to study the electrical effect of Ranvier node (Lopreore et al., 2008). Recent advent in estimating the voltage changes at a sub-micrometer resolution (Araya et al., 2006, 2014; Hochbaum et al., 2014; Jayant et al., 2017) revealed electrical properties of dendritic spines (Harnett et al., 2012; Holcman and Yuste, 2015; Savtchenko et al., 2017), but the heterogeneity of the results (Popovic et al., 2015; Acker et al., 2016) and the absence of a robust computational framework and theory to interpret data challenges our understanding of electrical properties of these structures and cellular microdomains in general.

To better understand how spines function, we develop here an electro-diffusion framework to compute the voltage-current relation and the local voltage variations generated by synaptic inputs. We present a deconvolution procedure to recover the timescale of voltage responses from voltage-sensitive indicators in hippocampal neurons. Genetically encoded voltage indicators (GEVIs) (Brinks et al., 2015; Gong et al., 2015; Han et al., 2013; Jin et al., 2012; St-Pierre et al., 2014) can be expressed in neuronal membrane through plasmid transfection (Kwon et al., 2017) and thus it reports internal changes of the membrane voltage. The deconvolution procedure transforms the voltage dye Arclight response into voltage dynamics. To interpret the drop of voltage between the spine head and dendrite, we use the Poisson-Nernst-Planck theory for electro-diffusion. We further compute how a current flowing inside the spine head is converted into voltage and determine the electrical resistance. Numerical simulations of the voltage drop in the entire spine reveal how a change in the neck length and radius alters voltage. The manuscript is divided in two parts: first, we present the general method of time series deconvolution applied here to voltage dyes and we construct an electro-diffusion model to extract parameters from data. In the second part, we use our electro-diffusion model to generate three-dimensional simulations to investigate how the spine geometry modulates its electrical properties. We conclude here that while the numbers and the types of synaptic receptors determine the injected current, the geometry of a dendritic spine controls the conversion of current into voltage.

RESULTS

Converting Arclight Fluorescent Signals into Voltage Responses

Arclight dye indicators respond to voltage with an intrinsic delay (Kwon et al., 2017), such that a fast voltage response leads to a convolved fluorescence response. In that context, a synaptic input entering a dendritic spine generates a fluorescent response that needs to be deconvolved in order to recover the electrical genuine time course. As the voltage intensity has already been deconvolved in Kwon et al. (2017), we focus here on the temporal response. The basis of the method is to find the causal kernel K(t), which is computed empirically by comparing the electro-physiology and the fluorescence responses in the soma (see STAR Methods). Once the kernel is found, we will use it to recover the noisy voltage dynamics in much smaller structures such as dendritic spines and portions of dendrites.

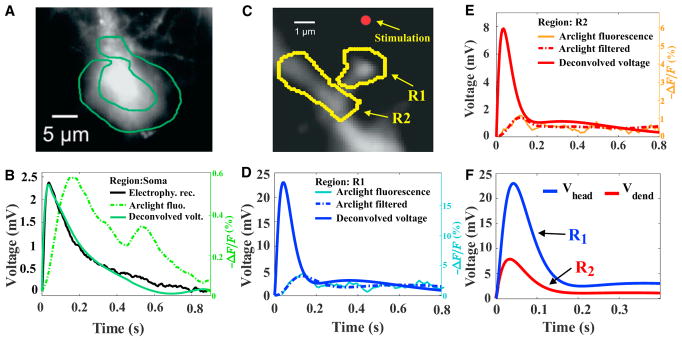
We apply the deconvolution procedure on the soma region (Figure 1A), which transforms the fluorescence dye signal (dashed green) into the voltage response (black) (Figure 1B; see STAR Methods and Figure S1). The deconvolved signal is shown by a line (green) that superimposes with the electrophysiological recordings (continuous black line). This result confirms the validity of the method. Indeed, by using the direct convolution of the electrophysiological recording by the kernel, we obtain the response (black curve) that exactly super-imposes with the fluorescence soma signal (Figure S1A). We note that the second bump in the fluorescence signal (dashed green) in Figure 1B is removed by the fitting procedure before the deconvolution kernel K(t), as expected because the electrophysiological recordings do not exhibit this second bump. We extended the deconvolution procedure for several spikes in Figure S2.

Figure 1. Voltage Drop across a Dendritic Spine Measured from Arclight.

(A) A region of interest is selected around the soma to estimate the fluorescence during a synaptic stimulation.

(B) The deconvolution of the fluorescence signal (dashed green) in the soma uses the electrophysiological recording (continuous black) to obtain the deconvolved voltage (continuous green) (we refer also to Figures S1C–S1E for further details on the filtering procedure). Fluorescence and electrophysiology are both traces averaged over 6 spines (Figure S3 for 5 other examples).

(C) Regions of interest (ROIs) R1 and R2 representing the spine and the dendrite, respectively. The red dot shows the location where glutamate is uncaged.

(D and E) Deconvolution of the fluorescence signal (single trial) in the dendritic spine R1 (D) and the dendrite R2 (E) using the kernel K(t) found in the soma deconvolution in (see B).

(F) Comparison of the filtered and deconvolved voltage signal in the spine head and parent dendrite.

Based on the deconvolution kernel K(t), we shall now deconvolve the fluorescent responses in the regions of interest (ROIs) R1 and R2 shown in Figure 1C and Figure S3. Indeed, after we found the deconvolution kernel K(t) from the soma data, we applied it to deconvolve the signal in spines because the distribution of dyes is the same in the entire neuron (Kwon et al., 2017). The results are shown in Figures 1D and 1E for the voltage in the spine head and dendrite. We note that the original fluorescence (thin line) contains fluctuations (Figures 1D and 1E) and an additional step is needed to remove the fluctuations (see STAR Methods and Figures S1C–S1E). We found that the voltage timescale in the dendritic spines, recovered from the present de-convolution procedure, is slower than the expected direct synaptic response. Probably, this slow timescale compared to direct synaptic electrical stimulation is due to glutamate uncaging, that can last for hundreds of milliseconds. To conclude, we can now recover the voltage in region R1, which represents the head, and in R2, which refers to the adjacent portion of the dendritic shaft at the base of the spine (Figure 1F). This deconvolution step is crucial because it allows us a direct comparison with the electro-diffusion model that we shall describe in the next section.

Electro-diffusion Theory for Ionic Flows in Dendritic Spines

To interpret the voltage dynamics in a dendritic spine, we use the electro-diffusion model that couples positive c_p(x, t) and negative c_m(x, t) charge concentrations with the electrical potential V(x, t). The model is based on the phenomenological Poisson-Nernst-Planck (PNP) equations, where the ionic flow is driven by diffusion and the electric field. The voltage is described by the classical Poisson equation (Jackson, 2007, Sect.1.7) (see STAR Methods). We use the PNP equations to model the flow of ions when a current I_stim(t), composed exclusively of positive charges, is injected at the top of a dendritic spine. We recall that the electrical potential generated by a flow of ions is defined up to an additive constant.

We start with the description of the voltage response produced by an input current I(t) inside the spine neck. The current I(t) that arrives at the neck entrance results from the stimulation current I_stim(t) received by the head. We applied the electro-diffusion approach at the nano-micrometer scale, by reducing the neck geometry to a one-dimensional wire of length L (Figures 2A–2C). Due to its large size, compared to a dendritic spine, the dendrite constitutes an ionic reservoir (fixed concentrations).

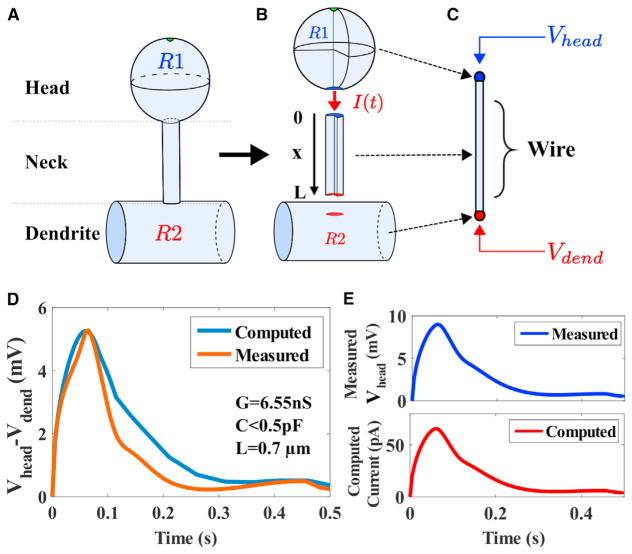
Figure 2. Extracting the Electrical Parameters of a Dendritic Spine from a Reduced Model and Voltage Dynamics.

(A and B) Schematic representation of a dendritic spine, divided into three regions: the head R1, the neck of length L, and the close dendrite R2. The current I(t) represents the axial current escaping from the head to the dendrite.

(C) Reduced geometry of a dendritic spine neck of length L, approximated as a dielectric wire. The input is the measured voltage V_head(t) of ROIs (Figure 1C) R1 at the head (x = 0) and we use voltage V_dend(t) (R2) in the parent dendrite (x = L) as an output for comparison with the numerical computation.

(D) Comparison of measured (trace averaged over 6 spines) (orange) and computed (blue) voltages. The parameters C and G are used in (1) to estimate the injected current.

(E) Measured membrane potential (blue) in the spine head is used to compute the ionic current (red) from (1), after the parameters (C, G) are extracted from the iterative method developed in the STAR Methods.

Furthermore, using for the internal resistivity the value 109 Ω.cm (Koch, 2004, Chapter 11), we find that the fluctuations of the voltage in the portion of the dendrite R2 (Figure 1C) are negligible, and in that case, the region R2 is expected to be iso-potential. Consequently, we fix in the dendrite the value for the voltage V(0, t) = 0mV. We thus interpret the potential V(t) = V(L, t) computed at the end of the neck (Figures 2A–2E) as the difference of potential between the entrance and the end of the spine neck. Consequently, we describe the electro-diffusion inside the neck by the ensemble of Equations 37, 39, and 40, where I(t) has yet to be estimated.

From the classical theory of electricity (Jackson, 2007), it is not possible to extract the current passing through a passive device from the difference of potential when the resistance is unknown. However, using an electrical model for the axial current, escaping from the spine head to the neck, we shall reconstruct the voltage in the neck and recover the current in the entire spine. Because there is no direct measurement of the current I(t), we develop here a procedure (STAR Methods) to estimate this current from the measured membrane potential ϕ(t) in the spine head. We decompose the current as the sum of a resistive and a capacitive term:

$$I(t)=G\varphi (t)+C\frac{d\varphi (t)}{dt}.$$ (Equation 1)

The conductance G and the capacitance C reflect how the current I_stim(t), injected in the spine, is processed by the head, depending on the intrinsic properties of the spine head (in the next section, we will simulate the entire voltage using PNP starting from the current entering through the channels). Consequently, we will refer to G and C as intrinsic conductance and intrinsic capacitance, respectively. We now estimate the two constants C and G and the voltage drop across a spine neck by solving numerically Equations 37, 39, and 40 and compare the results to the simulations with the deconvolved Arclight fluorescent voltage response. The response is generated following glutamate uncaging stimulations at the top of the spine head (Figure 1C, red dot). We solve numerically the PNP equations for the distribution of positive c_p(x, t) and negative c_m(x, t) charges, as well as the potential difference V(x, t) (Figures 2D and 2E). To estimate the voltage difference ΔṼ(t) across the neck, we grounded the potential to 0 mV at the dendritic shaft (before stimulations, the voltage is described by Equation 38).

To assess whether the potential difference ΔṼ(t) = V_head(t) − V_dend(t) can be predicted from the electro-diffusion model, we fix the input voltage ϕ(t) = V_head(t). We then compare the voltage obtained by solving Equations 37, 39, and 40 (Figures 2D and 2E) to the measured voltage V_dend(t) in region R2 (blue) at the dendritic shaft (Figure 2C). Although region R1 includes the head and the neck, we neglected the fluorescence in the neck due to its small thinness ≤100nm. We found a good agreement between the experimental data and numerical simulations (Figure 2D) showing that the difference of voltages between the head and dendrite can be predicted from the input voltage V_head(t). In addition, we estimated the injected current (Figure 2E, see STAR Methods and Equation 1) directly without any direct electrophysiological recordings. Note that the deconvolved voltage in the head (blue) and the computed current (red) are exactly proportional, because the capacitance C, reported in Table 1 and used to compute I(t) in Equation 1, is negligible. Thus, the current is simply proportional to the voltage. We conclude at this stage that the electro-diffusion theory allows estimating the electrical properties of the spine red neck and the injected current (of the order of tens of pA) in the spine neck, triggered by a synaptic current I_stim(t).

Table 1.

Extracted Parameters from Modeling

Spine	Neck Length L (μm)	Head Radius rhead (μm)	Intrinsic Capa. C (pF)	Intrinsic Res. 1/G (MΩ)	Effective Neck Res. Rneck (MΩ)
1	0.6	1.2	<0.5	128.5	73.3
2	0.7	0.8	<0.5	163.4	57.1
3	0.8	0.7	18	212	99.15
4	1.0	0.8	10	252	132.6
5	1.2	0.6	<0.5	261	134.1

Columns 1: spine indices. Column 2: neck length L. Column: 3 radius r_head of the spine head computed using formula 2. Column 4: intrinsic capacitance C (section 2 of the SI). Column 5: Intrinsic resistance of the spine 1/G (section 2 of the SI). Column 6: spine neck resistance, computed from formula R_neck = 〈V(0, t) − V(L, t)〉/〈I(t)〉 (see section S3 for the definition and computation), where V(0,t) and V(L,t) represent the voltage at 0 (entrance of the neck) and L (based of the spine) respectively and 〈·〉represents the time averaging between 0 and 0.5 s. We computed V(0,t) and V(L,t) from formula 9 and the current I(t) from Equation 1.

We apply systematically the electro-diffusion approach, based on (1), to extract the capacitance C and the conductance G of several spines (Figures S3 and S4). Using an optimization procedure, we explore the parameter space for computing C and G (Figure S4). We minimize the error between the solution of the electro-diffusion equation and the voltage output of the dendrite during a small time interval at the beginning of the response (Figure S4). The resistance is computed by averaging the voltage changes in time. We use for the estimator the expression R_neck = 〈V(0, t) − V(L, t)〉/〈I(t)〉 (where the average is performed over the time interval t ∈ [0, 0.4]s). In all cases, we find a good agreement (Figure 4) between the measured and computed voltage drop across the spine neck, where we estimated the current injected in the neck from the head of several spines.

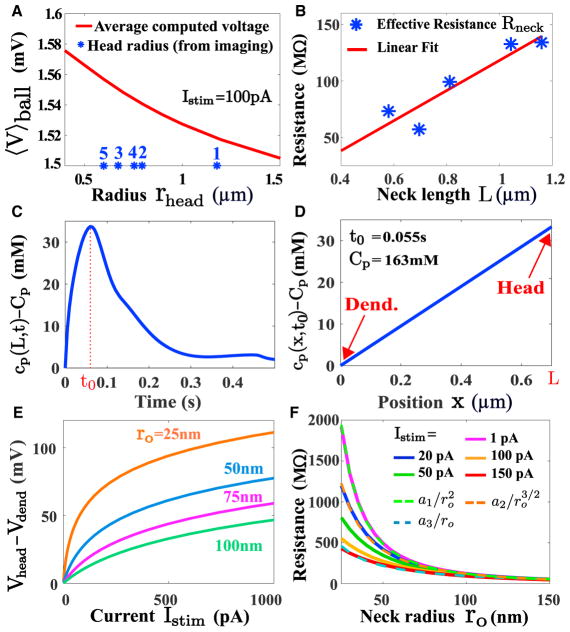
Figure 4. Electrical Properties of Dendritic Spines.

(A) Averaged voltage computed in a spine head using PNP (see Figure 3B): for various head radius, the voltage is almost constant (〈V〉_ball∈[1.52, 1.56]mV). The stars (blue) correspond to the radii of different spine heads based of their surface, determined from one photon image. The indexes refer to the different spines in Table 1. (B) Estimated spine neck resistance (blue stars) computed as the ratio of the voltage to the current averaged over the time responses R_neck = 〈V(0, t)〉/〈I(t)〉 for 5 different spines, revealing how the spine resistance depends on the neck length.

(C) PNP simulation showing the concentration of positive charges at the end of the neck for the injected current described in Figure 2E. The response peaks at t₀ = 0.055s.

(D) Distribution of charges at the peak, computed from PNP, showing a large concentration difference of 33 mM (the total concentration 163 mM).

(E) Predicted I–V relation in a dendritic spine for different spine neck radius.

(F) The spine neck resistance is defined by the ratio R_neck = 〈V〉_head/I_stim. The neck length is L = 1μm and a radius r_head = 0.5μm. The different injected current I_stim = 20; 50; 100; 150pA. The averaged voltage in the head 〈V〉_head is computed from system of PNP Equation 57. The computed resistance R_neck is fitted to power laws $a_1/r_o^2$ (dashed green) and $a_2/r_o^{3/2}$ (dashed orange) and a₃/r_o (dashed blue) where a₁ = 1.23·10⁶ a₂ = 1.57·10⁵ and a₃ = 1.22·10⁴.

In summary, we found that the average spine neck resistance (for a mean neck radius r_o = 100nm) is 〈R〉≈100 ± 35MΩ (Table 1). We also reported here a large variability in the spine resistance, while the intrinsic capacitance is negligible. To conclude, the electro-diffusion model allows computing the current injected in the spine neck after a synaptic stimulation, thus recovering the neck resistance.

Voltage Transduction in a Spine and Predictions of Electro-diffusion

We have shown in the previous section that electro-diffusion PNP-based model can be used to analyze Arclight fluorescence recording and this model allows estimating the current flowing in the spine neck. We shall now extend the PNP model to geometries that characterize the peculiar shape of the dendritic spines. To analyze how a dendritic spine influences the voltage response to a synaptic input, we simulate the three-dimensional PNP equations (see STAR Methods) for two geometries: a ball of radius r_head and a spine-like geometry (Figure 3). We computed the distribution of the electrical potential for short spine necks (Figure 3A), where the head contains two narrow openings: one of radius r_o = 100nm representing the junction with the neck, and the other of radius r_i = 10nm that receives the steady current I_stim of positive charges (Figure 3B). Note that we have dropped the time t in the expression of the current I_stim, since we consider now steady-state current. In addition we neglected the membrane capacitance because the current I_stim represents already the ionic flow entering the head. We show (Figure S5) that the capacitance has almost no contribution to the voltage drop. We computed the distribution of positive c_p(x) and negative c_m(x) charge concentrations as well as the voltage V(x) when it is grounded to 0 V at the end of the spine neck, which represents the connection to the dendrite, considered as a large ionic reservoir with fixed concentration (see Table 2). Consequently, V(x) represents the voltage difference induced by the injected current I_stim. We find the distribution of the voltage along the x axis (blue) Figure 3B when I_stim = 150pA is injected in the spherical geometry as shown in Figures 3A and 3B.

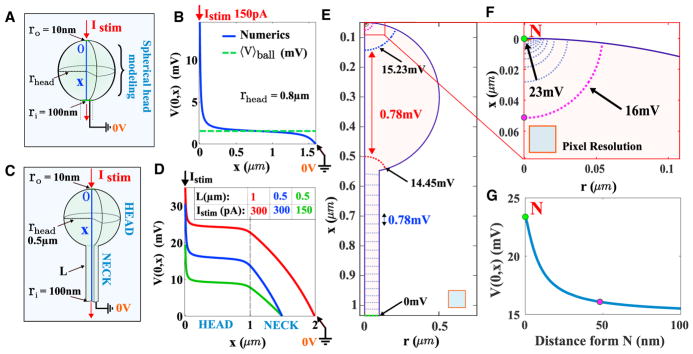
Figure 3. Simulation of PNP Equations for Electro-diffusion in a Dendritic Spine.

(A) Representation of a spine head where a current is injected in a 3D spherical cavity of radius r_head = 0.5μm.

(B) Voltage profile (blue) along the x axis obtained from three-dimensional simulations of the PNP equations that we compare to the potential averaged over the entire head (dashed green line) when the injected current is I_stim = 150pA. The south pole is grounded at V = 0V.

(C) Representation of a 3D spine geometry composed by a spherical head of radius r_head = 0.5μm and a neck of length L = 1μm. The head has two narrow openings, one of radius 10nm where the steady current I_stim is injected (north) and a second one (south) of 100nm at the junction with the neck.

(D) Potential drop along the x axis computed from the top of the head to the bottom of the spine. We compare the voltage drop between a spine where L = 1μm and I_stim = 300pA (red) with L = 0.5μm and I_stim = 150pA (blue).

(E) Voltage isolines in a longitudinal cross-section of a spine-like geometry.

(F) Magnification near the north pole N where the current is injected.

(G) Voltage in the neighborhood of the north pole N, computed in 100 nm along the z axis.

Table 2.

Biophysical and Geometrical Parameters

Parameter	Description	Value
z	Valence of ions	1
D	Diffusion coeffcient	200 μm2/s (Chen and Nicholson, 2000)
Dp	Diff. coeff. for + charges	D
Dm	Diff. coeff. for − charges	D
Cp	+ charge concentration	167 mol/m3 (Hille, 2001, Chapter 1)
Cm	− charge concentration	167 mol/m3 (Hille, 2001, Chapter 1)
Ω	Spine head	Ω (volume |Ω| ≈1fL) (Yuste, 2010, Chapter 3)
ro	Spine neck radius	(typical) 0.1 μm (Takasaki et al., 2013)
L	Spine neck length	(typical) 1 μm
T	Temperature	293.15K
E	Energy	kT = 2.58·10−2 eV
e	Electron charge	1.6·10−19 C
ε	Dielectric constant	ε = 80
ε0	Abs. Dielectric constant	8.8·10−12 F/m
k	Boltzmann constant	1.38·10−23 J/K
F	Faraday constant	96, 485 As/mol

In summary, inside a spherical domain, diffusion is the dominant driving force and the potential drop is reduced significantly, which is equivalent of having a small spine head resistance. Indeed, applying the electro-diffusion model (Equations 37 and 38) to a spine-like geometry (Figure 3C), we observe that most of the voltage drop is carried by the spine neck (Figure 3D). Interestingly, it is not equivalent to decrease the neck length to compensate for a decrease in the injected current (see result with an injected current of 150 versus 300pA), suggesting that changing the synaptic weight by adding or removing receptors or modifying spine neck length have different consequences on the spine voltage distribution.

We also observed in Figures 3E–3G that there is a narrow layer located at the entrance of the PSD region where the synaptic current I_stim is injected. We found a 7 mV drop occurring in a small distance (≈50nm) inside the spine head. This small region of large convection is at the limit of actual resolution (≈0.116μm/pixel). We could thus define a boundary layer resistance R_bl. Outside this layer, the voltage is quite uniform, leading to a reduced field convection e/k_BT∇ϕ (Equation 37), demonstrating that diffusion is dominant inside the spine head. To conclude, we demonstrated numerically using PNP equations that the voltage drop in the spine head is negligible (less than a quarter of mV), except in a small region where the current is injected. These results are in contrast with the classical cable theory (Figure S6), which suggests that the motion of ions is driven by the voltage gradient. At this stage, electro-diffusion theory predicts that the voltage in the spine head V_head(t) is spatially homogeneous, confirming the approximation of Equation 1, except near the post-synaptic density or at the entrance of the spine neck. The global spine head resistance is thus negligible, since the potential drop occurs just at the end of the neck, and thus the entire spine resistance is carried by the neck and the boundary layer: R_spine≈R_neck + R_bl. Note that in practice the resistance R_bl is not accessible to experimental measurements due to the thin region where it is generated. Thus, experimental results give access values for the neck resistance R_neck.

Spine Geometry Determines the I–V Conversion

To study the influence of the geometrical parameters on the electrical property of a spine, we first estimated the effect of the spine head radius r_head for five spines (Figure S3). By measuring their projected area S_head from the two-photon images, we use relation (Figure 4A)

$$r_{\mathit{head}}=\sqrt{\frac{S_{\mathit{head}}}{\pi }}$$ (Equation 2)

to extract the equivalent radius (blue stars). We then use the PNP model associated to the short spine with no neck (Figure 3A) to estimate the average voltage difference 〈V〉_ball (for a current of 100pA) between the north and the south pole of a spine head. We find that the mean voltage varies in a range of 1.5 − 1.6mV, when the radius of the head varies in the range 0.3 − 1.5μm. This result shows that the head radius had little influence on the mean voltage.

We then estimated how the spine neck resistance R_neck depends on the neck length and width, usually unaccessible using classical microscopy approaches: we find both theoretically and experimentally that the resistance increases (blue stars) with the neck length L (Figures 4B, 2D, and 2E). Note that the size of the head is not correlated with the resistance (Table 1). Furthermore, electro-diffusion simulations in a segment using (37–38) predicts that for the mean current input extracted from data, there is a significant change in the local concentration of positive charges (simulations of the 1D neck) of length L = 0.7μm at the time-to-peak (t₀ = 55ms). Indeed, we find a concentration gradient of 33mM between the tip and the base of the neck, when the concentration of ions is fixed at 163 mM in the dendrite (Figures 4C and 4D). Although the injected current I(t) is composed of positive charges, the concentration gradient in the neck is driven by positive and negative charges. Such phenomenon is called concentration polarization (Strathmann, 2004, Chapter 4). Finally, we confirmed this result using a simulation in a three-dimensional spine (neck plus head), where we injected transiently a current with an amplitude I_stim = 150pA (resp. I_stim = 150pA) at the top of a spine domain (Figure S6) and found a concentration gradient of 22mM (resp. 45mM) in the neck.

Finally, using the electro-diffusion theory and the spine parameter r_head = 0.5μm, L = 1μm, we estimated the I–V relation for various neck radius, showing a saturation for large current (Figure 4E). These curves show that the neck radius is one of the most critical parameters in defining the conversion of current into voltage. Then to clarify the dependency of the spine neck resistance R_neck on its radius, we simulated the PNP equations by solving Equation 58, where a steady-state current I_stim = 20; 50; 100; 150pA is injected inside the spine head (Figure 3C). We obtained the average voltage inside the head 〈V〉_head. We plotted the resistance of the neck versus the neck radius r₀, computed by R_neck = 〈V〉_head/I_stim in Figure 4F. Interestingly, we find that depending on the injected current, the spine resistance can decay inversely proportional to the radius of the neck. This is in contrast with classical results based on electrical circuit approximation (Koch, 2004, Chapter 12), where the classical Ohm’s law for a resistance predicts that resistance depends on $1/r_0^2$. When the injected current is large I_stim = 150pA, the resistance seems to decay with a power law 1/r₀ (dotted red) but changes to $1/r_0^{3/2}$ (dotted blue) for I_stim = 20pA. We recover the classical law for a small current I_stim = 1pA. Finally, for I_stim = 50pA and a spine neck radius of r₀ = 50nm (resp. 100 nm), the overall spine resistance that is mostly carried by the neck would be R_spine≈R_neck = 120MΩ. These results show a clear deviation from the classical Ohm’s law and also a limitation of the diffusion approach (Svoboda et al., 1997).

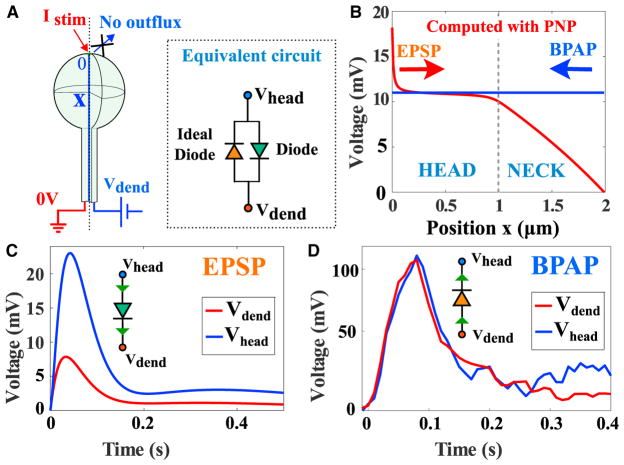
In summary, we used the electro-diffusion theory and the Arc-light fluorescent data to characterize the electrical properties of a dendritic spine. With respect to a synaptic input, a spine can be electrically characterized as a diode device (Figures 5A and 5B) with a finite resistance (for a small current), saturating for large currents (Figure 5C). The voltage difference varies from few to tens of mV. However, from the perspective of a Back Propagation Action potential, the equivalent circuit of a spine is a diode with zero resistance (no leak current; Horowitz and Hill, 1989, Chapter 1; Figure 5D).

Figure 5. Summary of Dendritic Spine Electrical Responses.

(A) Schematic representation of a dendritic spine. Left: a current is injected in the head. Right: modeling the effect of the BPAP on the spine voltage. The inset is an electrical circuit representation of the spine electrical properties, composed by a diode (green) with a resistance R_neck in the direction spine to dendrite and by ideal diode in the opposite direction (orange).

(B) Electrical response of a spine (length and radius of the head are L = R = 1μm) and the radius of the neck r₀ = 0.1μm, following a synaptic input (I_stim = 100pA) and a BPAP, where the value depends on the voltage in the dendrite, but it is constant in the spine.

(C) Modulation of the voltage between the spine head and the dendrite: the voltage attenuation can be modeled as a diode to account for the saturation behavior (Figure 3F).

(D) Response to a BPAP showing no voltage change between the head and the dendrite, as predicted by the electro-diffusion model.

DISCUSSION

We developed here a computational approach based on the electro-diffusion theory to estimate the electrical properties of dendritic spines. We first deconvolved the Arclight fluorescent signal and then applied the electro-diffusion theory to estimate the resistance and the capacitance from hippocampal neuron data. Our approach contrasts with classical estimation of the spine neck resistance and dendritic spine electric properties, extracted in the context of the electrical circuit approximation, passive cable theory and even diffusion approximation (Svoboda et al., 1997; Popovic et al., 2015; Acker et al., 2016; Koch, 2004, Chapter 2). In contrast to those studies, we find here that the electro-diffusion coupling is the main driving force for ionic current in the spine neck (Figure 3), while diffusion is sufficient to describe the motion of ions inside the head. The electric field is negligible in the head, except very close to the entrance of the synaptic input and at the exit with the neck.

In fact, electro-diffusion theory reveals that the spine head geometry imposes that the voltage is almost constant in the head, while the neck is responsible for most of the voltage drop. This is in contrast with the predictions of the cable theory or previous approximations of electro-diffusion (Koch and Segev, 1998), based on electroneutrality and no gradient of charges. We also demonstrated here that the ion conduction is mostly driven by diffusion in the spine head, suggesting that the head resistance is negligible compared to the neck.

We showed here that the synaptic current leads to a gradient of concentrations and thus the Poisson-Nernst-Planck theory should be used to describe the voltage at the submicron level. We presented in Figure 3 a resistance R_bl in a small boundary layer associated to a drop of voltage. This model may suggest that scaffolding proteins and receptors located in the PSD are experiencing large voltage drop that could regulate the electrical properties of charged C terminus of the receptors such as AMPA and thus their trafficking in dendritic spines (Nicoll, 2017; Herring and Nicoll, 2016). For slower electrical events, ionic concentrations should follow the changes of the local voltage and there is a significant gradient of charges of the order of 150 mM in a spatial scale of 1 μm, although the average concentration is stable around 100 mM. However, this effect does persist for a transient current lasting 100 ms, where the concentration gradient at time to peak is of the order of 30 mM. Most likely, fast oscillations or voltage fluctuations due to the opening and closing of the channels will not lead to an extended concentration gradient and, in that case, the electro-diffusion could be neglected.

It remains difficult to study the exact local balance of positive by negative charges, because in transient regimes or at equilibrium, positive charges are all the time in excess. Possibly the sum of negatively ionic charges plus the negative charges located on immobile proteins can balance positive charges at a tens to hundreds of nanometers. Long-range electro-diffusion effects have already been described for directing the current flow in the synaptic cleft into the post-synaptic terminal (Sylantyev et al., 2008, 2013), showing in a different context that electro-diffusion drives ionic flows and the voltage in neuronal microdomains.

Time Deconvolution of the Arclight Fluorescent Signal

Neuronal voltage is reported by recording electrodes and we showed here how the Arclight signal can be deconvolved in small and large microdomains, so that we can now access the voltage dynamics and electrical properties from microdomains. Genetically encoded activity sensors combined with microscopies are now classically used (Emiliani et al., 2015) to record and manipulate the activity of neural circuits. We show here how fluctuations contained in the fluorescent signal can be filtered and the voltage time course is recovered from the empirical kernel K(t) (STAR Methods). This approach can be applied to any encoded activity sensor expressed in neurons and only requires the comparison of the electrophysiological recording with the florescence in the soma. The present deconvolution could also be used to recover the electrical activity from slow calcium indicators (Emiliani et al., 2015).

Influence of the Neck Radius on the Spine Resistance

The spine neck radius cannot be spatially resolved, so any geometrical fluctuation is likely to result in a drastic change in the resistance. For diffusion alone, the rate of extrusion (Holcman and Schuss, 2013) (for Brownian particle) from a dendritic spine is given in first approximation as $(\mid {\mathrm{\Omega }}_{\mathit{spine}}\mid L/D\pi r_o^2)+(C_2\mid {\mathrm{\Omega }}_{\mathit{head}}\mid R_c^{3/2}/D{r}_o^{3/2})$, where D is the diffusion coefficient, |Ω_spine| is the volume of the spine, L the length of the neck, R_c the radius of curvature at the base of the neck-head junction, |Ω_head | the volume of the head and C₂ a constants, and r_o is the radius of the neck. This expression shows that a small change in the radius r_o (dividing by two for example) leads to a significant change of at least 4 for the diffusion time-scale. We addressed the radius neck uncertainty here in the context of electro-diffusion by computing the neck resistance for different radii (Figure 4F).

Spine-intrinsic electrical characteristics are revealed by the impedance, which is the ratio of the voltage to the injected current. For example, for a steady-state current of I = 50pA, the Ohmic resistance of a spine of radius 100nm (resp. 50nm) is 〈R_neck〉 = 120MΩ, (resp. 〈R_neck〉 = 350MΩ). This high resistance value for longer spine necks could be relevant for the statistics collected in brain slices (see our computations for the spine neck resistance in Figures S7D and S7E, where we find that the key parameter remains the spine neck radius; confirmed in Beaulieu-Laroche and Harnett, 2018). However, there is still no consensus about the large range of spine resistances, reported in the literature with direct and indirect measurements: the conclusions of different optical studies are mixed: some suggest an attenuation of EPSPs (Araya et al., 2006, 2014; Harnett et al., 2012), other suggest instead that spines are isopotential with the dendrites and do not alter EPSPs (Svoboda et al., 1997; Tønnesen et al., 2014). Diffusional studies of small fluorescent molecules through spines have predicted neck resistances of 4 – 50MΩ (fluorescein dextran) or 56MΩ (Alexa Fluor 488), (Svoboda et al., 1997; Tønnesen et al., 2014). Other studies suggested a lack of voltage filtering of dendritic spines during glutamate uncaging (Popovic et al., 2015; Acker et al., 2016) with a resistance of 30MΩ. We find here for the neck resistances a range of [100 – 300]MΩ, compared to 13 – 297MΩ, reported in Kwon et al. (2017). However, this large range of values may reflect the heterogeneous distribution of neck radii and in particular the smallest constriction along the neck. The decay of the EPSPs from the spine head to the parent dendrites can be explained by the law of electro-diffusion in the spine geometry. We have shown here that the electrical compartmentalization is mostly due to the resistance of the neck.

Interestingly, we also found here that the resistance of a dendritic spine is inversely proportional to the radius of the neck r₀, and not by the square $r_0^2$, as classically described for electrical devices (Figure S6) (Svoboda et al., 1997). This result shows that the neck size has a key effect in modulating the spine electrical resistance. Another prediction of the present theory is that a synaptic current injected in a spine head should be of the order of 100pA (as suggested in Figure 2E). The shortest diameter of a spine neck along its length is certainly a key factor that could drastically affect its resistance. Indeed, the critical geometrical parameter is the minimal shortest constriction along the neck (Holcman and Schuss, 2013), which could further be influenced by the crowding due to the internal endoplasmic reticulum (Holcman and Yuste, 2015).

The Geometry of Dendritic Spines Modulate the Voltage Changes Independently of the Input Current

Dendritic spines are involved in modulating two- and three-dimensional receptor trafficking (Huganir and Nicoll, 2013; Elias and Nicoll, 2007; Kessels and Malinow, 2009), molecular post-synaptic density composition, calcium diffusion (Yuste, 2010; Korkotian et al., 2004), synaptic transmission, and plasticity. We have shown here using the electro-diffusion framework that the voltage in dendritic spines can also be controlled by changing the neck length geometry. This modulation obtained by changing the geometry is complementary to the possible changes in the number of receptors, resulting in a long-term modification of the synaptic current, reflecting synaptic plasticity.

Changing the spine neck length can thus regulate the local dendritic voltage that contributes to the genesis of an action potential. We further confirm previous experimental findings in brain slices (Araya et al., 2006, 2014), showing that the synaptic voltage amplitude is inversely correlated with the neck length, but we found here a much stronger effect compared to previously evaluated (Popovic et al., 2015). However, in agreement with Popovic et al. (2015), we do not need to use any additional active channels in the electro-diffusion model to account for the voltage in the spine, suggesting that they might not play a predominant role.

To conclude, voltage changes in dendrites can now be detected at the nanometer scale and the electro-diffusion theory allows interpreting these data and predicts a nonlinear current-voltage relation imposed by the specific geometry of dendritic spines. While the spine geometry controls voltage, the synaptic current is set by the number of receptors (Huganir and Nicoll, 2013; Elias and Nicoll, 2007; Kessels and Malinow, 2009). These two mechanisms are supposed to be independent and they are both involved in controlling the synaptic response. It would certainly be interesting to study how changes in one affect the other.

Finally, spine twitching (hypothesized in Crick, 1982 and demonstrated experimentally in Korkotian and Segal, 2001a, 2001b) may impact the electrical property of spines. Indeed, the consequence of the spine head constriction might be negligible for the voltage inside the head but could influence the current inside the neck and thus reduces the effective resistance.

STAR ★ METHODS

Detailed methods are provided in the online version of this paper and include the following:

KEY RESOURCES TABLE

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Deposited Data
Fluorescence data	Kwon et al., 2017	N/A
Software and Algorithms
MATLAB 2015	MathWorks	https://fr.mathworks.com/; RRID: SCR_001622
COMSOL Multiphysics	COMSOL	https://www.comsol.com/; RRID: SCR_014767
Deconvolution algorithm	This paper	N/A

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, David Holcman (david.holcman@ens.fr).

METHOD DETAILS

Arclight signal

We briefly described here the experimental data we have used for our electro-diffusion theory and time deconvolution. There are fully described in (Kwon et al., 2017). The protein-based voltage indicator ArcLight is injected in primary cultured hippocampal neurons. ArcLight expressing dissociated hippocampal culture neurons in DIV 12–16 were recorded in artificial cerebrospinal fluid (ACSF) containing ions of various concentration. Two-photon glutamate uncaging was done with a custom-made two-photon laser scanning microscope. In glutamate uncaging, the location of stimulation was selected with 1–2 μm distance from dendritic spines, not closer than 1μm. The whole-cell patch clamp and the glutamate uncaging were performing while doing the wide-field one photon imaging of ArcLight fluorescence. Finally, we used the voltage deconvolved from the fluorescence signal, based on a two-state model of voltage dependent ArcLight fluorescence described in (Kwon et al., 2017).

Distribution of the arclight genetically encoded voltage indicator

We used here the genetically encoded voltage indicators (GEVIs) (Brinks et al., 2015; Gong et al., 2015; Han et al., 2013; Jin et al., 2012; St-Pierre et al., 2014), which can be expressed in neuronal membrane through plasmid transfection. This dye is used for an optical measurements of the membrane potential. ArcLight was expressed in cultured mouse hippocampal neurons and the fluorescence was imaged with an upright fluorescence microscope and a fast sCMOS camera. To monitor somatic electrophysiology, imaged neurons also were patched in whole-cell, current clamp mode. In neurons expressing ArcLight, fluorescent signals were clearly visualized in dendritic spines as well as soma.

To test how the ArcLight fluorescence responsed to bAPs generated by somatic current injection, the eletrophysiological signals were recorded from areas of interest (ROI) in somata, proximal dendrites and spines. To quantify optical signals, we measured the relative change in fluorescence intensity −ΔF/F, a quantity directly proportional to membrane potential (Peterka et al., 2011).

Intracellular ArcLight proteins located in ER and Golgi may contaminate baseline fluorescence (F) because they are fluorescent, but insensitive to membrane potential, as they are too far from the Debye length of the membrane’s electric field. Although ArcLight is in a dark state at the lower pH of intracellular organelles (Han et al., 2014), its contribution to background could be critical to determine −ΔF/F, if averaged together with a membrane responding ArcLight. To evaluate this possibility, it was calculated (Kwon et al., 2017) the activity probability of each pixel in response to voltage by using a constrained non-negative matrix factorization (CNMF) algorithm (Pnevmatikakis et al., 2016) and compared the resulted weight matrix image to the base fluorescence image. Through this comparison, we identified regions of non-responding intracellular ArcLight in the soma, which has strong base fluorescence yet low activity weight, while there were no such regions in dendrites and spines. This result implies that the trafficking mechanism of ArcLight proteins is by ER translation at inactive sites of soma, and then targeting to adjacent somatic cell membrane and by diffusion to the rest of the cell along the cell membrane. In summary, the Arclight dye is inserted in the membrane where the voltage sensor is located in the cytoplasm and thus it reports internal changes of the membrane, that we analyze here.

We also recall that spines are potentially electrotonically (Kwon et al., 2017) far from the soma and experiments with CsCl-based internal solution to block leak K+ channels make the neuron electronically compact. The average amplitude of bAP in spines was indistinguishable from that of parent dendrites (Kwon et al., 2017). Voltage step depolarizations in voltage clamp show that the measured somatic voltage was same as the optically measured voltages of spines and dendrites. Somatic voltage before background noise subtraction were larger than voltages of spines and dendrites because of the closer proximity to the brighter somatic region. These results confirm that the voltage dyes in the spines and dendrites are reliable reporters of the voltage and thus no further recalibration is necessary to analyze the fluorescent in the spine compared to the soma.

Deconvolution Kernel

To recover the intrinsic voltage dynamics h(t) from the slow Arclight signal A_rc(t), we compare the electrophysiological patch-clamp recording in the soma with the ArcLight fluorescence extracted from the somatic region delimited in the image (Figure 1A). This comparison is at the basis of the deconvolution method of the causal fluorescent signal. Indeed, the slow Arclight reporter convolves the fast electrical voltage signal, modeled by a kernel function K(t) with the intrinsic dye dynamics, leading to a slow fluorescent response. The kernel K(t) describes the time delay of the fluorescence activation compared to the voltage dynamics. We model the kernel by the function

$$K(t)=\frac{A}{{\tau }^2}t{e}^{-\frac{t}{\tau }},$$ (Equation 3)

where the value of the parameters A and τ are obtained by comparing the Arclight response in the soma with the convolution of the electrophysiological recordings (Figure S1). Indeed, for a voltage signal h(t), the Arclight signal A_rc(t) is expressed by the convolution product

$$A_{rc}(t)={\int }_0^{t}K(t-s)h(s)ds$$ (Equation 4)

To recovered h(t) from the Arclight signal A_rc(t), we first calibrated the kernel K(t) so that the Arclight signal peaks exactly at the one monitored by the electrophysiological signal (Figure 1B) and we obtain τ = .05s. The other parameter A is a scaling that will be adjusted for each experimental data. The kernel K(t) is plotted in Figure S1B.

Noise filtering and approximation

In small dendrite and dendritic spine regions, the Arclight data contains a large noise that should be removed. For that purpose, we use a Savitzky-Golay filter (Savitzky and Golay, 1964), to increase the signal-to-noise ratio. We shall now describe how we have removed the high frequency fluctuations present in the fluorescence signal (Figure S1C). We use the Savitsky-Golay (SG) filter, which is based on local least-squares polynomial approximation. The filter reduces the fluctuations while maintaining the shape and height of the initial signal (Savitzky and Golay, 1964).

Savitsky-Golay filter

The Savitsky-Golay filter is based on decomposing the input fluorescent signal A_rc that we now denote by F into polynomials. We start with the sampling,

$$F(t)=\sum _{k=1}^{N}F(t_k)\delta (t-t_k),$$ (Equation 5)

where N is the number of points. We define the discrete time subinterval I_k = {t_k − nΔt ···, t_k · · · t_k + nΔt} of size 2n + 1 time points, separated by a time step Δt. The filter is constructed by finding an ensemble of polynomials iteratively on each time window I_k. We define the sequences F_q of functions q = 0..N, where F₀ = F. To compute the polynomial of degree p,

$$P_k(t)=\sum _{i=0}^p{a}_{k,i}{t}^i,t\in I_k$$ (Equation 6)

that approximate the function F, we start with k = 1: the coefficients a_1,i are computed by minimizing on the interval I₁

$$\underset{t\in I_1}{min}{R}_1^2(t),$$ (Equation 7)

where

$$R_1^2(t)=\sum _{s=0}^n{(F_0(t_1+s\mathrm{\Delta }t)-P_1(t_1+s\mathrm{\Delta }t))}^2.$$ (Equation 8)

The function F₁ is constructed from F, by replacing F(t₁) by P₁(t₁),

$$F_1(t)=\{P_1(t_1),F(t_2),\cdots ,F(t_N)\}.$$ (Equation 9)

In general, the k^th – iteration is obtained by minimizing on I_k,

$$\underset{t\in I_k}{min}{R}_k^2(t),$$ (Equation 10)

where

$$R_k^2(t)=\underset{t_k+s\mathrm{\Delta }t\in I_k}{min}\sum _{s=-n}^n{(F_{k-1}(t_k+s\mathrm{\Delta }t)-P_k(t_k+s\mathrm{\Delta }t))}^2.$$ (Equation 11)

The filtered function F_k at the k^th – iteration is given by

$$F_k(t)=\{P_1(t_1),\cdots ,P_k(t_k),F(t_{k+1}),\cdots ,F(t_N)\}.$$ (Equation 12)

The coefficients {a_k,i}, for i = 0..p are obtained by differentiating $R_k^2$ (Equation 10) with respect to the coefficients a_k,i,

$$\{\begin{array}{c}\frac{\partial R_k^2}{\partial a_{k,0}}=0\\ ⋮\\ \frac{\partial R_k^2}{\partial a_{k,p}}=0.\end{array}$$ (Equation 13)

The system of Equation 13 is a linear matrix equation,

$$\left[\begin{array}{c}{F}_{k-1}(t_k-n\mathrm{\Delta }t)\\ ⋮\\ F_{k-1}(t_k+n\mathrm{\Delta }t)\end{array}\right]=\mathbf{V}\left[\begin{array}{c}{a}_{k,0}\\ ⋮\\ a_{k,p}\end{array}\right],$$ (Equation 14)

where V is the (2n + 1, p + 1) matrix

$$\mathbf{V}=\left(\begin{array}{ccccc}1& t_k-n\mathrm{\Delta }t& {(t_k-n\mathrm{\Delta }t)}^2& \cdots & {(t_k-n\mathrm{\Delta }t)}^p\\ 1& t_k-(n-1)\mathrm{\Delta }t& {(t_k-(n-1)\mathrm{\Delta }t)}^2& \cdots & {(t_k-(n-1)\mathrm{\Delta }t)}^p\\ ⋮& ⋮& ⋮& \ddots & ⋮\\ 1& t_k+n\mathrm{\Delta }t& {(t_k+n\mathrm{\Delta }t)}^2& \cdots & {(t_k+n\mathrm{\Delta }t)}^p\end{array}\right).$$ (Equation 15)

This matrix is inverted numerically in MATLAB. To conclude, the filtering procedure is summarized by

$${\mathcal{S}}_G(F(t))=\sum _{k=1}^N{P}_k(t_k)\delta (t-t_k).$$ (Equation 16)

We can iterate N_SG times the SG filter,

$$f(t)={({\mathcal{S}}_G)}^{N_{SG}}(F(t)),$$ (Equation 17)

where (S_G)^N_SG = S_G∘... ∘ S_G, N_SG times.

Preliminary treatment before using the Savitsky-Golay filter

We now segment the fluorescence signal: the first time interval starts at t_unc = 0 which is the initiation of the voltage response until the maximal response at time t_peak (see Figure S1C). Because the physical modeling of the dye kinetics (Kwon et al., 2017) predict a single exponential decay, we shall treat, after the time t_peak, any fluctuations as noise and we will apply the iteratively the SG filter (17). In summary, we divide the fluorescent response F(t) into three subregions Figure S1C:

1. before the time of glutamate uncaging t_unc,

2. from the time t_unc to the time-to-peak t_peak,

3. after the time-to-peak t_peak.

In region 1 (before t_unc), we use the following parameters: polynomial degree p = 2, the size of the window |I_k | = 40 points and the number of iteration of the filter N_SG = 1 to 3 (depending on the signal). This filtering reduces the noise amplitude in this first region by 80%. The filtered signal is f₁. In regions 2 and 3, to preserve the signal peak amplitude, we use a hight degree polynomial and the parameters p≥25, |I_k| = 100, and N_SG = 6 ± 2 to remove small fluctuations (Figure S1C). However, we note that the second bump of smaller amplitude around t = 0.65s in Figure S1C is generated by the random fluctuations of the fluorescence signal. Nevertheless, these fluctuations do not impact our analysis because we use for our computations the time interval: [0, 0.4]s. In region 3, we remove large fluctuations using parameters p≥5, |I_k | = 80, and N_SG = 5. The filtered signals in regions 2 and 3 are f₂ and f₃ respectively.

To glue continuously the results on each region, we use the sigmoid function,

$$\sigma (t,t_{\mathit{cut}})=\frac{1+tanh(\zeta (t-t_{\mathit{cut}}))}{2},$$ (Equation 18)

where ζ = 150s⁻¹ and t_cut is a parameter. Finally, from the input A_rc(t), we obtain the filtered signal

$$f(t)=\sigma (t,t_{\mathit{unc}})(f_2(t)+f_3(t)-f_1(t))+\sigma (t,t_{\mathit{peak}})(f_3(t)-f_1(t)-f_2(t))+2f_1(t)+f_2(t),$$ (Equation 19)

shown in Figure S1C.

Analytical approximation of the filtered signal and time deconvolution

We now described in detail the analytical approximation of the filtered signal f (previous section). The goal of this approximation is to remove any fluctuations that could be amplified in the deconvolution procedure. First, we project the filtered signal f on the two functions

$$f_{\alpha ,{\beta }_1,{\beta }_2,{\gamma }_1,{\gamma }_2}(t)=t^{\alpha }({\beta }_{1}exp(-{\gamma }_{1}t)+{\beta }_2\text{exp}(-{\gamma }_{2}t))$$ (Equation 20)

where the parameters α, β₁, β₂, γ₁, γ₂ are obtained by the MATLAB optimization procedure polyfit (Figure S1D). This step eliminates any small fluctuations that could have been amplified in the deconvolution step (Figure S1E). Another advantage of having an analytical representation is to obtain an explicit Laplace’s transformation used in the deconvolution. Indeed,

$${\widehat{f}}_{\alpha ,{\beta }_1,{\beta }_2,{\gamma }_1,{\gamma }_2}(s)=\mathrm{\Gamma }(\alpha +1)\left(\frac{{\beta }_1}{{(s+{\gamma }_1)}^{\alpha +1}}+\frac{{\beta }_2}{{(s+{\gamma }_2)}^{\alpha +1}}\right),$$ (Equation 21)

where Γ(·) is the Gamma function (Abramowitz and Stegun, 1966, Chapter 6). We now use the exact form of the kernel to obtain an explicit formula for the deconvolution. We recall that the convolution kernel is given by

$$K(t)=\frac{A}{{\tau }^2}texp\left(-\frac{t}{\tau }\right)$$ (Equation 22)

and its Laplace’s transform is

$$\widehat{K}(s)=\frac{A}{{(s\tau +1)}^2}.$$ (Equation 23)

The convolution product

$$f_{\alpha ,{\beta }_1,{\beta }_2,{\gamma }_1,{\gamma }_2}(t)=(K\ast h)(t)$$ (Equation 24)

can be written in the Laplace’s variable s

$${\widehat{f}}_{\alpha ,{\beta }_1,{\beta }_2,{\gamma }_1,{\gamma }_2}(s)=\widehat{K}(s)\widehat{h}(s).$$ (Equation 25)

Thus using expression 23 and 21, we obtain

$$\widehat{h}(s)=\frac{{\widehat{f}}_{\alpha ,{\beta }_1,{\beta }_2,{\gamma }_1,{\gamma }_2}(s)}{\widehat{K}(s)}=\frac{\mathrm{\Gamma }(\alpha +1){(s\tau +1)}^2}{A}\left(\frac{{\beta }_1}{{(s+{\gamma }_1)}^{\alpha +1}}+\frac{{\beta }_2}{{(s+{\gamma }_2)}^{\alpha +1}}\right).$$ (Equation 26)

We can now compute h using the analytical result for the inverse Laplace of function

$$M(s)=\frac{C{(s\tau +1)}^2}{{(s+\gamma )}^{\alpha +1}}$$ (Equation 27)

with α≥2 and 0≤γ which is given by

$$m(t)=\frac{C{e}^{-\gamma t}{t}^{\alpha -1}}{\mathrm{\Gamma }(\alpha +1)}(t(1-2\tau \gamma )+2\tau \alpha )+\frac{C{\tau }^2{e}^{-\gamma t}{t}^{\alpha -2}}{\mathrm{\Gamma }(\alpha +1)}\left({(t\gamma )}^2+{\alpha }^2-\alpha -2\gamma \alpha t\right).$$ (Equation 28)

Finally, we obtain the expression for the deconvolved voltage signal

$$h(t)=\frac{{\beta }_1{e}^{-{\gamma }_{1}t}}{A}\left(t^{\alpha -1}(t(1-2\tau {\gamma }_1)+2\tau \alpha )+{\tau }^2{t}^{\alpha -2}\left({(t{\gamma }_1)}^2+{\alpha }^2-\alpha -2{\gamma }_1\alpha t\right)\right)+\frac{{\beta }_2{e}^{-{\gamma }_{2}t}}{A}\left(t^{\alpha -1}(t(1-2\tau {\gamma }_2)+2\tau \alpha )+{\tau }^2{t}^{\alpha -2}\left({(t{\gamma }_2)}^2+{\alpha }^2-\alpha -2{\gamma }_2\alpha t\right)\right).$$ (Equation 29)

To conclude, we obtain here the expression for the deconvolution of (29) from the analytical approximation of the Arclight fluorescent signal A_rc, described in Figure S1E. Note that the value of the parameter A is calibrated for each dataset, such that the maximum amplitude between the Arclight response and the deconvolved voltage remains identical.

Deconvolution method applied on several peaks

The deconvolution procedure described in the above section can be extended to signals with several peaks. To illustrate the result of the deconvolution method, we use an input made of two consecutive spikes (Figure S2A), generated for example from a post-synaptic voltage response (Tsodyks and Markram, 1997). The two spikes are shown in Figure S2B (dashed black). We now summarize the steps of this deconvolution procedure:

1. We first simulate the fluorescent response by convolution of the two spikes with the kernel (22) K(t) = A/τ² te^−t/τ where τ = 18ms.

2. To account for possible fluorescence fluctuations, we added a colored noise ζ(t) that represents fluctuations of the fluorescence signal. The model for the colored noise is an Ornstein-Uhlenbeck process (Schuss, 2009, Chap.1)

   $$d\zeta (t)=\mu \zeta (t)dt+\sigma dW(t),$$ (Equation 30)

   where W(t) is a Wiener process and μ = 0.045 and σ = 0.025. The resulting fluorescence signal is shown Figure S2B (blue). We will then consider this signal as the input of the deconvolution.

3. The deconvolution starts with the fluorescence A_rc(t) shown Figure S2C (same as in S2B). Following the deconvolution procedure described above for a single peak, we approximate the input A_rc(t) (Figure S2D (dashed green)), using a sum of exponentials

   $$A_{rc}(t)=\sum _{j=0}^n{\beta }_j{(t-t_j)}^{{\alpha }_j}{e}^{-{\gamma }_j(t-t_j)}\mathrm{H}(t-t_j),$$ (Equation 31)
   where the spikes are initiated at time t_j (see Figure S2B, red dashed lines), β_j, α_j > 2 and γ_j are positive constants, n is the number of spikes and H(t − t_j) is the Heaviside function defined by

   $$\mathrm{H}(t-t_j)=\{\begin{array}{ll}1,\hfill & \text{if}t\ge t_j\hfill \\ 0,\hfill & \text{if}t\ge t_j.\hfill \end{array}$$ (Equation 32)

   All parameters are obtained by a fitting procedure.

4. To recover the voltage V(t) from the fluorescence A_rc(t), we invert the convolution equation, following the procedure described in the previous section

   $$A_{rc}(t)=(V\ast K)(t)$$ (Equation 33)
   We apply the Laplace transform to obtain an analytical representation of the solution

   $$\widehat{V}(s)=\frac{{\widehat{A}}_{rc}(s)}{\widehat{K}(s)}=\sum _{j=0}^n\frac{{\beta }_j\mathrm{\Gamma }({\alpha }_j+1)}{A}\frac{{(1+\tau s)}^2}{{(s+{\gamma }_j)}^{{\alpha }_j+1}}{e}^{-s{t}_j}.$$ (Equation 34)
5. The voltage V(t) is then recovered computing the inverse Laplace transform of expression (34) and we get

   $$V(t)=\sum _0^n\frac{{\beta }_j}{A}{e}^{-{\gamma }_j(t-t_j)}\mathrm{H}(t-t_j)P_{\tau ,{\alpha }_j,{\gamma }_j}(t-t_j),$$ (Equation 35)
   where

   $$P_{\tau ,\alpha ,\gamma }(t)=t^{\alpha }{(\tau \gamma -1)}^2-2\alpha \tau (\gamma \tau -1)t^{\alpha -1}+\alpha {\tau }^2(\alpha -1)t^{\alpha -2}.$$ (Equation 36)

The deconvolved voltage is shown Figure S2E. Note that the fluctuations disappear completely because the fitting procedure (31) removes them completely. The result of the deconvolution is compared to the initial voltage response (dashed black) in Figure S2F. The deconvolution of the voltage V(t) in step 4 relies on the apriori knowledge of the time of spike initiation t_j. These values could be identified when the spikes are sufficiently separated: when the time interval between two consecutive peaks Δt_i = t_{i + 1} − t_i is large enough, the times t_j can be recovered directly from fluorescence measurements: as shown in Figures S2G–S2I for Δt₀ = 75, 100 and 150ms respectively, the two peaks (red star) are clearly distinguishable and the time t₁ can be identified. However, when Δt₀ = 50ms (Figure S2C), the two peaks overlap such that the time t₁ cannot be read from the fluorescence time series but could be identified in the electrophysiology time series.

We conclude that the present deconvolution procedure can be applied to several spikes or EPSP, as long as the time between spikes is not less than 50ms. When the time between the events is less than 50ms, the information of their precise position could be retrieved from direct electrophysiological recordings, in that case, the deconvolution procedure still recover the fast time evolution.

Optimization procedure to extract the capacitance C and conductance G of a dendritic spine from the voltage drop between the head and the base of a spine

We describe here an optimization procedure for extracting the capacitance C and conductance G from the measured voltage time series. The procedure consists in fitting a very small portion of the voltage time response curve and to predict from this short time interval, the entire time response. Furthermore, this procedure permits to compute the current I(t) injected in the spine neck, based on Equation 1. We start with the one-dimensional electro-diffusion equations to model the current and voltage in the spine neck. These equations consist of the classical Poisson equation for the voltage and the ionic concentrations coupled to the Fokker-Planck equations for the concentrations and the voltage.

$$\begin{gathered} \frac{{\partial }^{2}V}{\partial x^2}(x,t)=-\frac{F}{\epsilon {\epsilon }_0}(c_p(x,t)-c_m(x,t)) \\ \frac{\partial c_p}{\partial t}(x,t)=D_p\frac{\partial }{\partial x}\left(\frac{\partial c_p}{\partial x}(x,t)+\frac{e}{k_{B}T}{c}_p(x,t)\frac{\partial V}{\partial x}(x,t)\right) \\ \frac{\partial c_m}{\partial t}(x,t)=D_m\frac{\partial }{\partial x}\left(\frac{\partial c_m}{\partial x}(x,t)-\frac{e}{k_{B}T}{c}_m(x,t)\frac{\partial V}{\partial x}(x,t)\right), \end{gathered}$$ (Equation 37)

where D_p, D_m are diffusion coefficients, e the electronic charge, the valencies for each specie is z = ± 1 and k_BT is the thermal energy. Equation 37 is used to compute the voltage drop when a current I(t) is injected at the tip of the spine neck. During the simulations, the ionic concentrations in the dendrite (ionic reservoir) are the boundary conditions fixed at the values C_p and C_m (see Table 2). We recall that the electrical potential is defined to an additive constant. The initial and boundary conditions are

$$V(x,0)=0$$ (Equation 38)

$$c_p(x,0)=C_p\text{and}{c}_m(x,0)=C_m.$$

$$\begin{gathered} {\frac{\partial V}{\partial x}(x,t)|}_{x=0}=0 \\ {\frac{\partial c_m}{\partial x}(x,t)|}_{x=0}=0 \end{gathered}$$ (Equation 39)

$$\frac{\partial c_p}{\partial x}(x,t)+\frac{e}{k_{B}T}{c}_p(x,t){\frac{\partial V}{\partial x}(x,t)|}_{x=0}=\frac{I(t)}{D_{p}F\pi r_i^2},$$

$$V(L,t)=0,c_p(L,t)=C_p\text{and}{c}_m(L,t)=C_m,$$ (Equation 40)

where r_i is the radius of the circular opening where the synaptic current is injected in our simulations (see Figure 3A). In summary, Equations 37, 39, and 40 describe the ionic response of an input current I(t) inside a thin cylinder reduced to a one dimensional segment. We simulate these equations using Comsol to determine the voltage drop (Figure 2).

To determine the unknown parameters (C, G), we use an iterative algorithm, where we solve numerically the boundary value problem Equations 37, 38, and 39, from which we obtain a ionic current I_C,G(t) (Equation 1) injected at the tip of the neck and the voltage V_C,G(x, t) in the neck at position x and at time t. Because V_C,G(L, t) = 0, the voltage V_C,G(0, t) represents the difference of potentials between the head and the dendrite. We start the iteration algorithm with a value for the parameters C₀, G₀: C₀ = 0.1pF and G₀ = 1nS (Figure S4A). Following each iteration, we compare the computed voltage V_C,G(0, t) (from Equation 37) with the measured potential difference V_head(t) − V_dend(t) extracted on a short time interval [t_i, t_f] (usually [0.2 − 0.4]ms). We chose this small time window because it allows us differentiating clearly the response from the background noise during glutamate uncaging (Figures S4B–S4D).

The value for the parameters C, G are the minimizers of the error functional

$$\underset{\{C,G\in S\}}{min}{\int }_{t_i}^{t_f}{\mid V_{C,G}(0,t)-(V_{\mathit{head}}(t)-V_{\mathit{dend}}(t))\mid }^{2}dt,$$ (Equation 41)

where the ensemble S of parameters is described below. We approximated the difference by a linear function V_head(t) − V_dend(t)

$$\xi (t)=a(t-t_i)+b,$$ (Equation 42)

where a and b are constants fitted to data in the interval [t_i, t_f]. This approximation reduces possible fluctuations (see fig. S4B–D). Finally, we score the different couple (C,G) using the estimator

$$S_{C,G}=\sum _{\{t_k\in [t_i,t_f]\}}{(V_{C,G}(0,t_k)-\xi (t_k))}^2.$$ (Equation 43)

At the beginning of each iteration, we use possible values for (C, G) among which we retain the optimal values (C^*, G^*) that minimizes the score S_C,G. The possible values for (C, G) can be represented by a square matrix, centered around the initial value (C₀, G₀), where we have chosen C₀ = 0.1pF and G₀ = 1nS (Koch, 2004). Each couple differs from one another by an increment ΔG = 0.05 and each line and ΔC = 0.01 on each raw. In total, there are (2α + 1)² values, presented in a matrix

$$\mathrm{S}=\left(\begin{array}{ccccc}(C+\alpha \mathrm{\Delta }C,G-\alpha \mathrm{\Delta }G)& \cdots & (C+\alpha \mathrm{\Delta }C,G)& \cdots & (C+\alpha dC,G+\alpha \mathrm{\Delta }G)\\ ⋮& & ⋮& & ⋮\\ (C,G-\alpha \mathrm{\Delta }G)& \cdots & ({\mathbf{C}}_0,{\mathbf{G}}_0)& \cdots & (C,G+\alpha \mathrm{\Delta }G)\\ ⋮& & ⋮& & ⋮\\ (C-\alpha dC,G-\alpha \mathrm{\Delta }G)& \cdots & (C-\alpha \mathrm{\Delta }C,G)& \cdots & (C-\alpha dC,G+\alpha \mathrm{\Delta }G)\end{array}\right).$$ (Equation 44)

We first look for the minimum of expression 43 for all entries of the matrix. For a given precision (ε_G, ε_C), we evaluate whether or not the conditions

$$\Vert C^{\ast }-C_0\Vert <{\epsilon }_C\text{and}\Vert G^{\ast }-G_0\Vert <{\epsilon }_G,$$ (Equation 45)

are satisfied and in that case, we have chosen V_C^*,G^* (x, t) = V(x, t), otherwise we continue the iteration by replacing the initial condition with the new values:

$$(C_0,G_0)\leftarrow (C^{\ast },G^{\ast })$$ (Equation 46)

$$(\mathrm{\Delta }C,\mathrm{\Delta }G)\leftarrow \left(\frac{\mathrm{\Delta }C}{2},\frac{\mathrm{\Delta }G}{2}\right).$$ (Equation 47)

This iteration shows how the new ’S’ matrix (Equation 45) is refinement near (C^*, G^*). In practice, we always find a unique solution for the final parameter C^* and G^*.

We show in Figure S3 several examples of dendritic spines, where we applied the present algorithm to extract the current, G and C from the voltage deconvolved time series. Figure S3A shows the different region of interest ROIs. In Figure S3B, we compare the deconvolved voltage signal with the one computed from PNP. In Figure S3C, we plot the computed injected current (from voltage) inside the spine neck.

Relation between the intrinsic 1/G and the effective neck R_neck resistance

We discuss here the relation between the spine effective and intrinsic resistance. The effective neck resistance is computed from the difference of voltage 〈V(t)〉 between the entrance and the exit of the neck, when the injected current is 〈I(t)〉. By definition, averaging over time, we have

$$R_{\mathit{neck}}=\frac{\langle V(t)\rangle }{\langle I(t)\rangle }.$$ (Equation 48)

When the injected current follows the model equation

$$I(t)=G{V}_1(t)+C\frac{d{V}_1(t)}{dt},$$ (Equation 49)

where V₁(t) is the voltage in the entrance of the neck, the intrinsic conductance and capacitance are G and C respectively. We thus obtain the following relation with 〈V(t)〉 = V₁ − V₂,

$$R_{\mathit{neck}}=\frac{1}{G+C\frac{dln{V}_1}{dt}(t)}\left(1-\frac{V_2(t)}{V_1(t)}\right),$$ (Equation 50)

where V₂ is the voltage at the end of the neck. In particular, when C = 0,

$$R_{\mathit{neck}}=\frac{1}{G}\left(1-\frac{V_2(t)}{V_1(t)}\right)<\frac{1}{G}.$$ (Equation 51)

Transient current in a three dimensional spine

We generated a transient current with a timescale of 100 ms (Figures S7A and S7B) from the PNP equations in the geometry consisting of a cylindrical neck plus round head. The equations are given for positive and negative species by

$$\mathrm{\Delta }V=\frac{-F}{\epsilon {\epsilon }_0}(c_p-c_m)$$ (Equation 52)

$$\frac{\partial c_p}{\partial t}=D_p\nabla \left(\nabla c_p+\frac{e}{k_{B}T}{c}_p\nabla V\right)$$ (Equation 53)

$$\frac{\partial c_m}{\partial t}=D_m\nabla \left(\nabla c_m-\frac{e}{k_{B}T}{c}_m\nabla V\right),$$ (Equation 54)

where D_p, D_m are diffusion coefficients, e the electronic charge, the valencies for each specie is z = ± 1 and k_BT is the thermal energy. Note that the electro-neutrality is not necessarily satisfied. Equations 52, 53, and 54 are used to compute the voltage drop when the injected current I_stim(t) at the tip of the spine is given by

$$I_{\mathit{stim}}(t)=\frac{I_{max}}{\tau }texp(-t/\tau +1),$$ (Equation 55)

where τ = 100ms is the decay time constant and I_max is the maximal current. During the simulations, the ionic concentrations are computed from the boundary conditions:

$$\begin{gathered} \frac{\partial V}{\partial n}=0\text{on}\partial {\mathrm{\Omega }}_r\cup \partial {\mathrm{\Omega }}_i \\ \frac{\partial c_p}{\partial n}=\frac{\partial c_p}{\partial n}=0\text{on}\partial {\mathrm{\Omega }}_r \\ \frac{\partial c_p}{\partial n}+\frac{e}{k_{B}T}{c}_p\frac{\partial V}{\partial n}=\frac{I_{\mathit{stim}}(t)}{\pi r_i^{2}F{D}_p}\text{on}\partial {\mathrm{\Omega }}_i \\ \frac{\partial c_m}{\partial n}-\frac{e}{k_{B}T}{c}_m\frac{\partial V}{\partial n}=0\text{on}\partial {\mathrm{\Omega }}_i \\ V=0\text{on}\partial {\mathrm{\Omega }}_o \\ {c}_p=C_p\text{on}\partial {\mathrm{\Omega }}_o \\ {c}_m=C_m\text{on}\partial {\mathrm{\Omega }}_o. \end{gathered}$$ (Equation 56)

We solve Equations 52, 53, 54, 55, and 56 numerically for I_max = 150 and 300pA using Comsol. Results are shown in Figure S7, where we find a concentration gradient at time to peak between the base and the tip of the neck of Δc_p = Δc_m = 22mM (resp. 45mM) when I_max = 150pA (resp. 300pA). We conclude that a transient current leads to a gradient of concentration inside a dendritic spine, showing that the assumption of a constant ionic concentration, which is at the basis of the cable equation, is not satisfied.

Three dimensional steady-state PNP-equations in a Ball and a dendritic spine shape

We present now the steady-state PNP equations, that describe the concentration of positive c_p(x) and negative c_m(x) charge concentrations and the voltage ϕ(x) inside a three dimensional bounded domain that we use in Figure 3. The equations are given by

$$\begin{gathered} \mathrm{\Delta }\varphi (\mathit{x})=\frac{-F}{\epsilon {\epsilon }_0}(c_p(\mathit{x})-c_m(\mathit{x})) \\ 0=D_p\nabla \left(\nabla c_p(\mathit{x})+\frac{e}{k_{B}T}{c}_p\nabla \varphi (\mathit{x})\right) \\ 0=D_m\nabla \left(\nabla c_m(\mathit{x})-\frac{e}{k_{B}T}{c}_m\nabla \varphi (\mathit{x})\right). \end{gathered}$$ (Equation 57)

The boundary is decomposed into three subdomains: the current is injected into ∂Ω_i. Charges can exit in ∂Ω_o and the impermeable membrane is represented by ∂Ω_r. The boundary conditions are

$$\begin{gathered} \frac{\partial \varphi }{\partial n}(\mathit{x})=0\text{on}\partial {\mathrm{\Omega }}_r\cup \partial {\mathrm{\Omega }}_i \\ \frac{\partial c_p}{\partial n}(\mathit{x})=\frac{\partial c_p}{\partial n}(\mathit{x})=0\text{on}\partial {\mathrm{\Omega }}_r \\ \frac{\partial c_p}{\partial n}(\mathit{x})+\frac{e}{k_{B}T}{c}_p(\mathit{x})\frac{\partial \varphi }{\partial n}(\mathit{x})=\frac{I_{\mathit{stim}}}{\pi r_i^{2}F{D}_p}\text{on}\partial {\mathrm{\Omega }}_i \\ \frac{\partial c_m}{\partial n}(\mathit{x})-\frac{e}{k_{B}T}{c}_m(\mathit{x})\frac{\partial \varphi }{\partial n}(\mathit{x})=0\text{on}\partial {\mathrm{\Omega }}_i \\ \varphi (\mathit{x})=0\text{on}\partial {\mathrm{\Omega }}_o \\ {c}_p(\mathit{x})=C_p\text{on}\partial {\mathrm{\Omega }}_o \\ {c}_m(\mathit{x})=C_m\text{on}\partial {\mathrm{\Omega }}_o. \end{gathered}$$ (Equation 58)

In that model, only positive charges can enter the spine domain. We use the Comsol platform to solve numerically Equation 57, presented and discussed in Figure 3.

Computing the neck resistance for long spines

We computed the spine neck resistance R_neck = 〈V_head〉/I_stim (Figure S7D) from the simulations of the PNP Equation 57 with boundary conditions (58) with the new parameter values for the neck length L = 1μm (typical for culture hippocampal neurons) versus L = 2μm (slices). We find that the neck resistance is small for shorter spine (culture hippocampal neurons) compared to brain slices. Indeed, by doubling the neck length the neck resistance increases from 117MΩ to 203MΩ. However, the most sensitive parameter is the neck radius which remains unaccessible. Reducing the neck radius from 100 to 50nm in both cases of L = 1 (resp. L = 2μm) increases the neck resistance from 117MΩ to 339MΩ (resp. from 203MΩ to 518MΩ).

Limitation of the cable theory

To confirm the limitation of the cable theory in describing the potential change across the spine neck, we use the cable Equation 60 below for the potential V(x, t) at position x and time t along a one dimensional segment (Koch, 2004). We impose a first condition for the voltage at the entrance of the spine neck from the head V(0, t) = V_head(t), while the boundary condition at x = L assumes a zero electric field at the connection with the dendrite. We use for V_head(t) the deconvolved voltage measured in the head.

The diffusion equation for voltage is

$$\tau \frac{\partial V(x,t)}{\partial t}={\lambda }^2\frac{{\partial }^{2}V(x,t)}{\partial x^2}-V(x,t)$$ (Equation 59)

$$V(0,t)=V_1(t)$$ (Equation 60)

$${\frac{\partial V(x,t)}{\partial x}|}_{x=L}=0.$$ (Equation 61)

where the two independent parameters $\lambda =\sqrt{r_m/r_a}$ and τ = r_mc_m (Koch, 2004, Chapter 2) are related to the membrane capacitance c_m, the resistance r_m and the intracellular resistance r_a. By definition, r_m = R_m/πd and c_m = C_m·πd, where R_m is the specific membrane resistance and C_m the specific membrane capacitance and d is the diameter of the cable (Koch, 2004).

Voltage changes computed from the cable model (green dashed) when the input is the measured voltage in the head (blue) does not match the measured response in the dendrite (red). To obtain a response comparable to the output, the intracellular resistivity should be increased by a factor 3.10⁵, showing the limitation of the cable equation to account for the voltage propagation in a dendritic spine (Figure S6).

We recall that the cable theory is an approximation derived the 1D Nernst-Planck equations (Koch, 2004, p. 261) that assumes there is no concentration fluctuations along the cable: ∂c_i(x, t)/∂x = 0. However as pointed out in (Koch, 2004, p. 28), within a compartment with a small diameter (<1μm) the concentration should vary: ∂c_i(x, t)/∂x≠0. We found using numerical simulations of PNP in the neck that the longitudinal concentration is not zero. Indeed, as shown in the main text Figure 4D and in Figure S7, we have ∂c_i(x, t)/∂x≈50 mMμm⁻¹≠0.

Furthermore, the cable theory predicts a decay of the voltage characterized by a space constant

$$\lambda =\sqrt{\frac{R_{m}d}{4R_i}},$$ (Equation 62)

where d is the diameter of the cable, R_m the membrane capacitance and R_i the intracellular resistivity. It characterizes the exponential decay of the voltage along an infinite cable such that V(x) = V_inite^−|x|/λ (Koch, 2004, p. 32). Consequently, at a distance λ the initial voltage V_init is decreased of e⁻¹ (36.7%). For example, choosing R_m = 2·10⁴ Ωcm², R_i = 200 Ωcm we have λ = 1mn for a 4μm thick dendrite (Koch, 2004). A spine neck radius of 100nm or 50nm gives λ = 220μm and 160μm respectively. However, the data of the voltage transduction in the spine neck (Figure S3) shows that more than 50% of the voltage amplitude is attenuated in a neck of length L = 1μm ≪ λ. The present analysis confirms that the cable theory cannot be used to predict the electrical behavior of a dendritic spine (Qian and Sejnowski, 1989; Koch, 2004).

Modeling the spine membrane capacitance

To account for the possible effect of the membrane capacitance in our model, we modified the boundary condition in the Poisson equation

$$\frac{\partial V(\mathit{x},t)}{\partial n}=0\text{on}\partial {\mathrm{\Omega }}_r$$ (Equation 63)

to (Feynman et al., 2005, Chapter 6)

$$\frac{\partial V(\mathit{x},t)}{\partial n}={\epsilon }_r\frac{V_{\mathit{ext}}-V(\mathit{x},t)}{d}\text{on}\partial {\mathrm{\Omega }}_r.$$ (Equation 64)

where V_ext is the extracellular voltage (assumed fixed at 65mV). The constants ε_r = 5 and d = 8nm are the membrane relative permitivity and thickness respectively (Ashrafuzzaman and Tuszynski, 2012, Chapter 2) (Figure S5A).

We simulate the voltage V near the membrane and in the bulk for a steady-current I = 50pA. We compare the two voltages obtained numerically for each condition (63) and (64 s). The difference between the mean voltages was less than <1.5% (Figure S5B) and the axial (bulk) voltages by accounting or not for the capacitance, only differs from 0.015% (Figure S5C). We conclude that the neck capacitance can be neglected and the reflecting boundary condition ∂V/∂n = 0 that we imposed is a good enough approximation.

DATA AND SOFTWARE AVAILABILITY

The PNP equations were solved using the finite element method implemented in the software COMSOL Multiphysics. We used the default MUltifrontal Massively Parallel solver (MUMPS). We applied an adaptive mesh refinement to eliminate mesh dependency. Any time-derivative functions were approximated by a n^th order backward differentiation formulas, n ∈ [|1, 3 |], where the maximal time-step is dt = 5·10⁻³s. The convergence of the method was ensured by setting an absolute tolerance at 0.001.

The optimization and filtering procedures were performed using the software MATLAB 2015. The numerical codes are available on our platform http://www.bionewmetrics.org.

Highlights.

• Deconvolution of fluorescence Arclight to recover voltage in dendritic spines

• The voltage distribution in spines modulated by geometry and electro-diffusion

• A concentration gradient appears in the spine neck following a synaptic input

• Spine electrical resistance depends on the injected current, Ohm’s law not valid