Cortical travelling waves: mechanisms and computational principles

Abstract

Multichannel recording technologies have revealed travelling waves of neural activity in multiple sensory, motor and cognitive systems. These waves can be spontaneously generated by recurrent circuits or evoked by external stimuli. They travel along brain networks at multiple scales, transiently modulating spiking and excitability as they pass. Here, we review recent experimental findings that have found evidence for travelling waves at single-area (mesoscopic) and whole-brain (macroscopic) scales. We place these findings in the context of the current theoretical understanding of wave generation and propagation in recurrent networks. During the large low-frequency rhythms of sleep or the relatively desynchronized state of the awake cortex, travelling waves may serve a variety of functions, from long-term memory consolidation to processing of dynamic visual stimuli. We explore new avenues for experimental and computational understanding of the role of spatiotemporal activity patterns in the cortex.

Synchrony in the activity of neuronal populations has long been of interest in neuroscience^1,2, but its function has remained elusive. Neural oscillations are rhythmic fluctuations of spiking activity within neuronal populations. It is proposed that synchrony of neural oscillations in different neural populations might be able to shape input gain and aid information transfer between these populations^3,4 because the synchronous occurrence of action potentials in many neurons is known to increase their ability to drive spikes in shared target neurons^5,6. Indeed, experimental evidence suggests that oscillation synchrony modulates the effective connectivity of populations in the cortex^7,8, shapes plasticity between neurons⁹ and drives processing of stimulus features between visual cortex areas V1 and V4 (REF. 10).

These proposed functions have traditionally been thought to involve precise zero-lag synchrony^11,12, in which oscillations across single areas or distant regions in the cortex are aligned perfectly in time. However, with the advent of simultaneous multichannel recording technologies, we have begun to appreciate that the relative timing of neural population activity is constantly changing. Instead of precise zero-lag synchrony, a range of flexible phase offsets is possible. These flexible phase relationships can, in their simplest form, be travelling waves of various shapes (including plane, radial and spiral waves). The combination of multiple travelling waves can form complex spatiotemporal patterns.

Stimulus-driven and internally generated travelling waves occur across different brain states and sensory conditions. Brain state and synaptic activity strongly shape these waves so that they differ profoundly from sleep¹³ to wake¹⁴. In turn, these waves transiently modulate neuronal excitability^15–19 and shape responses to external input²⁰ over a wide range of spatial and temporal scales. They travel over spatial scales that range from the mesoscopic (single cortical areas and millimetres of cortex) to the macroscopic (global patterns of activity over several centimetres) and extend over temporal scales from tens to hundreds of milliseconds. Although, in initial studies, mesoscopic travelling waves were pronounced only under conditions of low visual luminance contrast^21,22 and were mostly reported in anaesthetized states^23–28, recent work has shown that stimulus-evoked mesoscopic travelling waves robustly appear in the awake visual cortex^14,29 and can influence intracortical dynamics during the viewing of natural stimuli³⁰.

In vitro and in vivo cortical travelling waves have been reviewed previously^22,31,32. In this article, we cover a series of recent studies that have led to important advances in our understanding of travelling waves and the generality of their role in cortical processing. We first summarize experimental observations of travelling waves in the cortex, focusing on advances in recording and analysis techniques that have enabled the detection of waves in single cortical regions. Next, we briefly review the broad computational and mathematical literature on travelling waves in neural networks, focusing on theoretical mechanisms for wave generation and possible experimental tests of these predictions. Finally, we discuss emerging computational roles for cortical travelling waves, from sensory processing to memory consolidation. As we describe, at the macroscopic scale, these waves allow the formation of the large-scale, distributed cell assemblies thought to underlie long-term memory^33,34. At the mesoscopic scale, multiple lines of experimental evidence suggest that evoked waves are a way for neural circuits to flexibly store and use information from the recent past. In closing, we highlight open questions for new experiments and theoretical work to further elucidate the biological mechanisms underlying cortical travelling waves and their role in neural computation.

Travelling waves in neural systems

Travelling waves were first observed at the macroscopic, whole-brain scale. More recently, new high-resolution optical and electrophysiological recording technologies have led to the observation of travelling waves at the mesoscopic scale of single regions in the cortex. Distinct axonal fibre tracts carry waves at the two scales, and there are observable differences in the resulting dynamics — most notably, spatial extent and propagation speed — that make clear distinctions between the two possible. Macroscopic waves are generally recorded using electroencephalography (EEG) or electrocorticography (ECoG), in which arrays of electrodes either outside the skull (EEG) or directly on the cortical surface (ECoG) record potentials from neural populations with high temporal (millisecond) resolution but low spatial (centimetre) resolution. These waves generally have propagation speeds from 1 to 10 metres per second, falling within the range of the axonal conduction speeds of myelinated white matter fibres in the cortex³⁵. Mesoscopic waves are generally observed in the local field potential (LFP) using multielectrode arrays (MEAs) or in optical imaging signals recorded with voltage-sensitive dyes (VSDs). These techniques record from single regions in the cortex with high temporal and spatial resolution^36,37. Stimulus-evoked mesoscopic waves can appear in the sensory cortex during the fast onset transient that follows the presentation of a stimulus; these waves are thus time-locked to the stimulus. Alternatively, they may appear during sustained responses in a manner that is not necessarily locked to stimulus onset (often called induced waves). Mesoscopic waves generally have propagation speeds from 0.1 to 0.8 metres per second, consistent with the axonal conduction speed of the unmyelinated long-range horizontal fibres within the superficial layers of the cortex³⁸.

Macroscopic travelling waves

Neuroscientists first observed oscillations in EEG through the work of clinicians in the late nineteenth and early twentieth centuries³⁹. In 1929, Hans Berger reported the 10 Hz alpha oscillation in EEG recordings of human occipital lobes⁴⁰. Shortly thereafter, there was much interest in understanding the spatial organization of alpha oscillations through multielectrode recordings, which often appeared to show a wave travelling from occipital to frontal regions⁴¹. Alpha-band travelling waves in EEG recordings under both spontaneous and stimulus-driven conditions continue to be a subject of active interest^42,43. In subsequent studies, it also has been reported that the 0.1-1.0 Hz slow oscillation that occurs during sleep is an anterior-to-posterior travelling wave⁴⁴ (FIG. 1a) and that auditory-induced 30–80 Hz gamma oscillations make a coherent anterior-to-posterior sweep across the cortex (observed using magnetic field tomography)⁴⁵. Signal distortion by cranial tissues⁴⁶ and volume conduction, however, pose substantial possible confounds for detection of travelling waves in EEG. Understanding the generation of electric and magnetic fields by neural activity remains an active pursuit for experimental and theoretical research^46,47; however, in the absence of a general physical theory^48,49, the origin and interpretation of travelling waves observed solely in EEG is problematic (see REF. 50 for an initial comparison).

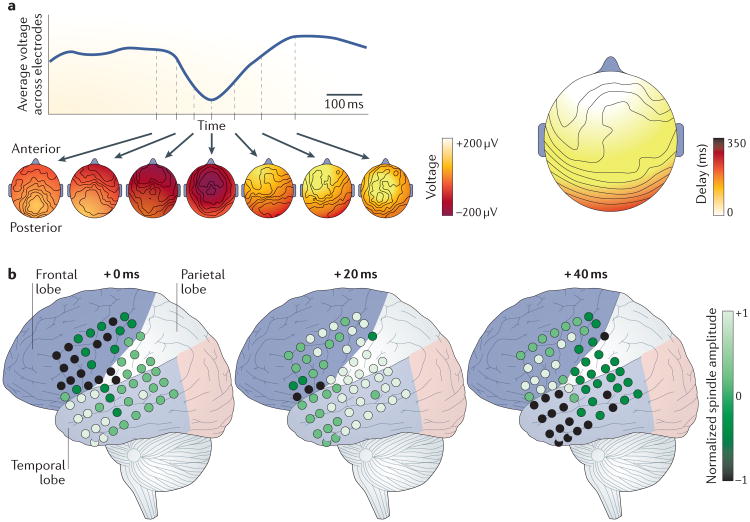
Figure 1. Macroscopic waves during human sleep.

a | The slow oscillation of deep non-rapid-eye-movement (non-REM) sleep has been reported to be a travelling wave that moves globally from anterior to posterior regions⁴⁴. The upper left panel represents the time course of one slow oscillation averaged across electroencephalogram (EEG) channels. The lower left panels illustrate the evolution of voltages across the scalp at different times during the slow wave. At the start of the slow oscillation, negative EEG potentials begin in anterior sections of the scalp, and as the oscillation progresses, these travel to posterior regions. The negative peak of the slow oscillation is delayed in posterior regions by hundreds of milliseconds, reflecting the propagation time of the travelling wave (right panel). b | Sleep ‘spindles’ are 11–15 Hz oscillations that occur during stage 2 non-REM sleep and have long been known to be important for learning and memory. These spindles systematically travel as global rotating waves from the temporal to the parietal to the frontal cortex (and are therefore called TPF waves) in intracranial electrocorticography (ECoG) recordings¹³. The panels illustrate the normalized spindle amplitude at each ECoG electrode (small circles) at successive points in the spindle cycle. From the start of an oscillation cycle (+0 ms), spindle amplitudes peak successively in the temporal (+0 ms), parietal (+20 ms) and frontal (+40 ms) lobes. The amplitudes recorded for each channel are normalized to their maximum amplitude. Part a is republished with permission of the Society of Neuroscience, from The sleep slow oscillation as a traveling wave. Massimini, M et al. J. Neurosci. 24 (31), 6872–6870 (2004); permission conveyed through Copyright Clearance Center, Inc. (REF. 44). Part b is adapted with permission from REF 13, eLife.

In recent years, intracranial ECoG recordings in clinical patients have made detailed analyses of human cortical dynamics possible. Following a technique developed by Penfield and Jasper for mapping the cortical sites involved in generating epileptic seizures⁵¹, surgeons typically implant two-dimensional ECoG electrode arrays on the surface of one cortical hemisphere, with coverage of temporal, parietal and frontal lobes supplemented by additional linear strips of electrodes on the same or the contralateral hemisphere. ECoG recordings have a high signal-to-noise ratio and spatial localization, reflecting neural activity spanning less than 1 centimetre of the cortex^52,53. Furthermore, by capturing power in the 80-150 Hz high-gamma band, which serves as an index for neuronal firing near the electrode⁵⁴, ECoG recordings can link oscillatory patterns with local population spiking activity.

Analysis of ECoG recordings has revealed travelling waves during both awake and sleep states. The spatial range of these oscillatory patterns can vary from relatively small patches of cortex to the global, whole-brain scale. In the awake state, travelling alpha waves in ECoG recordings have a dorsoventral direction of propagation that is markedly different from waves observed in EEG recordings⁵⁵. Similarly, the sleep slow oscillation⁵⁶ and the related K-complex⁵⁷ have complicated and variable patterns of propagation in ECoG recordings, in contrast to the smooth anterior-to-posterior propagation observed in EEG. Thus, at the higher spatial resolution afforded by intracranial recordings, oscillatory activity generally has different and more complicated dynamical patterns than those observed with EEG. However, ECoG recordings have shown that sleep spindles in humans exhibit robust spatiotemporal travelling waves that either radiate out from a point source or rotate across the cortex in a preferred direction, travelling from the temporal cortex to the parietal cortex, on to the frontal lobe and back again to the temporal cortex¹³ (FIG. 1b). These rotating waves represent a large proportion (50.8%) of all spindle cycles, with radial waves constituting a smaller fraction (15.6%) and the other cycles likely reflecting only local activity (33.6%)^58,59. The observed wavelengths of these waves are similar to the size of the brain, blurring out any effects of the folds of cortical sulci and gyri; however, with higher-resolution imaging techniques, a more detailed impact of the cortical folds may become apparent. The speeds at which these waves travel are concentrated between 2 and 5 metres per second, consistent with the conduction speed of short-range³⁸ and long-range^35,60 association fibres in the cortical white matter. These association fibres thus provide a possible substrate for propagation of ECoG travelling waves, suggesting that the waves have a functional role in building distributed cell assemblies in the cortex¹³.

Mesoscopic travelling waves

Advances in multichannel recording technologies now allow single-trial recordings in individual cortical areas with very high spatial (up to 20 micrometres) and temporal (up to 1 millisecond) resolution. For the first time, the responses of distributed neuronal populations in the cortex to sensory stimuli can be monitored through both optical and electrophysiological approaches. These new recordings can give important clues about the neural code and the role of topographic maps in sensory systems. Furthermore, the analysis of single trials gives new insights into sources of variability in cortical responses to repeated presentations of the same sensory stimulus.

To understand results from these recordings in single regions, an important distinction must be made between two theoretical models of the cortical sensory response: stationary bumps of neural activity and cortical travelling waves¹⁴. A stationary bump of neural activity would remain centred on the point of strongest input to the cortex, perhaps increasing in amplitude and expanding in range over time (FIG. 2). In V1, the point of strongest input is the retinotopic representation in the cortex of the stimulus in the visual field. Here, spikes carried by thalamocortical fibres enter layer 4, which then projects to layer 2/3 of V1. Thus, the spatiotemporal pattern of activation of a stationary bump is mainly driven by the input and shaped to a lesser degree by intracortical axons^61–63. In a stimulus-evoked cortical travelling wave, on the other hand, the cells at the point of strongest input would emit a peak of activity that expands progressively across the retinotopic map (FIG. 2). This pattern would indicate the presence of dominant recurrent interactions in the cortex, which are largely attributed to propagation along intracortical axons^64,65. This distinction leads to quite different hypothesized downstream effects: in a cortical area receiving input from V1, cells would receive their strongest input at any point in time either from the central point (stationary bump) or from a progressively expanding ring of activation (cortical travelling wave)¹⁴. We expand on the computational consequences of each model for the sensory response below.

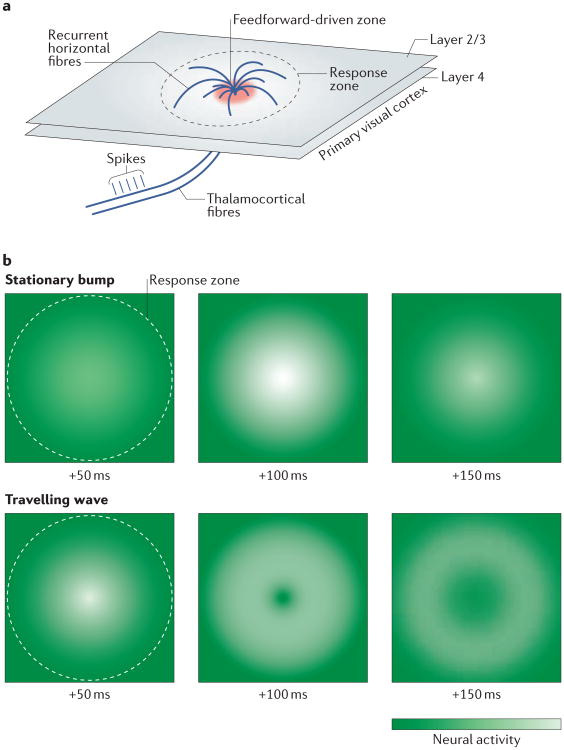
Figure 2. Two models for the stimulus-evoked response in the visual cortex.

a | Small visual stimuli evoke spikes in a set of thalamocortical fibres targeting layer 4 of the primary visual cortex, which, in turn, synapses onto a small segment of layer 2/3 (the feedforward-driven zone). Recurrent horizontal fibres synapse widely across layer 2/3, spanning up to 8 millimetres of distance in the cortex (response zone)¹⁰⁷. b | Within the response zone, the activity pattern is proposed to take two main forms: a stationary bump of activity, suggesting a relatively input-driven system, or a travelling wave, suggesting a circuit dominated by recurrent activity¹⁴. Schematic diagrams indicate these hypothesized activity patterns and are based on results reported in REF. 14.

Whether the stimulus-evoked response in the awake sensory cortex is a stationary bump or a travelling wave is debated. Initial evidence that visual stimuli evoke travelling waves came from optical imaging during sustained responses in semi-isolated turtle cortex⁶⁶. This was followed by intracellular recordings in V1 of anaesthetized cats, in which it was shown that the visually evoked response became progressively more delayed with increasing distance from the receptive field of the neuron⁶⁷ (FIG. 3a), with the relationship between the distance and delay being consistent with the axonal conduction speeds of the unmyelinated horizontal fibres in layer 2/3 (0.1–0.8 metres per second³⁸). By contrast, the initial VSD studies in V1 of awake behaving monkeys found a stationary bump of activation in the evoked response⁶⁸ (FIG. 3b). These results, however, required averaging over many trials to increase the signal-to-noise ratio, which may have masked travelling waves. The first VSD studies able to image cortical dynamics at the single-trial level were in V1 of anaesthetized rodents^69,70. These studies found an active travelling wave propagating out from the stimulus location in the cortex. A later study used a spike- triggered averaging (STA) approach in multielectrode array recordings to reveal spontaneous and stimulus-evoked waves in V1 of anaesthetized cats and macaques²¹. The validity of these findings, however, was later called into question because STA is open to artefacts caused by low-pass filtering⁷¹ (see REF 72 for a rebuttal) or by not fully accounting for the point process statistics of spike trains⁷³. Furthermore, in another VSD study performed in V1 of awake monkeys, again at the level of trial- averaged data, no delay across cortical space (2.5 millimetres) in the initial rise of the neural response was found, suggesting that the delays of the response peak are explained by intracortical gain- control mechanisms rather than by horizontal-fibre travelling waves⁷⁴.

Figure 3. Mesoscopic waves in the visual cortex.

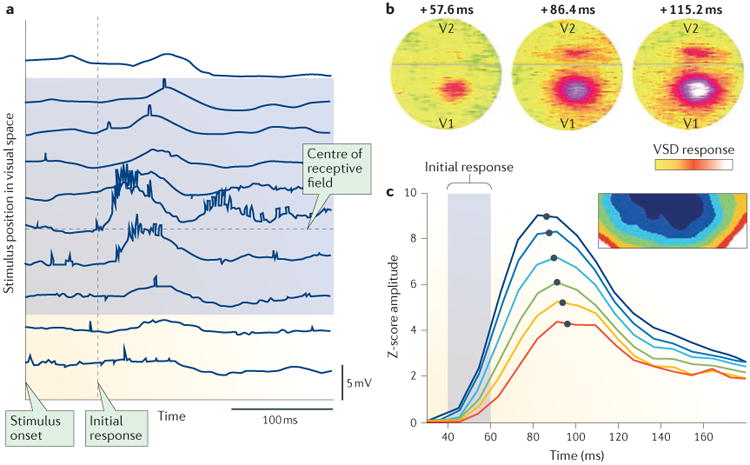
a | These intracellular recordings of a complex cell in the cat visual cortex area V1 during anaesthesia show responses to an optimally oriented bar stimulus⁶⁷. The middle row is the response to stimulation in the centre of the receptive field of the cell. Response deflections become weaker and more delayed as the stimulus is presented farther away in visual space (top and bottom traces). This delay suggests that individual small visual stimuli evoke waves travelling across the retinotopic map of visual space. b | The first voltage-sensitive dye (VSD) studies in area V1 of an awake monkey exhibited only stationary bump responses to small visual stimuli, questioning the existence of travelling waves in V1 during waking states⁶⁸. These plots show time from stimulus onset (above) and the VSD response in V1 and V2 (coloured in intensity from yellow to red to white). c | Single-trial analysis of VSD data in V1 of an awake monkey demonstrated that the stimulus onset transient (which occurs 40-140 ms after the start of stimulus presentation) is indeed a travelling wave, which is masked in trial-averaged data. Plotted are the average amplitudes of the VSD response in regions of interest located at increasing distances from the point of afferent input (indicated by colours from blue to red, as shown in inset box). The dark blue region contains the afferent input zone. Evoked amplitudes show increasing temporal offset in both the initial (40-60 ms) and peak (80-100 ms) response. Grey dots represent interpolated maxima illustrating the temporal offset in the peak response. Part a is adapted with permission from REF. 67, AAAS. Part b is adapted with permission from Slovin, H. et al. Long-term voltage-sensitive dye imaging reveals cortical dynamics in behaving monkeys. J. Neurophysiol. 88, 3421–3438 (2002) (REF 68). Part c is adapted from REF 14, Macmillan Publishers Limited.

New methods for the analysis of single-trial recordings have clarified this issue. A general phase-based algorithm was introduced that can detect arbitrarily shaped waves in high-noise multichannel data¹⁴. Applied to single- trial VSD recordings in awake behaving monkeys, this approach revealed that a small, high-contrast visual stimulus consistently evoked a single-cycle wave travelling across several millimetres of V1 (FIG. 3c), which was previously obscured by trial averaging. The isolated waves occurred during the fast stimulus onset response and exhibited consistent delays in initial rise times across the cortex (FIG. 3c), providing evidence against the gain-control mechanism previously suggested⁷⁴. Furthermore, the waves were shown to possess an intrinsic reliability: although wave onset was variable across trials, their cross-trial variability did not increase as they travelled across the cortex, indicating a propagation substrate with a highly consistent speed. These shifts in wave onset time relative to stimulus onset strongly contribute to attenuation of the waves in trial-averaged data. Together with the measured propagation speeds and shift in initial rises, this result implicates the horizontal fibres in layer 2/3 as the physical substrate for a wave of neural activity evoked by sensory input.

Importantly, these evoked waves in awake monkeys appear not to cross anatomical boundaries in the cortex (that is, between V1 and V2)¹⁴, unlike those observed in anaesthetized rodents⁶⁹. In V1 and V2, the waves evoked in rapid succession by feedforward input are aligned so that they travel simultaneously across their respective retinotopic maps. This alignment is important because it could allow integration of retinotopic information in parallel across multiple regions of the visual system. Whether this stimulus-evoked alignment of travelling waves indeed occurs in multiple visual areas, in addition to whether spontaneous waves exhibit such alignment, remains an open question. However, consistent phase relationships have been observed both within individual visual areas (for example, in LFP recorded from V4 (REF 75) and across different visual areas (in magnetoencephalography⁴³), indicating that such spatiotemporal patterning may be apparent in visual cortical dynamics during the awake state⁷⁶.

Previous work noted that the phase of gamma oscillations changed across retinotopic domains in V1 of awake monkeys⁷⁷ and rabbits⁷⁸ as well as across orientation domains in V1 of awake monkeys⁷⁹. This suggests that these multicycle high-frequency oscillations ride on top of a broader stimulus-evoked travelling wave and form sustained complex patterns that reflect features of the input. Furthermore, using a measure of directed information transfer across recording sites, a recent study found that shifts of the phase of gamma oscillations between pairs of electrodes in V1 of anaesthetized primates during stimulation with Hollywood movies are consistent with the presence of complex travelling waves propagating in the direction of maximal information transfer³⁰. Importantly, these interactions were consistent with propagation along the horizontal-fibre network and not with input changes, illustrating that the effect of the horizontal-fibre networks in the visual cortex (and their intrinsic time delays) does not disappear in more naturalistic high-input situations. Taken together, these results indicate that stimulus-evoked travelling waves are a general and important feature of dynamics in the visual system that can affect neuronal processing. The functional importance of these waves, however, remains unclear.

The importance of finding travelling waves evoked by high-contrast visual stimuli lies in what it implies about cortical dynamics during normal sensory processing. It has previously been noted that stimulus-evoked travelling waves, which modulate the excitability of neurons as they travel across a topographic sensory map, appear inconsistent with the precise retinotopy and orientation topography described by Hubel and Wiesel at the columnar level^22,80,81. If the visual system works to localize activity through retinotopic projections at each stage of processing, then why would it distribute activity across the map through travelling waves? Although initial results suggested that stimulus-evoked travelling waves were pronounced only at low luminance contrast²¹, thus minimizing consideration of their impact during normal visual processing²², the results reviewed above demonstrate that they are indeed an important feature of cortical dynamics that must be taken into account in describing the stimulus-evoked visual response at normal levels of contrast. These results indicate that activity evoked at one point in the visual cortex can, through the generation of a travelling wave, impact neurons quite far across the retinotopic map, and this affects how subsequent inputs are processed across visual space⁸². Rather than being a detriment to precise neuronal selectivity, however, these dynamic activity patterns may in fact be mediating previously unappreciated computations at the single-trial level. Theoreticians have postulated that a travelling wave with total phase offset between 0 and 2π could mark locations in the cortex with a unique phase that is useful for visual coding⁸³; however, it remains unclear how this can be used for neural computations with relevant ensembles of visual stimuli. We consider emerging ideas for computation with travelling waves below. Before this, however, we briefly consider the network-level mechanisms responsible for generating travelling waves at the mesoscopic and macroscopic scales.

Network mechanisms for travelling waves

As a paradigmatic example of a neural dynamic requiring the participation of millions of neurons and the recurrent connectivity of the cortex, the question of how travelling waves are generated and propagate has long attracted the attention of mathematicians and physicists. Computational and theoretical neuroscientists study cortical dynamics with a range of techniques, spanning from the mathematical continuum approximation of Wilson and Cowan⁸⁴ to the simulation of millions of neurons and billions of synapses on multicore and parallel computers⁸⁵. With recent advances in neural recording and optogenetic stimulation technologies, experimental tests of predictions generated by these approaches are now being realized. The results of mathematical and computational studies on travelling waves in neural networks have been reviewed previously^32,83,86,87; here, we focus briefly on results that concern the waves and regime most pertinent to the studies reviewed above — that is, the sparse, weakly modulating waves that occur during the asynchronous and irregular state of neocortex in awake, behaving animals. We do not address the strongly modulating travelling waves that occur during pathological states, such as seizures and spreading depression; furthermore, we note that sparse travelling waves in the awake adult entail fundamentally different mechanisms than the slowly propagating waves observed during development^88,89.

Macroscopic network mechanisms

At the whole-brain scale, neural recordings capture the effects of interaction among many billions of neurons across the cortex. Here, phase relationships among oscillations in individual cortical regions constitute the travelling wave, and interactions among regions can be effectively modelled by large-scale population descriptions, such as the Wilson-Cowan equations or coupled oscillator networks. Connections are mediated by cortical white matter fibres, which can traverse just below the grey matter when connecting two nearby regions or can run in the deep, long-range white matter tracts^60,90. These connections have axonal conduction delays up to tens of milliseconds^35,60 and, as with mesoscopic waves, these distance-dependent delays can strongly influence the emergence of spatiotemporal patterns at the macroscopic level. It has been shown that distance- dependent delays lead to a rich repertoire of spatiotemporal dynamics, including radial and spiral waves, in networks of coupled oscillators⁹¹. Furthermore, in simplified networks, mathematical analysis has established that highly structured, geometric connection patterns for networks arranged on a sphere can lead to rotating waves⁹². Further work is required, however, to understand how alpha band and spindle macroscale travelling waves emerge through the dynamics and time delays of the corticothalamic system.

Mesoscopic network mechanisms

In the cortex, neurons are embedded in a sea of so-called spontaneous activity. Pyramidal cells in V1 have dense recurrent synaptic connectivity, each receiving from 6,000 to 13,000 inputs per cell⁹³. Roughly 80% of these connections come from within the same cortical area, 95% of which arise from neurons within 2 millimetres of the receiving cell⁹⁴. Long-range horizontal fibres can span several milli metres across the supragranular layers of the cortex⁹⁵. These axons thus connect neurons spanning multiple functional hypercolumns within a cortical map. During the awake state, pyramidal cells in V1 of monkeys exhibit a median spontaneous firing rate of 7 Hz (REF. 96). This indicates that neurons in V1 of primates receive tens of thousands of synaptic inputs per second, with most arriving from the mesoscopic, intracortical circuit. This synaptic noise has well-known effects on the integration properties of cortical neurons⁹⁷, allowing them to respond quickly to transient input fluctuations⁹⁸, and forms the basis for the difference in network state between anaesthetized to awake⁹⁹.

Travelling waves transiently modulate this ongoing synaptic noise as they pass. For example, there is evidence that, depending on the specific cell-type recruitment, oscillations in the hippocampus may either excite or inhibit neurons in the local circuit at various points during the cycle¹⁰⁰. Similarly, during normal cortical function in awake animals, travelling waves weakly modulate neural spiking activity in the motor cortex¹⁹. This is consistent with observations at single points in the visual cortex, where alpha and gamma oscillations weakly entrain spiking activity^101–103, increasing and decreasing spike probability over the oscillation cycle. Here, we refer to this type of wave (in which the probability of any individual neuron participating in the wave is low) as a sparse wave (FIG. 4). This stands in contrast to the travelling waves observed in in vitro models of epilepsy^104,105, where dense waves dominate the spiking activity of the local circuit as they pass. Under these in vitro conditions, networks lack a large fraction of the spontaneous synaptic input that is present in vivo and furthermore are often studied in disinhibited conditions

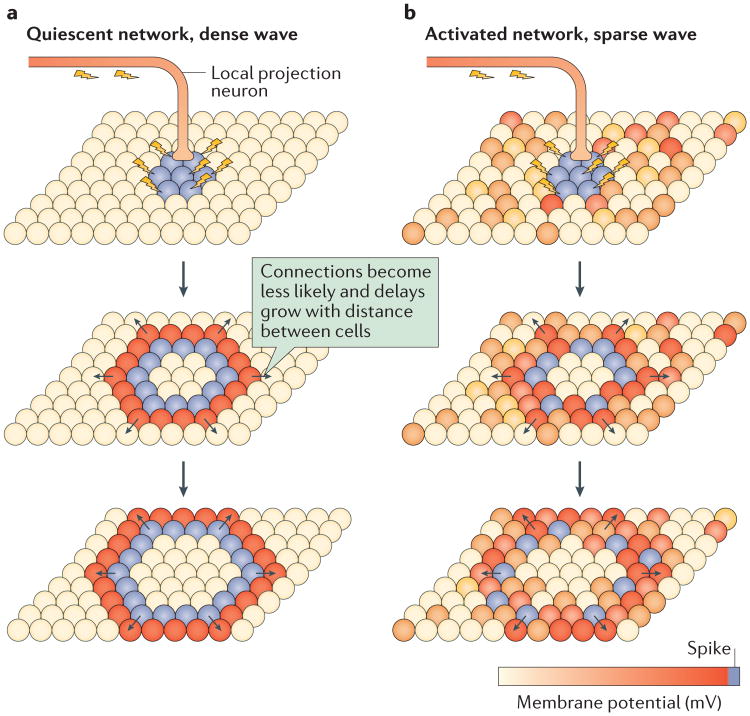
Figure 4. Two models for the generation of mesoscopic travelling waves.

Two schematic models for wave generation in topographic networks of neurons with local, random connections and linearly increasing axonal conduction delays are illustrated. Spheres represent neurons whose membrane potential is indicated by colour. a | In a cortical network with no background activity (as observed in deep anaesthesia or often in cortical slices in vitro), we hypothesize that local stimulation will elicit strong travelling waves, which recruit nearly all cells as they pass. Arrows indicate directions of wave propagation. b | In a cortical network with strong background activity (as observed in normal waking states), we hypothesize that local stimulation can elicit waves that weakly entrain neuronal spiking as they travel across the network.

When a burst of spikes arrives at a local patch of the cortex, it evokes a brief increase in spiking that can propagate out across the network^24,67,69. As outlined above, while most studies have focused on waves during the stimulus onset response, travelling waves may be induced during sustained stimulation responses and during the brief increase of spiking activity at stimulus offset in the sensory cortex of awake, behaving animals, and these waves may not be time-locked to the stimulus. Bursts during the fast onset transient arise through feedforward input; however, during spontaneous and induced waves, these bursts can result from recurrent fluctuations or feedback connections^26,106. Nevertheless, initial evidence indicates that induced waves travel over similar fibre networks as waves evoked during stimulus onset^66,77.

The key factor governing the generation and propagation of stimulus-evoked, induced and spontaneous travelling waves at the mesoscale is the axonal conduction delay of the horizontal fibres of superficial layers in the cortex^14,23,67. These fibres project over long distances across the cortical sheet^95,107, providing the substrate for travelling waves and governing their amplitude decay. Computational and mathematical studies have demonstrated the role of distance-dependent axonal conduction delays in generating stimulus-evoked waves in recurrent networks^87,108,109. Specifically, it has been shown that distance- dependent delays can destabilize synchrony in coupled oscillator networks, leading to travelling waves¹¹⁰. However, it remains unknown whether and how spontaneous and stimulus-evoked waves can be generated in large-scale spiking networks with biologically realistic synaptic noise, in which model neurons exhibit the irregular asynchronous (IA) state that is the hallmark of cortical dynamics¹¹¹. Stochastic neural field theory has studied the effect of noise on propagation of travelling waves in neural systems¹¹²; however, because the noise generated by networks in the IA state has a specific and nonstationary signature¹¹³, the dynamics of large-scale spiking networks may differ substantially from those of stochastic neural fields, and few detailed comparisons have been done.

In computational models of spiking networks, the degree to which neurons are entrained by travelling waves is a key factor in determining the dynamics and interactions of waves. In small models, in which synaptic weights are strong and correlations are increased¹¹⁴ (a rough analogue of biological networks in vitro), travelling waves are dense and strongly entrain neurons in the local circuit as they pass (FIG. 4a). Waves in such networks generally exhibit repelling interactions^115,116, in which two colliding waves will either disappear or deflect each other onto new paths. In larger networks, however, with network states matching those in the cortex and sparse (weakly entraining) waves (FIG. 4b), these interactions could be much different, with waves weakly interacting while passing through each other as they travel. These differences in wave interaction suggest vastly different general computational principles, to which we turn in the next section.

Emerging computational principles

As introduced above and noted previously²², spontaneous and stimulus-evoked travelling waves add a spatiotemporal context to the orderly response properties of the visual cortex first described by Hubel and Wiesel^80,81. In the canonical model of visual processing (and, indeed, of sensory processing in general), cortical neurons are independent feature detectors that build progressively more complex representations through successive elaboration of receptive field selectivity in each cortical region¹¹⁷. Stimulus-evoked travelling waves in the visual cortex introduce strong contextual influences into this model of cortical dynamics: for example, if two nearby sensory stimuli are presented in succession, the first may generate a travelling wave that has an effect on the response to the second, transiently modulating the receptive field properties of neurons whose receptive fields contain the second stimulus. Such contextual modulations have been discussed previously in connection with the notion of ‘non-classical’ receptive fields^118–121, which can implement spatial interactions that are well captured by the theory of association fields (REFS 122–124). Evidence that travelling waves actively influence visual processing, for example, by producing cortical correlates of low-level visual percepts such as the line-motion illusion^24,125 or the perceived speed of apparent motion stimuli^126,127, has been reported by linking cortical dynamics during anaesthetized states to human psychophysical data. An overview of observed cortical travelling waves and their potential computational roles is given in TABLE 1. A comprehensive conceptual framework for travelling waves and dominant recurrent interactions during normal awake sensory processing is, however, lacking.

Table 1. Observed cortical travelling waves and potential computational roles.

Neural system	Specific regions	Appearance in single electrode recordings	Proposed role	Refs
Visual	V1 and V2	Stimulus-evoked onset response (40–140 ms after stimulus onset)	Distributed computations with spatiotemporal patterns in sensory maps	14,21,67
	V1	Gamma oscillation (30–80 Hz)	Distributed computations with spatiotemporal patterns in sensory maps	30,77,79
Sensorimotor	V4	Saccade-evoked LFP transient	Perisaccadic suppression of visual processing or motor guidance for the following saccade	29
Motor	M1 and PMd	Beta oscillation (10–45 Hz) during movement planning	Sequencing activation in proximal-to-distal muscle representations in the motor cortex	19,131–134
Hippocampus	CA1	Theta oscillation (6–12 Hz)	Patterning pyramidal spiking from small to large place fields in each theta cycle	17,18,140
		Ripple oscillation (140–200 Hz)	Patterning spiking in either direction of the dorsoventral axis in hippocampus	146
Macroscopic	NA	Slow oscillation (0.1-1.0 Hz)	Orchestrating large-scale neural spiking in slow-wave sleep	44,56
		Spindle oscillation (11–15 Hz)	Building distributed neuronal assemblies in the cortex during memory consolidation in sleep	13

LFP, local field potential; M1, primary motor cortex; NA, not applicable; PMd, dorsal premotor cortex; V1, primary visual cortex; V2, secondary visual cortex; V4, visual area V4.

Converging evidence shows that the canonical model of visual processing is excellent for coding stationary images but has difficulty explaining processing of dynamic, nonstationary naturalistic stimuli¹²⁸. For example, standard models of cortical neurons based on this framework capture only a fraction of the response variance observed under natural sensory conditions¹²⁹. Below, we first review specific examples of functional roles for waves recently found in sensorimotor conditions and the hippocampus and then, inspired by a physical process for information storage by dynamic wave fields, introduce a general conceptual framework for cortical travelling waves in the processing of visual scenes.

Waves and sensorimotor coordination

Beta-frequency (15–30 Hz) oscillations have a strong connection to movement preparation and motor coordination¹³⁰, and their spatiotemporal properties have been a subject of much interest in recent years. In the motor cortex of monkeys, beta oscillations before movement initiation during an instructed-delay reach task are waves travelling in a consistent anatomical direction¹³¹. Similar dynamics were found in the motor cortex of humans¹³². It was later confirmed that these LFP travelling waves modulate spiking activity at the single-unit level¹⁹. In the context of the instructed-delay reach task, the travelling waves in the motor cortex have a plausible proposed functional role: they have been suggested to facilitate sequences of activation in proximal-to-distal muscle representations in preparation for reaching behaviour^133,134. While detailed future studies could illustrate the effect of recorded cortical activity on specific resulting patterns of muscle activation¹⁹, these observations provided a first link between cortical travelling waves and physiologically relevant neural outputs, suggesting that they play distinct functional roles.

In similar sensorimotor conditions in the visual system, saccades have been found to induce beta frequency travelling LFP waves in visual area V4 (REF. 29). These waves travel from foveal to peripheral regions of the V4 retinotopic map, creating a spatiotemporal pattern of post-saccadic excitability. Various functional roles are possible for this pattern, including saccadic suppression (useful in eliminating blurred visual scenes during eye movements)¹³⁵ and motor guidance in planning the following saccade. While their exact functional role remains unclear, these saccade-induced travelling waves in the visual system represent a second sensorimotor condition that may be probed by future work for a clear link between cortical travelling waves and physiological function.

Travelling waves in the hippocampus

Hippocampal population rhythms are some of the most well-studied oscillations in the brain and are of particular interest because of their important connections to learning and long-term memory¹³⁶. The 6–12 Hz theta oscillation modulates hippocampal LFP and pyramidal cell spiking during active exploration and rapid-eye-movement sleep^15,137, organizing the firing of hippocampal place cells in a crucial manner¹³⁸. Long thought to be approximately synchronous throughout the hippo campal formation¹³⁹, theta oscillations have recently been shown to be waves travelling along the dorsoventral axis of CA1 (REFS 17,18,140) (FIG. 5a). Because hippocampal place fields become progressively larger along this axis^141,142 (FIG. 5b), these travelling theta waves organize CA1 place cell spikes into a sweep from the finest to the coarsest scales of spatial selectivity^17,18 (FIG. 5c), possibly linking high-precision spatial information with broader contextual content. In addtion, the specific spatiotemporal structure of the LFP during these travelling theta waves has been shown to contain precise information about an animal's location¹⁴³

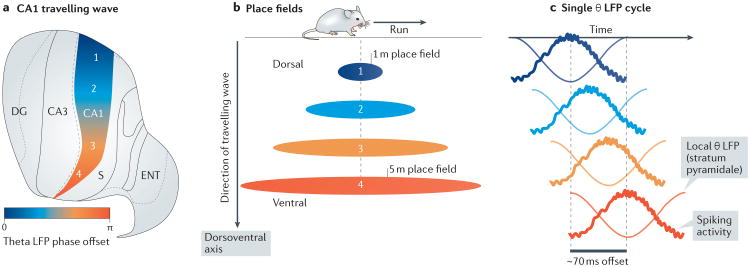
Figure 5. Patterning of place field firing by hippocampal travelling waves.

a | The 6–12 Hz hippocampal theta oscillation, which appears during active behavioural exploration and rapid-eye-movement sleep, is a wave travelling from dorsal to ventral hippocampal CA1 (REFS 17,18). This flattened map view of the rodent hippocampus shows the positions of the dentate gyrus (DG), CA3, CA1, subiculum (S) and entorhinal cortex (ENT). The phase offset of the theta oscillation is plotted in colour along the dorsoventral axis of CA1 (colour axis, bottom left). b | As the rodent runs on a linear track, pyramidal neurons in CA1 fire. These neurons exhibit place fields that become progressively larger as their location in CA1 changes from dorsal to ventral regions^141,142. The schematic illustrates a typical example of the place fields of neurons that fire when the rodent is at a particular spatial location during the run and is based on data in REF 17. The place fields are arranged according to their location in CA1 and with their colour illustrating the phase offset of the theta oscillation at that location on the dorsoventral axis. c | Because of the phase offset of the theta local field potential (LFP; as recorded in stratum pyramidale18; shown as light transparent lines) owing to the travelling wave (represented by the distance between the dotted lines) and the modulation of neuronal firing by theta (solid lines), neurons with CA1 place fields centred at the rodent's position fire in a temporal sweep from those with the smallest scales of spatial selectivity to those with the largest scales of spatial selectivity. Part a is reproduced from REF. 17, Macmillan Publishers Limited. Part c is adapted with permission from REF. 18, Elsevier.

High-frequency 140-200 Hz ripple oscillations, which appear during awake resting and slow-wave sleep¹⁴⁴ and are involved in replay of waking hippocampal spike sequences during sleep¹⁴⁵, have also been shown to be travelling waves, starting at discrete points along the dorsoventral axis and propagating in either the dorsal or ventral direction¹⁴⁶. The computational consequences of this exquisite mesoscopic organization of firing patterns by theta and ripple travelling waves in the hippocampus have not yet been investigated in detail; however, they have implications for theories involving synaptic plasticity as a mechanism for linking neurons across the hippocampus^147,148.

Potential computational roles for stimulus-evoked travelling waves

In the specific examples presented above, the existence of travelling waves is not in conflict with what is known about the underlying physiology: in both cases, travelling waves may organize population spiking along some behaviourally relevant axis (in a sweep from proximal to distal muscle representations, foveal to peripheral visual fields or small to large place fields). As outlined at the beginning of this section, however, a coherent account of computational roles for stimulus- evoked waves in the sensory cortex is lacking. At present, we cannot exclude the possibility that no specific computational role exists for spontaneous and stimulus-evoked waves and that they may be an epiphenomenon of the massive recurrent connectivity in the cortex. A direct demonstration of the function of these waves in sensory processing is lacking, most importantly, in the awake animal. However, it is clear that the information carried by these waves could play important computational roles. Stimulus-evoked travelling waves in V1 extend well beyond the locus of the initial stimulus- evoked response, broadly influencing neurons over several millimetres of the retinotopic map^14,24,25,67. Furthermore, it is important to consider that these waves travel over other functional maps such as ocular dominance and orientation maps in V1 and have been shown to distribute orientation specific information across the cortex (though this specificity decreases over a moderately short distance in the cortex)^25,149,150. This suggests that waves will be useful in visual processing on scales beyond the imprint of feedforward activation, opening up interesting new computational capacities. To explore this further, we now consider general models for computation with evoked waves travelling over sensory maps in the cortex.

Computation with waves has been a subject of continued interest in reaction-diffusion systems¹⁵¹, with some applications to spiking neural networks¹¹⁶. In these models, a localized wave state (generally a small travelling excitation) is considered a unit (or packet) of information, with computations implemented by interactions between localized wave states. For example, the merging of two waves might serve to compute an AND logic operation, while the annihilation of two waves may represent a dynamic XOR gate. These collision-based computations¹⁵², however, require dense wave interactions of the kind observed in small spiking networks with low numbers of synaptic connections per cell (see above). In the weakly entrained regime consistent with the low-correlated firing in physiologically normal cortex^153,154, sparse waves may interact much less strongly as they travel than dense waves. In this situation, multiple evoked waves could lead to a global spatiotemporal pattern of activation whose usefulness in computation must be considered within a different context.

What computations can be done with evoked, weakly interacting travelling waves in single cortical regions? For inspiration, we can look to a recently described physical process as an analogue. A recent study examined the dynamics of a silicone droplet bouncing on a vibrating oil bath¹⁵⁵. The vibrations of this medium propel the droplet upward and cause it to bounce continually, creating a pattern of successive impacts across the surface (FIG. 6a). With each bounce, the droplet creates a set of waves in the oil bath. In our analogy, these droplet waves may be similar to those created in the sensory cortex by the impact of afferent, stimulus-driven action potentials. The waves evoked by each impact of the droplet then create a pattern across the oil bath that leaves a trace of the path of the droplet. With sufficient knowledge of the dynamic properties of the medium, one could decode the history of the path of the droplet simply from the observed spatial pattern at each point in time. Furthermore, temporal reversibility is preserved for waves even in chaotic systems; this property, along with a clever manipulation of the experimental apparatus, can be used to cause the droplet to exactly reverse its trajectory (FIG. 6a). It is argued that this last manipulation shows that the global wave field stores information about the trajectory of the droplet with sufficient precision that it can be read back out. While the authors did not have neuroscience in mind and, indeed, note that they have not yet considered practical implementations, they posit that this system implements the basic elements for general computations that could find application in future work.

Figure 6. Computation with cortical waves.

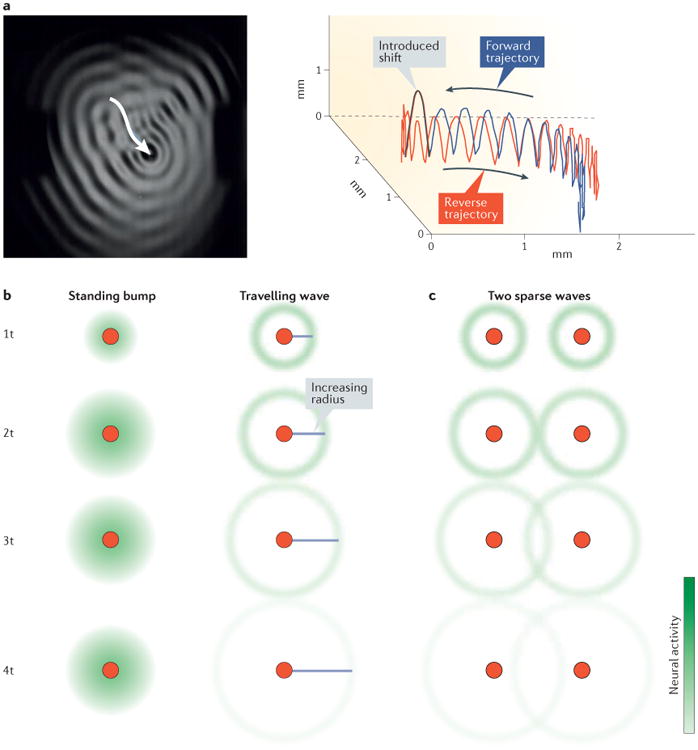
a | A droplet emits travelling radial waves as it bounces and creates a trajectory (white arrow) across the surface of a silicone oil bath (left panel)¹⁵⁵. As it bounces, the droplet creates a forward trajectory (blue line, right panel). The x axis, y axis and z axis represent the position of the droplet in space. With a simple manipulation, or introduced shift (a higher bounce, black line), the droplet can reverse its trajectory (red line), illustrating that the evoked wave field stores information about the recent past. b | Schematic models of standing bumps and travelling waves evoked by an external stimulus (red dot) are shown. As time increases (from 1 to 4 time units (t)), the standing bump reaches a steady pattern, whereas the travelling wave continues to expand across the network. It is therefore hypothesized that time from stimulus onset can be decoded in the case of travelling waves but not standing bumps. c | It is hypothesized that two sparse waves interacting in the cortex will weakly interact, passing through each other (unlike dense waves) and creating a global wave field with excitations that are symmetric about each stimulated point. Part a is adapted with permission from REF. 155. Copyrighted by the American Physical Society.

This physical system, though in many ways an imperfect analogy to the sensory cortex, provides a suggestive example for possible computations that could be performed by waves radiating from the retinotopic loci of stimulus-evoked input. The key difference between stimulus-driven stationary bumps of activity and active travelling waves is that the latter contain information about time from stimulus onset (FIG. 6b). While stationary bumps contain information about stimulus position in a retinotopic map, in a network with active stimulus-evoked travelling waves, one could decode both stimulus position and onset time. During the lifetime of waves travelling over a retinotopic map, they could therefore encode both stimulus position and the recent past in a distributed spatiotemporal pattern of activation (FIG. 6c). The availability of information about the recent past may be useful in processing dynamic, non-stationary sensory scenes, which present difficulties for the static feedforward framework^128,129. It is important to note that, though other activity patterns (such as expanding bumps) could encode both stimulus position and onset time, such activity patterns will be less robust than travelling waves arising from multiple points of stimulation. Similar ideas for computation have been discussed previously¹⁵⁶ but never before in the context of sensory systems and cortical topographic maps. Finally, because of their timing relative to sensory stimuli, induced waves during sustained responses may exhibit a much richer interaction between feedforward and feedback pathways in the cortex; thus, they may serve different computational roles than waves evoked by the initial feedforward input. However, because induced waves will propagate similarly across topographic maps in the sensory cortex, the framework discussed here can serve as a guiding example for further investigations.

This framework could potentially provide a general outline for computation with travelling waves in the sensory cortex, helping to resolve the difficulties posed by stimulus-evoked travelling waves to the canonical feedforward model of visual processing. Further experimental and theoretical work will be needed to further refine our understanding of travelling waves in these regions. Here, however, we have highlighted the importance of multi-wave interactions and suggest that they provide fertile ground for future experimental and theoretical work. Analysis of multichannel recordings will make it possible to test whether stimulus position and timing can be reliably decoded from responses at the single-trial level. While it has been noted that cortical travelling waves may structure visual responses to dynamic natural scenes³⁰, it remains unclear how the spatiotemporal interactions revealed following simple sensory stimuli¹⁴ generalize to multi-stimulus paradigms and natural scenes. Nevertheless, the effect of the abundant horizontal connections highlighted in this work (and their intrinsic axonal time delays) is not expected to disappear. Furthermore, it remains unknown how spontaneous and stimulus-evoked mesoscopic waves may influence computations in downstream cortical areas. Improved imaging techniques^52,157 and new optogenetic approaches in awake, behaving primates^158,159 may allow future studies to directly test the functional roles for cortical travelling waves discussed here. Central to this framework is the recognition that the fine-scale dynamics of neural populations can carry important additional information over sensory topographic maps. Even more complex interactions in higher-order association regions and in prefrontal cortex could be involved in cognitive functions such as planning and decision making.

Conclusions

In this Review, we have covered recent advances in travelling waves in neural systems. While initial evidence indicated that travelling waves were pronounced only in weak input regimes^21,22, recent studies have shown that travelling waves are evoked following small, high-contrast visual stimuli¹⁴, and they appear to play a role in cortical dynamics driven by dynamic sensory input and sensorimotor planning³⁰. It has previously been noted that the existence of stimulus-evoked travelling waves in the sensory cortex presents a challenge to the orderly topographic arrangement of selectivity first described by Hubel and Wiesel at the trial-averaged level²². Here, we have outlined an initial conceptual framework for computations with travelling waves in the sensory cortex. This regime, in which activity patterns generated by intracortical circuits actively shape responses to external stimuli, is well matched to the basic anatomy of the cortex, where neurons receive a large fraction of their input from a local patch of cells in the same region⁹⁴. Much theoretical and experimental work remains to test the feasibility of computations with travelling waves in the cortex; however, the development of large-scale, high-precision recording technologies is a priority in neuroscience, which will drive advances in these fields.

Glossary

Phase offsets

The differences in phase (an amplitude-invariant measure of position in an oscillation cycle) between two (or more) oscillations

Travelling waves

A disturbance that travels through a physical medium that may be water, air or a neural network

Complex spatiotemporal patterns

Patterns that can result from the summation of many individual waves. Depending on the properties of the medium the pattern resulting from these interactions can differ greatly

Mesoscopic

A scale between microscopic and macroscopic. In neuroscience, the mesoscopic scale describes single regions (such as cortical areas or subcortical nuclei) spanning millimetres to centimetres. Cortical networks at this scale can be imaged through recently developed recording technologies

Macroscopic

The scale of the whole brain traditionally recorded with extracranial techniques (electroencephalography and magnetoencephalography) and more recently recorded with intracranial methods (electrocorticography)

Electroencephalography

(EEG). A neural recording technique in which electrodes are placed on the scalp outside the skull (extracranial) that is of great use in studying the sensory and cognitive processes of normal human subjects

Electrocorticography

(ECoG). A recording technique in which electrodes are placed directly on the cortical surface, offering both high spatial (up to 2 millimetres or greater) and high temporal resolution

Local field potential

(LFP). The electric potential recorded in the extracellular space of the cortex. The LFP is thought to reflect the synaptic currents from neurons within a few hundred micrometres around the electrode

Multielectrode arrays

(MEAs). One-dimensional or two-dimensional grids of electrodes, which offer the ability to sample local field potential and spiking activity at the mesoscopic scale

Voltage-sensitive dyes

(VSDs). Fluorescent dyes applied directly to the surface of the cortex that allow the subthreshold membrane potential of neural populations to be recorded. The resulting signals are linearly related to the average membrane potential of neurons at each point in the cortex. This technique captures neural activity over a large field of view with very high spatial (up to 20 micrometres) and temporal (up to 1 millisecond) resolution

Slow oscillation

The large, 0.1-1.0 Hz rhythm of deep non-rapid-eye-movement sleep

Volume conduction

Passive transmission of an electric field through biological tissue. The fields can be created from a single source of neural activity and will appear as identical, highly synchronous waveforms across electrodes; a cause of spatial smoothing (blurring) in scalp electroencephalography

K-Complex

A brief (∼1 second), biphasic waveform composed of a strong negative potential followed by a positive deflection. K-Complexes occur predominantly during stage 2 non-rapid-eye-movement sleep and are driven by transitions from cortical down to up states

Sleep spindles

Thalamocortical 11–15 Hz oscillations prevalent in stage 2 non-rapid-eye-movement sleep. These oscillatory periods have long been associated with learning and memory, including sleep-dependent consolidation of long-term memory

Cell assemblies

A group of interconnected, repeatedly co-activated neurons whose signature spike pattern is thought to collectively represent a specific sensory stimulus or memory

Coupled oscillator networks

Models of emergent collective behaviour in large ensembles. In these networks, individual units are characterized by a state (or phase) between 0 and 2π. Interactions among units are typically modelled as attractive, such that units with different states tend to synchronize depending on the coupling strength of the interaction

Irregular asynchronous (IA) state

A state of asynchronous, highly irregular firing in spiking network models. This state exhibits the low-correlated firing that is the hallmark of cortical dynamics under general conditions of excitatory and inhibitory balance

Stochastic neural field theory

An extension of the neural field model of Wilson and Cowan to include the effects of neural and synaptic noise

Dorsoventral axis

In rodents, the long axis of the hippocampus, running from a dorsal, medial position to a ventral, lateral position; synonymous with septotemporal axis

Reaction–diffusion systems

Models of chemical dynamics that take into account local reactions and diffusion across space. These reactions exhibit complex dynamics, including travelling waves and emergent patterns

Temporal reversibility

A property of a system whose dynamics remain the same when time is reversed. This feature implies important mathematical properties for the system under study