Longer-Term Impact of High and Low Temperature on Mortality: An International Study to Clarify Length of Mortality Displacement

Abstract

Background:

In many places, daily mortality has been shown to increase after days with particularly high or low temperatures, but such daily time-series studies cannot identify whether such increases reflect substantial life shortening or short-term displacement of deaths (harvesting).

Objectives:

To clarify this issue, we estimated the association between annual mortality and annual summaries of heat and cold in 278 locations from 12 countries.

Methods:

Indices of annual heat and cold were used as predictors in regressions of annual mortality in each location, allowing for trends over time and clustering of annual count anomalies by country and pooling estimates using meta-regression. We used two indices of annual heat and cold based on preliminary standard daily analyses: a) mean annual degrees above/below minimum mortality temperature (MMT), and b) estimated fractions of deaths attributed to heat and cold. The first index was simpler and matched previous related research; the second was added because it allowed the interpretation that coefficients equal to 0 and 1 are consistent with none (0) or all (1) of the deaths attributable in daily analyses being displaced by at least 1 y.

Results:

On average, regression coefficients of annual mortality on heat and cold mean degrees were 1.7% [95% confidence interval (CI): 0.3, 3.1] and 1.1% (95% CI: 0.6, 1.6) per degree, respectively, and daily attributable fractions were 0.8 (95% CI: 0.2, 1.3) and 1.1 (95% CI: 0.9, 1.4). The proximity of the latter coefficients to 1.0 provides evidence that most deaths found attributable to heat and cold in daily analyses were brought forward by at least 1 y. Estimates were broadly robust to alternative model assumptions.

Conclusions:

These results provide strong evidence that most deaths associated in daily analyses with heat and cold are displaced by at least 1 y. https://doi.org/10.1289/EHP1756

Introduction

In many locations worldwide, daily time-series analyses have identified adverse associations between daily mortality and temperatures that are toward the hot and cold ends of the temperature range for each location (Gasparrini et al. 2015; Guo et al. 2014). Many of these analyses employed distributed lag models (Armstrong 2006; Schwartz 2000) that discount mortality displacement or harvesting (Zanobetti et al. 2000) within the lag interval, typically 2–3 wk in recent studies. However, they cannot identify the extent of displacement of mortality beyond this period. Such displacement may be quite short, for example, just a few months. The uncertainty about this makes it hard to estimate the actual life lost to weather and thereby judge the priority that should be given to public health policies to reduce those excesses.

One way to clarify the extent of mortality displacement due to the acute effects of heat and cold is to estimate associations between annual mortality and annual summaries of heat and cold. If such associations were null, it would indicate that excess deaths due to acute effects were wholly compensated by deficits later in the same year, as would be the case if all reflected mortality displacement. Positive associations of annual series would indicate that all or some of the excess deaths were displaced at least into the next period, suggesting that mortality was advanced by at least 1 y.

Two published single-city studies have used this method. In both London between 1947 and 2006 (Rehill et al. 2015) and Hong Kong from 1976 to 2012 (Goggins et al. 2015), years with cold winters and those with hot summers were associated with high mortality, though in temperate London, the association with heat was not significant. Those studies were not linked to daily studies, so it was not possible to directly estimate from them whether a proportion of heat and cold deaths found in daily studies were nevertheless displaced by less than 1 y.

In this multicountry study, we estimated the association between annual mortality and annual summaries of heat and cold in 278 locations from 12 countries. We also develop the method further to give insight, for positive associations, into whether the magnitude of association indicates partial or total absence of short-term displacement. This is easily the largest study to date addressing this question, indeed the only study including more than one location.

Methods

The data were assembled from daily counts of deaths and mean temperatures from 278 locations from 12 countries of total durations of 10–40 y from years between 1972 and 2012. These data are those that have been previously described (Gasparrini et al. 2015), with the addition of six locations from Ireland (all the island of Ireland: two regions in Northern Ireland and four in the Republic). We also used a longer series from some countries, Japan in particular, and excluded locations with less than 10 y of qualifying data (see below). Descriptive data on included locations are summarized in Table 1 and given in more detail in Supplementary Material (Table S1).

Table 1.

Summary descriptive statistics by country.

Country	$n$	Period	MMT (percentile)	Mean (SD) AF%		Mean (SD) °C
				Heat	Cold	Heat	Cold
Australia	3	1988–2008	22.8 (82%)	0.5 (0.2)	5.9 (0.5)	0.4 (0.1)	4.8 (0.3)
Brazil	15	1997–2010	25.1 (62%)	0.7 (0.3)	2.5 (0.5)	0.5 (0.1)	1.7 (0.2)
Canada	21	1986–2010	17.2 (82%)	0.5 (0.2)	5.1 (0.3)	0.5 (0.2)	11.1 (0.8)
Ireland	6	1984–2006	17.5 (97%)	0.0 (0.0)	11.3 (1.1)	0.0 (0.0)	7.8 (0.5)
Italy	2	1988–2009	21.8 (78%)	1.7 (1.4)	9.8 (0.9)	0.7 (0.3)	7.5 (0.5)
Japan	47	1972–2011	24.8 (84%)	0.4 (0.2)	10.5 (0.8)	0.4 (0.2)	10.1 (0.6)
South Korea	7	1992–2009	25.6 (90%)	0.3 (0.3)	6.6 (0.2)	0.2 (0.1)	12.0 (0.5)
Spain	50	1990–2009	21.4 (78%)	1.1 (0.5)	5.6 (0.7)	0.6 (0.2)	6.6 (0.5)
Taiwan	3	1994–2006	25.8 (55%)	0.9 (0.2)	3.8 (0.6)	1.1 (0.1)	2.9 (0.3)
United Kingdom	10	1993–2005	17.2 (90%)	0.3 (0.2)	8.4 (0.8)	0.2 (0.1)	6.9 (0.4)
United States	114	1985–2005	24.3 (83%)	0.3 (0.2)	5.4 (0.3)	0.4 (0.1)	9.8 (0.6)

Note: The table shows number $n$ of locations, period of study (start years of first to last complete Nov–Oct year), and the mean over locations of MMT from daily analyses (in degrees and as percentile), mean, and SD over included years of annual attributable fraction of deaths estimated due to heat and cold using methods identical those for a previously published daily analysis (Gasparrini 2015), and mean (SD) of annual mean degrees above and below the MMT. AF, attributable fraction; MMT, minimum mortality temperature; SD, standard deviation.

Broadly, statistical methods follow those of the previous single-location annual studies (Goggins et al. 2015; Rehill et al. 2015). Mortality and temperature daily series were collapsed to an annual series using two different year dividers: a) starting years at the beginning of summer (the month before that including the summer solstice, May, in the northern hemisphere) to allow maximum time for shorter-term displacement of heat-related deaths to be discounted; b) similarly, starting years at the beginning of winter (November) for optimal cold analysis. Location years with more than 1% of days missing key variables were excluded.

In these annual series, (logged) annual mortality was regressed on annual indices of heat and cold. We used two indices described below; the first (“Basic Model”) is simpler and we hope easier to follow, and the second (“Modified Model”) more informative at the expense of some additional complexity.

Basic Model

In a preliminary step, conventional daily analysis was used to identify minimum mortality temperature (MMT), the daily mean temperature at which mortality was predicted to be minimum, at each location. Specifically, we used exactly the same model specification as Gasparrini et al. (2015), a distributed lag nonlinear model (lags to 21 d) with spline control for seasonality and trend [8 degrees of freedom (df)/year] and day of week indicators.

Then, after collapsing daily to annual data as described above, in each country, location i and year t, mean daily deaths ${\mathrm{Y}}_{it}$ were regressed on mean of degrees above (below) these ${\text{MMT}}_i\mathrm{s}$ in that year and location:

$$\log \left({\mathrm{Y}}_{it}\right)={\mathrm{\alpha }}_i+{\mathrm{\beta }}_{\text{heat}}{\text{heat}\_\text{degrees}}_{i,t}+{\mathrm{\beta }}_{\text{cold}}{\text{cold}\_\text{degrees}}_{i,t}+{\mathrm{s}}_i\left(t{,\text{df}}_i\right)+{\mathrm{\omega }}_t+{\mathrm{\epsilon }}_{it}$$ [1]

Where

• •${\text{heat}\_\text{degrees}}_{i,t}={\sum }_{d=\mathrm{1,365}}\{\max \left[\left({\text{temp}}_{i,t,d}-{\text{MMT}}_i\right),0\right]\}/365,$ with ${\text{temp}}_{i,t,d}$ being mean temperature on day d, year t, location i.
• •${\text{cold}\_\text{degrees}}_{i,t}={\sum }_{d=\mathrm{1,365}}\{\max [\left({\text{MMT}}_i-{\text{temp}}_{i,t,d}\right),0]\}/365$.
• •${\mathrm{s}}_i\left(t{,\text{df}}_i\right)$ is a natural cubic spline of year t specific to location i with two df per decade (rounded).
• •${\mathrm{\omega }}_t$ and ${\mathrm{\epsilon }}_{it}$ are Gaussian independent and identically distributed noise at year and location–year levels, respectively.

In model (1), a Gaussian distribution was adopted in preference to the quasi-Poisson models used in daily analysis for modeling simplicity and because the large size of annual death counts made the Gaussian approximation very good (Goggins et al. 2015; Rehill et al. 2015). For presentation of results, we transform the coefficients ${\mathrm{\beta }}_{\text{heat}}$ and ${\mathrm{\beta }}_{\text{cold}}$ to percent excess relative risks (ERR%) per degree of annual high and low temperatures: $\text{ERR}\%=100[\text{exp}\left(\mathrm{\beta }\right)-1]$.

In these models, R code and data for one country are given in Supplemental Material, R code and data.

That model (1) is at country rather than location level is unusual, and indeed, we initially planned to fit a regression model of annual mortality model separately for each location, as did the previous single-location studies, and then combine results in a second-stage meta-analysis of location coefficients. However, exploratory analyses showed appreciable correlations of mortality and temperature anomalies across locations in the same country; years with anomalous mortality residuals in one location tended to be similarly anomalous in other locations also, even after allowing for temperature effects. This falsified the assumption of independence of estimates over locations necessary for conventional two-stage analysis with location-specific analyses at first level, leading to spurious precision in coefficients. We therefore reformulated the model for our analysis to have first-level regressions using all data from each country combined and a second-level meta-analysis of country (heat and cold) coefficients. The country-level regressions allowed separate intercepts and time spline curves for each location and an additional random effect of calendar year to allow for the shared year anomalies in mortality noted above.

Modified Model to Relate Results to Those from Daily Analyses

Model (1) allows concluding whether some deaths were displaced by more than 1 y by heat or cold (if the coefficients of the annual heat_degrees and cold_degrees are positive), but does not easily provide evidence whether such longer-displaced deaths comprised all or just a fraction of the deaths found attributable to heat and cold in daily analyses. To provide this more quantitative evidence, we replaced the heat degrees and cold degrees variables in model (1) with annual fraction of deaths attributable to heat and cold, ${\text{heat}\_\text{AFdaily}}_{i,t}$ and ${\text{cold}\_\text{AFdaily}}_{i,t}$, where AF stands for attributable fraction. These were estimated in the preliminary daily analyses by aggregating to annual level daily fractions of deaths attributable to heat and cold obtained as described in Gasparrini (2015), using the forward method described in Gasparrini and Leone (2014). The model was in other respects the same as model (1):

$$\log \left({\mathrm{Y}}_{it}\right)={\mathrm{\alpha }}_i+{\mathrm{\beta }}_{\text{heat}}{\text{heat}\_\text{AFdaily}}_{i,t}+{\mathrm{\beta }}_{\text{cold}}{\text{cold}\_\text{AFdaily}}_{i,t}+{\mathrm{s}}_i\left({t,\text{df}}_i\right)+{\mathrm{\omega }}_t+{\mathrm{\epsilon }}_{it}$$ [2]

Under model (2), if in each year t, the excess fraction of deaths due to heat (cold) found in annual regression analyses are the same as the fraction found by aggregating the daily attributable deaths, then the coefficients ${\mathrm{\beta }}_{\text{heat}}$ and ${\mathrm{\beta }}_{\text{cold}}$ would, to a close approximation, be 1. The approximation is addressed with a complexity cost in a sensitivity analysis, but we motivate the argument with a simplified example: Suppose in one location in just 1 y, daily analyses indicated that 2% of deaths were due to heat (none to cold), so ${\text{heat}\_\text{AFdaily}}_{i,t}=0.02$. Then, if all of those deaths were displaced by 1 y or more, mortality would be raised by a factor (rate ratio) of close to 1.02, and log mortality be 0.02 higher. To fit this, the coefficient ${\mathrm{\beta }}_{\text{heat}}=1$.

Thus, we can interpret the actual coefficients estimated from model (2) as follows: A coefficient of 0 is consistent with all deaths attributed to heat by daily analyses being displaced by less than 1 y. A coefficient of 1 is consistent with all the daily attributable deaths being displaced more than 1 y. Intermediate values are consistent with some but not all the daily attributable deaths being displaced by more than 1 y. Effects of heat and cold at longer lags than those considered in daily analyses may also play a part. If all the daily attributable deaths were displaced by more than 1 y, such additional longer lags would lead to coefficients $>1$. If there was some short-term displacement, this might be compensated by longer lag effects, so, for example, a coefficient of 1 might reflect the two things balancing exactly. However, public health importance seems independent of whether a coefficient of 1, say, is due to absence of short-term displacement or its compensation by longer lag effects.

Sensitivity Analyses

To identify sensitivity to specific features of the model (2) it was modified as follows:

• 1.Time spline changed from 2 to 1 and 3 df/decade.
• 2.The benchmark for excluding years dues to missing values changed from 1% to 0% (excluded 9 locations entirely) and 10% (added 18 locations).
• 3.Influenza data were available only for locations in Canada, Ireland, Japan, Spain, and the United Kingdom (137 locations). For these countries, a term $\mathrm{\lambda }{\left(\text{influenza}\%\right)}_{it}$ was added, where influenza% is the proportion of deaths coded as due to influenza (International Classification of Diseases Eighth Revision (ICD-8) 470-474, Ninth Revision (ICD-9) code 487, and Tenth Revision (ICD-10) (WHO 1966, 1978, 2016)]. Unadjusted results restricted to the same five countries are also given for comparison.
• 4.Step changes in death rates at calendar-year changes (1 January) were included wherever significant at a) $p<0.01$, and b) $p<0.001$. These corresponded to false discovery rates of included steps of about 50% and 20%, respectively (estimated by Storey’s q-value). Steps were selected first in calendar year analyses, modeled as indicators $\text{step}{\left(\mathrm{T}\right)}_{it}=1$ if $t>\mathrm{T}$, 0 otherwise. In the main models with years starting in May and November, the indicators were modified to $\text{step}{\left(\mathrm{T}\right)}_{it}=1$ if $t>\mathrm{T}$, $\text{step}{\left(\mathrm{T}\right)}_{it}=4/12\left(\text{May}\right)$ or 10/12 (November), 0 otherwise.
• 5.Three alternative approaches to clustering by year were undertaken: a) ignoring clustering by applying a conventional two-stage analysis with each location analyzed separately; b) using the country-level model as for the main model, but without random year effect with standard error of heat and cold index coefficients estimated by jackknife clustering on year; and c) the main model with addition of allowance for random variation in heat and cold coefficients (slopes) across locations.
• 6.To allow interpretation of coefficients with respect to proportion of deaths attributable to heat and cold in daily analyses without approximation, the explanatory variables in model (2) were modified to ${\text{heat}\_\text{index}}_{i,t}=-\log \left(1–{\text{heat}\_\text{AFdaily}}_{i,t}\right)$, and equivalently for cold. This we deduced from standard theory (Steenland and Armstrong 2006), by which for an explanatory variable value $x$ for 1 y, the AF is: $\text{AF}\left(x\right)=1-\text{exp}\left(-\mathrm{\beta }x\right)$. Changing the subject of this expression, the value $x=-\log \left[1-\text{AF}\left(x\right)\right]$ gives the x variable that would give a coefficient of 1 if $\text{AF}\left(x\right)$ were known. Thus, if ${\text{heat}\_\text{AFdaily}}_{i,t}$ indeed were the same as the AF from annual analysis, ${\text{heat}\_\text{AFannual}}_{i,t}$, then the coefficient of $x=-\log \left(1–{\text{heat}\_\text{AFdaily}}_{i,t}\right)$ would be 1. We did not anticipate replacing AF by $-\log (1-\mathrm{AF})$ would make much difference to results, since at the low values for AF in these data (maximum 0.08 for heat, 0.2 for cold), $\text{AF}\approx -\log \left(1-\text{AF}\right)$ to a good approximation.
• 7.An approximate correction was made for estimation uncertainty in the annual ${\text{AF}}_{\text{daily}}$ used as explanatory variables in our main analysis. Because of the complexity of the structure of this error in variables (highly correlated across years within a location), we chose the SIMEX method (Carroll et al. 2006) in which additional error is simulated at various magnitudes and the pattern of mean ERRs and their standard errors estimated from (100) simulations at each magnitude extrapolated to estimate what would have been observed at zero error if the pattern persisted. Specifically, we took values of additional error variance multiplier $\mathrm{\lambda }=0.5$, 1, 1.5, and 2, and used a quadratic polynomial to extrapolate the association between mean of estimated $\mathrm{\beta }$ values (${\mathrm{\beta }}_{\mathrm{\lambda }}$) with $\mathrm{\lambda }$ back to $\mathrm{\lambda }=-1$ to predict a value ${\mathrm{\beta }}_{\text{SIMEX}}$. To obtain $\text{SE}\left({\mathrm{\beta }}_{\text{SIMEX}}\right)$, we similarly extrapolated variance differences: $\text{mean}\left[{\text{Var}}_j\left({\mathrm{\beta }}_{\mathrm{\lambda }j}\right)\right]-\text{Var}\left({\mathrm{\beta }}_{\mathrm{\lambda }j}\right)$ to $\mathrm{\lambda }=-1$, where $j$ is the simulation number.

Results

A summary of distributions of key variables in the 278 included locations is shown by country in Table 1, and the values of those variables for each location are in Table S1. The United States, Japan, and Spain stand out as having the most locations, and Japan had easily the longest series (40 y). In some countries, the average location-specific variation over years of our two heat indices (fraction of deaths attributable to heat and degrees above MMT) is rather small, which limits study precision and power in those places. Ireland in particular, with mean MMT at the 97th percentile of temperature, showed an average heat-attributable fraction of just 0.03%, with standard deviation of 0.05%.

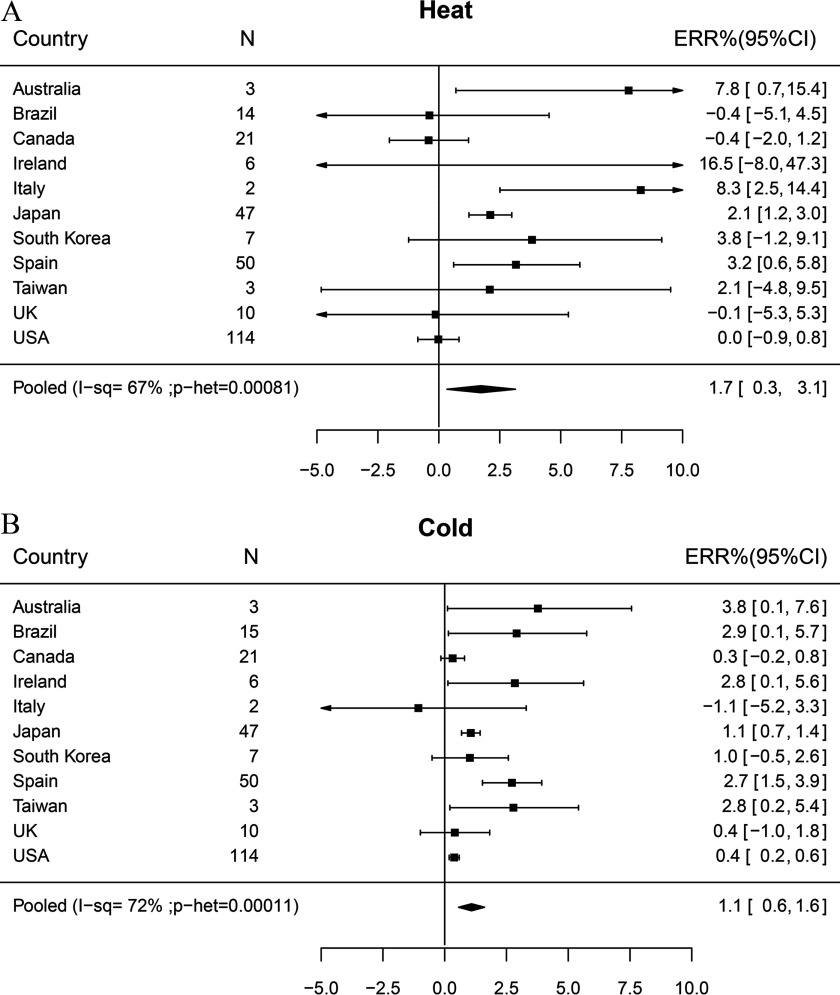
The association of mortality with mean annual degrees of heat and cold was positive on average and in most countries (Figure 1), with overall estimates of ERR per degree of heat above MMT 1.7% [(95% confidence interval (CI): 0.3, 3.1] and of cold below MMT 1.1% (95% CI: 0.6, 1.6), though variation between countries in ERRs was appreciable (${\mathrm{I}}^2=67\%$ and 72%). This indicates that some deaths associated with heat and cold were indeed brought forward by at least 1 y.

Figure 1.

Association of annual mortality with mean annual degrees above and below minimum mortality temperature (MMT) by daily analysis (model 1): (A) Heat, (B) Cold. Percent excess relative risks ERR% are increments in RRs (%) per 1°C increase in annual mean degrees above/below MMT.

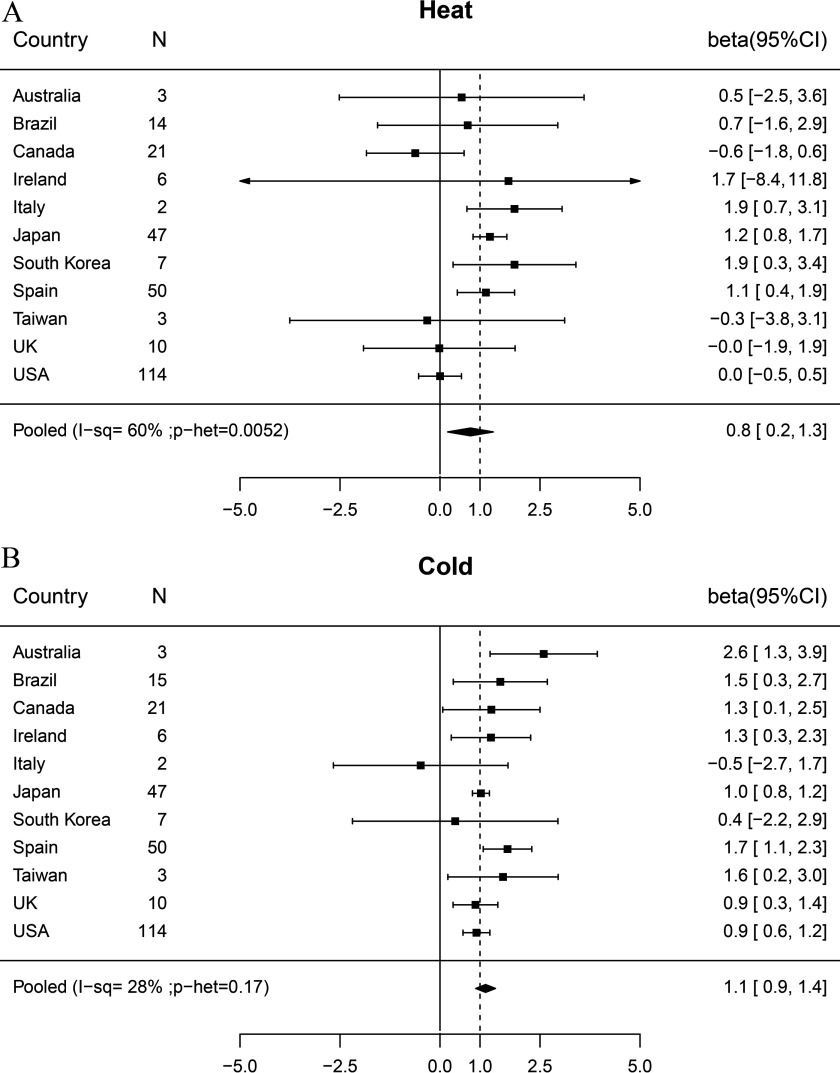
An ERR% of 1.0% has no special significance in the results in Figure 1 [model (1)], which cannot elucidate what proportion the excesses found comprise of all deaths found attributable to heat and cold in daily analyses. The results in Figure 2 from model (2) do this; if all the deaths found attributable to heat and cold in daily analyses were displaced by at least 1 y, then the regression coefficient $\mathrm{\beta }$ would be 1. For both heat and cold, our pooled annual analysis coefficients were indeed close to 1, at 0.8 (95% CI: 0.2, 1.3) and 1.1 (95% CI: 0.9, 1.4), respectively. This indicates that about the same numbers of deaths were found associated with these weather conditions in annual as in daily analyses, evidence that most of the latter were brought forward (displaced) by at least 1 y (not just harvested).

Figure 2.

Association of annual mortality with mean annual deaths attributed to heat and cold by daily analysis (model 2). (A) Heat, (B) Cold. Betas are regression coefficients for log(mortality) on fraction of deaths attributable to heat and cold in daily analyses; a value of 1.0 indicates exactly the deaths expected from daily analyses if all such deaths were displaced beyond the year end.

For cold, the country-specific associations in Figure 2 varied no more than expected by chance. There was, however, appreciable heterogeneity of heat coefficients across countries ($\mathrm{I}-\text{sq}=60\%$), despite these being less precise than for cold. Most of the results that were not clearly positive were very imprecise, but for the United States and Canada, the incremental risks, 0 (95% CI: $-0.5$, 0.5) and $-0.6$ (95% CI: $-1.8$, 0.6), had CIs excluding 1.0, thus providing some evidence that in these countries, some deaths shown in daily analyses to be associated with heat were displaced by less than 1 y.

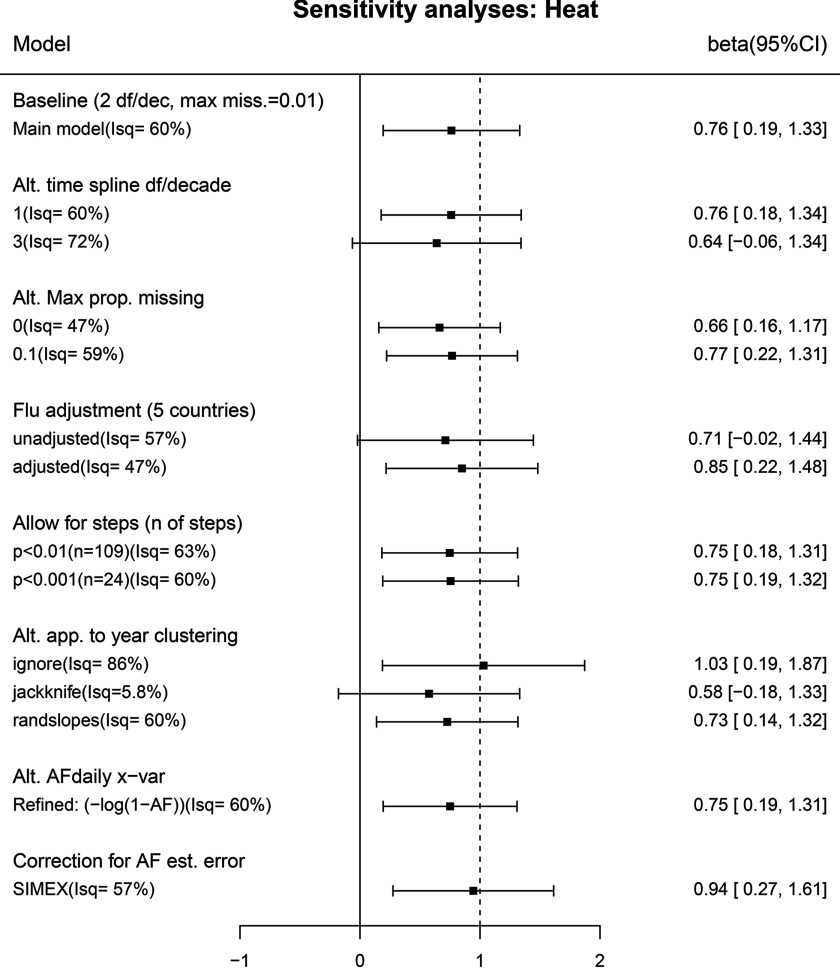
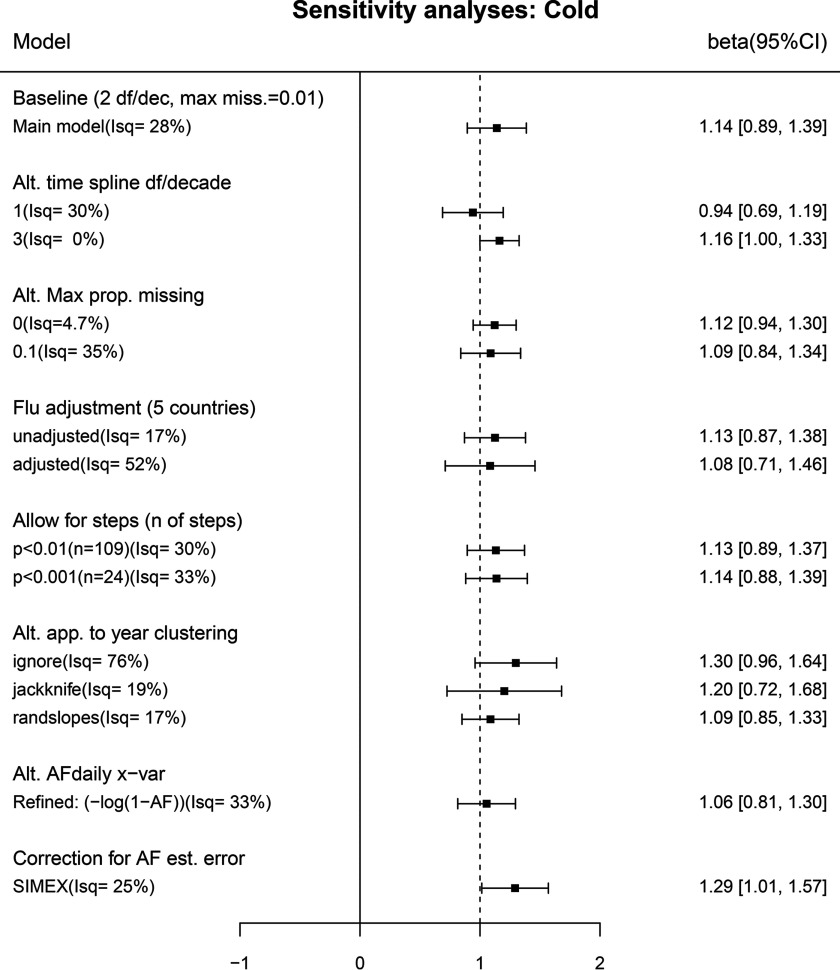
Few of the alternative models explored in sensitivity analyses changed the overall estimates appreciably (Figures 3 and 4). Models ignoring the year clustering across locations within countries (“Alt. app. to year clustering” first row) had much narrower confidence intervals for country-specific coefficients, which is reflected in the high heterogeneity I-sq values. Conversely, those using a jackknife to allow for clustering (second row) had wider country-level intervals leading to low I-sq values. Allowing for error in the ${\text{AF}}_{\text{daily}}$ values by SIMEX (“Correction for AF est. error”) moved estimates away from the null and slightly widened CIs. Here, overall estimates increased by multiples of 1.24 and 1.13 for heat and cold, respectively, and patterns by country remained the same (Figure S1). Investigation of sensitivity to the choice of month marking the start of years for annual aggregation (May and November in main analyses) showed little such variation for cold and somewhat more for heat, with November and February start months showing higher estimates, though all CIs overlapped considerably (Figure S2; not on Figures 3 and 4).

Figure 3.

Sensitivity of overall heat–mortality association (baseline model 2) to changing model features. Alt. time spline: Degrees of freedom (df)/decade changed from 2 df/decade (baseline) to 1 or 3 df/decade. Alt. max. prop. missing: criterion for excluding years with missing values changed from 1% (baseline) to 0% (9 locations excluded) or 10% (18 locations added.) Flu adjustment: adjusted for the proportion of deaths with influenza as the cause of death; data available only for locations in Canada, Ireland, Japan, Spain, and the United Kingdom (137 locations); unadjusted estimate restricted to the same countries for comparison. Allow for steps: Steps (breaks) were allowed for by including any single-step indicator variables significant at each of the two stated levels, which were estimated to result in false discovery rates of 0.5 ($p<0.01$; 109 steps) and 0.2 ($p<0.001$; 24 steps). Alt. app. to year clustering: The estimate ignoring clustering (“ignore”) was a conventional analysis with each location analyzed separately; the jackknife estimate was from the country-level model without random year effect, but standard error estimated by jackknife clustering on year; the “randslopes” estimate (baseline model) allowed for random variation in coefficients for heat and cold across locations. Alt. AFdaily x–var: Explanatory variables modified to ${\text{heat}\_\text{index}}_{i,t}=-\log \left(1-{\text{heat}\_\text{AFdaily}}_{i,t}\right)$ and ${\text{cold}\_\text{index}}_{i,t}=-\log \left(1-{\text{cold}\_\text{AFdaily}}_{i,t}\right)$, respectively, to allow interpretation of coefficients with respect to proportion of deaths attributable to heat and cold in daily analyses without approximation. Correction for AF estimation error: SIMEX correction made for error in ${\text{AFdaily}}_{i,t}$ values.

Figure 4.

Sensitivity of overall cold–mortality association (baseline model 2) to changing model features. Alt. time spline: Degrees of freedom (df)/decade changed from 2 df/decade (baseline) to 1 or 3 df/decade. Alt. max. prop. missing: criterion for excluding years with missing values changed from 1% (baseline) to 0% (9 locations excluded) or 10% (18 locations added.) Flu adjustment: adjusted for the proportion of deaths with influenza as the cause of death; data available only for locations in Canada, Ireland, Japan, Spain, and the United Kingdom (137 locations); unadjusted estimate restricted to the same countries for comparison. Allow for steps: Steps (breaks) were allowed for by including any single-step indicator variables significant at each of the two stated levels, which were estimated to result in false discovery rates of 0.5 ($p<0.01$; 109 steps) and 0.2 ($p<0.001$; 24 steps). Alt. app. to year clustering: The estimate ignoring clustering (“ignore”) was a conventional analysis with each location analyzed separately; the jackknife estimate was from the country-level model without random year effect, but standard error estimated by jackknife clustering on year; the “randslopes” estimate (baseline model) allowed for random variation in coefficients for heat and cold across locations. Alt. AFdaily x–var: Explanatory variables modified to ${\text{heat}\_\text{index}}_{i,t}=-\log \left(1-{\text{heat}\_\text{AFdaily}}_{i,t}\right)$ and ${\text{cold}\_\text{index}}_{i,t}=-\log \left(1-{\text{cold}\_\text{AFdaily}}_{i,t}\right)$, respectively, to allow interpretation of coefficients with respect to proportion of deaths attributable to heat and cold in daily analyses without approximation. Correction for AF estimation error: SIMEX correction made for error in ${\text{AFdaily}}_{i,t}$ values.

Discussion

This study found strong evidence that, on average, over all country studies, annual mortality was associated with deviations of temperatures from normal, in particular rising in years that experienced long or severe high or low temperatures. The strength of the association was consistent with all of the deaths found associated acutely with cold in daily analyses being brought forward by at least 1 y. These deaths thus represent significant life shortening rather than short-term mortality displacement. The associations with heat in the United States and Canada were exceptions, however. These suggested that in those countries, many of the deaths attributable in daily analyses to heat (though not cold) were advanced by less than 1 y.

Our overall results are broadly in line with the two previously published studies using a broadly similar approach, each with data from a single location but much longer periods (37 and 57 y) (Goggins et al. 2015; Rehill et al. 2015). Direct quantitative comparison is difficult. Many other studies have considered the mortality-displacement issue for heat-related deaths using distributed lag models with daily data, some finding evidence of significant proportions of heat-related deaths being displaced by only a few weeks (Basu and Malig 2011; Hajat et al. 2005; Kyselý 2004), but others found no such evidence (Kysely and Kim 2009; Le Tertre et al. 2006). In recent years, many studies have considered distributed lag models with maximum lag of several weeks (Gasparrini et al. 2015), so that temperature-related excesses of deaths with very short-term displacement will be matched by deficits later on in the total lag interval, so the overall cumulative risk for that interval will not include the deaths displaced within it. However, it is difficult for such studies to exclude displacement, which, though short, is more than a month or two.

Some studies have considered patterns of deaths after heat waves to elucidate displacement. From considering mortality for the 50 d following the 1995 Chicago heat wave, it was estimated that 26% of excess deaths during the heat wave were displaced by less than 50 d (Kaiser et al. 2007). From the experience in the year following the 2003 heat wave in Paris, it was concluded that deficits of mortality in next year could explain no more than 5,000 of the 15,000 excess due to heat in 2003 (Toulemon and Barbieri 2008). It would be interesting to explore whether duration of displacement differed for such extreme temperatures and the more moderate heat and cold dominating the temperature-related excesses found by Gasparrini (Gasparrini et al. 2015).

The patterns of reduced vulnerability to heat following winters of high mortality found in several studies (Ha et al. 2011; Qiao et al. 2015; Rocklöv et al. 2009; Stafoggia et al. 2009) provide some indirect evidence that some cold-related deaths are among those who would otherwise be vulnerable to heat, so they would likely have died within the next several months if they had survived the cold. However, it seems impossible from these studies to quantify the proportion of cold-related deaths that this would affect. Our results indicated that it is small.

The robustness of our results to quite extensive sensitivity analyses adds credibility to our conclusions. A further strength of this study is the wide geographic coverage and large number of locations. However, the gain in precision we hoped to achieve by multiple replication was somewhat reduced by the correlation of annual anomalies of mortality (year clustering) across cities in the same country. This meant that most country-specific results lack the precision for detailed comparison. A notable exception is Japan, where precise estimates illustrate the value of long (40 y) series for analyses of annual data.

There were some other limitations. Because we did not have annual population data for many locations, we could not allow for population changes, as did Goggins et al. (2015), relying rather on the spline curve to allow for this and other gradual temporal changes. We also did not consistently have cause- or age-specific death counts, precluding an investigation of these potential modifiers of the associations. Although our geographic coverage was wide, it is not globally representative, in particular overwhelmingly being comprised of more developed countries.

Conclusion

This study provides new evidence that over a wide range of locations, for the deaths associated acutely with extremes of heat and cold, most lives were shortened by at least 1 y. Adverse health effects of high and low temperatures are thus confirmed as significant public health concerns and not merely short-term displacement of times of death. Future research could usefully use similar methods, preferably with longer series, to clarify how much longer than 1 y temperature-attributable deaths are displaced, and whether extent of displacement varies by factors such as age, poverty, and preexisting conditions, and how extreme were the heat and cold.