Abstract
Osteoporosis is a life threatening disease which commonly affects women mostly after their menopause. It primarily causes mild bone fractures, which on advanced stage leads to the death of an individual. The diagnosis of osteoporosis is done based on bone mineral density (BMD) values obtained through various clinical methods experimented from various skeletal regions. The main objective of the authors’ work is to develop a hybrid classifier model that discriminates the osteoporotic patient from healthy person, based on BMD values. In this Letter, the authors propose the monarch butterfly optimisation-based artificial neural network classifier which helps in earlier diagnosis and prevention of osteoporosis. The experiments were conducted using 10-fold cross-validation method for two datasets lumbar spine and femoral neck. The results were compared with other similar hybrid approaches. The proposed method resulted with the accuracy, specificity and sensitivity of 97.9% ± 0.14, 98.33% ± 0.03 and 95.24% ± 0.08, respectively, for lumbar spine dataset and 99.3% ± 0.16%, 99.2% ± 0.13 and 100, respectively, for femoral neck dataset. Further, its performance is compared using receiver operating characteristics analysis and Wilcoxon signed-rank test. The results proved that the proposed classifier is efficient and it outperformed the other approaches in all the cases.
Keywords: diseases, bone, neural nets, optimisation, sensitivity analysis, pattern classification, medical diagnostic computing, patient diagnosis, orthopaedics
Keywords: Wilcoxon signed-rank test, receiver operating characteristics analysis, lumbar spine dataset, femoral neck dataset, 10-fold cross-validation method, monarch butterfly optimisation-based artificial neural network classifier, osteoporotic patient, hybrid classifier model, skeletal regions, clinical methods, BMD values, bone mineral density, osteoporosis diagnosis, mild bone fractures, menopause, life threatening disease, monarch butterfly optimisation algorithm, osteoporosis classification
1. Introduction
Osteoporosis is a silent, chronic and common metabolic bone disease characterised by low bone mass due to the loss of bone tissues. This leads to the micro-architectural deterioration of bone tissues with the increased risk of bone fragility and bone fractures mainly at spine and femur area. It also reduces the patient's height [1, 2]. It should be properly diagnosed at the earliest stage, so that a proper treatment can be given to prevent serious condition. Dual-energy X-ray Absorptiometry (DEXA) is the famous technique for measuring bone mineral density (BMD) values that is used to confirm a diagnosis of osteoporosis. The measurements are commonly done at lumbar spine, femoral neck and hip area. BMD testing is a vital component in the diagnosis, prediction and management of osteoporosis. A real BMD is expressed in absolute terms of grams of mineral per square centimetre scanned (g/cm2) and as a relationship to two norms the patient's T-score and Z-score provided by DEXA. T-score is the BMD value compared with that of young healthy adults of the same age who are at their BMD. World Health Organization (WHO) criteria defined for osteoporosis based on BMD measurements by DEXA, as T-score ≥–1 to be normal, T-score between –1 and –2.5 as low bone mass (osteopenia) and T-score ≤–2.5 as osteoporosis [3]. The difference between the patient's score and the norm is expressed in standard deviation above or below the mean. It also provides the patient's Z-score, which reflects a value compared with that of person matched for age and sex. The low BMD values can also be identified at dental region with a mandibular cortical width derived from digital dental panoramic radiographs (DPRs). This inexpensive method also helps in the identification of osteoporosis [4–6]. Mostly, women between 45 and 90 years of age are easily prone to osteoporosis.
The remaining of this letter is organised as follows: Section 2 outlines the related work carried out in the literature, the details of the methods used are briefly discussed in Section 3, its simulation results are explained in Section 4, and Section 5 concludes the proposed work.
2. Related work in the literature
The related works carried out in the literature are discussed henceforth. The ability of radial basis support vector machine (RB-SVM) for the osteoporotic risk detection using digital hip radiographs of 50 subjects are evaluated [7]. The hybrid genetic swarm fuzzy (HGSF) classifier to diagnose females with osteoporosis using DPRs of Korean women was developed in [8]. The input attributes are partitioned to generate an initial membership function and a rule set. Further, classification and optimisation are performed using fuzzy inference system and genetic swarm algorithm, respectively in [8]. The regression-based SVM developed in [9] predicts the BMD values based on the factors determined from the dietary and lifestyle habits of 305 women by a survey conducted on the same. The output is fed into the regression trees to identify the factors that have a significant bearing on BMD to prevent osteoporosis. The classifiers such as RB-SVM and k-nearest neighbours (kNNs) in [10] are created by combining several features that are extracted from 200 micro-CT images using micro-CT software and volumetric topological analysis is used for osteoporosis diagnosis. The automatic approach by combining histogram-based automatic clustering algorithm (HAC) with RB-SVM presented in [11] screens osteoporosis in postmenopausal Japanese women. The SVM classifier presented in [12] classifies osteoporotic data based on the features extracted from X-ray images using a fractional Brownian motion model. In [13], the three classification algorithms namely multilayer feed-forward neural network (MFFN), Naïve Bayes, and logistic regression (LR) with and without wrapper-based feature selection approach based on genetic factors are compared for predicting osteoporosis in Taiwanese women.
Several meta-heuristic algorithms such as the ant colony optimisation (ACO) [14], artificial bee colony (ABC) algorithm [15], biogeography-based optimisation (BBO) [16], differential evolution (DE) [17], and the stud genetic algorithm (SGA) [18] are also used to train artificial neural network (ANN). It is also found that these hybrid algorithms gave good results for other specific applications in which they were employed but were not previously used in osteoporosis related work. In this work, a recently devised meta-heuristic algorithm called monarch butterfly optimisation (MBO) [19] is selected among many heuristic algorithms to optimise the weights and biases for training ANN with the purpose of classifying osteoporotic data from healthy ones. The simple and robust nature of the algorithm with the ability to deal with the trade-off between exploration and exploitation process inspired us to use this for solving our problem. Many meta-heuristic algorithms may sometimes get trapped in local minima [20] and give only feasible values instead of optimal values. Sometimes may fail to produce optimal values with high-dimensional data and also slow down the convergence of the algorithm yielding less convergence rate. In some cases, the generalisation ability of these algorithms is also not appreciable. Our algorithm overcomes these issues. Only a very few osteoporotic related works are carried out in the past. The main objective of our work is to build a robust classifier which gives very accurate decision in the early detection of osteoporosis. This helps in giving necessary treatment in order to prevent the serious conditions caused at the advanced stage.
3. Methods
The overall approach is represented using a flow diagram in Fig. 1.
Fig. 1.
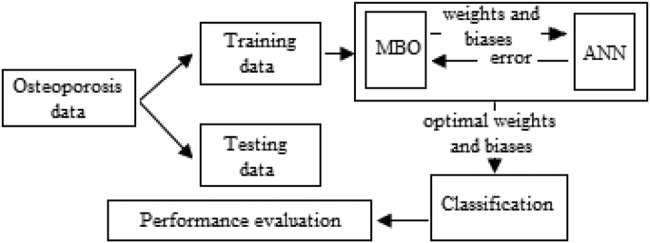
Flow diagram of MBO-ANN
3.1. Artificial neural network
The simple ANN is a three-layered architecture described as; the first layer is the input layer, a middle hidden layer and the output layer at last. It is massive, parallel and strongly connected network architecture. Back propagation network (BPN) algorithm is mostly used to train MLP. It uses a gradient descent approach to minimise the errors produced during training [21]. The architecture of ANN with three layers is shown in Fig. 2.
Fig. 2.
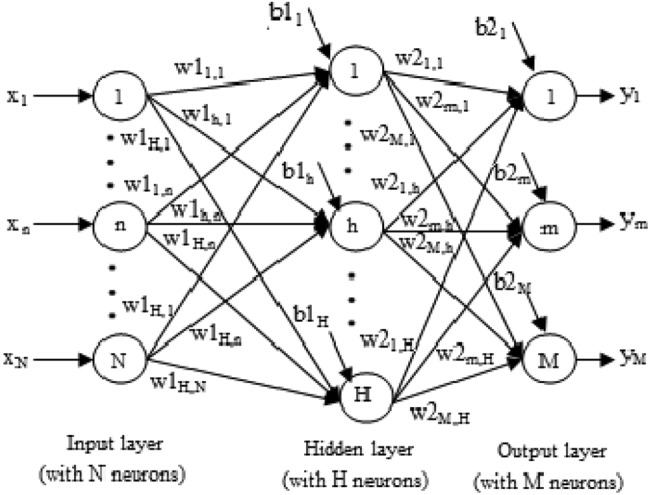
Three-layered ANN architecture
The steps for training ANN are gave below:
1: Initialise the synaptic weights and biases with random values.
2: Load the training data.
For the jth sample,
- 3: The net input at the hidden layer is calculated as
where w1h, n is the weight between input neuron ‘n’ and hidden neuron ‘h’, N and H are the sizes of input and hidden layers, respectively, and b1h is the bias value of hidden neuron ‘h’. The hidden layer output is calculated as(1) (2) - 4: Calculation of net input using at output layer is done as
where w2m, h is the weight between hidden neuron ‘h’ and output neuron ‘m’, b2m is the bias value of output neuron ‘m’. M is the number of output nodes. The network output is calculated below:(3) (4) - 5: The difference between the target output and network output gives the error value, which is calculated using the following equation:
where and are the target output and network output, respectively.(5) 6: The weight and bias values are updated.
7: Repeat from steps 2 to 6, for all training data till the error is minimised, which indicates the completion of the training process.
The final set of weights and biases at the end of the training is used to classify any unseen data. It is observed that optimum weights and biases are the primary parameters needed for training ANN.
3.2. MBO algorithm
It is a population-based algorithm devised from the inspiration of migration behaviour of the monarch butterflies between land1 and land2 based on the seasons. The total population of butterflies, NP is divided into two based on their fitness. The number of monarch butterflies in land1 and land2 are calculated as subpopulation1 (NP1) = ceil (p*NP) (NP1) and subpopulation2 (NP2) = NP − NP1, respectively, where ‘p’ is the migration ratio. The positions of monarch butterfly individuals are updated using migration operator (MO) and butterfly adjusting operator (BAO).
3.2.1. Migration operator
The offspring are generated (position updating) in subpopulation1 by MO and adjusted based on ‘p’, the ratio of monarch butterflies in land1. The position of each butterfly ‘m’ from subpopulation1 is based on that of individuals from subpopulation1 or subpopulation2. This is formulated as follows:
| (6) |
where is the jth element of at generation t + 1, t is the current generation. r1 and r2 are the monarch butterflies randomly selected from subpopulation1 and subpopulation2, respectively. r = rand*peri, where rand is the random number between [0, 1] and peri is the migration period.
3.2.1. Butterfly adjusting operator
The offspring of subpopulation2 is produced by BAO. The position of each butterfly individual is given as
| (7) |
where denotes the kth element of global best individual among the whole population, r3 is the randomly selected monarch butterfly from subpopulation2, rand is the random number generated between [0, 1], BAR is the butterfly adjusting ratio, dz is the walk step of butterfly ‘q’ calculated using Levy flight as dz = Levy and α = (Smax/t2) is the weighting factor, where Smax is the maximum walk step.
Finally, the newly generated butterfly with best fitness is replaced with its parent and moved to the next generation; else it is discarded to keep the population size as same.
3.3. Proposed MBO-ANN approach
3.3.1. Encoding of weights and biases
Each monarch butterfly ri from the population of size NP is encoded as a D-dimensional vector given below:
| (8) |
where is the weight vector representing the synaptic weights between input and hidden layers, is the weight vector containing synaptic weights between hidden and output layers, and are the bias vectors of hidden layer and output layer neurons, respectively. These weight and biases constitutes the elements of a butterfly which represents its position. The butterfly vector length ‘D’ is calculated as
| (9) |
where N, H and M are the number of input neurons, hidden neurons and output neurons, respectively.
3.3.2. Fitness function formulation
The MSE for one training sample is calculated using (5). The performance of ANN is based on the entire training data of size S. Hence the fitness function, F of MBO is the average MSE of the entire training samples, which is formulated as
| (10) |
The minimum MSE is considered as fitness value.
3.3.3. MBO-ANN implementation
Initially, the weights and biases for ANN are initialised with the random values and the fitness is calculated. In the next generation, weights and biases for ANN training are updated with the best position of the butterfly with best fitness value, calculated by MBO. The average MSE is calculated by the ANN. Thus the MBO algorithm calculates the best butterfly in the forward path for training ANN and receives the average MSE in the reverse path. This process is iteratively done till the minimum average MSE is achieved or the maximum generation is reached. Finally, after the training process, a set of optimal weight and bias values are given by the proposed MBO-ANN classifier. It is used to discriminate any unknown data as osteoporotic or non-osteoporotic. The MBO-ANN promises for the faster convergence with good convergence rate as most butterflies produce same fitness values with best global optimum values.
4. Simulation results
The proposed model is developed using MATLAB R2015b in the Intel core i5 processor with the speed of 2.7 GHz and 4 GB RAM. In this section, the details of the simulation results produced by MBO-ANN for the classification of two osteoporotic datasets are discussed. The experiments are conducted using the 10-fold cross-validation method. The performance is validated based on the classifiers learning ability and generalisation ability for the two datasets. The classifier is further statistically evaluated using receiver operating characteristics (ROC) analysis and Wilcoxon signed-rank test. To provide a meaningful result, the performance of the proposed MBO-ANN classifier is compared with that of five similar hybrid ANNs such as ACO-ANN, ABC-ANN, BBO-ANN, DE-ANN and SGA-ANN. For the purpose of comparison, these five algorithms are developed from the scratch with the relevant parameters based on optimisation algorithms [14–18].
4.1. Osteoporotic dataset
The datasets from the literature [8] are used for classification. Each dataset consists of 141 records, each containing 10 input attributes (first four attributes represents the patient's demographics and remaining six are the attributes of mandibular cortical bone and trabecular bone derived from the digital DPR of the patients) and one output attribute which denotes class labels. This value is based on the BMD values of the lumbar spine (L2–L4) (dataset1) and the femoral neck (dataset2). Based on some standard values for bone density, if the patient's BMD is within some range it would be healthy (non-osteoporotic), then the class label assigned as 1 else the class label assigned is 0 (osteoporotic). In the lumbar spine (LS) dataset, 21 patients are found to be osteoporotic and 120 as non-osteoporotic. Whereas in the femoral neck (FN) dataset, 20 patients are found to be osteoporotic and 121 as non-osteoporotic. Table 1 gives the details of the attributes.
Table 1.
Details of the input attributes in osteoporotic dataset (lumbar spine and femoral neck)
| Attribute number | Attribute name | Attribute description |
|---|---|---|
| 1 | age | age of the patient |
| 2 | height | height of the patient |
| 3 | weight | weight of the patient |
| 4 | BMI | body mass index |
| 5 | C.Width | cortical bone width or thickness |
| 6 | C.FD | cortical bone fractal dimension |
| 7 | Tr.thick | trabecular bone thickness |
| 8 | Tr.FD | trabecular bone fractal dimension |
| 9 | Tr.Numb | trabecular number |
| 10 | Tr.separa | trabecular separation |
4.2. Network setting
As it is widely accepted that the ANN with three layers is sufficient to approximate most of the functions, it is selected. The input layer size (N) and output layer size (M) is set to 10 and 1, respectively, based on the structure of the dataset. A less number of hidden neurons lower the function approximation and the more neurons cause over fitting with increased computation time. To avoid these issues, the number of hidden neurons is carefully selected among the three different values 7, 10 and 21 derived from the rules 0.75 × N, N and 2 × N + 1, respectively, based on Kolmogorov's theorem and the suggestions given in [22, 23]. Experimentally, it is found that the network with 7 hidden neurons performed well with the datasets. Hence, the ANN architecture is fixed as 10-7-1. The sigmoidal function is selected to act as the activation function in both hidden layer and output layer. To obtain the optimal weights and biases, the MBO parameters are set based on [19], as Smax = 1.0, peri = 1.2(as 12 months in a year), BAR = 5/12, p = 5/12, NP = 30, hence NP1 and NP2 are 13 and 17, respectively, and maximum generation = 100. At first, the MBO-ANN model is trained as discussed in Section 4, with the optimal values and then its performance is evaluated.
4.3. Learning ability
The main goal of the learning process is to find the optimal set of weights and biases on performing the mapping between input and output to gain good accuracy. The learning ability of the MBO-ANN for LS and FN datasets are discussed based on its convergence behaviour during its training. It is visually shown using Figs. 3 and 4, plotted with the MSE values obtained in different generations. It is observed from both the figures that the performance curve of MBO-ANN steeps down quickly to reach the minimum MSE value within 20 generations. It gradually converges to the fitness value of 0.001 for LS and FN datasets. The best fitness value of 0.00073 and 0.00068 is returned by MBO-ANN after all iterations. This obtained low value gives evidence that the global search is performed by MBO-ANN to yield the best optimum training parameters. BBO-ANN is found to be competitive with MBO-ANN as it produces MSE of 0.002 which is significantly a closer value. ACO-ANN performed moderately. However, the other algorithms such as ABC-ANN, SGA-ANN and DE-ANN get trapped in local minima and shows premature convergence. This shows that MBO-ANN has good learning ability for the two datasets when compared with other approaches.
Fig. 3.
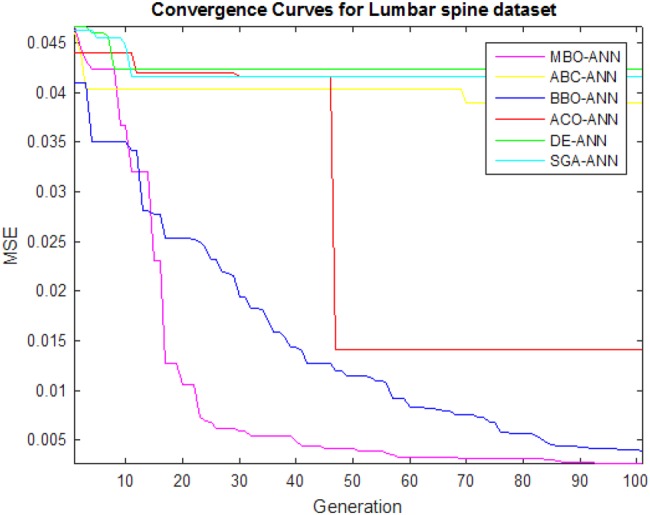
Convergence curves of algorithms for LS dataset
Fig. 4.
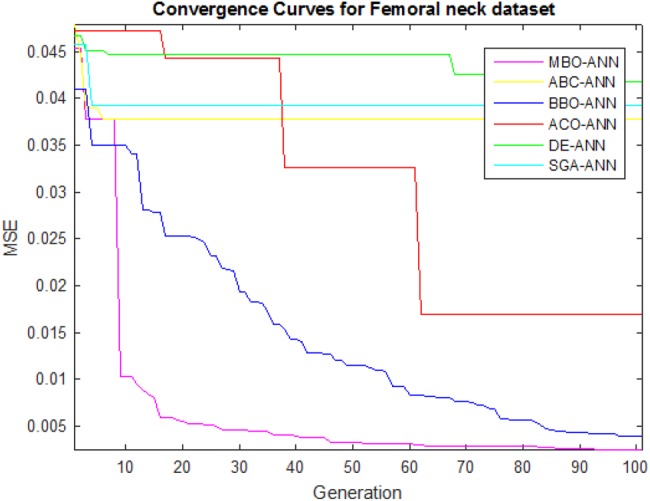
Convergence curves of algorithms for FN dataset
4.4. Generalisation ability
The generalisation ability of MBO-ANN classifier for the two datasets is evaluated using 10-fold cross-validation. For this, each dataset is divided into ten equal subsets. Then nine subsets are used to train the classifier, while the remaining one subset is used for testing. This process is repeated for ten times such that each subset is given a chance for testing and the classifier performance is noted. The performance parameters are estimated by averaging the ten appropriate values yielded by the classifier. The experiments are conducted for all the approaches using 10-fold cross-validation method with ten independent trials with the purpose to reduce the influence of randomness.
The performance parameters such as average fitness values (mean), standard deviation of fitness values (Std), best fitness value (best), average of correctly classified data in percentage (Cc), average of incorrectly classified data in percentage (Inc) and average computation time in seconds (Ct), from all the trials are calculated. The performance of MBO-ANN is compared with other classifiers using these parameters and it is reported in Table 2. The results indicate that the MBO-ANN classifier yielded a good classification accuracy of 97.9 and 99.3% for LS and FN datasets, respectively. This is comparatively higher than other approaches. BBO-ANN is found to be competitive with MBO-ANN as it yields the accuracy of 95 and 96.5% for LS and FN datasets, respectively, which is significantly closer to MBO-ANN accuracy.
Table 2.
Summary of performance comparison for osteoporotic datasets on 10-fold cross-validation
| Approach | Data | Mean | Std | Best | Cc | Inc | Ct |
|---|---|---|---|---|---|---|---|
| MBO-ANN | LS | 0.00132 | 0.00021 | 0.00073 | 97.9 | 2.1 | 36.09 |
| FN | 0.00105 | 0.00019 | 0.00068 | 99.3 | 0.7 | 36.13 | |
| ACO-ANN | LS | 0.01438 | 0.0.0073 | 0.01218 | 92.2 | 7.8 | 36.68 |
| FN | 0.01791 | 0.00574 | 0.00975 | 92.9 | 7.1 | 36.80 | |
| ABC-ANN | LS | 0.14112 | 0.01297 | 0.02752 | 90.8 | 9.2 | 37.38 |
| FN | 0.08602 | 0.01002 | 0.02147 | 87.23 | 12.77 | 36.17 | |
| BBO-ANN | LS | 0.00280 | 0.00126 | 0.00183 | 95 | 5 | 40.15 |
| FN | 0.00254 | 0.00092 | 0.00217 | 96.5 | 3.5 | 41.04 | |
| DE-ANN | LS | 0.10189 | 0.14021 | 0.07231 | 90.1 | 9.9 | 42.20 |
| FN | 0.09271 | 0.09120 | 0.09221 | 88.65 | 11.35 | 42.91 | |
| SGA-ANN | LS | 0.04183 | 0.01496 | 0.11918 | 88.7 | 11.3 | 32.79 |
| FN | 0.03872 | 0.19002 | 0.11149 | 85.8 | 14.2 | 32.71 |
Among all the approaches it is noted that the computation time of MBO-ANN is 36.09/36.13 s and SGA-ANN is only 32.79/32.71 s, respectively, for the lumbar spine and femoral neck datasets, but it is found that the accuracy of SGA-ANN is only 88.7 and 85.8% for lumbar spine and femoral neck datasets, respectively. In the medical domain, it is expected that the diagnostic accuracy of the disease should be high even if it takes a little more time for providing the proper treatment given to the patients. It is observed that ABC-ANN and DE-ANN have similar performance but better than SGA-ANN.
4.5. ROC analysis
The statistical evaluation of the test results is done based on ROC curve. It is a plot of all the sensitivity/(1−specificity) value pairs got by varying the decision threshold over its entire range of the test carried out. It depicts the trade-off between hit rates and false-alarm rates of the classifier. It is repeated with all the classifiers for both the datasets. The area under curve (AUC) is calculated and the classifiers are ranked with these values. The results are reported as AUC (rank) format in Table 3. The last row shows the average rank (Avg. rank) obtained by the classifiers. It is also observed from the table that the maximum AUC values obtained using MBO-ANN are 0.989 and 0.996 for LS and FN datasets, respectively. MBO-ANN ranks first among all the approaches. The average and standard deviation of specificity/sensitivity of the MBO-ANN are calculated as 98.33% ± 0.03/95.24% ± 0.08 and 99.2% ± 0.13/100 for LS and FN datasets, respectively. This shows that the classifier is good and accurate in discriminating the data samples into osteoporotic and non-osteoporotic.
Table 3.
Results of ROC analysis
| Data | MBO-ANN | ACO-ANN | ABC-ANN | BBO-ANN | DE- ANN | SGA-ANN |
|---|---|---|---|---|---|---|
| LS | 0.989(1) | 0.926(3) | 0.912(4) | 0.965(2) | 0.906(5) | 0.897(6) |
| FN | 0.996(1) | 0.931(3) | 0.887(5) | 0.972(2) | 0.891(4) | 0.866(6) |
| avg. rank | 1 | 3 | 4.5 | 2 | 4.5 | 6 |
4.6. Wilcoxon signed-rank test
The algorithms may perform differently in different runs. To examine whether MBO-ANN presents a significant improvement over other hybrids, the non-parametric two-tailed Wilcoxon signed-rank test [24] is employed at a significance level of 5%, (α = 0.05). A pairwise comparison is made between MBO-ANN and other approaches for the two datasets based on accuracy in different runs. The null hypothesis (H0) and alternate hypothesis (H1) are set as H0: There is no significance difference occurred in performance between two algorithms and H1: There is a significant difference occurred between in performance two algorithms. The results of the Wilcoxon signed-rank test are given in Table 4.
Table 4.
Results of Wilcoxon signed-rank test at α = 0.05
| Comparison | R+ | R− | Z-value | p-value | Null hypothesis |
|---|---|---|---|---|---|
| MBO-ANN versus ACO-ANN | 204 | 6 | −3.695 | 0.00022 | rejected |
| MBO-ANN versus ABC-ANN | 207 | 3 | −3.807 | 0.00014 | rejected |
| MBO-ANN versus BBO-ANN | 174 | 36 | −2.576 | 0.00988 | rejected |
| MBO-ANN versus DE-ANN | 204 | 6 | −3.695 | 0.00022 | rejected |
| MBO-ANN versus SGA-ANN | 207 | 3 | −3.807 | 0.00014 | rejected |
The difference in their accuracy is ranked as, R+ is the sum of ranks where MBO-ANN outperforms the other approach and R− is the sum of rank for the second algorithm taken in that comparison. In all the cases, it is found that p-value <α and Z-value <−1.96 for the rejection of the null hypothesis at the significance level of 0.05. The results provide strong evidence in the favour of MBO-ANN for its efficiency.
Further, Table 5 gives the comparison of our work with others in the literature that is based on the accuracy (Acc), specificity (Sp) and sensitivity (Sn).
Table 5.
Comparison with other works in the literature on osteoporosis classification
| Work carried | Approach | Performance |
|---|---|---|
| [7] | RB-SVM + hip radiographs | 90% Acc, 90% Sn, 87% Sp |
| [8] | HGSF classifier + DPRs of lumbar spine | 96.01% Acc, 95.3% Sn, 94.7% Sp |
| HGSF classifier + DPRs of femoral neck | 98.9% Acc, 99.1% Sn, 98.4% Sp | |
| [9] | regression SVM + factors from dietary and lifestyle habits | values not mentioned |
| [10] | RB-SVM + kNN + micro-CT images | values not mentioned |
| [11] | HAC algorithm + RB- SVM + DPRs of lumbar spine | 93% Acc, 95.8% Sn, 86.6% Sp |
| HAC algorithm + RB-SVM + DPRs of femoral neck | 89% Acc, 96% Sn, 84% Sp | |
| [12] | SVM + X-ray images | 95% Acc, Sn and Sp not mentioned |
| [13] | MFFN + WFS | Acc not mentioned, 57.9% Sn, 68.9% Sp |
| Naïve Bayes + WFS | Acc not mentioned, 0% Sn, 62% Sp | |
| LR + WFS | Acc not mentioned, 40.7% Sn, 62.3% Sp | |
| our proposed method | MBO-ANN + DPRs of lumbar spine | 97.9% Acc, 95.2% Sn, 98.3% Sp |
| MBO-ANN + DPRs of femoral neck | 99.3% Acc, 100% Sn, 99.2% Sp |
5. Conclusion
In this Letter, the recently devised MBO algorithm is used to optimise the weights and biases for training the ANN. This MBO-ANN classifier is used to classify two real world osteoporotic datasets namely LS and FN datasets, from healthy ones. The experiments were conducted using the 10-fold cross-validation method. The proposed classifier performance is analysed based on its learning ability and generalisation ability. Further, the statistical analysis was performed using ROC analysis and Wilcoxon signed-rank test to justify the performance of the proposed classifier. The results were compared with other approaches in the literature and other similar ANN hybrids. The accuracy, specificity, sensitivity values are given by MBO-ANN are 97.9% ± 0.14, 98.33% ± 0.03, 95.24% ± 0.08 and 99.3% ± 0.16%, 99.2% ± 0.13, 100 for LS and FN datasets, respectively. These estimated values of MBO-ANN are relatively found to be higher than other approaches. The MBO-ANN is ranked first among other hybrids based on AUC comparison. It is evidently found that MBO-ANN outperforms all other approaches to the discrimination of osteoporotic samples from healthy ones. It also reveals that MBO has made a better trade-off between exploration and exploitation process leading to global search in the way of finding optimal values to train ANN. It would have to be considered that MBO-ANN is suitable for very high dimensional medical data classification. In future, it is planned to focus on problems related to the medical domain.
6. Acknowledgment
The authors sincerely thank Prof. M.S. Kavitha, Kyungpook National University, Korea in [8] for providing the datasets.
7. Funding and declaration of interests
None declared.
8 References
- 1.World Health Organization: ‘Assessment of fracture risk and its application to screening for postmenopausal women for osteoporosis’. Geneva, Switzerland, 1994 [PubMed] [Google Scholar]
- 2.Klibanski A., Adams-Campbell L., Bassford T., et al. : ‘Osteoporosis prevention, diagnosis, and therapy’, J. Am. Med. Assoc., 2001, 285, (6), pp. 785–795 (doi: 10.1001/jama.285.6.785) [DOI] [PubMed] [Google Scholar]
- 3.National Osteoporosis Foundation: ‘Clinician's guide to prevention and treatment of osteoporosis’ (National Osteoporosis Foundation, Washington, DC, 2010) [Google Scholar]
- 4.Law A.N., Bollen A.M., Chen S.K.: ‘Detecting osteoporosis using dental radiographs: a comparison of four methods’, J. Am. Dent. Assoc., 1996, 127, pp. 1734–1742 (doi: 10.14219/jada.archive.1996.0134) [DOI] [PubMed] [Google Scholar]
- 5.Devlin H., Karayianni K., Mitsea A., et al. : ‘Diagnosing osteoporosis by using dental panoramic radiographs: the OSTEODENT project’, Oral Surg., Oral Med., Oral Pathol., Oral Radiol. Endod., 2017, 104, (6), pp. 821–828 (doi: 10.1016/j.tripleo.2006.12.027) [DOI] [PubMed] [Google Scholar]
- 6.Klemetti E., Kolmakow S.: ‘Morphology of the mandibular cortex on panoramic radiographs as an indicator of bone quality’, Dentomaxillofac. Radiol., 1997, 26, pp. 22–25 (doi: 10.1038/sj.dmfr.4600203) [DOI] [PubMed] [Google Scholar]
- 7.Sapthagirivasan V., Anburajan M.: ‘Diagnosis of osteoporosis by extraction of trabecular features from hip radiographs using support vector machine: an investigation panorama with DXA’, Comput. Biol. Med., 2013, 43, pp. 1910–1919 (doi: 10.1016/j.compbiomed.2013.09.002) [DOI] [PubMed] [Google Scholar]
- 8.Kavitha M.S., Ganesh Kumar P., Park S.-Y., et al. : ‘Automatic detection of osteoporosis based on hybrid genetic swarm fuzzy classifier approaches’, Dentomaxillofac Radiol., 2016, 45, pp. 1–3 (doi: 10.1259/dmfr.20160076) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ordóñez C., Matías J.M., de Cos Juez J.F., et al. : ‘Machine learning techniques applied to the determination of osteoporosis incidence in post-menopausal women’, Math. Comput. Model., 2009, 50, pp. 673–679 (doi: 10.1016/j.mcm.2008.12.024) [Google Scholar]
- 10.Xu Y., Li D., Chen Q., et al. : ‘Full supervised learning for osteoporosis diagnosis using micro-CT images’, Microsc. Res. Tech., 2013, 76, pp. 333–341 (doi: 10.1002/jemt.22171) [DOI] [PubMed] [Google Scholar]
- 11.Kavitha M.S., Asano A., Taguchi A., et al. : ‘The combination of a histogram-based clustering algorithm and support vector machine for the diagnosis of osteoporosis’, Imaging Sci. Dent., 2013, 43, pp. 153–161 (doi: 10.5624/isd.2013.43.3.153) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Tafraouti A., Hassouni M.E., Toumi H., et al. : ‘Osteoporosis diagnosis using fractal analysis and support vector machine’. IEEE Tenth Int. Conf. Signal-Image Technology & Internet-Based Systems, 2014, (doi: 10.1109/SITIS.2014.49) [Google Scholar]
- 13.Chang H.-W., Chiu Y.-H., Kao H.-Y., et al. : ‘Comparison of classification algorithms with wrapper-based feature selection for predicting osteoporosis outcome based on genetic factors in a Taiwanese women population’, Int. J. Endocrinol., 2013, 2013, pp. 1–8 (doi: 10.1155/2013/850735) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dorigo M., Maniezzo V., Colorni A.: ‘Ant system: optimization by a colony of cooperating agents’, IEEE Trans. Syst. Man Cybern. B, Cybern., 1996, 26, (1), pp. 29–41 (doi: 10.1109/3477.484436) [DOI] [PubMed] [Google Scholar]
- 15.Karaboga D., Basturk B.: ‘A powerful and efficient algorithm for numerical function optimization: artificial bee colony (ABC) algorithm’, J. Global Optim., 2007, 39, (3), pp. 459–471 (doi: 10.1007/s10898-007-9149-x) [Google Scholar]
- 16.Simon D.: ‘Biogeography-based optimization’, IEEE Trans. Evol. Comput., 2008, 12, (6), pp. 702–713 (doi: 10.1109/TEVC.2008.919004) [Google Scholar]
- 17.Storn R., Price K.: ‘Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces’, J. Global Optim., 1997, 11, (4), pp. 341–359 (doi: 10.1023/A:1008202821328) [Google Scholar]
- 18.Khatib W., Fleming P.: ‘The stud GA: a mini revolution?’. Proc. of the 5th Int. Conf. Parallel Problem Solving from Nature, New York, 1998, pp. 683–691 [Google Scholar]
- 19.Wang G.-G., Deb S., Cui Z.-H.: ‘Monarch butterfly optimization’, Neural Comput. Appl., 2015, pp. 1–20, (doi:10.1007/s00521-015-1923-y) [Google Scholar]
- 20.Gori M., Tesi A.: ‘On the problem of local minima in backpropagation’, IEEE Trans. Pattern Anal. Mach. Intell., 1992, 14, (1), pp. 76–86 (doi: 10.1109/34.107014) [Google Scholar]
- 21.Fine T.L.: ‘Feedforward neural network methodology’ (Springer Verlag, New York, NY, USA, 1999) [Google Scholar]
- 22.Kurkova V.: ‘Kolmogorov's theorem is relevant’, Neural Comput., 1991, 3, pp. 617–622 (doi: 10.1162/neco.1991.3.4.617) [DOI] [PubMed] [Google Scholar]
- 23.Hegazy T., Moselhi O., Fazio P.: ‘Developing practical neural network application using backpropagation’, J. Microcomput. Civil. Eng., 1994, 9, (2), pp. 145–159 (doi: 10.1111/j.1467-8667.1994.tb00369.x) [Google Scholar]
- 24.Wilcoxon F.: ‘Individual comparisons by ranking methods’, Biometrics Bull., 1945, 1, pp. 80–83 (doi: 10.2307/3001968) [Google Scholar]


