Relative Precision, Efficiency and Construct Validity of Different Starting and Stopping Rules for a Computerized Adaptive Test: The GAIN Substance Problem Scale

Abstract

Substance abuse treatment programs are being pressed to measure and make clinical decisions more efficiently about an increasing array of problems. This computerized adaptive testing (CAT) simulation examined the relative efficiency, precision and construct validity of different starting and stopping rules used to shorten the Global Appraisal of Individual Needs’ (GAIN) Substance Problem Scale (SPS) and facilitate diagnosis based on it. Data came from 1,048 adolescents and adults referred to substance abuse treatment centers in 5 sites. CAT performance was evaluated using: (1) average standard errors, (2) average number of items, (3) bias in person measures, (4) root mean squared error of person measures, (5) Cohen’s kappa to evaluate CAT classification compared to clinical classification, (6) correlation between CAT and full-scale measures, and (7) construct validity of CAT classification vs. clinical classification using correlations with five theoretically associated instruments. Results supported both CAT efficiency and validity.

Introduction

Over the past 30 years Medicaid, states, managed care, and accrediting bodies have increasingly emphasized the need for substance abuse treatment agencies to accurately measure and make clinical decisions (e.g., diagnosis, placement) about an increasingly wider array of areas while demanding that these systems simultaneously improve their efficiency. The Global Appraisal of Individual Needs (GAIN; Dennis et al., 2003) is a family of instruments that is in use in over 200 agencies around North America and which includes a 1 to 2 hour comprehensive biopsychosocial instrument explicitly designed for intake into substance abuse treatment. While the instrument is relatively efficient for the amount of information it collects (103 scales, five axis diagnosis, placement, treatment planning, outcome monitoring, and economic data in 8 domains), the average agency spends 2 to 4 hours to complete its whole intake process including any further health/mental exams, drug testing and financial paper work (McLellan et al., 2003). This has led to repeated calls from programs to see if the GAIN can be made even more efficient. This paper uses a series of simulations to examine the feasibility of using computerized adaptive testing (CAT) to shorten the GAIN’s Substance Problem Scale (SPS) without losing its validity. The SPS is the GAIN’s main measure of substance use disorder severity and is used to make diagnostic (none/abuse/dependence) and placement (outpatient/residential) decision.

Computerized assessment systems, in general, and the GAIN specifically, directly save time by eliminating need for a separate data entry step, providing real time quality assurance on following instructions/skips/answers, and by immediately generating clinical reports to support diagnosis, placement, and interventions (Alexander and Davidoff, 1990; Borland, Balmford, and Hunt, 2004; Halberg, Duncan, Mitchell, Hendrick, and Jones, 1986). Research on the use of computerized assessment systems revealed that clients responded favorably to them (Carr and Ghash, 1983; Lewis et al., 1988; Lucas et al., 1977; Reich, Cottler, McCallum, Corwin, and VanEerdewegh, 1995). When combined with an appropriate measurement model, a computerized administrative system can also use more complex “skips” to create a more sensitive measure while simultaneously reducing the number of questions/respondent burden.

Computerized Adaptive Testing

Computerized Adaptive Testing (CAT) is an example of such a system. CAT was originally developed to improve the efficiency of achievement testing for secondary and post secondary placement decisions (Cory and Rimland, 1977; DeWitt, 1974; McKinley and Recase, 1980; Weiss and Kingsbury, 1984), and was later applied to more general psychosocial measurement and health care practice (See Wendt and Surges Tatum, 2005).

CAT generally uses item response theory (IRT; Lord and Novick, 1968; see also Lord, 1980) or Rasch (1960; Wright and Stone, 1979) measurement models to locate items along a single latent dimension. By calibrating responses based on the location (i.e., by severity/ability/rarity), these models typically produce a more reliable and sensitive measure than simple counts of symptoms or sums of responses (Halkitis, 1998; Kreiter, Ferguson, and Gruppen, 1999; Lunz and Bergstrom, 1994; Lunz and Deville, 1996). CAT can also use the order of these items to make a more efficient test. Unlike fixed-item formats that base severity estimates on a total symptom count, CAT re-estimates client severity after each response and determines whether there was a significant change from the prior responses. Based on the answers, it can ask a more or less severe question or suggest that it is time to stop. The result is that each CAT-selected item is “tailored” to respondent ability and the process often requires fewer questions to obtain the same amount of information.

While both IRT and Rasch measurement models place an individual on an assessment continuum, they have different strengths. IRT models can result in greater reduction of items administered, but are much more sensitive to the sample on which the norms are based (Hornke, 1999)—hence their dominant use in specific population/settings, such as educational testing, workplace performance. The Rasch model, in contrast, can produce measures that are independent of the sample’s distributional properties (Wright and Stone, 1979) and more appropriate for use across the kind of heterogeneous populations with multiple co-occurring problems which are more the norm in clinical and health services settings (Chang and Gehlert, 2003; Dijkers, 2003; Lai, Cella, Chang, Bode, and Heinemann, 2003; Lai et al., 2005; Wisniewski, 1986; Wright and Stone, 1979).

Using CAT to Place Individuals into Treatment Categories

Whereas numerous studies have examined CAT efficacy and efficiency for constructing a measurement continuum, relatively few studies have examined CAT’s success at placing individuals into the kind of diagnostic categories used in treatment practice. One approach that has been examined involves the use of confidence intervals of the estimated measure. That is, item administration continues until the confidence interval no longer crosses one or more cut points separating categories. The starting rule for item selection can occur by selecting the most informative item (i.e., the item that is likely to produce the greatest improvement in measurement precision given the current estimate of the measure) at a random point, the middle, a key cut point or the currently estimated ability level. In their simulation study, Eggen and Straetmans (2000) observed that selecting the most informative item at the currently estimated trait level provided the most accuracy in classification with fewer items administered; with the relative advantage of this starting rule increasing as the required level of accuracy (i.e., precision) is increased. Where the goal is to classify people into one of three levels of clinical severity (i.e., triage), the balance between CAT accuracy and efficiency may also be optimized if the level of measurement precision used in the stopping rule (i.e., required to stop asking questions) is “tighter” around the clinical decision-making cut points to achieve accurate classification but can be more lenient on the low and high end (where differences do not affect classification into low/moderate/high) to reduce the number of items and improve efficiency.

Present Study

The purpose of this CAT simulation is to examine the relative efficiency, precision and construct validity of different starting and stopping rules used to shorten the Global Appraisal of Individual Needs’ (GAIN) Substance Problem Scale (SPS) and facilitate triage based on it. For starting rules, it compares a random start versus one based on the GAIN short screener (GAIN-SS) for substance use disorders. For stopping rules, it compares several different combinations allowing for increasingly relaxed precision at the low and high end. For validity, it compares the resulting classifications with each other and with other variables to which substance use disorder classification is expected to be correlated.

The specific research questions this paper is designed to address are:

1. Is there a difference between CAT starting values based on a random value vs. starting values based on a screener in terms of the efficiency, precision and construct validity of the Substance Problems Scale (SPS)?

2. How does relaxing CAT stopping rule precision at the low and high ends of the scale affect measurement efficiency, i.e., fewer items, and classification precision?

3. Can construct validity of classification based on the CAT do as well as validity based on the raw Substance Problem Scale (SPS) and the Rasch based classification?

Methods

Data Sources

Data for this simulation came from baseline interviews conducted in two experiments that have been reported on extensively elsewhere and will only be summarized here. The Cannabis Youth Treatment Experiment (CYT; Dennis et al., 2002; 2004) was a multi-site randomized field experiment conducted between 1997 and 2000 that examined five “manual-guided” approaches to outpatient treatment of adolescent cannabis abuse or dependency. The experiment involved 600 adolescents (83% males, 17% females) recruited from 4 outpatient clinics around the country who were between the ages 12 to 18, reported one or more Diagnostic and Statistical Manual, Fourth Edition (DSM-IV) criteria for cannabis abuse or dependence (American Psychiatric Association [APA], 1994), had used cannabis in the past 90 days (or 90 days prior to being in a controlled environment), and met the American Society of Addiction Medicine (ASAM) patient placement criteria for Level I (outpatient) or Level II (intensive outpatient) treatment.

The Early Re-Intervention (ERI) experiment (Dennis, Scott, and Funk, 2003; Scott, Dennis and Foss, 2005) was conducted between 2000 and 2004 and examined the effect of monitoring and early re-intervention for adult drug users who had completed treatment. The experiment involved 448 adults (41% males, 59% females) recruited from a large central intake unit for over a dozen clinics. The participants had to be 18 years or older (47% were in their 30s), to meet lifetime criteria of substance abuse or dependence, have used alcohol or other drugs during the past 90 days, complete a central intake unit (CIU) assessment, and receive a referral to substance abuse treatment at a collaborating treatment agency. Thus, the sample for the present study includes people in outpatient, intensive outpatient, and residential levels of care.

Instruments

Both studies used the Global Appraisal of Individual Needs (GAIN; Dennis et al., 2003), measured severity of substance use with the Substance Problem Scale (SPS) and made presumptive diagnoses based on a categorization of responses to the SPS. The SPS consists of 16 items that assess “recency” (past month, 2–12 months, 1+ years, never) of symptoms of substance related problems: Seven items are based on DSM-IV criteria for substance dependence (tolerance, withdrawal, loss of control, inability to quit, time consuming, reduced activity, continued use in spite of medical/mental problems), four items for substance abuse (role failure, hazardous use, continued use in spite of legal problems, continued use in spite of family/social problems), two items for substance-induced disorders (health and psychological), and three items for lower severity symptoms commonly used in screeners (hiding use, people complaining about use, weekly use).

These items can be used in several different ways. A subset of 5 items (weekly use, family/ friends complaining, hiding use, continued use in spite of fights, time consuming) are often used as a screener for who is a likely case before committing to the full 1–2 hour GAIN interview. The subset of the seven dependence items is also scored as a Substance Dependence Subscale (SDS). The recency rating (overall or for just dependence) can be used to make symptom counts for the past month, year or lifetime. Higher scores on all of the overall scales and subscales represent greater severity of drug problems. The raw scores are used to classify people into low / moderate / high severity for both the full SPS (0/1–9/10–16) and the SDS (0–2/3–5/6–7). Based on DSM-IV criteria (American Psychiatric Association, 1994), individual items are used to classify people based on a “presumptive” diagnosis of dependence (3 to 7 of the dependence items), abuse (1–4 of the abuse items and no dependence), or other (including 1–2 symptoms of dependence and any number of non-abuse/dependence items). Generally substance abuse treatment is limited to those with abuse or dependence and residential treatment is further limited to those with higher severity dependence. In both experiments SPS was found to have good internal consistency (Cronbach’s alpha of .8 or more), test-retest reliability (Rho = .7 or more) and good test-retest reliability in terms of diagnosis (kappa = .5 or more). Table 1 summarizes variations of SPS scales and classification rules that will be used in this paper. Below is a further description of the development of the Rasch and CAT based measures.

Table 1.

Variable Definitions

Measures Based On The Substance Problem Scale (SPS)

Screener SPS—Count of 5 SPS items (weekly use; family. friends complaining; hiding use; continued use in spite of fights; time consuming) in the past year, treating past month or 2–12 months as 1 and more than a year ago or never as 0.

SPS Raw Score—Count of the 16 SPS items in the past year (see Table 2), treating past year (past month or 2–12 months recency) as 1 and more than a year ago or never as 0.

Rasch SPS—Measure based on the 16 SPS items using a recency rating scale (2=past month, 1=2 to 12 months ago, and 0 = more than a year ago or never) and the Rasch based severity calibration of the item.

CAT SPS—Measure based on the SPS items (same rating scale as in Rasch SPS) using a stopping rule based on the Rasch SPS triage cut points for low/moderate/high that target overall severity (see below).

SDS—The Substance Dependence Subscale consists of 7 of the 16 SPS items that represent symptoms of substance dependence, based on DSM-IV criteria.

CAT SDS—Similar to CAT SPS, but using a stopping rule based on the Rasch SDS triage cut points for low/ moderate/high that target the severity of dependence (see below).

Triage Categorizations Of Measures To Support Clinical Decision Making

SPS Raw Triage Group—The SPS raw symptom (Sx) count triage was based on 0 symptoms = low; 1 to 9 symptoms = moderate; and 10 to 16 symptoms = high. Those with moderate or high are generally assumed to have a substance disorder (abuse or dependence) and the high group would normally be placed into higher levels of care (e.g., intensive outpatient, methadone, residential)

Full Rasch and CAT SPS—The parallel Rasch/CAT measures was triage based on logits of less than −2.50 = low; −2.50 to −0.10 logits = moderate and −.10 or more logits = high. .

SDS Raw Triage Group—The SDS raw symptom (Sx) count triage was based on 0 to 2 symptoms = low; 3 to 5 symptoms = moderate; and 6 to 7 symptoms = high. Those with moderate or high generally have dependence, with those in high having more severe dependence and probably needing residential treatment

Full Rasch and CAT SPS—The parallel Rasch/CAT measure was triaged based on logits of less than −.75 = low; −.75 to +.70 logits = moderate; +.70 or more logits = high.

Criterion Validation

Current Withdrawal Scale (CWS; alpha =.95; test-retest rho = .59). The GAIN CWS is a count of past-week psychological (tired, anxious) and physiological (e.g., diarrhea, fever) symptoms of withdrawal and is based on DSM-IV (American Psychiatric Association, 2000).

Substance Frequency Scale (SFS; alpha = .85; test-retest rho = .94). The GAIN SFS is a multiple-item measure that averages percent of days reported of any AOD use, days of heavy AOD use, days of problem from AOD use, days of alcohol, marijuana, crack/cocaine, and heroin/opioid use.

Emotional Problems Scale (EPS; alpha = .90; test-retest rho = .56). This is an average of items (divided by their range) for recency of mental health problems, memory problems, and behavioral problems and the number of days (during the past 90) of being bothered by mental problems, memory problems, and behavioral problems, and the number of days the problems kept participant from responsibilities.

Recovery Environmental Risk Index (RERI; alpha = n.a. test-retest rho = .75). This is an average of items (divided by their range) for the days (during the past 90) of alcohol in the home, drug use in the home, fighting, victimization, homelessness, and structured activities that involved substance use and the inverse (90 minus answer) percent of days going to self-help meetings and involvement in structured substance-free activities.

Health Problem Scale (HPS; alpha = .82; test-retest rho = .65). This is an average of items (divided by their range) related to being bothered by physical/medical problems including days these problems kept client from meeting his/her responsibilities, and the recency of problems.

Development of a Rasch Based Version of SPS

Principal component analysis of Rasch item residuals indicated that the SPS was composed of one clear, strong dimension, which explained nearly 70% of the total variance. The person reliability of the SPS was .82 with separation of 2.12. The item reliability was .99 with separation of 13.21. Analysis of the original recency rating scale (3 = past month, 2 = 2–12 months, 1 = more than a year, 0 = never) suggested that a 3 point rating would be more reliable than a 4 point rating (Conrad, Dennis, et al., under review). Therefore, the rating scale was revised from 3210 to 2100 (i.e., 2 = past month, 1 = 2–12 months ago, 0 = more than a year ago/never). Raw scores using the revised rating scale were then transformed to Rasch measures using Winsteps (Linacre, 2005). These measures use the logarithm of odds unit or logit as the scaling unit on a scale that typically runs between –5 to +5 where persons and items are calibrated on the same interval measure (Rasch, 1960; Wright and Masters, 1982).

Table 2 shows the SPS items sorted by their calibrated difficulty level. Note that while much of drug treatment research has focused on abstinence or weekly use, “weekly use” is actually the lowest criterion in terms of SPS severity. The Rasch analysis indicated that abuse and dependence criteria are intermixed: rather than abuse representing “low severity” dependence and dependence high severity. This helps to demonstrate that abuse symptoms actually represent other reasons why individuals receive treatment in the absence of a fully developed syndrome (much as suicidal ideation is to depression). Consistent with DSM, the physiological symptoms of dependence help to mark moderate (tolerance) to high (withdrawal). In this table we have indicated which items are used in the screener and regular SPS (both past year symptom counts) and in the full and CAT versions of the Rasch measures.

Table 2.

Substance Problem Scale Item Calibration and Relations to Scales

Calibration	DSM Criteria [GAIN Variable] question: When was the last time	Past year Sx counts Screener	SPS	Avg. of Calibration Rasch/CAT
−1.39	S3.[e] you used alcohol or drugs weekly?	X	X	X
−0.81	D5.[s] you spent a lot of time either getting alcohol or drugs, using alcohol or drugs, or feeling the effects of alcohol or drugs (high, sick)?	X	X	X
−0.69	S2.[d] your parents, family, partner, co-workers, classmates or friends, complained about your alcohol or drug use?	X	X	X
−0.33	D3.[q] you used alcohol or drugs in larger amounts, more often or for a longer time than you meant to?		X	X
−0.32	A1.[h] you kept using alcohol or drugs even though you knew it was keeping you from meeting your responsibilities at work, school, or home?		X	X
−0.28	A4.[m] you kept using alcohol or drugs even though it was causing social problems, leading to fights, or getting you into trouble with other people?	X	X	X
−0.18	S1.[c] you tried to hide that you were using alcohol or drugs?	X	X	X
−0.06	D4.[r] you were unable to cut down or stop using alcohol or drugs?		X	X
0	D1.[n] you needed more alcohol or drugs to get the same high or found that the same amount did not get you as high as it used to?		X	X
0.13	I1.[f] your alcohol or drug use caused you to feel depressed nervous, suspicious, uninterested in things, reduced your sexual desire or caused other psychological problems?		X	X
0.22	D7.[u] you kept using alcohol or drugs even after you knew it was causing or adding to medical, psychological or emotional problems you were having?		X	X
0.28	D6.[t] your use of alcohol or drugs caused you to give up, reduce or have problems at important activities at work, school, home or social events?		X	X
0.6	A2.[j] you used alcohol or drugs where it made the situation unsafe or dangerous for you, such as when you were driving a car, using a machine, or where you might have been forced into sex or hurt?		X	X
0.66	A3.[k] your alcohol or drug use caused you to have repeated problems with the law?		X	X
0.71	D2.[p] you had withdrawal problems from alcohol or drugs like shaking hands, throwing up, having trouble sitting still or sleeping, or that you used any alcohol or drugs to stop being sick or avoid withdrawal problems?		X	X
1.46	I2.[g] your alcohol or drug use caused you to have numbness, tingling, shakes, blackouts, hepatitis, TB, sexually transmitted disease or any other health problems?		X	X

Notes: Criteria are S-Screener, A-Abuse, D-Dependence, I–Induced, where the number refers to their order in DSM-IV criteria and the letter in [ ] refers to the order in the GAIN on question sequence S9; the “X” means this variable is included in the scale (0/1 for symptom [Sx] counts; Rasch calibration x revised recency rating for the Rasch and CAT). Items marked with an “X” in the Rasch/CAT column indicate that the item is used as part of the full-scale Rasch measure and is included in the item bank used for the SPS CAT.

Defning Triage Categories for Clinical Decision Making

As noted earlier, the SPS is used clinically to triage individuals into low (0 past year symptoms), moderate (1 to 9 past year symptoms) and high (10 to 16 past year symptoms) ranges of substance use disorder severity, where substance abuse treatment is typically targeted at the upper two ranges and those in the high range are typically placed into more intensive levels of care (e.g., intensive outpatient, methadone, residential). The SDS is a subset of seven dependence symptoms that are also used to make a categorization focused just on residential treatment in states/agencies using the American Society of Addiction Medicine’s (ASAM, 2001) placement criteria. The SDS is categorized into low (0 to 2 past year symptoms), moderate (3 to 5 past year symptoms) and high (6 to 7 past year symptoms), where moderate represents dependence, and high represents severe dependence.

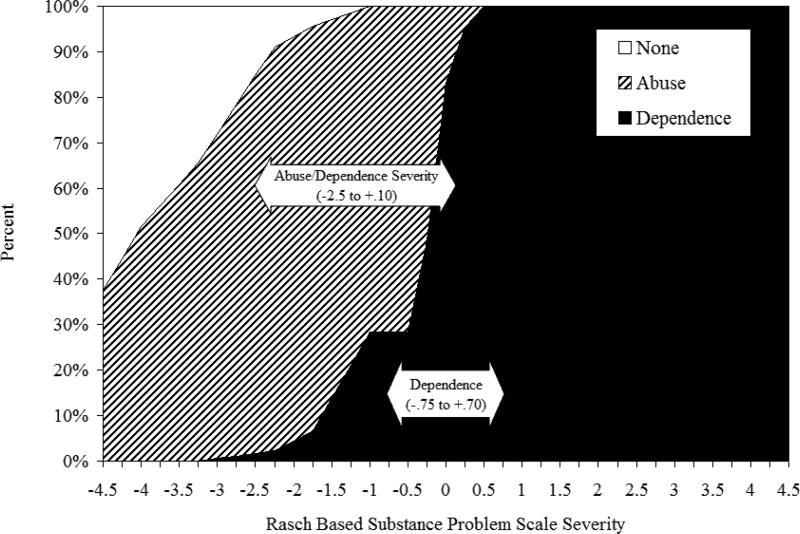
To determine cut points for the full and CAT versions of the Rasch measure we crossed each of the above triage groups with the Rasch measure to identify their location, and then compared this with diagnosis to verify that it had approximately the same relationship. Figure 1 illustrates the cumulative prevalence of “abuse” and “dependence” (recall that if they have both it is treated as dependence) as the Rasch severity goes up. The arrows show the middle ranges, with the SPS triage groups reflecting overall abuse/dependence severity while the SDS triage groups gauge the severity of dependence. In both cases, the middle range is where there is a lot of variability and need for more precision. To the left (low) and right (high), further changes in the measure do not have much effect on the dependence rate. Employing these cut points, the kappa coefficient indicating level of agreement between the raw and Rasch based categorizations were high for SPS overall (kappa = .82) and good for SDS (kappa = 0.66) Both compared favorably with the extent to which two psychiatrists would agree with each other (typically kappa of .4 for adolescents and .6 for adults). This paper will also compare the categorizations in terms of their construct validity as indicated by their relationship with substance-abuse associated symptoms (e.g., the severity of withdrawal symptoms, frequency of substance use, emotional problems, recovery risk environment, and health problems).

Figure 1.

Rasch Based Substance Problem Scale Severity (x-axis) by the prevalence of past year abuse/dependence (stacked area) with the mid point ranges for triage groups focused on overall abuse/dependence (general severity) and just dependence (high severity).

CAT Development and Simulation Procedures

We developed a simulation program using Visual Basic version 6.0 to execute an item selection algorithm. This program used item calibrations and step thresholds that were previously estimated in Winsteps (Linacre, 2002). The simulation program calculated estimates of person measures using algorithms of the Rasch rating scale model described by Linacre (1998). Item and person estimation, as well as pre-calibration starting value optimization and variable stopping rules are described below.

The baseline databases were analyzed to establish whether CAT administration would decrease the number of items presented, as well as facilitate classification of clients into treatment categories. The procedure is referred to as a simulation because data were not collected during a live CAT session. Rather, a starting item was chosen from each client’s data, and the existing response was used as though the client had responded. Then, based on that “response,” the algorithm selected the next item that would maximize information. This continued until a stopping rule criterion, of several described below, was achieved. Note that this was done twice, once using the SPS triage groups to drive the stopping rules (focusing on overall severity) and again using the SDS triage groups to drive the stopping rules (focusing more explicitly on the severity of dependence).

Starting Rules (Random vs. Screener)

For the first research question, we compared two methods that apply to different situations in practice. In many cases, there is no formal information available before doing a full assessment. In other cases a priori information on severity may be available from a screener that has the potential to improve the efficiency of the CAT. For this simulation we used the five item GAIN Substance Disorder Screener (SDScr) as the CAT starting value. Specifically, we compared the following two “start rules” for determining the initial value of the measure: (1) set the initial value of the measure using a random value between –0.5 and 0.5 logits, or (2) set the initial value based on the respondent’s measure from a substance abuse screening measure. The screener-based procedure makes use of the GAIN’s five-item substance abuse screener to (a) provide an initial estimate of the person’s measure on the SPS for purposes of selecting the first item, and (b) pre-set the standard error of measurement based on the standard error of measurement of the screener.

Stopping Rules

The second research question, concerning CAT efficiency, focuses on stopping the CAT when asking more questions does not produce a significant change in the estimated Rasch measure. The goal of CAT is to identify and stop at this point in order to reduce the number of questions asked and improve efficiency. The simulation’s variable stopping rule was defined by a standard error of measurement (SEM) criterion. From a practical standpoint, a lower SEM criterion means more accuracy (relative to the full Rasch measure) but also more items. Rather than using a single criterion, we defined a stringent criterion (SEM = .35 logits) for the middle range (where there was a lot of variability) and then varied a set of higher SEM criteria (SEM = .50, .60, .75) for the low and high ranges where less precision was needed (i.e., someone either clearly had no/low problem; or clearly had a severe problem).

Person Measure Estimation Using CAT Starting and Stopping Rules

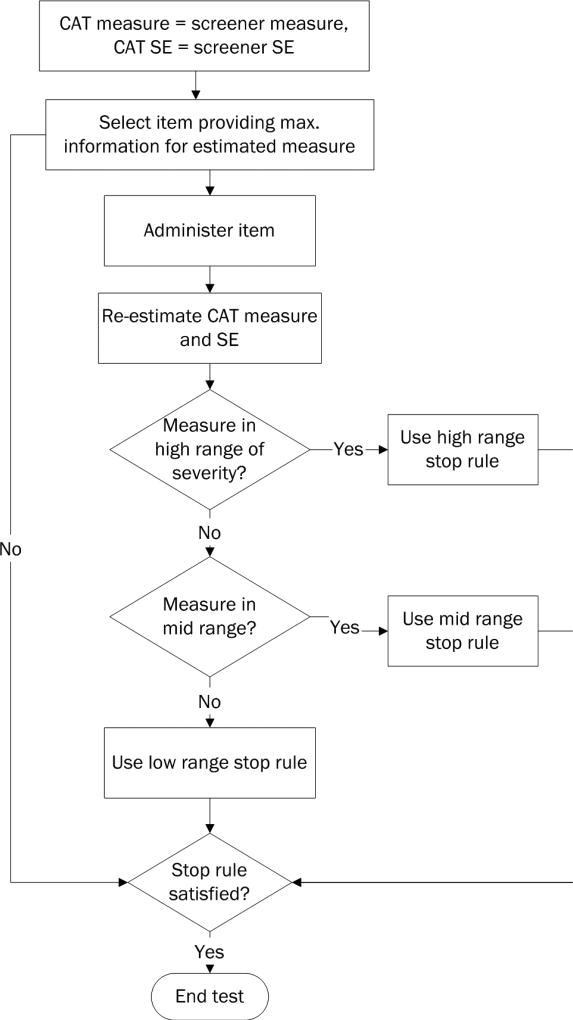
Person measure estimation using random and screener-based starting values is summarized as follows:

this is a test

1. For the random condition, set the initial (pre-CAT) measure by selecting a random value between −0.5 and 0.5 logits; for the screener condition, estimate the person starting value and standard error of measurement using the measure from the substance abuse screener.

2. Identify the item that provides maximum information given the currently estimated person measure.

3. Administer the item identified in Step 2.

4. Re-estimate the person measure and standard error.

5. Set the stopping rule according to the currently estimated measure and the defined cut points for low, medium and high [for SDS or SPS] severity.

6. Determine if the stopping rule established in Step 5 is satisfied, i.e., that the standard error of measurement falls at or below the standard error specified by the stopping rule.

7. If the stopping rule criterion is not met, go to Step 2; otherwise, end the test.

Appendix A also provides a flow chart describing the CAT procedure using variable stop rules and the screener to set the start value.

Criteria for CAT Evaluation

We assessed the results of the CAT using several established computerized adaptive testing criteria (Wainer, 2000). Efficiency was measured in terms of mean number of items (M), mean number of items for those in mid range (M MR), and efficiency ratio (E; see Hambleton, Swaminathan, and Rogers, 1991; Simms and Clark, 2005). E is the average amount of psychometric information provided during each CAT administration (i.e., the inverse square of the mean standard error of measurement) relative to the number of items administered. The formula for calculating E is:

$$E=\frac{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${(\overline{\mathit{\text{SE}}})}^2$}\right.}{{\overline{L}}_c}$$ (1)

where SE is the mean standard error across all CAT administrations and Lc is the mean number of items administered by the CAT. The smaller the mean standard error or the fewer number of items administered during the CAT, the higher the efficiency.

Precision was measured in terms of the mean standard error of measurement (M SEM), Bias, and the root mean square error (RMSE). Bias is calculated by subtracting the mean of the CAT-derived measure from the mean of the full-scale measure, and can indicate whether person measures obtained from the CAT are overestimating or underestimating trait levels relative to the full scale. Ideally, bias should be equal to zero. RMSE is calculated by computing the square root of the average squared differences between each respondent’s CAT-estimated measure and their measure on the full scale. The RMSE can be thought of as the standard deviation of the differences between the CAT and full-scale measurements, with lower RMSE values indicating greater consistency between measures derived from the CAT compared with measures derived from the full measure.

Construct Validity

Construct validity was evaluated in different ways. First, we examined the correlation and kappa coefficients of CAT to the raw and full Rasch scales and triage groups. Because the CAT is based on the Rasch measure, the CAT should be more closely related to the Rasch scale. Given the high correlation between the raw and full Rasch scale and triage groups for both SPS (R = .98; kappa = .82) and SDS (R = .99; kappa = .66), the CAT was also expected to have a similar relationship with the Rasch scale. This first method focused only on the extent to which the three methods were producing similar results. Second, we evaluated construct validity by comparing correlations of the triage groups based on the raw, Rasch and CAT measures to several other variables that are generally related to substance use, i.e., past week withdrawal symptoms, frequency of use, emotional problems, recovery environment risk, and health problems (see Table 1 for definitions). To determine whether observed differences in simulations were reliably measured (p<.05), we converted the differences to a z-score using Formula 2 for correlations and Formula 3 for kappa.

$$Z=\{(1/2\text{ log}((1+{\mathrm{R}}_1)/(1-{\mathrm{R}}_1))-(1/2\text{ log}((1+{\mathrm{R}}_2)/(1-{\mathrm{R}}_2))\}/\{\text{sqrt}(1/(\mathrm{N}-3)\}$$ (2)

$$Z=({\text{kappa}}_1-{\text{Kappa}}_2)(\text{sqrt}(N)\ast \mathit{\text{SE}})$$ (3)

Results

Research question 1: Is there a difference between CAT starting values based on a random value vs. starting values based on a screener in terms of the efficiency, precision and construct validity of the Substance Problems Scale (SPS)?

The performance of the various CAT simulations optimized for the SPS and SDS triage groups are summarized in Tables 3 and 4 respectively. This first section focuses on the bolded rows in the tables showing the average (across stopping rules) for a random value versus a screener based start. Stopping rule results are discussed further below. Relative to the random start, simulations using the screener to set the starting value required fewer items overall (SPS: 13 vs. 10; SDS: 13 vs. 8), fewer items for mid range scores (SPS: 16 vs. 15; SDS: 15 vs. 13), and were generally more efficient in terms of the E statistic (SPS: .37 vs. .47; SDS: .39 vs. .49). With fewer items, however, the screener based simulations were less precise than the random start simulations in terms of standard errors of measurement (SPS: .45 vs. .48; SDS: .46 vs. .52), bias (SPS: .02 vs. .06; SDS: −.01 vs. −.04), and RMSE (SPS: .19 vs. .39; SDS: .18 vs. .48). The screener based estimate was also lower in terms of its correlation with the raw score (SPS: .69 vs. .73; SDS: .76 vs .78), kappa with the raw score triage groups (SPS: .57 vs. .59; SDS: .62 vs. .68), correlation with the full Rasch measure (SPS: .99 vs. .95; SDS: .98 vs. .93), and kappa with the full Rasch score triage groups (SPS: .68 vs. .62; SDS: .59 vs. .57). With respect to these associations, however, only the differences in CAT to full Rasch correlations between random and screener start rules for both SPS and SDS were statistically significant (p’s < .05).

Table 3.

Summary of Simulation Results Optimized to Substance Problem Scale Triage Groups

	Efficiencyc			Precisiond			Construct Validatione
Start Rule	M MR						CAT to Raw		CAT to Rasch
(Stop Ruleb)	M Items	Items	E	M SEM	Bias	RMSE	Corr.	Kappa	Corr.	Kappa
Random Start (average)	13	16	0.37	0.46	0.02	0.19	0.73	0.68	0.99	0.68
(0.50, 0.35, 0.50)	13	16	0.37	0.46	0.03	0.20	0.73	0.67	0.99	0.68
(0.60, 0.35, 0.60)	13	16	0.37	0.46	0.02	0.18	0.72	0.68	0.99	0.69
(0.75, 0.35, 0.50)	13	16	0.37	0.46	0.02	0.18	0.72	0.67	0.99	0.68
(0.75, 0.35, 0.75)	13	16	0.37	0.46	0.02	0.18	0.73	0.69	0.99	0.68
Screener Based (average)	10	15	0.44	0.48	0.06	0.39	0.69	0.62	0.95	0.68
(0.50, 0.35, 0.50)	11	15	0.45	0.44	0.02	0.26	0.73	0.69	0.98	0.71
(0.60, 0.35, 0.60)	10	15	0.44	0.48	0.08	0.41	0.70	0.63	0.94	0.66
(0.75, 0.35, 0.50)	11	15	0.45	0.45	0.00	0.30	0.67	0.65	0.97	0.67
(0.75, 0.35, 0.75)	8	15	0.42	0.56	0.15	0.60	0.67	0.51	0.89	0.68

^aStart Rule specifies a random start between −.5 and +.5 logits versus a mean/standard error based start using a screener.

^bStop Rule specifies standard error for low, mid and high range (mid range = −2.50 to +0.10 Logits).

^cEfficiency measured in terms of the mean number of items (M), mean number of items for those in the mid range (M MR), and the efficiency ratio (E) calculated by dividing the amount of psychometric information by the number of items administered (See equation 1).

^dPrecision measured in terms of the mean standard error of measurement (M SEM), Bias (CAT minus full RASCH), root mean square error (RMSE) of the differences between the CAT and full Rasch score.

^eConstruct validation measured in terms of correlation and Kappa of CAT to the raw and full Rasch scale and triage groups with all correlations and kappa significant greater than 0 at p<.05. SPS Raw to Rasch correlation is .98 And the kappa between their triage groups is .82.

Table 4.

Summary of Simulation Results Optimized to Substance Dependence Scale Triage Groups

	Efficiencyc			Precisiond			Construct Validatione
Start Rule	M MR						CAT to Raw		CAT to Rasch
(Stop Ruleb)	M Items	Items	E	M SEM	Bias	RMSE	Corr.	Kappa	Corr.	Kappa
Random Start (average)	13	15	0.37	0.46	−0.01	0.18	0.78	0.59	0.98	0.59
(0.50, 0.35, 0.50)	14	15	0.37	0.44	0.004	0.129	0.78	0.61	0.99	0.59
(0.60, 0.35, 0.60)	14	15	0.37	0.44	0.007	0.133	0.78	0.57	0.99	0.58
(0.75, 0.35, 0.50)	10	15	0.35	0.53	−0.045	0.334	0.78	0.58	0.96	0.54
(0.75, 0.35, 0.75)	14	15	0.37	0.44	0.003	0.132	0.78	0.60	0.99	0.63
Screener Based (average)	8	13	0.49	0.52	−0.04	0.48	0.76	0.57	0.93	0.53
(0.50, 0.35, 0.50)	10	13	0.49	0.44	−0.003	0.256	0.79	0.61	0.98	0.58
(0.60, 0.35, 0.60)	8	13	0.51	0.50	−0.014	0.441	0.75	0.57	0.94	0.55
(0.75, 0.35, 0.50)	8	13	0.45	0.52	−0.135	0.52	0.78	0.57	0.92	0.50
(0.75, 0.35, 0.75)	5	13	0.51	0.60	−0.023	0.685	0.73	0.52	0.86	0.47

^aStart Rule specifies a random start between −.5 and +.5 logits versus a mean/standard error based start using a screener.

^bStop Rule specifies standard error for low, mid and high range (mid range = −0.75 to +0.70 Logits).

^cEfficiency measured in terms of the mean number of items (M), mean number of items for those in the mid range (M MR), and the efficiency ratio (E) calculated by dividing the amount of psychometric information by the number of items administered (See equation 1)

^dPrecision measured in terms of the mean standard error of measurement (M SEM), Bias (CAT minus full RASCH), root mean square error (RMSE) of the differences between the CAT and full Rasch score.

^eConstruct validation measured in terms of correlation and Kappa of CAT to the raw and full Rasch scale & triage group with all correlations and kappa significant greater than 0 at p<.05. Note that the SDS Raw to Rasch correlation is 99 And the kappa between their triage groups is .66.

Research question 2: How does relaxing CAT stopping rule precision at the low and high ends of the scale affect measurement efficiency, i.e., fewer items, and classification precision?

Figure 2 illustrates the effect of relaxing the variable stopping rules on the standard error distribution across the range of the SDS measure for a simulation that used the screener-based estimated starting value where the mid range for SDS extended from –0.75 to 0.7 logits and the low, mid and high range SE was set to 0.75, 0.35, and 0.50 logits, respectively. This figure illustrates that the CAT performed quite consistently with the pre-set standard error and mid range specifications. Between –0.67 and 0.69 logits, the standard error of measurement was at or below 0.35. In the low range, standard errors ranged from 0.38 to 0.9 logits, whereas in the high range, standard errors ranged from 0.4 to 0.9 logits. Standard error values only exceeded stopping rule criteria (i.e., greater than 0.5 logits in the high range and greater than 0.75 logits in the low range) at the extreme end of the scale (>= 2.0 logits or <= –3.79 logits) where there were no more items to use. The performance of all eight stopping rules for SPS (see Table 3) and eight stopping rules for SDS (see Table 4) were checked in the same way and performed similarly though generally with smaller standard errors.

Figure 2.

Illustration of the Effect of Screener Based Starting Rule and Variable Stopping Rule on Standard Error of CAT-Estimated SDS Measures Across the SDS Continuum (screener-based estimated starting value, Low SE=0.75, Mid SE=0.35, High SE=0.75)

The effect of variable stopping rules on CAT precision and efficiency can be seen in Tables 3 and 4. It can be seen after examination of the findings summarized in Tables 3 and 4 that the effect of the variable stopping rules on CAT efficiency and precision was dependent on which item selection algorithm was employed. That is, variable stopping rules had a much stronger effect on CAT precision and efficiency when the screener was used to set the starting value, whereas they had relatively little effect within the context of the random starting value item selection method. When the screener was used to pre-calibrate the measure, measurement precision (as indicated by mean standard error and RMSE) decreased and CAT efficiency (as measured by the E statistic and the mean number of items administered) increased as the stopping rule criteria for high and low symptom severity became larger (i.e., more lenient). This was particularly true when the standard error for the high and low range of the measure was set to 0.75 logits (last stopping rule) and when the scale was optimized on the SDS mid range (−0.75 to 0.70 logit). Within the random start group, in contrast, there were no statistically significant differences between the stopping rule simulations in terms of construct validity measured by the correlation and kappa compared to the raw and full Rasch scales and triage groups. Among the screener-based simulations, the first stopping rule (.50/.35/.50) performed significantly better than the last (.75/.35/.75) for both SPS and SDS with respect to correlations and kappa coefficients between the raw score and full Rasch measures (with the other two stopping rules falling in between).

Research question 3: Can the construct validity of classifications based on the CAT do as well as those based on the raw Substance Problem Scale (SPS) and the Rasch based classification?

Table 5 presents the zero-order correlations between the triage groups based on the raw, full Rasch, and CAT-derived measures for SPS and SDS and substance abuse related symptoms as measured by the GAIN’s Current Withdrawal Scale, Substance Frequency Scale, the Emotional Problem Scale, Recovery Environment Risk Index, and the Health Problem Scale. For the CAT-derived measure we reported the average correlation for each starting rule and the range of correlations for the stopping rules within a given starting rule (none of which are significantly different from each other). While the full Rasch based triage groups (second row of each set) had higher correlations than the raw symptom count based triage groups with 4 of 5 related constructs for SPS and all five for SDS—the differences were not statistically significant. For the SPS triage groups, the correlations for 4 of the 5 related constructs for the CAT based groups were between those observed for raw and Rasch based group and the fifth variable (health problems) was slightly lower—none of the differences was statistically significant. For the SDS triage groups, correlations with CAT-defined groups were higher than those with triage groups based on the raw or full Rasch measure for all five associated constructs– though again, none of the differences was statistically significant.

Table 5.

Construct Validity of Raw, Rasch and CAT Clinical Triage Groups

	Related Construct Variablea
Categorization (low/mod/high) based on	Current Withdrawal Scale (CWS)	Substance Frequency Scale (SFS)	Emotional Problem Scale (EPS)	Recovery Environment Risk Index (RERI)	Health Problem Scale (HPS)
Substance Problem Scale Triage Groupb
Raw Sx Count	0.46	0.33	0.36	0.33	0.21
Full Rasch	0.53	0.39	0.44	0.38	0.23
CAT Rasch w/Random Average (range for stopping rules)	0.47 (.40–.50)	0.36 (.34–.38)	0.33 (.28–.36)	0.32 (.30–.36)	0.16 (.14–.17)
CAT Rasch w/Screener Average (range for stopping rules)	0.48 (.47–.48)	0.39 (.38–.39)	0.34 (.33–.34)	0.34 (.32–.35)	0.15 (.14–.16)
Substance Dependence Scale Triage Groupsc
Raw Sx Count	0.53	0.38	0.36	0.37	0.19
Full Rasch	0.54	0.43	0.41	0.39	0.22
CAT Rasch w/Random Average (range for stopping rules)	0.57 (.56–.58)	0.45 (.44–.46)	0.44 (.43–.45)	0.40 (.38–.41)	0.23 (.22–.23)
CAT Rasch w/Screener Average (range for stopping rules)	0.57 (.55–.59)	0.43 (.42–.43)	0.43 (.40–.45)	0.39 (.36–.41)	0.22 (.20–.23)

^aAll correlations significantly different than 0 at p<.05; None of the column differences within SPS or within SDS are statistically significant.

^bThe SPS raw symptom (Sx) count triage is based on 0\ 1 to 9 \ 10 to 16 symptoms; For the Rasch/CAT versions the triage is based on less than −2.50 / −2.50 to −0.10 / > −.10 logits.

^cThe SDS raw symptom (Sx) count triage is based on 0 to 2 \ 3 to 5 \ 6 to 7 symptoms; For the Rasch/CAT versions the triage is based on less than −.75 / −.75 to +.70 / > +.70 logits.

Discussion

Reprise

The use of a screener to set the starting value and relaxing stopping rules requirements at the low and high end reduced the number of required items and improved overall efficiency. While this reduced precision, the effect on classification for clinical triage was minimal and did not produce any statistically significant changes in construct validity relative to other constructs related to substance use. This is significant because the various simulations represent an average reduction of 13% to 66% in the 16 item SPS with little loss in construct validity. Given that the full GAIN includes 103 scales and takes over 2 hours, this could result in a significant savings of client and staff time/resources if the CAT were applied throughout. Moreover, the algorithms employed in the present study involving the use of a screener to set the start rule and the application of variable stop rules can easily be applied to other CAT applications designed to group individuals by trait level.

Strengths and Limitations

While this study had many strengths (large and diverse sample, testing several methods, using several types of construct validity), it does have some important limitations that need to be acknowledged. Generally, CAT simulations have been done with many more items. Additional questions and/or alternative forms of collateral information to set the starting value of the CAT may help to improve classification accuracy while improving CAT efficiency. Extending the CAT across GAIN scales (e.g., to substance specific measures of abuse/dependence or to other measures of psychopathology) may also help in this regard. Further research is needed to explore the possibility of using demographic and other available clinical information that could improve the effectiveness of CAT pre-estimation procedures. As noted, this was a simulation rather than an assessment of a working CAT system. Although based on real data, it would be desirable to replicate the present findings using another dataset and to test with an actual CAT application.

Conclusion

To our knowledge this is the first study that has explored the use of measure-based estimated starting values and variable stopping rules in a computerized adaptive test designed to categorize individuals for treatment assignment. This approach capitalizes on useful aspects of the Rasch measurement model; namely, that standard errors vary across the measurement continuum. Not only can a CAT adapt to a person’s estimated measure on a latent trait, the present study demonstrates that it can also adapt to the need for greater precision in certain areas of the measurement continuum and less precision in other areas. This simulation has implications for improving the efficiency of clinical care assessment, which is important in addressing the conflicting pressure to measure more with fewer resources.

Appendix

Appendix A.

Flow chart of CAT Procedure Using Variable Stop Rules and the SPS Screener to Set the Start Valu