Comparison of methods that use whole genome data to estimate the heritability and genetic architecture of complex traits

Abstract

Multiple methods have been developed to estimate narrow-sense heritability, h², using single nucleotide polymorphisms (SNPs) in unrelated individuals. However, a comprehensive evaluation of these methods has not yet been performed, leading to confusion and discrepancy in the literature. We present the most thorough and realistic comparison of these methods to date. We utilized thousands of real whole genome sequences to simulate phenotypes under varying genetic architectures and confounding variables, and used array, imputed, or whole genome sequence SNPs to obtain “SNP-heritability” estimates (ĥ²_SNP). We show that ĥ²_SNP can be highly sensitive to assumptions about the frequencies, effect sizes, and levels of linkage disequilibrium (LD) of underlying causal variants, but that methods that bin SNPs according to minor allele frequency and LD are less sensitive to these assumptions across a wide range of genetic architectures and possible confounding factors. These findings provide guidance for best practices and proper interpretation of published estimates.

Narrow-sense heritability, h², the proportion of a trait’s phenotypic variance attributable to additive genetic variance, is a fundamental concept in quantitative genetics. In addition to being the central descriptor of the genetic bases of traits, h² determines the response to selection and the potential utility of individual genetic prediction^1,2. h² estimated in traditional designs using pedigrees or twins, ${\hat{h}}_{\mathit{\text{PED}}}^2$, relies on strong assumptions about the causes of covariance between close relatives and can be biased to the degree these assumptions are unmet^3,4. Over the last eight years, alternative “SNP-based” methods⁵ have been developed to estimate h² using measured SNPs, denoted ${\hat{h}}_{\mathit{\text{SNP}}}^2$. When estimated in samples of nominally unrelated individuals, ${\hat{h}}_{\mathit{\text{SNP}}}^2$ is unlikely to be confounded by common environmental or non-additive genetic effects that increase similarity of close relatives, and should reflect the proportion of phenotypic variation due to causal variants (CVs) tagged by SNPs. When common SNPs are used in the analysis, ${\hat{h}}_{\mathit{\text{SNP}}}^2$ is expected to be less than h² and ${\hat{h}}_{\mathit{\text{PED}}}^2$ because rare CVs are typically poorly tagged by common SNPs, and indeed ${\hat{h}}_{\mathit{\text{SNP}}}^2$ is substantially lower than ${\hat{h}}_{\mathit{\text{PED}}}^2$ for most complex traits in such analyses, with schizophrenia⁶ ( ${\hat{h}}_{\mathit{\text{SNP}}}^2~0.23$ versus ${\hat{h}}_{\mathit{\text{PED}}}^2~0.8$) a typical example.

More recently, imputed SNPs have been used to capture the effects of rarer CVs and to gain insight into the genetic architecture of traits, examine genetic networks and annotation classes, and test evolutionary hypotheses^6–18. For example, the substantial fraction of the variance in prostate cancer risk due to rare variants suggests that negative selection has reduced the frequency of risk alleles¹⁸, and across a range of traits, young alleles explain more of the heritability than old alleles, suggesting widespread purifying selection^13,14. Whole genome sequence (WGS) SNPs are likely to be increasingly used for such purposes in the future.

As SNPs in these analyses begin to more accurately reflect the density and frequency distributions of CVs, ${\hat{h}}_{\mathit{\text{SNP}}}^2$ should approach total h², making it important to understand the factors that can bias ${\hat{h}}_{\mathit{\text{SNP}}}^2$. Moreover, the proliferation of methods (Table 1) has led to discrepancies in estimates. For example, schizophrenia ${\hat{h}}_{\mathit{\text{SNP}}}^2$ has been reported as 0.56 (LD score regression¹⁹) and 0.23 (univariate GREML¹⁶). Recently, Speed et al.¹⁵ argued that typical assumptions about the relationships between SNP effect size, minor allele frequency (MAF), and linkage disequilibrium (LD) are inaccurate, and reported ${\hat{h}}_{\mathit{\text{SNP}}}^2$ values significantly higher than previous estimates under different assumptions. How should such discrepancies be interpreted? Under which conditions do biases exist across different methods and when should researchers prefer one method over another? Answers to these questions are important, yet to date, comparisons across methods have been restricted to a small subset of methods in the primary papers they were introduced in, and have been compared across simulations that are unrealistic with respect to properties of real genomes. For example, simulating CVs from imputed genotypic data rather than measured WGS data¹⁵ can lead to CVs with highly atypical levels of LD and therefore to conclusions about ${\hat{h}}_{\mathit{\text{SNP}}}^2$ that apply to genetic architectures unrepresentative of real traits.

Table 1.

Summary of commonly applied methods and a description of findings from simulations.

Method & original ref	Description	Major Assumptions	Simulation findings regarding ${\hat{h}}_{\mathit{\text{SNP}}}^2$	Computational Issues
GREML-SC5	Often called the “GCTA approach.” Originally applied to common array SNPs only. Estimates ${\hat{h}}_{\mathit{\text{SNP}}}^2$, the amount of h2 caused by CVs tagged by SNPs used to create the GRM.	1) Genetic similarity is uncorrelated with environmental similarity; 2) an infinitesimal model; 3) SNP effects are normally distributed, independent of LD, and inversely proportionate to MAF (α=−1).	Biased to the degree that the average LD among SNPs is different than the average LD between SNPs and CVs. This occurs in stratified samples and when MAF & LD distributions of SNPs do not match those of CVs.	Simple model tractable with large samples (>100K).
GREML-MS11	The first multi-component approach, usually applied by binning SNPs according to their MAF, annotation, or physical regions in order to explore genetic architecture.	Requires that the same assumptions of GREML-SC hold within each GRM.	Biased if CVs have generally higher or lower levels of LD than the SNPs used to make the GRM. Relatively large standard errors.	Run times and memory requirements higher than GREML-SC and increase as a function of the number of variance components estimated.
GREML-LDMS-R7	A multi-component approach that bins imputed SNPs by their MAF and regional LD.	Same as GREML-MS	Use of regional LD scores can lead to biases if CVs have different LD on average than surrounding SNPs. Relatively large standard errors.	Same as GREML-MS.
GREML-LDMS-I	A multi-component approach introduced here that bins imputed SNPs by their MAF and individual LD.	Same as GREML-MS	Appears to be the least biased approach, even when traits have complex genetic architectures. Relatively large standard errors.	Same as GREML-MS.
LDAK-SC15,20	Introduced to account for redundant tagging of CVs by common SNPs. Recently modified to incorporate error due to imputation and to alter the MAF-effect size relationship.	Same as GREML-SC, except that allelic effects are a function of LD. Extended to assume that effects are also a function of imputation quality and weakly inversely proportionate to MAF (α=−0.25).	Can correct for the overestimation observed in GREML-SC from redundant tagging of CVs, but otherwise about as biased as GREML-SC when assumptions are unmet, although the biases are sometimes in different directions.	Same as GREML-SC.
LDAK-MS15	A multi-component extension of LDAK-SC that bins SNPs by MAF.	Requires that the same assumptions of LDAK-SC hold within each GRM.	Less biased on average than LDAK-SC, but more biased than GREML-LDMS (-I or -R). Relatively large standard errors.	Same as GREML-MS.
Threshold GRMs24	A multi-component approach with two GRMs: the normal (unthresholded) GRM built from all SNPs, and a second GRM with entries set to 0 if below a threshold. Conducted in samples that include close relatives.	Same as GREML-SC for the unthresholded GRM. Assumes no shared environmental influences among close relatives.	Estimates associated with unthresholded GRM similar to those of GREML-SC. When used in samples that include close relatives, the second GRM captures pedigree-associated variation but can be upwardly biased by shared environmental influences.	See GREML-SC.
LD Score Regression19	Uses the slope from χ2 (from GWAS) regressed on SNPs’ LD scores to estimate the h2 due to CVs in LD with common SNPs.	Infinitesimal model with allelic effects normally distributed.	Largely robust to confounding due to stratification and shared environmental influences. Estimates h2 due to common CVs only, even when used on imputed or WGS data. Underestimates h2 if the trait is not highly polygenic.	The most computationally efficient method of those compared and is tractable for very large datasets.

Here, we utilized thousands of fully sequenced genomes to simulate traits across different genetic architectures and degrees of population stratification, and compared the performance of the most popular SNP heritability estimation methods using three different SNP types (array, imputed, and WGS). By simulating phenotypes from real WGS data rather than from simulated or array/imputed SNPs, we were able to mimic patterns of LD and stratification found in real genomes and to include the effects of CVs down to a MAF of 0.0003. We then estimated heritability and the allelic spectra of six complex traits in the UK Biobank. Our findings provide insight into the most important factors influencing, and best practices for estimating, ${\hat{h}}_{\mathit{\text{SNP}}}^2$.

RESULTS

Comparison of ${\hat{h}}_{\mathit{\text{SNP}}}^2$ across estimation methods under typical assumptions about CV effect sizes

For all methods described here other than LD score regression, evidence for ${\hat{h}}_{\mathit{\text{SNP}}}^2$ occurs to the degree to which the genome-wide average correlation between pairs of individuals i, j at measured SNPs, A_ij, is related to phenotypic similarity. A_ij values between all pairs of individuals are stored in an n×n genomic relationship matrix (GRM), used to estimate ${\hat{h}}_{\mathit{\text{SNP}}}^2$ with restricted maximum likelihood (REML). Such models can be fit using a single GRM (“single-component GREML”)^5,20 or by binning SNPs according to MAF, LD, and/or other annotations into multiple GRMs (“multi-component GREML”)^7,11, akin to multiple regression and leading to one ${\hat{h}}_{\mathit{\text{SNP}}}^2$ per GRM, which can be summed to derive total ${\hat{h}}_{\mathit{\text{SNP}}}^2$.

We used WGS data from the Haplotype Reference Consortium²¹ to mimic four levels of stratification found within Europe by varying the ancestry compositions of samples (each n=8201; Online Methods). We simulated traits using 1000 randomly chosen WGS CVs within five different MAF ranges under typical assumptions (CV effect sizes independent of LD and inversely proportionate to MAF, per-CV contribution to h² invariant across MAF). Later, we tested alternative assumptions. While all CVs are SNPs in our simulations (i.e., we do not simulate non-SNP CVs, such as repeat polymorphisms), we hereafter restrict our usage of “SNPs” to denote the markers used to create GRMs and “CVs” to denote underlying causal variants. We estimated h² using commonly applied methods (see Supplemental Note for additional methods) and used SNPs on a typical commercial platform (the UK Biobank Axiom array²²), SNPs imputed from an independent reference panel, or WGS SNPs to create GRMs. When WGS SNPs were used to create GRMs, CVs were necessarily included in the markers that created the GRMs, whereas this occurred sporadically for array and imputed SNPs. We simulated 100 phenotypes for each parameter combination and found the means of ${\hat{h}}_{\mathit{\text{SNP}}}^2$ and their empirical 95% confidence intervals (CIs) across replicates. We did not simulate any phenotypic effects as a function of ancestry, and thus biases related to stratification in our results were due to the genotypic (e.g., long-range LD), not environmental, effects of stratification.

We note that in some contexts, it is useful to compare ${\hat{h}}_{\mathit{\text{SNP}}}^2$ to a corresponding population parameter, ${\hat{h}}_{\mathit{\text{SNP}}}^2$, defined as the true proportion of variance explained by the set of SNPs used in the analysis²³, and which in most cases is less than the full h² due to imperfectly tagged CVs. However, such a formulation is cumbersome in the current context because ${\hat{h}}_{\mathit{\text{SNP}}}^2$ changes across each combination of genetic architecture and SNP data type. Instead, in all cases we compare ${\hat{h}}_{\mathit{\text{SNP}}}^2$ to the full (simulated) h², with the recognition that downward biases in ${\hat{h}}_{\mathit{\text{SNP}}}^2$ are expected when CVs are imperfectly tagged by (array and imputed) SNPs used in the analysis, and that such underestimates do not necessarily reflect estimation problems. Because this expected underestimation does not apply to WGS data, and because these methods will be increasingly applied to WGS data in the future, in this section we focus primarily on results from WGS data; results from imputed SNPs (which were similar) and array SNPs (which were often dissimilar) are discussed briefly below but are presented in full in the Supplement.

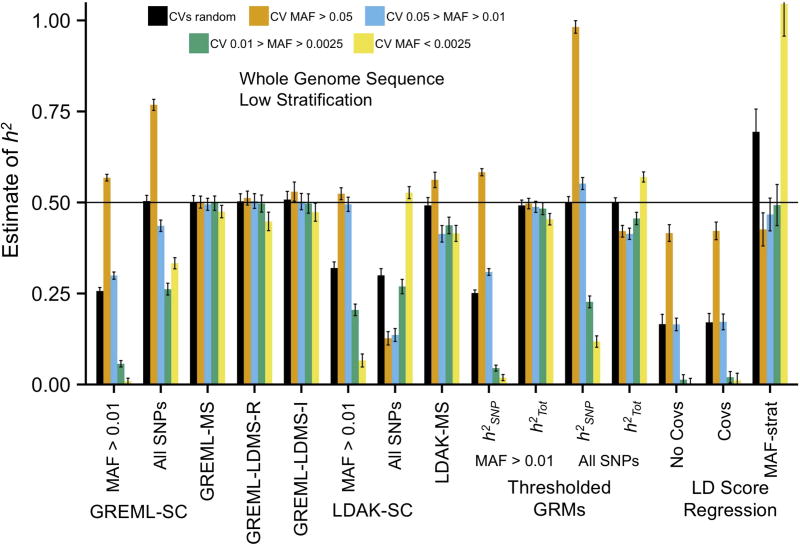
The most-widely used estimation method, single-component GREML⁵ (GREML-SC, or the “GCTA” approach¹⁵), underestimated h² when average CV MAF < average SNP MAF, such as when CVs were rare and array SNPs were analyzed, and overestimated h² when average CV MAF > average SNP MAF, such as when CVs were common and WGS SNPs were analyzed (Figure 1; Supplementary Figs. 1–6, Supplementary Tables 1–3). These biases are predictable based on SNP-SNP versus SNP-CV LD: when the mean LD between CVs and SNPs $({\overline{r^2}}_{\mathit{\text{QM}}})$ is less than the mean LD between all SNPs $({\overline{r^2}}_{\mathit{\text{MM}}})$, which occurs when CVs are on average rarer than SNPs, ${\hat{h}}_{\mathit{\text{SNP}}}^2$ under-estimates h², and vice-versa when ${\overline{r^2}}_{\mathit{\text{QM}}}>{\overline{r^2}}_{\mathit{\text{MM}}}$ (Supplementary Fig. 7, ref.⁷). GREML-SC analyses using array SNPs led to modest overestimation of h² when CVs were common (Supplementary Fig. 1), presumably because array SNPs are chosen to maximally tag surrounding genomic regions. Stratification led to long-range tagging between ancestry specific (rare) CVs and ancestry informative common SNPs, which altered these biases. In the most stratified sample, average LD for very rare SNPs was higher than average LD for common SNPs (Supplementary Fig. 7), which led to overestimation of h² when CVs were very rare and underestimation of common CV h² when using WGS or imputed variants (Supplementary Figs. 3–5). Controlling for ancestry principal components as fixed effects had no influence on these biases. Thus, stratification, CV MAF, and data type strongly influenced patterns of CV and SNP LD, leading to over- or under-estimated h² using GREML-SC.

Figure 1.

Mean ${\hat{h}}_{\mathit{\text{SNP}}}^2$ across 100 replicates from GRMs built from WGS SNPs in the least structured subsamples. Methods on the x-axis as follows: Single-component GREML (GREML-SC) with all SNPs or only MAF > 0.01; MAF-stratified GREML (GREML-MS); LD and MAF-stratified GREML (GREML-LDMS-R [regional LD] & -I [individual SNP LD]); Single-component Linkage Disequilibrium-Adjusted Kinships (LDAK-SC) with all SNPs or only MAF > 0.01; MAF-stratified LDAK (LDAK-MS); Extended Genealogy with Thresholded GRMs with all SNPs or only common (MAF > 0.01), presenting both h²_SNP and h²_Tot (=h²_SNP + h²_ibs>t); LD score regression (LDSC) using no PCs as covariates in GWAS, using PCs as covariates, or partitioned using PCs with MAF-stratification. Estimates are from samples of unrelated individuals (relatedness <0.05) except for those from the Threshold GRM method, which included all individuals. Simulated (true) h² = 0.5. Colors represent the MAF range of the 1,000 randomly drawn CVs. See Online Methods for descriptions of each method and Supplementary Figures for additional estimates and Supplementary Table 2 for numerical results. Error bars represent 95% confidence intervals.

Speed et al. introduced an approach (LDAK) to LD-weight SNPs in order to account for the redundant tagging of CVs by multiple SNPs, which can bias ${\hat{h}}_{\mathit{\text{SNP}}}^2$ in certain situations²⁰. We limit discussion here to LDAK-SC as originally described²⁰, and explore recent extensions of this model¹⁵ below with different simulations. As with GREML-SC, LDAK-SC estimates were highly sensitive to stratification, CV MAF, and SNP data type. When using common SNPs for the analysis (array, imputed, or WGS), LDAK-SC underestimated h² arising from rare CVs, but corrected the overestimation arising from common CVs observed with GREML-SC (Fig 1; Supplementary Fig. 1–2). However, when using all SNPs from WGS data, LDAK weighted SNPs inversely proportionate to their LD, resulting in near-zero weights for common SNPs and very high weights for rare SNPs (Supplementary Fig. 8–9). This led to underestimated h² when CVs were common and overestimated h² when CVs were very rare (Fig. 1; Supplementary Fig. 4). This over-weighting of rare SNPs appeared to exacerbate biases arising from stratification versus the unweighted (GREML-SC) approach (Supplementary Fig. 3–5). On the other hand, when all imputed SNPs were modeled in unstratified samples, LDAK appeared to provide decent estimates of h² (Supplementary Fig. 5), although results in the next section suggest that this was due to offsetting biases that happened to cancel out across this particular combination of parameters. Overall, the LDAK-SC results reiterate that single-component GREML models are highly sensitive to assumptions about genetic architecture.

We compared four multi-component approaches: 1) GREML-MS⁷ (4 GRMs) which binned SNPs into 4 MAF categories; 2) GREML-LDMS-R⁷ (16 GRMs) which binned SNPs by MAF crossed by the average LD of SNPs in the surrounding ~200kb region; 3) GREML-LDMS-I (16 GRMs), which we introduce here and which binned SNPs by MAF crossed by their individual levels of LD; and 4) LDAK-MS^15,20 (4 GRMs), which binned SNPs by MAF and weighted them according to the LDAK model. There were no major differences between the results of the first three approaches: all provided ~ unbiased total ${\hat{h}}_{\mathit{\text{SNP}}}^2$ (the sum of ${\hat{h}}_{\mathit{\text{SNP}}}^2$ from each GRM) when used on imputed or WGS data (Fig. 1, Supplementary Fig. 1–5). The similarity of these estimates is unsurprising in this set of simulations because CV effects were unrelated to LD, but below we demonstrate that GREML-LDMS-I provides the most robust estimates when this is not the case. LDAK-MS provided less biased ${\hat{h}}_{\mathit{\text{SNP}}}^2$ than LDAK-SC but more biased ${\hat{h}}_{\mathit{\text{SNP}}}^2$ than the other three multi-component GREML methods when CVs were rare. Biased ${\hat{h}}_{\mathit{\text{SNP}}}^2$ from LDAK-MS could occur because the simulation model does not match the LDAK assumption that CV effect sizes are a function of LD; we explore this issue below. In general, multi-component models outperform single-component models because ${\overline{r^2}}_{\mathit{\text{QM}}}$ is closer to ${\overline{r^2}}_{\mathit{\text{MM}}}$ within narrower MAF/LD ranges, and therefore ${\hat{h}}_{\mathit{\text{SNP}}}^2$ associated with each partitioned GRM—and their sums—are likely to be ~unbiased, consistent with previous work⁷. For similar reasons, these models were less biased in stratified samples than single-component models (Supplementary Fig. 3–5). However, the empirical standard errors of ${\hat{h}}_{\mathit{\text{SNP}}}^2$ from GREML-LDMS-I were ~20%–50% higher than those from GREML-LDMS-R, which were in turn ~100% higher than those from GREML-SC (Supplementary Fig. 10–12). Thus, multi-component GREML models require large sample sizes (e.g., n > 30k) to be informative.

Zaitlen et al.²⁴, proposed a two GRM approach to obtain ${\hat{h}}_{\mathit{\text{PED}}}^2$ and ${\hat{h}}_{\mathit{\text{SNP}}}^2$ in samples containing close relatives. The first GRM contains A_ij for all pairs of individuals, while A_ij values below a threshold, t (=.05 here), are set to 0 in the second GRM. The first GRM contains information on sharing of CVs tagged by SNPs and is used to obtain ${\hat{h}}_{\mathit{\text{SNP}}}^2$, while the second GRM only contains information from closely related individuals, reflecting sharing of CVs not tagged by SNPs, and is used to obtain ${\hat{h}}_{\mathit{\text{IBS}}>t}^2$, the additional h² captured by close relatives. The sum of ${\hat{h}}_{\mathit{\text{IBS}}>t}^2$ and ${\hat{h}}_{\mathit{\text{SNP}}}^2$ therefore provides an estimate of ${\hat{h}}_{\mathit{\text{PED}}}^2$. In our simulations, ${\hat{h}}_{\mathit{\text{PED}}}^2$ was an unbiased estimate of h² across most situations examined (Supplementary Fig. 13–14). However, ${\hat{h}}_{\mathit{\text{IBS}}>t}^2$ and ${\hat{h}}_{\mathit{\text{SNP}}}^2$ were often severely over- or under-estimated individually, depending on the CV MAF range and data type, with patterns of ${\hat{h}}_{\mathit{\text{SNP}}}^2$ similar to those observed for GREML-SC. Thus, attempts to use this method to infer genetic architecture should be treated with caution. Moreover, as acknowledged by Zaitlen et al.²⁴ and demonstrated in additional simulations, ${\hat{h}}_{\mathit{\text{PED}}}^2$ may be biased upward when environmental factors cause similarity within nuclear or extended families (Supplemental Fig. 15).

LD score regression (LDSC) is an alternative, computationally-efficient approach that estimates h² from the relationship between LD-tagging of individual SNPs and their expected GWAS test statistics under an infinitesimal model^10,19. Results from LDSC were similar when utilizing array, imputed, or WGS SNPs (Fig. 1, Supplementary Fig. 1–2, 16–18), as were estimates of the intercept, which reflect the contribution of stratification and cryptic relatedness to the GWAS test statistics (see Supplementary Note for further discussion of LDSC statistics). Across data types, LDSC generally underestimated h² by 5–10% when CVs were common. LDSC increasingly underestimated h² when CVs were rare, regardless of data type, because rare SNPs and CVs generally have very low LD scores. However, LDSC was largely immune to the genomic effects of stratification (see Supplementary Note), and we found no upward bias when unmodeled shared environmental effects were included in the simulations (Supplementary Fig. 15), suggesting that ${\hat{h}}_{\mathit{\text{SNP}}}^2$ from LDSC is robust to familial environmental effects and provides a reasonable estimate of the lower bound of h² tagged by common CVs.

We also simulated ascertained, case-control phenotypes applying the standard transformation to the liability scale²⁵. While the smaller sample size from ascertainment increased standard errors, patterns of ${\hat{h}}_{\mathit{\text{SNP}}}^2$ estimates across methods were similar to those found with continuous phenotypes (Supplementary Fig. 19), suggesting that our conclusions here apply to categorical outcomes.

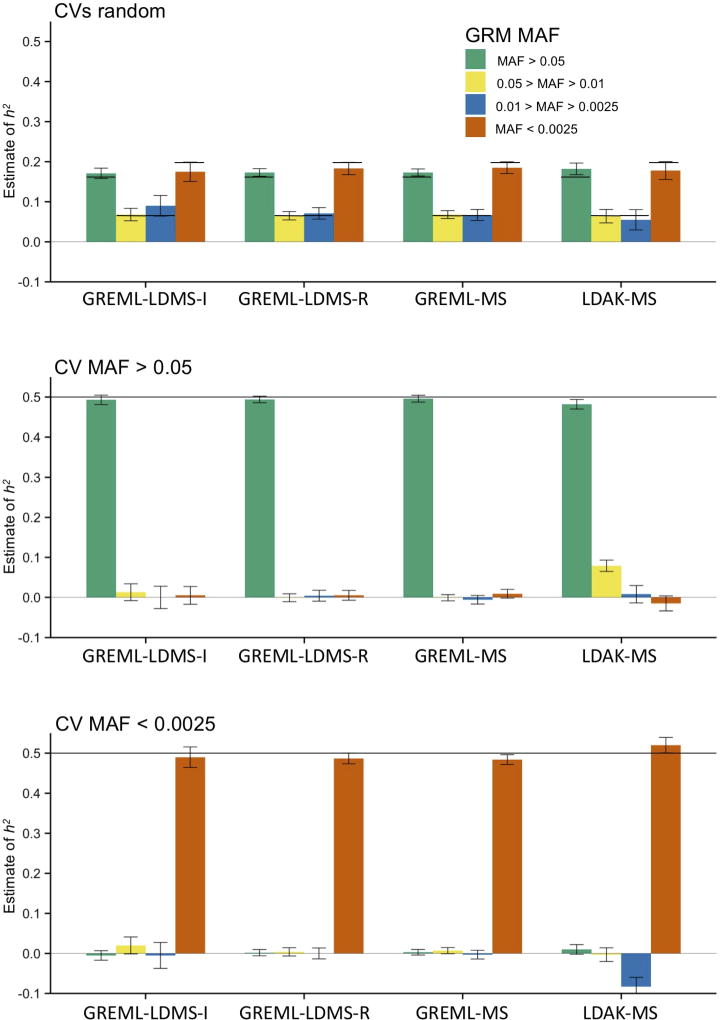
Finally, multi-component methods can also estimate h² across different annotations or different MAF bins (the “allelic spectra” of traits). Multi-component GREML approaches accurately estimated the allelic spectra when using WGS data (Fig. 2, Supplementary Fig. 20). However, these approaches underestimated the contribution of very rare CVs by up to 20% using imputed data (Supplementary Fig. 21), due to the poorer imputation quality of rare SNPs, and highly underestimated their contribution when using array SNPs (Supplementary Fig. 22) due to the low LD typically observed between array SNPs and rare CVs (Supplementary Tables 4–5).

Figure 2.

Mean ${\hat{h}}_{\mathit{\text{SNP}}}^2$ for four MAF bins across 100 replicates from multi-component approaches in unrelated individuals using WGS SNPs in the least structured subsample. See Fig. 1 for specific methods. Black lines are the true (simulated) h² values; note that in the top panel, the true h² values differ across MAF. See Online Methods for descriptions of each method and Supplementary Figures for additional estimates and Supplementary Table 4 for numerical results. Error bars represent 95% confidence intervals.

Comparison of ${\hat{h}}_{\mathit{\text{SNP}}}^2$ models under alternative assumptions

Recent work has shown that, conditioning on MAF, SNPs with individually low levels of LD contribute disproportionately to the heritability of multiple complex traits¹³, suggesting that CV effects are not independent of their levels of LD. The simulations above assumed that CV effect sizes, β_k, were independent of LD and that rare CVs had, on average, larger effect sizes than common CVs, and therefore that the per-CV h² was invariant on average across MAF. This is achieved by applying an α of −1, which governs the MAF-effect size relationship and assuming β_k~N(0,1), the default scaling of GREML-SC, -LDMS-R, and LDMS-I^5,7 (Online Methods). Recently, Speed et al.¹⁵ argued that less biased ${\hat{h}}_{\mathit{\text{SNP}}}^2$ estimates are obtained using a single-component model, but by assuming a higher contribution of common CVs (i.e., α=−0.25), by assuming SNP effect sizes, w_k, are inversely proportionate to LD, (Supplementary Fig. 8–9), and by weighting SNPs by imputation quality (r²) (the LDAK model). Across numerous traits, they observed LDAK-SC-based ${\hat{h}}_{\mathit{\text{SNP}}}^2$ 25–43% higher than ${\hat{h}}_{\mathit{\text{SNP}}}^2$ from GREML-SC and GREML-LDMS-R, as well as higher log-likelihoods from LDAK-SC models.

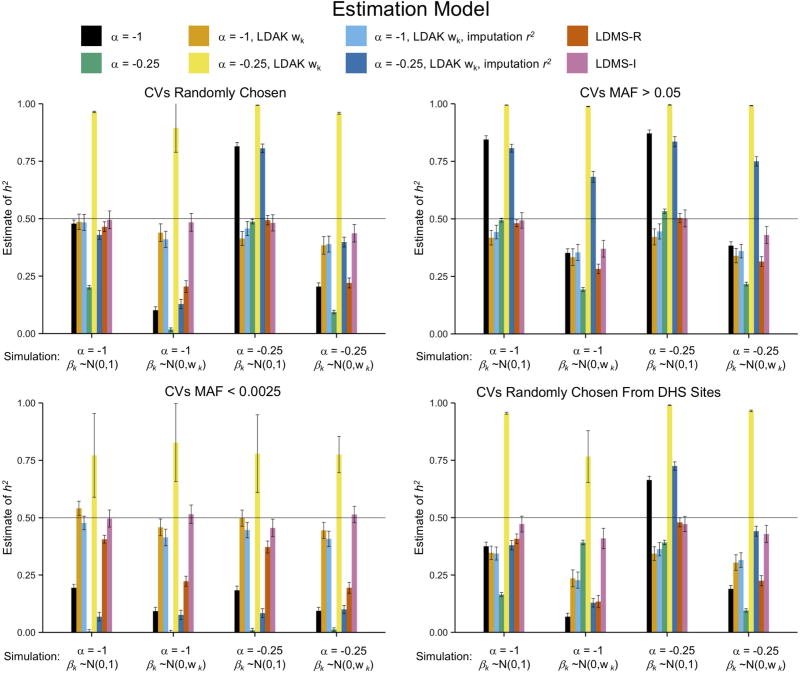
We compared the performance of these alternative assumptions of MAF, LD, and CV effect size relationships with simulated phenotypes using CVs drawn from different MAF ranges under four different combinations of MAF-effect size (α=−1 or −0.25) and LD-effect size (β_k ~N(0,1) or ~N(0,w_k)) relationships. We also simulated phenotypes from two distinct, functionally relevant genetic architectures. First, we simulated with CVs randomly chosen from all DNase-I Hypersensitivity Sites, which have systematically lower LD¹⁷. Second, we simulated phenotypes using the empirically-estimated, LD-dependent effect size distribution, β_k~N(0, τ_k), where τ_k was estimated across 31 traits using partitioned LD score regression¹³ (Online Methods). This latter simulation is particularly important because the functional, LD-dependent genetic architecture it used was independent of the assumptions made in the GREML and LDAK models used in estimation. Because LDAK-SC was intended to be used on imputed data, our primary results below are based on imputed SNPs, but results from WGS data are also presented in the Supplement.

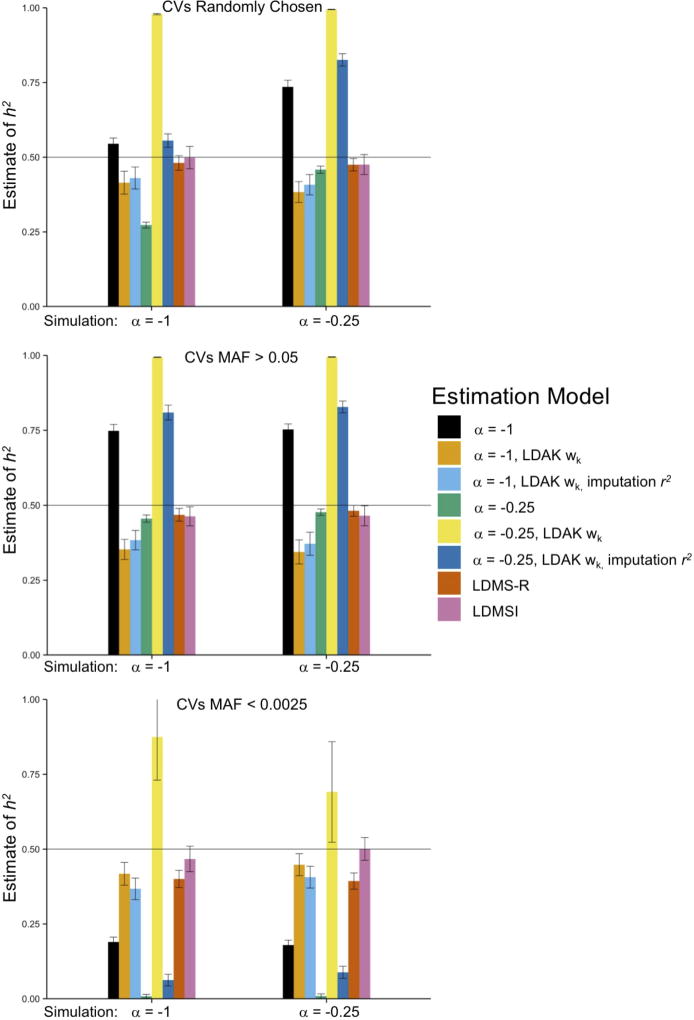
${\hat{h}}_{\mathit{\text{SNP}}}^2$ from single-component models, including GREML-SC and LDAK-SC, were highly sensitive to model assumptions about MAF- and LD-effect size relationships, as well as to differences between CV and SNP MAF distributions (Fig. 3, Supplementary Figs. 23–24, Supplementary Tables 6–7). Moreover, in simulations with empirically derived genetic architectures¹³ (β_k~N(0, τ_k)), both GREML-SC and LDAK-SC (Fig. 4, Supplementary Fig. 25–26) were highly biased. On the other hand, multi-component GREML models were much more robust to model misspecification (Figs. 3–4, Supplementary Fig. 23–28). In particular, when we binned SNPs by their individual LD scores (GREML-LDMS-I), ${\hat{h}}_{\mathit{\text{SNP}}}^2$ estimates were robust across every genetic architecture we investigated (Fig. 3), including when CV effect sizes were drawn from the empirically estimated genetic architectures (Fig. 4). Across all genetic architectures and all data types investigated, GREML-LDMS-I had the lowest absolute bias of any method (Fig. 5). This suggests that particular assumptions regarding MAF- and LD-effect size relationships are mitigated by the use of multiple-component models.

Figure 3.

Mean ${\hat{h}}_{\mathit{\text{SNP}}}^2$ across 100 replicates from GRMs built from imputed SNPs in the least structured subsamples across different model assumptions (bars) and different ways of simulating CVs (x-axes). The x-axes of each panel show the simulated CV MAF-scaling parameter, α, and the CV effect size distribution, β_k. The four panels show different MAF ranges of the 1,000 randomly-drawn CVs. DHS sites were randomly sampled without respect to MAF. Bar colors indicate the fitted model, with a single GRM used except for the “LDMS” models, which used 16 GRMs (α=−1) stratified by MAF and either regional (-R) or individual SNP (-I) LD score. See Online Methods for descriptions of each method and Supplementary Figures for additional estimates and Supplementary Table 6 for numerical results. Error bars represent 95% confidence intervals.

Figure 4.

Mean ${\hat{h}}_{\mathit{\text{SNP}}}^2$ across 100 replicates from GRMs built from imputed SNPs in the least structured subsamples across different model assumptions (bars) and different ways of simulating CVs (x-axes). CV effect sizes were simulated from ~N(0,τ_k). The x-axes of each panel show the simulated CV MAF-scaling parameter, α. The three panels show different MAF ranges of the 1,000 randomly-drawn CVs. Bar colors indicate the fitted model. See Online Methods for descriptions of each method and Supplementary Figures for additional estimates and Supplementary Table 6 for numerical results. Error bars represent 95% confidence intervals.

Figure 5.

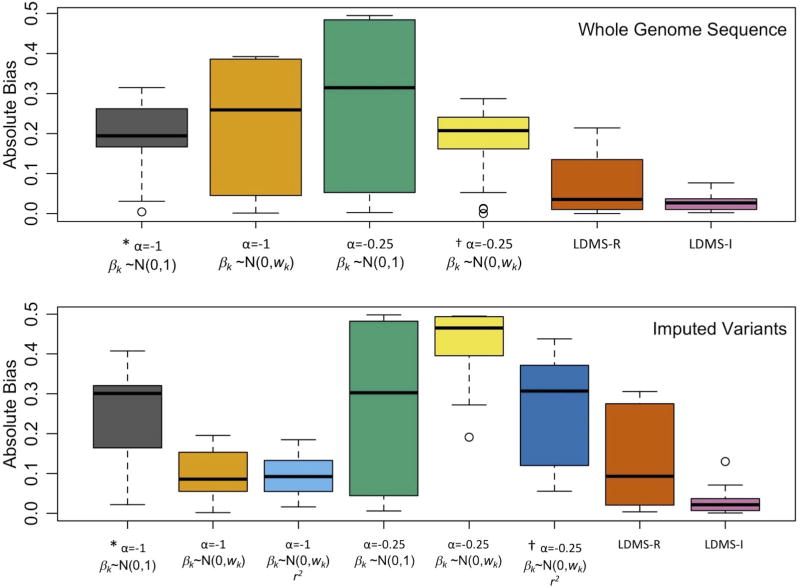
Boxplots of the absolute bias of heritability estimates $(|E({\hat{h}}_{\mathit{\text{SNP}}}^2)-h^2|)$ across all simulated phenotypes from Supplementary Figures 24 & 26 using WGS data to estimate GRMs (top), and from Figures 3–4 using imputed variants to estimate the GRMs (bottom). X axis indicates the parameters for the estimation model, including the MAF scaling factor, α, and the assumed effect size distribution, β_k, specified in the GRM and whether imputation scores (r²) were used in the GRM estimation. All used a single GRM except for LD- & MAF-stratified GREML (LDMS), which used 16 GRMs (α=−1) stratified by MAF and either regional (-R) or individual SNP (-I) LD score. * Typical GREML-SC parameters. † Typical LDAK-SC parameters. Boxplots show the median and interquartile, with whiskers extending 1.5 times the quartiles and more extreme points shown for N=22 (WGS) and 26 (imputed) mean estimates of heritability.

Of note, log likelihood was not a reliable indicator of degree of bias. Speed et al.¹⁵ argued that higher log-likelihood assuming α=−0.25 than α=−1 suggested that the former was more tenable. Across single-component models, which had the same number of predictors and therefore comparable log likelihoods, models with higher log likelihoods were typically less biased. However, we observed multiple cases where negligible differences in log likelihood translated into large differences in bias, as well as situations where models with higher average log likelihoods produced more biased results than models with lower average log likelihoods (Supplementary Figs. 23–26).

Heritability of Complex Traits in the UK Biobank

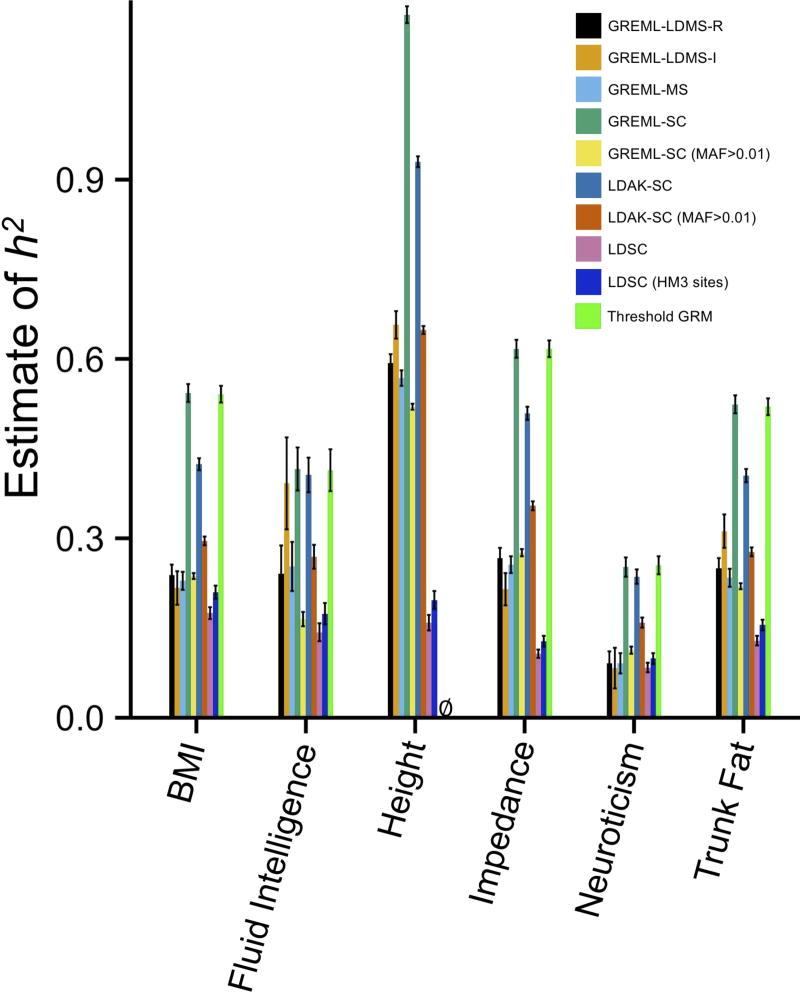
We applied seven approaches using imputed SNPs to six complex traits in the UK Biobank²⁶ (Fig. 6, Supplementary Fig. 29–30, Supplementary Table 8). Differences in ${\hat{h}}_{\mathit{\text{SNP}}}^2$ across methods were consistent with our simulations. Estimates from single-component models were often higher than those from multi-component models that bin SNPs by MAF and LD. For instance, the majority of height h² is attributable common CVs²⁷, and GREML-SC and LDAK-SC ${\hat{h}}_{\mathit{\text{SNP}}}^2$ of height were unrealistically high $(>{\hat{h}}_{\mathit{\text{PED}}}^2)$, which can occur when CVs are more common than SNPs used to build the GRM (Fig. 1,3–4). On the other hand, estimates from multi-component GREML were much more reasonable. These results provide context for understanding previously published estimates (see Supplementary Note), including those from Speed et al.¹⁵ showing higher LDAK ${\hat{h}}_{\mathit{\text{SNP}}}^2$, and highlight the dangers of using single-component models that rely on strong assumptions about CV effect sizes and MAF distributions.

Figure 6.

Estimated ${\hat{h}}_{\mathit{\text{SNP}}}^2$ using multiple methods with imputed variants for six complex traits in the UK Biobank. MAF>0.01 indicates common SNPs were used to create the GRMs. ∅ = information matrix was not invertible. HM3 indicates that only imputed HapMap3 sites were used in the LDSC analysis. Sample sizes as follows: height N=94,769; BMI N=94,595; impedance N=93,451; trunk fat N=93,414; fluid intelligence N=31,724; neuroticism N=78,565. See Supplementary Table 8 for numerical results. Error bars are 1 S.E.M.

Our results also suggest that the allelic spectra differ across the six traits, as estimated using GREML-LDMS-I, the most accurate approach in our simulations (Supplementary Fig. 31, Supplementary Tables 9–10). For example, while the majority of height heritability was explained by common SNPs, 59% of fluid intelligence h² was due to rare CVs, with a total ${\hat{h}}_{\mathit{\text{SNP}}}^2(~0.35)$ that approached ${\hat{h}}_{\mathit{\text{PED}}}^2$. Nevertheless, our simulations suggest that variance due to increasingly rare CVs was underestimated by ~20% for all traits due to low imputation quality at lower MAF. This under-estimate was probably more severe because the imputation reference panel (combined UK10K and 1,000 Genomes) used in the UK Biobank data was smaller by ~half and less diverse than the reference panel used in our simulations.

DISCUSSION

We have demonstrated that estimates of h² and allelic spectra using SNP data can be biased in a number of sometimes difficult to foresee ways, and depend strongly on a complex interplay between the method and type of data used in the analysis, trait genetic architecture, degree of sample stratification, shared environmental effects, and whether close relatives are included or excluded. Understanding how these influence ${\hat{h}}_{\mathit{\text{SNP}}}^2$ is crucial for proper interpretation of often-conflicting published estimates and for optimal design of future studies. Additional factors that we did not investigate might also influence the biases of ${\hat{h}}_{\mathit{\text{SNP}}}^2$ across methods, such as technical artifacts²⁸, environmental factors that covary with ancestry^29,30, CVs with MAF <0.0003, or non-SNP CVs.

LD is central to the performance of all the methods compared here, in particular, the LD among SNPs used to create the GRM and that between CVs and SNPs^7,20. Single-component models, such as GREML-SC and LDAK-SC, are highly sensitive to assumptions, especially when rare imputed or WGS SNPs are used to create the GRM. This is problematic given that it seems unlikely that a single set of assumptions will hold for all traits and across the entire allelic spectrum. Alternatively, multi-component models that partition ${\hat{h}}_{\mathit{\text{SNP}}}^2$ across multiple LD and MAF bins provide the most robust estimates across the majority of contexts explored here while simultaneously providing insight into the allelic spectra of complex traits. However, they are more computationally intensive and have higher standard errors than single-component models, and require larger datasets to achieve reliable estimates. Nevertheless, such data is now at hand, and if the goal is to obtain the least biased estimates of h² or to estimate allelic spectra, we recommend using multi-component GREML models. Even when using multi-component approaches, h² is likely underestimated, but will improve as sample sizes increase and larger imputation panels and/or WGS data are utilized.

Based on the results of the present and previous studies, we summarize our suggestions for using SNPs to estimate h² and allelic spectra of complex traits. First, quality control of genetic data is crucial, particularly for case-control and/or multiple cohorts datasets where technical artifacts can inflate or deflate ${\hat{h}}_{\mathit{\text{SNP}}}^2$³¹. Covariates (ancestry principal components, cohorts, plates, etc.) that might be confounded with genetic similarity should be included as fixed effects in GREML models and in the GWAS models for LD score regression³². Related individuals may share common environmental and non-additive genetic effects, upwardly biasing estimates of h²; using unrelated individuals should provide estimates not inflated by such factors³³.

Second, the model and data type used in the analysis strongly influence estimates. When genotype data are unavailable or impractical to use, LDSC provides a lower bound of the h² captured by common CVs and is unaffected by confounding due to stratification and the common environment. Single component methods such as GREML-SC and LDAK-SC are highly sensitive to model misspecification, which can lead to severely biased estimates of heritability. Moreover, they are also sensitive to the effects of stratification, which are not mitigated by inclusion of ancestry covariates. We recommend these approaches only when sample sizes are small (e.g., n < 30,000) and homogeneous. Multi-component approaches with WGS or imputed SNPs provide the most accurate estimates of h² and allelic spectra across a range of genetic architectures and stratification levels. When using imputed data, SNPs should be imputed using the largest and most diverse reference panel possible (e.g., HRC²¹) in order to more reliably capture the effects of rare CVs. However, more GRMs lead to larger standard errors, necessitating larger sample sizes (n > 30,000). Of the multi-component approaches, GREML-LDMS-I, which we introduce here and bins SNPs by MAF and individual LD levels, appears to perform the best.

ONLINE METHODS

Samples and Population Structure

We simulated continuous phenotypes derived from WGS data in the Haplotype Reference Consortium (HRC)²¹. The HRC comprises ~32,500 individuals from multiple WGS studies, with called genotypes at all sites with minor allele count ≥5. We had access to a subset (Supplementary Note) of 21,500 individuals with genotype calls at 38,913,048 biallelic SNPs. This large WGS dataset allowed phenotype simulation with differing genetic architectures under realistic patters of LD structure, stratification, and relatedness.

The HRC is mainly of European ancestry. To reduce the effects of worldwide stratification, we identified European individuals using principal components analysis (PCA). We used flashpca³⁴ on 133,603 MAF- and LD-pruned SNPs (plink2³⁵ commands –maf 0.05 --indep-pairwise 1000 400 0.2), extracted the first ten PCs. We used the 1000 Genomes individuals in the HRC as anchor points for ancestry and identified 19,478 individuals of European descent, including individuals of Finnish and Sardinian ancestry using K-means clustering in R³⁶ (Supplementary Fig. 32).

To identify subsets of these 19,478 individuals spanning different levels of genetic heterogeneity, we reran PCA with only these individuals, then identified four increasingly homogenous subgroups within them using K-means clustering (Supplementary Fig. 33 and Supplemental Note). We sampled an equal number of individuals from each subset at a relatedness cutoff of 0.1 (N=8,201), and also identified individuals with relatedness less than 0.05 within each group (N=7,792; 8,115; 8,129; and 8,186 for the four subsamples) to examine how relatedness and stratification influence ${\hat{h}}_{\mathit{\text{SNP}}}^2$ estimates.

Simulation of Phenotypes and Whole Genome Data Types

To assess how methods performed on a range of genetic architectures, we simulated phenotypes from CVs drawn randomly from five MAF ranges from the WGS data: common (MAF≥0.05), uncommon (0.01≤MAF<0.05), rare (0.0025≤MAF<0.01), very rare (0.0003≤MAF<0.0025), and all SNPs that had a minor allele count (MAC) ≥5 (MAF≥0.0003). We generated phenotypes from 1,000 CVs from the model y_i=g_i+e_i, where g_i=ΣX_ikβ_k and X_ik=(z_ik−2p_k)[2p_k(1−p_k)]^α/2, where z_ik was the genotype coded as 0, 1, or 2 of individual i at the k^th CV, p_k was the MAF within a population subset, and β_k was the k^th allelic effect size, drawn from ~N(0,1). In these simulations, we used α=−1, assuming larger average effect sizes for rarer SNPs. The g_i’s were standardized and added to residual error drawn from ~N(0,(1−h²)/h²) for h²=0.5. A total of 100 replicated phenotypes were simulated for each CV MAF range and each of the four population stratification subsets. Note that simulations did not include any ancestry (i.e., PC) effects, and thus stratification-driven biases were due to the genotypic (e.g., long-range LD) effects of stratification.

To simulate ascertained case-control phenotype data, in samples with some and low stratification (Supplementary Fig. 33B–C), we converted the continuous phenotypes simulated above to dichotomous case-control data using a prevalence of 20% (K=0.2). We then combined the cases with an equal number of randomly sampled controls to simulate ascertained datasets, which reduced sample sizes (~40% of the continuous trait data). Note that this altered sample size reduces the genetic variance for phenotypes derived from rarer CVs. We transformed estimates of h² to the liability scale using the transformation described in Lee et al.²⁵.

To simulate array, imputed, and WGS data types, we first extracted from the WGS data SNP positions corresponding to a widely-used commercially available genotyping array, the UKBiobank Affymetrix Axiom array (the array SNP dataset). We then imputed genome-wide variants using these Axiom SNPs and independent HRC samples as a WGS reference panel (the imputed dataset). Finally, we used the HRC WGS data directly (the WGS dataset). See Supplementary Note for details of each dataset. MAF distributions of the different data types for two of the structure subsamples are shown in Supplementary Fig. 34.

Heritability Estimation Methods Tested

We briefly describe our implementation of the most commonly used methods to estimate h² and partition genetic variation using genome-wide data (see Supplementary Note for descriptions of and results from additional, less commonly used methods). For all methods except LD score regression (described below), we generated GRMs following the standard procedures of each method, and estimated h²_SNP using GCTA³⁷. In all models, variance component estimates were unconstrained (e.g., by using the –reml-no-constrain option of GCTA), and included 20 PCs (10 from worldwide PCA and 10 from the specific subsample PCA) and sequencing cohort as fixed effects.

Single-component GREML (GREML-SC)

Yang et al.⁵ introduced the single-component approach using a mixed-effects model, with GRM entries:

$$A_{\mathit{\text{ij}}}=\frac{1}{m}{\sum }_k^m\frac{(x_{\mathit{\text{ik}}}-2p_k)(x_{\mathit{\text{jk}}}-2p_k)}{2p_k(1-p_k)}$$ (1)

where m is the number of SNPs, x_jk is the genotype (coded as 0, 1, or 2) of individual j at the k^th locus, and p_k is the MAF of the k^th locus. The variance of the phenotypes is

$$\mathit{\text{var}}(\mathit{y})=\mathit{A}{\sigma }_v^2+\mathit{I}{\sigma }_e^2$$ (2)

where the variance explained by the SNPs (σ²_v) and error variance (σ²_e) are estimated using restricted maximum likelihood (REML) implemented in the GCTA package³⁷. The proportion of the total variance explained by all SNPs is then a measure of heritability $({\hat{h}}_{\mathit{\text{SNP}}}^2={{\sigma }^{\mathit{2}}}_v/({{\sigma }^{\mathit{2}}}_v+{{\sigma }^{\mathit{2}}}_e))$. Typically, the set of m SNPs used to build the GRM is the set of SNPs with MAF≥0.01 (hereafter “common SNPs”) and unrelated individuals (relatedness ≤ 0.05). We compared this typical approach to one using all SNPs with MAC≥5 (hereafter “all SNPs”) in each particular stratification subsample and for each data type (note that ~9.5% of Axiom array positions have MAF <0.01 in our sample), as well as to an approach using less stringent relatedness thresholds (relatedness < 0.10 and no relatedness threshold). For analyses that used no relatedness threshold, inclusion of close relatives increased our sample sizes to 9,916; 8,701; 8,715; and 8,506 for the samples with most, some, low, and least stratification, respectively (Supplementary Fig. 33).

MAF-Stratified GREML (GREML-MS)

${\hat{h}}_{\mathit{\text{SNP}}}^2$ is expected to be a biased estimate of h² when using the GREML-SC method if the MAF distribution of the CVs does not match the MAF distribution of SNPs used to generate the GRM¹¹. Stratifying SNPs into MAF bins in a multiple GRM GREML approach can mitigate this bias and can partition ${\hat{h}}_{\mathit{\text{SNP}}}^2$ into that explained by different SNP MAF bins, lending insight into the allelic spectra of complex traits^6,7. For each data type, we applied this approach using 4 MAF bins, matching the CV MAF binsused for phenotype simulation.

LD- and MAF-Stratified GREML (GREML-LDMS-R and GREML-LDMS-I)

Extending the GREML-MS method to account for different levels of LD throughout the genome, Yang et al.⁷ introduced an approach (originally termed GREML-LDMS but which we term GREML-LDMS-R here) that stratifies SNPs jointly by their MAF and regional LD scores, defined as the sum of r² between the focal SNP and all other SNPs in a 200Kb sliding window. We estimated LD scores using the default settings in GCTA (200Kb block size with a 100Kb overlap), and stratified SNPs into LD score quartiles (see Yang et al.⁷ for details). This resulted in 16 GRMs (4 MAF bins by 4 LD bins) and therefore 16 values of ${\hat{h}}_{\mathit{\text{SNP}}}^2$, which were summed to derive total ${\hat{h}}_{\mathit{\text{SNP}}}^2$. SNPs with individually low levels of LD contribute disproportionately to the heritability for multiple complex traits, particularly low LD SNPs in regions of high LD¹³. Because these results suggest individual rather than regional LD levels influence heritability, we developed and compared results from an alternative approach (GREML-LDMS-I) that stratified by individual (rather than regional) SNP LD scores, again binning SNPs by LD quartiles and four MAF bins, for a total of 16 GRMs.

Single- and multi-component LD-Adjusted Kinships (LDAK-SC and LDAK-MS)

Speed et al.²⁰ noted that because LD varies across the genome, CVs in regions of high LD receive disproportionate weight by eqn. (1) above. The original LDAK²⁰ approach weights SNPs according to individual LD, potentially correcting for the bias introduced when there is variation in how well CVs are tagged by SNPs, and assumes standard MAF-CV effect size scaling (α = −1). We used LDAK5²⁰ to estimate these LD-weighted GRMs, which first thins SNPs in very high LD to reduce redundant tagging, then estimates SNP weights, w_k, that are inversely proportional to their average LD with other SNPs. We also applied the MAF-stratified approach described above but using LDAK weights (LDAK-MS). For the single-component model (LDAK-SC), we used all SNPs (MAC≥5) as well as only common SNPs (MAF≥0.01) to build the GRM for each data type. For the MAF-stratified approach, following recommendations in the LDAK documentation, we estimated SNP weights over the union of all SNPs (MAC≥5), then computed GRMs for each MAF class separately. We then applied the multiple GRM method with these LDAK-weighted GRMs to estimate h²_SNP using GCTA. Results from the first set of simulations (Figs. 1 and 2) come from the traditional LDAK approach described above; results from the second set of simulations (Figs. 3–5) come from the updated LDAK approach described in the section below, Simulation of data and comparison of ${\hat{h}}_{\mathit{\text{SNP}}}^2$ under alternative assumptions about CV effect sizes.

Extended Genealogy with Thresholded GRMs

Zaitlen et al.²⁴ introduced a method to simultaneously obtain ${\hat{h}}_{\mathit{\text{SNP}}}^2$ and ${\hat{h}}_{\mathit{\text{PED}}}^2$ by using two GRMs in a sample containing close relatives. The first GRM contains all A_ij, whereas the second GRM sets A_ij, values below a threshold, t, to 0. The first GRM, therefore, contains information on allele sharing of (mostly common) variants in unrelated and related individuals (estimating h²_SNP), while the second only contains information from closely related individuals (estimating h²_IBS>t, following Zaitlen et al.²⁴). We tested two relatedness thresholds (t ≤ 0.05 and 0.1) for the second GRM. The sum of ${\hat{h}}_{\mathit{\text{IBS}}>t}^2$ and ${\hat{h}}_{\mathit{\text{SNP}}}^2$ provides an estimate of total h², similar to ${\hat{h}}_{\mathit{\text{PED}}}^2$, with all the same potential biases that exist in ${\hat{h}}_{\mathit{\text{PED}}}^2$ from designs that use close relatives. By necessity, all analyses using this approach included close relatives, which could lead to confounding between genetic and environmental similarity if shared environmental effects are not modeled^38,39. Indeed, Zaitlen et al.²⁴ argue that such shared environmental effects were the likely cause of higher ${\hat{h}}_{\mathit{\text{PED}}}^2$ estimates among relatives who shared an environment through cohabitation (e.g., half-siblings) compared to equally related relatives that did not share a cohabitation environment (e.g., grand-parents and grand-children). We therefore assessed whether ${\hat{h}}_{\mathit{\text{SNP}}}^2$ and ${\hat{h}}_{\mathit{\text{PED}}}^2$ estimates from this method (as well as from GREML-SC and LDSC) were biased when extended shared environmental effects were present but unmodeled in samples of closely related individuals (see Supplementary Note).

LD Score Regression (LDSC)

LDSC uses a different approach to estimate the heritability tagged by common CVs. Rather than estimating relatedness within a sample for use in mixed-model GREML analysis, LDSC regresses GWAS test statistics (χ²) on SNPs’ LD scores, which reflect the degree to which each SNP is correlated with surrounding SNPs^10,19. For a polygenic model, the expected GWAS test statistic of SNP j, χ²_j, is

$$\mathrm{E}[{{\mathrm{\chi }}^2}_{\mathrm{j}}|l_j]=N({h^{\mathit{2}}}_{\mathit{\text{SNP}}})l_j/M+\mathit{\text{Na}}+1$$ (3)

where N is the sample size, M is the number of SNPs, l_j is the LD score (= Σ_kr²_jk) measuring the tagging of surrounding variants by SNP j, and a is a measure of confounding biases arising from stratification and cryptic relatedness. Thus, regressing GWAS test statistics on per-SNP LD scores allows for both estimation of ${\hat{h}}_{\mathit{\text{SNP}}}^2$ and assessing the degree of confounding or polygenicity of a trait¹⁹. Bulik-Sullivan et al.¹⁹ argue that LDSC provides unbiased estimates of h² tagged by common SNPs regardless of whether GWAS test statistics are estimated with or without controlling for ancestry or environmental covariates or relatedness. Here, we estimated GWAS test statistics using plink2 without controlling for ancestry covariates or controlling for ancestry covariates (20 PCs and sequencing cohort as above). We used the ldsc package with default parameters (see URLs) to perform LDSC. We calculated LD scores for all SNPs using WGS data, including common and rare SNPs. As recommended by Bulik-Sullivan et al.¹⁹, we used unrelated individuals (relatedness ≤ 0.05) and only common SNPs to perform the regression itself, because the relationship between the GWAS χ² and LD-score is unclear for rare (MAF<.01) SNPs. We examined the relationship among ${\hat{h}}_{\mathit{\text{SNP}}}^2$, the intercept, the mean χ², and the genomic control inflation factor, λ_GC (see Supplementary Note).

LDSC can also be used to partition heritability among annotations¹⁰. We applied this approach using the four MAF bins described above. Because our MAF bins included very rare SNPs, for this MAF-stratified LDSC, we used GWAS test statistics from all SNPs (MAF≥0.0003, using the --not-5–50 flag in the ldsc package) while controlling for covariates as above.

Simulation of Phenotypes and Comparison of ${\hat{h}}_{\mathit{\text{SNP}}}^2$ under Alternative Assumptions about CV Effect Sizes

We tested the LDAK-SC, GREML-SC, and GREML-LDMS (-R & -I) methods on phenotypes imulated under alternative assumptions about CV effect sizes in order to determine the degree to which the methods were robust to model misspecification. To simulated phenotypes under alternative effect size assumptions, in the low stratification sample only (Supplementary Fig. 33C), we varied the MAF-effect size relationship (α=−1 or −0.25), and the effect size distribution (β_k~N(0,1) or ~N(0,w_k), where w_k is the LDAK weight of the k^th CV estimated from the WGS data, which is inversely proportional to the SNP LD score (Supplementary Fig. 8–9)). When β_k~N(0,1) and α=−1, this model is the same as above and as previously described⁷. WGS CVs were drawn randomly from common SNPs (MAF > 0.05), very rare SNPs (MAF < 0.0025), all SNPs (MAF≥0.0003) or randomly from all DHS sites (systematically lower LD¹⁷), annotated for all UK10K SNPs with MAC≥2. Note that in Speed et al.¹⁵, effect sizes, β_k, are also assumed to be proportionate to the imputation quality scores (r²). Because we were simulating CVs from WGS data rather than imputed variants, we did not include the r² term for simulating CV effect sizes.

Additionally, we simulated phenotypes using an independent LD architecture derived from the 75 annotations baseline-LD model described in ref.¹³, which contains coding, conserved, DHS and other functional annotations, 10 MAF bins, and 6 LD-related annotations modeling multiple LD-related architectures (including predicted allele age, recombination rate and CpG-content). For these simulations, we annotated 20,678,452 SNPs with allele count greater or equal than 2 in 3,567 UK10K unrelated individuals, and modeled the variance of the k^th SNP, τ_k, proportional to ${\sum }_{c=1}^{75}{a}_c(k){\theta }_c$, where a_c(k) was the continuous value annotations of CV k for annotation c and θ_c was the per-SNP contribution of one unit of the annotation a_c to the heritability. We used the values of θ_c estimated with stratified LD score regression on 31 independent traits¹³ and constrained θ_c to be positive. Finally, as θ_c and stratified LD score regression hold only for common SNPs, we rescaled the variance of all τ_k so that the heritability explained by the four rarest of the 10 MAF bins (delimited by 0, 0.1%, 0.5%, 1% and 5% boundaries) were equal to the expected variance of the bin (=Σ(p_k(1 − p_k))^1+α, where α=−0.28, estimated by Loh et al.¹²). We then simulated phenotypes as described above with effect sizes β_k drawn from ~N(0,τ_k).

We compared estimates from models applying different assumptions of α and β_k. The traditional GREML-SC, -LDMS-R, and -LDMS-I estimate GRMs using α=−1 and β_k ~N(0,1), while the updated LDAK-SC model of Speed et al.¹⁵ uses α=−0.25 and β_k ~N(0,w_k) as well as weighting SNPs by imputation r². To test these assumptions, we estimated GRMs using either α=−1 or −0.25 and either weighting by LDAK weights or not. For imputed data, we also weighted SNP contributions to the GRM by imputation r². For GREML-LDMS-R and -I, we used α=−1 and no LDAK or imputation r² weighting.

Heritability of Complex Traits in the UK Biobank

We estimated heritability for six continuous phenotypes in the initial release of the UK Biobank²⁶ (N~150,000) using the most commonly applied methods (Fig. 6). To reduce the effects of stratification, we used individuals of European ancestry (Supplementary Fig. 33). To estimate the GRMs, we separately used directly genotyped Axiom array positions as well as imputed genome-wide SNPs with IMPUTE info score ≥0.3. See Supplementary Table 8 for the list of all methods we applied. See Supplemental Note for additional methods and details.