Modular discovery of monomeric and dimeric transcription factor binding motifs for large data sets

Abstract

In some dimeric cases of transcription factor (TF) binding, the specificity of dimeric motifs has been observed to differ notably from what would be expected were the two factors to bind to DNA independently of each other. Current motif discovery methods are unable to learn monomeric and dimeric motifs in modular fashion such that deviations from the expected motif would become explicit and the noise from dimeric occurrences would not corrupt monomeric models. We propose a novel modeling technique and an expectation maximization algorithm, implemented as software tool MODER, for discovering monomeric TF binding motifs and their dimeric combinations. Given training data and seeds for monomeric motifs, the algorithm learns in the same probabilistic framework a mixture model which represents monomeric motifs as standard position-specific probability matrices (PPMs), and dimeric motifs as pairs of monomeric PPMs, with associated orientation and spacing preferences. For dimers the model represents deviations from pure modular model of two independent monomers, thus making co-operative binding effects explicit. MODER can analyze in reasonable time tens of Mbps of training data. We validated the tool on HT-SELEX and ChIP-seq data. Our findings include some TFs whose expected model has palindromic symmetry but the observed model is directional.

INTRODUCTION

In transcriptional regulation, proteins called transcription factors (TFs) bind to specific DNA motifs, to have a regulatory effect on the transcription rate of particular genes. The regulating TFs may bind co-operatively in clusters of two or more factors which makes the regulation combinatorial by nature (1–4). Therefore, it is of interest not only to find the binding motifs for individual monomeric TFs but also motifs for dimeric and higher order co-operative binding of several TFs on the same regulatory area in DNA. With the massive training data currently available from, e.g. high-throughput SELEX (5,6) and ChIP-seq experiments (7), it is possible to learn complex binding models from quite weak signals.

In a large number of dimeric cases of TF binding, the specificity of the dimeric motif has recently been observed to differ notably from what would be expected were the two factors to bind to DNA independently of each other (4,6,8). Current automatic motif discovery tools do not learn monomeric and dimeric motifs soundly within one probabilistic framework in modular fashion such that the effects of co-operative binding on motifs could be shown and analyzed. In this paper, we propose such a learning algorithm and a software tool for modular discovery of monomeric and dimeric binding motifs for TFs.

The algorithm uses a class of probabilistic mixture models for (possibly multi-profile) monomeric binding motifs and all their dimeric combinations. Our model represents each monomeric motif as a standard position-specific probability matrix (PPM) (9,10). Each dimeric motif is represented in modular fashion as a pair of monomeric PPMs, with associated information on the relative orientation and spacing of the two monomeric components. In our model, the monomeric components need not be spatially separate but their sites may overlap; such overlaps have been reported, e.g. in (4,11). A novel feature of our model is that it includes a deviation matrix that represents explicitly how much the discovered dimeric PPM deviates from the expected PPM for independent component monomers. Another novelty is that monomeric and dimeric models are learned such that the effect of the noise from dimeric occurrences on monomeric models is minimized. Moreover, the mixing parameters of the model reveal the relative abundances of different motif combinations. In particular, the mixing parameters for the dimeric variants give precise quantitative indication of orientation and spacing preferences of the two monomers that make the dimer.

For learning our binding model we describe an expectation maximization (EM) algorithm (12), called MODER (MOtif DEtectoR). Given a data set of sequences that contain enriched motif instances, MODER learns by EM search the parameters of all model components simultaneously, as a mixture of several PPMs, by optimizing the alignment of the model with the training data using maximum likelihood estimation. The EM search is initialized with user-given seed sequences for the monomeric profiles of the model. It finds PPMs for the monomers as well as for their dimeric combinations within given range of spacings and orientations. Higher-order combinations are not included, as it would exponentially increase the complexity and the size of the model. Monomer PPMs are learned using pruning techniques that minimize contamination from near-by motifs occurrences and from background. The requirement to provide seeds is a limitation of MODER which depends on prior knowledge (such as motif databases) or the use of other motif discovery algorithms. On the other hand, seed-based initialization makes MODER fast and capable of processing in reasonable time a training data consisting of sequences that are hundreds of bps long and are several Mbps in total size. MODER was designed for motif discovery from HT-SELEX reads, but other type of training data, such as ChIP-seq data sets, can be used as well.

Validation experiments of MODER show robust and fast performance both on HT-SELEX and ChIP-seq data. We applied MODER on six HT-SELEX data sets, each consisting of 10⁵–10⁶ reads of length 30 or 40, and found varying amounts of difference between observed and expected motifs: for example, for factors FLI1 and PKNOX2 the expected homodimeric model has palindromic symmetry but the observed model is directional, reconfirming an earlier observation in (6). From ChIP-seq data MODER finds for factor CTCF essentially the same dimeric model as reported in (13,14), and for modular receptor RXRA a dimeric model that the Tomtom tool (15) matches with a known RXRA heterodimer. For factor NRSF, MODER finds from ChIP-seq data essentially the same multi-profile model as in (16).

In previous research, a dimer model quite similar to ours but without explicit modular structure and overlaps of monomers within dimers was introduced, with an entropy minimization learning algorithm Bipad/Maskminent (17–19). Discovery of spaced dyads (pairs of relatively short motifs) was considered in (20,21). Gibbs sampling based BioProspector (22) is another early dimer search algorithm. Recent dimer prediction methods include SpaMo (23), iTFs (24), and TACO (25). All start from given monomeric PPMs and find, using thresholding, the occurrence sites of the PPMs in the training data. Then enrichment of specific spacings of pairs of occurrences is detected, with an analysis of the statistical significance but without an analysis of co-operative effects of dimer components. SpaMo was designed for finding preferred distances between the site of the primary TF and the sites of secondary TFs in ChIP-seq data. The dimer model of iTFs includes relative orientation of the components but it does not consider overlaps and uses binned distances. Finally, TACO’s model includes orientation and distance and allows the components to overlap, but does not analyze the effect of overlap on the binding profile.

Using the EM algorithm in motif discovery was initiated by Lawrence and Reilly (26) and was used for finding motifs with spacers by Cardon and Stormo (27). The mixture model and the EM learning of MODER generalize the techniques of MEME (28,29) to multi-profile dimeric case. As compared to MEME, an important feature of MODER is that it learns all submodels simultaneously, using all training data symmetrically. coMOTIF (30) is another simultaneous multi-profile motif finder based EM algorithm. It does not, however, keep track of the distances between binding sites and does not allow overlaps of binding sites, nor does it have the modeling of deviation or learning of the motif in the gap positions between the dimer components. MODER can be seen as a generalization of coMOTIF. Recent EM algorithm based finders of monomer motifs include GADEM and rGADEM (31,32) which use genetic algorithm with EM to improve starting PPMs, SEME (33) which uses importance sampling to speed-up the search, EXTREME (16) which achieves speed-up by using the on–line version of the EM algorithm, and STEME (34) which resorts to suffix-trees. Moreover, Liu et al. (35) use Gibbs sampling and Ikebata and Yoshida (36) use a repulsive MCMC version of MEME type search for simultaneous discovery of several motifs, Alipanahi et al. (37) use deep learning for motif discovery with good validation results but non-modular structure of the underlying model, and Colombo and Vlassis (38) find monomeric motifs with a fast spectral learning algorithm. Recent motif finders specially designed for large ChIP-seq data include rGADEM (32), HOMER (39), ChIP-Munk (40), and MEME-ChIP (41), evaluated in (42).

In the rest of the paper, the next section defines the mixture model of MODER, the next one gives the associated EM algorithm for estimating the model parameters, then our implementation of MODER is described, with techniques to initialize and prune the search, and finally we report some validation and comparison experiments and discuss motifs found by MODER for TFs FLI1, HOXB13, HNF4A, TFAP2A, FOXC1, PKNOX2, NRSF, CTCF and RXRA.

MATERIALS AND METHODS

Model structure

The binding affinity model learned by MODER, specified by parameters η = (θ, ψ, λ), gives a probability distribution for sequences in some alphabet Σ. We will use always the DNA alphabet Σ = {A, C, G, T} but the model works for arbitrary alphabets.

Model η is a mixture of distributions for monomeric sequences that contain one occurrence of a monomeric motif, and distributions for dimeric sequences that contain two monomeric motifs in a specific relative orientation and spacing, and a distribution for background sequences. Monomeric distributions are built from the PPMs of the monomers and the background. For all orientation and spacing alternatives between the two monomers in a dimer, dimeric distributions are built either from the PPMs of the monomers and the background or from the PPM of the entire dimer and the background. If the two monomers of a dimer do not overlap and have a long gap in between, then the dimeric distribution is just the product of the two monomer PPMs, that is, the model assumes that there is no co-operative effect affecting the independence of the two binding profiles. If the monomers overlap or the gap between them is short, then the binding profiles of two monomers do not necessarily remain independent. There can be interaction between the components of a dimer as they may physically contact each other, or the interaction can be DNA mediated (4). Therefore the model allows deviating from pure reduction to monomer PPMs and also represents, using the so-called deviation matrix, how the PPM learned from data differs from the product of monomer PPMs which would be the expected model if there are no interactions.

The three parameter groups of η = (θ, ψ, λ) and the parametrization of the dimeric structures are defined in detail in the following subsections.

Monomeric PPMs θ_k and background θ₀

Parameter θ = (θ₀, θ₁, …, θ_p) gives the background distribution θ₀ and p monomeric motifs θ_k. Each θ_k, k ≠ 0, is a 4 × ℓ_k PPM

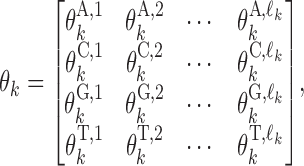where gives the probability for an alphabet symbol (nucleotide) a to occur in position h of θ_k, and ℓ_k denotes the length of θ_k. The reverse complement 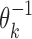of θ_k is a PPM such that 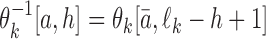for each a and h, where 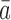is the complementary base of a (e.g., ).

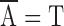The mononucleotide background model 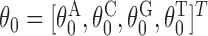gives the occurrence probabilities of each alphabet symbol in a position that is outside the occurrences of monomers or dimers. The background model is position-independent.

Dimer specification k₁k₂od

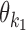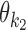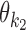The model uses monomeric motifs θ_k as building blocks of dimeric motifs. The possible dimeric motifs are indexed with quadruples (k₁, k₂, o, d) which we abbreviate as k₁k₂od (this should not be confused with the multiplication of these symbols). A dimer with index k₁k₂od is composed of monomers and whose orientation is o and distance (spacing) from the end of to the start of is d, where 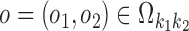and 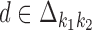. Because of co-operative binding effects, monomer motifs alone are not enough for building dimeric models. To model such effects we will use an additional PPM (see the next subsection) that covers the middle area of the dimer, called the bridging segment. Figure 1 illustrates our parametrization of dimeric structures; cf. (17).

Figure 1.

Parametrization of dimeric structures. On top, a non-overlapping dimer with spacing d and head-to-tail orientation. Parameter δ gives the lower bound such that monomers separated by a space ≥δ are assumed independent. Below, a dimer with reversed first monomer and overlap of length d. When d < δ, the model also includes the bridging PPM ψ that covers the bridging segment of the dimer.

The set of possible pairwise orientations o is if k₁ = k₂ (homodimer), and 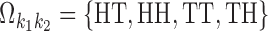otherwise (heterodimer). Table 1 describes different orientations o = (o₁, o₂) giving the directions of motifs 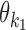and . Note that for homodimers the orientations HT and TH are identical, and one can use HT to represent them both. We assume that motif 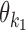always occurs before motif when moving from 5′ end to 3′ end and using motif start position as reference point. The reverse order of the two motifs transforms back to this case by considering the complementary strand.

Table 1. Relative orientation of two motif occurrences within a dimer.

Orientation o	Short-hand		o 1	o 2
Head-to-Tail	HT	→ →	+1	+1
Head-to-Head	HH	→ ←	+1	−1
Tail-to-Tail	TT	← →	−1	+1
Tail-to-Head	TH	← ←	−1	−1

Exponents o₁ and o₂ give the orientation of the first and the second PPM: for a PPM θ_k, 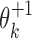leaves the matrix intact but 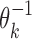takes the reverse complement.

The possible distances between the two occurrences are given as an interval 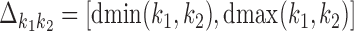. If 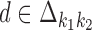is non-negative, it gives the number of gap positions between the two occurrences. If d < 0, then the occurrences overlap by −d positions. The smallest possible distance 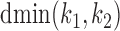has to be 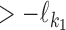. MODER implementation uses (optionally adjustable) default value 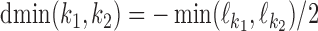, that is, overlaps only up to half of the length of the monomers are allowed. The longest distance possible for sequences of maximum length L_max is .

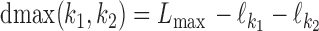We use parameter δ ≥ 0 to give the minimum spacing such that if the space between the two monomers of a dimer is ≥δ then the monomer profiles are assumed independent, i.e. in this case the model ignores the possible co-operative interactions that would change the binding preferences of the two TFs or the gap between them. Parameter δ is a user-given constant (default value δ = 4 in our implementation).

In what follows, we refer to the available monomeric and dimeric motifs with index k that may belong to the following three separate sets:

M = {1, …, p}: the indices for monomeric motifs.

D ⁺ = {k₁k₂od: d ≥ δ, k₁, k₂ ∈ M}: the indices for dimeric motifs whose monomers and 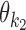have a gap of length ≥δ in between. This is called the independent case.

D ⁻ = {k₁k₂od: d < δ, k₁, k₂ ∈ M}: the indices for dimeric motifs whose monomers 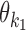and 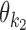have a gap of length <δ in between. This is called the dependent case. Note that this case includes dimers whose monomers overlap.

Dimeric PPMs τ_k1k₂od, bridging PPMs ψ_k1k₂od and deviation matrices κ_k1k₂od

We use 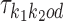to denote the PPM (which is a 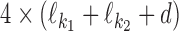matrix) for motif k₁k₂od ∈ D⁺∪D⁻. Each is a derived parameter, composed of free parameters, such that if k₁k₂od ∈ D⁺ then 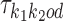is built from 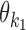, , and background θ₀, and if k₁k₂od ∈ D⁻ then 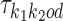is built from 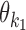, , and the bridging PPM 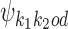to be defined below. Constructions are as follows.

If k₁k₂od ∈ D⁺, then we put simply

(1)

where • concatenates matrices. There are d column-matrices θ₀ in the middle of 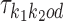, that is, the middle gap is filled with the background.

If k₁k₂od ∈ D⁻, then a middle segment of 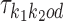is a free parameter learned from data: for d < 0, the columns that are on the overlap area (plus one more column on both sides) are free parameters, and for 0 ≤ d < δ, the columns that are on the area between the monomers (plus one more column on both sides) are free parameters. This area of length |d| + 2 in the middle of a dimer is called the bridging segment, and the 4 × (|d| + 2) PPM for the bridging segment is called the bridging PPM. We let 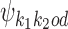denote the bridging PPM. Now, the columns of 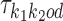that cover the bridging segment come from 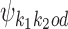while the columns outside this segment are supposed to reduce to the monomer motifs, i.e. they are as in the implied prefix and suffix segments of monomer matrices 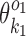and 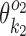. So we get

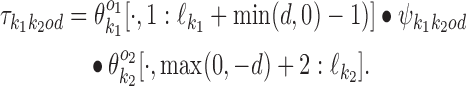(2)

Next, we make it explicit how PPM 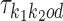differs from the PPM that would be expected were the monomer motifs independent in the dimer. We denote such an expected PPM as 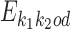. It models the situation that motifs 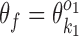and 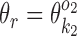have independent instances at distance d from each other in sequences 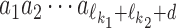with an occurrence of θ_f at the left end and θ_r at the right end.

Let first d ≥ 0. Consider the occurrence probability P(a_i) of the ith symbol a_i. Obviously, if 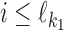, then P(a_i) = θ_f[a_i, i]; if 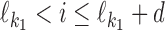, then P(a_i) = θ₀(a_i), i.e., we expect to see the background distribution between the two motifs; and if 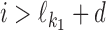, then 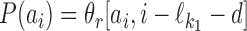. This means that 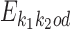is just θ_f followed by d columns, each equal to θ₀, followed by θ_r; c.f., the definition of 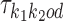in the independent case (1).

Let then d < 0, i.e., the motifs overlap by |d| symbols. Consider again the probability P(a_i). If 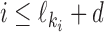, then P(a_i) = θ_f[a_i, i], and hence the ith column of the expected PPM is 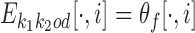. Similarly, if 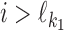, then 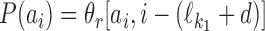, and hence 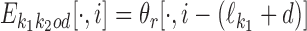. In the remaining case we have , and the ith symbol a_i belongs to the area where the two motifs overlap. Hence a_i is generated by both θ_f and θ_r, under the condition that both generate the same symbol because in the overlapping area the two motifs have to coincide. Therefore P(a_i) would be equal to , normalized by the condition that both motifs generate the same symbol. This gives

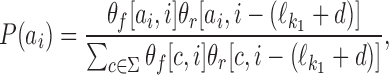(3)

and therefore the ith column becomes

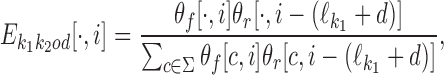(4)

where × denotes element-wise product.

Finally, the deviation matrix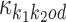, defined as

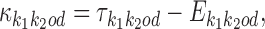gives the difference between observed and expected model. Deviation matrices will be visualized using a variant of the sequence logo in which positive values are shown above a separating line and negative values below it, see Figure 2. Note also that the expected PPM of homodimers is always palindrome symmetric for orientations HH and TT.

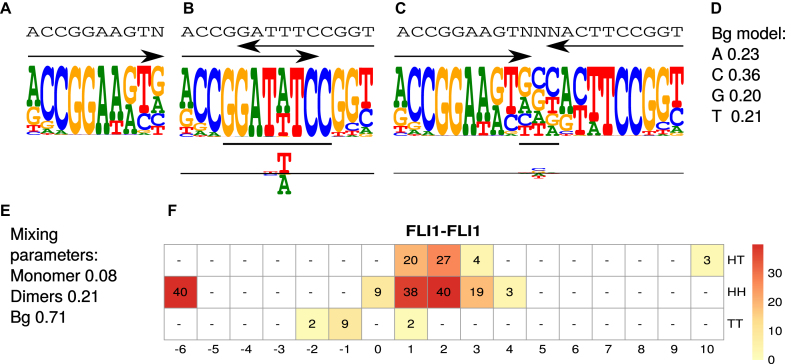
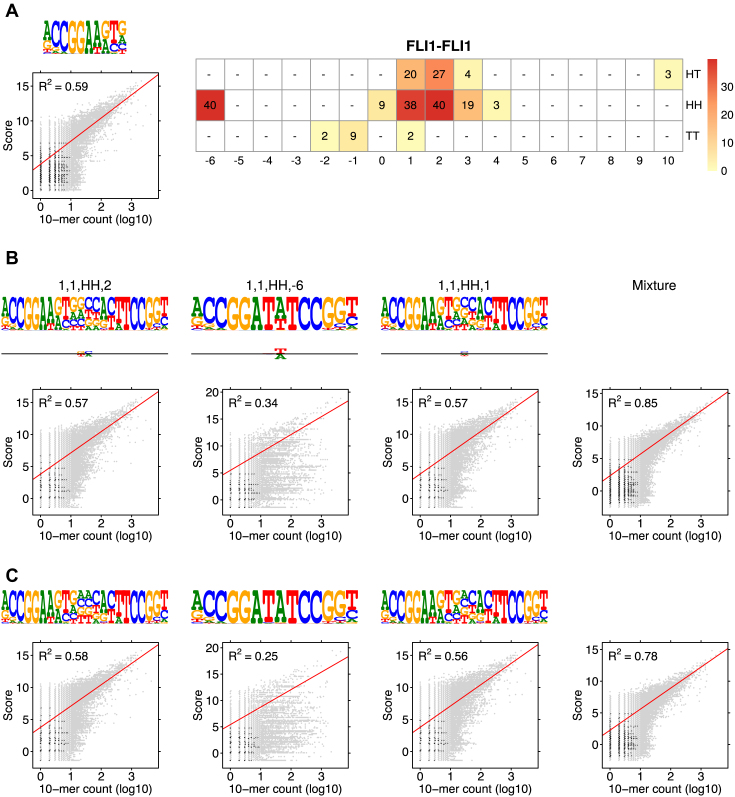
Figure 2.

Example model η for factor FLI1. The model was learned by MODER from a HT-SELEX data set (PRJEB14550, 143 389 reads of length 40), see Section Validation results. (A) Monomeric PPM θ₁ with original seed ACCGGAAGTN. (B) Dimeric PPM with (above) the seed and arrows indicating the orientation, and (below) horizontal bar indicating the bridging segment, and deviation matrix 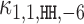with the positive values visualized above and the negative values below the horizontal line. (C) Dimeric PPM 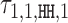and its deviation matrix. (D) Background PPM θ₀. (E) Mixture break-down into monomer, all dimers, and background. For example, 0.21 is the sum of mixing parameter values λ_k, k ∈ D⁺∪D⁻. Note that the proportion of background is larger than the signal, because data from an early SELEX cycle with lots of background was used. (F) Heat map of COB table (λ_{1, 1, o, d}) for homodimers of FLI1, giving the break-down into individual dimers and indicating that 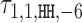(panel b), 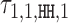(panel c), and 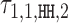are the strongest dimers. Horizontal axis gives the distance d, and a cell with no value indicates that the corresponding dimeric case was pruned during the EM search; see Section Pruning the search. The units in the COB table are integer multiples of 0.001.

Mixing parameters λ

Mixing parameters λ = {λ_k: k ∈ {0}∪M∪D⁺∪D⁻} give the probability of each component of the mixture as follows:

λ_k, k ∈ M, is the probability that the sequence contains exactly one monomeric occurrence of motif θ_k and no other occurrences.

λ_k, k = k₁k₂od ∈ D⁺∪D⁻, is the probability that the sequence contains exactly one occurrence of motif 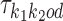and no occurrences of other motifs.

λ₀ is the probability that the sequence contains no motif occurrences.

For each pair (k₁, k₂), the array 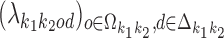of mixing parameter values is called the co-operative binding table (COB table) of motifs 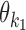and . The values in a COB table indicate the orientation and spacing preferences of the dimeric structures that are composed of 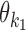and .

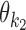Figure 2 illustrates model η for binding motifs of TF FLI1.

Learning by expectation maximization

Given a training data set X = {X₁, X₂, …, X_n} consisting of n DNA sequences 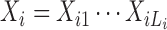, where L_i is the length of the ith sequence, we use the EM algorithm (12,28) to find model parameters η which maximize the expectation of the likelihood L(η|X, Z) = P(X, Z|η), where latent variables Z give the ’missing information’ used by an EM algorithm.

Latent variables are 0–1-valued random variables that indicate how the data X is aligned to the model. To align X_i, there are latent variables Z_{ik ·}, k ∈ {0}∪M∪D⁺∪D⁻, with exactly one of them having value 1, that code the alignment as follows.

Case Z_i0 = 1: Sequence X_i has no occurrences of motifs and is generated by the background model θ₀ alone.

Case Z_ikj = 1: If k ∈ M, then the sequence X_i has an occurrence of motif θ_k starting at position j. The rest of X_i is generated by the background model. If k = k₁k₂od ∈ D⁺∪D⁻ then the sequence X_i has an occurrence of motif τ_k at position j, that is, an occurrence of motif 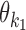at position j and an occurrence of motif 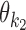at 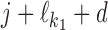such that the occurrences of 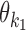and have relative orientation o.

We denote by S_ik the set of positions j at which motif k may occur in X_i. For k ∈ M we have S_ik = {1, …, L_i − ℓ_k + 1}, and for k = k₁k₂od ∈ D⁺∪D⁻, .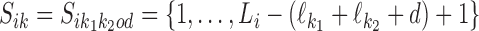

The probability of X_i in model η, given the missing information Z_{i ·}, is straightforward to evaluate as follows. If sequence X_i contains no motif occurrences, i.e. Z_i0 = 1, its probability is

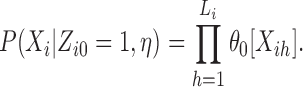(5)

If the sequence X_i contains one motif occurrence, i.e. Z_ikj = 1 for some k ∈ M, j ∈ S_ik, its probability is

(6)

where B₁ = {1, …, L_i}∖[j, j + ℓ_k).

For the dimeric binding we have two cases: independent (d ≥ δ) and dependent (d < δ). Let first k = k₁k₂od ∈ D⁺. Define the set 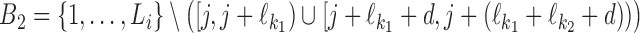. Then the probability of X_i is

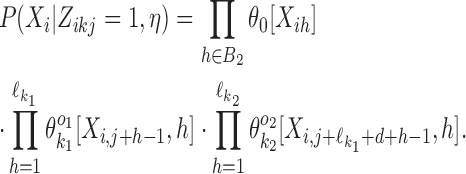(7)

Let then k = k₁k₂od ∈ D⁻. The probability of X_i is

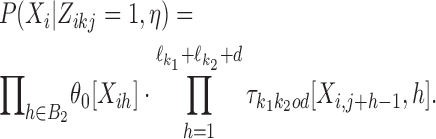(8)

Recall from (2) that 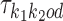is composed of bridging PPM 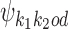in the middle and of flanking segments taken from PPMs 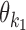and .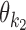

Now the joint likelihood of the model parameters, given data X and missing information Z, is the product of mixture probabilities of each X_i:

It is important to note here that, to simplify notation, we have ignored the fact that we should consider motif occurrences appearing in the reverse DNA strand as well. For this algorithm to work in the two-stranded case, a new index should be added, which specifies the direction (+1 or –1) of a monomer or a dimer occurrence. Then in all the places where we sum over j, we should sum over the directions as well. Moreover, to make sure that the probabilities add up to one, an additional division by two should be performed where we currently divide by |S_ik|.

As for each i, exactly one of the latent values Z_{i ·} equals 1 and the others are zeros, the log-likelihood has the following form:

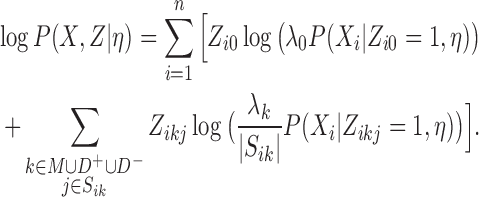(9)

The EM algorithm repeatedly applies the following rule to update η = (θ, κ, λ) until convergence:

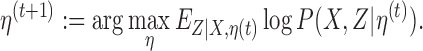One iteration of the algorithm, indexed with t, consists of an E-step and an M-step. These steps are described next.

Expectation step

E-step finds the expectation of log-likelihood (9) for current parameter values η^(t). By linearity of expectation, this reduces to finding the expected values 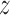_{i ·} of latent variables Z_{i ·}. By noting that 0 and 1 are the only possible values of a latent variable, and by applying the Bayes rule, one can see that the expected values and hence the update rule of the E-step becomes, for k ∈ {0}∪M∪D⁺∪D⁻ and j ∈ S_ik, as follows:

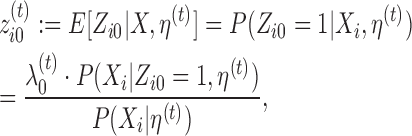(10)

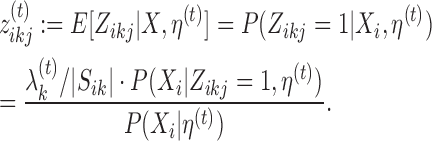(11)

Here, probability P(X_i|Z_i0 = 1, η^(t)) is given by (5) and probability P(X_i|Z_ikj = 1, η^(t)) by (6), (7) or (8), and

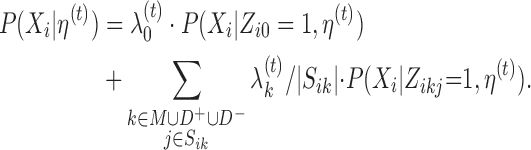(12)

Maximization step

M-step maximizes the expectation of log-likelihood for current ^(t) by updating parameters η = (θ, ψ, λ). The form of log-likelihood (9) is such that the M-step is of Baum–Welch type: parameters are updated by normalizing the expected counts of using different components of the model when X is aligned to the model according to 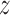^(t).

The update rules for mixing parameters become:

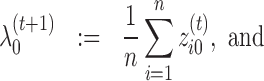(13)

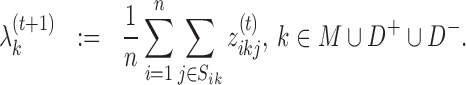(14)

To update θ and ψ we first accumulate the expected counts of how many times each mixture component is used when X is aligned with η^(t). For all k ∈ M, we get the 4 × ℓ_k matrices of expected counts of the monomer motifs as

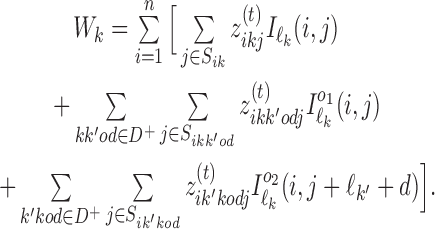Here 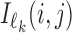is 4 × ℓ_k matrix-valued indicator function such that 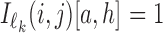if X_i[j + h − 1] = a, and otherwise 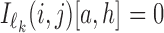. Again, 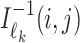is the reverse complement of 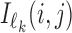. Note that the above aggregation of W_k implements the modularity of binding: a monomer model θ_k gets its counts from monomeric occurrences of θ_k as well as from occurrences of θ_k as an independent component of a dimer. Since the monomer models are not learned from the overlapping cases, there is no coupling between the monomers and the deviations matrices, i.e. both are uniquely defined.

For k ∈ D⁻, the matrix of the expected counts is

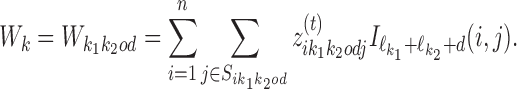According to our modularity constraint the columns of 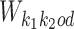that are outside the bridging segment should be modeled with 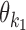and 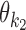. They should therefore be added to 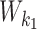and 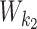as follows

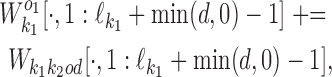(15)

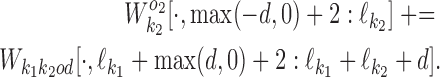(16)

The count vector of the background model is obtained as

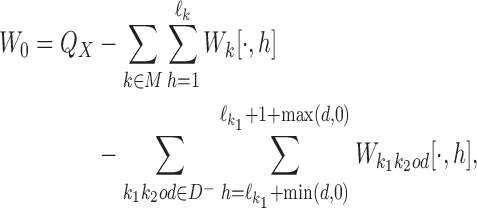where 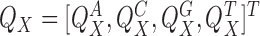is the column-vector of total counts of alphabet symbols in the data set X.

When normalized column-wise, the matrices W_k (with pseudo-counts possibly added) give updated θ_k for k ∈ {0}∪M:

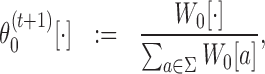(17)

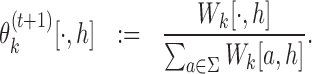(18)

Similarly, the bridging segments of W_k, k = k₁k₂od ∈ D⁻, give updated bridging PPMs ψ_k:

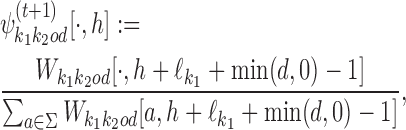(19)

where h = 1, …, |d| + 2.

Implementation of MODER

In this section we give practical details of our implementation of the MODER algorithm and provide some modifications to improve its efficiency.

Input

The input of MODER consists of the following items.

1. Data set X that consists of DNA sequences X₁, X₂, …, X_n, with |X_i| = L_i for all i = 1, …, n.

2. The seeds s₁, s₂, …, s_p. Each s_k is an IUPAC sequence of length |s_k| = ℓ_k. Seeds should be high-affinity representative sequences, one for each monomeric motif to be learned from data X. They will be used for constructing initial values for PPMs θ_k.

3. Set R⊂{1, 2, …, p}² of pairs that restrict the set of dimeric motifs represented in η. MODER learns only dimers k₁k₂od such that (k₁, k₂) is in R.

4. Minimum gap length in dimers whose monomers are assumed independent, δ; maximum number of EM-iterations, maxiter; and the convergence threshold for parameter change in consecutive EM-iterations, ε.

EM iterations

As the EM algorithm converges to a local optimum, it is crucial to use good initial values for the parameters. Initial PPMs 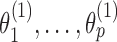are obtained from input data X and seeds s₁, …, s_p using the multinomial method (5). Initial bridging PPMs 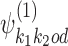are obtained from input data X and combined seeds using the multinomial method. A combined seed is constructed by orienting seeds 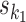and 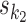according to o, spacing them by d symbols, and replacing the symbols in the bridging segment by the neutral IUPAC symbol N. This gives sequence y. Then the combined seed 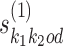is the highest counting non-palindromic subsequence of input data X that matches with y. A non-palindromic seed makes it possible for the EM search to break the symmetry and find non-palindromic PPMs. 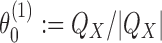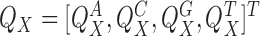Background model is initialized as where is the column-vector of total counts of alphabet symbols in X. The mixing parameters λ⁽¹⁾ are initialized as follows:

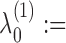• 0.5,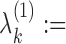

• 

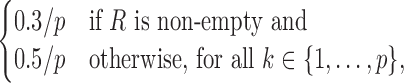
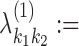• 0.2/|R|, for all (k₁, k₂) ∈ R. Within a COB table the value 0.2/|R| is divided evenly among the cells as .

The EM iterations then proceed as follows:

It should be noted that the above algorithm outputs the deviation matrix κ just for completeness. As κ is a derived parameter, it could be evaluated from θ and ψ in a post-processing phase as well.

Pruning the search

MODER implementation makes some heuristic modifications to the EM framework of Section 3 in order to speed-up the search and to utilize prior knowledge of data quality.

First, as the information content of well-known binding affinity PPMs is on average quite high while low information content may indicate contamination from background, MODER trims during the EM all overlapping dimeric mixture components k whose average column-wise information content in the overlapping area goes below a threshold (default 0.40 bits). This is done by setting λ_k ≔ 0. Similarly, any dimeric component k whose λ_k gets below a small threshold (default 0.001) is eliminated as k is too weak. Blank entries of COB tables indicate eliminated dimers.

Second, MODER learns new values 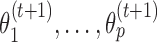of monomeric PPMs not from the full data but from dimeric occurrences of the monomer such that the distance d between the components is large enough (default d ≥ δ = 4). This is because such isolated occurrences within a dimer are supposed to give the best data for a monomer PPM, not distorted by close-by other sites such as the other component of a dimer. However, if the share of these dimeric cases in the mixture is less than 0.02, then the dimeric data is treated too small. In this case distances d ≥ 0 are included into the analysis.

The third modification is motivated by the fact that transcription factors may have different binding motifs whose consensus sequences are only a few Hamming steps apart. To minimize disturbance from such similar motifs and from background, MODER tends to restrict the learning of PPMs 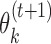and 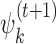to high-affinity training sequences. Such sequences are identified by the heuristic rule that they are in small Hamming neighbourhood of the consensus sequences (sequences with highest probability) of the PPMs found so far. Monomer PPM 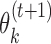is learned from data sites that are in the 1-Hamming neighbourhood of the seed (using the consensus sequence as the seed) of 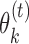. Bridging PPM is learned from data sites that are in the 1-Hamming neighbourhood of combined seed . The combined seed is obtained as the initial combined seed (see Section EM Iterations) but using the seeds of 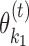and 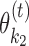. MODER uses this seed-guided EM search by default, with the standard search as an option.

RESULTS

Generated data

As an initial sanity test we created a model η, generated a data set using it, and checked that MODER is able to learn η back from the generated data. We first created one monomeric PPM and deviation matrices κ_{HH − 4} and κ_{HT − 4}. From these we constructed a model that had uniform background (λ = 0.71) and PPMs for homodimers HH 5 (λ = 0.12), HH –4 (0.08) and HT –4 (0.09). Using this model, we generated 100 000 sequences of length 40 bp. The sequences contained dimeric motifs and background only, no monomeric sequences were included. MODER accurately relearned the model from this data as the learned parameter values deviated from the original at most by 0.036; see Supplementary Figure S1 for details.

Validation using HT-SELEX data

Next we measured the quality of PPM models produced by MODER using correlation (R²) between occurrence counts and PPM scores of 8–mers or 10–mers of SELEX data. When counting the k–mers, all occurrences and both directions were considered. As the score of a k-mer x by a single PPM ρ we used the maximum value of 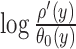when y and ρ′ go over all intersections of ρ and x and of ρ and reverse complement 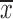. As the score of x by a mixture of PPMs ρ₁, …, ρ_t, whose mixing parameters by MODER are λ₁, …, λ_t, we used λ₁S₁ + ⋅⋅⋅ + λ_tS_t where S₁, …, S_t are the individual scores of x by the PPMs. The scatter plots in the figures visualize the counts and scores of different 8- or 10-mers in hexagonal bins. The color of a bin reflects the number of different k–mers in that bin, with a darker color meaning higher number of different k–mers. As the early cycles of SELEX data can contain large proportion of nonspecific sequences (i.e. background), the counts were corrected against background using the data of the previous SELEX cycle, as described in (5).

We report results for the monomer and dimer PPMs of factors HOXB13, HNF4A, TFAP2A, FLI1, FOXC1 and PKNOX2 learned from HT-SELEX data. A basic correlation analysis is done for factor HOXB13. For HNF4A, TFP2A, FLI1, FOXC1, and PKNOX2 we also analyse the differences between observed and purely modular motifs. In all validations, the SELEX data sets were randomly divided into two halves, one half used for learning the model and other half used for validating it.

We used the following HT-SELEX data sets: HOXB13 (PRJEB14550, 164 768 reads), HNF4A (ERX169045, (6), 655 432 reads), TFAP2A (ERX1085476, (43), 168 053 reads), FLI1 (PRJEB14550, 143 389 reads), FOXC1 (ERX169015, (6), 189 009 reads), and PKNOX2 (ERX1084652, (43), 423 339 reads). Each read was 40 bp long except for FOXC1 whose reads were 30 bp long. The following seeds, selected by hand using the models published in (6), were used as input: HOXB13 (CTCGTAAAA, CCAATAAAA), HNF4A (RGGTCA, RGTCCA), TFAP2A (GGGCA), FLI1 (ACCGGAAGTN), FOXC1 (RTAAAYA), and PKNOX2 (TGACANN). Note that it was essential to use non-palindromic seeds for overlapping dimers as, for example, the observed cases HH -6 for FLI1 and HH -2 for PKNOX2 are directional; see Figure S3 in (6) and Section EM iterations.

Selecting strong components of the model

The learned total model is likely to contain useless, weak components (weak dimeric motifs) that should be removed before the model is applied, e.g. to predict new putative binding sites. One could, for example, include model components in decreasing order of weight λ until a certain fraction of the non-background sequences is covered. Here we used the fraction of 85% to select the models for validation experiments. In addition, we also studied the effect of parameter δ (minimum gap length in the independent case) by experimenting with large values (up to L_max) of δ. As all larger deviations from expected were observed to usually occur in dimers with gap <4, default value δ = 4 was selected.

Factors HOXB12, HNF4A, TFAP2A, FLI1, FOXC1 and PKNOX2

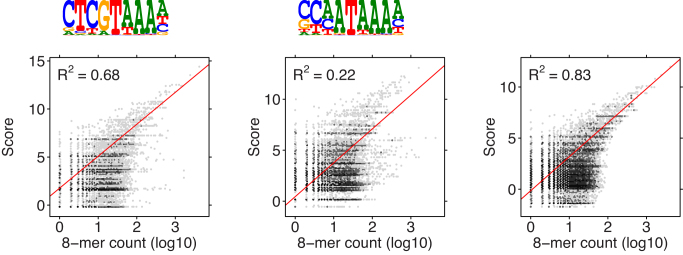
Figure 3 shows the sequence logos of the learned PPMs for factor HOXB13 and reports correlations of the scores of individual PPMs and of their mixture with counts of 8-mers. Since MODER did not find any strong dimeric motifs, the model for this factor is composed of two monomers only. The power of multi-motif modeling can be seen: the combined mixture consistently gives the highest R².

Figure 3.

Correlation analysis of HOXB13 binding motifs. Two monomer PPMs and their mixture (last panel) with weights λ₁ = 0.187, λ₂ = 0.198 were used. No dimer models were included. The combined model has higher correlation than the component models.

HNF4A, TFAP2A, FLI1, FOXC1 and PKNOX2 are examples of TFs for which many dimeric PPMs deviate clearly from the purely modular PPMs. Analyses of these factors are shown in Figures 4–8, where the correlations are shown for both the expected (purely modular) and the learned models, and the deviation matrices are also visualized. The number of dimeric models included into the mixture by the 85% rule ranged from 3 to 14 for different factors, only the top three dimeric models shown in the Figures. The full set of models, weights, and resulting correlations are available in the Supplementary File S1. Not surprisingly, the learned model has always higher correlation, but with varying margin. Sometimes (TFAP2A) deviating from the expected model gives strongly improved model while sometimes (FOXC1) the difference to the expected model is minor. As for the directionality of the motifs, sometimes both the expected and learned motifs are palindromic (Figure 5) while sometimes expected palindromes become directed in the learned motif (Figures 6 and 8).

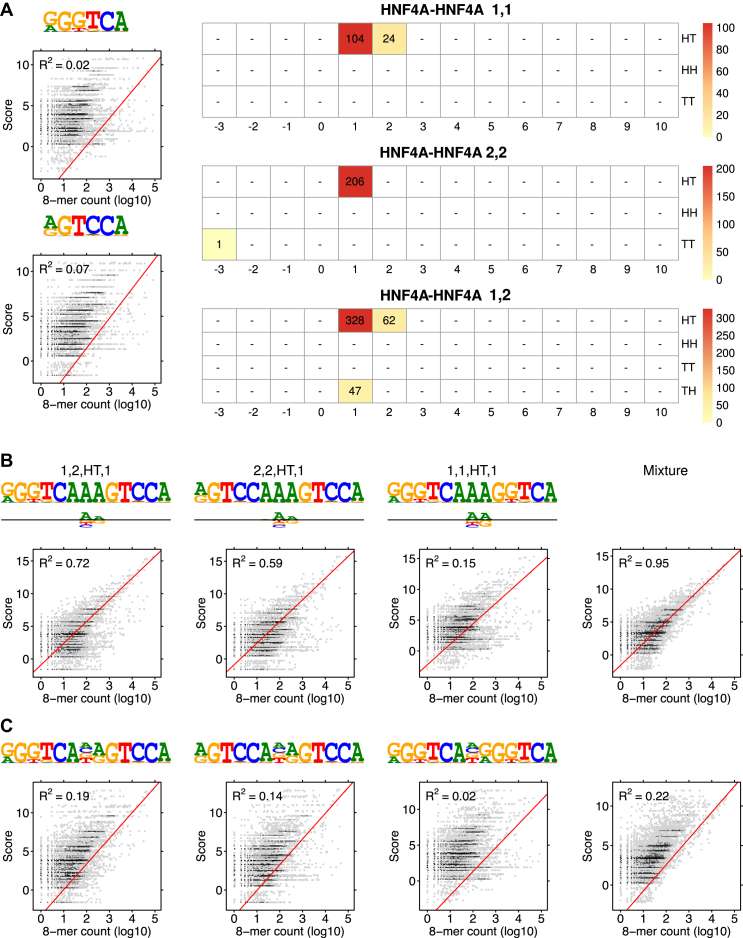
Figure 4.

Modularity analysis of HNF4A binding motifs. (A) Monomer models 1 and 2 (λ₁ = 0.073, λ₂ = 0.056) and the COB tables in units of integer multiples of 0.001. Since all the mixing parameters are in the same scale, comparison of λ values is also possible between two distinct COB tables. Also shown is correlation analysis for the two monomer models. (B) The first monomer PPM and dimeric models τ_{1, 2, HT, 1}, τ_{2, 2, HT, 1}, τ_{1, 1, HT, 1}, and τ_{1, 2, HT, 2} were included in the analysis by the 85% rule (only the best three dimeric models are shown in the Figure). Deviation matrices are depicted below the logos of the dimeric PPMs. Their mixture used corresponding weights λ = 0.073, 0.328, 0.206, 0.104, 0.062. The combined model has much higher correlation than any individual model. (C) Correlation analysis as in B but for the PPMs E_{1, 2, HT, 1}, E_{2, 2, HT, 1}, E_{1, 1, HT, 1} and E_{1, 2, HT, 2} that are expected under the independence assumption. All R²-values for the learned and expected PPMs differ remarkably, reflecting the large deviations between the learned and the expected PPMs. The purely modular model cannot detect the AAA sequence connecting the half-sites.

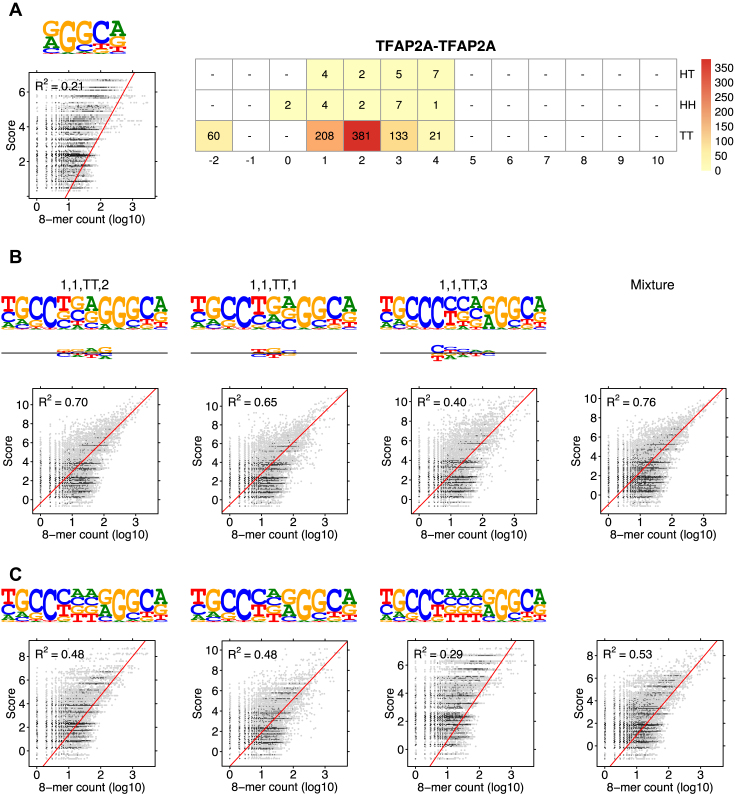
Figure 5.

Modularity analysis of the binding motifs of TFAP2A. (A) The monomer model (λ₁ = 0.003) and the COB table in units of integer multiples of 0.001. The monomer model was not included in the correlation analysis of the mixture by the 85% rule. (B) Correlation analysis of the model learned for TFAP2A by MODER: three dimeric PPMs τ_{1, 1, TT, 2}, τ_{1, 1, TT, 1} and τ_{1, 1, TT, 3}, and their mixture. Deviation matrices are depicted below the logos of the dimeric PPMs. The mixture of the PPMs uses weights λ = 0.381, 0.208, 0.133. (C) Correlation analysis as in B but for the PPMs E_{1, 1, TT, 2}, E_{1, 1, TT, 1}, E_{1, 1, TT, 3} that are expected under the independence assumption. All R²-values for the learned and expected PPMs differ remarkably, reflecting the large deviations between the learned and the expected PPMs. It is obvious that the purely modular model is not able to capture the binding affinity of TFAP2A. Note that all three PPMs TT 1, TT 2 and TT 3 that are palindromic in the expected model, stay palindromic in the learned model.

Figure 6.

Modularity analysis of the binding motifs of FLI1. (A) The monomer model (λ₁ = 0.08) and the COB table in units of integer multiples of 0.001. Also shown is the correlation analysis using only the monomer model. (B) Correlation analysis of the model learned for FLI1 by MODER: the monomer model and six dimeric PPMs τ_{1, 1, HH, 2}, τ_{1, 1, HH, −6}, τ_{1, 1, HH, 1}, τ_{1, 1, HT, 2}, τ_{1, 1, HT, 1}, τ_{1, 1, HH, 3} (only three best are shown in the Figure) were included in the analysis by the 85% rule. Deviation matrices are depicted below the logos of the dimeric PPMs. The mixture of the PPMs uses weights λ = 0.080, 0.040, 0.040, 0.038, 0.027, 0.020, 0.019. (C) Correlation analysis as in B but for the expected PPMs E_{1, 1, HH, 2}, E_{1, 1, HH, −6}, E_{1, 1, HH, 1}, E_{1, 1, HT, 2}, E_{1, 1, HT, 1}, E_{1, 1, HH, 3} under the independence assumption. The R²-values for the learned and expected PPMs differ clearly for the mixture and the dimeric case HH –6. The purely modular model cannot handle the dimeric case HH –6 properly, since expected PPMs are always palindromic for orientations HH and TT, while here the learned model HH –6 turns out to be directed. Albeit quite weak, the directionality has a clear effect on R².

Figure 7.

Modularity analysis of the binding motifs of FOXC1. (A) The monomer model (λ₁ = 0.071) and the COB table in units of integer multiples of 0.001. Also shown is the correlation analysis using only the monomer model. (B) Correlation analysis of the model learned for FOXC1 by MODER: the monomeric model and five dimeric PPMs τ_{1, 1, HH, −2}, τ_{1, 1, HH, −3}, τ_{1, 1, HT, −3}, τ_{1, 1, TT, 10}, τ_{1, 1, TT, 9} were included in the analysis by the 85% rule. Deviation matrices are depicted below the logos of the dimeric PPMs. The mixture of the PPMs uses weights λ = 0.071, 0.080, 0.033, 0.029, 0.012, 0.011. (C) Correlation analysis as in B but for the PPMs E_{1, 1, HH, −2}, E_{1, 1, HH, −3}, E_{1, 1, HT, −3}, E_{1, 1, TT, 10}, E_{1, 1, TT, 9} that are expected under the independence assumption. The R²-values for the learned and expected PPMs differ quite clearly, for HT –3 and HH –3 in particular, as also suggested by their large deviation matrices, while the difference is small for HH –2, the heaviest component of the mixture. It is obvious that the purely modular model is not able to fully capture the binding affinity of FOXC1. Note that expected palindromic PPM HH –3 becomes directed while expected PPM HH –2 stays palindromic in the learned model.

Figure 8.

Modularity analysis of the binding motifs of PKNOX2. (A) The monomer model (λ₁ = 0.256) and the COB table in units of integer multiples of 0.001. Also shown is the correlation analysis using only the monomer model. (B) Correlation analysis of the model learned for PKNOX2 by MODER: 14 dimeric PPMs were included in the analysis by the 85% rule but only the best three, τ_{1, 1, HH, −2}, τ_{1, 1, HT, 3}, and τ_{1, 1, HT, 4}, are described here. In the mixture the weight for the monomer and three best dimeric models were λ = 0.256, 0.177, 0.068, 0.065. The sum of the lambdas for the last 11 dimeric models was 0.267. Deviation matrices are depicted below the logos of the dimeric PPMs. (C) Correlation analysis as in A but for the PPMs E_{1, 1, HH, −2}, E_{1, 1, HT, 3}, E_{1, 1, HT, 4} that are expected under the independence assumption. Here the 85% rule selected very many dimeric models, because the lambda values have quite even distribution in this case. Again the R²-values for the learned and expected PPMs differ quite clearly. It can be seen that the purely modular model is already satisfactory but can be improved somewhat by allowing deviations. Note that the palindromic HH -2 motif of the expected model becomes directed in the learned model.

Validation using ChIP-seq data

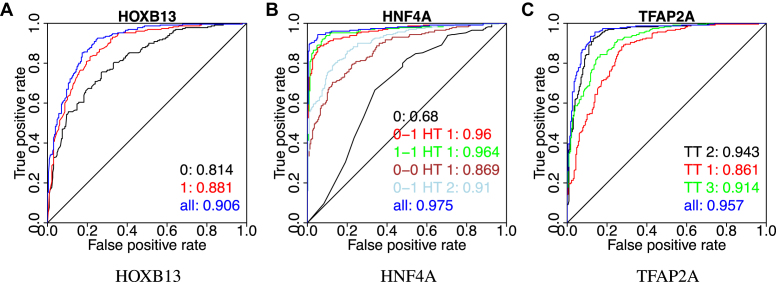
We then tested for factors HOXB13, HNF4A, and TFAP2A the validity of the obtained in vitro models on in vivo data. We performed standard ROC analysis to measure the performance of the models learned from SELEX data on binary classification of ChIP-Seq peaks. The following ChIP-seq data was used: HOXB13 (European Nucleotide Archive accession ERX332516, IgG: ERX332513) (44), HNF4A (Sequence Read Archive accession SRR952427, IgG: SRR952608) (45) and TFAP2A (SRR952485,IgG: SRR952608) (45). To find the peaks, the reads were aligned with BWA (46), and peak calling was done with Peakzilla (47). The genome assembly used was GRCh37 (hs37d5). From each ChIP-seq peak set, top n = 230 peaks with highest quality score were selected, and for each peak a sequence of length L = 190 bp flanking the peak summit was chosen for the positive set. A negative set of the same size was chosen randomly from the human genome, making sure that the positions were mappable. Sequences were scored using the SELEX models of HOXB13, HNF4A and TFAP2A shown in Figures 3, 4 and 5. The resulting ROC curves of the (very good) classification performance of PPM scores are shown in Figure 9.

Figure 9.

Classification performance of multi-motif models for HOXB13, HNF4A, and TFP2A. ROC curves of classification using the scores by PPMs and their mixtures on ChIP-seq data. The area under each curve is also shown. Same models were used as in the correlation analysis (Figures 3–5).

We also applied MODER on the ChIP-seq data set of factor NRSF on the GM12878 cell line produced by (48) and further analyzed by (16). To obtain the seeds, we first took all the k-mers of lengths 9–11 from the data set, applied hierarchical clustering, and selected two best clusters and their representative k-mers (TTCAGCACC and GGACAGCTCC) by using the order given by the 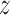-score. MODER finds 9 out of 10 models reported by Quang and Xie, for details, see Figure 2 of (16) and Supplementary Figure S2. Note that as NRSF has two monomeric motifs, MODER discovers heterodimeric motifs whose COB-table has all four orientations.

Next, we tried to detect the core and side motifs of factor CTCF. This should test MODER’s capabilities in detecting long sites, as together these motifs are known to form a site of length about 34 bp (13). We used raw ChIP-exo data from human LoVo cells targeting factor CTCF from Katainen et al. (49) (ENA accession ERX986066). Mapping and peak calling was done as in Hartonen et al. (50), briefly: alignment was done using BWA (46) against assembly GRCh37 and the peaks were called using PeakXus (50). Five thousand highest scoring peaks were selected, and around the peak summits sequences of length 60 were extracted (blacklisted regions (51), ENCODE accession ENCFF001TDO, and centromeres were removed). Results in Supplementary Figure S3 show that MODER is able to detect similar configurations of distances and orientations between the core and side motifs of CTCF as in Schmidt et al. (13) (Figure 2) and Nakahashi et al. (14) (Figure 4). The strongest dimer formed by the core and side motifs, namely τ_{1, 2, HT, 8}, was found in 20% of the top 5000 peaks.

As nuclear receptors commonly bind as dimers (52), we chose another factor, in addition to HNF4A, from this family to display the performance of MODER. ChIP-seq data from ENCODE for factor RXRA in cell line HepG2 was used (ENCODE accession ENCFF002CKZ). Ten thousand highest scoring peaks were selected, and around the peak summits sequences of length 40 were extracted (blacklisted regions and centromeres were removed). The monomer seed GGGGTCA for the experiment was handpicked based on the Rxra mouse model in Jaspar (53). The seed finding method used with NRSF for k-mer lengths 6–15 would give AGGTCA, which could have been used as well. Supplementary Figure S4 shows that MODER detects a strong dimeric binding motif τ_{1, 1, HT, 0}, which could either be a homodimer of RXRA or a heterodimer such as NR1H2-RXRA, as suggested by Tomtom (15).

MODER versus MEME

When comparing MODER with the popular tool MEME it should be noted that the models of motifs of the two methods are different. MEME learns separate monomer models in successive passes, deleting the found sites of a model from data before the next pass, while MODER aims at discovering the modularity of motifs and hence learns the entire modular structure of monomeric and dimeric motifs in the same probabilistic framework in one run. The difference is illustrated in Supplementary Figure S5 that compares the models learned for factors TFAP2A and FLI1 by the two methods.

MODER versus Bipad/Maskminent

We also compared MODER with Bipad/Maskminent (17,19) which among the previous tools comes closest to MODER. An example qualitative comparison using alignment of models is illustrated in Supplementary Figure S6. Similarities between motifs obtained using these two algorithms are obvious, although Maskminent seems to introduce some background noise into the motifs. Comparison using correlation analysis was not performed since Maskminent does not learn the monomer model and the two orientation classes of dimers (DR and IR) in the same commensurate model, and hence the weights for models of different types could not be decided.

In order to make a quantitative comparison to Maskminent, we used the data sets for which a bipartite Maskminent model is available from Lu et al. (19). There were 53 such data sets in ENCODE (51), and we used 40 of those (6 had been revoked from ENCODE, 7 were unidentifiable). The identification problems were due to Lu et al. not giving the accession codes, but merely describing the used data sets. For all the data sets we managed to identify, we have now included the accessions in the Supplementary Table S1. The same number of top scoring peaks were used as in (19), but only 100 bp around the peak summit was selected, and these data sets were randomly divided into learning and validation sets of equal size. We selected the initial seeds for MODER based on Jaspar (53) in the following way: for JUN-like factors (ATF3, BACH1, BATF, FOS, FOSL1, FOSL2, JUN, JUNB, JUND, NFE2) we used the seed ATGA, for EBF1 the seed TCCC, for ESR1 the seed AGGTCA, for MAFF and MAFK the seed TCAGCA, and for STAT1 the seed TTC. Then MODER was run on learning data sets, and the best dimeric PPM (according to lambda) was chosen for each data set. For Maskminent we used their published model for each data. The results displayed in Supplementary Table S1 and Figure S7 show that MODER gets better AUC value in 35 cases out of 40. Note also that MODER wins in 33 out of 35 cases, when considering only the optimal IDR-thresholded data sets (the other five data sets are initial peaksets, marked with a star in the table). The selection of factors used by Lu et al. (19) was unfortunately quite repetitive, but the comparison shows consistent behaviour for both methods.

DISCUSSION

The MODER algorithm is based on reductionist view that PPM models for dimers can be built in a modular fashion from monomer PPMs.

As noted e.g. by (4), such modularity is not always valid as in a number of dimeric cases the specificity of the dimeric motif differs notably from what could be expected from its monomeric components. The deviation matrix of MODER represents such differences explicitly. These deviations from the expected models are especially important for orientations HH and TT, for which all expected models are always symmetric (palindromes), whereas the real binding motifs might have a direction (6). This was demonstrated by several examples in our validation experiments. In addition, the deviations from expected motif commonly occur when the core segments of the motifs of two factors are closely packed and the overlapping flanks are distorted from the expected model. In TF-DNA binding, the core positions in a motif are usually recognized by direct bonds to the bases, whereas the weaker positions are recognized by contacts to DNA backbone (4) and are hence more prone to deviations.

The motif discovery algorithm of MODER considers simultaneously all possible orientation–distance pairs and finds the preferred dimeric motifs. Learning multiple motifs in serial manner—first finding one motif, then removing its occurrences from the data, and then running the algorithm again—does not treat symmetrically the sequences that may belong to several motifs. MODER improves over the similar coMOTIF algorithm (30) by including the spacing information in the overall model, and by adding overlapping motifs and the deviations from the expected motif. Allowing overlaps of monomer motifs within a dimer turned out a very useful feature. In fact, for factors FLI1, FOXC1 and PKNOX2 the strongest dimer has such an overlap.

Simultaneous learning of all motif components and their mixing parameters makes direct comparison of the relative strengths of the motifs possible by using the mixing parameters. Depending on the application, it might be useful to rescale the obtained mixing parameters, after the actual algorithm is finished. This was done, when we chose the motifs for performance testing by the 85% rule: the mixing parameters were rescaled to exclude the background. Then motifs were included in descending order, until the motifs covered 85% of the signal. Sometimes it might also be useful to rescale the mixing parameters in each COB table separately, although this would prevent the comparison of mixing parameters between distinct COB tables.

MODER is not too sensitive to noise in the seeds. For factor HOXB13, we mutated the first initial seed in two positions and the second seed in three positions, including informative positions. Still the algorithm managed to obtain the same results as with the original seeds. MODER is reasonably fast. For example, it took 2 min 18 s wall-clock time and 15 min 30 s CPU time when run simultaneously on eight cores to learn the model for FLI1 in Figure 2 from a 2 865 880 bp long HT-SELEX data set. The seeds for MODER can be found from existing PPM databases or can be produced by seed-finding tools such as DREME (54) or by using the procedure in section Validation using ChIP-seq data to find representative k-mers.

AVAILABILITY

MODER is implemented in C++ on Linux platform and is available from https://github.com/jttoivon/MODER. European Nucleotide Archive, accession code PRJEB14550.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR online.

FUNDING

EU FP7 project SYSCOL [UE7-SYSCOL-258236]; Leverhulme Trust [VP1-2014-044 to E.U.]. Funding for open access charge: University of Helsinki.

Conflict of interest statement. None declared.