Abstract
Background
The recently developed test-negative design is now standard for observational studies of influenza vaccine effectiveness (VE). It is unclear how influenza test misclassification biases test-negative VE estimates relative to VE estimates from traditional cohort or case-control studies.
Methods
We simulated populations whose members may develop acute respiratory illness (ARI) due to influenza and to non-influenza pathogens. In these simulations, vaccination reduces the risk of influenza but not of non-influenza ARI. Influenza test sensitivity and specificity, risks of influenza and non-influenza ARI, and VE were varied across the simulations. In each simulation, we estimated influenza VE using a cohort design, a case-control design, and a test-negative design.
Results
In the absence of influenza test misclassification, all three designs accurately estimated influenza VE. In the presence of misclassification, all three designs underestimated VE. Bias in VE estimates was slightly greater in the test-negative design than in cohort or case-control designs. Assuming the use of highly sensitive and specific reverse-transcriptase polymerase chain reaction tests for influenza, bias in the test-negative studies was trivial across a wide range of realistic values for VE.
Discussion
Although influenza test misclassification causes more bias in test-negative studies than in traditional cohort or case-control studies, the difference is trivial for realistic combinations of attack rates, test sensitivity/specificity, and VE.
Keywords: Influenza, Human, Methodology, Bias (Epidemiology), Vaccine effectiveness
1. Introduction
In recent years, the so-called “test-negative” design has become the standard approach for observational studies of influenza vaccine effectiveness (VE) [1–3]. In a test-negative design, the study population comprises patients who present to an outpatient clinic or hospital with acute respiratory illness (ARI) and who are tested for influenza infection [4]. VE is defined as one minus the ratio of the risk of influenza among the vaccinated to the corresponding risk among the unvaccinated. In case-control and test-negative studies, VE is estimated as one minus the odds ratio of influenza for vaccinated vs. unvaccinated. Relative to some other observational designs, the test-negative design offers the advantage of reduced confounding from differences in healthcare-seeking behavior between vaccinated and unvaccinated persons [5].
Misclassification of influenza leads to biased VE estimates, regardless of the study design. Assuming the misclassification is not differential by vaccination status, misclassification will introduce bias that will tend to underestimate VE. The degree of bias due to misclassification has been believed to be low in test-negative studies, primarily due to a 2007 paper by Orenstein and colleagues [6]. In that paper, the authors concluded that case-control and test-negative studies were less biased than cohort studies in populations subject to similar amounts of misclassification of influenza. That paper, however, had an important flaw. The authors based their calculations on a cumulative design [7] for the case-control and test-negative studies, in which the controls are sampled from those who did not get influenza during the follow-up period. Controls in a case-control study correspond to the denominator information in a cohort study. The cumulative sampling strategy excludes those who get influenza from the sampled denominators, biasing study results away from the null [7]; this bias is small for rare disease but is larger if the disease is common. In the paper by Orenstein et al, the bias toward the null in VE stemming from misclassification of disease was countered in the test-negative and case-control design by a bias away from the null due to the cumulative design sampling strategy. With no misclassification, a properly designed case-control study would give expected results equivalent to those from a cohort study, but the cumulative design considered by Oren-stein et al. would not. Thus, the work of Orenstein et al. does not allow a valid conclusion about the effects of test sensitivity and specificity on VE estimates in test-negative studies.
In this paper, we compare the effects of imperfect test sensitivity and specificity on VE estimates from cohort, case-control, and test-negative studies. We correct the problem in the paper by Oren-stein et al. by using simulations based on sampling controls from the full population at risk (sometimes referred to as “case-cohort sampling”) [7] rather than a cumulative design for the case-control and test-negative studies.
2. Methods
To focus on the effects of imperfect sensitivity and specificity, we assumed that other sources of bias are absent. Specifically, we assumed that there is no confounding, no selection bias, and no misclassification of exposure (vaccination) status. We simulated populations at risk for two outcomes: medically attended influenza infection and medically attended infection with other pathogens. We assumed infection with influenza to be independent from infection with other pathogens. We also assumed that subjects could only be infected once with influenza, but could be infected multiple times with non-influenza pathogens. Our simulation involves five parameters (Table 1):
Table 1.
Parameter values for simulations.
| Parameter | Description | Values | |
|---|---|---|---|
|
| |||
| All ages | Young children | ||
| VEtrue | Vaccine effectiveness | 50% | 70% |
| IPflu | Incidence proportion of ARI* due to influenza | 5% | 15% |
| IPother | Incidence proportion of ARI due to other pathogens | 10% | 30% |
| Sens (RT) | Rapid test sensitivity | 80% | |
| Spec (RT) | Rapid test specificity | 90% | |
| Sens (PCR) | RT-PCR sensitivity | 95% | |
| Spec (PCR) | RT-PCR specificity | 97% | |
ARI = acute respiratory illness.
VE = influenza vaccine effectiveness against medically attended influenza
IPflu = incidence proportion (risk) of influenza ARI in unvaccinated persons
IPother = incidence proportion of ARI due to non-influenza pathogens
sens = sensitivity of influenza test
spec = specificity of influenza test
For consistency with Orenstein et al., we performed one set of “young children” simulations, in which we assumed that IPflu = 15%, IPother = 30%, and VE = 70%, based on expected incidence and VE in children 6–24 months of age [6]. We also performed a set of “all ages” simulations assuming IPflu = 5%, IPother = 10%, and VE = 50%, which are more realistic values for the population of all ages that is a frequent target of test-negative VE studies. Following Oren-stein et al., we assumed influenza test sensitivity to be 0.8 and specificity to be 0.9. These values were based on the use of rapid antigen tests for detecting influenza. In practice, nearly all modern studies use reverse-transcriptase polymerase chain reaction (RT-PCR) assays for influenza testing, which are both more sensitive and more specific than rapid antigen tests [8–10]. We therefore repeated our analyses using sensitivity and specificity parameters based on RT-PCR (Table 1).
We ran a series of 1000 simulations to compare the study designs. In each, we simulated a population of 50,000 subjects, which gives study sizes roughly equal to those in existing observational VE studies [1,3,11]. We assumed that 40% of subjects received influenza vaccine at the start of follow-up. Within the follow-up period, subjects could be infected (up to once) with influenza, with risk equal to IPflu, and infected (up to once) with a non-influenza pathogen, with risk equal to IPother. We assumed that risk of influenza is independent of the risk of non-influenza ARI, as analyses of the effects of hypothetical non-independence on test-negative VE estimates have been performed previously [12]. After running the simulation to determine the simulated disease events, we randomly allowed these simulated events to be misclassified according to the rapid test and RT-PCR values for sensitivity and specificity.
We estimated VE using three separate designs, first using the correctly classified outcomes. In the cohort design, we calculated the risk of influenza infection in the vaccinated and the unvaccinated. We then estimated as (1 − RR), where RR is the risk ratio. In the case-control design, for each detected influenza case, we randomly sampled three controls from the total study population. We estimated as (1 − ORcc), where ORcc is the odds ratio from the case-control study, which estimates the risk ratio [7]. For the test-negative design, we included all ARI events testing positive for influenza as cases. All ARI events testing negative for influenza were selected as a comparison group. We estimated as (1 − ORtn), where ORtn is the odds ratio from the test-negative study. We calculated 95% confidence limits from the 2.5th and 97.5th percentiles of the simulations.
After estimating VE in the simulated population based on the true disease status, we repeated the analysis using the rapid test misclassified outcomes, and again using the RT-PCR misclassified outcomes. We calculated the bias of each design from each simulation as a percent: . For each design at each level of misclassification, we calculated the mean bias with 95% confidence limits.
We further assessed the independent effects of influenza test sensitivity and test specificity on VE estimates in the test-negative design, using the “all ages” scenario. For this, we ran 1000 simulations assuming IPflu = 5%, IPother = 10%, and VE = 50%. In each simulated population, we calculated VEtn at a range of test sensitivities (from 0.8 to 1.0, keeping specificity at 1.0) and at a range of specificities (from 0.8 to 1.0, holding sensitivity at 1.0). Finally, we assessed the degree to which bias in the cohort and test-negative designs varies with varying VE. For this, we ran 1000 simulations, assuming PCR sensitivity and specificity, IPflu = 5%, and IPother = 10%, while varying VE between 10 and 70%.
Finally, we conducted sensitivity analyses of the “young children” and “all ages” scenarios, where we allowed subjects to have multiple influenza and non-influenza ARI events during follow-up. Instead of incidence proportions, the number of events per person was randomly sampled from a Poisson distribution with mean equal to IPflu (for influenza ARI) and IPother (for non-influenza ARI). Results were trivially different from the main analyses for all study designs in both scenarios (less than one percentage point difference in estimated VE at PCR levels of misclassification) and are not further presented here. Analyses were conducted using SAS Version 9.3 (SAS Institute, Cary NC) and R Version 3.0.2 (The R Foundation for Statistical Computing, Vienna, Austria).
3. Results
In the absence of misclassification, all three designs accurately estimated VE in the “young children” scenario, with mean across the simulations of 70% (Table 2). In the presence of misclassification at the level of RT-PCR tests, all three designs slightly underestimated VE (mean bias = −6% for cohort and case-control and −7% for test negative). Underestimation of VE was more pronounced in the presence of rapid test misclassification, and this underestimation was greater in the test-negative design (mean bias = −26%) compared with the case-control and cohort designs (mean bias = −20% for each).
Table 2.
Estimated vaccine effectiveness (VE) and bias from 1000 “young children” simulations under different study designs and levels of misclassification, assuming 70% VE.
| Design | Misclassification | Estimated VE | Percent bias |
|---|---|---|---|
| Cohort | None | 70% (68–72%) | 0% |
| Cohort | RT-PCR | 66% (63–68%) | −6% |
| Cohort | Rapid test | 56% (53–58%) | −20% |
| Case-control | None | 70% (68–72%) | 0% |
| Case-control | RT-PCR | 66% (63–68%) | −6% |
| Case-control | Rapid test | 56% (53–58%) | −20% |
| Test-negative | None | 70% (68–72%) | 0% |
| Test-negative | RT-PCR | 65% (63–68%) | −7% |
| Test-negative | Rapid test | 53% (50–56%) | −24% |
Similar results were seen in the “all ages” scenario where true VE was 50%, with mean across the simulations of 50% in the absence of outcome misclassification (Table 3). Underestimation of VE was slight in the presence of RT-PCR misclassification (−6% for cohort and case-control, −8% for test-negative) and more pronounced in the presence of rapid test misclassification (−20% for cohort and case-control and −26% for test-negative).
Table 3.
Estimated vaccine effectiveness (VE) and bias from 1000 “all ages” simulations under different study designs and levels of misclassification, assuming 50% VE.
| Design | Misclassification | Estimated VE | Percent bias |
|---|---|---|---|
| Cohort | None | 50% (45–55%) | 0% |
| Cohort | RT-PCR | 47% (42–52%) | −6% |
| Cohort | Rapid test | 40% (34–45%) | −20% |
| Case-control | None | 50% (44–55%) | 0% |
| Case-control | RT-PCR | 47% (40–52%) | −6% |
| Case-control | Rapid test | 40% (33–46%) | −20% |
| Test-negative | None | 50% (44–55%) | 0% |
| Test-negative | RT-PCR | 46% (39–52%) | −8% |
| Test-negative | Rapid test | 37% (29–43%) | −26% |
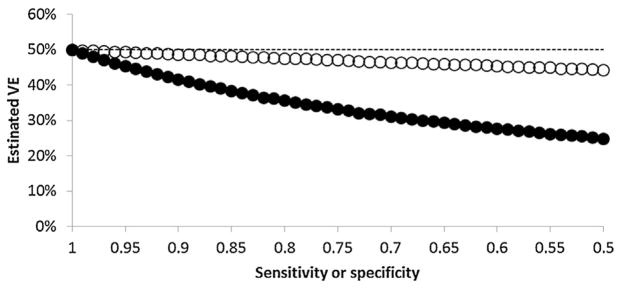
In the test-negative design, low specificity caused greater bias in VE estimates than did low sensitivity. Assuming true VE of 50%, in simulations holding specificity constant at 1.0, VEtn ranged from 50% when sensitivity was 1.0 to 48% when sensitivity was 0.8 (Fig. 1). In simulations holding sensitivity constant at 1.0, VEtn ranged from 50% when specificity was 1.0 to 36% when specificity was 0.8.
Fig. 1.
Mean estimated influenza vaccine effectiveness (VE) from 1000 simulations of a test-negative study at different cut-points of influenza test sensitivity (open circles) and specificity (filled circles), assuming true VE of 50% (dashed line).
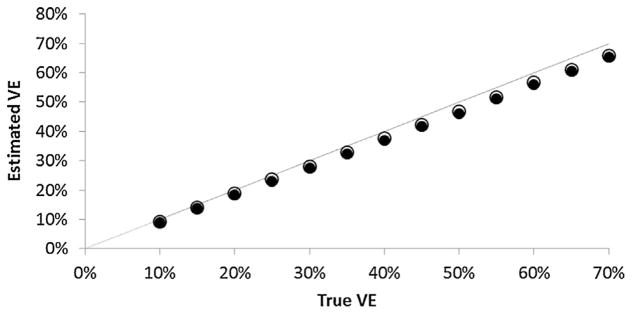
When using RT-PCR for diagnosing influenza, the difference in mean between cohort and test-negative designs was trivial across a wide range of VE values (Fig. 2); from the test-negative design tended to be one percentage point lower than from the cohort design.
Fig. 2.
Mean estimated influenza vaccine effectiveness (VE) from 1000 simulations of a cohort study (open circles) and a test-negative (filled circles) study at different values of true VE assuming RT-PCR sensitivity and specificity; the dashed line shows perfect agreement between true and estimated VE.
4. Discussion
Although first introduced in 1980 [13], the test-negative design was little used until it began to be applied to influenza vaccine studies less than 10 years ago [14]. Much remains unknown about the relative impact of potential biases on VE estimates from test-negative studies. One source of bias is misclassification of disease status due to the imperfect sensitivity and specificity of influenza tests. A priori, we would expect disease misclassification to cause greater bias in a test-negative study than in a cohort or a case-control study. In the cohort and case-control designs, persons falsely testing positive only contribute to the study in proportion to the rate of false positive tests in the entire population, which is a product of test specificity and incidence of non-influenza ARI. In contrast, in the test-negative design, persons falsely testing negative contribute to the study in proportion to the rate of false positive tests among persons with non-influenza ARI. Our findings con-firm this expectation: in the presence of disease misclassification, VE estimates from the test-negative design are more biased than VE estimates from case-control or cohort designs. However, when highly sensitive and specific tests such as RT-PCR are used, the difference in bias between these designs is small and does not lead to meaningful differences in estimated VE between study designs.
We found that imperfect specificity of influenza testing caused greater bias in the test-negative design than did imperfect sensitivity. This finding agrees with the expected effects of imperfect sensitivity and specificity of traditional case-control studies [15]. In selecting influenza tests for test-negative studies, high specificity is much more important than high sensitivity for avoiding bias. For individual test results that are inconclusive (such as RT-PCR results with high cycle times), erring on the side of considering these to be negative results is expected to cause less bias than considering these to be positive.
Multiple influenza types or subtypes can co-circulate in a given season, and therefore people may remain at risk for a second influenza infection within a single season even after being infected. In such settings, an individual who was previously infected with influenza is still at risk for influenza and should still be eligible to be sampled into the control group of a case-control study, including the test-negative group in a test-negative case-control study. Sampling subjects into the control group if they have previously had influenza may bias VE estimates if sampling of such subjects is associated with vaccine status. Our primary simulation analysis assumed that only one influenza infection occurred, and did not address this potential bias.
Although most commonly used for influenza VE studies, the test-negative design has also been used for rotavirus VE studies, with subjects being children with diarrheal illness (e.g., [16,17]). Enzyme immunoassay tests for rotavirus have sensitivities of 75–80% and specificities of 98% or more [18,19]. Rotavirus test-negative studies have found positive rotavirus tests for 11–17% of subjects tested [16,17]. Given the high proportion of subjects with diarrhea due to non-rotavirus causes, test specificity will be more important than sensitivity for causing biased rotavirus VE estimates. Given the high specificity of rotavirus tests, our results suggest that rotavirus VE estimates from test-negative designs will also not be meaningfully biased relative to VE estimates from other designs in the presence of imperfect diagnostic tests.
Several limitations of our study are worth considering. We assumed that misclassification was non-differential by vaccination status, i.e., that the accuracy of influenza test results was not affected by vaccination. Serologic testing for influenza infection has been shown to have reduced sensitivity in vaccinated persons, but data are less clear for RT-PCR [20]. Our results will not hold true if sensitivity or specificity is differential by vaccination status. We also assumed that influenza test results (either correct or misclassified) are known for all persons with ARI, and that patients with prior influenza infection can be excluded from the study population. In practice, potential study subjects may have had prior ARI that was not tested for influenza, and so persons with prior influenza infection may continue to contribute person time (in a cohort study) or be included as controls (in a case-control or test-negative study). The degree to which this phenomenon may bias VE results is uncertain, and the issue is further complicated by the possibility that persons may be infected with influenza multiple times during a single season (from infection with different virus types or subtypes). Finally, we did not examine the effect of other sources of bias, including selection bias, inaccurate exposure measurement, or confounding.
5. Conclusions
Influenza VE estimates from test-negative studies are biased in the presence of outcome misclassification, and this bias is greater than in corresponding VE estimates from cohort or case-control studies. However, the relative increase in bias is slight when using RT-PCR for diagnosing influenza. Given that observational studies of influenza VE can be dramatically confounded by differences in care-seeking and disease risk between vaccinated and unvaccinated persons [21,22], the gains in control of confounding by use of the test-negative design are likely to outweigh the bias due to misclassification.
Acknowledgments
This work was supported by grant U01 IP000466 from the Centers for Disease Control and Prevention.
Footnotes
Conflicts of interest statement
The authors declare no conflicts of interest.
References
- 1.Kissling E, Valenciano M, Larrauri A, Oroszi B, Cohen JM, Nunes B, et al. Low and decreasing vaccine effectiveness against influenza A(H3) in 2011/12 among vaccination target groups in Europe: results from the I-MOVE multicentre case-control study. Euro Surveill. 2013:18. doi: 10.2807/ese.18.05.20390-en. [DOI] [PubMed] [Google Scholar]
- 2.McNeil S, Shinde V, Andrew M, Hatchette T, Leblanc J, Ambrose A, et al. Interim estimates of 2013/14 influenza clinical severity and vaccine effectiveness in the prevention of laboratory-confirmed influenza-related hospitalisation, Canada, February 2014. Euro Surveill. 2014:19. doi: 10.2807/1560-7917.es2014.19.9.20729. [DOI] [PubMed] [Google Scholar]
- 3.Ohmit SE, Thompson MG, Petrie JG, Thaker SN, Jackson ML, Belongia EA, et al. Influenza vaccine effectiveness in the 2011–2012 season: Protection against each circulating virus and the effect of prior vaccination on estimates. Clin Infect Dis. 2013 doi: 10.1093/cid/cit736. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Foppa IM, Haber M, Ferdinands JM, Shay DK. The case test-negative design for studies of the effectiveness of influenza vaccine. Vaccine. 2013;31:3104–9. doi: 10.1016/j.vaccine.2013.04.026. [DOI] [PubMed] [Google Scholar]
- 5.Jackson ML, Nelson JC. The test-negative design for estimating influenza vaccine effectiveness. Vaccine. 2013;31:2165–8. doi: 10.1016/j.vaccine.2013.02.053. [DOI] [PubMed] [Google Scholar]
- 6.Orenstein EW, De Serres G, Haber MJ, Shay DK, Bridges CB, Gargiullo P, et al. Methodologic issues regarding the use of three observational study designs to assess influenza vaccine effectiveness. Int J Epidemiol. 2007;36:623–31. doi: 10.1093/ije/dym021. [DOI] [PubMed] [Google Scholar]
- 7.Rothman KJ, Greenland S, Lash TL. Modern epidemiology. 3. Chapter 7 Philadelphia PA: Lippincott Williams & Wilkins; 2008. [Google Scholar]
- 8.Atmar RL, Baxter BD, Dominguez EA, Taber LH. Comparison of reverse transcription-PCR with tissue culture and other rapid diagnostic assays for detection of type A influenza virus. J Clin Microbiol. 1996;34:2604–6. doi: 10.1128/jcm.34.10.2604-2606.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Irving SA, Vandermause MF, Shay DK, Belongia EA. Comparison of nasal and nasopharyngeal swabs for influenza detection in adults. Clin Med Res. 2012;10:215–8. doi: 10.3121/cmr.2012.1084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Lopez Roa P, Catalan P, Giannella M, Garcia de Viedma D, Sandonis V, Bouza E. Comparison of real-time RT-PCR, shell vial culture, and conventional cell culture for the detection of the pandemic influenza A (H1N1) in hospitalized patients. Diagn Micr Infec Dis. 2011;69:428–31. doi: 10.1016/j.diagmicrobio.2010.11.007. [DOI] [PubMed] [Google Scholar]
- 11.Kissling E, Valenciano M, Buchholz U, Larrauri A, Cohen JM, Nunes B, et al. Influenza vaccine effectiveness estimates in Europe in a season with three influenza type/subtypes circulating: the I-MOVE multicentre case-control study, influenza season 2012/13. Euro Surveill. 2014:19. doi: 10.2807/1560-7917.es2014.19.6.20701. [DOI] [PubMed] [Google Scholar]
- 12.Suzuki M, Camacho A, Ariyoshi K. Potential effect of virus interference on influenza vaccine effectiveness estimates in test-negative designs. Epidemiol Infect. 2014;142:2642–6. doi: 10.1017/S0950268814000107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Broome CV, Facklam RR, Fraser DW. Pneumococcal disease after pneumococcal vaccination: an alternative method to estimate the efficacy of pneumococcal vaccine. N Engl J Med. 1980;303:549–52. doi: 10.1056/NEJM198009043031003. [DOI] [PubMed] [Google Scholar]
- 14.Skowronski DM, Gilbert M, Tweed SA, Petric M, Li Y, Mak A, et al. Effectiveness of vaccine against medical consultation due to laboratory-confirmed influenza: results from a sentinel physician pilot project in British Columbia, 2004–2005. Can Commun Dis Rep. 2005;31:181–91. [PubMed] [Google Scholar]
- 15.Koepsell TD, Weiss NS. Epidemiologic methods: studying the occurrence of illness. Chapter 10 New York City, NY: Oxford University Press; 2003. [Google Scholar]
- 16.Castilla J, Beristain X, Martinez-Artola V, Navascues A, Garcia Cenoz M, Alvarez N, et al. Effectiveness of rotavirus vaccines in preventing cases and hospitalizations due to rotavirus gastroenteritis in Navarre. Spain Vaccine. 2012;30:539–43. doi: 10.1016/j.vaccine.2011.11.071. [DOI] [PubMed] [Google Scholar]
- 17.Patel M, Pedreira C, De Oliveira LH, Umana J, Tate J, Lopman B, et al. Duration of protection of pentavalent rotavirus vaccination in Nicaragua. Pediatrics. 2012;130:e365–72. doi: 10.1542/peds.2011-3478. [DOI] [PubMed] [Google Scholar]
- 18.Gautam R, Lyde F, Esona MD, Quaye O, Bowen MD. Comparison of Premier Rotaclone(R), ProSpecT, and RIDASCREEN(R) rotavirus enzyme immunoas-say kits for detection of rotavirus antigen in stool specimens. J Clin Virol. 2013;58:292–4. doi: 10.1016/j.jcv.2013.06.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Paul SK, Tabassum S, Islam MN, Ahmed MU, Haq JU, Shamsuzzaman AK. Diagnosis of human rotavirus in stool specimens: comparison of different methods. Mymensingh Med J. 2006;15:183–7. doi: 10.3329/mmj.v15i2.41. [DOI] [PubMed] [Google Scholar]
- 20.Petrie JG, Ohmit SE, Johnson E, Cross RT, Monto AS. Efficacy studies of influenza vaccines: Effect of end points used and characteristics of vaccine failures. J Infect Dis. 2011 doi: 10.1093/infdis/jir015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Jackson LA, Jackson ML, Nelson JC, Neuzil KM, Weiss NS. Evidence of bias in estimates of influenza vaccine effectiveness in seniors. Int J Epidemiol. 2006;35:337–44. doi: 10.1093/ije/dyi274. [DOI] [PubMed] [Google Scholar]
- 22.Jackson ML, Nelson JC, Weiss NS, Neuzil KM, Barlow W, Jackson LA. Influenza vaccination and risk of community-acquired pneumonia in immunocompetent elderly people: a population-based, nested case-control study. Lancet. 2008;372:398–405. doi: 10.1016/S0140-6736(08)61160-5. [DOI] [PubMed] [Google Scholar]