Observations of Hydrogen and Oxygen Isotopes in Leaf Water Confirm the Craig-Gordon Model under Wide-Ranging Environmental Conditions

Abstract

The Craig-Gordon evaporative enrichment model of the hydrogen (δD) and oxygen (δ¹⁸O) isotopes of water was tested in a controlled-environment gas exchange cuvette over a wide range (400‰ δD and 40‰ δ¹⁸O) of leaf waters. (Throughout this paper we use the term “leaf water” to describe the site of evaporation, which should not be confused with “bulk leaf water” a term used exclusively for uncorrected measurements obtained from whole leaf water extractions.) Regardless of how the isotopic composition of leaf water was achieved (i.e. by changes in source water, atmospheric vapor δD or δ¹⁸O, vapor pressure gradients, or combinations of all three), a modified version of the Craig-Gordon model was shown to be sound in its ability to predict the δD and δ¹⁸O values of water at the site of evaporation. The isotopic composition of atmospheric vapor was shown to have profound effects on the δD and δ¹⁸O of leaf water and its influence was dependent on vapor pressure gradients. These results have implications for conditions in which the isotopic composition of atmospheric vapor is not in equilibrium with source water, such as experimental systems that grow plants under isotopically enriched water regimes. The assumptions of steady state were also tested and found not to be a major limitation for the utilization of the leaf water model under relatively stable environmental conditions. After a major perturbation in the δD and δ¹⁸O of atmospheric vapor, the leaf reached steady state in approximately 2 h, depending on vapor pressure gradients. Following a step change in source water, the leaf achieved steady state in 24 h, with the vast majority of changes occurring in the first 3 h. Therefore, the Craig-Gordon model is a useful tool for understanding the environmental factors that influence the hydrogen and oxygen isotopic composition of leaf water as well as the organic matter derived from leaf water.

The stable isotopes of hydrogen (δD) and oxygen (δ¹⁸O) in meteoric water vary in both space and time. When incorporated into the organic matter of plant tissues, analyses of these isotopes can provide valuable environmental information regarding patterns of plant water use (Dawson, 1993) and climatic variation (Schiegl, 1974; Gray and Thompson, 1976; Epstein and Krishnamurthy, 1990). One of the first steps in understanding how the stable isotopes of water are incorporated into plant organic matter is to model how leaf water is altered as a result of transpiration (Roden et al., 1999). (Throughout this paper we use the term “leaf water” to describe the site of evaporation, which should not be confused with “bulk leaf water” a term used exclusively for uncorrected measurements obtained from whole leaf water extractions.)

A freely evaporating surface tends to enrich leaf water in heavy isotopes, since the lighter isotopes of hydrogen and oxygen in water vapor escape from liquid surfaces more readily that the isotopically heavy water molecules. Craig and Gordon (1965) were the first to model this isotopic-fractionation effect for evaporation from large bodies of water. Flanagan et al. (1991b) modified the Craig-Gordon model to include the effects of a turbulent boundary layer on the kinetic fractionation factors that were appropriate for molecular diffusion only. In some cases the Craig-Gordon model predicts a greater isotopic enrichment than was actually observed in bulk leaf water (Allison et al., 1985; Leaney et al., 1985; Flanagan and Ehleringer, 1991; Flanagan et al., 1991a; Wang and Yakir, 1995). Since the value of leaf water at the site of carbohydrate metabolism is an essential component of models predicting the hydrogen and oxygen isotopic composition of plant organic matter, carefully controlled experiments are needed to determine how sound these leaf water models are under different environmental conditions. This is particularly critical when plants are grown experimentally under conditions in which the source water and atmospheric water vapor are not in isotopic equilibrium with each other.

Important environmental parameters included in all leaf water models are the vapor pressure and isotopic composition of the air near the leaf and the isotopic composition of the source water supplying the leaf. The parameters involving atmospheric vapor are often not measured rigorously in growth experiments and are assumed to have limited effects on plant isotopic composition. However, White et al. (1994) demonstrated that the isotopic composition of atmospheric vapor plays an important role in the isotopic composition of cellulose (presumably through its effect on leaf water), and asserted that studies that ignore the influence of atmospheric vapor are potentially flawed.

White and Gedzelman (1984) have shown that the δD of atmospheric vapor can vary seasonally by as much as 70‰ at a single site and that the assumption of isotopic equilibrium of atmospheric vapor with surface water may not always be valid. It may be that the discrepancies between the Craig-Gordon model and measured leaf water δD and δ¹⁸O values under field conditions are related to variations in atmospheric vapor δD and δ¹⁸O that are unaccounted for. In addition, experiments that study the incorporation of stable isotopes in plant material by artificially enriching water sources can produce nonequilibrium conditions in which large isotopic differences are generated between the isotopic composition of the source water and that of the atmospheric water vapor (Roden and Ehleringer, 1999).

While the Craig-Gordon model has strong theoretical support, it has not been tested over an extended range of leaf waters under conditions of isotopic nonequilibrium between source water and atmospheric vapor. Thus, it is important to know how sensitive leaf water is to variations in the isotopic composition of atmospheric vapor and whether models can accurately predict leaf water enrichment under a variety of environmental conditions.

Another important feature of all leaf water models is the assumption of steady state. In natural systems this assumption is often violated due to the continual diurnal variation in environmental parameters (Harwood et al., 1998; Yakir, 1998). The time needed for a leaf to equilibrate with its environment after a perturbation is of interest for modeling efforts. The length of time to reach steady state could also be affected by humidity, and thus it is important to understand the significance of variation in vapor pressure gradients. In addition, understanding how humidity affects the isotopic composition of leaf water is important as a first step in clarifying some of the disparate observations in the literature regarding humidity signals recorded in plant cellulose. While some studies contend that humidity information is recorded in the isotopic composition of plant cellulose (Edwards and Fritz, 1986; Lipp et al., 1993), others find no evidence for a humidity signal (DeNiro and Cooper, 1989; White et al., 1994; Terwilliger and DeNiro, 1995).

The objectives of this study were: (a) to determine if the leaf water model is accurate at steady state over a wide range of leaf water isotopic compositions and vapor pressure gradients and under conditions in which the isotopic signatures of atmospheric vapor are substantially different from source water signatures; and (b) to determine the dynamic response of leaf water to step changes in both atmospheric vapor and source water isotopic composition.

MATERIALS AND METHODS

Plant Material and Growth Conditions

Three-year-old saplings of two species, water birch (Betula occidentalis Hook) and cottonwood (Populus angustifolia James), were obtained from local nurseries. The saplings were grown hydroponically in 190-L tanks (stock tanks, Rubbermaid, Wooster, OH) with aquarium pumps and airstones providing oxygen to the roots as described in detail previously (Roden and Ehleringer, 1999). The initial tank water isotopic composition was derived from Salt Lake City municipal water (δD = −120‰; δ¹⁸O = −15‰). Additions of D₂O and 10 atom % ¹⁸O water (Europa Scientific, Crewe, UK) were mixed with Salt Lake City water when the experiment called for a change in source water (δD = +87‰; δ¹⁸O = +6‰). Nutrients were supplied to the roots as one-tenth-strength Hoagland solution. The plants were grown in a greenhouse set to 25°C and ambient humidity (20%–60%). Plants were grown for 1 month in the greenhouse under constant hydroponic conditions prior to any gas exchange measurements. A second experiment utilized only cottonwood saplings grown hydroponically in individual 10-L buckets under three different source water δ¹⁸O compositions (−15‰, 0‰, and +15‰).

Gas Exchange Measurements

A steady-state gas exchange system described previously (Comstock and Ehleringer, 1993) was utilized to measure water vapor and CO₂ exchange in mature leaves. The temperature, humidity, light, and CO₂ concentration within the cuvette were controlled and measured. Boundary layer conductance to water vapor in the cuvette was 2 mol m⁻² s⁻¹. Leaf temperatures ranged from 23°C to 26°C. Light levels were saturating (>1,500 μmol photons m⁻² s⁻¹, 400–700 nm), and the CO₂ concentration was 360 μL L⁻¹. The leaf-to-air water vapor mole fraction gradient (ν) was controlled by adjusting flow rates and temperature of a dew point column for vapor input, and was maintained for the entire 5- to 7-h experiment between 0.005 and 0.01 and between 0.018 and 0.025 (dimensionless, mole per mole) for the “low” and “high” ν treatments, respectively. Total conductance to water vapor differed between ν treatments for birch (low ν; range 0.16 to 0.54 mol m⁻² s⁻¹, mean of 0.4 and high ν; range 0.14 to 0.34 mol m⁻² s⁻¹, mean of 0.24) but not for cottonwood (low ν, range 0.17 to 0.55 mol m⁻² s⁻¹, mean of 0.35 and high ν range 0.13 to 0.57 mol m⁻² s⁻¹, mean of 0.33).

Stomatal conductance to water vapor and leaf transpiration rates were recorded throughout the experiment. Although not critical for calculations of leaf water isotopic composition, carbon assimilation rates ranged from 10 to 25 μmol CO₂ m⁻² s⁻¹ and intercellular CO₂ concentrations from 200 to 300 μL L⁻¹.

Experiment 1: Change in Input Vapor Isotopic Composition

At the start of the experiment, a sapling was transferred from the 190-L tank in the greenhouse to an 8-L bucket containing the same source water as the tank (the bucket was actually filled with tank water), brought to the gas exchange system, and a root aeration system was installed. A leaf was placed into the gas exchange cuvette for 1 h to allow physiological adjustment to the cuvette environment and the stomata to open fully. The input water vapor was manipulated by altering the isotopic composition of the water reservoir that humidified the air stream prior to the dew point column (the bubbler).

For the 1st h, input water vapor was set to a value close to the ambient conditions in the greenhouse, then the water in the bubbler was enriched by approximately 180‰ to 240‰ (δD) and/or 20‰ to 25‰ (δ¹⁸O). Prior to the step change, both input and output water vapor was collected in a 9-mm Pyrex tube fitted to an ethanol/dry ice trapping system (−78°C) connected to the air flow tubing either just before (input vapor) or just after (output vapor) the leaf cuvette. After the step change, output water vapor was sampled every 20 to 30 min for the first 2 h and less frequently thereafter to determine the time required for the leaf to reach isotopic steady state.

Experiment 2: Change in Water Source Isotopic Composition

In this experiment, the saplings were handled in the same initial manner as described above, except instead of a step change in input vapor isotopic composition, the water in the bucket was enriched from −120‰ to +120‰ in δD and/or from −15‰ to +10‰ in δ¹⁸O. Output water vapor was sampled (as above) at progressively longer time intervals over a 30-h period to determine the time required for the leaf to reach isotopic steady state after a step change in source water isotopic composition. In addition to output vapor, source water was also sampled periodically.

Experiment 3: Dependence of Leaf Water on ν and Isotopic Composition of Vapor

In this experiment, the saplings were handled in the same initial way as in experiment 1, except dynamic changes in output vapor were not tracked. The isotopic composition of the input water vapor was changed by enriching the bubbler (as above), and the leaf was allowed to reach steady state for a minimum of 5 h. The experiment did not end unless the estimates of stomatal conductance, transpiration rate, and ν did not systematically vary for at least 1 h. The leaves did not show any midday depressions in stomatal conductance, and for the most part had flat-line responses for the entire experimental period. At the end of the experiment, the output water vapor, source water, and leaf water were sampled. This experiment was performed on both species with two source water treatments, both low and high ν (see above), as well as four to five different input vapor isotopic compositions for a total of 32 experiments. The data from these experiments were also used to test the ability of a leaf water model to predict the observed variations in leaf water δD generated by the imposed environmental conditions.

Due to analysis problems with the ¹⁸O measurements in the original experiments, a second round of experiments was performed that varied δ¹⁸O in source water and the cuvette vapor to generate variation in leaf water δ¹⁸O to test the leaf water model for ¹⁸O. This experiment used three source water treatments (−15‰, 0‰, and +15‰ δ¹⁸O), with all other measurements similar to the steady-state experiment described above.

Isotope Sampling

Approximately 2 mL of water was sampled from the tank or buckets for analysis of source water δD and δ¹⁸O. At the end of each experiment, leaf material with the midvein removed was placed into a glass vial, sealed with laboratory film, and placed into a freezer (−5°C) until the water could be extracted for isotopic analysis. Leaf water was obtained by cryogenic extraction as described by Ehleringer and Osmond (1989). The sample was frozen in liquid nitrogen (−190°C) and once evacuated, the system was then isolated from the vacuum pump and immersed in boiling water. The water from the leaf was then collected in a tube immersed in liquid nitrogen until all water was extracted.

The δD of water samples from the tanks, leaves, and output vapor were obtained by reducing the H in 2 μL of H₂O to H₂ using 100 mg of a Zn catalyst in a 500°C oven (modification of Coleman et al., 1982). The δ¹⁸O values of the water samples were obtained by a modified micro-equilibration technique in which 20 to 60 μL of water was sealed in a 9-mm Pyrex tube with approximately 240 μL of CO₂ in a 25°C water bath for over 7 d. In this method the CO₂ is extracted cryogenically using liquid nitrogen and dry-ice/ethanol traps (Ehleringer and Osmond, 1989). Because of the small volume of CO₂ in the micro-equilibration technique, an external “cold-finger” was used to increase the amount of CO₂ input into the mass spectrometer. Both the H₂ and CO₂ were analyzed on an isotope ratio mass spectrometer (MAT Delta S, Finnigan, San Jose, CA) with a precision of ±1‰ for δD and ±0.2‰ for δ¹⁸O.

Leaf Water Model

Throughout this paper we will be using the conventional “delta” notation, which expresses the isotopic composition of a material relative to that of a standard on a per mil deviation basis:

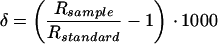1

where δ is the isotope ratio and R is the molar ratio of heavy to light isotopes. The standard for both hydrogen and oxygen is Standard Mean Ocean Water (SMOW).

A general model for the evaporative enrichment of a free water surface for both δD and δ¹⁸O was developed by Craig and Gordon (1965). The model includes both an equilibrium isotope effect resulting from the phase change from liquid to vapor and a kinetic isotope effect caused by different rate of diffusion of the heavy and light isotopes of water vapor in air. The Craig-Gordon model was expanded by Flanagan et al. (1991b) to include leaf boundary layers (see also Farquhar et al., 1989):

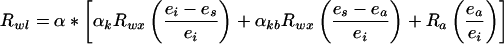2

where the subscripts a, wl, and wx refer to bulk air, leaf water, and xylem water, respectively, and e is the vapor pressure (subscripts a, s, and i refer to bulk air, leaf surface, and intercellular air spaces, respectively). (Leaf surface vapor pressures were determined from the equations of Ball [1987]. The fractionation factors differ depending on whether hydrogen or oxygen isotopes are being modeled, but the same general model applies to both species.) α* is the liquid-vapor equilibrium fractionation factor and varies with temperature according to the equations of Majoube (1971) for both H/D and ¹⁶O/¹⁸O, α_k is the kinetic fractionation associated with diffusion in air (H/D = 1.025 and ¹⁶O/¹⁸O = 1.0285), and α_kb is the kinetic fractionation associated with diffusion through the boundary layer and is calculated by raising α_k to the 2/3 power (H/D = 1.017 and ¹⁶O/¹⁸O = 1.0189). Other studies (Buhay et al., 1996; Wang et al., 1998) have accounted for boundary layer effects by modifying the kinetic fractionation for different species from leaf aerodynamic and morphological properties.

The Craig-Gordon model contains a number of assumptions that may not be strictly valid for leaves, causing potential discrepancies between the model and bulk leaf water δD and δ¹⁸O measurements. For leaves the assumption of: (a) isotopic steady state (b) constant water volume, and (c) isotopic homogeneity may not always be valid (Yakir, 1998). Significant spatial heterogeneity in δD and δ¹⁸O of water within a leaf has been observed, because all parts are not equally exposed to evaporation (Yakir et al., 1989; Luo and Sternberg, 1992). Some of this heterogeneity may be caused by compartmentation (vein and mesophyll tissues), patchy stomatal conductances (Mott, 1995), contrasting effects of diffusion of isotopically enriched water from the evaporating surfaces into the leaf tissues against the convective flux of source water from the xylem (Péclet effect, Farquhar and Lloyd, 1993), or all of the above. In addition, some researchers have found that leaf morphological and physiological characteristics can enhance predictions of the isotopic composition of leaf water (Buhay et al., 1996; Wang et al., 1998). Due to the many potentially interacting effects described above, we chose to bundle them all into empirical equations (Flanagan, 1993) that are used to correct bulk leaf water measurements for comparisons with predictions of the Craig-Gordon model:

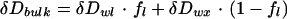3

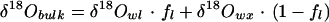4

where ƒ_l is the proportion of the bulk leaf water subjected to evaporative enrichment, the subscripts bulk and wx refer to bulk leaf water and xylem water, respectively, and wl refers to the values of δD and δ¹⁸O from Equation 2 above. An electronic spreadsheet version of the model is available at (ftp://ecophys.biology.utah.edu/treering/).

RESULTS

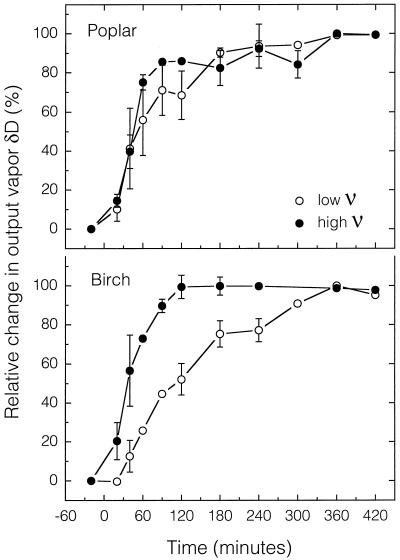
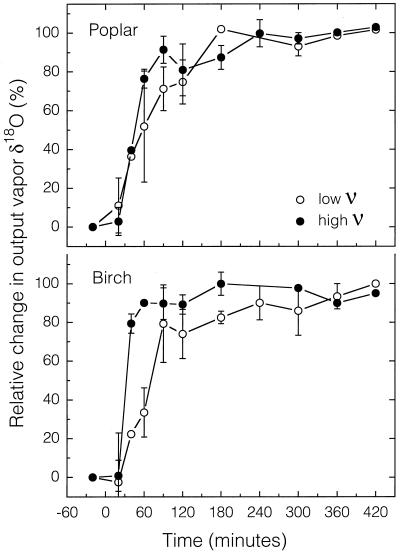
To compare the curves during step changes in either source water or input water vapor isotopic composition, the data were normalized such that the relative change in output vapor at steady state was set to 100%. For both δD and δ¹⁸O, leaves reached isotopic steady state in 5 to 6 h (Figs. 1 and 2). For plants exposed to high ν, the leaves reached equilibrium in as little as 2 h, with 50% of the changes occurring within 30 to 60 min. Plants exposed to low ν took longer to reach steady state (3–5 h) as well as half maximum (1–2 h). There was no apparent difference in the amount of time to reach steady state between δD and δ¹⁸O, although there is not enough replication (n = 2) to determine fine scale differences. Birch leaves may take longer to reach equilibrium that poplar leaves, but, again, the differences were generally minor.

Figure 1.

Time course of the relative change in output vapor δD after a step change in input vapor δD (time 0) for leaves of birch or poplar exposed to high or low ν. Values are means ± se (n = 2). A missing error bar implies that a sample was lost (n = 1) unless the data are near 0% or 100%, in which case the error bars are often within the symbol. If a symbol is missing then both samples were lost due to technical difficulties.

Figure 2.

Time course of the relative change in output vapor δ¹⁸O after a step change in input vapor δ¹⁸O (time 0) for leaves of birch or poplar exposed to high or low ν. Values are means ± se (n = 2). A missing error bar implies that a sample was lost (n = 1) unless the data are near 0% or 100%, in which case the error bars are often within the symbol. If a symbol is missing then both samples were lost due to technical difficulties.

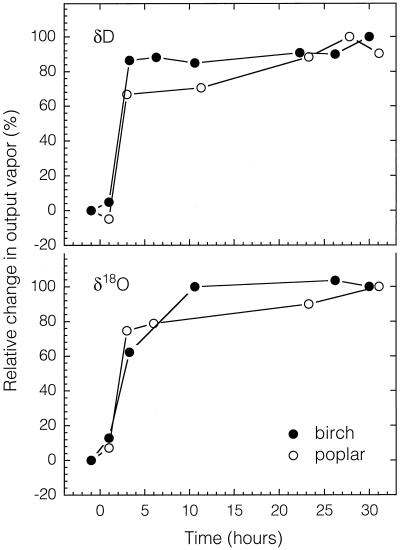
When there was an abrupt change in source water to the roots the output vapor changed little over the 1^st h, then changed rapidly by 3 h, and exhibited gradual changes thereafter (Fig. 3). The leaf reached steady state by 24 h and somewhat earlier for birch than cottonwood. Both plants were exposed to moderate ν (0.01–0.018) and had stable conductances to water vapor (0.4–0.6 mol m⁻² s⁻¹) and transpiration rates (5–7 mmol m⁻² s⁻¹) during the daytime periods.

Figure 3.

Time course of the relative change in output vapor δD and δ¹⁸O after a step change in source water δD and δ¹⁸O (time 0) for leaves of birch and poplar.

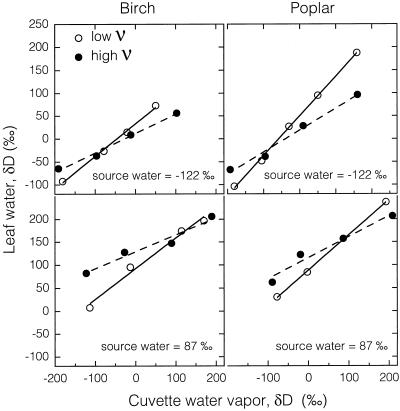
Various combinations of the isotopic composition of source water and input vapor produced leaves with a range of 400‰ in leaf water δD. For a given source water and ν, both species produced linear relationships between cuvette water vapor δD and leaf water δD (Fig. 4). The cuvette water vapor (the output vapor) isotopic composition is a combination of both the input vapor and transpiration and is analogous to atmospheric vapor in natural systems. The leaf not only undergoes evaporative enrichment with its environment but also isotopic vapor exchange. The degree to which the isotopic composition of the cuvette water vapor affected leaf water was dependent on ν (Fig. 4).

Figure 4.

Relationship between the isotopic composition of cuvette water vapor (output vapor) and the isotopic composition of leaf water for birch and poplar leaves exposed to high and low ν and grown in source water of either −122‰ or 87‰ δD.

At low ν (high humidity) there is a greater probability for the water vapor in the cuvette to exchange with the leaf, causing the differences in the observed slopes between high and low ν. The intersection of the high and low ν lines occurred when the cuvette water vapor δD was close to the source water δD. If there is no gradient in δD between atmospheric vapor and source water, then ν becomes irrelevant, as it relates to isotopic vapor exchange and the leaf water isotopic signature reflects evaporative enrichment only. The reason the cuvette water vapor δD at the intersection of the high and low ν lines is not exactly equal to the source water δD value is that ν will still affect evaporative enrichment even if isotopic gradients for vapor exchange are minimized.

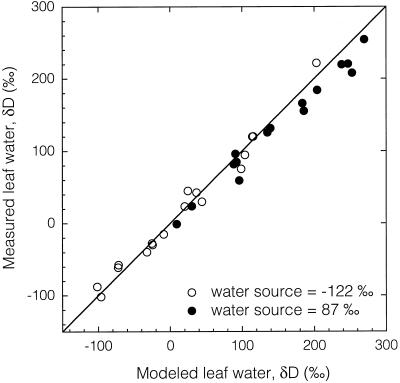
Using the detailed environmental and physiological measurements derived from the steady-state gas exchange experiments, the leaf water isotopic composition was predicted from the leaf water model (Eq. 2). These predictions were then compared with the measured leaf water δD values. Clearly, the model does a good job of predicting leaf water δD over a wide range of leaf water values (400‰) and only deviated from the 1:1 line at highly enriched values (Fig. 5). These leaf waters were generated by extremely diverse means, including both depleted and enriched source waters, high and low ν, and highly depleted and enriched cuvette water vapor input. The Craig-Gordon model handled these disparate environmental conditions and produced plausible leaf water predictions.

Figure 5.

Relationship between the δD of modeled and measured leaf water. Variations in leaf water were generated in a gas exchange cuvette through altering input vapor δD, source water δD, and vapor pressure deficits and flow rates. The line represents a 1:1 relationship.

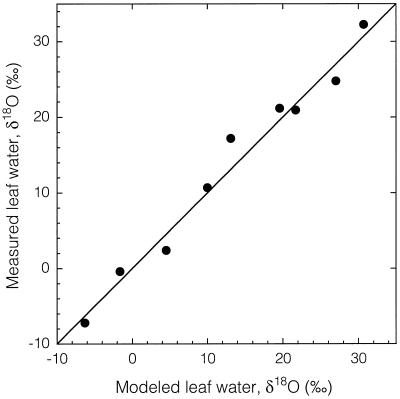
The leaf water model accurately predicted measured leaf water δ¹⁸O over a range of nearly 40‰ (Fig. 6). In this experiment, we used only cottonwood. The species-specific parameters in the leaf water model (stomatal conductance and transpiration rate) are only used to estimate the water vapor at the leaf surface (Ball, 1987; Roden et al., 1999), and sensitivity analysis has shown that their effects on leaf water isotopic composition are limited. Although Wang et al. (1998) have observed substantial differences between species, the similar morphology and physiology of birch and cottonwood leaves, as well as the lack of observed species effects when modeling leaf water δD, indicated that a single species (cottonwood) test for δ¹⁸O was sufficient.

Figure 6.

Relationship between the δ¹⁸O of modeled and measured leaf water. Variations in leaf water were generated in a gas exchange cuvette through altering input vapor δ¹⁸O, source water δ¹⁸O, and vapor pressure deficits and flow rates. The line represents a 1:1 relationship.

DISCUSSION

Despite a variety of approaches to alter the isotopic composition of leaf water (i.e. changing the ν, the source water δD and δ¹⁸O, or the atmospheric vapor δD and δ¹⁸O), the Craig and Gordon (1965) evaporative enrichment model as modified by Flanagan et al. (1991b) did an excellent job in predicting leaf water isotopic composition over a wide range (400‰ in δD and 40‰ in δ¹⁸O) of values (Figs. 5 and 6). Some previous studies have found that the Craig-Gordon model predicted a higher degree of heavy isotopic enrichment than observed in bulk leaf water measurements (Allison et al., 1985; Leaney et al., 1985; Flanagan and Ehleringer, 1991; Flanagan et al., 1991a; Wang and Yakir, 1995). Although the results of this study also showed a similar trend between modeled and measured bulk leaf water values, the generality of the model is still clearly evident over the range of leaf waters that far exceeds natural conditions (Figs. 5 and 6).

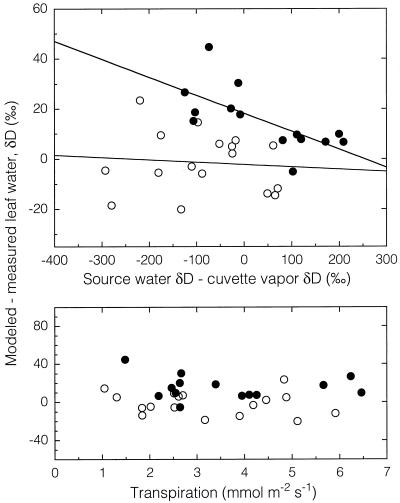
Although some researchers have attributed the difference between observed and modeled leaf water to the inclusion of unfractionated vein water in the bulk leaf water isotopic composition (Allison et al., 1985; Leaney et al., 1985; Walker et al., 1989), the results presented in this study were corrected (Eqs. 3 and 4) for this effect. The unfractionated pool of water has been estimated to be from 13% to 30% of the total water volume (Allison et al., 1985; Leaney et al., 1985; Walker et al., 1989; Flanagan et al., 1991b). Since the major vein was cut out of the leaf just prior to sampling, a smaller fraction (10%) produced the best fit between observed and measured values in this study. Alternatively, some researchers have attributed discrepancies between observed and modeled leaf water to high transpiration rates (Flanagan et al., 1991b). Transpiration rates could potentially shift the balance between the back diffusion of heavy isotopes from the sites of evaporation and the bulk flow of source water into the leaf (Farquhar and Lloyd, 1993). However, there was no relationship between transpiration rate and differences between modeled and measure leaf water isotopic composition in our data (Fig. 7), although the transpiration rates were much lower than reported in Flanagan et al. (1991b).

Figure 7.

Difference between modeled and measured leaf water δD as a function of leaf transpiration rate or the difference between source water δD and cuvette vapor δD. •, Plants grown in enriched source water (87‰ δD); ○, plants grown in depleted source water (−122‰ δD).

Modeling bulk leaf water is more problematic than modeling leaf water at the site of evaporation. The Craig-Gordon model contains a number of assumptions that may not be strictly valid for whole leaves, such as isotopic steady state, constant water volume, and isotopic homogeneity (Flanagan, 1993; Yakir, 1998). Many of the bulk leaf water corrections in the literature require detailed anatomical, morphological, and physiological information for each species (Buhay et al., 1996; Wang et al., 1998; Yakir, 1998). In addition, the Péclet correction (Farquhar and Lloyd, 1993), in which the effects of diffusion of isotopically enriched water from the evaporating surfaces into the leaf tissues opposes the convective flux of source water from the xylem, requires knowledge of the leaf transpiration rate and the effective mixing pathlength. In practice, the effective mixing length is calculated from the discrepancies between the Craig-Gordon model and the measured bulk leaf water along with gas exchange measurements of leaf transpiration. The proportion of bulk leaf water subjected to evaporative enrichment (ƒ_l) in Equations 3 and 4 is an empirical value that incorporates all of the factors that influence bulk leaf water isotopic heterogeneity for the species tested. Mechanistic models of the δD and δ¹⁸O values of bulk leaf water may still be unable to account for all of the potential influences on leaf heterogeneity (e.g. patchy stomatal conductance).

The ƒ_l value of 10% used in this study produced excellent fits between modeled and measured observations over an extended range of leaf water δD and δ¹⁸O values for both species (Figs. 5 and 6). This implies that if ƒ_l is determined for a species using detailed micro-environmental and gas exchange information, as well as the isotopic composition of bulk leaf water, then it may be used to correct bulk leaf water observations over a wide range of values. However, the utilization of the Craig-Gordon model in studies of the isotopic composition of plant organic matter (e.g. tree rings, Roden and Ehleringer, 1999), as well as studies of global and canopy CO₂ exchange of ¹⁸O with the atmosphere (Farquhar and Lloyd, 1993; Flanagan et al., 1994), is not dependent on the various corrections for bulk leaf water heterogeneity. For these studies what is important is the δD and δ¹⁸O values in the chloroplast, where carbohydrate metabolism and CO₂ exchange take place. The proximity of chloroplasts to the air-water interface suggests that chloroplast water should be very close to that predicted by the Craig-Gordon model, as shown by Flanagan et al. (1994, but see also contrasting results from Yakir et al., 1993).

There was a slight trend for the difference between modeled and measured leaf water isotopic composition to be related to the magnitude of the difference between source water and cuvette vapor δD (for the enriched source water treatment only [Fig. 7]). Sensitivity analysis of the leaf water model indicates (Roden et al., 1999) that as the difference between source water δD and atmospheric vapor δD increases, any errors in humidity measurements will magnify errors in model prediction. In addition, at high humidities, any errors in atmospheric vapor δD measurements will also magnify errors in the prediction of leaf water δD. Thus, although the model is effective in handling even large differences between source water and atmospheric vapor δD (as high as 300‰ in this study), extreme care must be taken when estimating environmental parameters for use in the leaf water model. However, these concepts are less likely to apply to differences observed in field studies, since the differences between the isotopic composition of local water sources and atmospheric vapor are not as large as those generated in these experiments.

These results have implications for conditions in which the isotopic composition of atmospheric vapor is not in equilibrium with source water, such as experimental systems that grow plants under isotopically enriched water regimes (Roden and Ehleringer, 1999) and natural systems in which trees are exposed to seasonably variable atmospheric water vapor but tap water sources that are less variable than meteoric input (ground water).

There was excellent agreement between modeled and measured leaf water δ¹⁸O evident over the entire leaf water range (approximately 40‰, Fig. 6). There did not appear to be any relationship between transpiration rate and discrepancies between modeled and measure leaf water δ¹⁸O values, nor was there a relationship between the magnitude of source water and cuvette vapor δ¹⁸O differences (data not shown). Some of the differences between modeled and observed oxygen isotope ratios in leaf water from the earliest studies relate to the noninclusion of boundary layer effects in the Craig-Gordon model (Flanagan et al., 1991b). Boundary layer effects are quantitatively more important for oxygen than for hydrogen because the relative magnitudes of the kinetic and equilibrium fractionation factors differ between the two species (Flanagan, 1993).

Following a change in the isotopic composition of vapor in the cuvette, approximately 2 to 5 h was required for the leaf to reach isotopic steady state depending on ν. A number of other studies (Farris and Strain, 1978; Yakir et al., 1993) have also found that 2 h are required to reach steady state. Flanagan et al. (1991b) found that common bean leaves required approximately 1 h to reach isotopic steady state when exposed to an increase in irradiance. Flanagan et al. (1991b) used dry air as an input to create very high ν; the resulting high transpiration rates may explain some of the differences in the response dynamics, since lower ν tend to extend the equilibration time (Figs. 1 and 2).

There could also be species differences, since the turnover time for leaf water depends on the ratio of leaf water to the transpiration rate. On the other hand, birch, poplar, and common bean leaves all have fairly thin leaves and relatively high transpiration rates, so turnover rates may not be the critical factor. Longer time periods would be required to reach steady state for thick, schlerophylous leaves, plants in very humid environments, or leaves with low stomatal conductance. However, it should also be noted that the step change in these experiments was fairly drastic (output vapor changed by as much as 270‰ in δD and 15‰ in δ¹⁸O over the 5- to 7-h experiment), and in natural systems, perturbations in the environment would be far less drastic and more gradual.

Leaves may actually be very close to isotopic steady state in the field even though the environmental conditions are not constant, so the steady-state assumptions of the leaf water model may not invalidate its use in natural systems. A recent study by Harwood et al. (1998) showed that leaves of Piper aduncum were not at isotopic steady state while vapor pressure deficits were changing and isotopic steady state was achieved for only 2 h around midday. However, isotopic steady state was achieved for a time, and sampling protocols should consider the best time of day to collect leaves so as to avoid changing environmental conditions.

After a change in source water isotopic composition, approximately 3 h was required for the majority of changes in leaf water to show up in the output vapor and approximately 24 h was required to be assured of complete equilibration for the small trees used in these experiments (Fig. 3). Using typical transpiration rates (5 mmol m⁻² s⁻¹), specific leaf area, and relative water content of a poplar leaf, turnover of the entire leaf water volume should have occurred in as little as 15 min. The amount of time it takes for a leaf to come into equilibration with a step change in the isotopic composition of source water depends on the capacitance of the system (especially stem water storage capacity) and on the mixing rate within the leaf (apoplastic to symplastic water exchange). In natural systems the isotopic composition of source water can change, but seldom is this change rapid or to as large an extent as in these experiments (240‰ in δD and 25‰ in δ¹⁸O). These results are more applicable to experimental systems in which stable isotopes of water are used as tracers. A spike in either ²H or ¹⁸O could be detected within 24 h, depending on the water flux rates through the plant.

The degree of isotopic enrichment in a leaf is not only dependent on evaporation, but also on the difference between the isotopic composition of the water supplying the leaf and that of the atmospheric water vapor. In general, the isotopic composition of vapor in the air is related to the isotopic composition of meteoric waters for that region, making it difficult to study atmospheric vapor effects in the field. The advantage of a gas exchange system is that artificial differences between the isotopic composition of source water and atmospheric vapor can be imposed and effects on leaf water studied while other factors such as ν are controlled. The differences in slope between the high and low ν (Fig. 4) demonstrate that the heavy isotopes in atmospheric vapor influence leaf water isotopic composition depending on the gradients that drive vapor flux. There is often the perception that vapor moves in one direction only (out of the leaf), but our data support the concept of a bidirectional isotopic flux until isotopic equilibrium is reached.

In conclusion, the models describing evaporative enrichment developed by Craig and Gordon (1965) and modified by Flanagan et al. (1991b) are sound in their ability to predict both hydrogen and oxygen isotopic composition over a wide range of leaf waters. As such, these equations are a useful tool to determine the environmental factors that may influence leaf water and, ultimately, plant organic matter isotopic composition. It is clear from the present study that when making estimates of leaf water isotopic composition in natural or artificial environments, careful measurements of atmospheric humidity and the isotope ratios of that vapor are needed. The model assumption of isotopic steady state is probably achieved under relatively stable environmental conditions and should not be a deterrent for using the model in field situations.

Abbreviations:

δD

stable hydrogen isotope ratio

δ¹⁸O

stable oxygen isotope ratio

ν

leaf-to-air water vapor mole fraction gradient