Skillful object manipulation requires learning the dynamics of objects, linking applied force to motion 1,2. This involves the formation of a motor memory 3,4, which has been assumed to be associated with the object, independent of the point on the object that one chooses to control. Importantly, in manipulation tasks, different control points on an object, such as the rim of a cup when drinking or its base when setting it down, can be associated with distinct dynamics. Here we show that opposing dynamic perturbations, which interfere when controlling a single location on an object, can be learned when each is associated with a separate control point. This demonstrates that motor memory formation is linked to control points on the object, rather than the object per se. We also show that the motor system only generates separate memories for different control points if they are linked to different dynamics, allowing efficient use of motor memory. To account for these results, we develop a normative switching state-space model of motor learning, in which the association between cues (control points) and contexts (dynamics) is learned rather than fixed. Our findings uncover an important mechanism through which the motor system generates flexible and dexterous behavior.
Understanding how humans learn to use tools is a central challenge in neuroscience 5. Tool use requires knowledge of the dynamics of objects (relating applied force to motion), which depend on both the physical properties of objects (e.g., mass, mass distribution and friction) and how objects are used to interact with the environment (e.g., for transport or percussion). Numerous paradigms have been developed to explore how humans learn the dynamics of objects. In conventional object manipulation tasks, participants grasp and lift physical objects with familiar dynamics e.g., 3,6,7. When lifting an object for the first time, visual cues about size and surface material strongly influence lift forces 8–10. However, after several lifts, participants learn the dynamics of the object, as demonstrated by adaptation of grip and lift forces measured at the fingertips prior to object lift off 4,11. If the dynamics of the object are simple, learning can occur in a single trial 8. However, even for objects with simple dynamics, interference can be seen when alternately lifting the same object and grasping it at different locations 12,13.
Robotic manipulanda offer an alternative testbed for object manipulation studies 14. These interfaces can simulate objects with unfamiliar dynamics 15–20 and provide an opportunity to manipulate the relationship between haptic and visual feedback 21,22. In a typical adaptation experiment, participants grasp the handle of a robotic manipulandum and make reaching movements that are perturbed by the robot. For example, a perturbation that has been examined extensively is a viscous curl field that generates forces on the hand that act perpendicular to the velocity of the hand and proportional to its speed 15,23–25. Over repeated movements, participants learn to generate the forces required to compensate for the perturbation, forming a motor memory of the grasped object 26,27. However, the capacity to learn different dynamics in such paradigms appears to be surprisingly limited when the same movement is made (under veridical visual feedback) in force fields that act in opposite directions 28,29.
In the standard force-field adaptation paradigm, the ‘object’ being moved to a target is a small disk and the task involves controlling the center of the disk. However, in natural object manipulation tasks involving objects with more complex geometries, we can exert control over different locations, or ‘control points’, on the object. For example, when using a wide broom to sweep along a wall, we could control the edge of the broom that is nearest to the wall so as to make contact with the wall. Such contact will perturb the head of the broom, rotating it in opposite directions for walls on the left and right; that is, when controlling the left and right side of the broom. Similarly, when drinking from a wine glass, we can control the near rim as we lift the glass to our mouth and then control the base of the stem as we replace the glass. Numerous studies of object manipulation have examined how memories of object dynamics transfer across changes in grasp configurations 12,13,30–34. However, none of these previous studies have explicitly manipulated the location of the control point independently of either the grasp location or the required movement of the object.
Here we tested the hypothesis that the motor system can flexibly engage separate memories when controlling different points on a single object, allowing different dynamics to be learned and associated with these control points. Using a planar robotic interface and virtual reality system, we linked the movement of a rectangular virtual object to the motion of the hand. The hand was clearly visible at all times and located at the center of the object (Fig. 1). There were two control points, located on the left and right of the object, and two corresponding targets. The two control points were linked to opposing viscous curl fields. On each trial, the participant was required to generate a straight ahead hand movement to align either the left or right control point to its corresponding target. Thus, the required movement was the same for both control points.
Figure 1.
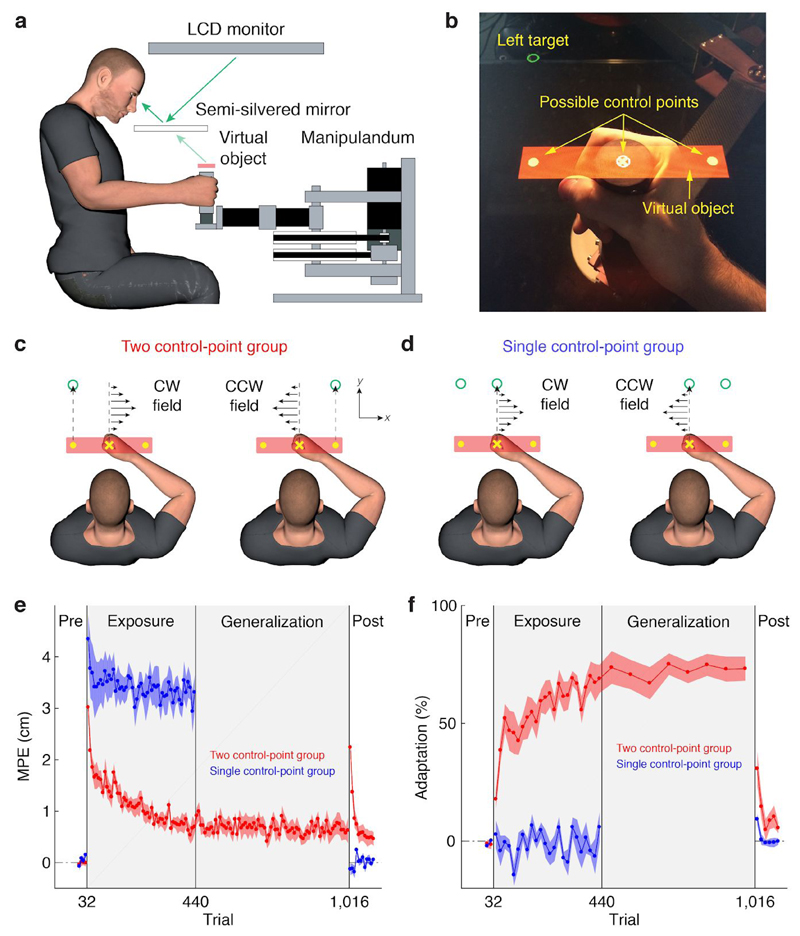
Separate motor memories are formed for different control points. Experimental paradigm and learning curves for Experiment 1. (a) Participants grasped the handle of a robotic manipulandum. A semi-silvered mirror allowed the participant to view their hand as well as a virtual object that was reflected from the monitor. (b) Photograph of the hand, the virtual object and target, as seen from the perspective of the participant. Depending on the experiment and trial type, one of three control points on the object had to be aligned with a target placed above it. (c) Participants in the two control-point group moved the left or right control point to its corresponding target. The direction of the force field applied to the hand was determined by the target/control point. (d) Participants in the single control-point group moved the central control point to a central target. The direction of the field applied to the hand was cued by which lateral 'target' was displayed. (e) Kinematic error measured as the maximum perpendicular error (MPE: deviation from a straight line to the target) over the course of the experiment. Data were first averaged over blocks of eight exposure trials and then plotted as mean across participants ± 1 s.e.m. Gray background shows the period when the force field was turned on. (f) same as (e) but for percentage adaptation measured on channel trials. The generalization phase was performed by the two control-point group (n = 10) but omitted for the single control-point group (n = 8).
We found that participants could learn opposing dynamics when they were linked to these different points. By testing generalization we show that this learning is associated with control points, rather than hand or target locations. In addition, we show that the motor system only assigns distinct memories to control points if they are linked to different dynamics, allowing flexible and efficient use of motor memory. Finally, we show that our results are best accounted for by a switching state-space model. Unlike standard state-space models, our model can learn the probability of cues (i.e., control points) given the context (i.e., force field) and can infer the state for each context based on motor errors. Our results uncover an important mechanism through which the human motor system can generate flexible and dextrous motor behaviour.
We carried out two experiments to examine the mapping of motor memories to control points. In Experiment 1, we examined the ability of participants to learn opposing dynamics when these are associated with either different control points or a single control point. We then examined the reference frame in which control points are represented by testing generalization of learning. In Experiment 2, we test whether the assignment of separate memories to control points is obligatory, or whether this only occurs when necessary.
Participants grasped the handle of a robotic interface (Fig. 1a) and a semi-silvered mirror was used to display a rectangular virtual object centered on the hand. The object translated with the hand. The workspace under the mirror was illuminated so that both the hand and the object were always visible (Fig. 1b). The object had three visible control points: circles displayed on the left and right of the object and a cross at the center of the object. For participants in the two control-point group (n = 10), a target appeared above one of the two lateral control points at the start of each trial, and participants were instructed to move the corresponding control point to the target (Fig. 1c). The target location (left or right) cued the direction of the force field on exposure trials (see below). For participants in the single control-point group (n = 8), a central target appeared above the central control point and participants were instructed to move the central control point to this target (Fig. 1d). In this group, as in the two control-point group, a lateral ‘target’ was also displayed to cue the direction of the force field. Crucially, for both groups the start position of the hand and the required final position of the hand were the same in all trials.
In the pre-exposure phase participants made movements in a null field. In the exposure phase, opposing force fields were associated with the two lateral targets. Hence, for participants in the two control-point group, each force field was also associated with the point on the object that had to be controlled. To produce the same movement of the hand in both force fields, participants would need to learn the opposing dynamics.
Participants performed 52 blocks of 8 trials (416 trials) in the exposure phase with an equal number of trials for each target in a pseudorandom order. So that predictive force compensation could be assessed independently from co-contraction, one randomly selected trial in each block was a channel trial 25,35, in which the movement was confined to a simulated mechanical channel to the target. On these trials, the forces generated by participants into the wall of the channel could be measured.
To assess performance we measured kinematic error, defined as the maximum perpendicular error (MPE) between the actual and ideal (i.e., straight) hand path. We also measured force compensation on channel trials, defined as the percentage of the force required to fully compensate for the force field (adaptation). During the pre-exposure phase, as expected the kinematic error and the adaptation were close to zero (Fig. 1e-f). At the start of the exposure phase, the force fields produced substantial deviations of the hand path from a straight line (Supplementary Figure 1). To assess learning, we compared adaptation, which unlike MPE is not influenced by stiffness, in the final two blocks of the pre-exposure and exposure phases. This revealed a significant interaction between group and epoch (mixed-design ANOVA, F1,16 = 73.31, p = 2e-7). Adaptation reached 68.1% ± 6.6% and -0.2% ± 4.3% of full force compensation by the end of the exposure phase for the two and single control-point groups (Fig. 1f), respectively. For the two control-point group, the increase in adaptation was significant (two-tailed paired t-test, 69.4% ± 6.7%, t(9) = 10.99, p = 2e-6).
The failure to learn when controlling a single control point is consistent with previous studies showing that arbitrary visual cues do not facilitate learning of opposing force fields 28,29,36, and indicates that the learning observed when controlling two different control points — despite making similar hand movements — is not simply due to the contextual cues provided by the lateral targets.
We performed two additional control experiments. In the first (Supplementary Figure 2), we show that participants (n = 8) can learn opposing fields, linked to different control points, even when they are required to fixate a central fixation point. This rules out the possibility that learning is due to associating field direction with gaze position. The second control was designed to rule out the possibility that subjects might be treating the two control points (small circles) as separate objects, despite the fact that they move coherently and are bounded by a rectangle. In this control, we used an object where the control points are defined by the geometry of the object and there are no distinct visual elements (Supplementary Figure 3). We show that participants (n = 8) can still learn opposing fields, linked to these different control points (Supplementary Figure 3).
Our hypothesis that separate memories can be formed for different control points on manipulated objects assumes that these points are represented in object-centered coordinates; i.e., that translating the object would not interfere with the learned memories associated with these points. However, other interpretations are possible based on the results for the two control-point group. Specifically, whereas our hypothesis assumes that memories formed for the two fields are linked to the locations of the control points relative to the object (object-centered representation), it is possible that these memories are linked to the locations of the targets relative to the body (body-centered representation) or the locations of the targets and control point relative to the hand (hand-centered representation).
Based on our hypothesis and pilot data, we anticipated that participants in the two control-point group would learn the two force fields. Therefore, for this group only, we included a generalization phase following the exposure phase, in which we tested the alternative interpretations outlined above. As shown in Figure 1e-f, performance, measured by both the kinematic error and adaptation, was stable during this phase.
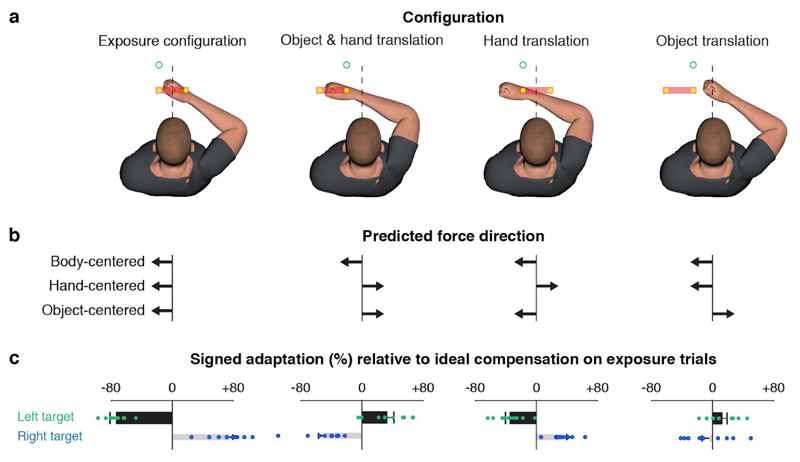
In the generalization phase, we used channel trials to measure the forces produced in four configurations (Fig. 2a), where: (1) the hand and object were in the original exposure configuration; (2) both the object and hand translated; (3) only the hand translated; and (4) only the object translated. Note that Figure 2a shows the generalization trials involving the left target. In trials involving the right target, the hand and/or object were translated in the opposite direction. In all configurations, the object still moved with the hand with the appropriate offset throughout the movement. Figure 2b shows the direction of force we expect the participants to generate for each possible representation (i.e., body-, hand-, or object-centered) for each configuration. All predictions are for the case in which the left and right targets/control points were associated with clockwise (CW) and counterclockwise (CCW), respectively. In the exposure configuration, we expect that participants will generate forces in the appropriate (in this case leftward) direction and this is consistent with all three possible representations (Fig. 2b left). Importantly, however, the pattern across the other three configurations is different for each possible representation.
Figure 2.
Control points are represented in an object-centered frame of reference. (a) Configurations used to examine generalization of learning for trials with the left target. For trials with the right target all translations were reversed. All these trials were channel trials. (b) Predictions of the direction of force according to the three possible representations. Note these are for the scenario in which the left and right targets/control points were associated with the CW and CCW fields, respectively. The predictions for the right target (not shown) are in the opposite directions. (c) Mean + 1 s.e.m. signed adaptation across participants (n = 10) relative to the ideal compensation on exposure trials. The sign of the bars, positive and negative, indicate compensatory forces appropriate for CCW and CW fields, respectively. Black and gray bars correspond to trials with the left and right targets, respectively. Dots represent data from individual participants.
The thick black bars in Figure 2c show the measured force compensation (signed adaptation) in all four configurations, relative to the force required to fully compensate for the force field in the exposure configuration. (The thin gray bars show the force compensation in trials involving the right target, in which all predicted forces are in the opposite direction.) Separate t-tests revealed that adaptation was significantly different from zero for both the left and right targets in the object-and-hand (two-tailed one-sample t-test, left target: 32.6% ± 9.2%, t(9) = 3.75, p = 0.005; right target: -48.0% ± 8.3%, t(9) = 6.12, p = 2e-4) and hand translation configurations (two-tailed one-sample t-test, left target: -34.4% ± 5.9%, t(9) = 6.14, p = 2e-4; right target: 34.5% ± 5.0%, t(9) = 7.28, p = 5e-5). Furthermore, the direction of adaptation in these configurations was only consistent with the object-based predictions. Although adaptation was not significantly different from zero for either target in the object translation configuration (two-tailed one-sample t-test, left target: 12.5% ± 6.5%, t(9) = 2.03, p = 0.072; right target: -3.5% ± 9.9%, t(9) = 0.38, p = 0.714), the sign of adaptation was again consistent with the object-based predictions. Note that the magnitude of force compensation (i.e., length of the bars), relative to the exposure configuration, decreased in all three generalization configurations, involving translation of the hand-and-object, object, or hand. This decrease is consistent with a large body of literature showing that motor learning is generally local with graded reduction with changes in context 2,37. Overall, these results clearly support the hypothesis that separate memories are formed for control points represented in object-centered coordinates.
Having established that participants can form separate motor memories for different control points, we asked whether this process is obligatory or flexible. Specifically, we tested whether separate memories are formed even when the dynamics experienced for the different control points are the same. In contrast to Experiment 1, here, a single motor memory would be sufficient for representing the dynamics of both control points and would also support efficient allocation of neural resources. Two groups were examined: participants in the opposing-field group (n = 8) experienced a different (opposing) force field for each control point whereas participants in the same-field group (n = 8) experienced the same force field for each control point. To assess the separation of motor memories, after learning we de-adapted one control point with null-field trials and then assessed the state of adaptation when controlling the other control point. If the memories are separate, then de-adapting one control point should not de-adapt the memory for the other control point.
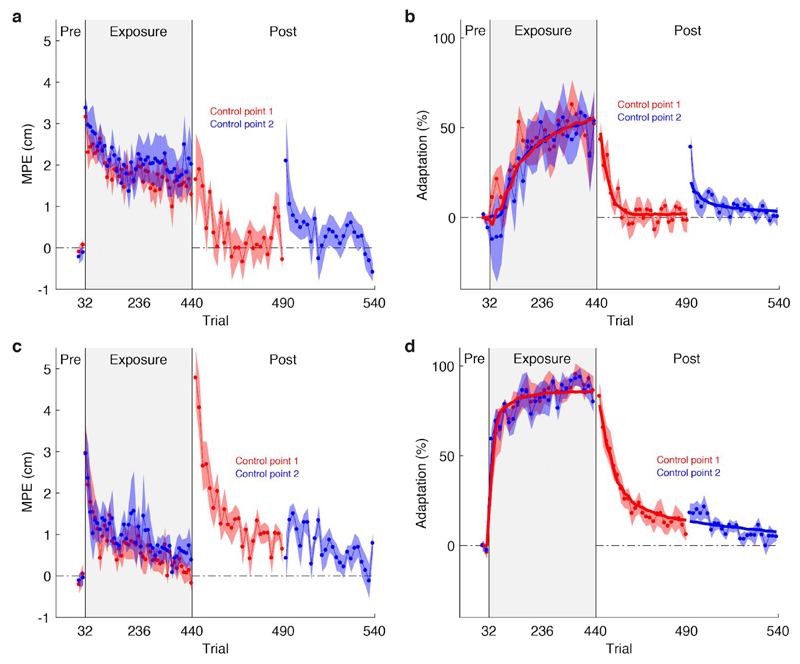
Both groups learned to compensate for the perturbation and, as expected, learning was greater for the group who learned the same field for both control points. By the final block of the exposure phase, there was no significant difference in adaptation between the opposing-field group (52.8% ± 12.1%) and the two-control point group (Experiment 1) (68.9% ± 5.9%) who performed the same task (two-tailed unpaired t-test, 16.1% ± 13.1%, t(16) = 1.27, p = 0.222). To assess whether de-adapting one memory led to de-adaptation of the other memory, we compared the mean of the last two channel trials in the post-exposure phase for the first control point with the first channel trial in the post-exposure phase for the second control point. For the group who learned opposing force fields, after de-adapting one control point, substantial adaptation re-emerged (Fig. 3b, two-tailed paired t-test, 37.6% ± 8.6%, t(7) = 4.69, p = 0.002) when controlling the other control point. Although this effect is primarily driven by the first channel trial, this first trial provides a critical test for the separation of memories. This suggests that separate representations existed for each control point. In contrast, for the group who experienced the same force field for both control points, when we de-adapted one control point there was minimal adaptation remaining (Fig. 3d, two-tailed paired t-test, 9.4% ± 7.8%, t(7) = 1.31, p = 0.232) when switching to the other control point. This is despite the greater adaptation observed in the same-field group, which increases the power to detect a difference in adaptation between the two control points during de-adaptation. This suggests a single representation existed for both control points in this case.
Figure 3.
The encoding of dynamics for different control points depends on the fields experienced. (a) MPE ± 1 s.e.m. and (b) adaptation ± 1 s.e.m. for each control point in the group that experienced opposing force fields at each control point (n = 8). Data in the pre-exposure and exposure phases were first averaged over blocks of eight trials. The post-exposure phase has been expanded for clarity. For simplicity, the sign of adaptation for control point 2 has been inverted. (c) & (d) are the same as (a) & (b) but for the group that experienced the same force field at each control point (n = 8). Solid lines in (b) and (d) show the mean switching state-space model fits across participants.
We fit several candidate models to the data and performed model comparison. Context-dependent state-space models (SSMs) have been used to account for motor learning of opposing perturbations 38–40. Briefly, these models assume that each context (force field) is associated with separate states of adaptation that are updated based on the error from the previous trial. Contexts can be coupled, such that errors in one context update the states associated with the other context, and states associated with both contexts contribute to the final output. However, critically, these models assume that the coupling between contexts is known in advance and remains fixed over time. Therefore, they predict that (1) with no coupling two separate memories will be formed, (2) with complete coupling a single memory will be formed, and (3) with partial coupling two overlapping memories will be formed. While it is difficult to account for our results with either no coupling or complete coupling, it is possible that a context-dependent state-space model with partial coupling could explain the data.
Context-dependent state-space models can be either single rate 33,41 or dual rate, in which the total adaptation involves two memory processes: (1) a fast process that both adapts and decays quickly and (2) a slow process that adapts and decays more gradually 24,42. We examined 7 variants of the context-dependent state-space model (Supplementary Table 1) 38,40, which vary as to whether single-rate or dual-rate states are included and also which states are coupled (see Methods for details).
As an alternative, we also developed a normative switching state-space model (SSSM) 43–45 of motor learning. The switching state-space model is a generalization of the state-space model to systems with multiple operating modes (here contexts), each of which can be associated with different, and even evolving, dynamics. On each trial, the system is in one context which determines both the dynamics experienced and the cues observed. Between trials, contexts switch stochastically. On each trial, the learner must infer the probability of each context (from control point cues and prediction errors) and use this information to partition control and learning between two context-specific dual-rate states (see Methods for details). Importantly, although the association between cues and contexts is deterministic (the control point perfectly predicts the force-field direction), this association must be learned through experience. We therefore reasoned that the formation of separate motor memories may arise from participants learning the association between cues and contexts. Critically, in the switching state-space model, the probabilities of cues (control points) given contexts (force fields) are therefore learned online.
We fit each model to the data from both the opposing- and same-field groups simultaneously, and performed model comparison using the Bayesian information criterion (BIC) (Supplementary Table 2). Although the context-dependent state-space models qualitatively capture the difference in post-washout adaptation between the same-field and opposing-field groups (Supplementary Figure 4), the switching state-space model fits the overall time course of adaptation and de-adaptation in the opposing-field group better (Fig. 3b & d, solid lines; slow and fast states shown in Supplementary Figure 5) and has much stronger support (ΔBIC of 112.4 relative to the next best model).
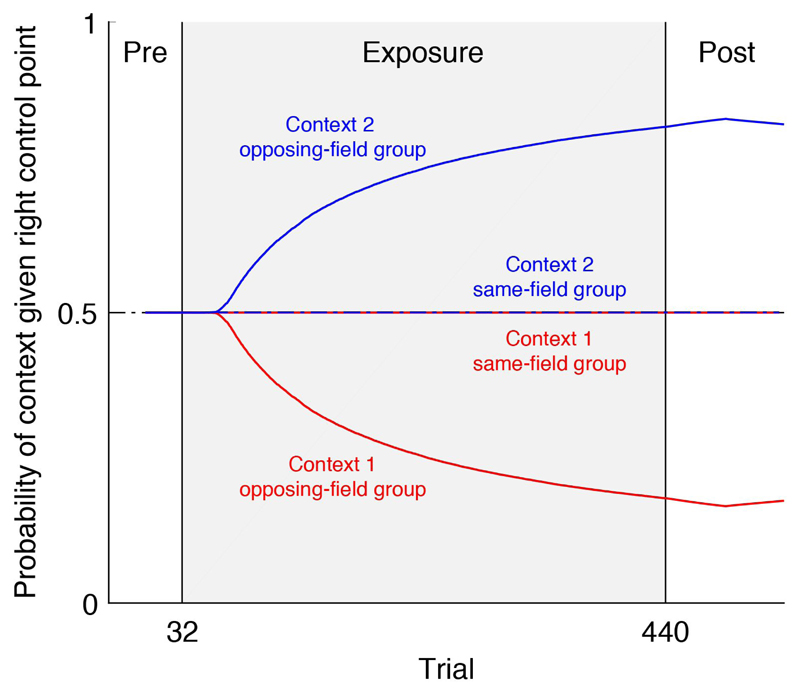
To understand how the switching state-space model works, we examined how the estimated probability of each context given a cue evolves for each group. As shown in Figure 4, at the start of the experiment both contexts are activated equally by the right control point (i.e., the probability of each context given the right control point is 0.5). Therefore, the model starts naive with respect to how control points relate to contexts. In the same-field group, both contexts are activated equally throughout the experiment, regardless of the control point, leading effectively to a single motor memory. In contrast, in the opposing-field group, each context becomes paired with a different control point, resulting in separate motor memories.
Figure 4.
Learning to associate contexts with cues in the switching state-space model. The switching state-space model estimates the probability of each context given the cue (plotted here for the right control point cue prior to movement). Following exposure to opposing force fields, participants learn to differentiate between the two contexts given the right control point. Participants trained on the same force field at each control point do not learn to differentiate between contexts, leading to a single motor memory. Traces show mean model fits across participants. The plot for the left control point (not shown) is the mirror image about the line 0.5.
Our results demonstrate that the motor system can form separate memories for different control points on the same object, even when the movements associated with these points are the same. By examining generalization, we found that learning was associated with control points on the object and not with the location of the object in extrinsic space or the location of the control point relative to the hand. Moreover, we found that the motor system only forms distinct memories if the dynamics of the control points differ, allowing efficient and flexible allocation of motor memory. Finally, we developed a probabilistic model of context-dependent motor adaptation that can account for such flexible parcellation of motor memories.
Humans have a remarkable capacity to manipulate objects with different dynamics, and a central focus of research in motor control has been to elucidate how the brain learns and represents these dynamics. To investigate how contextual information can be used to learn different dynamics, numerous studies have used opposing novel dynamics (e.g., viscous curl fields) that perturb the hand in opposite directions. This work has shown that the ability to learn opposing dynamics, when each is associated with a visual cue such as color of the cursor or background, is generally highly limited 28,29,36. Similarly, when lifting physical objects with different mass distributions, substantial interference is observed when each mass distribution is associated with a different visual geometric cue 12,13. In agreement with these findings, we show that when controlling a single control point, participants cannot learn opposing fields when they are associated with the location of peripheral visual cues that corresponded to the targets in the two control-point group.
Several studies have shown that opposing fields can be learned if the perturbed movement is preceded or followed by a separate movement that differs for each field, or if the perturbed movement is accompanied by a concurrent movement of the other hand that again differs for each field 23,36,46–48. Furthermore, previous studies have shown that opposing fields can be learned if they are associated with different states of the limb, as when the arm operates in a different region of the workspace for each field 29,49–51 a visual-proprioceptive discrepancy is introduced so that the perceived state of the limb is different for each field 29,52. Critically, in our experiment, and in contrast to these previous studies, veridical visual feedback of the hand was provided throughout the movement and the movement start and end points were the same for the opposing fields. Consequently, participants’ estimates of the state of the limb did not differ for the two fields. Therefore, we can be confident that it is the control of different points on the object that allows the formation of separate memories for different dynamical contexts. Moreover, we show clearly that the learning of each control point is linked to the location on the object.
Tool use generally involves controlling a specific location, or ‘control point’, on the tool as it interacts with the environment, such as the face of a hammer striking a nail or the eraser of a pencil rubbing a page. Skilled performance when using tools requires knowledge of the dynamics of the tool (relating applied force to motion) as well as contact mechanics 53,54, which may vary across control points. Most natural manipulation tasks involve a series of action phases separated by contact events 4,11. Consider, for example, grasping a pencil, lifting it out of a container and transporting it to a piece of paper, using it to erase a pencil mark, and then replacing it in the container. Here contact between the fingertips and pencil marks the end of the reach phase, contact between the pencil and paper marks the end of the transport phase, the breaking of contact between the pencil and paper marks the end of the erase phase, and so on. By comparing predicted and actual sensory signals associated with these contact events, the motor system can monitor task progress, launch corrective actions as needed, and calibrate internal models of objects and their interactions 4,11. Critically, both the control point on the object and the dynamics may change from phase to phase. For example, while erasing, the eraser end of the pencil is controlled and the dynamics include the friction between the eraser and paper. The ability to form separate motor memories for different control points may thus be an essential component of skilled object manipulation and tool use.
Recent studies in neurophysiology, neuroimaging and neuropsychology support the idea that tools are incorporated into a body schema. For example, Iriki and colleagues 55 trained monkeys to use a rake to retrieve a pellet of food that could not be reached by hand. Following tool use, the visual receptive fields of intraparietal neurons expanded beyond the space surrounding the hand to include the tip of the rake. Similar incorporation of tools is supported by studies in humans when making temporal order judgements of tactile stimuli on the hand 56. Importantly, such incorporation is seen only for the functional part of a tool 57 and a tool must be actively controlled for assimilation to occur 55,58. This suggests that the point being controlled on a tool determines how the body schema changes with tool use. Interestingly, the body schema is thought to consist of distinct neural modules which represent different body parts 59,60. It is therefore conceivable that different control points are assimilated by different body schema modules. Indeed, one may expect to find intraparietal neurons that respond differently for different control points on a tool. Furthermore, following incorporation of control points into the body schema, the effective 'state' of the body may include the control point, allowing different dynamics to be associated with different states linked to control points.
We found that the formation of distinct motor memories for different control points is not obligatory but only occurs if the dynamics for each control point are different. Therefore, the allocation of motor memory is both flexible and efficient. To explain this result, we developed a model of motor adaptation based on a switching state-space model 43–45, which is a generalization of the mixture-of-experts architecture in neural networks 61,62 to dynamical systems 63. The switching state-space model is, unlike these previous models, normative and therefore derived from first principles. Moreover, although the context-dependent state-space models could qualitatively capture the difference in post-washout adaptation between the same-field and opposing-field groups, model comparison convincingly selected this SSSM over existing models. Switching state-space models combine a hidden Markov model with linear dynamical systems and can be used to model systems with multiple discrete operating regimes, termed modes. A switching state-space model with one mode is a state-space model. The key innovation of the switching state-space model is that only one of the state-space modes is active at any one time and that over time the system can transition between modes. For example, a switching state-space model would be appropriate when handling different objects. The transition between the use of different objects can be considered as a Markov process specifying the probability of switching from one object to another (e.g., from kettle to cup) and the dynamics of each object can be different and change over time (e.g., as the kettle empties and the cup fills).
Within this framework, the problem for the sensorimotor system in our experiment is twofold. First, it must infer the current mode (e.g., context) and the state of the dynamics (e.g., force-field perturbation) based on the parameters of the switching state-space model. The expected perturbation is then a weighted sum of the perturbations expected for each mode, with weights given by the probabilities of each mode. Second, it must update the parameters of the switching state-space model online to ensure that these inferences are as accurate as possible. Here we provide evidence to support the idea that motor adaptation consists not only in state inference but also in parameter learning or system identification 64–67.
For simplicity, the switching state-space model we used had two modes. However, in general, switching state-space models can have any number of modes. Central to the performance of the model here is its capacity to learn through experience (i.e., during the experiment) the associations between cues (e.g., control points) and contexts (e.g., force fields) via parameter estimation. To reduce the degrees of freedom of the model, we restricted the simulation to only update the parameters (during the experiment) that determine the probabilities of the cues given the contexts. However, in general, all parameters of the model can be updated online. The fits of the switching state-space model suggest that participants only develop distinct memories for each control points if the dynamics are different (Fig. 4). In nonparametric extensions of this standard switching state-space model, the number of modes are learned through experience, rather than fixed a priori 68. Such models would allow the motor system to be efficient by recruiting additional context-dependent memories (i.e., modes) when control points have different dynamics and, conversely, removing modes that are redundant when control points have the same dynamics.
Our results suggest that objects are not represented by the motor system as holistic entities but are instead parcellated in a task-dependent manner according to control points. Interestingly, the results of the switching state-space model suggest that effective contextual cues, such as control points, do not necessarily engage distinct motor memories a priori. Instead, they engage online parameter learning processes that form distinct motor memories if and when needed.
Methods
Participants
Fifty neurologically intact participants (22 males and 28 females; age 28.2 ± 7.8, mean ± SD) were recruited to participate in four experiments, which had been approved by the Cambridge Psychology Research Ethics Committee. All participants provided written informed consent and were right-handed according to the Edinburgh handedness inventory 69.
Experimental Apparatus
All experiments were performed using a vBOT planar robotic manipulandum with virtual-reality system and air table 70. The position of the handle was measured using optical encoders sampled at 1 kHz and torque motors allowed forces to be generated on the handle. A monitor mounted above the vBOT projected virtual images into the plane of movement via a horizontal semi-silvered mirror (Fig. 1a). Participants were seated in front of the vBOT and grasped its handle with their right hand. A lamp was used to illuminate the hand below the mirror with the illumination adjusted so that both the vBOT, hand, arm and virtual images were clearly visible (Fig. 1b). This was done to ensure that participants always had an accurate estimate of the state of their hand and arm. The right forearm was supported on an air sled which constrained arm movements to the horizontal plane and reduced friction.
On each trial, the vBOT could generate forces associated with either a velocity-dependent curl field (field trials) or a force channel (channel trials). Alternatively, in the case of the null field, no forces were generated (null trials). For the curl field, the force generated on the hand was given by
| (1) |
where Fx, Fy, ẋ and ẏ are the forces and velocities at the handle in the x- and y-directions (mediolateral and anteroposterior, respectively). The field gain g was set to ±15 Ns/m and the sign of g specified whether the curl field was clockwise (CW) or counterclockwise (CCW). On channel trials, the hand was constrained to move along a straight line to the target. This was achieved by simulating forces associated with a stiff spring and damper, with the forces acting perpendicular to the long axis of the channel. A spring constant of 6,000 N/m and a damping coefficient of 5 Ns/m were used. Channel trials allowed the feedforward forces generated by participants to be measured orthogonal to the direction of reach 25,35.
In all experiments, participants first performed a familiarisation phase of between 96 and 128 trials, consisting of null-field trials and channel trials for each control point in a pseudorandomized order.
In order to have precise control over vision and dynamics in our experiment we used a robotic interface and virtual reality system. Importantly, a number of previous object manipulation studies using robotic manipulanda have been shown to produce similar results to experiment that use real-world physical objects 5,12,32,70,71.
Experiment 1: The encoding of motor memories by control points
Two control-points
In the two control-point condition, we investigated whether participants could learn opposing (CW and CCW) force fields when each field is associated with a different control point on the object. The paradigm consisted of pre-exposure, exposure, generalization and de-adaptation (“wash-out”) phases as detailed below.
Pre-exposure, exposure and de-adaptation phases
Participants (n = 10) grasped the handle of the vBOT and a rectangular virtual object (solid red rectangle 16 x 3 cm) was displayed centered on the hand (Fig. 1b). The position of the object translated with the hand. The object had two potential control points (0.4 cm radius green disks) ±7 cm lateral to the center of the object.
To start each trial, participants aligned the center of the object (indicted by a yellow cross) with the home position (0.5 cm radius circle) situated in the midline approximately 30 cm in front of the participant's chest. The trial started after the center point was within 0.3 cm of the home position and had remained below a speed of 0.5 cm/s for 100 ms. After a 0.2 s delay a target (0.5 cm radius circle) appeared 12 cm away (anteriorly along the y-axis) above either the left or right control point. A tone indicated that the participants should initiate a reaching movement to the target. Participants were instructed to move the corresponding control point to the target. That is, if the target was aligned with the left control point, they should move the left control point to the target, and conversely for the target aligned with the right control point. Crucially, because each target was aligned with its respective control point, the hand moved to the same location to attain both targets.
A trial ended when the control point had remained within 0.3 cm of the target for 50 ms. If the peak speed of the movement was less than 50 cm/s or more than 70 cm/s, a low-pitch tone sounded and a 'Too Slow' or 'Too Fast' message was displayed, respectively. At the end of each trial, the vBOT actively returned the hand to the home position.
After familiarization, participants performed blocks of 8 trials in which one of the trials (not the first) was randomly chosen as a channel trial and the remainder were either null trials or field trials. The paradigm consisted of a pre-exposure phase (4 blocks/32 trials), an exposure phase (52 blocks/416 trials), a generalization phase (71 blocks/568 trials; see below) and a de-adaptation phase (12 blocks/96 null-field trials). Each target appeared an equal number of times within a block in a pseudorandom order.
During the exposure phase, the location of the target (left or right) determined the direction of the force field (CW or CCW) applied during the movement. As such, the field direction was associated with the particular control point on the object (left or right) and its corresponding target (Fig. 1c). The direction of the force field for each control point was counterbalanced across participants. A 45 s rest break was given after blocks 12, 25, 38 and 51 of the exposure phase.
Generalization
The generalization phase (immediately after the exposure phase) was used to investigate the representation of the memories for the two force fields. Specifically, we tested whether the representations were object-centered (associated with the control points on the object), target-centered (associated with the target locations in space) or hand-centered (associated with the location of the targets/control points relative to the hand). The generalization phase included force field trials (to maintain adaptation) as well as channel trials (to monitor ongoing adaptation and examine generalization). To monitor adaptation, we used standard channel trials (as in the exposure phase). To examine generalization, participants performed channels trials during lateral translations (±14 cm) of either the object or the hand or both the object and the hand. This gave three kinds generalization trials (Fig. 2a).
During object and hand (O-H) translation trials, participants translated the hand and the object ±14 cm along the x-axis before the trial started. For rightward translations of the object and hand, the right target was cued and the participant moved the left control point towards the target (which was now aligned with the right target). The converse was true for leftward translations. Importantly, as on all trials in the study, the control points and targets were always aligned along the y-axis, thus requiring a straight movement.
During hand (H) translation trials, participants translated their hand ±14 cm along the x-axis while the object remained in the center of the workspace. For rightward translations of the hand, the right target was cued and the participant moved the right control point towards the target. The converse was true for leftward translations.
During object (O) translation trials, the object was visually translated ±14 cm along the x-axis while the hand remained in the center of the workspace. For rightward translations of the object, the right target was cued and the participant moved the left control point towards the target. The converse was true for leftward translations.
In all conditions, the object tracked the hand during the movement with the fixed offset associated with the particular generalization type maintained throughout the trial.
A 2.5 s delay was imposed at the start of each channel trial to allow time for the participant to translate their hand and/or the object, if required. A 15 s rest break was given every 9 blocks during the generalization phase starting at block 8. A block of fields trials (with no channel trials) followed each rest break to mitigate the effects of any time-dependent decay. Each of the channel types (2 to monitor ongoing adaptation and 6 for generalization) was repeated 8 times and there were 7 pure exposure blocks post-rest giving 64 + 7 = 71 blocks (568 trials).
Note that the familiarization phase in the two-control point condition included trials for each of the generalization conditions described above.
Single control-point
In the single control-point condition, we examined whether the visual targets alone could provide a contextual cue for learning. A separate group of participants (n = 8) performed the single control-point condition. As in two control-point condition (described above), the left and right control points were displayed on the object. Similarly, the left and right targets were displayed and were always associated with the particular field direction (CW or CCW). However, participants were instructed to move the central control point (yellow cross) on the object to a central target (which remained on the screen at all times) (Fig. 1d) and to ignore the lateral targets. Participants were thus required to control a single control point. The paradigm consisted of the same pre-exposure (4 blocks/32 trials), exposure (51 blocks/408 trials), and de-adaptation (12 blocks/96 trials) phases as in two control-point condition. However, in this case, the generalization phase was omitted.
Gaze fixation control
During target-directed reaches, people tend to fixate the target 72–74. The gaze fixation experiment (n = 8) was performed to exclude the possibility that gaze direction, rather than the control point on the object, was the contextual cue responsible for adaptation to opposing force fields.
An EyeLink 1000 eye tracker was used to track the position of the left eye at 500 Hz. The eye tracker was mounted at an oblique angle between the handle of the manipulandum and a transparent reflective sheet of plastic that was used to project visual feedback (replacing the semi-silvered mirror). A forehead rest was used to stabilize the head. The eye-tracker was calibrated at the start of the experiment and after every rest break using a 9-point grid.
The paradigm include both fixation and free-gaze trials. On fixation trials, participants had to fixate a small cross (located 8 cm above the home position) while performing the task (moving the left or right control point to left or right target, respectively). Because movements were being guided by peripheral vision, the spatial tolerance of the target was increased to 0.6 cm. If the participant broke fixation (> 2 cm) the trial was aborted and repeated. The central control point on the object was not displayed in order to prevent participants from using it to guide the movement toward the fixation point. The home position was indicated by a rectangular frame which was visible at all times during the experiment. On free-gaze trials, no fixation cross was displayed and eye movements were unconstrained.
After familiarization (as described above), participants performed a fixation pre-exposure phase (4 blocks/32 trials), a fixation exposure phase (65 blocks/520 trials), a free-gaze exposure phase (64 blocks/512 trials) and finally a free-gaze de-adaptation phase (12 blocks/96 trials). The direction of the force field associated with each control point was counterbalanced across participants. Each block had the same structure as in the two control point condition, with 7 exposure trials and 1 channel trial.
A 45 s rest break was given every 13 blocks during the exposure phase starting at block 12. A block of fields trials (with no channel trials) followed each rest break to mitigate the effects of any time-dependent decay.
Uniform object control
The object used in the main experiment consisted of different visual elements (green circular control points embedded in a red rectangle) that could conceivably be interpreted as distinct objects. We therefore repeated the exposure phase in the two control-point group using an object that no longer contained different visual elements. A separate group of participants (n = 8) controlled a new uniform object with control points that were not discriminable from the rest of the object by color (Supplementary Figure 3). The rectangle was removed from the original object and the control points (0.4 cm radius green disks) were connected by a bar (solid green rectangle 14 x 0.6 cm) that was the same color as the control points. Importantly, these control points were the same size and in the same location as those of the original experiment. We reduced the size of the central cross so that it would fit inside the connecting bar.
As in two control-point experiment (described above), participants moved the corresponding control point to the displayed target, which was always associated with a particular field direction (CW or CCW). The paradigm consisted of the same pre-exposure (4 blocks/32 trials), exposure (51 blocks/408 trials), and de-adaptation (12 blocks/96 trials) phases as in single control-point experiment.
Experiment 2: Are separate motor memories obligatory for different control points?
This experiment was performed to investigate whether separate motor memories are formed even when the dynamics experienced at the two control points on the object are the same.
After familiarization, participants performed a pre-exposure phase, an exposure phase and a de-adaptation phase. The pre-exposure phase (4 blocks/32 trials) and exposure phases (51 blocks/408 trials) were the same as in Experiment 1. Participants performed blocks of 8 trials consisting of 7 null (pre-exposure) or field (exposure) trials and one channel trial. In the exposure phase, half the participants (n = 8) experienced opposing fields at each control point (as in Experiment 1) and the other half (n = 8) experienced the same field at each control point. In both the opposing-field and same-field conditions, the direction of the fields was counterbalanced across participants. A 45 s rest break was given after blocks 12, 25 and 38 of the exposure phase. A block of fields trials (with no channel trials) followed each rest break to mitigate the effects of any time-dependent decay.
The exposure phase was followed by 50 blocks of de-adaptation, with each block consisting of 1 null-field trial and 1 channel trial. Importantly, one control point was cued throughout the first half of the de-adaptation phase (first 25 blocks/50 trials) and the other control point was cued throughout the second half (last 25 blocks/50 trials). The order in which each control point (left or right) was cued was counterbalanced across participants.
If the dynamics at both control points are encoded by a single representation, de-adaptation at one control point should also lead to de-adaptation at the other control point. Alternatively, if the representations are separate, de-adaptation at one control point should have minimal effect on the representation associated with the other control point.
Data Analysis
Data analysis was performed using MATLAB R2017a. Two measures of performance were calculated. On exposure and null-field trials, we calculated the maximum distance between the path of the hand and a straight line connecting the start position and the target (maximum perpendicular error, MPE). On channel trials, we calculated the percentage of the force field that was compensated for (adaptation) by regressing the actual forces Fa(t) generated by participants in the channel on the ideal forces Fi(t) that would fully compensate for the force field in an exposure trial (defined in equation 1):
| (2) |
| (3) |
where b is the regression coefficient and t is the discrete time step in the trial. The offset of the regression was constrained to zero. For this analysis, we used the portion of the movement where the hand velocity was greater than 1 cm/s. To combine maximum perpendicular error (MPE) and adaptation results across participants, data from individual participants was sign-adjusted according to the direction of the field.
To identify changes in MPE and adaptation over the course of multiple experiments, mixed-design ANOVAs and paired t-tests were performed. Comparisons of adaptation between experiments were performed using between-subjects ANOVAs and unpaired t-tests. All statistical tests were two-sided with significance set to p < 0.05. Where values are reported they represent mean ± s.e.m..
Models
We fit two classes of model to Experiment 2. The first class is a deterministic, context-dependent state-space model based on 38–40. The second class is a probabilistic switching state-space model. We did not fit the models to Experiment 1 as this experiment was not designed to distinguish between the model classes. Note, however, that and the initial part of Experiment 1 is identical to the initial part for the opposing field group in Experiment 2.
Context-dependent state-space model
We used a context-dependent state-space model that includes separate states for different contexts and also different rates of adaptation (slow versus fast adaptive processes). In the current study, there are 2 contexts (the left and right control points) and each context can include states that update with slow and fast rates. This gives a total of 4 states (two contexts and two rates) which can be represented by the elements of a state vector
| (4) |
where superscripts represent which context the state is associated with (e.g., 1 = left and 2 = right control points) and the subscripts represent the slow and fast adaptation processes. The motor output on trial t is a weighted sum of the elements in the state vector, with the weighting determined by the context:
| (5) |
where the context weighting vector, c, varies according to the context for the trial (left or right control point). The error on a trial is the difference between the motor output and the task perturbation:
| (6) |
In the current study, the task perturbation, f, is zero for null-field trials, +1 for CW field trials and -1 for CCW field trials. The state vector is updated across trials:
| (7) |
where ⊙ represents element-wise multiplication. Trial-by-trial decay is determined by the retention vector A. Error-dependent adaptation of states is determined by the context weighting vector and the learning-rate vector B.
We considered 7 variants of the model which determine the way A, B and c are parameterized (Supplementary Table 1). The models vary as to whether there is a single context-dependent state (SSM 1), a slow/fast context-independent state and a fast/slow context-dependent state (SSMs 2-4), or both fast and slow context-dependent states (SSMs 5-7). For context-dependent states, the values in the context weighting vector determine the coupling (if any) between contexts. Models which include parameters cs and cf can have coupling between the contexts for the slow and/or fast processes, respectively.
Switching state-space model
The generative model
Here we develop a probabilistic switching state-space model that allows the sensorimotor system to optimally partition learning across contexts. We assume that the environment consists of distinct contexts which switch in a probabilistic manner according to a hidden Markov model (Supplementary Figure 6). Each context is associated with its own perturbations which evolve according to linear-Gaussian dynamics. We assume that participants possess an internal generative model of perturbations that matches the environment. We characterize this model as a switching state-space model, a generalization of the state-space model to systems with multiple operating regimes or modes. Switching state-space models define a probability density over a time series of discrete and continuous states. Here the discrete states represent contexts, and the continuous states represent perturbations. We implement the model with two contexts, although the extension to more than two contexts is straightforward.
On trial t, the environment is in one of two contexts, ct ∈ {1, 2}, and between trials the context either remains the same or switches in a stochastic manner. The context transition probabilities are defined by the matrix π, where
| (8) |
To reduce the number of free parameters in the model, we assume that the context remains the same or switches with equal probability, that is πij = 0.5 for all i, j. This is consistent with the exposure phase of our experiment in which each force field is presented with equal frequency and in a pseudorandom order.
On each trial, the context gives rise to one of two observable cues, qt ∈ {1, 2}, corresponding to the location of the control point. The matrix ϕ defines the cue emission probability
| (9) |
The perturbations in each context evolve independently according to linear-Gaussian dynamics, as defined by the state transition function
| (10) |
where is a vector of slow and fast states (subscripts) for contexts 1 and 2 (superscripts), A is a diagonal matrix of the form diag (as, af, as, af) and wt is zero-mean Gaussian process noise with covariance Q = diag(qs, qf, qs, qf). Thus we implement a probabilistic context-dependent dual-rate model.
The context determines which perturbations are observed, as defined by the output function
| (11) |
where C(1) = [1 1 0 0] is the observation vector for context 1, C(2) = [0 0 1 1] is the observation vector for context 2 and υt is zero-mean Gaussian observation noise with variance r.
State inference
To operate effectively, the sensorimotor system must keep track of perturbations in the environment, as well as the contexts in which they occur. However, both perturbations and contexts are hidden variables, which must be inferred from a sequence of observations {y1:t, q1:t}. Several techniques have been developed to infer the joint state, {ct, xt}, of a switching state-space model 43–45,63,75,76. Here we focus on a technique known as the generalized pseudo-Bayesian estimator of order 1 (GPB1) 76, which we adapt for a switching state-space model in which the context, ct, emits observable cues qt. GPB1 is an assumed density filtering method that approximates the exact posterior of the state (a mixture of Gaussians with MT components, where M is the number of modes and T is the number of trials) with a single Gaussian.
To maintain an estimate of the state, two Kalman filters operate in parallel (Supplementary Figure 6). Each filter has a different observation vector, C(j) (defined above), and is thus specialized for a different context; all remaining parameters are the same for both filters. On trial t, both filters operate on the same Gaussian estimate of the continuous state from the previous trial, with mean x̂t−1|t−1 and covariance Vt−1|t−1, to generate a Gaussian estimate of the continuous state on the current trial, with mean and covariance This produces a mixture of Gaussians with mixing weights given by the probability of each context Because the number of possible context sequences doubles with every trial, the number of components in this mixture will also double if no approximations are made, making inference intractable. Therefore, after each trial, the mixture of Gaussians is approximated by a single Gaussian via moment matching (Supplementary Figure 6), rendering inference tractable but approximate.
Upon observation of the contextual cue qt, but prior to movement, the probability of each context (assuming equiprobable context transitions) is
| (12) |
The predicted observation used for control is
| (13) |
where is the observation predicted for each context. We assume that the predicted observation is expressed through a motor action that is corrupted by zero-mean Gaussian noise (see Model Fitting).
After the movement, once the perturbation yt has been observed, the likelihood of each context is
| (14) |
Here we use to denote the PDF for the normal distribution with mean and variance where is the standard Kalman filter innovation covariance. The final probability of each context is given by Bayes' rule:
| (15) |
Finally, a single Gaussian estimate of the perturbations is obtained via moment matching:
| (16) |
| (17) |
Parameter learning
To perform state inference, the sensorimotor system must set the parameters, θ = {A, Q, C(1), C(2), r, π, ϕ}, of the switching state-space model. Importantly, these parameters need not be fixed but may be learned online. In general, the sensorimotor system could learn all of these parameters online. However, to reduce the degrees of freedom of the model for our dataset, we assume that the sensorimotor system only learns the cue emission probabilities and that all other parameter estimates are fixed.
To learn the cue emission probabilities, we perform expectation maximization (EM), an iterative method for obtaining maximum likelihood estimates of unknown parameters in probabilistic models involving latent variables 77. We utilize a sufficient-statistics formulation of EM that supports online parameter learning. A detailed description of this method can be found in 78,79. Here we provide a brief outline as applied to our perturbation study.
The algorithm iterates between an E step, in which the joint probability of c and q is estimated, and an M step, in which the joint probability of c and q is normalized to obtain the probability of q given c.
Stochastic E step
The aim of the E step is to count the number of times that each combination of c and q co-occur. If both ct and qt were known, this would involve summing 2 × 2 matrices, each of which would have a single unity entry defined by the indicator function
| (18) |
However, because ct is a latent variable, 𝓼t(qt, ct) can only be estimated in the form of an expectation:
| (19) |
Here, and elsewhere, the hat notation is used to indicate an estimated value. After each new set of observations, {qt, yt}, the quantity 𝓢t–1 is updated:
| (20) |
with 𝓢0 initialized to a matrix of zeros. In general, the expectations in equation (19) will show trial-to-trial variability due to noise. Therefore, an adaptive stepsize, ηt = α/(α + t – 1), is used to average the sequence of estimates and promote convergence 80. Because the stepsize decreases to zero according to the requirements of stochastic approximation theory, and the effects of noise are eliminated in the long run 81. Increasing α slows the rate at which the stepsize decreases, placing greater weight on more recent observations compared with older observations. We treat α as a free parameter of the model.
It is possible to compute smoothed estimates of the sufficient statistics in equation (18) online using forward smoothing recursions 82. However, in general, exact computation of these smooth statistics is intractable, requiring sequential Monte Carlo sampling techniques 83. For simplicity, we only compute filtered estimates of the sufficient statistics, as in equation (19).
M step
To calculate ϕ̂t, we normalize 𝓢t by dividing each element by its corresponding column sum to ensure that the probability of either cue being emitted in each context is 1. Note all elements of 𝓢t must be nonzero for the solution of the EM algorithm to be well defined (otherwise some probabilities will always remain zero). Therefore, we omit the M step for the first 8 trials to ensure that both contextual cues have been observed.
Importantly, to infer the probability of each context given an observed cue, the model of how contexts emit cues (equation 9) is inverted (equation 12).
Model implementation
We applied the above inference and learning algorithms to a sequence of noiseless observations, y1:T, assigned values of 0 (null-field trials) or ± 1 (force-field trials), corresponding to the actual perturbations delivered by the robot. We also examined adding zero-mean Gaussian noise (variance r) to the delivered sequence of perturbations to include observation noise. However, because the observation noise that participants perceived is unknown to us, it must be marginalized out (e.g., using Monte Carlo integration). The inclusion of observation noise also results in a stochastic objective function, which requires alternative parameter optimization techniques. For simplicity, we only report fits to noiseless observations as the addition of observation noise did not qualitatively change the model fit or the outcome of model comparison.
To update the estimate of the continuous state, we applied the standard Kalman filter recursive equations 84. The prior estimate of the continuous state was initialized with mean, x̂0|0, and covariance, V0|0, equal to zero and the mean steady-state covariance matrix across Kalman filters, respectively. The prediction error of each Kalman filter, was set to zero on channel trials.
We set C(j) and π as described above and initialized ϕ̂0 as a symmetric matrix
| (21) |
where β = 0.5 + ϵ and ϵ = 10−6. Thus the learner starts naive with respect to how cues relate to contexts. ϕ̂t was updated recursively using the online EM algorithm. The small amount of jitter, ϵ, was added to allow symmetry breaking. We used q = 1 and q = 2 for the left and right control points, respectively.
Model Fitting
We simulated each model separately for each participant using the particular sequence of cues they observed. We then calculated the mean model data across participants for each group and each control point. We assume that adaptation measured on channel trials represents predicted observations that have been corrupted by Gaussian motor noise. Maximum likelihood estimates of the free parameters of the models (Supplementary Table 2) were therefore obtained by minimizing the sum-of-squared errors between the mean model data (equation (5) for the SSMs and equation (13) for the SSSM) and the mean experimental data measured on channel trials (b in equation (2)). As each model involved fitting both same- and opposing-field groups jointly with the same set of parameters, we chose to fit the mean adaptation data across participants to reduce variability in the dataset.
Model comparison
Model selection was performed using the Bayesian Information Criterion (BIC):
| (22) |
where n (204) is the number of data points, k is the number of free parameters and the constant does not depend on the model. The first term in the BIC penalizes underfitting, whereas the second term penalizes model complexity, as measured by the number of free parameters in the model. Taking the difference in BIC values for two competing models approximates half the log of the Bayes' factor 85. A BIC difference of greater than 4.6 (a Bayes factor of greater than 10) is considered to provide strong evidence in favour of the model with the lower BIC value 86.
Supplementary Material
Acknowledgements
We thank Goda Žalalytė and Alex Pantelides for assistance with the experiments and Sumeetpal Singh for advice on the model. We thank the Wellcome Trust, the Royal Society (Noreen Murray Professorship in Neurobiology to D.M.W.), the Engineering and Physical Sciences Research Council and the Canadian Institutes of Health Research for support. The funders had no role in the conceptualization, design, data collection, analysis, decision to publish, or preparation of the manuscript.
Footnotes
Author contributions
All authors conceived and designed the experiments. JH performed the experiments and developed and fit the switching state-space model. All authors wrote the paper, discussed the results and edited the manuscript.
Competing interests
The authors declare no competing interests.
Code availability
The code used to generate the data in this study is available from the corresponding author on request.
Data availability
Data that support the findings of this study are available from the corresponding author on request.
References
- 1.Shadmehr R, Smith MA, Krakauer JW. Error correction, sensory prediction, and adaptation in motor control. Annu Rev Neurosci. 2010;33:89–108. doi: 10.1146/annurev-neuro-060909-153135. [DOI] [PubMed] [Google Scholar]
- 2.Wolpert DM, Diedrichsen J, Flanagan JR. Principles of sensorimotor learning. Nat Rev Neurosci. 2011;12:739–751. doi: 10.1038/nrn3112. [DOI] [PubMed] [Google Scholar]
- 3.Johansson RS, Westling G. Roles of glabrous skin receptors and sensorimotor memory in automatic control of precision grip when lifting rougher or more slippery objects. Exp Brain Res. 1984;56:550–564. doi: 10.1007/BF00237997. [DOI] [PubMed] [Google Scholar]
- 4.Johansson RS, Flanagan JR. Coding and use of tactile signals from the fingertips in object manipulation tasks. Nat Rev Neurosci. 2009;10:345–359. doi: 10.1038/nrn2621. [DOI] [PubMed] [Google Scholar]
- 5.Ingram JN, Wolpert DM. Naturalistic approaches to sensorimotor control. Prog Brain Res. 2011;191:3–29. doi: 10.1016/B978-0-444-53752-2.00016-3. [DOI] [PubMed] [Google Scholar]
- 6.Westling G, Johansson RS. Factors influencing the force control during precision grip. Exp Brain Res. 1984;53:277–284. doi: 10.1007/BF00238156. [DOI] [PubMed] [Google Scholar]
- 7.Johansson RS, Westling G. Coordinated isometric muscle commands adequately and erroneously programmed for the weight during lifting task with precision grip. Exp Brain Res. 1988;71:59–71. doi: 10.1007/BF00247522. [DOI] [PubMed] [Google Scholar]
- 8.Gordon AM, Westling G, Cole KJ, Johansson RS. Memory representations underlying motor commands used during manipulation of common and novel objects. J Neurophysiol. 1993;69:1789–1796. doi: 10.1152/jn.1993.69.6.1789. [DOI] [PubMed] [Google Scholar]
- 9.Flanagan JR, Beltzner MA. Independence of perceptual and sensorimotor predictions in the size--weight illusion. Nat Neurosci. 2000;3:737–741. doi: 10.1038/76701. [DOI] [PubMed] [Google Scholar]
- 10.Baugh LA, Kao M, Johansson RS, Flanagan JR. Material evidence: interaction of well-learned priors and sensorimotor memory when lifting objects. J Neurophysiol. 2012;108:1262–1269. doi: 10.1152/jn.00263.2012. [DOI] [PubMed] [Google Scholar]
- 11.Flanagan JR, Bowman MC, Johansson RS. Control strategies in object manipulation tasks. Curr Opin Neurobiol. 2006;16:650–659. doi: 10.1016/j.conb.2006.10.005. [DOI] [PubMed] [Google Scholar]
- 12.Fu Q, Santello M. Context-dependent learning interferes with visuomotor transformations for manipulation planning. J Neurosci. 2012;32:15086–15092. doi: 10.1523/JNEUROSCI.2468-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Fu Q, Santello M. Retention and interference of learned dexterous manipulation: interaction between multiple sensorimotor processes. J Neurophysiol. 2015;113:144–155. doi: 10.1152/jn.00348.2014. [DOI] [PubMed] [Google Scholar]
- 14.Wolpert DM, Flanagan JR. Q&A: Robotics as a tool to understand the brain. BMC Biol. 2010;8:92. doi: 10.1186/1741-7007-8-92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Shadmehr R, Mussa-Ivaldi FA. Adaptive representation of dynamics during learning of a motor task. J Neurosci. 1994;14:3208–3224. doi: 10.1523/JNEUROSCI.14-05-03208.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Dingwell JB, Mah CD, Mussa-Ivaldi FA. Manipulating objects with internal degrees of freedom: evidence for model-based control. J Neurophysiol. 2002;88:222–235. doi: 10.1152/jn.2002.88.1.222. [DOI] [PubMed] [Google Scholar]
- 17.Dingwell JB, Mah CD, Mussa-Ivaldi FA. Experimentally confirmed mathematical model for human control of a non-rigid object. J Neurophysiol. 2004;91:1158–1170. doi: 10.1152/jn.00704.2003. [DOI] [PubMed] [Google Scholar]
- 18.Nagengast AJ, Braun DA, Wolpert DM. Optimal control predicts human performance on objects with internal degrees of freedom. PLoS Comput Biol. 2009;5:e1000419. doi: 10.1371/journal.pcbi.1000419. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Nasseroleslami B, Hasson CJ, Sternad D. Rhythmic manipulation of objects with complex dynamics: predictability over chaos. PLoS Comput Biol. 2014;10:e1003900. doi: 10.1371/journal.pcbi.1003900. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Flanagan JR, Wing AM. The role of internal models in motion planning and control: evidence from grip force adjustments during movements of hand-held loads. J Neurosci. 1997;17:1519–1528. doi: 10.1523/JNEUROSCI.17-04-01519.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ahmed AA, Wolpert DM, Flanagan JR. Flexible representations of dynamics are used in object manipulation. Curr Biol. 2008;18:763–768. doi: 10.1016/j.cub.2008.04.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Danion F, Diamond JS, Flanagan JR. The role of haptic feedback when manipulating nonrigid objects. J Neurophysiol. 2012;107:433–441. doi: 10.1152/jn.00738.2011. [DOI] [PubMed] [Google Scholar]
- 23.Sheahan HR, Franklin DW, Wolpert DM. Motor Planning, Not Execution, Separates Motor Memories. Neuron. 2016;92:773–779. doi: 10.1016/j.neuron.2016.10.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Smith MA, Ghazizadeh A, Shadmehr R. Interacting adaptive processes with different timescales underlie short-term motor learning. PLoS Biol. 2006;4:e179. doi: 10.1371/journal.pbio.0040179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Scheidt RA, Reinkensmeyer DJ, Colborn MA, Rymer WZ, Mussa-Ivaldi FA. Persistence of motor adaptation during constrained, multi-joint, arm movements. J Neurophysiol. 2000;84:853–862. doi: 10.1152/jn.2000.84.2.853. [DOI] [PubMed] [Google Scholar]
- 26.Cothros N, Wong JD, Gribble PL. Are there distinct neural representations of object and limb dynamics? Exp Brain Res. 2006;173:689–697. doi: 10.1007/s00221-006-0411-0. [DOI] [PubMed] [Google Scholar]
- 27.Kluzik J, Diedrichsen J, Shadmehr R, Bastian AJ. Reach adaptation: what determines whether we learn an internal model of the tool or adapt the model of our arm? J Neurophysiol. 2008;100:1455–1464. doi: 10.1152/jn.90334.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Gandolfo F, Mussa-Ivaldi FA, Bizzi E. Motor learning by field approximation. Proceedings of the National Academy of Sciences. 1996;93:3843–3846. doi: 10.1073/pnas.93.9.3843. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Howard IS, Wolpert DM, Franklin DW. The effect of contextual cues on the encoding of motor memories. J Neurophysiol. 2013;109:2632–2644. doi: 10.1152/jn.00773.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Salimi I, Hollender I, Frazier W, Gordon AM. Specificity of internal representations underlying grasping. J Neurophysiol. 2000;84:2390–2397. doi: 10.1152/jn.2000.84.5.2390. [DOI] [PubMed] [Google Scholar]
- 31.Bursztyn LL, Flanagan JR. Sensorimotor memory of weight asymmetry in object manipulation. Exp Brain Res. 2008;184:127–133. doi: 10.1007/s00221-007-1173-z. [DOI] [PubMed] [Google Scholar]
- 32.Ingram JN, Howard IS, Flanagan JR, Wolpert DM. Multiple grasp-specific representations of tool dynamics mediate skillful manipulation. Curr Biol. 2010;20:618–623. doi: 10.1016/j.cub.2010.01.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ingram JN, Howard IS, Flanagan JR, Wolpert DM. A single-rate context-dependent learning process underlies rapid adaptation to familiar object dynamics. PLoS Comput Biol. 2011;7:e1002196. doi: 10.1371/journal.pcbi.1002196. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Ingram JN, Flanagan JR, Wolpert DM. Context-dependent decay of motor memories during skill acquisition. Curr Biol. 2013;23:1107–1112. doi: 10.1016/j.cub.2013.04.079. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Milner TE, Franklin DW. Impedance control and internal model use during the initial stage of adaptation to novel dynamics in humans. J Physiol. 2005;567:651–664. doi: 10.1113/jphysiol.2005.090449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Howard IS, Ingram JN, Franklin DW, Wolpert DM. Gone in 0.6 seconds: the encoding of motor memories depends on recent sensorimotor States. J Neurosci. 2012;32:12756–12768. doi: 10.1523/JNEUROSCI.5909-11.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Berniker M, Franklin DW, Flanagan JR, Wolpert DM, Kording K. Motor learning of novel dynamics is not represented in a single global coordinate system: evaluation of mixed coordinate representations and local learning. J Neurophysiol. 2014;111:1165–1182. doi: 10.1152/jn.00493.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Nozaki D, Scott SH. Multi-compartment model can explain partial transfer of learning within the same limb between unimanual and bimanual reaching. Exp Brain Res. 2009;194:451–463. doi: 10.1007/s00221-009-1720-x. [DOI] [PubMed] [Google Scholar]
- 39.Lee JY, Schweighofer N. Dual adaptation supports a parallel architecture of motor memory. J Neurosci. 2009;29:10396–10404. doi: 10.1523/JNEUROSCI.1294-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Kim S, Oh Y, Schweighofer N. Between-Trial Forgetting Due to Interference and Time in Motor Adaptation. PLoS One. 2015;10:e0142963. doi: 10.1371/journal.pone.0142963. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Thoroughman KA, Shadmehr R. Learning of action through adaptive combination of motor primitives. Nature. 2000;407:742–747. doi: 10.1038/35037588. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Trewartha KM, Garcia A, Wolpert DM, Flanagan JR. Fast but fleeting: adaptive motor learning processes associated with aging and cognitive decline. J Neurosci. 2014;34:13411–13421. doi: 10.1523/JNEUROSCI.1489-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Ackerson G, Fu K. On state estimation in switching environments. IEEE Trans Automat Contr. 1970;15:10–17. [Google Scholar]
- 44.Chang CB, Athans M. State Estimation for Discrete Systems with Switching Parameters. IEEE Trans Aerosp Electron Syst. 1978;AES-14:418–425. [Google Scholar]
- 45.Shumway RH, Stoffer DS. Dynamic Linear Models With Switching. J Am Stat Assoc. 1991;86:763. doi: 10.1080/01621459.1991.10475086. [DOI] [PubMed] [Google Scholar]
- 46.Howard IS, Wolpert DM, Franklin DW. The Value of the Follow-Through Derives from Motor Learning Depending on Future Actions. Curr Biol. 2015;25:397–401. doi: 10.1016/j.cub.2014.12.037. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Nozaki D, Kurtzer I, Scott SH. Limited transfer of learning between unimanual and bimanual skills within the same limb. Nat Neurosci. 2006;9:1364–1366. doi: 10.1038/nn1785. [DOI] [PubMed] [Google Scholar]
- 48.Yokoi A, Hirashima M, Nozaki D. Gain field encoding of the kinematics of both arms in the internal model enables flexible bimanual action. J Neurosci. 2011;31:17058–17068. doi: 10.1523/JNEUROSCI.2982-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Richter S, Jansen-Osmann P, Konczak J, Kalveram K-T. Motor adaptation to different dynamic environments is facilitated by indicative context stimuli. Psychol Res. 2004;68:245–251. doi: 10.1007/s00426-003-0140-y. [DOI] [PubMed] [Google Scholar]
- 50.Yeo S-H, Wolpert DM, Franklin DW. Coordinate Representations for Interference Reduction in Motor Learning. PLoS One. 2015;10:e0129388. doi: 10.1371/journal.pone.0129388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Hwang EJ, Smith MA, Shadmehr R. Dissociable effects of the implicit and explicit memory systems on learning control of reaching. Exp Brain Res. 2006;173:425–437. doi: 10.1007/s00221-006-0391-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Hirashima M, Nozaki D. Distinct motor plans form and retrieve distinct motor memories for physically identical movements. Curr Biol. 2012;22:432–436. doi: 10.1016/j.cub.2012.01.042. [DOI] [PubMed] [Google Scholar]
- 53.Chib VS, Krutky MA, Lynch KM, Mussa-Ivaldi FA. The separate neural control of hand movements and contact forces. J Neurosci. 2009;29:3939–3947. doi: 10.1523/JNEUROSCI.5856-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Casadio M, Pressman A, Mussa-Ivaldi FA. Learning to push and learning to move: the adaptive control of contact forces. Front Comput Neurosci. 2015;9:118. doi: 10.3389/fncom.2015.00118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Iriki A, Tanaka M, Iwamura Y. Coding of modified body schema during tool use by macaque postcentral neurones. Neuroreport. 1996;7:2325–2330. doi: 10.1097/00001756-199610020-00010. [DOI] [PubMed] [Google Scholar]
- 56.Yamamoto S, Kitazawa S. Sensation at the tips of invisible tools. Nat Neurosci. 2001;4:979–980. doi: 10.1038/nn721. [DOI] [PubMed] [Google Scholar]
- 57.Farnè A, Iriki A, Làdavas E. Shaping multisensory action–space with tools: evidence from patients with cross-modal extinction. Neuropsychologia. 2005;43:238–248. doi: 10.1016/j.neuropsychologia.2004.11.010. [DOI] [PubMed] [Google Scholar]
- 58.Witt JK, Proffitt DR, Epstein W. Tool use affects perceived distance, but only when you intend to use it. J Exp Psychol Hum Percept Perform. 2005;31:880–888. doi: 10.1037/0096-1523.31.5.880. [DOI] [PubMed] [Google Scholar]
- 59.Haggard PW, Wolpert DM. Disorders of Body Scheme. Higher-Order Motor Disorders. 2004:7. [Google Scholar]
- 60.Benton AL. Right-left discrimination and finger localization: Development and pathology. 1959 doi: 10.1001/archneurpsyc.1955.02330180001001. [DOI] [PubMed] [Google Scholar]
- 61.Jacobs RA, Jordan MI, Nowlan SJ, Hinton GE. Adaptive Mixtures of Local Experts. Neural Comput. 1991;3:79–87. doi: 10.1162/neco.1991.3.1.79. [DOI] [PubMed] [Google Scholar]
- 62.Wolpert DM, Kawato M. Multiple paired forward and inverse models for motor control. Neural Netw. 1998;11:1317–1329. doi: 10.1016/s0893-6080(98)00066-5. [DOI] [PubMed] [Google Scholar]
- 63.Ghahramani Z, Hinton GE. Variational learning for switching state-space models. Neural Comput. 2000;12:831–864. doi: 10.1162/089976600300015619. [DOI] [PubMed] [Google Scholar]
- 64.Baddeley RJ, Ingram HA, Miall RC. System identification applied to a visuomotor task: near-optimal human performance in a noisy changing task. J Neurosci. 2003;23:3066–3075. doi: 10.1523/JNEUROSCI.23-07-03066.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Burge J, Ernst MO, Banks MS. The statistical determinants of adaptation rate in human reaching. J Vis. 2008;8:20.1–19. doi: 10.1167/8.4.20. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Zarahn E, Weston GD, Liang J, Mazzoni P, Krakauer JW. Explaining savings for visuomotor adaptation: linear time-invariant state-space models are not sufficient. J Neurophysiol. 2008;100:2537–2548. doi: 10.1152/jn.90529.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Huang VS, Shadmehr R. Persistence of motor memories reflects statistics of the learning event. J Neurophysiol. 2009;102:931–940. doi: 10.1152/jn.00237.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Fox E, Sudderth EB, Jordan MI, Willsky AS. Nonparametric Bayesian Learning of Switching Linear Dynamical Systems. In: Koller D, Schuurmans D, Bengio Y, Bottou L, editors. Advances in Neural Information Processing Systems 21. Curran Associates, Inc; 2009. pp. 457–464. [Google Scholar]
- 69.Oldfield RC. The assessment and analysis of handedness: the Edinburgh inventory. Neuropsychologia. 1971;9:97–113. doi: 10.1016/0028-3932(71)90067-4. [DOI] [PubMed] [Google Scholar]
- 70.Howard IS, Ingram JN, Wolpert DM. A modular planar robotic manipulandum with end-point torque control. J Neurosci Methods. 2009;181:199–211. doi: 10.1016/j.jneumeth.2009.05.005. [DOI] [PubMed] [Google Scholar]
- 71.Ingram JN, Sadeghi M, Flanagan JR, Wolpert DM. An error-tuned model for sensorimotor learning. PLoS Comput Biol. 2017;13:e1005883. doi: 10.1371/journal.pcbi.1005883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Land MF, Furneaux S. The knowledge base of the oculomotor system. Philos Trans R Soc Lond B Biol Sci. 1997;352:1231–1239. doi: 10.1098/rstb.1997.0105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Johansson RS, Westling G, Backstrom A, Flanagan JR. Eye-hand coordination in object manipulation. J Neurosci. 2001;21:6917–6932. doi: 10.1523/JNEUROSCI.21-17-06917.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Land MF, Mennie N, Rusted J. Eye movements and the roles of vision in activities of daily living: making a cup of tea. Perception. 1999;28:1311–1328. doi: 10.1068/p2935. [DOI] [PubMed] [Google Scholar]
- 75.Doucet A, Gordon NJ, Kroshnamurthy V. Particle filters for state estimation of jump Markov linear systems. IEEE Trans Signal Process. 2001;49:613–624. [Google Scholar]
- 76.Bar-Shalom Y, Rong Li X, Kirubarajan T. Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software. John Wiley & Sons; 2004. [Google Scholar]
- 77.Dempster AP, Laird NM, Rubin DB. Maximum Likelihood from Incomplete Data via the EM Algorithm. J R Stat Soc Series B Stat Methodol. 1977;39:1–38. [Google Scholar]
- 78.Cappé O, Moulines E. On-line expectation–maximization algorithm for latent data models. J R Stat Soc. 2009 [Google Scholar]
- 79.Cappé O. Online EM Algorithm for Hidden Markov Models. J Comput Graph Stat. 2011;20:728–749. [Google Scholar]
- 80.George AP, Powell WB. Adaptive stepsizes for recursive estimation with applications in approximate dynamic programming. Mach Learn. 2006;65:167–198. [Google Scholar]
- 81.Robbins H, Monro S. A Stochastic Approximation Method. Ann Math Stat. 1951;22:400–407. [Google Scholar]
- 82.Del Moral P, Doucet A, Singh S. Forward Smoothing using Sequential Monte Carlo. arXiv [stat.ME] 2010 [Google Scholar]
- 83.Özkan E, Lindsten F, Fritsche C, Gustafsson F. Recursive Maximum Likelihood Identification of Jump Markov Nonlinear Systems. IEEE Trans Signal Process. 2015;63:754–765. [Google Scholar]
- 84.Kalman RE. A New Approach to Linear Filtering and Prediction Problems. J Basic Eng. 1960;82:35–45. [Google Scholar]
- 85.Kass RE, Raftery AE. Bayes Factors. J Am Stat Assoc. 1995;90:773–795. [Google Scholar]
- 86.Jeffreys H. The Theory of Probability. OUP Oxford; 1998. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.