Universality of clone dynamics during tissue development

Abstract

The emergence of complex organs is driven by the coordinated proliferation, migration and differentiation of precursor cells. The fate behaviour of these cells is reflected in the time evolution their progeny, termed clones, which serve as a key experimental observable. In adult tissues, where cell dynamics is constrained by the condition of homeostasis, clonal tracing studies based on transgenic animal models have advanced our understanding of cell fate behaviour and its dysregulation in disease (1, 2). But what can be learned from clonal dynamics in development, where the spatial cohesiveness of clones is impaired by tissue deformations during tissue growth? Drawing on the results of clonal tracing studies, we show that, despite the complexity of organ development, clonal dynamics may converge to a critical state characterized by universal scaling behaviour of clone sizes. By mapping clonal dynamics onto a generalization of the classical theory of aerosols, we elucidate the origin and range of scaling behaviours and show how the identification of universal scaling dependences may allow lineage-specific information to be distilled from experiments. Our study shows the emergence of core concepts of statistical physics in an unexpected context, identifying cellular systems as a laboratory to study non-equilibrium statistical physics.

Biological systems, being highly structured and dynamic, function far from thermal equilibrium. This is particularly evident in embryonic development where, through large-scale cellular self-organisation, highly complex structures emerge from a group of genetically identical, pluripotent stem cells. To achieve the stereotypic ordering of organs and tissues, the fate of embryonic stem cells and their progeny must be tightly-regulated, such that the correct number and type of cells is generated at the right time and place during development. Mechanisms regulating such cell fate decisions are at the center of research in stem cell and developmental biology (3). Efforts to resolve the mechanisms that regulate cell fate behaviour place emphasis on emerging technologies, including single-cell genomics and genome editing methods, which provide detailed information on the subcellular and cellular processes. However, by focusing on gene regulatory programmes, such approaches often fail to engage with how collective cell behaviour, and the formation of functioning organs, emerges from the network of complex interactions at the molecular scale.

To understand how complexity at the microscopic scale translates into coherent collective behaviour at the macro-scale, statistical physics provides a useful theoretical framework. For critical systems, where fluctuations are scale-invariant, successive coarse-graining can yield effective theories describing macroscopic behavior. In such systems, different “microscopic” systems can give rise to indistinguishable macroscopic behavior – a concept known as universality. As a reflection of scale invariance, statistical correlations, such as size distributions, obtain simple scaling forms, which depend only on one or few dimensionless composite variables. But, given the complexity of embryonic development, can such concepts be applied to study cellular behaviour?

At the cellular scale, the patterns of cell fate decisions during embryonic development are reflected in the time-evolution of individual developmental precursors cells and their progeny, which together constitute a clone. While the dynamics of individual clones maybe complex, subject both to intrinsic and extrinsic influences, statistical ensembles of clones may provide robust (predictive) information about the relationship between different cell types and mechanisms regulating cellular behaviour. In mammals, where live-imaging of developing embryonic organs is typically infeasible, efforts to resolve clonal dynamics have relied on cell lineage tracing studies using transgenic animal models (1). In this approach, the activation of a reporter gene allows individual cells to be marked with a fluorescent reporter. As a genetic mark, this label is then inherited by all progeny of a marked cell, and allows clone sizes and cell compositions to be recorded at specific times post-labelling (Figure 1A). Lineage tracing studies therefore provide a “two-time” measure of clonal dynamics in the living embryo. In adult tissues, where cell dynamics is heavily constrained by the steady state condition of homeostasis, efforts to resolve cell fate behaviour from clonal tracing studies have drawn successfully upon concepts from statistical physics and mathematics (4–6). However, in developing tissues, the interpretation of these experiments is complicated by the fact that clonal dynamics is, in principle, less constrained. Moreover, due to large-scale cellular rearrangements as well as stochastic forces from surrounding tissues, labelled clones may fragment into disconnected clusters, or they merge and form larger compounds of labelled cells (Figure 1B-F).

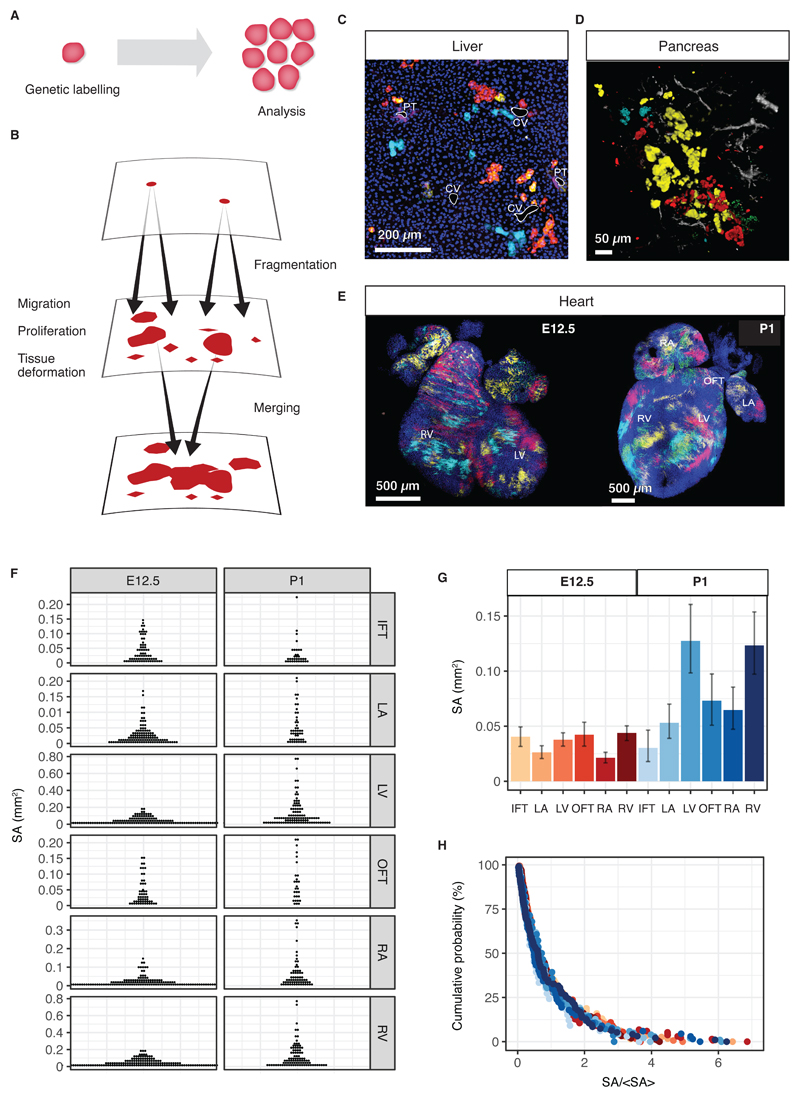
Fig. 1. Clonal dynamics during tissue development.

(A) Lineage tracing allows resolving clonal dynamics using a “two-time” measurement in living organisms. (B) Merger and fragmentation of labelled cell clusters occur naturally because of large-scale tissue rearrangements during the growth and development of tissues. (C,D) Illustration of clone fragmentation in mouse during the development of (C) liver and (D) pancreas (collection at post-natal day (P)45 and P14, respectively) following pulse-labelling using, respectively, R26R-CreERT2;Rainbow and R26R-CreERT2; R26-Confetti at E9.5 and E12.5, respectively. Portal tracts (PT) and central veins (CV) are highlighted in white, osteopontin (a ductal marker) is shown in purple and nuclei are marked in blue. Pancreatic ducts are shown in grey. (E) High density (mosaic) labelling of mouse heart using the Mesp1-Confetti system showing the left/right atrium (L/RA), left/right ventricle (L/RV) and the in/out-flow tracts (I/OFT). (F) Distributions of cell cluster sizes on the surface of the developing mouse heart at E12.5 (680 clusters from 4 mice) and P1 (373 clusters from 3 mice). (G) Average cluster sizes in different heart compartments and time points during development. Error bars denote 95% confidence intervals. (H) Rescaled cluster size distributions showing scaling behaviour.

Here, by establishing a formal mapping between clonal dynamics and a generalization of the theory of aerosols, we show that, during embryonic development, clonal dynamics converges to a critical state, giving rise to universal scaling behaviour of the size distributions of labelled clusters. Further, we explore how understanding the origins of scaling and universality can form the quantitative basis for recovering information on cell fate behaviour during development. We thus find the emergence of core concepts of statistical physics in the unexpected context of embryonic development. As well as being of interest in the study of tissue development, these findings have important implications for the study of tissue regeneration and tumour growth.

To develop this programme, we begin with an example of clonal evolution during the development of mouse heart. The gene Mesp1 is transiently expressed between embryonic day (E)6.5 and E7.5 in mice in the earliest precursor cells of the heart (7–9). Quantitative analysis of hearts labelled at low density (1-2 clones per heart) have established the temporal progression in differentiation and proliferative capacity of these precursors (8, 9). However, with just 1 or 2 clones per embryo, and inherent variability in the efficiency of labelling, low-density labelling is highly inefficient in probing evolutionary processes during development. By contrast, at high (mosaic) labelling density, each embryo provides a potentially rich dataset. The situation is exemplified in Figure 1E, which shows mouse hearts at E12.5 and postnatal day P1 after mosaic labelling between E6.5 and E7.5 using the multicolour Mesp1-Cre/Rosa-Confetti reporter construct (with 50% of the cardiac surface being fluorescently labelled with each of three colours, cyan, yellow and red, roughly equally represented). However, at this density of labelling, a single contiguous cluster of labelled cells can be derived from the chance fusion of two or more independent clones induced with the same colour (10). Given that clone sizes are not constrained by tissue size, and the ambiguity arising from clone merger and fragmentation, to what extent can information on cell fate behaviour be recovered?

To address this question, we quantified the surface area (SA) covered by each cluster in a given heart compartment at different developmental time points. From the SAs, we then determined their distributions in each heart region (Fig. 1F). Although cardiac development involves complex cell fate decisions, with regional and temporal variations in proliferation (11, 12), we found that the resulting cluster size distribution was remarkably conserved: After rescaling the SA of each cluster by the ensemble average for each compartment at a given time point, the resulting rescaled size distributions perfectly overlapped (Fig. 1G,H). This result implies that, despite the complex and variable histories, the resulting SA distribution is fully characterized by the average alone, the defining property of scaling. Formally, the frequency f(x,t)dx of a cluster with a SA between x and x + dx at time t post-labelling acquires the statistical scaling form, f(x,t) = ϕ(x/〈x(t)〉), where ϕ denotes the scaling function.

The simplicity of the cluster size distribution that is reflected in scaling behaviour suggests that its origin may not rely on details of the morphogenic programme in heart. Rather, to uncover its origin, we began by considering the simplest set of processes that could determine cluster size: First, as labelled cells divide, clusters may grow at a rate proportional to their size. Second, in expanding tissues, clones may fragment into disconnected clusters as cells disperse or the tissue deforms. If the rate of growth and fragmentation increase in proportion to cluster size, the SA distribution would be predicted to become stationary. However, although clonal tracing studies indicate that growth and fragmentation occur on a similar time scale during the early phase of heart development (E6.5 and E12.5) (9), average cluster sizes at E12.5 and P1 differ by a factor of 2.7, showing that steady-state is not reached. More importantly, such a simple line of argument neglects the possibility that clusters of the same colour can merge into larger, cohesively labelled regions. Yet the number of clusters varies only marginally between E12.5 and P1 (9), indicating that merger and fragmentation could be equally abundant.

To resolve the origin of scaling, it is instructive to leave temporarily the realm of biology and consider the growth dynamics of “inanimate” compounds. Indeed, processes involving merger and fragmentation occur in multiple contexts in physics, including the nucleation of nano-crystals, amyloid fibrils, polymerisation, endocytosis and the dynamics of aerosols (13–16). In common with clonal evolution in tissues, droplets in aerosols may merge (coagulate) or they may fragment (Fig. 2A). By analogy with clonal growth due to cell division, droplets may also expand by condensation of free molecules, while cell loss due to death or migration out of the imaging window is mirrored in the evaporation and shrinking of droplet sizes. Finally, by analogy with the migration of cells into the field of view, new droplets may nucleate from free molecules. Through this correspondence, can the statistical physics of aerosols provide insight into the dynamics of cell clusters in tissues and the emergence of scaling?

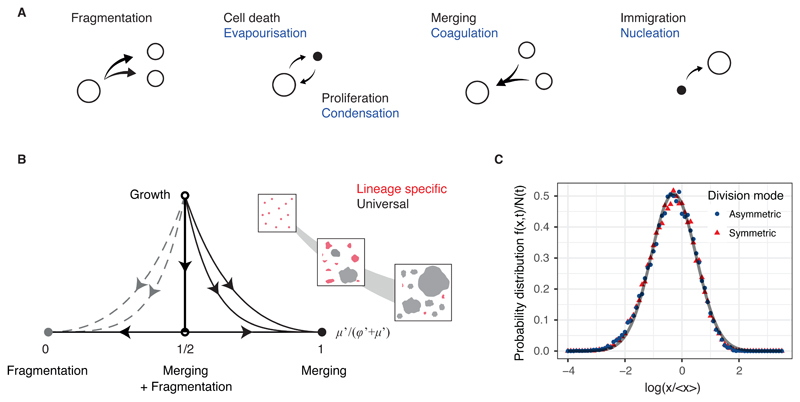
Fig. 2. Origin of scaling and universality in clonal dynamics during development.

(A) Sizes of labelled cell clusters in developing tissues are determined by processes analogous to the kinetics of droplets in aerosols, as depicted. (B) Sketch of the renormalisation flow diagram showing how the relative contributions of different processes to the cluster size distribution evolve during development. At long times and/or larger cluster sizes, the time evolution of the cluster size distribution becomes controlled by three fixed points (dependent on the details of the merging and fragmentation processes), where it acquires a universal scaling dependence (Supplementary Information). The inset shows a schematic of the renormalization process, with the largest cluster sizes (grey) converging more rapidly onto the universal distribution than the smallest cluster sizes (red). (C) Rescaled cluster size distributions for different division modes obtained by numerical simulations (Supplemental Theory) collapse onto a universal log-normal form (grey line).

The distribution of cluster sizes, f(x,t), is the result of different sources of variability including merger, fragmentation, cell division and loss. Formally, the time evolution of the cluster size distribution can be cast (symbolically) as a sum of operators that describe the effect of these contributions on the time evolution,

$${\partial }_{t}f(x,t)=L_{\text{growth}}\left[f(x,t)\right]+\phi L_{\text{fragmentation}}\left[f(x,t)\right]+\mu L_{\text{merger}}\left[f(x,t)\right]+\dots ,$$

where the parameters, φ, μ, etc. characterize the relative strength of these processes against that of growth (for details, see Supplementary Theory). To investigate the origin of scaling, we questioned what determines the long-term, large-scale dependence of the cluster size distribution. In statistical physics this question is typically answered by successively coarse-graining the dynamics and monitoring changes in the relative contributions of different processes. Under this renormalization, when a cell divides, cluster sizes are rescaled by the resulting increase in tissue size, x → x/(1 + δX) ≡ ρ. Simultaneously, time is rescaled in such way that the total rate of merging and fragmentation events remains constant in this process. Notably, after repeated rounds of dynamic renormalisation, the kinetic equation converges to a self-similar (critical) form, where the fluctuations in cluster sizes are dominated solely by a balance between merger and fragmentation events (Supplementary Theory), while the influence of other processes becomes vanishingly small,

$${\partial }_{\tau }f(\rho ,\tau )\approx \phi \prime L_{\text{fragmentation}}\left[f(\rho ,\tau )\right]+\mu \prime L_{\text{merging}}\left[f(\rho ,\tau )\right],$$

where φ′ and μ′ are rescaled parameters and τ is a rescaled time (Supplemental Theory). Intuitively, this means that, as the organ grows, different sources of variance contribute to the cluster size distribution by different degree (Fig. 2B and S1A). Crucially, in the long term, contributions relating to cell fate behaviour (e.g. cell division or loss) become dominated by merger and fragmentation processes, resulting in information on the former becoming erased (Supplementary Theory). Therefore, while cell fate decisions affect the mean cluster size, the shape of the distribution is determined entirely by merger and fragmentation events (Fig. 2C), leading to the emergence of scaling behaviour observed in heart development (Fig. 1F).

Importantly, these results suggest not only that the cluster size distribution is entirely determined by its average (scaling), but also that the shape of the distribution is independent of the biological context (universality). The form of the scaling function, ϕ, relies on the dependence of the merging and fragmentation rates on cluster size. In a uniformly growing tissue, clone merger and fragmentation events are the result of the slow diffusive motion of clusters originating from random forces exerted by the surrounding tissue (17). In this case, the resulting scaling form is well-approximated by a log-normal size dependence (Fig. 2C, Supplementary Theory). Indeed, such distributions are typical of merging and fragmentation processes and describe the empirical distribution of droplet sizes in aerosols (18, 19). Similar universal behaviour is recapitulated by a simple lattice-based Monte Carlo simulation of uniform tissue growth, where the stochastic nature of cell division alone leads to merger and fragmentation (Figure S1B and Supplementary Theory). Importantly, this analysis provides an explanation for the observed scaling behaviour of labelled cluster sizes of mouse heart, where the distribution indeed follows a strikingly log-normal size dependence (Fig. 3A,B and S2A,B). To further challenge the universality of the scaling dependences, we used a similar genetic labelling strategy to trace the fate of early developmental precursors in mouse liver and pancreas as well as the late stage development of zebrafish heart (20). In all cases, cluster size distributions showed collapse onto a log-normal size dependence (Fig. 3C-F and S2C-E), with the notable exception of a subpopulation of pancreatic precursors (see below).

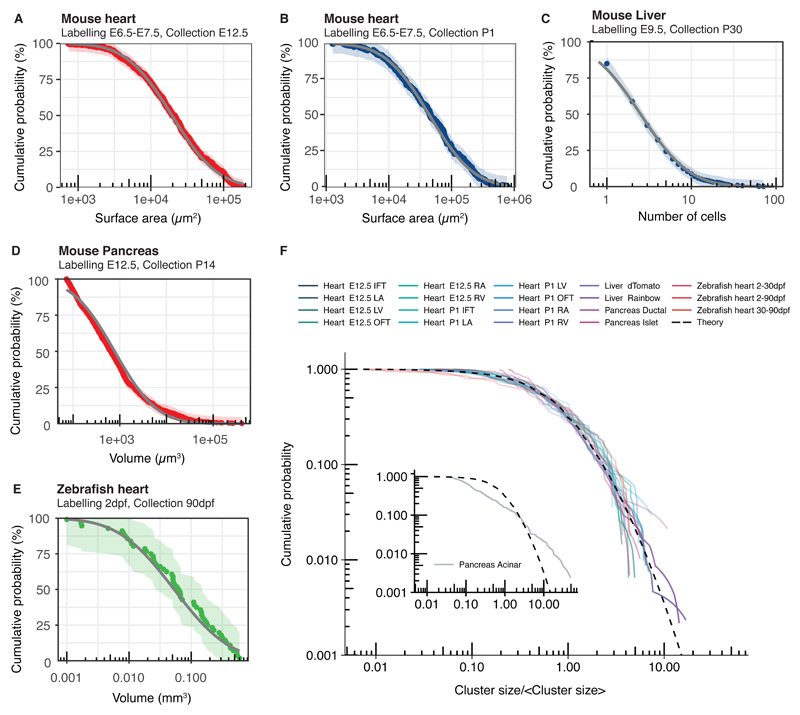
Fig. 3. Universality of cluster sizes in different tissue types and organisms.

(A-B) Cumulative cluster size distributions obtained from lineage tracing studies of the mouse heart. (C-E) Experimental cumulative cluster size distributions for (C) mouse liver (892 clusters from 4 mice), (D) mouse pancreas (988 clusters from 3 mice), and (E) zebrafish heart (from (20)) collapse onto the predicted universal log-normal dependence fitted by maximum likelihood estimation (grey). Data shown in colour and shading shows 95% Kolmogorov confidence intervals. (F) Experimental cumulative cluster size distributions (solid lines) separated by time, region, cell type labelling strategy collapse onto a universal shape (dashed line) with the exception of a subset of pancreatic acinar cells (inlay).

This analysis shows that, in the long term, the collective cellular dynamics leads to a critical state dominated by a balance between merging and fragmentation events. The emerging universal scaling distributions progressively become void of information on underlying biological processes on a time scale determined by the merging and fragmentation rates. But how can such information be recovered? In analogy to the turnover of adult homeostatic tissues, such as interfollicular epidermis or intestine (4, 21), the behaviour of the size distribution under renormalization (Fig. 2B and Supplemental Theory) shows how lineage-specific information can be recovered: First, it is preserved in the non-universal cluster size dependences at short times post-labelling, prior to convergence to the scaling regime. Second, convergence onto universal scaling dependences is the slowest for small cluster sizes (x ≪ 〈x〉). Third, if the rate of clone merger is negligibly small, different cluster size distributions can emerge according to the mode of cell division. The range of possible behaviours is summarised in Table 1. Finally, as merging and fragmentation are emergent properties of cell fate decisions, deviations from the scaling form can inform on structural properties of organ formation. As an example, in the developing pancreas, acinar cells initiate from precursors localized at the tips of a complex ductal network and aggregate as cohesive cell clusters thereby supressing clonal fragmentation. This results in a departure from scaling behaviour of the cluster size distribution (Figs. 3F and S2F).

Table 1. Non-universal dependencies of the cluster size distribution.

Analytical expressions for the cluster size distribution (top row in each cell) and average cluster size (bottom row). Shown are expressions in situations, where labelling density is clonal, labelling density is almost clonal but clones are subject to fragmentation, and where both merging and fragmentation of clones occur (left to right). As merging and fragmentation both result from tissue rearrangements merging should always imply fragmentation. Time is measured in units of the cell cycle time. Expressions are valid after convergence to the scaling regime, when the typical cluster size is much larger than the size of single cells, and in the mean-field limit, which is a good approximation for two and three dimensional tissues. In addition, it is assumed that the full spectrum of cluster sizes can be experimentally resolved. If clones fragment but not merge fragmentation and growth ultimately compensate to lead to a stationary distribution. In case of clonal merging and fragmentation expressions give empirical approximations, where depends on the details of the merging and fragmentation processes (see Supplemental Theory).

Growth mode	Clonal	Fragmentation	Merging & fragmentation
Exponential	〈x〉−1 exp (−x/〈x〉) 〈x〉 = exp(t)	φ exp (−φ−1x) 〈x〉 = φ−1	$\{\begin{array}{ll}{(x/\langle x\rangle )}^{\alpha }\hfill & x\ll \langle x\rangle \hfill \\ \text{exp}(-x/\langle x\rangle )\hfill & x\gg \langle x\rangle \hfill \end{array}$ 〈x〉 = exp(t)
Linear	$\frac{1}{\sqrt{2\pi \langle x\rangle }}\text{exp}\left[-\frac{{(x-\langle x\rangle )}^2}{2\langle x\rangle }\right]$ 〈x〉 = t	$\phi x\left(2+\sqrt{\phi }x\right)\text{exp}\left(-\sqrt{\phi }x-\frac{\phi }{2}{x}^2\right)$ 〈x〉 = φ−1/2	$\{\begin{array}{ll}{(x/\langle x\rangle )}^{\alpha }\hfill & x\ll \langle x\rangle \hfill \\ \text{exp}(-x/\langle x\rangle )\hfill & x\gg \langle x\rangle \hfill \end{array}$ 〈x〉 = t
Homeostasis	〈x〉−1 exp [−x / 〈x〉] (see Ref. 6) 〈x〉 ∝ t	J(x) (see Ref. 24) 〈x〉 = const.	$\{\begin{array}{ll}{(x/\langle x\rangle )}^{\alpha }\hfill & x\ll \langle x\rangle \hfill \\ \text{exp}(-x/\langle x\rangle )\hfill & x\gg \langle x\rangle \hfill \end{array}$ 〈x〉 = const.

In recent years, there has been a growing emphasis on genetic lineage tracing as a tool to resolve the proliferative potential and fate behaviour of stem and progenitor cells in normal and diseased tissues (1). Here, we have shown that the collective cellular dynamics in tissue growth and turnover lead to universal clone dynamics, where cluster size distributions become independent of the fate behaviour of cell populations. As well as highlighting the benefit of low-density labelling and the dangers of making an unguarded assessment of clonality in lineage labelled systems, these findings identify quantitative strategies to unveil cell fate-specific information from short-term or small cluster size dependencies, with potential applications to studies of clonal dynamics in both healthy and diseased states. At the same time, by highlighting the unexpected emergence of core concepts of statistical physics in a novel context, this study provides a model of how the cellular dynamics of living tissues can serve as a laboratory for statistical physics.

Methods

Surface area analysis of mosaically labeled hearts

To generate mosaically labelled hearts at high density, Mesp1-Cre mice (22) were crossed with the Rosa-Confetti reporter mice (23) kindly provided by Hans Clevers. Hearts collected at embryonic days E12.5 and P1 were fixed in 4% paraformaldehyde for 1hr at room temperature. Nuclei were counterstained with Topro3 (1/500, Invitrogen). The surface images were acquired with a confocal microscope (LSM780; Carl Zeiss). The surface area (SA) of each independent clusters was measured using Fiji software (24) on the maximum intensity projection.

Pancreas

R26R-CreERT2; R26-Confetti mice were intraperitoneally injected with Tamoxifen (from Sigma) at 0.030mg per gram of female at E12.5 of pregnancy under Home Office guidelines, Animal Scientific Procedure Act (ASPA) 1986. P14 pancreas was fixed in 4% Paraformaldehyde (PFA) overnight, and then washed in PBS. Samples were sucrose-treated (30%) and mounted in OCT, and subsequently thick 100μm cryostat sectioned. Sections were rehydrated in PBS, blocked overnight in PBS, 2% donkey serum and 0.5% Triton-100X. The samples were incubated in Dolichos biflorus agglutinin (DBA), biotinylated (from Vectorlabs) for 3 days at 4°C, and AF647-Streptavidin (from Life Technologies) was applied for 2 days at 4°C. Next, sections were cleared with RapiClear 1.52 (from SunJin Lab). Images were acquired with Leica TCS SP5 confocal microscope, using the tiling mode. The images were analyzed with Volocity and volumes and coordinates of centers of clonal clusters quantified. To obtain 3D reconstructions from Z stacks obtained with Leica SP5 microscope, Imaris (v8, Bitplane) was used.

Liver

R26R-CreERT2⁺;Rainbow⁺ mice were a kind gift from Magdalena Zernicka-Goetz (University of Cambridge, UK). R26R-CreERT2⁺;Rainbow⁺ male mice were crossed with wild-type MF1 females and labelling induced by intraperitoneal injection of pregnant dams with Tamoxifen (Sigma). Tamoxifen was prepared at 10 mg/mL in sunflower oil and induction performed using 0.025 mg Tamoxifen per gram of pregnant dam. Pregnant dams were induced at E9.5 and the resulting pups had livers collected at postnatal day P30 – P45. Livers were divided into pieces of thickness ~10mm, washed at least 3 times in PBS to remove blood and fixed in 4% Paraformaldehyde overnight before being washed twice in PBS. Liver pieces were mounted in 4% Low Melt Agarose (Bio-Rad) and 100µm thick sections cut using a vibratome (Leica VT1000 S). Thick sections were stored in PBS at 4 °C before immunostaining. Briefly, sections were blocked in PBS + 5% DMSO (Sigma) + 2% donkey serum (Sigma) + 1% Triton-X100 (Sigma) overnight before incubation in PBS + 1% DMSO + 2% donkey serum + 0.5% Triton-X100 + 1:40 goat anti-Osteopontin (R&D Systems, AF808) for 3 days at 4 °C. Following several washes in PBS + 1% DMSO + 0.5% Triton-X100 at 4 °C for 24 h, sections were incubated in PBS + 1% DMSO + 2% donkey serum + 0.5% Triton-X100 + 1:250 donkey anti-goat antibody conjugated to AF647 (Life Technologies) for 2 days at 4 °C. Following the staining, sections were cleared by increasing glycerol gradient before incubation with PBS + 1:1000 Hoechst 33342 (Sigma) for 1h at 4 °C to counterstain nuclei and mounted with Vectashield (Vector Laboratories). Images of liver sections were acquired using a Leica TCS SP5 confocal microscope and processed using LAS AF Lite software (Leica). Cell numbers for each labelled cluster were counted manually from acquired images.

Code availability

Custom code used to in this study is available from the corresponding authors upon reasonable request.

Data availability

The data that support the plots within this paper and other finding of this study are available from the corresponding author upon request.