Skip to main content
NCBI home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2019 May 17.
Published in final edited form as: J Biomech. 2018 Apr 12;73:177–184. doi: 10.1016/j.jbiomech.2018.04.011

Vocal Fold Contact Patterns Based On Normal Modes Of Vibration

Simeon L Smith 1,*, Ingo R Titze 1
PMCID: PMC5935250  NIHMSID: NIHMS960160  PMID: 29680310

Abstract

The fluid-structure interaction and energy transfer from respiratory airflow to self-sustained vocal fold oscillation continues to be a topic of interest in vocal fold research. Vocal fold vibration is driven by pressures on the vocal fold surface, which are determined by the shape of the glottis and the contact between vocal folds. Characterization of three-dimensional glottal shapes and contact patterns can lead to increased understanding of normal and abnormal physiology of the voice, as well as to development of improved vocal fold models, but a large inventory of shapes has not been directly studied previously. This study aimed to take an initial step toward characterizing vocal fold contact patterns systematically. Vocal fold motion and contact was modeled based on normal mode vibration, as it has been shown that vocal fold vibration can be almost entirely described by only the few lowest order vibrational modes. Symmetric and asymmetric combinations of the four lowest normal modes of vibration were superimposed on left and right vocal fold medial surfaces, for each of three prephonatory glottal configurations, according to a surface wave approach. Contact patterns were generated from the interaction of modal shapes at 16 normalized phases during the vibratory cycle. Eight major contact patterns were identified and characterized by the shape of the flow channel, with the following descriptors assigned: convergent, divergent, convergent-divergent, uniform, split, merged, island, and multichannel. Each of the contact patterns and its variation are described, and future work and applications are discussed.

Keywords: vocal fold biomechanics, contact area, medial surface, glottal geometry, normal mode vibration

Introduction

Many areas of biomechanics deal with the interactions between fluids and solid-like structures. The fluid-structure interaction and energy transfer from respiratory airflow to self-sustained vocal fold oscillation has challenged researchers for many decades (Ishizaka and Flanagan, 1972; Titze, 1988; Thomson et al., 2005). In particular, the temporal and spatial distributions of pressures on the vocal fold surfaces are only beginning to be described in detail (Luo et al., 2009; Mihaescu et al, 2010; Chen and Mongeau, 2011; Oren et al., 2014b). To accelerate this effort, an important step is to quantify the time-varying airspace between the vocal folds, known as the glottis. Given that this airspace can collapse, in whole or in part, it needs to be quantified in three dimensions over various time intervals of the vibration cycle.

The three-dimensional shape of the glottis during phonation is determined largely by contact between the vocal folds. The glottal shape in turn determines the pressure distribution in the glottis (Scherer et al., 2001; 2002). Since pressure is the driving force for vocal fold self-oscillation, glottal pressure distributions determine vibration patterns (van den Berg, 1957) as well as glottal airflow patterns (Scherer et al., 1983; Deverge et al., 2003). Subtleties in the glottal airflow waveform affect parameters such as voice quality and sound amplitude (Gauffin and Sundberg, 1989; Childers and Lee, 1991; Childers and Ahn, 1995; Södersten et al., 1995).

Although vocal fold contact is related to many aspects of vocalization, contact area patterns have been studied mainly indirectly. The electro-glottograph (EGG) signal has long been used to estimate average (integrated) contact area between the vocal folds (Fourcin, 1981; Baer et al., 1983; Childers et al., 1986; Rothenberg, 1992; Herbst and Ternström, 2006; Ma and Love, 2010), but much of the spatial detail of contact is not revealed. A first attempt at computational modeling and interpretations of the EGG signal has been offered in terms of spatial and temporal features (Titze, 1990), but the model parameters were highly selective. Transmission ultrasonic imaging across the larynx has been attempted to resolve vocal fold contact area (Hamlet and Reid, 1972), but the beam width was too wide to capture much spatial detail. Studies using high-speed digital imaging of human vocal folds from a superior view, along with similar data from physical models, have presented glottal area shapes for normal and pathological conditions (Neubauer et al., 2001; Zhang et al., 2010; Tsuji et al., 2014), as well as associated “constriction modes” of the glottis with acoustic outputs (Krebs et al., 2010). Excised larynx studies have considered medial surface dynamics by tracking surface points in multiple anterior-posterior coronal planes (Berry et al., 2001; Döllinger et al., 2005; Doellinger and Berry, 2006). Yet, no studies have visualized or characterized a large variety of contact area patterns.

A study of contact patterns is highly relevant for computational modeling of normal and abnormal vocalization. The patterns facilitate the development of simplified flow models for near realtime voice simulation when thousands of cases need to be tested. This is particularly important for modeling abnormal voices, which are marked by asymmetry in movement between the left and right vocal folds. Such asymmetries are linked to anatomical variation or altered vocal fold shape due to surgery or disease. Non-entrained modes of vibration then occur that result in complex contact patterns and glottal geometries. It has been shown that a few modes of vibration are dominant in self-sustained oscillation of the vocal folds, even when there is non-synchronized motion between the left and right folds (Berry et al., 1994; Berry et al., 2001; Döllinger et al., 2005; Neubauer et al., 2001). The modes are described with two indices (m,n), where m indicates the number of half-wavelengths in the anterior-posterior direction, and n indicates the approximate number of half-wavelengths in the inferior-superior direction (Titze, 2000, Fig. 4.9). The most dominant modes are the (1,0) and the (1,1) modes, but videostroboscopy has shown that the (2,1) and (3,1) modes can be excited in abnormal vibration (Švec et al., 2000; Neubauer et al., 2001; Berry, 2001).

The goal of this paper is to create a taxonomy for characterizing glottal contact patterns based on normal modes of vibration. The modes will not be pulse-excited or self-excited with fluid-structure interaction, but rather driven with a specific frequency governed by mucosal surface wave propagation (Titze, 1988). The phases and amplitudes of the modes will be determined parametrically as described in previous work (Titze, 1984; Story and Titze, 1998). This approach is preferable to pulse excitation or flow-induced excitation because it gives a wider range of possible contact patterns, even though not all patterns are routinely encountered. A subset of the patterns can be expected in normal vocal fold vibration and a greater subset in abnormal vibration. The ultimate purpose is to determine possible complex glottal flow situations during vocal fold contact, from which pressure-flow relations for self-sustained oscillation can be quantified, following the empirical work of Scherer et al. (2001; 2002), Oren et al. (2014a; 2014b), and the computational work of Luo et al. (2008), Xue et al. (2010), Zheng et al. (2010; 2011), Sciamarella and Le Quéré (2007), and Zañartu et al. (2014). These pressure-flow relations can then be used in models of voice simulation. Consideration of a wider range of possible contact patterns allows for development of robust pressure-flow models that can handle complex, and even unexpected, flow situations that will arise in pathological phonation. The set of contact patterns found here is not an end goal, but an initial step toward development of accurate models for simulating and studying voice disorders.

Methods

Medial Surface Geometry

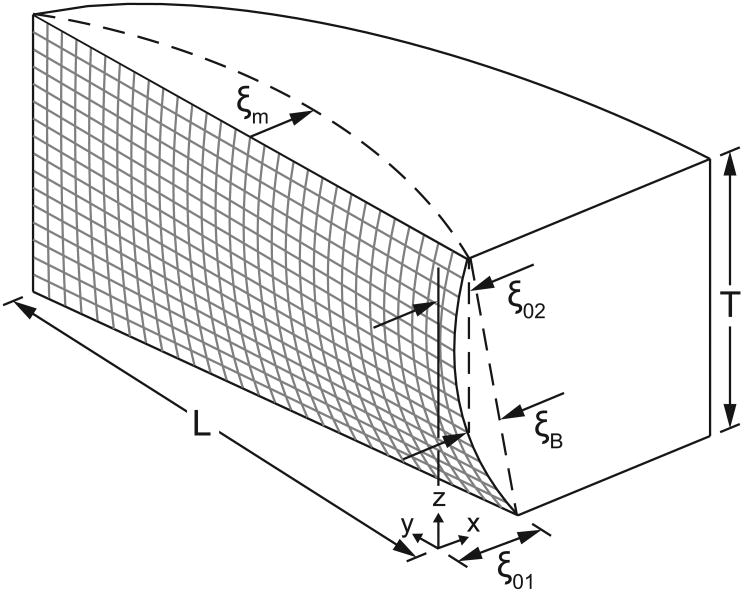
An idealized medial surface geometry was adopted from Titze (2006) and is shown in Figure 1. It consists of a rectangular surface of vertical thickness T and anterior-posterior length L, with posturing parameters to define the initial (prephonatory) three-dimensional geometry. Following the original mathematics given by Titze (1984), each point on the right prephonatory medial surface was defined by a glottal half-width, ξ 0R, (x-distance from the glottal midline) as a function of anterior-posterior (y) and inferior-superior (z) directions, given by the following equation:

Figure 1.

Figure 1

Open in a new tab

Schematic of medial surface dimensions and posturing parameters.

ξ0R(y,Z)=(1−y/L)[ξ0R2+(ξ0R1−ξ0R2−4ξBRz/T(1−z/T), (1)

where ξ 0R1 is the glottal entrance half-width at the vocal process (posterior edge of surface), ξ 0R2 is the glottal exit half-width at the vocal process, and ξ BR is a surface bulging parameter that governs the vertical curvature of the medial surface. The subscript R denotes the right vocal fold. Geometry for the left vocal fold follows the same equation with an L subscript.

The thickness, T, and the length, L, were defined as 0.8 and 1.5 cm, respectively. These dimensions are typical for human male vocal folds (Titze, 2006). Three initial posturing configurations were considered for this study: convergent, uniform, and divergent. These were defined by the parameter values in Table I.

Table I.

Posturing parameter values defining each of the three prephonatory glottal configurations.

Posturing Configuration ξ0R1 ξ0R2 ξBR ξ0L1 ξ0L2 ξBL
Convergent 0.18 0.03 0.005 0.18 0.03 0.005
Divergent 0.03 0.18 0.005 0.03 0.18 0.005
Uniform 0.1 0.1 0.005 0.1 0.1 0.005
Open in a new tab

Normal Modes of Vibration

To simulate normal modes of vibration over time, modal displacements were superimposed on the prephonatory geometry based on the surface-wave approach (Titze, 1988). The modal displacement ξ R of the medial surface at any instant in time is defined by:

ξR(y,z,t)=ξmRsin(mπy/L)[sinωt−n(ω/c)(z−zmR)cosωt], (2)

along length of vocal fold), zmR is the inflection point for the vertical half wavelength, ω is angular frequency, and c is speed of the mucosal wave. The ω/c coefficient in Eq. (2) accounts for vertical modal displacement (mucosal wave), when n=1. When n=0, no mucosal wave is present. Again, equivalent equations exist for the left vocal fold (L subscript). The three-dimensional shape of each medial surface at any instant in time is given by the addition of the prephonatory medial surface coordinates and the modal displacement, as follows:

gR/L(y,z,t)=ξ0R/L+ξR/L(y,z,t). (3)

For this study, vibration frequency, f, was chosen to be 125 Hz, typical for a human male, although the value was irrelevant with normalized cycles. The modal displacement amplitude, ξ mR/L, was 1 mm. The angular frequency, ω, and the mucosal wave speed, c, were based on vibration frequency and defined as 2πf and Tπf, respectively. The inflection point zmR/L, was defined as T*(0.6 - 0.02 ξBR/L). In preliminary simulations, varying zmR/L alone within its realistic range (0.4-0.6), only showed quantitative, not qualitative changes in contact patterns.

Simulation of Contact Patterns

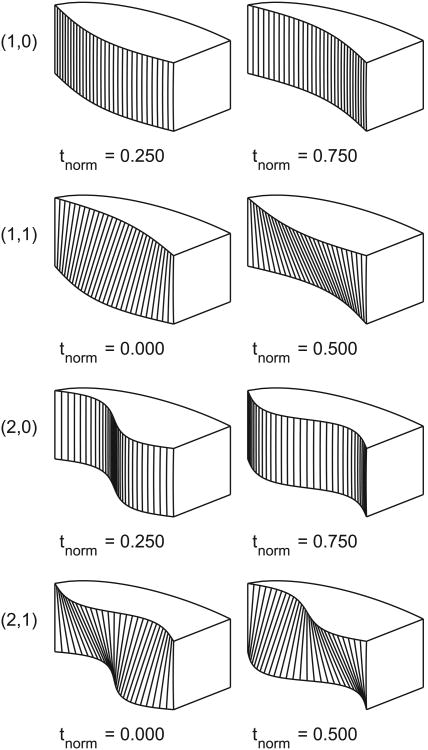
In this study, the lowest four modes of vibration were considered: (1,0); (1,1); (2,0); and (2,1). These are depicted in Figure 2. The (1,0) mode corresponds to medial-lateral translation of the vocal folds, while (1,1) captures both the vocal fold medial-lateral translation and the alternating convergent-divergent profile of the glottis that drives self-oscillation (Berry et al., 1994). Modes similar to these two account for more than 90% of the vibration energy (Berry et al., 1994; Berry et al., 2001; Döllinger et al., 2005; Neubauer et al., 2001). The other higher modes have been observed in vocal fold vibration (Švec et al., 2000; Neubauer et al., 2001; Berry, 2001), but they contribute much less to the overall energy. They were included here to consider other possible contact patterns. Contact patterns were investigated for all symmetrical and asymmetrical combinations of these modes with each of the three prephonatory glottal configurations (30 cases total). As for vocal fold dimensions, prephonatory glottal configuration, and vibration frequency, only symmetric cases are dealt with in this paper; asymmetry in these aspects will be addressed in future studies.

Figure 2.

Figure 2

Open in a new tab

Lowest four modes of vibration, denoted by (m,n), where m is number of half-wavelengths in anterior-posterior direction and n stands for approximate number of half-wavelengths in inferior-superior direction. Left and right images show extremes of displacement, with corresponding normalized times during the cycle.

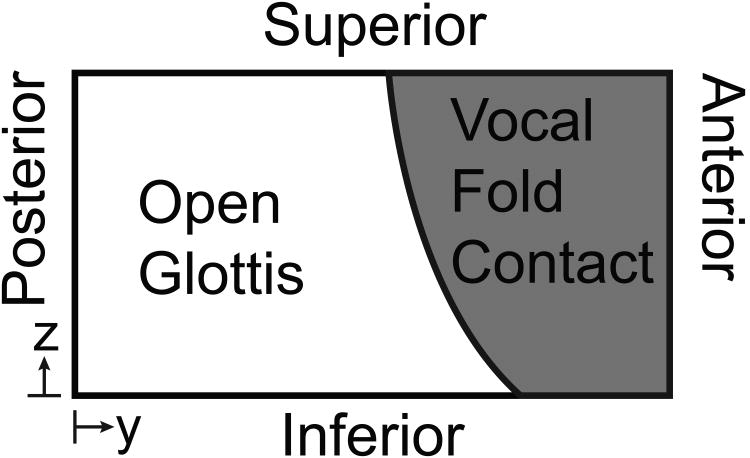
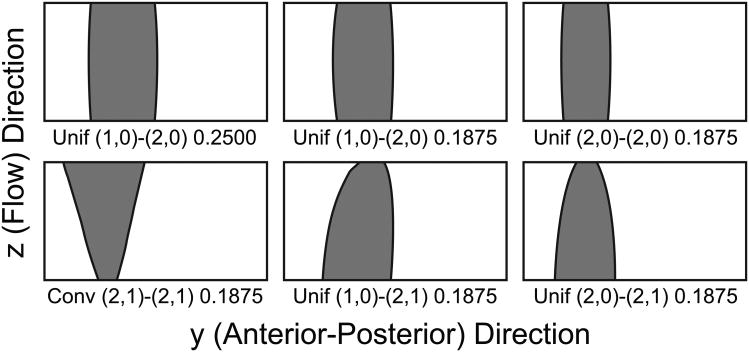
Simulations were performed using a MATLAB script, modeling opposing left and right medial surfaces with specified modal displacements. The medial surface was discretized into a mesh with 0.01 cm resolution, resulting in an 81 × 151 array of points to model each of the vocal fold surfaces. Modal vibration for each combination of left and right modes was simulated for one cycle. Contact occurred where left and right surfaces overlapped, and the contact surface was calculated as an average of the left and right surface coordinates. The contact area was plotted and viewed at 16 phases during the vibration cycle (normalized time steps of 0.0625), which gave sufficient temporal resolution to capture all contact patterns. An example contact area plot is provided in Figure 3 to orient the reader with the plots that will be presented in the results section. The plot shows a two-dimensional representation of the rectangular medial surface, with the posterior end of the glottis at the left edge and the inferior edge of the glottis at the bottom. Open glottal area is white, while vocal fold contact areas are colored gray. Contact areas were analyzed qualitatively to determine general, repeated contact patterns.

Figure 3.

Figure 3

Open in a new tab

Example contact area plot, representing rectangular medial surface, showing glottal orientation and areas of open glottis (white) and vocal fold contact (gray).

It should be noted that while vocal fold vibration has typically been reported as a combination of eigenmodes similar to the (1,0) and (1,1) modes, the (1,1)-like eigenmode observed in previous studies accounts more for the convergent-divergent motion (n=1 contribution) of the medial surface and less for the half-wavelength motion in the horizontal dimension (m=1 contribution) (Berry and Titze, 1996). In the current study, because the (1,1) mode provides an equal contribution of sinusoidal motion in both the horizontal and vertical directions, this mode alone can describe the full vibratory motion. The same applies to (2,1) and (3,1) modes. Thus, a combination of independent modes is not necessary to fully capture appropriate motion, and, in fact, a superposition of n=0 modes with n=1 modes - (1,0) combined with (1,1), for example - would be redundant. However, in the interest of addressing various contributions from m versus n motion to the overall energy, simulations were performed with a uniform glottis and various amplitude ratios of the m and n terms in Equation (2), for all left-right mode combinations with at least one vocal fold exhibiting n=1 motion. The results of these simulations showed changes in the occurrence of contact patterns throughout the cycle, along with quantitative differences in contact area and boundaries, but no additional qualitative differences in contact patterns were observed. Hence, the results presented in this paper are not limited by the use of principal modes.

Results

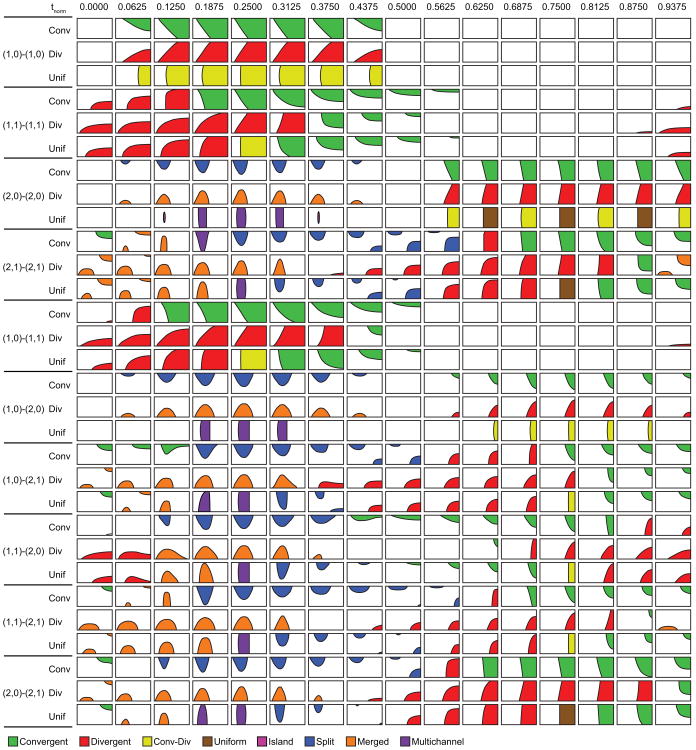
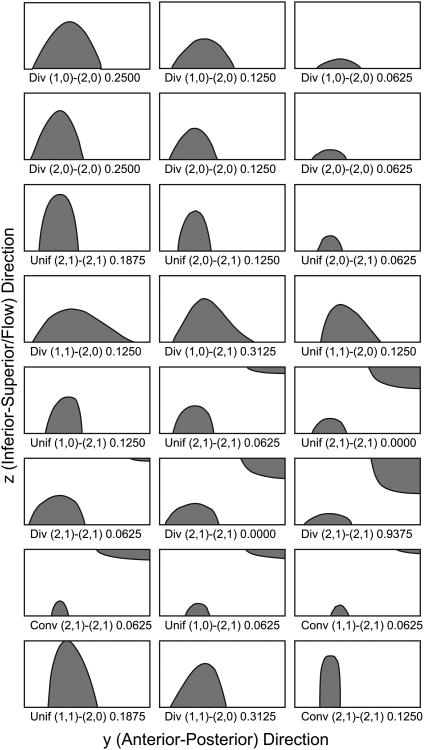
Figure 4 shows two-dimensional contact patterns at each normalized time step for all cases simulated in the present study. Patterns shown in Figure 4 are colored according to pattern type. In addition, videos showing full cyclic medial surface motion and contact for three cases, are included as Supplementary Material. Analysis of the contact areas for all cases identified eight major distinct patterns, which were named as follows: convergent, divergent, uniform, convergent-divergent, split, merged, multichannel, and island. Each of the contact patterns is described in detail below.

Figure 4.

Figure 4

Open in a new tab

Contact patterns for 16 phases of the cycle for each modal case, colored according to each pattern type.

Convergent

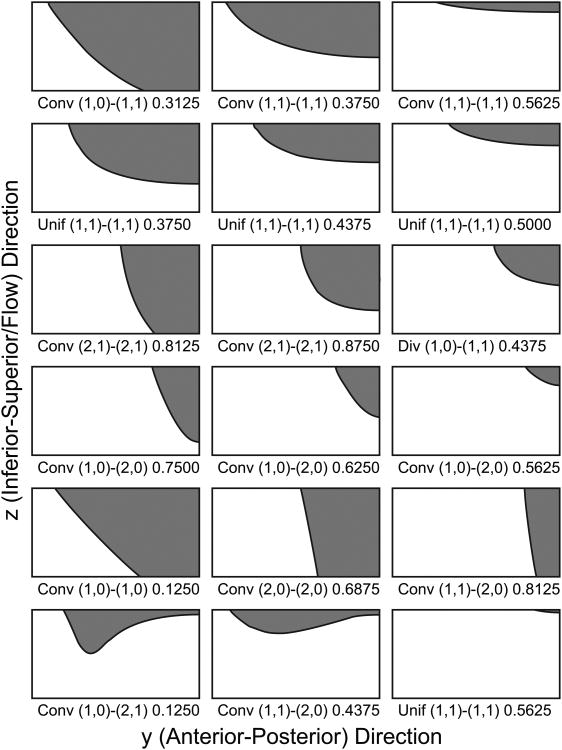
The convergent contact pattern consisted of a single flow channel that converged in the direction of flow. The convergent contact shapes exhibited various channel widths, angles of convergence, and contact boundary curvatures. Figure 5 gives examples of the convergent pattern and lists the case and phase where each was observed. Each row shows a different convergent shape that was observed, while each column in the row generally shows varying contact areas for the given shape. The bottom row shows some of the most complex shapes. It was observed that the contact areas can range from covering most of the medial surface to covering almost a negligible portion of the medial surface, as would be expected as the fold transitions between a closed and open glottis. The curvature of the contact boundary ranged from nearly straight to arc-shaped, and sometimes exhibited a change in the direction of curvature.

Figure 5.

Figure 5

Open in a new tab

Examples of convergent contact patterns observed, with notation below each image indicating for which case and phase the pattern was observed.

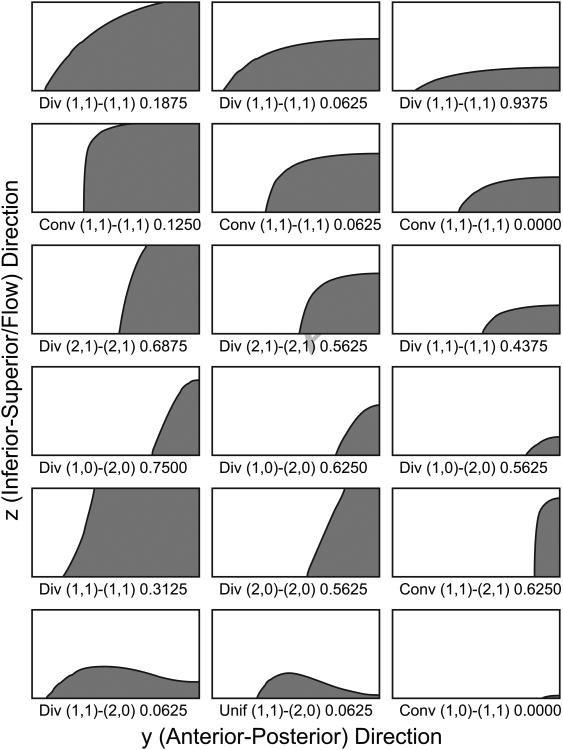
Divergent

The divergent contact pattern was characterized by a single flow channel that diverged in the flow direction - essentially the inversion of the convergent pattern. Figure 6 shows various manifestations of the divergent pattern. The various divergent contact patterns were highly similar to the convergent patterns, but inverted. However, the divergent pattern variations shown in Figure 6 are not all corresponding inversions of the convergent patterns shown in Figure 5. Other variations have been intentionally shown to present a greater extent of the variation.

Figure 6.

Figure 6

Open in a new tab

Examples of divergent contact patterns observed, with notation below each image indicating for which case and phase the pattern was observed.

Uniform and Convergent-Divergent

The uniform channel was characterized by a single, straight channel through the glottis, while the convergent-divergent pattern was a single channel that first converged and then diverged in the flow direction. The uniform and convergent-divergent patterns are presented together because, as contact boundary curvature straightens, the convergent-divergent pattern transforms into a uniform pattern. The variations in these patterns are presented in Figure 7. Both patterns varied in the contact area width and the contact boundary curvature, which ranged from highly curved to virtually straight.

Figure 7.

Figure 7

Open in a new tab

Examples of convergent-divergent, uniform, and island contact patterns, with notation below each image indicating for which case and phase the pattern was observed.

Island

The island pattern (bottom right image in Figure 6) consisted of an isolated contact area in the middle of the medial surface (not touching any edges). Thus, the glottal flow starts as one channel, splits, and then merges again within the glottis. The shape seen in these simulations was essentially a long ellipse and was nearly identical for the two cases where it was observed.

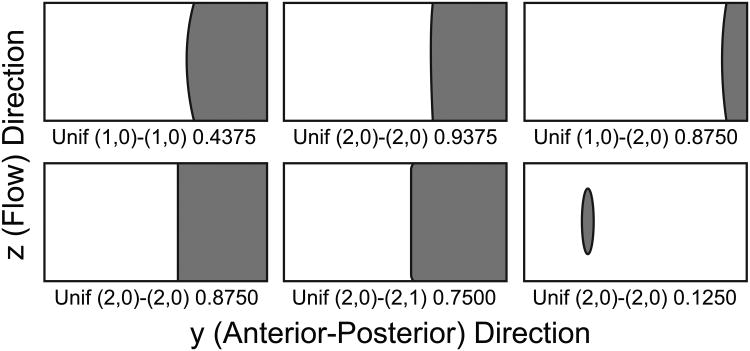
Split

The split contact pattern manifested as a bifurcation from one flow channel to two. Variations of the split pattern are given in Figure 8. Again for this pattern, there was variation in the total contact area, angles of convergence after the split, and contact boundary curvature. Here we also observed multiple contact areas, where one formed the split and another created a divergent section in the glottis preceding the split.

Figure 8.

Figure 8

Open in a new tab

Examples of split contact patterns, with notation below each image indicating for which case and phase the pattern was observed.

Merged

The merged contact pattern was defined by the joining of two flow channels into one within the glottis. Figure 9 shows the variety of merged patterns among the modal simulations. Again here, cases were intentionally chosen that do not correspond to exact inversions of the split pattern cases, for the sake of showing the extent of the variation. However, generally, all of the merged patterns seen were inversions of split cases. Thus, all of the various cases shown in the figures for the split and merged patterns were apparent in both patterns. As with the split pattern, both single and multiple contact areas were observed for the merged pattern.

Figure 9.

Figure 9

Open in a new tab

Examples of merged contact patterns, with notation below each image indicating for which case and phase the pattern was observed.

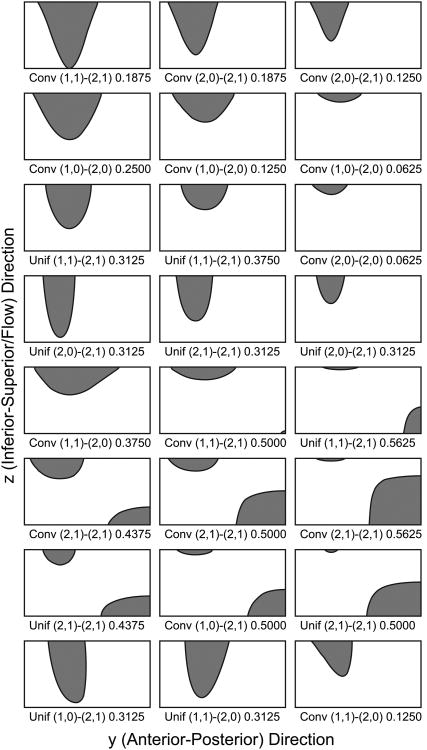
Multichannel

The multichannel pattern was characterized as two separate channels through the entire glottis. Figure 10 shows several cases that represent some of the variation in multichannel patterns. The patterns varied in the width of the contact area, as well as the shape in either channel. Some patterns exhibited convergent, divergent, or convergent-divergent (in flow direction) shapes in both channels, while others possessed a combination of shapes between the channels (e.g., one divergent, one convergent-divergent).

Figure 10.

Figure 10

Open in a new tab

Examples of multichannel contact patterns, with notation below each image indicating for which case and phase the pattern was observed.

Discussion

This study addressed visualizing and characterizing vocal fold contact patterns. Contact patterns were presented for left-right symmetric and asymmetric combinations of the lowest four normal modes of vibration superimposed on three prephonatory vocal fold configurations. Eight major vocal fold contact patterns were identified based on the shape of the resulting flow channel(s): convergent, divergent, convergent-divergent, uniform, island, split, merged, and multichannel. It is likely that patterns similar to the convergent, divergent, and uniform shapes would occur with normal opening and closing of the glottis, particularly since they are associated with the two lowest modes, (1,0) and (1,1), which account for much of the vocal fold vibration energy. The patterns associated with the m=2 modes and asymmetric modal combinations (split, merged, island, and multi-channel) might have a lower likelihood of being observed in normal human phonation, but could be more common in the disordered voice, where higher modes and asymmetry are present. The single-contact split and merged, as well as the island, patterns could reasonably occur in normal or abnormal phonation if the medial surface is bowed convexly. Patterns with multiple contact areas, however, might be more probable in abnormal physiology due to voice disorders.

Although many of the contact patterns based on normal modes might be observed in phonation, it must be kept in mind that these patterns are not based on flow-driven oscillation, and therefore these particular patterns might be less probable or might be significantly different with a fluid-structure interaction approach. However, it is acceptable that these patterns are not necessarily the exact patterns observed in normal or pathological vocal fold vibration. As stated in the introduction, the goal of this paper was to develop a wide range of possible contact patterns that create a set of complex flow situations that will be used to develop robust flow regimes for computationally efficient models of vocal fold vibration. We acknowledge an iterative process in model refinement toward clinical application. The first-order contact patterns described here lead to abbreviated first-order flow calculation, which then lead to more likely contact patterns with self-sustained oscillation, which then lead to further improvements and simplification in glottal flows and pressure, on so on. In our finite-element modeling (Titze et al., 2017), computation time is of essence because we test hundreds of conditions, each with hundreds of vibration cycles, which means that brute-force three-dimensional Navier-Stokes solutions are prohibitive. Our approach here is a cost-effective way of reaching the clinical application goal, and this process must start with general approximations of possible vocal fold contact areas as described here.

Two final notes are worthy of mention. First, because this is a kinematic approach, we do not conjecture on flow patterns resulting from the contact patterns, nor do we relate pattern types to any acoustic output or voice phenomena. Exploration of these types of kinetic relationships is an ongoing goal that will be described incrementally in future work. Second, in this paper we did not fully quantify the three-dimensional glottal shapes, only the two-dimensional patterns of contact. Glottal width varies in the “open” glottal regions. This adds another element of complexity to the pressure-flow relations that will be considered in future studies based on contact patterns in three-dimensional configurations.

In conclusion, vocal fold contact patterns can be estimated based on normal modes of vibration. A set of characteristic contact patterns was found for the lowest modes of vibration that provides a starting point for future studies to further characterize the contact patterns and, hence, three-dimensional glottal shapes that occur physiologically. These glottal shapes can be used in the development of self-oscillating vocal fold models that can accurately predict glottal pressure profiles and vocal fold motion for complex flow situations, specifically in modeling voice disorders. This study has added to the understanding of vocal fold mechanics and opens the door to more in-depth studies regarding the relationship of muscle activity and voice disorder mechanisms to three-dimensional glottal shapes and resulting vibration patterns.

Supplementary Material

1
Download video file (7MB, mp4)
2
Download video file (7.2MB, mp4)
3
Download video file (6.6MB, mp4)

Acknowledgments

This work was supported by the National Institutes of Health / National Institute on Deafness and Other Communication Disorders grant R01-DC014538.

Footnotes

Conflict Of Interest Statement: The authors have no conflicts of interest that might have influenced the research either financial or in kind

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  1. Baer T, Lofqvist A, McGarr NS. Laryngeal vibrations: A comparison between high-speed filming and glottographic techniques. Journal of the Acoustical Society of America. 1983;73(4):1304–1308. doi: 10.1121/1.389279. [DOI] [PubMed] [Google Scholar]
  2. Berry DA. Mechanisms of modal and nonmodal phonation. Journal of Phonetics. 2001;29:431–450. [Google Scholar]
  3. Berry D, Herzel H, Titze IR, Krischer K. Interpretation of biomechanical simulations of normal and chaotic vocal fold oscillations with empirical eigenfunctions. Journal of the Acoustical Society of America. 1994;95(6):3595–3604. doi: 10.1121/1.409875. [DOI] [PubMed] [Google Scholar]
  4. Berry DA, Montequin DW, Tayama N. High-speed digital imaging of the medial surface of the vocal folds. Journal of the Acoustical Society of America. 2001;110(5):2539–2547. doi: 10.1121/1.1408947. [DOI] [PubMed] [Google Scholar]
  5. Chen LJ, Mongeau L. Verification of two minimally invasive methods for the estimation of the contact pressure in human vocal folds during phonation. Journal of the Acoustical Society of America. 2011;130(3):1618–1627. doi: 10.1121/1.3613708. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Childers DG, Hicks DM, Moore GP, Alsaka YA. A model for vocal fold vibratory motion, contact area, and the electroglottogram. Journal of the Acoustical Society of America. 1986;80(5):1309–1320. doi: 10.1121/1.394382. [DOI] [PubMed] [Google Scholar]
  7. Childers DG, Lee CK. Voice quality factors: Analysis, synthesis, and perception. Journal of the Acoustical Society of America. 1991;90(5):2394–2410. doi: 10.1121/1.402044. [DOI] [PubMed] [Google Scholar]
  8. Childers DG, Ahn C. Meeting the glottal volume-velocity waveform for three voice types. Journal of the Acoustical Society of America. 1995;97(1):505–519. doi: 10.1121/1.412276. [DOI] [PubMed] [Google Scholar]
  9. Deverge M, Pelorson X, Vilain C, Lagrée PY, Chentouf F, Willems J, Hirschberg A. Influence of collision on the flow through in-vitro rigid models of the vocal folds. Journal of the Acoustical Society of America. 2003;114(6):3354–3362. doi: 10.1121/1.1625933. [DOI] [PubMed] [Google Scholar]
  10. Döllinger M, Berry DA, Berke GS. Medial surface dynamics of an in vivo canine vocal fold during phonation. Journal of the Acoustical Society of America. 2005;117(5):3174–3183. doi: 10.1121/1.1871772. [DOI] [PubMed] [Google Scholar]
  11. Doellinger M, Berry DA. Visualization and quantification of the medial surface dynamics of an excised human vocal fold during phonation. Journal of Voice. 2006;20(3):401–413. doi: 10.1016/j.jvoice.2005.08.003. [DOI] [PubMed] [Google Scholar]
  12. Fourcin AJ. Proceedings of the Conference on the Assessment of Vocal Pathology. American Speech and Hearing Association; Washington, DC: 1981. Laryngographic assessment of phonatory function. [Google Scholar]
  13. Gauffin J, Sundberg J. Spectral correlates of glottal voice source waveform characteristics. Journal of Speech, Language, and Hearing Research. 1989;32:556–565. doi: 10.1044/jshr.3203.556. [DOI] [PubMed] [Google Scholar]
  14. Hamlet SL, Reid JM. Transmission of ultrasound through the larynx as a means of determining vocal-fold activity. IEEE Transactions in Biomedical Engineering. 1972;BME-19(1):34–37. doi: 10.1109/tbme.1972.324156. [DOI] [PubMed] [Google Scholar]
  15. Herbst C, Ternström S. A comparison of different methods to measure the EGG contact quotient. Logopedics, Phoniatrics, Vocology. 2006;31(3):126–138. doi: 10.1080/14015430500376580. [DOI] [PubMed] [Google Scholar]
  16. Ishizaka K, Flanagan JL. Synthesis of voiced sounds from a two-mass model of the vocal cords. Bell Labs Technical Journal. 1972;51(6):1233–1268. [Google Scholar]
  17. Luo H, Mittal R, Zheng X, Bielamowicz SA, Walsh RJ, Hahn JK. An immersed-boundary method for flow-structure interaction in biological systems with application to phonation. Journal of Computational Physics. 2008;227(22):9303–9332. doi: 10.1016/j.jcp.2008.05.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Luo H, Mittal R, Bielamowicz SA. Analysis of flow-structure interaction in the larynx during phonation using an immersed-boundary method. Journal of the Acoustical Society of America. 2009;126(2):816–824. doi: 10.1121/1.3158942. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Ma EP, Love AL. Electroglottograph evaluation of age and gender effects during sustained phonation and connected speech. Journal of Voice. 2010;24(2):146–152. doi: 10.1016/j.jvoice.2008.08.004. [DOI] [PubMed] [Google Scholar]
  20. Krebs F, Artana G, Sciamarella D. Proceedings of the 10ème Congrès Français d'Acoustique. Lyon, France: 2010. Constriction modes and acoustic output in an in-vitro self-oscillating vocal-fold model. [Google Scholar]
  21. Mihaescu M, Khosla SM, Murugappan S, Gutmark EJ. Unsteady laryngeal airflow simulations of the intra-glottal vertical structures. Journal of the Acoustical Society of America. 2010;127(1):435–444. doi: 10.1121/1.3271276. [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Neubauer J, Mergell P, Eysholdt U, Herzel H. Spatio-temporal analysis of irregular vocal fold oscillations: Biphonation due to desynchronization of spatial modes. Journal of the Acoustical Society of America. 2001;110(6):3179–3192. doi: 10.1121/1.1406498. [DOI] [PubMed] [Google Scholar]
  23. Oren L, Khosla S, Gutmark E. Intraglottal geometry and velocity measurements in canine larynges. Journal of the Acoustical Society of America. 2014a;135(1):380–388. doi: 10.1121/1.4837222. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Oren L, Khosla S, Gutmark E. Intraglottal pressure distribution computed from empirical velocity data in canine larynx. Journal of Biomechanics. 2014b;47(6):1287–1293. doi: 10.1016/j.jbiomech.2014.02.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Rothenberg M. A multichannel electroglottograph. Journal of Voice. 1992;6(1):36–43. [Google Scholar]
  26. Scherer RC, Titze IR, Curtis JF. Pressure-flow relationships in two models of the larynx having rectangular glottal shapes. Journal of the Acoustical Society of America. 1983;73(2):668–676. doi: 10.1121/1.388959. [DOI] [PubMed] [Google Scholar]
  27. Scherer RC, Shinwari D, De Witt KJ, Zhang C, Kucinschi BR, Afjeh AA. Intraglottal pressure profiles for a symmetric and oblique glottis with a divergence angle of 10 degrees. Journal of the Acoustical Society of America. 2001;109(4):1616–1630. doi: 10.1121/1.1333420. [DOI] [PubMed] [Google Scholar]
  28. Scherer RC, Shinwari D, De Witt KJ, Zhang C, Kucinschi BR, Afjeh AA. Intraglottal pressure distributions for a symmetric and oblique glottis with a uniform duct. Journal of the Acoustical Society of America. 2002;112(4):1253–1256. doi: 10.1121/1.1504849. [DOI] [PubMed] [Google Scholar]
  29. Sciamarella D, Le Quéré P. Solving for unsteady airflow in a glottal model with immersed moving boundaries. European Journal of Mechanics - B/Fluids. 2007;27(1):42–53. [Google Scholar]
  30. Södersten M, Hertegård S, Hammarberg B. Glottal closure, transglottal airflow, and voice quality in healthy middle-aged women. Journal of Voice. 1995;9(2):182–197. doi: 10.1016/s0892-1997(05)80252-8. [DOI] [PubMed] [Google Scholar]
  31. Story BH, Titze IR. Parameterization of vocal tract area functions by empirical orthogonal modes. Journal of Phonetics. 1998;26:223–260. [Google Scholar]
  32. Švec JG, HoráČek J, Šram F, Veselý J. Resonance properties of the vocal folds: in vivo laryngoscopic investigation of the externally excited laryngeal vibrations. Journal of the Acoustical Society of America. 2000;108(4):1397–1407. doi: 10.1121/1.1289205. [DOI] [PubMed] [Google Scholar]
  33. Thomson SL, Mongeau L, Frankel SH. Aerodynamic transfer of energy to the vocal folds. Journal of the Acoustical Society of America. 2005;118(3):1689–1700. doi: 10.1121/1.2000787. [DOI] [PubMed] [Google Scholar]
  34. Titze IR. Parameterization of glottal area, glottal flow, and vocal fold contact area. Journal of the Acoustical Society of America. 1984;75(2):570–580. doi: 10.1121/1.390530. [DOI] [PubMed] [Google Scholar]
  35. Titze IR. The physics of small-amplitude oscillation of the vocal folds. Journal of the Acoustical Society of America. 1988;83(4):1536–1552. doi: 10.1121/1.395910. [DOI] [PubMed] [Google Scholar]
  36. Titze IR. Interpretation of the electroglottographic signal. Journal of Voice. 1990;4(1):1–9. [Google Scholar]
  37. Titze IR. Principles of Voice Production. Prentice Hall; Englewood Cliffs, NJ: 1994. Reprint: 2000 National Center for Voice and Speech, Denver, CO. Translated into Japanese and Portuguese. [Google Scholar]
  38. Titze IR. The Myoelastic-Aerodynamic Theory of Phonation. National Center for Voice and Speech, Denver, CO; 2006. [Google Scholar]
  39. Titze IR, Alipour F, Blake D, Palaparthi A. Comparison of a fiber-gel finite element model of vocal fold vibration to a transversely isotropic stiffness model. Journal of the Acoustical Society of America. 2017;142(3):1376–1383. doi: 10.1121/1.5001055. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Tsuji DH, Hachiya A, Dajer ME, Ishikawa CC, Takahashi MT, Montagnoli AN. Improvement of vocal pathologies diagnosis using high-speed videolaryngoscopy. International Archives of Otorhinolaryngology. 2014;18:294–302. doi: 10.1055/s-0034-1372512. [DOI] [PMC free article] [PubMed] [Google Scholar]
  41. van den Berg J, Zantema JT, Doorenbal P., Jr On the air resistance and the Bernoulli effect of the human larynx. Journal of the Acoustical Society of America. 1957;29(5):626–631. [Google Scholar]
  42. Xue Q, Mittal R, Zheng X, Bielamowicz S. A computational study of the effect of vocal-fold asymmetry on phonation. Journal of the Acoustical Society of America. 2010;128(2):818–827. doi: 10.1121/1.3458839. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Zañartu M, Galindo GE, Erath BD, Peterson SD, Wodicka GR, Hillman RE. Modeling the effects of a posterior glottal opening on vocal fold dynamics with implications for vocal hyperfunction. Journal of the Acoustical Society of America. 2014;136(6):3262–3271. doi: 10.1121/1.4901714. [DOI] [PMC free article] [PubMed] [Google Scholar]
  44. Zhang Y, Regner MF, Jiang JJ. Theoretical modeling and experimental high-speed imaging of elongated vocal folds. IEEE Transactions on Biomedical Engineering. 2011;58(10):2725–2731. doi: 10.1109/TBME.2010.2095012. [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Zheng X, Xue Q, Mittal R, Bielamowicz S. A coupled sharp-interface immersed-boundary-finite-element method for flow-structure interaction with application to human phonation. Journal of Biomechanics. 2010;132(11):111003. doi: 10.1115/1.4002587. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Zheng X, Mittal R, Xue Q. Direct-numerical simulation of the glottal jet and vocal-fold dynamics in a three-dimensional laryngeal model. Journal of the Acoustical Society of America. 2011;130(1):404–415. doi: 10.1121/1.3592216. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

1
Download video file (7MB, mp4)
2
Download video file (7.2MB, mp4)
3
Download video file (6.6MB, mp4)

RESOURCES