A resolution adaptive deep hierarchical (RADHicaL) learning scheme applied to nuclear segmentation of digital pathology images

Abstract

Deep learning (DL) has recently been successfully applied to a number of image analysis problems. However, DL approaches tend to be inefficient for segmentation on large image data, such as high-resolution digital pathology slide images. For example, typical breast biopsy images scanned at 40× magnification contain billions of pixels, of which usually only a small percentage belong to the class of interest. For a typical naïve deep learning scheme, parsing through and interrogating all the image pixels would represent hundreds if not thousands of hours of compute time using high performance computing environments. In this paper, we present a resolution adaptive deep hierarchical (RADHicaL) learning scheme wherein DL networks at lower resolutions are leveraged to determine if higher levels of magnification, and thus computation, are necessary to provide precise results. We evaluate our approach on a nuclear segmentation task with a cohort of 141 ER+ breast cancer images and show we can reduce computation time on average by about 85%. Expert annotations of 12,000 nuclei across these 141 images were employed for quantitative evaluation of RADHicaL. A head-to-head comparison with a naïve DL approach, operating solely at the highest magnification, yielded the following performance metrics: .9407 vs .9854 Detection Rate, .8218 vs .8489 F-score, .8061 vs .8364 true positive rate and .8822 vs 0.8932 positive predictive value. Our performance indices compare favourably with state of the art nuclear segmentation approaches for digital pathology images.

1. Introduction

Deep learning (DL) approaches have seen recent application in digital histology, from localising invasive ductal carcinomas (Cruz-Roa et al. 2014) to detecting mitosis (Cireşan et al. 2013; Wang et al. 2014). A typical digital tissue slide scanned on a whole slide scanner at 40× magnification can also be reconstituted at multiple lower magnifications (e.g. 20×, 10×, 5×). Unfortunately, most DL-based approaches when applied to digital pathology images typically tend to favour a single image scale where there is a linear correlation with the number of pixels which must be analysed and the amount of computation time required. In the case of 2k × 2k images, this process can take 15 hours using a M2090 GPU and the popular open source framework Caffe (Jia et al. 2014), known for its computational efficiency.

To alleviate the burden associated with large images, hierarchical approaches (Janowczyk et al. 2012) have been proposed with a number of image analysis tasks for digital pathology applications. For example, Doyle et al. (2012), use a multi-resolution approach to detect regions of prostate cancer from digitised needle biopsies. Since their task was to identify regions of cancer (large patches on the images), the approach does not require creating a very granular classifier to identify histologic primitives such as individual nuclei.

In this paper, we present a resolution adaptive deep hierarchical (RADHicaL) learning scheme ¹ which utilises a hierarchical approach to reduce computation time for pixel-wise analysis of large digital pathology images. Images obtained at a uniform magnification are resized to M different resolution levels. A set of M networks are trained (Figure 1, blue arrows) to classify pixels at each level. During testing (Figure 1, red arrows), images are resized to the lowest resolution and evaluated by the network trained at that resolution. Pixels classified as the target class are mapped to the next-highest magnification level for analysis. As a result, images at the highest resolution contain many fewer pixels to analyse, reducing overall computation time by about 85% compared with a naïve DL approach while maintaining comparable performance. Traditional approaches, wherein domain specific cues are manually identified and developed into task-specific “handcrafted” features, can require extensive tuning to accommodate these variances. However, DL is particularly well suited for resolution-specific pixel discrimination as it takes a more domain agnostic approach combining both feature discovery and implementation to maximally discriminate between the classes of interest. This is crucial as the object of interest presents differently at the various levels of magnification, thus motivating their necessitating unique features and variable settings for accurate detection or segmentation.

Figure 1.

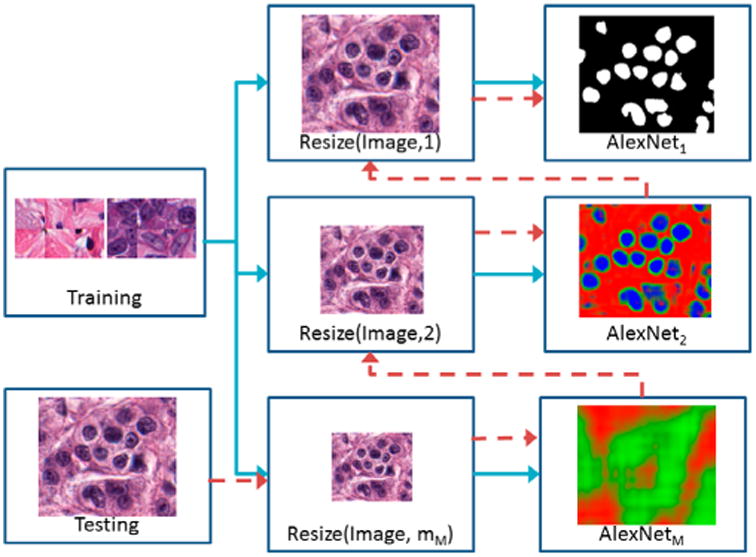
High-level flow chart illustrating RADHicaL. Training images (blue paths) are resized to train M different AlexNet networks at each of the different resolutions m. Test images (red path) are initially reduced to the smallest magnification, where a threshold is applied to the classifier's probability mask so that only relevant pixels are mapped into the next highest resolution for further analysis.

This method is the first, to our knowledge, which uses multiple DL networks, with the same architecture, to significantly reduce computation time for producing a precise, fully annotated, high-magnification digital pathology image. While this approach is generalisable to many other histology tasks, for evaluation purposes, we specifically focus on the task of nuclear segmentation using a cohort of 12,000 expertly annotated nuclei across 141 estrogen receptor positive (ER+) breast cancer (BCa) H&E slides scanned at 40×. Our RADHicaL approach compares favourably in terms of detection accuracy to other state of the art approaches (Veta et al. 2013; Irshad et al. 2014; Xu et al. 2015).

Nuclei segmentation is itself an important problem for two critical reasons: (a) evidence suggests that the organisation of nuclei is correlated with prognosis (Basavanhally et al. 2011), and (b) nuclear morphology is a key component in most cancer grading schemes (Genestie et al. 1998; Humphrey 2004). A recent review of nuclei segmentation literature (Irshad et al. 2014) shows that accurately delineating nuclei and dividing overlapping nuclei is still challenging. Since overlap resolution techniques are typically applied as post-processing on segmentation outputs, they are outside of the scope of this paper, but would likely further improve our segmentation results (Fatakdawala et al. 2010; Ali & Madabhushi 2012). We have specifically chosen to investigate breast cancer images because these nuclei can vary greatly in their presentation across patients and cancer grades, often by changes in area of over 200%. These large variances make developing domain inspired hand-crafted feature approach difficult since it would require understanding and explicitly modelling all possible variances in morphology, texture and colour appearances.

Our RADHicaL approach involves deriving a suitable feature space solely from the data itself without any pre-existing assumptions about the particular task or data-set. This is a critical attribute of the DL family of methods, as learning from training exemplars allows for a pathway to generalisation of the learned model to other independent test sets. Once the DL network has been trained with an adequately powered training set, it is usually able to generalise well to unseen situations, obviating the need of manually engineering features.

The rest of this paper is organised as follows: Section 2 introduces the methodology for RADHicaL, Section 3 describes the experimental setup and results, and lastly, Section 4 summarises our concluding remarks.

2. Methodology

We denote I as the set of images, I_n, n ∈ {1,…, N} each having an associated ground truth binary mask, G_n. Further, M = {m₁, …, m_M} is a set of M rescaling factors, where m_M = 1 is defined as the original base image. For example, an image pyramid using M = {1, .5, .25, .1}, would consist of an original image, a 50, 25 and 10% reduction in resolution, respectively.

2.1. Review of deep learning approach

Our approach towards efficiently analysing digital histology images leverages the smaller version of the popular AlexNet (Krizhevsky et al. 2012) used in the 32 × 32 CIFAR-10 challenge, discussed briefly below. For a thorough review, we encourage the reader to revert to the original paper and associated Caffe implementation (Jia et al. 2014). DL approaches consist of three main components: network selection, training, and testing.

2.1.1. Network selection

The patch size and the network description need to be tightly coupled as the size of the patch determines the lowest layer of the network and thus sets the framework for the additional layers. In this work, we use the 32 × 32 AlexNet, which fixes both our patch size and our network architecture.

2.1.2. Training

Training patches of size 32 × 32 are extracted from the image and assigned their associated class as defined by G, where a positive mask attribute indicates that the centre pixel belongs in the positive class. Examples of the patches are shown in Figure 2.

Figure 2.

Six examples of (a) the negative class show large areas of stroma which are notably different than (b) the positive nuclei class and tend to be very easily classified. To compensate, we supplement the training set with (c) patches which are exactly on the edge of the nuclei, forcing the network to learn boundaries better.

2.1.3. Testing

During testing, 32 × 32 windows around each pixel are fed into the classifier and a class probability is produced. An argmax on the class probabilities, or a threshold (θ) on a specific class, is used to generate the final output.

2.2. Improved patch selection

Since DL techniques learn models directly from the data, the selection of representative patches is critical. Here, we discuss a procedure by which can identify patches that lead to a superior model, and thus a more precise segmentation.

An example of a standard approach could involve selecting positive class patches from I_n using G_n, and applying a threshold to the colour deconvoluted image (Ruifrok & Johnston 2001) to locate likely negative class examples, since non-nuclei regions tend not to strongly absorb hematoxylin. Figure 2 shows that while the patches correctly correspond to their associated class, the negative class (i.e. Figure 2(a)) is not challenging, having selected mostly non-nuclei stromal patches. The resulting network has very poor performance in correctly delineating nuclei boundaries, as shown in Figure 3(d), since these edges are under represented in the training set.

Figure 3.

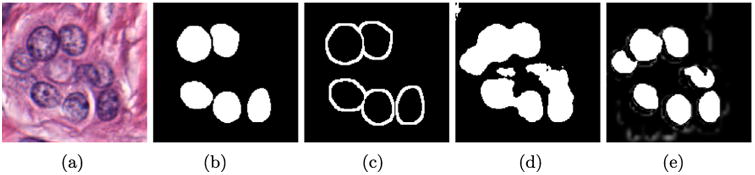
Training label creation. The original image (a) only has (b) a select few of its nuclei annotated, leaving it difficult to find patches which create a challenging negative class. Our approach is to create (c) a dilated edge mask. Sampling locations from (c) allows us to create negative class samples which are of very high utility for the DL algorithm. As a result, our improved patch selection technique leads to (e) notably better delineated nuclei boundaries as compared to (d) a typical approach.

To compensate, we intelligently sample “challenging” patches for the training set. Challenging in this case implies patches which are not obviously in one class or the other, for example, in transition regions or visual confounders. Figure 3(a) shows an example image I_n with its associated mask G_n in Figure 3(b). Note that only a subset of the nuclei are annotated (see Section 3). Using G_n, we can identify (a) positive pixels by randomly selecting from the annotated mask, and (b) randomly extracting negative patches by selecting from the pixels after applying a threshold to the hematoxylin channel of the colour deconvolution image. From a classifier trained with those patches, we obtain the segmentation Figure 3(d), which fails to identify nuclear boundaries. To enhance these boundaries, an edge mask is produced by morphological dilation of G_n (Figure 3(c)). From the dilated mask, we select negative training patches which are inherently difficult to learn due to their similarity to the positive class. Examples of these edge patches are shown in Figure 2(c), which are strikingly similar to the positive class (Figure 2(b)) but have their centre pixels outside of the nuclei. We still include a small proportion of the stroma data, as shown in Figure 2(a), to ensure it is represented. This patch selection technique, which intentionally over-samples edge regions, results in clearly separated nuclei with more accurate boundaries, as seen in Figure 3(e).

2.3. Resolution adaptive deep hierarchical learning scheme

The flow chart in Figure 1 illustrates this process, explained in detail below.

2.3.1. Training

Training proceeds along the blue paths illustrated in Figure 1. For classifier m_i, i ∈ {1, …, M}, each I_n is modified into Î_n by (a) convolving with a matrix $\mathbf{\Delta }=m_i^2{\mathbf{J}}_f$, where f = 1/m_i and J is a matrix of ones of size f × f and then (b) down sampled by a factor of m_i. As a result, three classes can be identified: (i) the positive class when all associated higher resolution pixels in G₁ are positive (i.e. Î_n = 1), (ii) the negative class when all associated higher resolution pixels in G₁ are negative (i.e. Î_n = 0), and (iii) the alternate class if the associated higher resolution pixels in G₁ are both positive and negative (i.e. Î_n ∉ {0, 1}). As shown in Figure 4, during test time, RADHicaL is able to indicate when a higher magnification is necessary to analyse a region as a result of being supplied exemplar patches during training of the three classes: positive (100% object of interest at m₁), negative (0% object of interest at m₁), and alternative (mixed object of interest at m₁). In Figure 4, the red indicates pixels which do not need additional computation at a higher magnification because there are no objects of interest present within them. The blue also represents pixels which do not require additional computation because all of their pixels belong to the object of interest. Lastly, the green pixels indicate where the additional computation is needed in order to obtain a highly accurate segmentation.

Figure 4.

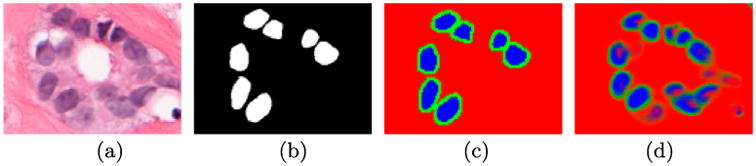
The original image (a) and (b) the associated ground truth. After convolution, the (c) three classes used in training can be identified. The output (d) from RADHicaL indicates that the deep learning classifiers are capable of learning the boundaries well, which forms the foundation of the computational savings.

2.3.2. Testing

During testing (Figure 1, red arrows), an image is first rescaled by a factor of m_M to the lowest resolution. Each pixel in this smaller image is then fed into the associated M AlexNet. The network returns three probabilities for each pixel p, n, and c (which sum to 1).The variables p and n represent the likelihood that the pixel does not need additional computation at a higher level because it is a superset of a region which, at the highest magnification, (a) entirely belongs (i.e. p) or (b) entirely does not belong (i.e. n) to the object of interest. The last probability, c, indicates the likelihood that this particular pixel does indeed need additional computation as it contains a boundary between the region of interest and the background.

Each probability map produced at each of the m ∈ M levels has a two thresholds, θ_m,ε and θ_m,ξ, applied to determine the class memberships. All pixels where p > θ_m,ξ are added directly to the output mask and are not analysed again because they are believed to be a part of the object class at the highest magnification (e.g. blue pixels in Figure 4). Similarly, all pixels where p + c < θ_m,ε are not analysed again and added to final output mask because they are believed to not be a part of the object class at the highest magnification (e.g. red pixels in Figure 4).

These values of θ represents a trade-off: higher values reduce overall computation time by reducing false positives, but at the cost of additional false negatives. In this context, a false positive is a pixel which is predicted to be part of the object of interest but ultimately is not, while a false negative is a pixel which is predicted to not be part of the object of interest, when indeed it truly is. Once the M layer is completed, the remaining pixels (e.g. green pixels in Figure 4) are mapped to the M − 1 layer. Classification proceeds again at this resolution level only for pixels identified as in the previous layer as boundary pixels, drastically reducing the cardinality of the computed set. This process continues through m₁, which produces a high-resolution segmented image after applying the associated threshold.

3. Experimental results and discussion

3.1. Dataset description

The data-set consists of 141 regions of interest (ROIs) from H&E ER+ BCa histology images from 137 patients, scanned at 40×, and cropped to 2k × 2k. We randomly split the ROIs, at the patient level, into three groups for training (112 images), validation (9 images) and testing (20 images). The ground truth consists of about 12,000 manually delineated nuclei, which coincides with about 13 million pixels in the positive class to sample from. An expert was given 10 min per image to segment as many nuclei as possible. As a result, no image consists of a complete nuclei segmentation, but each image contains a notable amount. Due to the laborious nature of the annotation task, it was more beneficial to have as many different ROIs and patients represented, versus far fewer single ROIs completely annotated. As a result, our evaluation metrics are accordingly modelled.

3.2. Method descriptions

3.2.1. Resolution adaptive deep learning (RADHicaL)

We use M = 4 resolution levels, where M = {1, .5, .25, .1}. Using the validation set, we empirically set θ_ξ = {N/A, .61, .8267, .16} and θ_ε = {.5267, .733, .18, .12} via the approach described in Section 3.4. Training sets are generated by randomly selecting 500 nuclei patches (positive), 500 edge patches (alternative) and 500 stroma patches (negative) from each training image as described in Section 2.2. Each patch is also rotated 90° and appended to the training set, yielding about 678,000 training patches per level. This is sufficiently large to prevent over-fitting of the AlexNet (note, CIFAR-10 only has 60k 32 × 32 images).

Our network architecture is the 32 × 32 AlexNet provided by the Caffe DL framework (Jia et al. 2014). To alleviate the need for accurate learning rate selection and an annealmeant schedule, thus simplifying our approach, we use the AdaGrad (Duchi et al. 2011) technique, where optimal gradients on a per variable basis are continuously estimated. An initial learning rate (LR) of .001 was selected, and adjusted on a per variables basis by AdaGrad at each iteration. This continues for a fixed set of 6,000,000 iterations. During training, each patch is randomly mirrored to augment the training set without increasing data size.

3.2.2. Naïve deep learning (NDL)

NDL is created using the same m₁ DL network above, except that this approach computes every pixel in the 40× image. This provides a baseline for which to compare RADHicaL, since RADHicaL obtains its efficiency by selectively computing the pixels at this level.

3.3. Performance measures

We use multiple measures to evaluate our algorithm. Since we do not have fully annotated ground truth images, we instead report the mean F-score, true positive rate (TPR) and positive predictive value (PPV) measures computed on a per nuclei basis thus allowing a comparison to results in Irshad et al. (2014). While those metrics evaluate how well the system can delineate nuclear boundaries, we also present the detection rate, which indicates how many nuclei in the ground truth overlap at least 50% with a segmented nuclei in our results.

3.4. Threshold selection

Selecting an appropriate threshold is very critical, as premature exclusion of pixels from the computation set will result in numerous false negatives later on. On the other hand, a low threshold will add many false positives. While these false positives will be pruned at higher levels of magnification, thus not greatly affecting the accuracy of the system, each additional pixel increases the computation time.

To investigate the relationship between the threshold and the TPR, we use the seven patients from the validation set (corresponding to nine images total). We compute the TPR at various thresholds of θ_m,ε against p + c, since ideally we would like a value of 1 to ensure that no pixels are accidentally pruned prematurely. Figure 5, which shows the TPR in blue and the percentage of pixels which would be computed in green, has the obvious property that when the threshold is set to 0, the TPR is 1, but also 100% of the pixels are computed. Figure 5 shows the expected trade off; the lower the threshold, the higher the TPR, but also an increase in the number of pixels, and thus computation time. We can see that as the level becomes higher, we can choose increasingly lower thresholds without affecting the expected accuracy of the system. For example, Figure 5(a) indicates that for RADHicaL, we can choose a relatively high threshold, say 0.4, which results in improved efficiency as only about 40% of the pixels need to be computed, without a large impact on TPR. On the other hand, if we can accept a TPR of 80%, corresponding to a threshold of 0.5, the number of pixels which need further analysis drops to 25%. We note that in general, the greater the area between the two curves, the greater the speed increase can be exploited.

Figure 5.

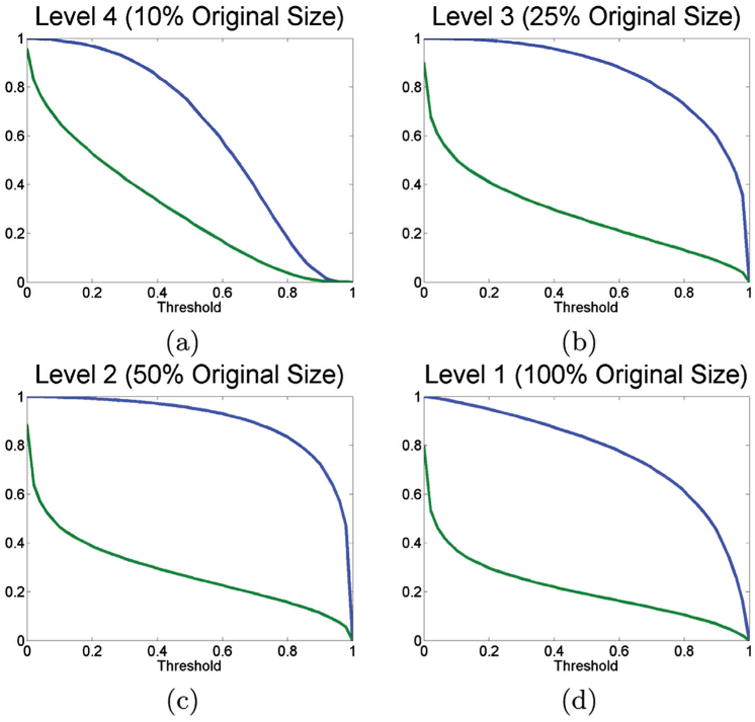
TPRs for RADHicaL computed at various thresholds for the various levels. The blue line corresponds to the TPR, while the green line identifies what percentage of the pixels would be computed at that specific threshold.

One may also glean from the graphs, especially Figure 5(d), is that there are few pixels in the image which represent the target class, allowing our approach to acquire its efficiency. While the TPR has a gentle decline, the number of pixels which meet the required computation threshold at even a low-threshold drop off significantly, for example, from 100% down to 30% at a threshold of 0.3.

To select the appropriate thresholds for a given level of error, we undertake the following procedure. Firstly, we compute the f-score, f_base, using the NDL approach on the validation set, to determine θ_1,ε. This supplies the upper bounded benchmark by which it is possible to measure the segmentation degradation as a result of various thresholds. We opted for a ∼2% decrease in f_base to yield improved efficiency, explicitly f_target = (1 − .02) × f_base. Then, for each level m, we iteratively determine the lowest θ_m,ξ and then the highest θ_m,ε, so that the f-score is greater than or equal to f_target.

3.5. Results

3.5.1. Efficiency

Using Caffe with a Tesla M2090 GPU, a 2k × 2k image takes 55,200 s using the NDL approach juxtaposed with 8952 s for our resolution-adaptive approach; indicating an 83 ± .05% (i.e. 6× fold) speed improvement. Although our resolution adaptive approach requires a one-time training of four separate networks (4 h each = 16 h total) instead of just one (4 h total); there is an obvious time benefit if we amortise over two or more images.

3.5.2. Qualitative evaluation

Figure 6 illustrates the probability maps produced at the various levels on a small cropped region. The blue channel, ranging from [0,1], indicates the confidence in a particular pixel belonging to a nuclei. The red channel indicates the confidence in a particular pixel not belonging to a nuclei. Lastly, the green channel indicated the confidence that a pixel needs additional computation at the next level of magnification. Even at the lowest resolution, Figure 6(d), our algorithm is able to approximate the location of nuclei, obviating the need for the computation of the entire image at the next level as all of the red pixels can be avoided. Mapping upwards to Figure 6(e) m₂ shows a much greater resolution, here the blue pixels will be added to the final segmented output and not computed again, while the green pixels merit additional computation at the next magnification level. Finally, when presenting (f) m₁, which is of the same magnification as Figure 6(c), the results are nearly identical, yet were produced 6× faster, leading us to believe that this approach is fit-for-purpose. We note that since the same classifier is applied at both (c) and (f) (the difference is in which pixels are evaluated), an improvement in the classifier model would likely cascade to improving the results in both, not solely the NDL version.

Figure 6.

Comparison of (f) our approach and (c) the NDL approach. The original image is shown in (a) with its ground truth in (b). Additionally, we show the (d) lowest level m₄ appears and (e) m₂.

Additionally, we note that there is very little noise in the result image in terms of islands of pixels or hollow nuclei as they are removed at the lower levels of magnification. Clearly, the inclusion of the edge patches in training has benefited the output by producing very concise boundaries for the nuclei, as seen in Figure 3(e).

3.5.3. Quantitative evaluation of performance

Table 1 shows the results of a per nuclei F-score, TPR, and PPV comparison between both our resolution adaptive and the NDL approaches. In all cases, our approach very closes mirrors the NDL approach, implying that the efficiency gained did not come at the cost of the quality of the results. Incidentally, our results are similar to those presented in the review (Irshad et al. 2014), including results obtained by Ali and Madabhushi (2012) (TPR 0.86, PPV 0.66) and Fatakdawala et al. (2010) (TPR 0.8, PPV 0.86). These studies employed post processing and cluster splitting approaches which would likely improve our results, but are outside the scope of this paper. Our detection rate, i.e. how well were we able to find the nuclei which were in the ground truth data-set, is over 94%.

Table 1.

Performance metrics comparing our hierarchical approach versus the NDL approach of computing all pixels.

	Detection	F-score	TPR	PPV	Timing
Naïve DL	.9854	.8489	.8364	.8932	∼55,000
Resolution adaptive DL	.9407	.8218	.8061	.8822	∼9000

Note: Timing, in seconds, shows a 6× speed improvement for a typical image.

The overall computational burden for a typical histopathology image can be thought of as the summation of the copmputational load at each of the magnification levels at which the classification or analysis is done. The percent of pixels to the total number of pixel in the image that are computationally interrogated at each magnification level (1, 2, 3, 4) correspond to roughly 5, 24, 43 and 100%, respectively. This in turn translates to contributions of 31, 40, 18 and 11% to the overall computation time. At the highest level of magnification at which the image analysis is done, it is necessary to computationally interrogate every pixel to identify large regions which do not contain the object of interest. Subsequently, at each magnification level, we see an approximate 50% reduction in the number of pixels interrogated at that particular level, which interestingly coincides with the ratio between the magnification reduction levels defined in M.

The trade-off between accuracy and computational load, for this particular problem of nuclei detection is based off the downstream requirements. For instance, if one is simply doing nuclei counting for grading, then one could potentially operate at lower resolutions with higher thresholds. If the need is for a quantitative assessment of nuclear shape or chromatin patterns, then one might need to operate at the maximum possible magnification (e.g. 40×) and use lower thresholds to ensure a precise delineation. Also, as described in Section 3.4, by selecting a higher f_target, the associated θs will change, resulting in better accuracy at the cost of additional computation time. This variance gives the user the ability to weight the accuracy versus the time.

4. Concluding remarks

We have presented are solution adaptive hierarchical deep learning scheme, which identifies object classes by calculating pixel-wise labels at low-resolutions and constrains high-resolution computations to just those pixel regions, significantly reducing execution times. DL is especially suitable as the classifier for RADHicaL, as it allows for a domain agnostic approach that automatically adjusts for the varying presentations of objects of interest at the various levels of magnification. We evaluated the method on a nuclei segmentation task using a database of 141 ER+ BCa images, employing a novel patch selection technique to refine the training and improve overall precision. We show that with a reduction of 85% of the computation time, we can accurately segment nuclei according to F-score (.818), TPR (.8016), PPV (.8822) and detection rate (.9407), which are comparable to a classifier applied directly to the high-resolution image. These results corroborate with currently published state of the art approaches on similar tasks, suggesting that our approach is a viable solution for scaling DL tasks to large digital histology images. There is the potential of improved accuracy and efficiency by augmenting the system with domain-specific post processing approaches (i.e. nuclei splitting) and increased sophistication of predictive pixel class memberships (e.g. Markov Random Fields for tighter coupling of classes of adjacent pixels).