Abstract
Electrochemical systems suffer from poor management of evolving gas bubbles. Improved understanding of bubbles behavior helps to reduce overpotential, save energy and enhance the mass transfer during chemical reactions. This work investigates and reviews the gas bubbles hydrodynamics, behavior, and management in electrochemical cells. Although the rate of bubble growth over the electrode surface is well understood, there is no reliable prediction of bubbles break-off diameter from the electrode surface because of the complexity of bubbles motion near the electrode surface. Particle Image Velocimetry (PIV) and Laser Doppler Anemometry (LDA) are the most common experimental techniques to measure bubble dynamics. Although the PIV is faster than LDA, both techniques are considered expensive and time-consuming. This encourages adapting Computational Fluid Dynamics (CFD) methods as an alternative to study bubbles behavior. However, further development of CFD methods is required to include coalescence and break-up of bubbles for better understanding and accuracy. The disadvantages of CFD methods can be overcome by using hybrid methods. The behavior of bubbles in electrochemical systems is still a complex challenging topic which requires a better understanding of the gas bubbles hydrodynamics and their interactions with the electrode surface and bulk liquid, as well as between the bubbles itself.
Keywords: Bubble growth, Gas-evolving electrode, Two-phase flow
1. Introduction
Electrochemical processes occur at the nano-, micro- and macro- scales in numerous applications such as fuel cells, batteries, hydrogen production, mineral extraction, water treatment, electrotherapy, sensors and many others. In most of these applications, gases evolve either at one electrode or at both electrodes due to electrolysis. These gases form bubbles that play a crucial role in electrochemical systems. For example, gas bubbles in Hall-Heroult cells have a significant positive role in both homogenization of alumina distribution and the temperature field in the bulk flow.1 Ultrasound surface cleaning applications use the bubble swarm to clean the solid/liquid interface surface. In this application, bubbles are generated from the electrode and then the ultrasonic irradiation drives the generated bubbles to clean the solid/liquid interface surface.2 In electrochemical groundwater remediation systems, the presence of electrochemically generated oxygen and hydrogen bubbles along with a suitable redox condition may stimulate anaerobic or aerobic processes in the bulk or create strong oxidizing or reducing conditions that improve abiotic contaminants degradation.3 In fuel cells, the channels will be blocked if the evolved gas bubbles are not removed efficiently which limits mass transport.4 In some electrochemical biosensor applications, the generated layer of gas bubbles on the electrode surface protects the electrode from erosion, which increases the working life of the electrodes.5
All electrochemical systems suffer from the adhering layer which is formed by bubbles evolution as a consequence of supersaturation of dissolved gas bubbles in the bulk.6 This adhering layer causes the formation of an inactive area on the electrode surface which prevents the fresh bulk solution from contacting the electrode surface to produce the necessary reaction. In addition to this effect on mass transfer, the adhering layer acts as an electrical shield that reduces the conductivity and increases the ohm resistance on the electrode surface.7 The characteristics of this layer depend on the interfaces between three-phases; solid, gas and liquid, which are respectively electrode, bubble, and bulk solution. These interfaces are strongly related to the electrode geometry, cavities, wettability, bubble composition, bulk solution chemistry, flow velocity and reaction components (e.g. current density).8, 9 On the other hand, the detachment and release of bubbles from the electrode surface induces a wake or micro-convection which enhances the mass transfer at the detachment location. This enhancement depends on the size of the bubbles and their detachment velocity. Similarly, the physics of the bubbles presence on the electrode surface happens on ion-exchange membrane surfaces as well.10 The released bubbles disperse into the electrolyte and form void fraction in the two-phase systems. The void fraction causes overpotential, increases the cell resistance and lowers the effective conductivity of the electrolyte.7, 11 The motion of bubbles inside the bulk has a role in mass transfer by inducing macro-convections inside the bulk.
The complex effects of these gas bubbles in electrochemical systems require efficient management in the reactors or cells. Techniques have been developed to enhance the bubbles detachment from the electrode surface and to provide better mixing by external sources such as magnetic, ultrasonic and super gravity fields or by studying the bulk flow pattern effect.8, 10–19 Other studies tried to develop new materials and surface treatments to reduce the surface tension on the electrode surface, which reduces the residence time of bubbles on electrode surface and expedites their release frequency.20–24 But very few have focused on improving the cell configuration and electrode geometry. All of these studies investigate the bubbles from one aspect only that are based on the specific application which leaves many unanswered questions and limited understanding of the hydrodynamics of bubble formation and behavior. For instance, what is the applicable range of supergravity fields on electrochemical systems to reduce the overpotential? Do the ultrasonic fields always have positive interaction on bubbles detachment? What are the best methods to simulate two-phase (liquid-bubble) electrochemical systems? What is the effect of changing bulk flow velocity on the bubble flow regime? Most importantly, the behavior of bubbles in electrochemical systems is still a complex challenging topic which requires a better understanding of the gas bubbles hydrodynamics and their interactions with the electrode surface and bulk liquid, as well as between the bubbles itself.
Extensive theoretical, numerical and experimental work has been carried out to understand the physicochemical hydrodynamics of gas bubbles in two-phase electrochemical systems. However, these studies tend to look at the problem from a specific angle relevant to their application, and there is a need to review the fundamentals and multi-scale aspects of the gas bubble processes. In this paper, we review the techniques to model, simulate, measure, and control bubbles in electrochemical systems, to establish a better understanding of these techniques and their strengths and limitations. The paper describes the fundamental hydrodynamics of gas bubbles on the electrode surface and the fundamental hydrodynamics of gas bubbles interaction with the liquid bulk solution. Also, the paper discusses the computational methods to simulate the two phase electrochemical systems. Then the available techniques to enhance gas management inside electrochemical cells are reviewed. Furthermore, the paper covers a review of experimental techniques that are used in the measurement of gas bubbles hydrodynamics.
2. Two phase electrochemical systems
Gas bubbles evolving mechanism at the electrode surface, in electrochemical reactors, can be divided into four micro process stages.25, 26 These stages occur simultaneously at the electrode surface (Fig. 1):
Figure 1.
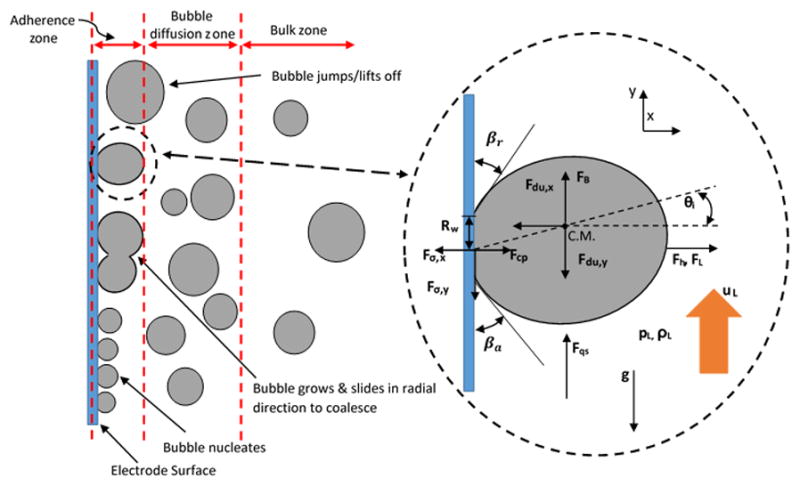
Schematic diagram for balance of forces on growing and detaching bubbles at adherence region for vertical electrode with absence of external sources
A. Nucleation
Gas bubbles start nucleating at the active sites of the electrode surface due to electrolysis once the liquid solution reaches supersaturation condition. It is convenient to express the state of the liquid solution in terms of the gas solubility, c (mol m−3), and supersaturation ratio, ζ, as follows:
| [1] |
| [2] |
where kH is Herny’s constant (mol N−1), which is specific to the gas-liquid pair at given temperature and Pgas is the partial pressure of the gas (N m−1). co is the concentration of the dissolved gas in liquid solution at given temperature and pressure (mol m−3). cs is the equilibrium (saturation) concentration of dissolved gas (mol m−3). ζ represents the excess amount of the dissolved gas, where supersaturation requires ζ>0.
Following from supersaturation of a dissolved gas, gas bubble nucleation occurs at the electrode surface. Gas bubbles may nucleate starting from an initial bubble size of zero, as assumed by classical nucleation theory (CNT). On the other hand, bubbles can also form within pre-existing gas pockets trapped on a surface in contact with the supersaturated liquid solution. Even though the CNT is more preferable in electrochemical cells models, Sequeria, C. A. C. et al., 2013 27 reported that the effectiveness of CNT for electrolytic gas evolution needs further examination and investigation about the effect of the electric field within the electric double layer.
B. Growth
Gas bubbles grow due to continuous electrolysis and the growing bubble may simultaneously slide on the electrode surface to coalescence with another bubble. The large growing bubble acts as a collector and attracts smaller growing bubbles. Bubbles continue to coalesce forming larger bubbles. One of the possible driving mechanisms of bubbles radial coalescence motion on the electrode surface is thermocapillary phenomena.28 The induced temperature gradient on the electrode surface causes thermocapillary effects. Two main reasons explain the presence of temperature gradient at the electrode surface; first, the reaction overpotential, which happens at the electrode surface, and second, the heat conduction losses because of the electrode material finite resistivity.
Sillen, C.W. 1983 29 stated that there are three controlling mechanisms occur during bubbles growth period as follows:
Mechanical forces (hydrodynamics).
Heat transfer, due to the temperature gradient.
Mass diffusion, due to the supersaturation of the surrounding liquid solution.
The dissolved gas concentration at time t (sec), after starting the electrolysis, c, is given by Fick’s second law for transient diffusion model of one species, at the electrode, as follows:
| [3] |
where D is the diffusion coefficient of the redox-active species (m2 s−1). The convective mass transfer near the electrode is considered negligible and it is assumed that only diffusion-controlled mass transfer occurs at the electrode. Sakuma, G. et al., 2014 30 provided solution for Eqn.3 in terms of electrochemical gas evolving reaction parameters and by assuming one-dimensional space, where the cell input current is completely converted to gas evolution. The dissolved gas concentration determines the supersaturation of dissolved gas, which controls the bubble growth.31 Moreover, the variation degree of supersaturation depends on interfacial curvature and the surface energy used to build the gas/electrode interface.30, 31
C. Detachment (Departure)
The bubble detaches from the electrode surface, once the bubble size reaches a critical volume (radius) at which the buoyancy force exceeds the interfacial tension between the gas bubble and the solid electrode surface. After the bubble jumps from the electrode surface, it moves into the bulk flow. At this stage, the detached bubble provides an active vicinity at the electrode surface for new fresh electrolytes to react and regenerate new bubbles.
In contrast to equilibrium bubble detachment, it has been found that the bubble which is formed by coalescence of two large bubbles would disassociate from the electrode surface, jump off and sometimes return to the electrode surface.27, 32
D. Rise (Buoyancy and Flow)
After the bubble diffuses into the bulk solution, it moves into the bulk flow under the influence of the driving flow mechanism (natural or forced convection). The interaction between the liquid bulk and gas bubbles is generally classified as two-phase flow interaction.
These stages form three distinguished zones around the electrode (Fig. 1).33 The first zone is the adherence region and it is located at the electrode surface where the bubble nucleates, grows and coalesces with other bubbles. The second zone is the bubble diffusion region, which is a thin-diffusion layer where bubbles enter and start their diffusion toward the bulk electrolyte. Lubetkin, S. 2002 reviewed the motion of bubble near the surface of electrode.32 The last zone is the bulk region, liquid-bubble interaction region, where bubbles rise and interact with electrolyte bulk flow away from the electrode.
In this section, we explore the governing equations of bubbles hydrodynamics inside the electrochemical cell two parts: bubble-electrode and bubble-bulk flow interactions, which provide an overall view of the physics of these interactions. Also, we assess the simulation methods of two-phase bubbly flow and the necessary governing equations for electrochemical systems (transport of momentum, species and mass equations).
2.1. Balance of forces acting on bubbles at electrode-bubble interaction region
Generally, the published Computational Fluid Dynamics (CFD) models do not consider that the electrode releases the generated bubbles from its surface with a certain frequency but assume it is a continuous process. For simplicity, these models use Faraday’s law to evaluate the generated gas flux from the electrode surface, which is given:
| [4] |
where jb is the production flux of the specific gas by electrolysis (m s−1), i is the current density (A m−2), Mw is the molecular mass of the produced gas bubble (kg mol−1), z is the number of participating electrons in electrochemical reaction, F is Faraday’s constant (= 96485 (c mol−1) and ρb is the gas bubble density (kg m−3). These models assume the electrode as a black box that produces a specific mass of a gas and/or other species into the solution at a constant rate, which means evolved gases are assumed to nucleate and detach from the surface of electrode as soon as reaction occurs and the amount of dissolved gases in the electrolyte solution is neglected. However, this is not accurate for two reasons. First, determination of bubbles detachment frequency is necessary, especially for electrodes with high surface tension parameters or reactors with small bulk flow velocity (e.g. natural convection flow pattern). In these cases, the bubbles detachment frequency is higher and the efficiency of detached bubbles with respect to the generated bubble should be considered. Second, the amount of the produced gases does not completely convert to bubbles nucleation, instead there is a portion which dissolves into the electrolyte.
Understanding the micro physics behind the electrode-bubbles interactions requires introduction of the forces that act on growing and detaching bubbles. These forces that influence the bubbles behavior at the adherence region are crucial to determining and controlling the bubbles detachment frequency. The balance of these forces promotes the understanding of the bubbles curtain around the electrode surface.34, 35 The cycle of bubble evolution at the electrode surface in electrochemical systems is similar to bubble evolution at a solid surface in boiling systems. The gas bubble growth in electrochemical cells is driven by concentration difference between the bulk solution and the gas bubble interface, where bubble growth in boiling systems is driven by the temperature difference. However, obtaining the concentration data from electrolysis reaction is not easy, and because of the bubble growth in electrochemical systems is less developed compared to bubble growth in boiling systems.36 The hydrodynamic forces that control the gas bubbles growth and their release from a vertical electrode can be analyzed into x and y acting forces. These forces are mainly a function of the electrode cavities, bulk flow parameters (e.g. supersaturation and velocity) and the cell configurations (shown in Fig. 1).
The balance of forces at x-direction:
| [5] |
The balance of forces at y-direction:
| [6] |
Where the Fdu is the unsteady growth force which acts as drag force (N), Fσ is the surface tension force between the bubble and electrode surface (N), Fh is the hydrodynamic force due to hydrodynamic pressure (N), FL is the shear lift force (N), Fcp is the contact pressure force (N), FB is the buoyancy force (N) and Fqs is the quasi-steady drag force due to bulk flow (N). The balances of forces are written in the absence of any external sources applied on the cell (e.g. ultrasound, magnetic fields).
As long as the resultant force is in negative x-direction and in negative y-direction, ΣFx < 0 and ΣFy < 0 respectively, bubbles remain attached to the surface of the electrode. But if the resultant force is no longer in negative x-direction, and it is still in negative y-direction, then the bubble will start sliding on the electrode surface. Once the resultant force is no longer in both negative x and negative y directions, then the bubble jumps off the electrode surface, detaches and moves toward the bubble’s diffusion region.35 In other words bubbles leave the electrode surface when the gas bubble size reaches a critical value at which the sum of both FB and Fqs forces exceeds the sum of both Fσ,y and Fdu,y forces, ΣFy ≥ 0.34 By assuming spherical shape for the bubble for simplicity, the forces in y-direction can be evaluated easily to determine bubble departure diameter, its growth rate and detachment frequency.
The surface tension force (Fσ,y) is a function of the advancing angle, receding angle and contact diameter between bubble and electrode surface, which are βa (degree), βr (degree) and dw = 2Rw (m) respectively. These parameters depend on the electrode cavities, surface condition and its polishing. The surface tension force causes the generated bubble to detach from the surface of electrode periodically. Because of the major effect of surface tension force, controlling the bubble detachment and its distribution in the adherence and diffusion regions can be achieved by controlling the electrode cavities. The Fσ,y force 35 can be estimated as:
| [7] |
where σ is surface tension (N m−1). The contact diameter can be written as:34
| [8] |
where db is the bubble diameter (m) and βm is the mean contact angle (degree).
Moving to the unsteady growth force (Fdu,y) which can be written as:
| [9] |
where ρL is the liquid bulk density, rb is the bubble radius that is related to the bubble growth rate (m), Cs is empirical coefficient and ṙb and r̈b are the first and second time derivative of the bubble radius respectively. θi is the inclination angle (degree) which is defined as the angle between the x-axis and the growth force and depends on the electrode surface cavities similar to βa and βr
The bubble radius is related to the growth rate of the individual bubble which is given in general form as:37
| [10] |
The value of A and γ constants are determined experimentally by a least-square procedure to fit rb(t). The growth rate depends mainly on the supersaturation; this growth explains how fast the bubble can be transported across the interface. Lubetkin, S.D. 1995 26 reported that the growth rate of diffusion-controlled growth can be given as following:
| [11] |
where A1 is a constant for given conditions of supersaturation and D is diffusion coefficient of the dissolved product (m2 s−1). The same relation has been suggested by Sakuma et al., 2014.30 The same relation can be used for faradic bubble growth rate; however, the results of constants product (S = 2A1(D)½) will be different (for example, it has been reported that S equals 0.5 for diffusion-controlled growth and S equals 0.3 for the faradic growth 38). Vogt and Stephan, 2015 25 reported similar relation for the growth rate in terms of Fourier number (Fo) by setting Fo = 1/(4 A12) in the growth rate equation. They mentioned that Fo remains constant shortly after the bubbles growth starts.
Additional relation for the bubble growth rate at high current densities had been reported by Donose B.C et al., 2012:38
| [12] |
where A2 is a coefficient that depends on the current and faradic stoichiometry and is given based on Faraday’s and Charles’s law:
| [13] |
where R is the universal gas constant (J mol−1 K−1), T is the absolute temperature (K) and P is the pressure value (N m−2).
The buoyancy force (FB) depends on the interphase density between the bubble and the bulk flow which represents the driving mechanism for this force and it can be written as:
| [14] |
where db is the gas bubble diameter (m), and Δρ is the interphase density which equals to the difference between the liquid and bubble (gas) density (kg m−3), ρL and ρg respectively.
The quasi-steady force (Fqs) is a drag force that influences the bubble in the direction of the bulk flow and is given as:
| [15] |
where CD is the drag coefficient, μL is the liquid bulk dynamic viscosity (N s m−2) and Reb is the bubble Reynolds number, which is given as:
| [16] |
ur is the relative velocity between the bubble center of mass (C.M.) and the liquid bulk velocity.
The bubble departure diameter and its release frequency from the electrode surface can be evaluated based on the previous hydrodynamic definitions of each force and by solving the equation ΣFy = 0. Modeling this type of interaction between bubble and electrode surface helps to evaluate the bubbles coverage area on the electrode surface area. The bubbles coverage area is related to the applied current density on the electrode, bubble production release from electrode surface and mass transfer physics around the electrode region.25 The coverage area due to bubbles accumulation on the electrode surface tells us the percent of the electrode inactive area because of the bubbles blanket. Vogt, H. 201731 has published a paper about the quantities that affect the bubble coverage of gas-evolving electrodes.
Liu, H. et al., 2016 39 simulated the growth of a single hydrogen bubble at electrode surface by using FLUENT to determine the bubble growth behavior and its effect on mass transfer. They stated that until now there are no reliable results to predict the break-off diameter of an electrolysis bubble diameter because i) the neighbor bubbles disturbance results in a premature departure from the electrode surface, ii) electrocapillarity, and iii) variations of surface tension in the presence of the dissolved gases.
The boundary conditions of the bulk liquid at the electrode surface is one of the important variables that should be considered at the electrode-bubble interaction region. The majority of the literature limits their modeling to the no-slip condition of the liquid on the electrode surface. However, due to the large number of produced bubbles and their direct formation on the electrode surface bubbles, a full slip or partial slip condition should be considered during modeling. 40 Furthermore, most literature simulated the behavior of growing and detachment of a single bubble without considering the presence of multiple bubbles which causes coalescence on the electrode surface. It is important to mention that the built-in codes in commercial simulation software treat the constant angle between the electrode surface and growing bubble as static while it is a dynamic contact angle which requires the user to code a user-defined function. Di Marco et al., 2013 41 studied the effect of electrical force on bubble shape and Zhang et al., 2012 42 found that at a higher cell voltage more fine bubbles detach from the electrode surface. However, further investigation is highly recommended and required to understand the effect of the electrical force, which is caused by electrode charges and the electrode surrounding charges/ions, on the bubbles detachment from the electrode surface. It is important to understand how this electrical force contributes in the bubbles residence time on the electrode surface.
2.2. Balance of forces acting on bubbles at bulk liquid-bubble interaction region
Modeling and simulation of multiphase problems are extremely challenging due to the inherent complexities, as the gas and liquid phases are not independent. The nonlinear and multiscale interactions between the two different phases characterize the interfacial transfer of mass, momentum, and energy. At the same time, combining the models of ion transport and reaction kinetics of electrochemistry to the two-phase flow dynamics increases the model complexity. CFD models provide accurate simulations of such complex systems. Hreiz et al., 2015 43 summarized CFD hydrodynamics investigations for vertical plane electrode simulated systems. The majority of these studies adapted 2D simulation; however, understanding the nonlinear motion of bubbles requires 3D modelling. Simulation of two phases and multiscale system of bubble columns is carried out either by using the Eulerian-Eulerian (E-E) model, Eulerian-Lagrangian (E-L) model or Direct Numerical Simulation (DNS) model. The E-E model is known as two-fluid models/formulation, which considers both phases interoperating liquids and employs a continuum approach to both gas bubble and liquid phases. In this approach, additional closure models are required to determine the bubble size distribution due to the bubble-liquid and bubble-bubble interactions.44–46
A more accurate approach compared to the E-E is the E-L model, which is usually employed on lab scale and is known as Discrete Bubble Modeling (DBM). The DBM model describes the liquid phase by Navier-Stokes continuum and considers it a carrier. On the other hand, it treats the bubbles as dispersed phase and describes these bubbles by Lagrangian approach. The Lagrangian approach tracks each bubble individually using Newton’s second law.47 The time step of the liquid phase (global) is divided into small time steps to evaluate the information of the bubbles. Mapping techniques are required here to relate the Eulerian and Lagrangian quantities. This approach does not require any additional closure to determine the bubble size distribution since it is considered as a part of the approach nature.48 However, additional closures in this model are still needed to account for the interaction forces between bubble-liquid phases.45 Even with the dynamic characteristics determination of bubbles superiority for E-L model over E-E model, E-L framework has downsides. One of the limitations of the E-L approach is the number of bubbles (e.g. maximum O (105)).44, 49 Since this approach solves the equation of motion for each bubble individually, the cost of simulation increases as compared to the E-E approach. Another drawback in E-L models is the gas-liquid free surface boundary interface treatment, which is estimated by artificial boundary condition or buffer zone technique and that ignores the dynamics of the free surface.48
E-E and E-L models are used widely in multiphase flow. However, DNS models are the most accurate models that are generally performed to obtain micro-scale data. The accuracy of DNS approach arises because it solves Navier-Stokes equations without prior assumptions. However, the cost of DNS models is very expensive and it can only be performed for a small number of bubbles (e.g. O (102)).45, 50 There are several methods for DNS models, which are varied in the description of interface boundaries and its treatment. The methods that treat the interface boundary with fixed grid are: Level Set (LS), Lattice Boltzmann (LB), Volume of Fluid (VOF) and Front Tracking (FT). Among all of these methods, FT method, which is an interface tracking method, only resolves the interface boundary explicitly by adapting Lagrangian surface/grid which makes it a superior method to locate the interface location and shape high resolution and thus reducing the numerical diffusion at interface without applying refine grid at the interface. The main drawback of the FT method is the mass conservation due to the mapping between the Eulerian and Lagrangian quantities. Also, the FT requires sub-grid models to account the physics of bubbles coalescence and break-up, since tracking the interface surface is very complex.45, 51 On the other hand, the two widely used methods of the class of interface capturing methods are VOF and LS, whereas these methods use an artificial scalar field for an implicit description of the interface. The advantages and drawbacks of VOF and LS methods are listed in Table 1.
Table 1.
Summary of advantages and disadvantages of DNS methods for multiphase flow 56
| Method | Advantages | Disadvantages |
|---|---|---|
| Front Tracking |
|
|
| Level Set (LS) |
|
|
| Marker Particles |
|
|
| SLIC VOF |
|
|
| PLIC VOF |
|
|
| Shock-Capturing |
|
|
| Lattice Boltzmann |
|
|
| Coupled LS-VOF (CLSVOF) |
|
|
| Coupled Marker Particles-LS |
|
|
Clearly, each method has its advantages and disadvantages which make it difficult to identify an optimum approach. Further research and development are required to implement hybrid CFD methods by coupling the available CFD methods; DNS (Table 1), DBM and E-E methods. The benefit of using hybrid simulation methods is mainly the opportunity to overcome downsides of one method by coupling another method that covers this downside successfully. For instance, Jain, D. et al., 2014 52 adopted a hybrid approach to simulate bubble column by treating the free surface using VOF and the rest of the system by using DBM. Also, Asad et al., 2017 53 implemented a similar hybrid approach in their study to resolve the free surface interface boundary properly. Another hybrid simulation method has been reported for bubble flow system by modeling the liquid (continuous) phase using LB method and the dispersed bubble by using Lagrangian scheme.54 At the same time, optimization of parallel computing techniques can reduce the simulation time of bubble flow systems. Table 1 lists two popular hybrid models, which are Coupled LS-VOF and Coupled Marker Particles-LS methods.
CFD simulations provide the opportunity to examine the wake phenomena of bubbles, which is one of the most important characteristics of bubbles hydrodynamics and mass transfer. Marschall, H. et al., 2012 55 stated that the bubble wake phenomena have a significant effect on mass transfer due to its influence on both rising trajectory and mixing pattern in the proximity of the bubble. They reported 55 that the wake patterns can be categorized into: i) steady wake without circulation, ii) steady wake with circulation and iii) unsteady wake with vortex structure and vortex shedding. Based on the wake type different bubble trajectories can be observed during bubbles rise. These trajectories are classified in bubble rise free flow system as: i) straight trajectory, ii) zigzag trajectory and iii) spiral/helical. These bubble trajectories can be easily visualized in CFD simulations.
In this paper, we are introducing the necessary governing equations to model two-phase bubbly flow in electrochemical system based on the E-L framework. The E-L model explains clearly the hydrodynamic forces on the bubbles. The governing equations of the E-L model, which will be introduced in the following section were adopted in Darmana, D. et al., 2005 49 for electrochemical systems.
A. Eulerian phase hydrodynamics
The mass conservation of liquid phase is introduced based on continuity equation:
| [17] |
where εL is the volume fraction of the liquid phase, uL is the velocity of the liquid phase (m s−1) and Ṁ is the interphase mass transfer (kg m−3 s−1). The effect of bubbles presence in the system is taken into account in the liquid phase volume fraction where εL + εb = 1 and in the absence of bubbles the volume fraction of bubbles phase εb is zero. Also, the source term of mass interphase transfer, Ṁ, accounts for bubbles presence in the system.
The hydrodynamics momentum conservation of Eulerian phase is given by average-volume Navier-Stokes momentum equation as:
| [18] |
P and τL are respectively the pressure and shear stress tensor of the liquid phase (N m−2). fL→b is the forcing term due to bubble-liquid interface interactions (N m−3). In the momentum equation, the presence of bubbles is taken into account by εL and fL→b terms.
B. Lagrangian phase hydrodynamics
The motion of each individual bubble is described by Newton’s second law, where bubbles are considered as incompressible fluid. The contributions of the liquid phase are considered via the mass interphase transfer rate, ṁ (kg s−1), and the net force, which acts on each individual bubble. The governing equation of bubbles hydrodynamics can be written as:
| [19] |
| [20] |
where ρb, Vb, ub are respectively the density (kg m−3), volume (m−3) and velocity (m s−1) of the bubble. FB,FL,FP,FV,M,FW,FD are respectively the uncoupled buoyancy, lift, pressure, virtual mass, wall and drag forces (N). The expressions of these forces are discussed in details in Darmana, D. et al., 2005 and Jain, D. et al., 2014 published papers.49, 52
The processes responsible for changing the size and shape of each bubble in the multiphase flow system are one of the most important points to consider during such simulation. These processes are described as: break-up, coalescence, gas compressibility, phase transition and deformation of bubbles due to the interface forces.57 Generally, the coalescence and break-up phenomena are the main reason for bubbles size distribution and shape deformation. The spherical shape of bubbles can be imposed for simplicity in simulation since the size of bubbles is very small.57 However, it should be taken into account that bubbles shape (shown in Fig. 2) could be spherical, ellipsoidal, wobbling (irregular), skirted or cap based on Reynolds, Eotvos and Morton numbers.58 The bubble interfacial area is an important parameter which influences the overall species transfer. The bubble interfacial area depends on its shape and because of that, it is advisable to study different shapes. The physics of coalescence and break-up are only considered in turbulent flows. It is assumed that in laminar (homogeneous) flows that bubbles do not coalesce or breakup since the chance collisions between gas particles in laminar flow are very small. However, it has been claimed that multi-phase flow systems are generally at least pseudo turbulent.59 For better understanding of mathematical simulation of coalescence and break-up of bubbles, we recommend the reader consider Lau, Y.M. et al., 2014 48 and Jain, D. et al., 2014 52 for better understanding and detailed explanations. As we see the flow pattern is very important to determining the bubbles size distribution inside the two phase flow, especially by controlling the frequency of collision between bubbles which leads to coalescence and breakup. To date, the literature does not include or consider coalescence and break-up physics when simulating electrochemical cells.
Figure 2.
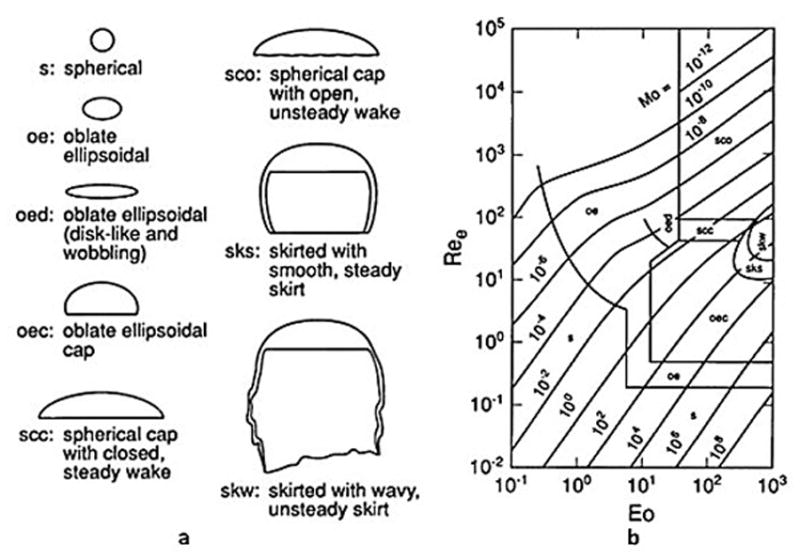
(a) Schematic diagram of commonly observed shapes of bubbles, (b)The shape-map of deformed bubbles based on Reynolds, Eotvos and Morton numbers60
C. Transport of chemical species
The reactive transport of chemical species (j) inside the liquid phase mixture is given for each species by:
| [21] |
where and are respectively the mass fraction of liquid and bubble. is the effective species diffusion transport coefficient (m−2 s−1). The source term Sj accounts for the rate of gain or loss of the species due to the chemical reaction (kg m−3 s−1).
The species transfer associated with bubble dynamics is still not fully understood. Different experimental correlations have been obtained. However, these experimental correlations are evaluated at specific experimental conditions, which ensure reproducibility.55 The CFD simulations can avoid these experimental limitations and provide evaluation at different conditions.
D. Interphase mass transfer
The gradient of mass fraction is considered the driving mechanism for the interphase mass transfer of the bubble. The mass transfer rate of the bubble due to this driving mechanism is given for each species as:49
| [22] |
where E is the mass transfer enhancement factor because of the chemical reaction and it can be given by approximated relation in terms of Hatta number.49 is the mass transfer coefficient for chemical species (m s−2), Ab is the interfacial area of the bubble (m2) and is the mass fraction on the liquid side of the bubble-liquid interface and can be determined using Herny’s law:
| [23] |
where kHj is Henry’s constant for chemical species j and is the mass fraction on the bubble side of the interface.
3. Experimental techniques to measure gas bubbles dynamics
Although the computational power of CFD methods has resulted in significant progress over the last decades, the development of CFD in multiphase flows requires high resolution and reliable experimental data for verification. Both Laser Doppler Anemometry (LDA) and Particle Image Velocimetry (PIV) have become standard experimental techniques in fluid dynamics measurement. LDA and PIV have been widely used in different applications to determine the flow patterns in multiphase systems using image processing procedures.61–64 Specifically, both techniques have been used to measure bubbles hemodynamics in electrolytic cells.15, 65–67
PIV technique determines the velocity fields of a fluid using an optical, non-intrusive instantaneous measurement method. PIV measures gas bubbles data in gas-liquid system by injecting small tracer particles that ideally follow the continuous phase flow. A laser light sheet is used to illuminate the tracer particles in a target plane of the flow between two successive light pulses with time delay. Then a digital camera records the two subsequent positions of the tracer particle to compute the particle displacement using image processing software and collect data about gas bubbles velocity.61 PIV can determine the velocities of two different phases simultaneously without disturbing the flow. LDA is a non-invasive method used to measure the instantaneous flow velocity of a particle or the speed of moving solid state surfaces in fluid. Due to its high degree of accuracy, spatial and temporal resolution, and the statistical data collected, the LDA method is known as a “gold standard”.68 LDA is an optical single point measurement technique, which can only measure the velocity of one single tracer particle injected into the continuous liquid phase at a time. Therefore, it cannot measure the velocities of different phases simultaneously. A comparison between PIV and LDA techniques is summarized in Table 2.61
Table 2.
Comparison between PIV and LDA
| Technique | Summary |
|---|---|
| Laser Doppler velocimetry |
|
| Particle image velocimetry |
|
Niels G. Deen et al., 2000 61 performed both PIV and LDA measurements on a bubble column to compare the efficiency of both techniques in gas-liquid flow system. They found the PIV velocity data appears to be much smoother compared to LDA data. It seems the sample period for LDA measurements is too short to obtain steady time-averaged data. However, PIV fails to determine which phase is measured by using a single camera. That means additional algorithm is needed to differentiate between the tracer particles and the dispersed phase (bubble). LDA is suitable technique to study the liquid phase in bubbly flows,63 where PIV is faster and preferable to collect data about bubble dynamics in multiphase flow. However, PIV has limitation of accuracy that should be considered during collection of measurements.69
4. Bubbles management by external sources
4.1. Super gravity field
Imposing an external source gives the potential to rotate the electrode/electrochemical cell, and generates a centrifugal field inside the electrochemical cell. It was found that applying such centrifugal fields increases the electrochemical cell performance.10, 12, 70–72 The rotation of the electrochemical cell creates an acceleration environment at both the electrode and bulk. The centrifugal rotating acceleration works along with the interphase buoyancy force, Δρg, to improve the bubbles removal from the electrode surface, reducing the gas blanketing on the membrane by increasing the interphase slip velocity between the gas and solid surface. The gravity coefficient or relative acceleration coefficient, G, for the cell is defined as the ratio of rotational cell acceleration, ω2r, to the normal gravity acceleration (g = 9.8 m s−2):
| [24] |
G acts like an amplification factor; when G equals 1 the cell will be operating under normal gravity field, and as G value increases beyond 1 the system will no longer be under normal gravity and instead be operating under a super gravity field. By introducing this type of gravity field, the ohmic voltage drops and the overpotential may be reduced by intensifying the interphase slip velocity, which weakens the gas bubbles coverage on the electrode surface and exposes more efficient active area of the electrode to interact with the electrolyte and decrease the negative effect of the gas bubbles shield layer. Wang et al. 12, 71 confirmed that under the super gravity effect the hydrogen evolution reaction has smaller critical radii for forming nucleate bubbles, and the rotation acceleration contributes to create larger buoyancy force which allows a rapid bubble disengagement or spillover from the electrode surface or electrolyte with shorter contact time. They investigated the effect of changing the G coefficient value on electrochemical reaction by conducting water electrolysis reaction under galvanostatic conditions in 0.1 NaOH solution under normal and super gravity effects. They obtained good linear relation between G value and the cell voltage (E) at different current densities which can be expressed by the formula: 71
| [25] |
where EG is the cell voltage under super gravity effect (V); γ is the change rate of EG with the logarithm of the gravity coefficient (G) and can be determined from the experiment data under specified conditions, and Eo (V) is the cell voltage for given current density under normal gravity. As the value of G increases the cell voltage increases for the same current density value. The previous formula is similar to results achieved by Cheng and Scott, 2003 70 during their study of the effect of centrifugal field as well. However, they found the maximum overpotential reduction occurs at 0.5 A cm−2 under super gravity. Increasing the current density beyond 0.5 A cm−2 causes an intense gas bubble evolution at the electrode surface. This high production of the gas bubble counteracts the effects of super gravity. The bubbles coverage area of the electrode surface is significant at high current density, even with the presence of super gravity effects. On the other hand, the super gravity has a dominant effect at low current density.
The increased convective bulk solution velocity due to the applied centrifugal source field is another benefit that has a positive effect on the cell chemical reactions. This positive effect can enhance the mass transfer in the reactor by introducing an increase in turbulence flows and mixing inside the cell. Under a normal gravity field, the buoyancy force drives the bubbles to evolve upwards against the gravity direction (Fig. 3a). On the other hand, under super gravity the bubbles will be forced to move in angular path (Fig. 3b). By this rotational movement the gas bubbles will disengage from the electrode surface with vorticity, the bulk electrolyte will gain forced convective velocity and bubbles dispersion through the electrolyte will be enhanced. These effects of turbulence promotion in the cell will result in better mass transfer coefficients. It was reported that by increasing the rotating speed of the electrode the mass transfer coefficient will increase due to the increasing convection factor of total mass transfer.73 From another angle the fluid turbulent flow has diffusive and dissipative characteristics due to the generated vorticity and velocity fluctuations inside the reactor which produces higher mass transfer-rate inside the reactor.74
Figure 3.
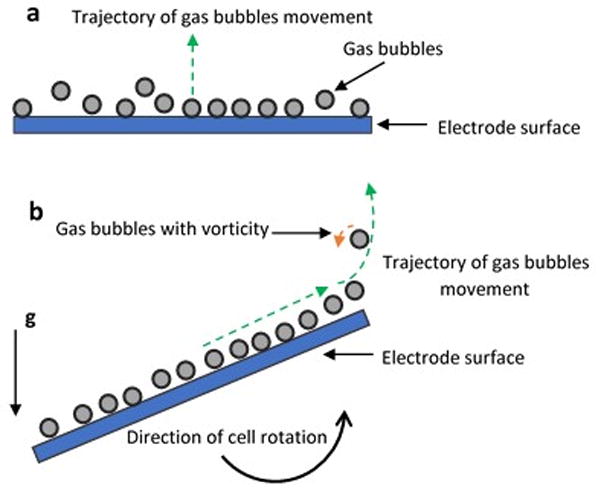
Pathways of bubbles movement: (a) Cell under normal gravity, (b) Cell under super gravity effect
External power consumption is one of the important points that must be taken into consideration when an external source applies to create super gravity environment. The super gravity field reduces the cell voltage drop because by enhancing bubbles management, operating the rotational movement of the cell or electrode requires input energy to the source of the super gravity field. This means an optimization between the consumed power by the external source and the saved power due to the enhanced bubbles management must be studied and considered carefully, especially in energy production cells such as fuel cells. As we explored there is a critical current density value on the electrode that limits the super gravity effect; increasing the current density beyond this critical value causes the intense gas bubbles generation to counteract the super gravity effect. Also, as reported 12 at certain values of gravity amplification, G, the reduction in overpotential will be at the peak and as we move toward higher value of gravity amplification the overpotential reduction decreases and the significant effect of super gravity will be less. This means as we input more power to achieve a higher value of gravity amplification beyond the critical value of G, the energy saving difference will be smaller and may not be worth the input of extra power.
Another important point that must be considered is the design restrictions of the electrochemical cell site, where integrating a rotating mechanism is inconvenient. For example, in groundwater remediation sites where they use electrochemical reactors in a well,3 it is not possible to generate rotational movement since the reactor is restricted in its location. In electrochemical nanotechnology applications it is not easy to impose centrifugal rotational source in such scales of nano-electrochemical cell.75, 76 Furthermore, the high centrifugal driving force on the reactor may affect the mechanics of reactor structure components.
4.2. Ultrasonic field
Using ultrasonic field (USF) is one of the promising applications to reduce gas bubbles accumulation on the electrode surface and the void fraction inside the bulk electrolyte.13 This external source technology induces acoustic waves, which oscillate the adhered gas bubbles on the electrode surface. The vibrating waves assist the attached bubble at the surface of the electrode to overcome the surface tension forces at gas-solid interphase and enhance the gas bubbles removal from the electrode surface.77 The disengagement of bubbles results in a reduction in the electrochemical cell voltage potential drop and it has effect on the mass transfer as well.
Li, S. -D. et al., 2009 13 reported that applying USF in a water electrolysis reactor enhances the hydrogen production rate by 5–18% at certain current densities, because the sound waves will carry the hydrogen bubbles away from the cathode as soon as the hydrogen bubbles generate and before they are able to coalesce. However, the oxygen bubbles generation decreases by 8% at high electrolyte concentration under the presence of USF.13, 78 Under normal conditions, oxygen bubbles grow and coalesce with neighboring bubbles. The buoyancy force can remove the bubbles from the surface of the electrode, once the bubble reaches a certain volume at which disengagement occurs at the interphase. Under USF the oxygen bubbles coalescence will be hindered by the oscillation dynamics on the bubbles, and since the oxygen bubble has a larger diameter compared to the hydrogen bubble, it requires a higher force to overcome the surface tension at the gas-solid interphase. The gas type affects the bubble hydrodynamics. In conclusion, the oxygen bubble size will not reach the critical diameter under USF to release it from electrode surface via buoyancy force, and the sound waves cannot disengage the oxygen bubble by itself. As we can see, applying USF has a noticeable effect on the mass transfer and this effect is directly related to gas bubbles size in electrochemical reaction.
At the same time, acoustic waves affect the fluid dynamics and interaction between the gas bubbles and electrolyte. The major forces that drive the bubbles through the liquid phase of the electrolyte are the buoyancy force, the drag force and the acoustic force, or Bjerknes force under USF. The Bjerknes force, Fp (N), is a body force acts on the bubble and given by:79
| [26] |
where Vb is the volume of the bubbles (m3) and ∇Ps is the liquid pressure gradient (N m−3) around the bubble which is the function of the acoustic wave amplitude, its frequency and the wave number, which are generated by the USF source. Bjerknes force changes its sign and fluctuates between positive and negative; this behavior causes instability in the bubbles motion into the bulk and yields lower rise velocity of bubbles.79, 80 These effects result in an increase in the gas hold-up in the electrochemical reactor.
The rapid removal of bubbles in presence of USF causes a reduction in the cell voltage drop in water electrolysis and the energy savings are estimated be between 4–25%,13, 78 depending on the electrolyte concentration and its type. However, the consumed power to run the USF source should be considered. Also, there is no clear study between varying the applied sound frequency in USF and the cell voltage drop to understand the required input power on external source versus the energy savings in the reactor. It is also necessary to consider the limiting acoustics parameters (e.g. amplitude and frequency) on the electrochemical reactions and on the structure mechanics of the electrodes to avoid unnecessary disadvantages (e.g. damage). One option is using pulsed USF, which lowers power consumption but produces similar effects.
4.3. Magnetic-Hydrodynamic field
There had been considerable interest in applying an external Magnetic-Hydrodynamic field (MHD) on electrochemical reactions as one of the potential areas to control bubbles evolution. The magnetic field generates a body force that induces a hydrodynamic stirring effect on the electrolyte; this force is called the Lorentz force and is given as , where ι⃗ is the current density and B⃗ is the magnetic flux (T). The direction of FMH (N), which is determined from the cross product operation, and its magnitude have a significant convective influence on the bubbles cycle inside the electrochemical reactor.11, 15, 17–19, 81–85 Accordingly, the direction and magnitude of FMH are very important; when the FMH acts in the same direction of the buoyancy force then the effect will be cumulative and will increase the bubbles release frequency from the electrode surface, and the released bubbles will have smaller diameters compared to the bubbles in absence of the MHD. On the other hand, when FMH acts in the opposite direction of the buoyancy force, it decreases the bubbles release frequency from the electrode surface, stabilizes the growth rate of bubbles and produces higher bubbles diameter. The influence of FMH magnitude on bubble frequency release at bubble-electrode regime has a noticeable effect by varying the magnetic flux strengths (B), but the magnitude of FMH with respect to varying the current density has a relatively small effect on the bubble release frequency at the same regime.82 A possible explanation for this observation is that changing the current density will change directly the production rate of the bubbles at the electrode, and at higher current frequency the bubbles reach a certain diameter to detach in shorter time compared to lower current density. For that reason, the high production rate of bubble’s influence on the bubbles detach frequency is the dominant factor compared to the contribution of FMH in this case, even though increasing the current density increases the magnitude of FMH.
The FMH induces stirring effect in the bulk flow, and acts on the electrolyte ions and charged redox molecules, which increases the velocity of the bulk flow and enhances the mass transfer inside the reactor, especially when the magnetic flux direction is perpendicular to the direction of the ion flux. The empirical relations of the limited current that is generated by disk milli-electrode, il, and the mass transport coefficient, m, are given as:81, 85
| [27] |
| [28] |
where n is the number of participating electrons of the redox process, A is the area of electrode (m2), D is the diffusion redox-active species (m2 s−1), υ and c are the kinematic viscosity (m2 s−1) and the concentration of the bulk electrolyte (mol m−3) respectively and F is Faraday’s constant. Both Eq. 27 and Eq. 28 are valid for steady-state, magnetic field intensity between 0.85–1.75 T and the current density is perpendicular to the magnetic flux.
The pumping effect of the forced convective motion of the charged species plays a significant role in accelerating the bubbles in the region of bubble-electrolyte interphase. These accelerated ascending bubbles contribute to the mass transfer enhancement inside the electrochemical cell and reduction of void fraction in the electrolyte bulk, which decreases the overpotential of the cell as well. The MHD has been recognized as one of the important imposed sources to affect the bubbles inside the electrochemical cells; however, further investigations are required to understand the direction of magnetic flux influence, bubbles growth and the effect of electrode geometry in the presence of MHD.
5. Effect of bulk flow on bubbles
The flow pattern has a direct significant control on the bubbles mass transfer, heat transfer and its superficial velocity in electrochemical reactors. The flow patterns in vertical electrodes reactor can be classified 7, 43 as (shown in Fig. 4): i) Forced Convection: where the electrolyte is being pumped into the electrochemical reactor which causes pressure gradient to drive the bubbles inside the reactor, ii) Free (Natural) Convection Induced Circulations: the rising bubbles, which are being driven by buoyancy force from the electrode vicinity, cause a net flow inside the reactor and exert motion to the stagnant liquid electrolyte, and iii) Blocked Convection (no net flow) where the rising bubbles drives the electrolyte near the electrode area, causing stirring; however, the far electrolyte regime from electrode suspends this motion by inducing an opposite loop motion. The last type is not commonly used in industrial applications and the focus is mainly on force and free convection flow types; however, it is helpful to develop better understanding of the bubble curtain layer characteristics.
Figure 4.
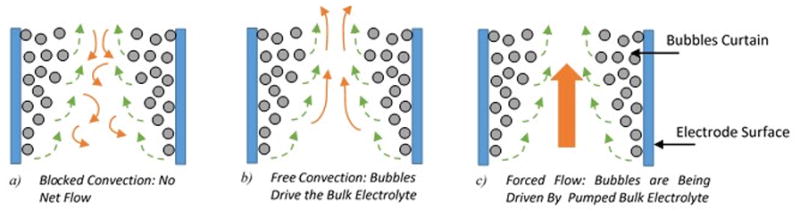
Flow Patterns in Vertical Electrode Reactors: bubbles motion, electrolyte motion
The natural flow type reactor has an important contribution in predicting diffusion-controlled electrochemical process.86 In this type of flow, the bubbles detach from the surface of the electrode once the gravitational buoyancy force exceeds the interfacial surface tension force between electrode-gas interphase; then the density difference between the electrolyte and the bubbles interphase causes buoyancy-induced flow that drives the bubbles inside the bulk. Mat and Aldas, 2005 87 investigated the natural convection flow pattern applications, and reported the gas release rate from the electrode surface increases as the current density increases. However, this behavior is nonlinear and at a high current density the bubbles coverage area on the electrode surface increases because of the high intensity production of bubbles at the electrode surface. The coverage area of the generated bubbles at the electrode surface diminishes the penetration of fresh electrolyte to active electrode areas. The micro-convection of the gas bubbles in this type of flow pattern is the dominant mechanism of mass transfer.
In forced convection flow the motion of electrolyte bulk exert drag force on the bubbles which is summed to buoyancy force to overcome the interfacial tension force at the vicinity of electrode-gas interphase and lift force tries to push the bubble away from the electrode surface. The growing bubbles on the electrode surface more likely move from the nucleation vicinity along the electrode surface until they coalesce/collide with another bubble, at which time the volume of the collided bubbles reaches the critical diameter. The increased volume enables both drag and buoyancy forces to overcome the interfacial tension force and release the bubble from the electrode surface.42, 88 Following this the bubbles move inside the bulk, which drives the bubbles by means of electrolyte flow momentum besides the interphase density (buoyancy force). The macro-convection motion of the electrolyte enhances the bubbles detachment from the electrode surface. As the bulk velocity increases the critical departure diameter of the bubbles from the electrode surface decreases.42 Also, the high bulk velocity lowers the void fraction (gas hold-up) by reducing the residence time of bubbles inside the electrolyte bulk (enhances bubbles rise). Increasing the bulk velocity improves the mass transfer by instigating turbulence and avoiding the recombination of the electrochemically produced gaseous species.88, 89 Understanding the bubble-electrolyte interphase flow is essential to optimizing the mass transfer and bubbles detachment efficiency.
The flow pattern affects the superficial gas velocity which plays a significant role with the reactor scale-up to determine the characteristics of the bubbles distribution regimes inside the electrochemical reactor (e.g. homogeneous, transition, heterogeneous bubbling regimes).90–94 The homogeneous (ideal bubbly) regime is characterized by laminar, uniform size of bubbles (coalescence and break-up interactions are negligible) and radially uniform gas hold-up. This regime occurs at low to moderate gas superficial velocity, almost in blocked or natural convection flow patterns, and the bubbles hold-up has a linear relation with superficial bubbles velocity. On the other hand, the heterogeneous regime is characterized by turbulent, non-uniform and wide distribution of bubble sizes due to the existence of coalescence and break-up interactions with the presence of a radial gas hold-up profile. This is called churn-turbulent flow because the large bubbles churn through the liquid phase. The transition regime represents the developing zone between homogeneous and heterogeneous bubbles. The hydrodynamics difference between each flow regime characteristics leads to different mass and heat transfer rates. Determination of the flow regime is very important to optimizing the geometry scales of the reactor and velocity ratio between the bubble and electrolyte phases; such information is usually indicated in a flow map that provides the essential information about geometry scale, gas velocity, liquid velocity and gas hold-up. Hine and Murakami, 1980 7 reported at high current density in narrow channels, which are operated under natural circulation, slug flow could be observed.
6. Bubbles management by cell components
The physical properties of electrode material, its size, surface characteristics and the configuration of electrochemical cells have a significant influence on gas evolution on the electrode surface and bubbles distribution inside the electrochemical cell. Understanding these physical properties and their effects are necessary to enhance bubbles hydrodynamics management by changing the electrochemical cell configuration or improve the physics of the electrode.
6.1. Electrode inclination angle
Many studies have reported the effect of the inclination angle of the electrochemical electrodes.97–100 However, the cathode and the anode should be always kept in parallel position to avoid any non-uniformity in potential and current distributions between the electrodes. Usually, when the electrode is oriented in a vertical or horizontal direction, the buoyancy acts in one direction on the growing bubbles at the electrode surface. However, by changing the electrode inclination angle, the buoyancy force will have two force components. One component acts on the growing bubbles in normal direction to the electrode and the other component acts in parallel direction to the electrode surface. Kreysa, G. and H.J. Külps, 1981 98 stated an optimum inclination angle for the electrodes based on the minimum voltage drop due to gas bubbles generation, which was −15° (considering zero angle at y-axis, 90° angle at x-axis and −90° at negative x-axis convention) based on experimental results. They observed a flat range of minimum voltage drop based by on changing the inclination between 15° and −45°. However, their study did not include information about the inclination angle effect on bubbles detachment frequency or considering bubbles size distribution. Fei, K. and C.W. Hong, 2006 99 simulated the effect of inclination angle on microchannel fuel cell system. They reported that the change of inclination angle has a direct effect on bubbles velocity inside the cell. By keeping the flow perpendicular to the gravity direction, the bubbles were able to reach the outlet in the simulated slug flow. However, moving away from this orientation and changing the inclination angle will require additional momentum by means of increasing the inlet flow velocity. The purpose of increasing the inlet velocity is to supply the bubbles with enough momentum to reach the outlet of the channel, because the buoyancy force will not be able to provide the necessary momentum. Abdelouahed, L. et al., 2014 97, 100 studied the lantern blade electrode cells where a group of electrodes with the same polarity are placed in successive parallel positions and a counter electrode is fixed in perpendicular position with respect to other electrodes. They found the inclination angle and the gap space between the parallel electrodes influence the bubbles distribution by less than 20%, but they stated that these parameters cannot be considered a key parameter for the properties of electrogenerated bubbles. On the other hand, the inclination angle influences the diversion of gas bubbles between the electrodes, and therefore the gap between the electrode must be adjusted based on the inclination angle to reach optimum design goals (e.g. bubble accumulation on electrode surface). This brings us to the next important parameter in the electrochemical cell configuration and its effect on bubbles inside the cell, which is the gap distance between the electrodes.
6.2. Distance between electrodes (Inter-electrode distance)
The gap between the electrodes is the main region where bubbles are generated; the flow of chemical species along with bubbles takes place inside the electrochemical cell. The spacing between the electrodes impacts the electrical resistance of the electrochemical cell. Nagai, N. et al., 2003 101 found at low current density the cell voltage drop decreases as the gap distance decreases with small void fractions in the cell, while at a large current density the increased production of bubbles due to high current density causes a higher voltage drop as gap distance decreases. The ohmic potential is affected directly by the gap distance between the electrodes; the drop of ohmic potential is proportional to the gap distance between electrodes.102, 103 Sajid Hossain, M. et al., 2017 104 reported that increasing the channel width between electrodes increases the non-uniformity of gas flow in conventional Z-type fuel cells. The cell cross section (gap distance between electrodes) and bulk flow rate velocity should be optimized to make sure the bubbles detach from the electrode surface. These parameters are the criteria of flow pattern determination as discussed in earlier sections.
6.3. Electrode Geometry/Arrays
The electrode geometry has a significant contribution in bubble detachment promotion. The electric current density and the mass transfer at the electrode are related directly to the electrode geometry. Because of these decisive roles, the electrode geometry should be optimized to increase the surface contact area between the bulk flow and electrode surface, and to obtain a uniform electrical field distribution. The most popular electrode geometries are the flat plate, cylindrical and spherical in different orientations (vertical, horizontal and inclined). Perforated plate geometry appears 105 to be slightly better than mesh geometry in the aspect of bubbles detachment from the electrode surface at low percolation velocities. Meshed plate electrodes are reported 106 to enhance the turbulence intensity and mass transfer due to its contribution in improving the liquid flow distribution inside the electrochemical reactor. However, this work does not cover the bubble flow or discuss bubble behavior. Chen, G., 2014 102 reported a novel arrangement of electrodes by placing anode and cathode in the same plane, where this arrangement causes a quick dispersion of the generated bubbles in the wastewater flow. This open configuration allows the bulk flow to contact the electrode surface directly which enhances bubbles dispersion into the bulk. Ultimately, literature primarily focuses on studying the effect of electrode geometries/arrays on electrode’s electrical properties.107, 108
Overall, research to understand or optimize electrode arrangement and configurations to control bubble formation in electrochemical reactors is lacking. Further understanding is needed for electrode geometry and its configuration as they are among the dominant parameters to control the bubbles detachment frequency, velocity, diversion in the reactor and size.
7. Summary and Conclusion
Bubble generation in electrochemical cells plays a significant role in the mass transfer and cell efficiency. Bubbles residence time on the surface of the electrode should be controlled to prevent accumulation of bubbles on the electrode surface. There are no reliable methods to predict the break-off diameter of bubbles from the electrode surface due to the complex transient physics that influence bubble behavior. Better distribution of bubbles inside the cell is to enhance the mass transfer rate; however, the void fraction due to the bubbles presence in bulk flow increases the overpotential and reduces the cell efficiency.
PIV method is preferable to measure bubble dynamics over LDA method. Experimental results using accurate technologies such PIV or LDA are expensive, time consuming and sometimes have limitations. Experimental techniques permit collection of data to be extracted from a limited number of locations in the system. With available supercomputing capabilities, computational method enhances understanding, allows visualization of bubble trajectories, allows great control over the physical processes, couple transport of species with hydrodynamic simulations and provides information about bubble growth and detachment behavior at the electrode surface. However, the available CFD studies ignore the physics of coalescence and break-up of bubbles because of process complexity. Bubbles coalescence and break-up works should be extended to fully understand bubbles behavior. Hybrid solvers should be considered to simulate the electrochemical cells in CFD for higher resolution and better outcomes.
Different external source technologies have been proposed to enhance bubble behavior inside the electrochemical cells; however, these technologies are efficient under specific conditions and rates. Optimization between power input to the external source and increased efficiency of the electrochemical cell should be considered when integrating external sources.
The electrode shape and the cell configuration have a major impact on bubbles behavior and management of bubbles can be enhanced by adopting novel electrode shapes and optimizing the distance between electrodes or cell orientation. Little work has been done in this area and further studies and research will valuable, especially in the study of new electrode shapes and their effect on bubbles release frequency. Also, the distance between electrodes (cell cross section) relative to the flow and current rate an important parameter to determine the flow pattern of bubbles inside the electrochemical cell along with bulk flow velocity. The flow bulk velocity significantly contributes to bubbles management.
Furthermore, electrode surface material determines the electrode cavities and surface tension, which is the dominant force that causes bubble residence on the electrode surface.
Supplementary Material
Figure 5.

Flow patterns: (a) Flow regime of gas-liquid phases in vertical flow95, (b) Flow regime of gas-liquid phase in horizontal flow96
Acknowledgments
This research work was supported by the US National Institute of Environmental Health Sciences (NIEHS, Grant No. P42ES017198). The content is solely the responsibility of the authors and does not necessarily represent the official views of the NIEHS or the National Institutes of Health.
References
- 1.Alam M, Yang W, Mohanarangam K, Brooks G, Morsi YS. Metallurgical and Materials Transactions B. 2013;44(5):1155–1165. [Google Scholar]
- 2.Birkin PR, Offin DG, Vian CJB, Leighton TG. Physical Chemistry Chemical Physics. 2015;17(33):21709–21715. doi: 10.1039/c5cp02933c. [DOI] [PubMed] [Google Scholar]
- 3.Mao X, Yuan S, Fallahpour N, Ciblak A, Howard J, Padilla I, Loch-Caruso R, Alshawabkeh AN. Environmental Science & Technology. 2012;46(21):12003–12011. doi: 10.1021/es301711a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Lu GQ, Wang CY. Journal of Power Sources. 2004;134(1):33–40. [Google Scholar]
- 5.Jin Y, Mao H, Jin Q, Zhao J. Analytical Methods. 2016;8(24):4861–4866. [Google Scholar]
- 6.Gabrielli C, Huet F, Nogueira RP. Electrochimica Acta. 2005;50(18):3726–3736. [Google Scholar]
- 7.Hine F, Murakami K. Journal of the Electrochemical Society. 1980;127(2):292–297. [Google Scholar]
- 8.Matsushima H, Iida T, Fukunaka Y. Journal of Solid State Electrochemistry. 2012;16(2):617–623. [Google Scholar]
- 9.Vogt H, Balzer RJ. Electrochimica Acta. 2005;50(10):2073–2079. [Google Scholar]
- 10.Cheng H, Scott K, Ramshaw C. Journal of The Electrochemical Society. 2002;149(11):D172–D177. [Google Scholar]
- 11.Weier T, Landgraf S. The European Physical Journal Special Topics. 2013;220(1):313–322. [Google Scholar]
- 12.Wang M, Wang Z, Guo Z. International Journal of Hydrogen Energy. 2010;35(8):3198–3205. doi: 10.1016/j.ijhydene.2010.04.183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Li SD, Wang CC, Chen CY. Electrochimica Acta. 2009;54(15):3877–3883. [Google Scholar]
- 14.Xi X, Cegla FB, Lowe M, Thiemann A, Nowak T, Mettin R, Holsteyns F, Lippert A. Ultrasonics. 2011;51(8):1014–1025. doi: 10.1016/j.ultras.2011.05.018. [DOI] [PubMed] [Google Scholar]
- 15.Baczyzmalski D, Karnbach F, Yang X, Mutschke G, Uhlemann M, Eckert K, Cierpka C. Journal of The Electrochemical Society. 2016;163(9):E248–E257. [Google Scholar]
- 16.Grant KM, Hemmert JW, White HS. Journal of Electroanalytical Chemistry. 2001;500(1–2):95–99. [Google Scholar]
- 17.Koza JA, Mühlenhoff S, Żabiński P, Nikrityuk PA, Eckert K, Uhlemann M, Gebert A, Weier T, Schultz L, Odenbach S. Electrochimica Acta. 2011;56(6):2665–2675. [Google Scholar]
- 18.Matsushima H, Iida T, Fukunaka Y. Electrochimica Acta. 2013;100:261–264. [Google Scholar]
- 19.Matsushima H, Kiuchi D, Fukunaka Y. Electrochimica Acta. 2009;54(24):5858–5862. [Google Scholar]
- 20.Brussieux C, Viers P, Roustan H, Rakib M. Electrochimica Acta. 2011;56(20):7194–7201. [Google Scholar]
- 21.Lee SG, Jeon DH. Journal of Power Sources. 2014;265:363–369. [Google Scholar]
- 22.Li Y, Zhang H, Xu T, Lu Z, Wu X, Wan P, Sun X, Jiang L. Advanced Functional Materials. 2015;25(11):1737–1744. [Google Scholar]
- 23.Xu J, Vaillant R, Attinger D. Microfluidics and Nanofluidics. 2010;9(4):765–772. [Google Scholar]
- 24.Wang NW Hongbin, Hang Tao, Li Ming, et al. Applied Surface Science. 2016;372:7–12. [Google Scholar]
- 25.Vogt H, Stephan K. Electrochimica Acta. 2015;155:348–356. [Google Scholar]
- 26.Lubetkin SD. Chemical Society Reviews. 1995;24(4):243–250. [Google Scholar]
- 27.Sequeira CAC, Santos DMF, Šljukić B, Amaral L. Brazilian Journal of Physics. 2013;43(3):199–208. [Google Scholar]
- 28.Guelcher SA, Solomentsev YE, Sides PJ, Anderson JL. Journal of The Electrochemical Society. 1998;145(6):1848–1855. [Google Scholar]
- 29.Sillen CW. The effect of gas bubble evolution on the energy efficiency in water electrolysis. 1983 [Google Scholar]
- 30.Sakuma G, Fukunaka Y, Matsushima H. International Journal of Hydrogen Energy. 2014;39(15):7638–7645. [Google Scholar]
- 31.Vogt H. Electrochimica Acta. 2017;235:495–499. [Google Scholar]
- 32.Lubetkin S. Electrochimica Acta. 2002;48(4):357–375. [Google Scholar]
- 33.Boissonneau P, Byrne P. Journal of Applied Electrochemistry. 2000;30(7):767–775. [Google Scholar]
- 34.Cho YJ, Yum SB, Lee JH, Park GC. International Journal of Heat and Mass Transfer. 2011;54(15):3234–3244. doi: 10.1016/j.ijheatmasstransfer.2011.04.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Hong G, Yan X, Yang Y-h, Xie T-z, Xu J-j. Nuclear Engineering and Design. 2012;247:202–211. [Google Scholar]
- 36.Hu X, Wang Y, Guo L, Cao Z. Advances in Condensed Matter Physics. 2014;2014 [Google Scholar]
- 37.Van Helden WGJ, Van Der Geld CWM, Boot PGM. International Journal of Heat and Mass Transfer. 1995;38(11):2075–2088. [Google Scholar]
- 38.Donose BC, Harnisch F, Taran E. Electrochemistry Communications. 2012;24:21–24. [Google Scholar]
- 39.Liu H, Pan L-m, Wen J. The Canadian Journal of Chemical Engineering. 2016;94(1):192–199. [Google Scholar]
- 40.Alexiadis A, Dudukovic MP, Ramachandran P, Cornell A, Wanngård J, Bokkers A. International Journal of Hydrogen Energy. 2011;36(14):8557–8559. [Google Scholar]
- 41.Di Marco P, Kurimoto R, Saccone G, Hayashi K, Tomiyama A. Experimental Thermal and Fluid Science. 2013;49:160–168. [Google Scholar]
- 42.Zhang D, Zeng K. Industrial & Engineering Chemistry Research. 2012;51(42):13825–13832. [Google Scholar]
- 43.Hreiz R, Abdelouahed L, Fünfschilling D, Lapicque F. Chemical Engineering Research and Design. 2015;100:268–281. [Google Scholar]
- 44.Darmana D, Deen NG, Kuipers JAM. Journal of Computational Physics. 2006;220(1):216–248. [Google Scholar]
- 45.Baltussen MW, Kuipers JAM, Deen NG. Chemical Engineering Science. 2014;109:65–74. [Google Scholar]
- 46.Liao Y, Rzehak R, Lucas D, Krepper E. Chemical Engineering Science. 2015;122:336–349. [Google Scholar]
- 47.Jain D, Lau YM, Kuipers JAM, Deen NG. Chemical Engineering Science. 2013;100:496–505. [Google Scholar]
- 48.Lau YM, Bai W, Deen NG, Kuipers JAM. Chemical Engineering Science. 2014;108:9–22. [Google Scholar]
- 49.Darmana D, Deen NG, Kuipers JAM. Chemical Engineering Science. 2005;60(12):3383–3404. [Google Scholar]
- 50.Tryggvason G, Esmaeeli A, Lu J, Biswas S. Fluid Dynamics Research. 2006;38(9):660–681. [Google Scholar]
- 51.Dijkhuizen W, Roghair I, Annaland MVS, Kuipers JAM. Chemical Engineering Science. 2010;65(4):1427–1437. [Google Scholar]
- 52.Jain D, Kuipers JAM, Deen NG. Chemical Engineering Science. 2014;119:134–146. [Google Scholar]
- 53.Asad A, Kratzsch C, Schwarze R. Engineering Applications of Computational Fluid Mechanics. 2016;11(1):127–141. [Google Scholar]
- 54.Sungkorn R, Derksen JJ, Khinast JG. Chemical Engineering Science. 2011;66(12):2745–2757. [Google Scholar]
- 55.Marschall H, Hinterberger K, Schüler C, Habla F, Hinrichsen O. Chemical Engineering Science. 2012;78:111–127. [Google Scholar]
- 56.Dijkhuizen W. Deriving closures for bubbly flows using direct numerical simulations. University of Twente; 2008. [Google Scholar]
- 57.Mukin RV. International Journal of Multiphase Flow. 2014;62:52–66. [Google Scholar]
- 58.Clift R, Grace JR, Weber ME. Bubbles, drops, and particles. Academic Press; New York: 1978. [Google Scholar]
- 59.El-Askary WA, Sakr IM, Ibrahim KA, Balabel A. Energy. 2015;90(Part 1):722–737. [Google Scholar]
- 60.Fan LS, Tsuchiya K. Bubble wake dynamics in liquids and liquid-solid suspensions. Butterworth-Heinemann; 1990. [Google Scholar]
- 61.Niels BHHaTS, Deen G, et al. 2000 [Google Scholar]
- 62.Ziegenhein MGT, Lucas D. Chemical Engineering Science. 2016;153:155–164. [Google Scholar]
- 63.Groen JS, Mudde RF, Van Den Akker HEA. Experiments in Fluids. 1999;27(5):435–449. [Google Scholar]
- 64.Kulkarni AA, Joshi JB, Kumar VR, Kulkarni BD. Chemical Engineering Science. 2001;56(21):6437–6445. [Google Scholar]
- 65.Hara K, Suzuki T, Yamamoto F. Experiments in Fluids. 2011;50(3):715–727. [Google Scholar]
- 66.Kuroda I, Sakakibara A, Sasaki T, Murai Y, Nagai N, Yamamoto F. JAPANESE JOURNAL OF MULTIPHASE FLOW. 2008;22(2):161–174. [Google Scholar]
- 67.Feng YQ, Yang W, Cooksey M, Schwarz MP. The Journal of Computational Multiphase Flows. 2010;2(3):179–188. [Google Scholar]
- 68.Browne P, Ramuzat A, Saxena R, Yoganathan AP. Annals of Biomedical Engineering. 2000;28(1):39–47. doi: 10.1114/1.252. [DOI] [PubMed] [Google Scholar]
- 69.Nobach H, Bodenschatz E. Experiments in Fluids. 2009;47(1):27–38. [Google Scholar]
- 70.Cheng H, Scott K. Journal of Electroanalytical Chemistry. 2003;544:75–85. [Google Scholar]
- 71.Wang M, Wang Z, Guo Z. International Journal of Hydrogen Energy. 2009;34(13):5311–5317. [Google Scholar]
- 72.Wang M, Wang Z, Guo Z, Li Z. International Journal of Hydrogen Energy. 2011;36(5):3305–3312. [Google Scholar]
- 73.Shen C, Afacan A, Luo J, Klimas SJ. International Journal of Heat and Mass Transfer. 2014;70:162–168. [Google Scholar]
- 74.Mollinedo-Ponce-de-León HR, Martínez-Delgadillo SA, Mendoza-Escamilla VX, Gutiérrez-Torres CC, Jiménez-Bernal JA. Industrial & Engineering Chemistry Research. 2012;51(17):5947–5952. [Google Scholar]
- 75.Wang H, Park JD, Ren ZJ. Environmental Science & Technology. 2015;49(6):3267–3277. doi: 10.1021/es5047765. [DOI] [PubMed] [Google Scholar]
- 76.Osaka T. Nanostruct Sci Techn. 2010:1–4. [Google Scholar]
- 77.Ellenberger J, van Baten JM, Krishna R. Catalysis Today. 2003;79–80:181–188. [Google Scholar]
- 78.Hung C-Y, Li S-D, Wang C-C, Chen C-Y. Journal of Membrane Science. 2012;389:197–204. [Google Scholar]
- 79.Fan JM, Cui Z. Industrial & Engineering Chemistry Research. 2005;44(17):7010–7018. [Google Scholar]
- 80.De Jagher PC. Journal of Geophysical Research: Atmospheres. 1990;95(D7):10017–10022. [Google Scholar]
- 81.Sen D, Isaac KM, Leventis N, Fritsch I. International Journal of Heat and Mass Transfer. 2011;54(25–26):5368–5378. [Google Scholar]
- 82.Fernández D, Diao Z, Dunne P, Coey JMD. Electrochimica Acta. 2010;55(28):8664–8672. [Google Scholar]
- 83.Fernández D, Martine M, Meagher A, Möbius ME, Coey JMD. Electrochemistry Communications. 2012;18:28–32. [Google Scholar]
- 84.Baczyzmalski D, Weier T, Kähler CJ, Cierpka C. Experiments in Fluids. 2015;56(8):162. [Google Scholar]
- 85.Leventis N, Chen M, Gao X, Canalas M, Zhang P. The Journal of Physical Chemistry B. 1998;102(18):3512–3522. [Google Scholar]
- 86.Zakaria Ebrahim M, Mansour IAS, Sedahmed GH. Surface Technology. 1984;22(1):81–87. [Google Scholar]
- 87.Mat MD, Aldas K. International Journal of Hydrogen Energy. 2005;30(4):411–420. [Google Scholar]
- 88.Eigeldinger J, Vogt H. Electrochimica Acta. 2000;45(27):4449–4456. [Google Scholar]
- 89.Schillings J, Doche O, Deseure J. International Journal of Heat and Mass Transfer. 2015;85:292–299. [Google Scholar]
- 90.Zahradník J, Fialová M, Růžička M, Drahoš J, Kaštánek F, Thomas NH. Chemical Engineering Science. 1997;52(21):3811–3826. [Google Scholar]
- 91.Vial C, Camarasa E, Poncin S, Wild G, Midoux N, Bouillard J. Chemical Engineering Science. 2000;55(15):2957–2973. [Google Scholar]
- 92.Ruzicka MC, Zahradník J, Drahoš J, Thomas NH. Chemical Engineering Science. 2001;56(15):4609–4626. [Google Scholar]
- 93.Kantarci N, Borak F, Ulgen KO. Process Biochemistry. 2005;40(7):2263–2283. [Google Scholar]
- 94.Shaikh A, Al-Dahhan Muthanna H. International Journal of Chemical Reactor Engineering. 2007;5 [Google Scholar]
- 95.Bhagwat SM, Ghajar AJ. Experimental Thermal and Fluid Science. 2012;39:213–227. [Google Scholar]
- 96.Barbosa PR, Crivelaro KCO, Seleghim P., Jr Journal of the Brazilian Society of Mechanical Sciences and Engineering. 2010;32:15–20. [Google Scholar]
- 97.Abdelouahed L, Hreiz R, Poncin S, Valentin G, Lapicque F. Chemical Engineering Science. 2014;111:255–265. [Google Scholar]
- 98.Kreysa G, Külps HJ. Journal of The Electrochemical Society. 1981;128(5):979–984. [Google Scholar]
- 99.Fei K, Hong CW. Microfluidics and Nanofluidics. 2007;3(1):77–88. [Google Scholar]
- 100.Abdelouahed L, Valentin G, Poncin S, Lapicque F. Chemical Engineering Research and Design. 2014;92(3):559–570. [Google Scholar]
- 101.Nagai N, Takeuchi M, Kimura T, Oka T. International Journal of Hydrogen Energy. 2003;28(1):35–41. [Google Scholar]
- 102.Chen G. Separation and Purification Technology. 2004;38(1):11–41. [Google Scholar]
- 103.Rajic L, Fallahpour N, Alshawabkeh AN. Applied Catalysis B: Environmental. 2015;174–175:427–434. doi: 10.1016/j.apcatb.2015.03.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Sajid Hossain M, Shabani B, Cheung CP. International Journal of Hydrogen Energy. 2017;42(8):5272–5283. [Google Scholar]
- 105.Albuquerque ILT, Cavalcanti EB, Vilar EO. Chemical Engineering and Processing: Process Intensification. 2009;48(9):1432–1436. [Google Scholar]
- 106.Li T, Li X, Chen F, Wang J. Journal of The Electrochemical Society. 2014;161(5):E81–E86. [Google Scholar]
- 107.Cao X, Lyu Q, Sui X, Chai X. 2014 International Conference on Information Science, Electronics and Electrical Engineering. 2014;1:385–389. [Google Scholar]
- 108.Bergues Pupo AE, Reyes JB, Bergues Cabrales LE, Bergues Cabrales JM. BioMedical Engineering OnLine. 2011;10:85–85. doi: 10.1186/1475-925X-10-85. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


