Robust Multicategory Support Vector Machines using Difference Convex Algorithm

Abstract

The Support Vector Machine (SVM) is one of the most popular classification methods in the machine learning literature. Binary SVM methods have been extensively studied, and have achieved many successes in various disciplines. However, generalization to Multicategory SVM (MSVM) methods can be very challenging. Many existing methods estimate k functions for k classes with an explicit sum-to-zero constraint. It was shown recently that such a formulation can be suboptimal. Moreover, many existing MSVMs are not Fisher consistent, or do not take into account the effect of outliers. In this paper, we focus on classification in the angle-based framework, which is free of the explicit sum-to-zero constraint, hence more efficient, and propose two robust MSVM methods using truncated hinge loss functions. We show that our new classifiers can enjoy Fisher consistency, and simultaneously alleviate the impact of outliers to achieve more stable classification performance. To implement our proposed classifiers, we employ the difference convex algorithm (DCA) for efficient computation. Theoretical and numerical results obtained indicate that for problems with potential outliers, our robust angle-based MSVMs can be very competitive among existing methods.

1 Introduction

Classification is an important type of supervised learning problems in machine learning. Given a training dataset with both inputs and class labels available for all subjects, one important goal of classification is to build a classification model, also known as a classifier, to predict the class label accurately for new subjects with inputs only. There are many existing classifiers in the literature (Hastie et al, 2009). Among various classifiers, the Support Vector Machine (SVM, Boser et al, 1992; Cortes and Vapnik, 1995) is a popular method that was first introduced in the machine learning literature. As a typical margin-based classifier, the SVM has achieved many successes in various scientific disciplines, such as artificial intelligence, cancer research, and econometrics. Theoretical properties of standard SVMs have been well established, including the Fisher consistency (more details are given in Section 2.2; see also Lin, 1999; Liu, 2007), and generalization error bounds (Bartlett et al, 2006; Steinwart and Scovel, 2007). For a comprehensive introduction of SVMs, we refer the readers to Cristianini and Shawe-Taylor (2000) and Hastie et al (2009), among others.

Binary SVM methods have been extensively studied in the literature. In particular, the original binary SVM searches for a hyperplane in the feature space that can maximally separate the two classes, and uses a single classification function for prediction. The signed distance between an observation and the separating boundary is called the functional margin. One can verify that the corresponding optimization problem is equivalent to using the hinge loss function on functional margins of training observations. Many useful results for binary SVMs, including the feature selection properties for high dimensional learning (Le Thi et al, 2008; Wang and Shen, 2007), have been obtained. Empirical studies in the literature have confirmed the usefulness of binary SVMs (see, for example, Justino et al, 2005; Caruana et al, 2008; Arora et al, 2010).

Despite the success, how to extend binary SVM methods to address multicategory problems is a challenging problem. In the simultaneous margin-based classification framework, a common approach to handle problems with k different labels is to use k classification functions, and the corresponding prediction rule is based on which function is the largest. To reduce the parameter space and to ensure theoretical properties of the classifier, a sum-to-zero constraint is often imposed on these k functions. In the literature, many existing Multicategory SVM (MSVM) methods follow this procedure, including Vapnik (1998), Crammer and Singer (2001), Lee et al (2004), Liu and Shen (2006), Liu and Yuan (2011), and Guermeur and Monfrini (2011). Recently, Zhang and Liu (2014) suggested that this procedure can be inefficient and suboptimal, and proposed angle-based classification as a new margin-based classification framework. Zhang and Liu (2014) showed that angle-based classifiers can enjoy better prediction accuracies and faster computational speeds, hence are very competitive.

For the extension from binary SVM to MSVM methods in the angle-based framework, there are still many open problems. For example, Zhang and Liu (2014) showed that the naive SVM generalization is not Fisher consistent. To overcome this drawback, Zhang and Liu (2014) proposed to use a large-margin unified machine loss function with appropriate parameters to approximate the hinge loss for consistency (more details of the large-margin unified machine can be found in Liu et al, 2011). Moreover, Zhang et al (2016) proposed a new reinforced MSVM classifier in the angle-based framework that can enjoy Fisher consistency. Another open problem is that existing angle-based MSVM methods may not be robust against outliers. In particular, consider the feature space of the predictors, and assume that a training observation with label 2 is deeply buried in the group of observations with label 1. In this case, the fitted functional margin of this outlier, whether using the classifier in Zhang and Liu (2014) or Zhang et al (2016), would be negative with a large absolute value. This leads to a very large loss value for this single observation. Consequently, the fitted angle-based MSVM classifier can be unstable and suboptimal. A similar phenomenon was also observed by Wu and Liu (2007). In particular, Wu and Liu (2007) proposed to employ truncated hinge loss functions for MSVMs using k classification functions and the sum-to-zero constraint. Because the angle-based framework can enjoy better efficiency and accuracy, it is desirable to explore how to develop angle-based MSVM classifiers that can achieve both Fisher consistency and robustness against potential outliers simultaneously. To fill this gap, in this paper, we propose two MSVM methods in the angle-based framework using truncated hinge loss functions. We show that both classifiers can enjoy Fisher consistency and other attractive theoretical properties. Our numerical results demonstrate that the new robust MSVM classifiers are very competitive among existing methods.

Because the truncated hinge loss functions we employ in this paper are non-convex, the corresponding optimization problems are more involved than the original quadratic programming or linear programming for MSVM methods. To overcome this difficulty, we notice that the nonconvex objective function can have a difference of convex functions decomposition (DC), and propose to apply the difference of convex functions algorithm, i.e., difference convex algorithm (DCA) (Le Thi and Pham Dinh, 1997). The DCA decomposes the original non-convex problems into a sequence of convex subproblems, and each subproblem can be solved efficiently. We propose several robust SVM formulations combining truncated hinge loss functions and a variety of regularizers. We further apply efficient algorithms to solve the corresponding convex subproblems. Through numerical examples, we demonstrate that the DCA can work very well for our new classifiers.

The rest of this article is organized as follows. In Section 2, we first give a review of some existing MSVM classifiers, then introduce our robust angle-based MSVM methods. In Section 3, we show how to implement the DCA to solve the corresponding optimization problems, and provide convergence results to our solution methods. Some statistical learning theory, including Fisher consistency of our new methods, is obtained in Section 4. We perform numerical studies to demonstrate the effectiveness of our new methods in Section 5. All proofs are collected in the Appendix.

2 Methodology

In this section, we first give a brief review of some margin-based classification methods in Section 2.1, then propose our new classifiers in Section 2.2.

2.1 Review of Some Margin-based Classifiers

Denote by P(X,Y) the underlying joint distribution of (X,Y), where X is the vector of predictors, and Y is the label. The learning goal is to find a classifier with the prediction rule ŷ(·), such that for any future observations, the misclassification rate E[I{Y ≠ ŷ(X)}] is minimized. Here I is the indicator function, and the expectation is taken with respect to the distribution P. Given a set of training observations {(x₁,y₁),…,(x_n,y_n) from P, an intuitive approach is to find a classifier by minimizing the empirical prediction error $\frac{1}{n}{\displaystyle {\sum }_{i=1}^{n}I\{y_i\ne \widehat{y}({\mathit{x}}_i)\}}$. However, because the indicator function is discontinuous, such an optimization can be very difficult.

To circumvent this difficulty, it is common to use a surrogate loss function in place of the indicator function. For binary classifiers with Y ∈ {+1,−1}, one uses a single function f (·) for classification, and the prediction rule is ŷ(x) = sign{f (x)}. In this case, the indicator function I{y ≠ ŷ(x)} is equivalent to I{yf (x) < 0, and the term yf (x) is referred to as the functional margin. Binary margin-based classifiers use surrogate loss functions to encourage large functional margins. In particular, the corresponding optimization problem is typically

$$\underset{f\in \mathcal{F}}{min}\frac{1}{n}{\displaystyle \sum _{i=1}^n\mathcal{l}\{y}f(\mathit{x})\}+\lambda J(f),$$

where $\mathcal{F}$ is the functional space, ℓ(·) is the surrogate loss function, J(f) is a penalty to prevent overfitting, and λ is a tuning parameter to balance the loss and penalty terms. Different binary margin-based classifiers use different surrogate loss functions. For example, the standard SVM uses the hinge loss ℓ(u) = [1−u]₊, where [u]₊ = max(u,0), logistic regression (Lin et al, 2000) uses the deviance loss ℓ(u) = log{1 + exp(−u)}, and AdaBoost in boosting (Freund and Schapire, 1997) is shown to be approximately equivalent to using the exponential loss ℓ(u) = exp(−u).

For multicategory problems, how to define the prediction rule and functional margins becomes more involved. The details of angle-based classification are as follows. For a problem with k classes, consider a centered simplex with k vertices W = {W₁,…, W_k} in ℝ^k−1 with

$${\mathit{W}}_j=\{\begin{array}{ll}{(k-1)}^{-1/2}1\hfill & j=1\hfill \\ -(1+k^{1/2})/\{{(k-1)}^{3/2}\}1+{\{(k-1)\}}^{1/2}{e}_{j-1}\hfill & 2\le j\le k,\hfill \end{array}$$

where 1 is a vector of 1, and e_j is a vector with its jth element 1 and 0 elsewhere. One can verify that the matrix W introduces a symmetric simplex in ℝ^k−1. Without loss of generality, assume that class j is assigned to W_j. The angle-based classifiers map x into ℝ^k−1 using k − 1 functions f = (f₁,…,f_k−1). This classification function vector f(x) defines k angles with respect to {W₁,…,W_k}, namely, ∠(W_j, f); j = 1,…,k. The prediction rule is based on which angle is the smallest, i.e., ŷ(x) = argmin_j∈{1,…,_k}∠(W_j, f). Note that the smaller ∠(W_j, f) is, the larger the corresponding inner product 〈W_j, f〉 would be. Thus, it is equivalent to maximizing 〈W_y, f(x)〉 in the optimization, where 〈W_j, f(x)〉 can be regarded as functional margins for angle-based methods. Zhang and Liu (2014) proposed to use the following optimization problem for angle-based classification

$$\underset{\mathit{f}\in \mathcal{F}}{min}\frac{1}{n}{\displaystyle \sum _{i=1}^n\mathcal{l}}\{\langle {\mathit{W}}_{y_i},\mathit{f}({\mathit{x}}_i)\rangle \}+\lambda J(\mathit{f}),$$ (1)

where ℓ is a binary margin-based loss function. For angle-based classifiers, we note that the functional margins sum to zero implicitly. Zhang and Liu (2014) showed that, without an explicit sum-to-zero constraint as that used by other existing methods, the angle-based classifier can achieve a faster computational speed, and better classification performance.

2.2 Robust Angle-based Support Vector Machines

A direct generalization of the SVM method in the angle-based framework is to use ℓ(u) = [1 − u]₊ in (1). However, Zhang and Liu (2014) proved that this naive MSVM is not Fisher consistent, and proposed to use a loss function in the large-margin unified machine family to approximate the hinge loss to achieve Fisher consistency. In particular, Fisher consistency is defined as follows. Consider an observation with fixed X = x, and denote by P_j(x) = pr(Y = j | X = x) the class conditional probability of class j ∈ {1,…,k}. One can verify that the best prediction rule, namely, the Bayes rule, which minimizes the misclassification rate, is ŷ_Bayes(x) = argmax_jP_j(x). For a classifier, denote by ϕ{f(x),y} its surrogate loss function for classification using f as the classification function, and ŷ_f the corresponding prediction rule. Define the conditional loss S(x) = E[ϕ{f(X),Y} | X = x], where the expectation is taken with respect to the marginal distribution of Y | X = x. We call f*(x) = arginf_fS(x) the theoretical minimizer of the conditional loss. Fisher consistency requires that ŷ_f* (x) = ŷ_Bayes(x). In other words, Fisher consistency means that if we are using infinitely many training observations and an appropriate functional space $\mathcal{F}$, then the obtained classifier can achieve the best prediction performance, which is a fundamental requirement for a classification method. Zhang et al (2016) proposed the following reinforced MSVM loss function in the angle-based framework,

$$\varphi \{\mathit{f}(\mathit{x}),y\}=\gamma {[(k-1)-\langle \mathit{f}(\mathit{x}),{\mathit{W}}_y\rangle ]}_{+}+(1-\gamma ){\displaystyle \sum _{j\ne y}{[1+\langle \mathit{f}(\mathit{x}),{\mathit{W}}_j\rangle ]}_{+},}$$ (2)

where γ ∈ [0,1] is the convex combination parameter. Note that the first term of (2) explicitly encourages 〈f(x),W_y〉 to be large. The second term of (2) encourages 〈f(x),W_y〉 to be small for j ≠ y. This implicitly encourages 〈f(x),W_y〉 to be large, because ${\displaystyle {\sum }_{j=1}^k\langle \mathit{f}(\mathit{x}),}{\mathit{W}}_j\rangle =0$. Zhang et al (2016) showed that their reinforced MSVM method using this convex combination of hinge loss functions with γ ∈ [0,0.5] enjoys Fisher consistency.

Despite the progress, neither Zhang and Liu (2014) nor Zhang et al (2016) addressed the problem of potential outliers in practical problems. Consequently, the fitted classifiers may be suboptimal. In Figure 1, we demonstrate the effect of outliers on the performance of the angle-based MSVM proposed by Zhang and Liu (2014), using a simulated example. In particular, we first generalize a training dataset that has no outliers, and find the best angle-based MSVM classifier. We plot the corresponding classification boundaries on the left panel of Figure 1. Next, the class labels of some observations in one group are changed to another randomly. In practical problems, this type of unobserved mislabeling can be common, such as recording errors, a misdiagnosis of a patient in clinical trials. We then train a new angle-based MSVM classifier, and plot the corresponding classification boundaries on the right panel of Figure 1. For both classifiers, we use L₂ penalized linear learning, and the best tuning parameters are selected via 5-fold cross validation. One can see that for the data without outliers, the angle-based method works well. In contrast, for the second classifier, the existence of outliers has a significant effect on the classification boundary estimation, and the prediction accuracy deteriorates.

Fig. 1.

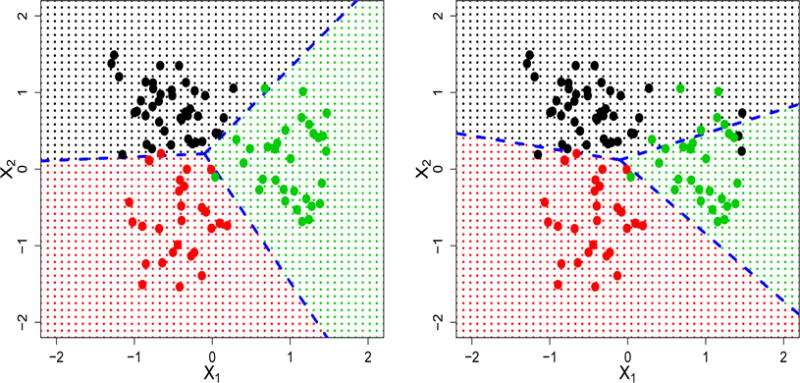
The training dataset on the left panel has no potential outliers, whereas the training set on the right panel has three (black) potential outliers in the green group of observations. The blue dashed lines are the fitted classification boundaries.

To better understand the effect of outliers on classification performance, we consider the reinforced MSVM loss (2) as an illustrating example. The first loss function term, [k – 1 − u]₊, increases linearly when u < k − 1 decreases, and the second loss term [1+u]₊ increases linearly when u > − 1 increases. For a potential outlier such as those in Figure 1, it is often to have 〈f(x),W_y〉 being negative with a large absolute value. Moreover, because of the implicit sum-to-zero property ${\displaystyle {\sum }_{j=1}^k\langle \mathit{f}(\mathit{x}),{\mathit{W}}_j\rangle }=0$, some of 〈f(x),W_j〉, j ≠ y can be positive with a large absolute value. This can result in a large ϕ{f(x),y} for this single observation, which, consequently, has a great influence on the final solution. For the angle-based MSVM using the approximate hinge loss, one can verify that a similar issue exists. Therefore, it is desirable to decrease the loss ϕ{f(x),y} for such outliers in MSVM methods. To this end, we propose to use truncated hinge loss functions in the angle-based classification framework. In particular, in this paper, we propose two such MSVM methods. We first explore how to implement the truncated hinge loss function for the reinforced MSVM by Zhang et al (2016). Then we propose a novel MSVM method in the angle-based framework, and show how to employ the truncated hinge loss function for this new classifier to alleviate the effect of potential outliers.

To begin with, define H_s(u) = [s − u]₊, and G_s(u) = [s + u]₊. One can rewrite (2) as

$$\varphi \{\mathit{f}(\mathit{x}),y\}=\gamma H_{k-1}\{\langle \mathit{f}(\mathit{x}),{\mathit{W}}_y\rangle \}+1(1-\gamma ){\displaystyle \sum _{j\ne y}{G}_1}\{\langle \mathit{f}(\mathit{x}),{\mathit{W}}_j\rangle \}.$$

To reduce the effect of outliers, we consider the truncated hinge losses T_s(u) = H_k−1(u) H_s(u) and R_s(u) = G₁(u) − G_s(u). Here s is a parameter that controls the location of truncation. In this paper we assume that k is a fixed constant, thus in the notation of T_s we suppress the dependency on k. When s > 0, T_s(u) and R_s(u) are constant within [−s,s]. In this case, one can verify that the loss for some correctly classified observations is the same as that of those misclassified ones, which is not desirable. Hence, we set s ≤ 0. For real applications, one can perform a data adaptive tuning method to select the best s ≤ 0. In our numerical experience, the choice of s = −1/(k−1) works well. We plot T_s(u) and R_s(u) in Figure 2.

Fig. 2.

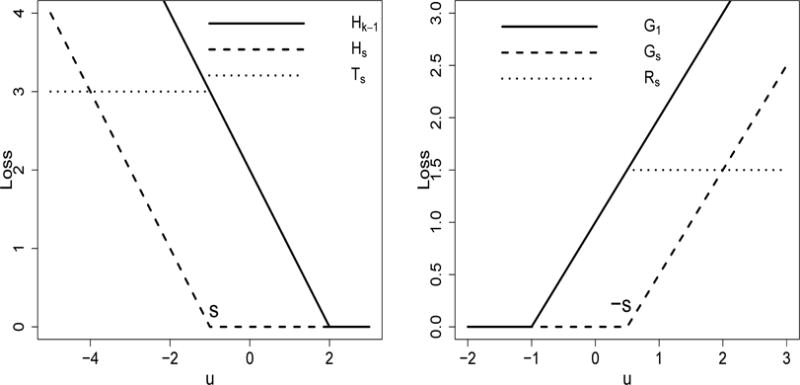
Plots of the loss functions T_s (left) and R_s (right).

With T_s(u) and R_s(u) defined as above, we propose the following loss function for our first robust angle-based MSVM

$${\varphi }_1\{\mathit{f}(\mathit{x}),y\}=\gamma T_{(k-1)s}\{\langle \mathit{f}(\mathit{x}),{\mathit{W}}_y\rangle \}+(1-\gamma ){\displaystyle \sum _{j\ne y}{R}_s}\{\langle \mathit{f}(\mathit{x}),{\mathit{W}}_j\rangle \},$$ (3)

where k is the number of classes. Note that T_(k−1)s = H_k−1 (u) − H_(k−1)s(u), and we choose T_(k−1)s such that the locations of truncation in (3) sum to zero, which is consistent with the implicit sum-to-zero property ${\displaystyle {\sum }_{j=1}^k\langle \mathit{f},{\mathit{W}}_j\rangle }=0$ of angle-based classifiers. One can see that for any potential outlier (x,y) with a large 〈f(x),W_y〉 < 0, its loss ϕ₁{f(x),y} is upper bounded by a constant for any f. Thus, the impact of outliers can be alleviated by our new method using the loss in (3).

Our second robust MSVM loss function is motivated by the following observation. An instance (x,y) is correctly classified using f if and only if 〈f(x),W_y〉 > 〈f(x),W_j〉, for all j ≠ y. This is equivalent to 〈f(x),W_y− W_j〉 > 0 for all j ≠ y. This is equivalent to 〈f(x),W_y− W_j〉 > 0 for all j ≠ y, or min_{j ≠ y}{〈f(x),W_y−W_j〉} > 0. Therefore, the theoretical misclassification error rate can be written as

$$E(I[\underset{j\ne Y}{min}\{\langle \mathit{f}(\mathit{X}),{\mathit{W}}_Y-{\mathit{W}}_j\rangle \}\le 0]).$$ (4)

To employ the SVM method in this framework, one can use a surrogate hinge loss function in place of the indicator function in (4)

$$\varphi \{\mathit{f}(\mathit{x}),y\}=H_1[\underset{j\ne y}{min}\{\langle \mathit{f}(\mathit{x}),({\mathit{W}}_y-{\mathit{W}}_j)\rangle \}]$$ (5)

However, for outliers with 〈f(x),W_y〉 < 0 and |〈f(x),W_y〉| ≫ 1, we have the corresponding min_j≠y {〈f(x), (W_y – W_j)〉} being negative with a large absolute value. To reduce the loss for such observations, we propose to use the following loss function for our second robust angle-based MSVM,

$${\varphi }_2\{\mathit{f}(\mathit{x}),y\}=T_s[\underset{j\ne y}{min}\{\langle \mathit{f}(\mathit{x}),({\mathit{W}}_y-{\mathit{W}}_j)\rangle \}],$$ (6)

where T_s = H₁(u) − H_s(u) with s ≤ 0. One can verify that for any instance with very small 〈f(x),W_y〉, its loss ϕ₂{f(x),y} is upper bounded by 1 − s. Therefore, compared to (5), the influence of outliers can be alleviated in our new robust angle-based SVM.

Note that for regular MSVM methods that use k functions for a k-class problem, Crammer and Singer (2001), Liu and Shen (2006) and Wu and Liu (2007) considered pairwise comparisons of the k functions for classification. To our knowledge, in the angle-based classification literature, there is no existing work that has considered pairwise comparisons of functional margins such as in (4), or the corresponding surrogate loss functions for the indicator function in (6). Hence, our second robust angle-based MSVM method is different from the methods mentioned above. We will examine the performance of these two robust methods in Section 5.

In the next section, we discuss how to implement the proposed classifiers using DCA.

3 Computational Implementation using Difference Convex Algorithm

In this section, we discuss how to implement our robust angle-based MSVM methods using DCA. DCA was introduced by Pham Dinh Tao in 1985 and further developed by Le Thi Hoai An and Pham Dinh Tao. More details about DCA and some of its recent developments can be found in Le Thi and Pham Dinh (2005, 2013, 2014); Le Thi et al (2014). We provide detailed algorithms for the two proposed MSVMs in Sections 3.1 and 3.2. In this section, we focus on linear learning with L₂, L₁, and mixed L₁ + L₂ penalties.

3.1 Algorithm for Robust Angle-based MSVM 1

We consider the DC formulation of (3)

$$\underset{\mathit{\beta }}{min}G(\mathit{\beta })-H(\mathit{\beta }),$$

where

$$G(\mathit{\beta })={\displaystyle \sum _{i=1}^n[\gamma H_{k-1}\{\langle \mathit{f}({\mathit{x}}_i),{\mathit{W}}_{y_i}\rangle \}}+(1-\gamma ){\displaystyle \sum _{j\ne y_i}{G}_1\{\langle \mathit{f}({\mathit{x}}_i),{\mathit{W}}_j\rangle }\}]+\lambda J(\mathit{f}),$$

and

$$H(\mathit{\beta })={\displaystyle \sum _{i=1}^n[\gamma H_s\{\langle \mathit{f}({\mathit{x}}_i),{\mathit{W}}_{y_i}\rangle \}+(1-\gamma ){\displaystyle \sum _{j\ne y_i}{G}_s\{}\langle \mathit{f}({\mathit{x}}_i),{\mathit{W}}_j\rangle \}]}.$$

For linear learning, we assume f_q(x) = x^Tβ_q, where β_q ∈ ℝ^p (q = 1,…,k − 1) are the vectors of parameters that we are interested in. For brevity, we denote f (x) by Bx, where B = (β₁,…,β_k−1)^T is a (k−1)× p parameter matrix, and $\mathit{\beta }={({\mathit{\beta }}_1^T,\dots ,{\mathit{\beta }}_{k-1}^T)}^T$ is the vectorization of B. For various choices for the penalty term J(·), we use different methods to solve the convex subproblems in DCA. First, we consider $J(\mathit{f})=\frac{1}{2}{\displaystyle {\sum }_{q=1}^{k-1}\langle {\mathit{\beta }}_q},{\mathit{\beta }}_q\rangle$. In this case, we have that the DC components G and H as

$$G(\mathit{\beta })={\displaystyle \sum _{i=1}^n[\gamma H_{k-1}\{\langle \mathit{B}{\mathit{x}}_i,{\mathit{W}}_{y_i}\rangle \}+(1-\gamma )]}{\displaystyle \sum _{j\ne y_i}{G}_1}\{\langle \mathit{B}{\mathit{x}}_i,{\mathit{W}}_j\rangle \}]+\frac{\lambda }{2}{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{\beta }}_q,{\mathit{\beta }}_q\rangle },$$

$$H(\mathit{\beta })={\displaystyle \sum _{i=1}^n[\gamma H_s\{\langle \mathit{B}{\mathit{x}}_i,{\mathit{W}}_{y_i}\rangle \}+(1-\gamma ){\displaystyle \sum _{j\ne y_i}{G}_s}\{\langle \mathit{B}{\mathit{x}}_i,{\mathit{W}}_j\rangle \}]}.$$

For DCA, note that the DC component H is a convex polyhedral function, thus for a point β^m, a subgradient g^m ∈ ∂H(β^m)(g^m ∈ ℝ^(k−1)p) can be computed efficiently. Define ${\mathit{g}}_q^m$ to be the q-th sub-vector in g^m that corresponds to β_q. In particular, for the m-th iteration, we solve the following convex optimization

$$\underset{\mathit{\beta }}{min}{\displaystyle \sum _{i=1}^n[\gamma H_{k-1}\{\langle \mathit{B}{\mathit{x}}_i,{\mathit{W}}_{y_i}\rangle \}+(1-\gamma ){\displaystyle \sum _{j\ne y_i}{G}_1}\{\langle \mathit{B}{\mathit{x}}_i,{\mathit{W}}_j\rangle \}]}+\frac{\lambda }{2}{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{\beta }}_q,{\mathit{\beta }}_q\rangle -}{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{g}}_q^m,{\mathit{\beta }}_q\rangle }.$$ (7)

We first introduce nonnegative slack variables ξ = (ξ₁₁,ξ₁₂,…,ξ_1k,…,ξ_n1,ξ_n2,…,ξ_nk)^T, and rewrite (7) as

$$\underset{\mathit{\beta },\mathit{\xi }}{min}{\displaystyle \sum _{i=1}^n\{\gamma }{\xi }_{i{y}_i}+(1-\gamma ){\displaystyle \sum _{j\ne y_i}{\xi }_{ij}\}}+\frac{\lambda }{2}{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{\beta }}_q,{\mathit{\beta }}_q\rangle -}{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{g}}_q^m,{\mathit{\beta }}_q\rangle },$$

$$\mathrm{s}.\mathrm{t}{\xi }_{i{y}_i}\ge k-1-\langle \mathit{B}{\mathit{x}}_i,{\mathit{W}}_{y_i}\rangle ;i=1,\dots ,n,$$

$${\xi }_{ij}\ge 1+\langle \mathit{B}{\mathit{x}}_i{\mathit{W}}_j\rangle ;i=1,\dots ,n,j\ne y_i,$$

$${\xi }_{ij}\ge 0;i=1,\dots ,n,j=1,\dots ,k.$$

Next, we introduce dual variables μ_ij ≥ 0 and α_ij ≥ 0; i = 1,…,n, j = 1,…,k, and the corresponding Lagrangian becomes

$$\mathbb{L}(\mathit{\beta },\mathit{\xi },\mathit{\mu },\mathit{\alpha })={\displaystyle \sum _{i=1}^n\{\gamma {\xi }_{i{y}_i}+(1-\gamma ){\displaystyle \sum _{j\ne y_i}{\xi }_{ij}}\}}+\frac{\lambda }{2}{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{\beta }}_q,{\mathit{\beta }}_q\rangle }-{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{g}}_q^m,{\mathit{\beta }}_q\rangle }+{\displaystyle \sum _{i=1}^n{\mu }_{i{y}_i}(k-1-\langle \mathit{B}{\mathit{x}}_i{\mathit{W}}_{y_i}\rangle -{\xi }_{i{y}_i})+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j\ne y_i}{\mu }_{ij}(1+\langle \mathit{B}{\mathit{x}}_i{\mathit{W}}_j\rangle -{\xi }_{ij})+}}}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j=1}^k{\alpha }_{ij}}(-{\xi }_{ij})},$$ (8)

where μ = (μ₁₁, μ₁₂,…, μ_1k,…, μ_n1, μ_n2,…, μ_nk)^T. After some calculation, one can show that $0\le {\mu }_{i{y}_i}\le \gamma ;i=1,\dots ,n$ and 0 ≤ μ_ij ≤ 1 − γ; i = 1,…,n, j = 1,…,k, j ≠ y_i. Furthermore, we have that

$${\mathit{\beta }}_q=\frac{1}{\lambda }({\mathit{g}}_q^m+{\displaystyle \sum _{i=1}^n{\mu }_{i{y}_i}{W}_{yi}^q{\mathit{x}}_i-{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j\ne y_i}{\mu }_{ij}{W}_j^q{\mathit{x}}_i}}}),$$ (9)

where $W_{y_i}^q$ and $W_j^q$ are the q-th elements of ${\mathit{W}}_y{ }_i$ and ${\mathit{W}}_j$, respectively. To simplify notation, we introduce (k − 1) matrices X^q; q = 1,…,k − 1, each with size kn × p. For X^q, its (ij)-th row is defined to be $W_j^q{\mathit{x}}_i^T$ if j ≠ y_i and $-W_j^q{\mathit{x}}_i^T$ otherwise, for i = 1,…,n, j = 1,…,k. One can verify that (9) can be written as ${\mathit{\beta }}_q=\frac{1}{\lambda }({\mathit{g}}_q^m-{\mathit{\mu }}^T{\mathit{X}}^q)$, where ${\mathit{g}}_q^m$ is the sub-vector in g^m that corresponds to β_q. Substitutng this into (8), we obtain the dual problem

$$\underset{\mathit{\mu }}{min}\frac{1}{2}{\mathit{\mu }}^T{\displaystyle \sum _{q=1}^{k-1}{\mathit{X}}^q{({\mathit{X}}^q)}^T}\mathit{\mu }-\lambda \langle \delta ,\mathit{\mu }\rangle -\langle {\displaystyle \sum _{q=1}^{k-1}{\mathit{X}}^q{({\mathit{g}}_q^m)}^T,\mathit{\mu }}\rangle ,$$

$$\mathrm{s}\text{.t.}0\le {\mu }_{i{y}_i}\le \gamma ;i=1,\dots ,n,$$

$$0\le {\mu }_{ij}\le 1-\gamma ;j\ne y_i,i=1,\dots ,n,j=1,\dots ,k,$$

where δ = (δ₁₁,δ₁₂,⋯,δ_1km⋯,δ_n1,δ_n2,⋯, δ_nk)^T, ${\delta }_{i{y}_i}=k-1,{\delta }_{ij,j\ne y_i}=1$. This dual problem is a quadratic programming problem with a positive semi-definite Hessian matrix and box-constraints. Due to the separability of the constraints, one can use the very efficient coordinate descent method to solve the optimization (Hsieh et al, 2008; Tseng, 2010).

In order to perform variable selection, we consider the L₁ penalization with $J={\displaystyle {\sum }_{q=1}^{k-1}\Vert }{\mathit{\beta }}_q{\Vert }_1$. In this case, one can derive the following optimization problem in an analogous manner as (7),

$$\underset{\mathit{\beta }}{min}{\displaystyle \sum _{i=1}^n[\gamma H_{k-1}\{\langle \mathit{B}{\mathit{x}}_i,{\mathit{W}}_{y_i}\rangle \}+(1-\gamma ){\displaystyle \sum _{j\ne y_i}{G}_1}\{\langle \mathit{B}{\mathit{x}}_i,{\mathit{W}}_j\rangle \}]}+\lambda {\displaystyle \sum _{q=1}^{k-1}\Vert {\mathit{\beta }}_q{\Vert }_1-}{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{g}}_q^m,{\mathit{\beta }}_q\rangle }.$$ (10)

To solve (10), we introduce nonnegative slack variables ξ_ij; i = 1,…,n, j = 1,…,k and β⁺. Then (10) becomes a linear programming problem as follows:

$$\underset{\mathit{\xi },\mathit{\beta },{\mathit{\beta }}^{+}}{min}{\displaystyle \sum _{i=1}^n\gamma {\xi }_{i{y}_i}+(1-\gamma )}{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j\ne y_i}{\xi }_{ij}+\lambda \langle 1,{\mathit{\beta }}^{+}\rangle }}-{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{g}}_q^m,{\mathit{\beta }}_q\rangle },$$

$$\mathrm{s}.\mathrm{t}\text{.}{\xi }_{i{y}_i}\ge k-1-\langle \mathit{B}{\mathit{x}}_i,{\mathit{W}}_{y_i}\rangle ;i=1,\dots ,n,$$

$${\xi }_{ij}\ge 1+\langle \mathit{B}{\mathit{x}}_i,{\mathit{W}}_j\rangle ;i=1,\dots ,n,j=1,\dots ,k,j\ne y_i,$$

$${\mathit{\beta }}^{+}-\mathit{\beta }\ge 0,{\mathit{\beta }}^{+}+\mathit{\beta }\ge 0,{\mathit{\beta }}^{+}\ge 0,$$

which can be solved efficiently using existing linear programming software.

Lastly, we consider the mixed L₁ and L₂ penalty $\lambda J(\mathit{f})={\lambda }_1{\displaystyle {\sum }_{q=1}^{k-1}\Vert {\mathit{\beta }}_q{\Vert }_1+\frac{{\lambda }_2}{2}}{\displaystyle {\sum }_{q=1}^{k-1}\langle {\mathit{\beta }}_q,{\mathit{\beta }}_q\rangle }$. In this case, the optimization problem becomes

$$\underset{\mathit{\beta }}{min}({\displaystyle \sum _{i=1}^n[\gamma H_{k-1}\{\langle \mathit{B}{\mathit{x}}_i,{\mathit{W}}_{y_i}\rangle \}+(1-\gamma ){\displaystyle \sum _{j\ne y_i}{G}_1\{\langle \mathit{B}{\mathit{x}}_i,{\mathit{W}}_j\rangle \}}}]+{\lambda }_1{\displaystyle \sum _{q=1}^{k-1}\Vert {\mathit{\beta }}_q{\Vert }_1+\frac{{\lambda }_2}{2}}{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{\beta }}_q,{\mathit{\beta }}_q\rangle }-{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{g}}_q^m,{\mathit{\beta }}_q\rangle }).$$ (11)

To solve (11), we employ the Alternating Linearization (AL, Kiwiel et al, 1999; Lin et al, 2014) algorithm. In particular, we consider the following decomposition of (11),

$$\underset{\mathit{\beta }}{min}F(\mathit{\beta })=F_1(\mathit{\beta })+F_2(\mathit{\beta }),$$

where F is the objective function in (11), F₁ corresponds to the robust MSVM loss term, and $F_2=\frac{{\lambda }_2}{2}{\displaystyle {\sum }_{q=1}^{k-1}\langle {\mathit{\beta }}_q,{\mathit{\beta }}_q\rangle -}{\displaystyle {\sum }_{q=1}^{k-1}\langle {\mathit{g}}_q^m,{\mathit{\beta }}_q\rangle +{\lambda }_1{\displaystyle {\sum }_{q=1}^{k-1}\Vert {\mathit{\beta }}_q{\Vert }_1}}$. The idea of our AL algorithm is that, at each iteration, we solve two sub-problems, each consisting of one component, linearizations of the other components, and a proximal term. From these two sub-problems, we obtain two candidate updates for the original optimization. We then evaluate the objective function (11) at these two candidate updates, and if a candidate solution delivers an improvement, we update it for the original objective function.

The details of our AL method for (11) can be summarized as follows:

Alternating Linearization Algorithm

Initialization

$\overline{\mathit{\beta }}\in {ℝ}^{(k-1)p}$ is the current solution vector, β ∈ ℝ^(k−1)p is the vector of unknown variables, and introduce z₁,z₂,d₁,d₂ ∈ ℝ^(k−1)p initialized to zero vectors, and ρ > 0. In our description, we use β_q, ${\overline{\mathit{\beta }}}_q$,d_1,q,d_2,q to denote the q-th sub-vector of the corresponding vectors respectively, where q = 1,2,⋯,k − 1.

Repeat

Sub-problem 1

$${\mathit{z}}_1=\underset{\mathit{\beta }}{\text{arg}min}{\displaystyle \sum _{i=1}^n\gamma }{H}_{k-1}\{\langle \mathit{B}{\mathit{x}}_i,{\mathit{W}}_{y_i}\rangle \}+(1-\gamma ){\displaystyle \sum _{j\ne y_i}{G}_1\{\langle \mathit{B}{\mathit{x}}_i,{\mathit{W}}_j\rangle \}}+{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{d}}_{2,q},{\mathit{\beta }}_q\rangle }+\frac{\rho }{2}{\displaystyle \sum _{q=1}^{k-1}\Vert {\mathit{\beta }}_q-{\overline{\mathit{\beta }}}_q{\Vert }_2^2,}{\mathit{d}}_1=-{\mathit{d}}_2-\rho ({\mathit{z}}_1-\overline{\mathit{\beta }}).$$

If z₁ improves the objective function, set $\overline{\mathit{\beta }}={\mathit{z}}_1$.

Sub-problem 2

$${\mathit{z}}_2=\underset{\mathit{\beta }}{\text{arg}min}\frac{{\lambda }_2}{2}{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{\beta }}_q,{\mathit{\beta }}_q\rangle }-{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{g}}_q^m,{\mathit{\beta }}_q\rangle }+{\lambda }_1{\displaystyle \sum _{q=1}^{k-1}\Vert {\mathit{\beta }}_q}{\Vert }_1+{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{d}}_{1,q},{\mathit{\beta }}_q\rangle }+\frac{\rho }{2}{\displaystyle \sum _{q=1}^{k-1}\Vert {\mathit{\beta }}_q-{\overline{\mathit{\beta }}}_q{\Vert }_2^2,}{\mathit{d}}_2=-{\mathit{d}}_1-\rho ({\mathit{z}}_2-\overline{\mathit{\beta }}).$$

If z₂ improves the objective function, set $\overline{\mathit{\beta }}={\mathit{z}}_2$.

Until convergence

Note that one can choose any ρ > 0 in the above algorithm. In our paper, we set ρ = 1. As a remark, we would like to point out that sub-problem 1 can be solved in an analogous manner as (7), using the coordinate descent algorithm. To make the algorithm more efficient, the solution of the previous iteration can be used as the starting point for the next iteration. Moreover, note that the L₁ and L₂ penalties are separable, therefore the sub-problem 2 has closed form solutions. This greatly enhances the computational speed of our method.

3.2 Algorithm for Robust Angle-based MSVM 2

For our second MSVM formulation (6), we can choose the DC components as

$$G(\mathit{\beta })={\displaystyle \sum _{i=1}^n{H}_1[\underset{j\ne y_i}{min}\{\langle \mathit{f}({\mathit{x}}_i),({\mathit{W}}_{y_i}-{\mathit{W}}_j)\rangle \}]}+\lambda J(\mathit{f}),$$

and

$$H(\mathit{\beta })={\displaystyle \sum _{i=1}^n{H}_s[\underset{j\ne y_i}{min}\{\langle \mathit{f}({\mathit{x}}_i),({\mathit{W}}_{y_i}-{\mathit{W}}_j)\rangle \}]}.$$

As in Section 3.1, we first consider the case when $J(\mathit{f})=\frac{1}{2}{\displaystyle {\sum }_{q=1}^{k-1}\langle {\mathit{\beta }}_q,{\mathit{\beta }}_q\rangle }$. In the m-th iteration of DCA, we solve the following optimization problem

$$\underset{\mathit{\beta }}{min}\left({\displaystyle \sum _{i=1}^n{H}_1[\underset{j\ne y_i}{min}\{\langle \mathit{B}{\mathit{x}}_i,({\mathit{W}}_{y_i}-{\mathit{W}}_j)\rangle \}]}+\frac{\lambda }{2}{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{\beta }}_q,{\mathit{\beta }}_q\rangle }-{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{g}}_q^m,{\mathit{\beta }}_q\rangle }\right).$$ (12)

Using nonnegative slack variables ξ_i, i = 1,…,n, (12) is equivalent to

$$\underset{\mathit{\beta },\mathit{\xi }}{min}{\displaystyle \sum _{i=1}^n{\xi }_i}+\frac{\lambda }{2}{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{\beta }}_q,{\mathit{\beta }}_q\rangle }-{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{g}}_q^m,{\mathit{\beta }}_q\rangle ,}$$

$$\mathrm{s}.\mathrm{t}.{\xi }_i\ge 1-\underset{j\ne y_i}{min}\langle \mathit{B}{\mathit{x}}_i,({\mathit{W}}_{y_i}-{\mathit{W}}_j)\rangle ;i=1,\dots ,n,$$

$${\xi }_i\ge 0;i=1,\dots ,n.$$

Next, by introducing nonnegative dual variables μ ∈ ℝ^(k−1)n and α ∈ ℝⁿ, we have the corresponding Lagrangian

$$\mathbb{L}(\mathit{\beta },\mathit{\xi },\mathit{\mu },\mathit{\alpha })={\displaystyle \sum _{i=1}^n{\xi }_i+\frac{\lambda }{2}{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{\beta }}_q,{\mathit{\beta }}_q\rangle }}-{\displaystyle \sum _{q=1}^{k-1}\langle {\mathit{g}}_q^m,{\mathit{\beta }}_q\rangle }+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j\ne y_i}{\mu }_{ij}(1-\langle \mathit{B}{\mathit{x}}_i,{\mathit{W}}_{y_i}-{\mathit{W}}_j\rangle -{\mathit{\xi }}_i)}+{\displaystyle \sum _{i=1}^n{\alpha }_i(-{\xi }_i)}}.$$ (13)

With some calculation, one can show that for a fixed i, ${\displaystyle {\sum }_{j\ne y_i}{\mu }_{ij}\le }1$. Furthermore, we have that

$${\mathit{\beta }}_q=\frac{1}{\lambda }({\mathit{g}}_q^m+{\displaystyle \sum _{i=1}^n{\displaystyle \sum _{j\ne y_i}{\mu }_{ij}(W_{y_i}^q-W_j^q){\mathit{x}}_i}}),$$ (14)

where β_q; q = 1,…,k − 1, is the parameter vector of the q-th classification function, and $W_j^q$ is the q-th entry of W_j.

Similar to Section 3.1, we define k−1 matrices X¹,…,X^k−1 with dimension (k − 1)n × p to simplify notation. In particular, for each q, and let the i j-th row of X^q be $(W_j^q-W_{y_i}^q){\mathit{x}}_i^T$; i = 1,…,n, j = 1,…,k, j ≠ y_i. One can verify that (14) can be written as ${\mathit{\beta }}_q=\frac{1}{\lambda }({\mathit{g}}_q^m-{\mathit{\mu }}^T{\mathit{X}}^q)$. By substituting this into (13), we obtain the dual problem

$$\underset{\mathit{\mu }}{min}\frac{1}{2}{\mathit{\mu }}^T{\displaystyle \sum _{q=1}^{k-1}{\mathit{X}}^q{({\mathit{X}}^q)}^T}\mathit{\mu }-\lambda \langle 1,\mathit{\mu }\rangle -\langle {\displaystyle \sum _{q=1}^{k-1}{\mathit{X}}^q{({\mathit{g}}_q^m)}^T,\mathit{\mu }}\rangle ,$$

$$s.t.{\displaystyle \sum _{j\ne y_i}{\mu }_{ij}\le 1;i=1,\dots ,n,}$$

$$\mathit{\mu }\ge 0.$$ (15)

The optimization problem (15) is a quadratic programming problem with box constraints and linear inequalities. Due to the block separability structure of the linear inequality constraints, we can solve this problem by iterating through each block (Nesterov, 2012; Tseng, 2010). In particular, for a fixed i, let $\mathit{Q}={\displaystyle {\sum }_{q=1}^{k-1}{\mathit{X}}^q}{({\mathit{X}}^q)}^T$, and let Q_i be the sub-matrix corresponding to μ_ij, j ≠ y_i. One can verify that the sub-problem is a small scale positive semi-definite quadratic programming problem with box constraints and a single inequality constraint

$$min\frac{1}{2}{\mathit{\mu }}_{i,j\ne y_i}^T{\mathit{Q}}_i{\mathit{\mu }}_{i,j\ne y_i}+v^T{\mathit{\mu }}_{i,j\ne y_i},$$

$$s.t.{\displaystyle \sum _{j\ne y_i}{\mu }_{ij}\le 1,{\mu }_{ij}\ge 0;j=1,\dots ,k,j\ne y_i},$$

where v is a vector that depends only on λ, X^q and g^m. When k = 3, the problem is a simple quadratic function with two variables and the solutions can be easily obtained. For k > 3, the sub-problem can be solved efficiently using the coordinate descent algorithm (Platt, 1998).

In the cases of L₁ and mixed L₁ + L₂ penalties, one can employ similar strategies as in Section 3.1, and we omit the details here.

4 Statistical Properties

In this section, we explore some statistical properties of our proposed classifiers using loss functions (3) and (6). In particular, we first establish the Fisher consistency of (3) and (6), then show how to estimate the future prediction error rate using the training dataset.

Fisher consistency was introduced in Section 2.2. The next theorem shows that the proposed robust angle-based MSVM can enjoy Fisher consistency with appropriately selected parameters s and γ.

Theorem 1

Our first robust angle-based MSVM (3) is Fisher consistent with γ ∈ [0,1/2] and s ≤ 0, and our second robust angle-based MSVM (6) is Fisher consistent with $s\in \left[-\frac{1}{k-1},0\right]$.

According to Theorem 1, with infinitely many training observations and an appropriate $\mathcal{F}$, our robust angle-based MSVMs can achieve the best classification accuracy.

In practice, it is desirable to study the prediction performance of the obtained classifier on future testing data, in terms of $E[I\{Y\ne {\widehat{y}}_{\widehat{\mathit{f}}}(\mathit{X})\}]$. To this end, one possible approach is to use the empirical prediction error rate on the training dataset, $\frac{1}{n}{\displaystyle {\sum }_{i=1}^{n}I\{y_i\ne {\widehat{y}}_{\widehat{\mathit{f}}}({\mathit{x}}_i)\}}$, to estimate the future error rate. However, it is well known that the empirical error rate often underestimates $E[I\{Y\ne {\widehat{y}}_{\widehat{\mathit{f}}}(\mathit{X})\}]$. The next theorem shows that for our new classifiers, the future error rate exceeds the empirical rate by a small amount that can converge to zero at a fast rate. Here we use linear learning with L₁ or L₂ penalties, and reproducing kernel Hilbert space learning (Wahba, 1999) as examples. With a little abuse of notation, we denote by $\widehat{\mathit{f}}$ the solution to our new MSVM methods (3) or (6).

Theorem 2

The solution $\widehat{\mathit{f}}$ to (3) or (6) satisfies that, with probability at least 1 − δ,

$$E[I\{Y\ne {\widehat{y}}_{\widehat{\mathit{f}}}(\mathit{X})\}]\le \left[\frac{1}{n}{\displaystyle \sum _{i=1}^{n}I\{y_i\ne {\widehat{y}}_{\widehat{\mathit{f}}}({\mathit{x}}_i)\}+3{\{\text{log}(2/\delta )/n\}}^{1/2}+Z}\right],$$ (16)

where

$$Z=\{\begin{array}{c}\frac{C_1}{\lambda }\sqrt{\frac{\text{log}(p)}{n}}\mathit{\text{for}}\mathit{\text{linear}}\mathit{\text{learning}}\mathit{\text{with}}{L}_1\mathit{\text{penalty}},\\ \frac{C_2}{{\lambda }^{1/2}}\sqrt{\frac{p}{n^{1/2}}}\mathit{\text{for}}\mathit{\text{linear}}\mathit{\text{learning}}\mathit{\text{with}}{L}_2\mathit{\text{penalty}},\\ \frac{C_3}{\lambda \sqrt{n}}\mathit{\text{for}}\mathit{\text{RKHS}}\mathit{\text{learning}}\mathit{\text{with}}\mathit{a}\mathit{\text{separable}}\mathit{\text{kernel}},\end{array}$$

and C₁,C₂,C₃ are constants (specified in the Appendix) that do not depend on n or p.

Theorem 2 shows that for our robust MSVM classifiers, one can obtain an upper bound for the future prediction error rate using the empirical error rate, and the corresponding difference can converge to zero at a fast rate. For example, as n → ∞, we can let λ → 0 (as is typical for general machine learning problems) at the rate of O{log(n)^−1/2}. In this case, we have that $Z=O_P\{\sqrt{\text{log}(p)\text{log}(n)/n}\}$ for L₁ learning, $Z=O_P\{\sqrt{p\text{log}{(n)}^{1/2}/n^{1/2}}\}$ for L₂ learning, and $Z=O_P\{\sqrt{\text{log}(n)/n}\}$ for kernel learning.

As a remark, we would like to point out that Theorem 2 also reveals the effectiveness of L₁ penalized methods over the L₂ ones on practical problems where the underlying signal is sparse. To see this, consider a problem where the classification signal depends only on a handful predictors, and the remaining predictors are noise variables. In this case, it is well known that L₁ penalized methods can deliver parsimonious classifiers that can fit the data well (Wang and Shen, 2007). On the other hand, L₂ penalized classifiers cannot deliver sparse classification models. Because we can typically expect a small empirical error rate on training datasets, Theorem 2 shows that when the dimension p is ultrahigh, the corresponding convergence rate of the difference term Z can be much faster in the L₁ case. In other words, the L₁ penalized classifiers can perform much better in terms of future prediction accuracy. This is consistent with many existing experiments in the literature.

5 Numerical Results

In this section, we investigate the performance of our proposed robust angle-based SVMs using simulated and real datasets.

5.1 Simulated Experiments

In this section, we conduct a simulation example to demonstrate the numerical performance of our new classifiers. We use 100 observations for training, and select the best regularization parameters via a grid search on a separate tuning dataset with 1000 observations. Then, we evaluate the prediction performance of the obtained classifiers on a testing dataset with size 10000. We compare the performance of RMSVM by Liu and Yuan (2011), MSVM by Liu and Shen (2006), and our proposed RSVMs (3) and (6).

We generate the simulated datasets as follows. We choose k = 3 with pr(Y = j) = 1/3 for j = 1,2,3. Among the observations in the training and tuning sets, we generate 5% and 10% outliers (denoted by perc = 5% and perc = 10%) to contaminate the data. The classification signal depends only on two predictors X₁ and X₂. For the uncontaminated observations, the marginal distribution of (X₁,X₂)^T for Y = j is N(μ_j,0.16I₂), where I₂ is the identity matrix, and μ_j’s are equally distributed on the unit circle with μ₁ = (1,0)^T. For the contaminated observations, the marginal distribution of (X₁,X₂)^T is N((3,0)^T, 0.16I₂) for Y = 1,2,3. Moreover, we generate noise variables to make the dimension p higher. In particular, the noise predictors are generated independently from a uniform distribution on [−1,1]. We report the results of p = 2,20,200.

We compare the performance of our two robust angle-based SVMs (RSVMs 1-2) (3) and (6), with truncation at s = 0 (denoted by T₀) and s = −1/(k − 1) (denoted by T_K). For the regularization terms, we employ three different penalty functions, namely, the L₂, L₁, and L₁ + L₂ penalties. In particular, the candidate sets of L₁ and L₂ tuning parameters consist of 30 candidates each, and the candidate sets of L₁ + L₂ tuning parameters consist of 30 × 30 = 900 different values. For each setting of the simulation, we run the experiments 100 times. We report some of the classification results in Figure 3. Full numerical results of the simulated studies are reported in Tables 1–3. From Figure 3 and the tables, one can see that our proposed RSVMs perform better than the original SVMs. Furthermore, our methods with truncation at s = 0 and s = −1/(k−1) perform similarly. To avoid intensive tuning of s and to obtain more stable results, we recommend to use s = −1/(k−1) in practice.

Fig. 3.

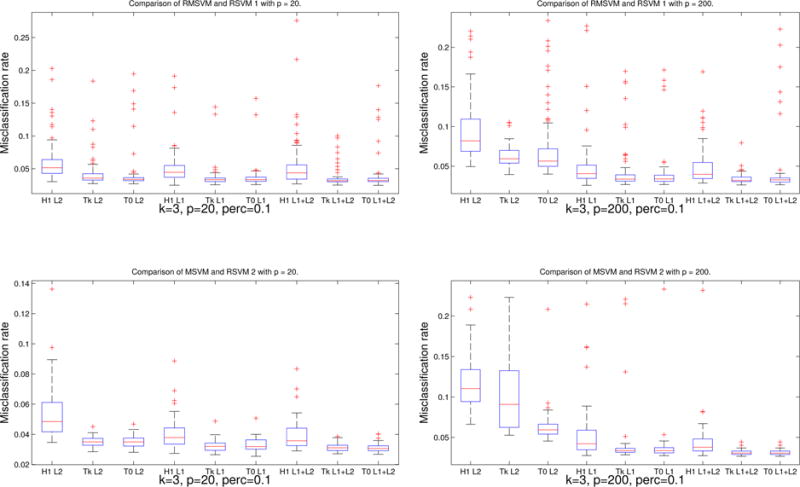
Boxplots of misclassification rates for RMSVM (denoted by H₁ on the top panels), our RSVM 1 with truncation at s = −1/(k − 1) (T_K on the top panels) and at s = 0 (T₀ on the top panels), MSVM (denoted by H₁ on the bottom panels), and our RSVM 2 with truncation at s = −1/(k − 1) (T_K on the bottom panels) and at s = 0 (T₀ on the bottom panels) on the simulated example.

Table 1.

Classification error rates for RMSVM, MSVM and our RSVMs 1-2 on the simulated data with k = 3, p = 2. Here Perc stands for the percentage of data that are contaminated.

Penalty		L2	L1	L1 + L2
Perc	Loss	Error	Error	Error
5 %	RMSVM	3.3600(0.0062)	3.5575(0.0063)	3.3990(0.0069)
	T0 RSVM 1	3.1159(0.0034)	3.3125(0.0057)	3.0756(0.0030)
	Tk RSVM 1	3.1148(0.0043)	3.2874(0.0045)	3.0968(0.0028)
	MSVM	3.2572(0.0032)	3.4097(0.0049)	3.2130(0.0031)
	T0 RSVM 2	3.0654(0.0023)	3.2780(0.0036)	3.0446(0.0027)
	Tk RSVM 2	3.0766(0.0021)	3.2346(0.0031)	3.0123(0.0023)
10 %	RMSVM	4.6710(0.0237)	5.0689(0.0202)	4.6662(0.0250)
	T0 RSVM 1	4.7892(0.0649)	3.8702(0.0241)	3.3646(0.0180)
	Tk RSVM 1	3.4628(0.0098)	3.7674(0.0174)	3.4748(0.0180)
	MSVM	4.3474(0.0214)	4.1759(0.0135)	4.5220(0.0209)
	T0 RSVM 2	3.2404(0.0194)	3.2075(0.0031)	2.9990(0.0023)
	Tk RSVM 2	3.2451(0.0170)	3.1844(0.0029)	2.9890(0.0022)

Table 3.

Classification error rates for RMSVM, MSVM and our RSVMs 1-2 on the simulated data with k = 3, p = 200. Here Perc stands for the percentage of data that are contaminated.

Penalty		L2	L1	L1 + L2
Perc	Loss	Error	Error	Error
5%	RMSVM	6.3898(0.0121)	3.4861(0.0098)	3.5316(0.0077)
	T0 RSVM 1	5.5830(0.0093)	3.5360(0.0063)	3.3142(0.0039)
	Tk RSVM 1	5.7684(0.0085)	3.3287(0.0045)	3.2944(0.0040)
	MSVM	7.8186(0.0250)	3.4781(0.0081)	3.5385(0.0131)
	T0 RSVM 2	5.9862(0.0093)	3.3206(0.0073)	3.3900(0.0061)
	Tk RSVM 2	6.3608(0.0183)	3.4235(0.0040)	3.2542(0.0051)
10%	RMSVM	9.1100(0.0410)	5.1094(0.0309)	5.2558(0.0292)
	T0 RSVM 1	5.7400(0.0241)	3.48940.0052)	3.5366(0.0127)
	Tk RSVM 1	6.6500(0.0362)	3.9901(0.0247)	3.4498(0.0100)
	MSVM	12.0516(0.0364)	5.3859(0.0346)	4.1383(0.0103)
	T0 RSVM 2	6.5674(0.0300)	3.8189(0.0275)	3.1750(0.0026)
	Tk RSVM 2	10.1318(0.0467)	4.0308(0.0334)	2.9816(0.0013)

Note that only the first 2 predictors contain useful classification signals, and the remaining are noise variables. In Table 4, we report the average numbers of selected variables for different classifiers and penalties with p = 200. The L₂ regularization chooses all variables in the resulting classifiers, while the L₁ and L₁ + L₂ penalties lead to more parsimonious classifiers. Note that all methods with L₁ and L₁ + L₂ penalties are able to identify the underlying two predictors. In terms of classification error rates, the two sparse penalties perform better than the pure L₂ method, with L₁ + L₂ slightly better than L₁.

Table 4.

The number of predictors selected by RMSVM, MSVM and our RSVMs 1-2 on the simulated example with p = 200 and data contamination percentage 10%.

Penalty	L2	L1	L1 + L2
RMSVM	200.0000	3.9800	8.4000
T0 RSVM 1	200.0000	6.0200	27.8000
TK RSVM 1	200.0000	6.1400	6.8000
MSVM	200.0000	6.9200	3
T0 RSVM 2	200.0000	5.4000	3
TK RSVM 2	200.0000	5.1600	3

As a measurement of computational speeds, for the simulated example with p = 200, we report the average running time of one replication for the compared methods in Table 5. One can see that since the optimization problems are more involved, our RSVMs with the DCA take longer to compute, compared with RMSVM and MSVM without truncation. However, they are still relatively efficient to implement. Note that the candidate set of tuning parameters for the L₁ + L₂ penalty is much larger than that of L₁ or L₂ penalties, hence the running time of the methods with the L₁ + L₂ penalty is longer.

Table 5.

Running time of one replication for various classifiers and penalty functions in the simulated example with p = 200.

Penalty	L2 Running time (sec)	L1 Running time (sec)	L1 + L2 Running time (sec)
RMSVM	0.3736	12.9099	152.0332
T0 RSVM 1	4.1636	31.7880	717.1089
Tk RSVM 1	3.8809	26.6204	674.5778
MSVM	2.2035	11.4896	1347.3421
T0 RSVM 2	8.5175	22.9063	4208.3969
Tk RSVM 2	6.4516	16.9095	2599.3510

5.2 Real Data Analysis

In this section, we investigate the performance of our proposed classifiers using a real application dataset Small Round Blue Cell Tumors (SRBCT, Demšar et al, 2013), which can be found on the UCI Machine Learning Repository (Bache and Lichman, 2013). The SRBCT dataset consists of 4 different types of children brain tumors, including Ewing sarcoma (EWS), neuroblastoma (NB), rhabdomyosarcoma (RMS), and Burkitt’s Lymphoma (BL). Because treatment options and responses to therapy vary widely depending on the diagnosis, accurate prediction of the SRBCT subtype is highly desirable. However, these cancer subtypes are similar in routine histology and are difficult to differentiate using regular clinical results. The dataset contains gene expression levels of 2308 genes, and there are 83 patients in total. In particular, we have 29 EWSs, 18 NBs, 25 RMSs, and 11 BLs. In our analysis, we split the data into 3 equal parts for training, tuning, and testing. We first compare the performance of RMSVM (Liu and Yuan, 2011), MSVM by Liu and Shen (2006), and our proposed RSVMs (3) and (6). Here, we choose the truncation locations in the same way as in Section 5.1. We also contaminate the dataset with outliers. In particular, we choose 10% of the observations, randomly relabel them into another class, and add a constant 2 to each of the corresponding predictors. Then we run the examples again using RMSVM, MSVM and our proposed RSVMs 1-2 to demonstrate the effect of outliers on classification accuracy.

We report the average misclassification error rates over 50 replicates for various methods in Table 6. We also report the running time in seconds for each method in Table 7. The running time for the method with L₁ + L₂ penalty is higher since the number of tuning parameters is much bigger. Note that when Perc = 0%, the results of MSVM and RSVMs 1-2 using L₁ or L₂ penalties are the same. This is because all these methods have perfect prediction on the training set, therefore no truncation is needed. From the results, we can see that our proposed methods with truncations are very competitive in terms of classification accuracy, especially when the data are contaminated with outliers. For this dataset, among 3 types of penalties, L₁ +L₂ works the best. This can be due to the grouping effects of this penalty which allows highly correlated input variables, commonly in genetic data, to have similar fitted coefficients and simultaneously allow automatic variable selection and shrinkage (Wang et al, 2006). Between two choices of truncated location, s = −1/(k − 1) works slightly better than s = 0.

Table 6.

Classification error rates for RMSVM, MSVM and our RSVMs 1-2 on the SRBCT dataset. Here Perc stands for the percentage of data that are contaminated.

Penalty		L2	L1	L1 + L2
Perc	Loss	Error	Error	Error
0%	RMSVM	3.6000(0.0542)	6.1333(0.0795)	4.3859(0.0705)
	T0 RSVM 1	3.8666(0.0540)	6.2666(0.0801)	3.2894(0.0638)
	Tk RSVM 1	3.3333(0.0526)	6.0000(0.0800)	4.3859(0.0705)
	MSVM	5.3333(0.0602)	7.2000(0.0850)	3.4736(0.0482)
	T0 RSVM 2	5.3333(0.0602)	7.2000(0.0850)	3.0526(0.0464)
	Tk RSVM 2	5.3333(0.0602)	7.2000(0.0850)	3.4736(0.0482)
10%	RMSVM	6.9333(0.0830)	11.0666(0.1171)	6.0000(0.0728)
	T0 RSVM 1	4.8000(0.0539)	8.5333(0.0852)	4.8000(0.0539)
	Tk RSVM 1	6.1333(0.0671)	9.0666(0.0891)	5.3333(0.0571)
	MSVM	8.8000(0.0743)	10.4000(0.0843)	5.1714(0.0670)
	T0 RSVM 2	7.4666(0.0695)	9.2000(0.0840)	3.7838(0.0559)
	Tk RSVM 2	8.4000(0.0748)	10.4000(0.0821)	4.0390(0.0545)

Table 7.

Running time in seconds for RMSVM, MSVM and our RSVMs 1-2 on the SRBCT dataset. Here Perc stands for the percentage of data that are contaminated.

Penalty		L2	L1	L1 + L2
Perc	Loss	Running time (sec)	Running time (sec)	Running time (sec)
0%	RMSVM	0.7095	78.7449	474.5619
	T0 RSVM 1	4.2161	88.7830	2770.0465
	Tk RSVM 1	4.0069	86.0682	2833.6601
	MSVM	0.5916	1292.2680	716.5681
	T0 RSVM 2	1.8748	3409.9990	3348.6898
	Tk RSVM 2	3.6891	3497.6771	3260.9417
10%	RMSVM	3.6029	84.5760	596.2820
	T0 RSVM 1	14.7556	111.6447	3053.0931
	Tk RSVM 1	14.7022	104.4469	3198.6766
	MSVM	0.5898	1639.3733	685.2144
	T0 RSVM 2	3.8194	5383.0758	2730.4939
	Tk RSVM 2	4.6654	5169.2126	2663.3808

In terms of variable selection, even when 10% of the data are contaminated, our proposed methods with the L₁ + L₂ penalty are able to identify important signature genes that can be used to predict SRBCT subtypes. In particular, we identify genes with ID 770394 and 1435862 that are known to be associated with EWS, genes 812105 and 325182 associated with NB, gene 796258 associated with RMS, and gene 183337 associated with BL (Demšar et al, 2013). Here, genes 770394 and 1435862 appear in the final classifier for all the repetitions, whereas gene 183337 is selected 47 times out of 50 repetitions (94%), partly because the number of samples of this tumor subtype is small.

6 Discussion

In this paper, we consider how to alleviate the effect of outliers in the angle-based classification framework. The existing angle-based methods impose heavy loss values on outliers, hence the resulting classifiers can be unstable and suboptimal. To overcome this difficulty, we employ truncated hinge loss functions, and propose two robust angle-based MSVM methods. Because the corresponding optimization problems are non-convex, we use the DCA to solve the corresponding optimization, and develop the algorithms for our RSVMs using various penalty functions. Theoretical results, including Fisher consistency and prediction error bounds are obtained. Numerical results with both simulated and real data demonstrate that our new classifiers are very competitive, especially at the presence of outliers in the data. One interesting future research direction is to further understand the solutions obtained by DCA for our two proposed robust angle-based MSVMs, along the line of the recent work by Pang et al (2016).

Table 2.

Classification error rates for RMSVM, MSVM and our RSVMs 1-2 on the simulated data with k = 3, p = 20. Here Perc stands for the percentage of data that are contaminated.

Penalty		L2	L1	L1 + L2
Perc	Loss	Error	Error	Error
5 %	RMSVM	4.0991(0.0089)	3.4977(0.0072)	3.4074(0.0047)
	T0 RSVM 1	3.4220(0.0103)	3.4978(0.0055)	3.1792(0.0032)
	Tk RSVM 1	3.6043(0.0050)	3.3798(0.0047)	3.2436(0.0037)
	MSVM	3.9090(0.0063)	3.3828(0.0046)	3.3400(0.0052)
	T0 RSVM 2	3.4982(0.0041)	3.3873(0.0043)	3.1500(0.0025)
	Tk RSVM 2	3.4442(0.0037)	3.3396(0.0035)	3.0922(0.0021)
10 %	RMSVM	4.0991(0.0140)	4.6318(0.0172)	5.0172(0.0257)
	T0 RSVM 1	3.5752(0.0055)	3.4000(0.0051)	3.3710(0.0116)
	Tk RSVM 1	3.4733(0.0044)	3.3798(0.0049)	3.4596(0.0084)
	MSVM	5.5827(0.0194)	4.6140(0.0252)	4.1241(0.0149)
	T0 RSVM 2	3.5240(0.0041)	3.3520(0.0042)	3.1598(0.0031)
	Tk RSVM 2	3.5147(0.0039)	3.4888(0.0204)	3.4147(0.0034)

Appendix

Proof to Theorem 1

To prove the theorem, we need the following lemma, of which the proof can be found in Zhang and Liu (2014).

Lemma 1 (Zhang and Liu, 2014, Lemma 1)

Suppose we have an arbitrary f ∈ ℝ^k−1. For any u,v ∈ {1,…,k} such that u ≠ v, define T_u,v = W_u − W_v. For any scalar z ∈ ℝ, 〈(f + zT_u,v),W_w〉 = 〈f, W_w〉 where w ∈ {1,…,k} such that u ≠ v, define T_u,v = W_u−W_v. For any scalar z ∈ ℝ, and w ≠ u,v. Furthermore, we have that 〈(f + zT_u,v),W_u〉 − 〈f,W_u〉 = − 〈(f + zT_u,v),W_u〉 + 〈f,W_u〉.

We first prove that the loss function (3) is Fisher consistent with γ ≤ 1/2 and s ≤ 0. Assume that, without loss of generality, P₁ > P₂ ≥ ⋯ ≥ P_k. The goal is to show that 〈f*,W₁〉 > 〈f*,W_j〉 for any j ≠ 1. Inspired by the proof in Liu and Yuan (2011) and Wu and Liu (2006), we complete our proof with four steps.

The first step is to show that there exists a theoretical minimizer f* such that 〈f*,W_j〉 ≤ k – 1 for all j. Otherwise, suppose 〈f*,W_j〉 > k – 1 for some i, there must exist q ∈ {1,…,k}, q ≠ i, such that 〈f*,W_q〉 > −1, by the sum-to-zero property of the inner products ${\displaystyle {\sum }_{j=1}^k\langle \mathit{f}\ast ,{\mathit{W}}_j\rangle }=0$. Now one can decrease 〈f*,W_i〉 by a small amount, and increase 〈f*,W_q〉 by the same amount (Lemma 1), and the variation of the conditional loss depends on s. Specifically, if $s<-\frac{1}{k-1}$, the conditional loss is decreased, which is a contradiction to the definition of f*. If $-\frac{1}{k-1}\le s\le 0$, the conditional loss remains the same. However, one can keep doing this till all 〈f*,W_j〉 ≤ k – 1, which is a contradiction to the assumption 〈f*,W_i〉 > k – 1.

The second step is to show that 〈f*,W₁〉 ≥ 〈f*,W_j〉 for any j ≠ 1 using contradiction. Suppose 〈f*,W₁〉 < 〈f*,W_i〉 for some i. By the definition of S(x) = E[ϕ₁{f(X),Y}|X = x], we can simplify it as

$$S(\mathit{x})\triangleq {\displaystyle \sum _{j=1}^k{P}_j{h}_{\gamma }(\langle \mathit{f},{\mathit{W}}_j\rangle )}+(1-\gamma ){\displaystyle \sum _{j=1}^k{R}_s(\langle \mathit{f},{\mathit{W}}_j\rangle )}.$$

Where h_γ(u) = γT_(k−1)s(u) − (1 − γ)R_s(u). Because h_γ(u) is monotone decreasing for any 0 ≤ γ ≤ 1, we have h_γ(〈f*, W₁〉) ≥ h_γ(〈f*, W_i〉). We claim that h_γ(〈f*, W₁〉) ≤ h_γ(〈f*, W_j〉) for all j ≠ 1. If it is not true, there must exist h_γ(〈f*, W₁〉) > h_γ(〈f*, W_j〉) for some j. Then we can define f′(x) ∈ ℝ^k−1 such that 〈f*,W₁〉 = 〈f*,W_j〉 and 〈f*,W_j〉 = 〈f*,W_j〉 (the existence of such f′ is guaranteed by Lemma 1). One can verify that f′ is the minimizer of S(x), not f*. This contradicts with the definition of f*. Therefore, we obtain h_γ(〈f*, W₁〉) = h_γ(〈f*, W_i〉). Because h_γ(·) is flat in (−∞, min(−1,(k−1)s)] and [max(k−1, −s), +∞), 〈f*,W₁〉 and 〈f*,W_i〉 lie in the same interval simultaneously. If 〈f*, W₁〉, 〈f*, W_i〉 ∈ (−∞, min(−1, (k−1)s)] < 0, then all 〈f*, W_j〉 < 0, which is a contradiction to the sum-to-zero property. Thus 〈f*, W₁〉, 〈f*, W_i〉 ∈ [max (k – 1, –s), +∞). If s < −(k – 1), then –s ≤ 〈f*, W₁〉 ≤ k−1, which is a contradiction. If 0 ≥ s ≥ −(k − 1), based on the fact that 〈f*, W_j〉 ≤ k−1 for all j, then 〈f*, W₁〉 = 〈f*, W_i〉 = k – 1, which contradicts with the assumption. Hence, we must have that 〈f*, W₁〉 ≥ 〈f*, W_j〉 for all j ≠ 1.

The third step is to show that when γ ≤ 1/2, 〈f*, W_j〉 ≥ −1 for all j. Suppose this is not true, and 〈f*, W_i〉 < −1 for some i ≠ 1. There must exist q ∈ {1,…,k}, q≠ 1, i, such that −1 < 〈f*, W_q〉 ≤ k – 1. In this case, we can decrease 〈f*, W_q〉 by a small amount and increase 〈f*, W_i〉 by the same amount, such that the conditional loss S(x) is decreased, which contradicts with the optimality of f*.

The last step is to show that 〈f*, W_j〉 ≤ 0 for any j ≠ 1. If 〈f*, W_i〉 > 0 for some i, then 〈f*, W₁〉 < k − 1. Otherwise, 〈f*, W₁〉 = k−1. According to third part, we have 〈f*, W_j〉 = −1, j ≠ 1. Especially, 〈f*, W_i〉 = −1 < 0, which is a contradiction to the assumption 〈f*, W_i〉 > 0. Then 〈f*, W₁〉 < k − 1. Now we can decrease 〈f*, W_i〉 by a small amount, and increase 〈f*, W₁〉 by the same amount (Lemma 1), and the conditional loss is decreased. Is It indicates that the current f* is not optimal, which is a contradiction. Based on the sum-to-zero property, we show the fact 〈f*, W₁〉 > 0 ≥ 〈f*, W_j〉 for any j ≠ 1. This completes the first part of the proof, that (3) is Fisher consistent when γ ≤ 1/2 and s ≤ 0.

We proceed to show the Fisher consistency of (6) when s ∈ [−1/(k − 1),0]. Again, without loss of generality, P₁ > P₂ ≥ ⋯ ≥ P_k. By similar arguments as above, one can verify that 〈f*, W₁〉 ≥ 0, and 〈f*, W_i〉 ≥ 〈f*, W_j〉 if i < j. Therefore, it remains to show that 0 is not the minimizer for the choice of s. To this end, notice that for $s\in [-\frac{1}{k-1},0]$, we have $\frac{1}{-s}\ge k-1$. Consequently, there exists t ∈ (0,1] such that $\frac{t}{-s}\ge k-1$. Consider a f such that $\langle \mathit{f},{\mathit{W}}_1\rangle =\frac{t(k-1)}{k}$ and $\langle \mathit{f},{\mathit{W}}_j\rangle =-\frac{t}{k}$ for j ≠ 1. One can verify that f yields a smaller conditional loss, compared to 0. Thus, the robust SVM (6) is Fisher consistent. ■

Proof to Theorem 2

We can prove the theorem using a recent technique in the statistical machine learning literature, namely, the Rademacher complexity (Bartlett and Mendelson, 2002; Koltchinskii and Panchenko, 2002; Shawe-Taylor and Cristianini, 2004; Bartlett et al, 2005; Koltchinskii, 2006; Mohri et al, 2012). To begin with, let σ = {σ_i; i = 1,…,n} be independent and identically distributed random variables, that take 1 and −1 with probability 1/2 each. Denote by S a sample of observations (x_i,y_i); i = 1,…,n, independent and identically distributed from the underlying distribution P(X,Y). For a function class $\mathcal{F}=\{f:f(\mathit{x},y)\}$ and given S, we define the empirical Rademacher complexity of $\mathcal{F}$ to be

$${\widehat{R}}_n(\mathcal{F})=E_{\sigma }\{\underset{f\in \mathcal{F}}{\text{sup}}\}\frac{1}{n}{\displaystyle \sum _{i=1}^n{\sigma }_{i}f}({\mathit{x}}_i,y_i)\}.$$

Here E_σ means taking expectation with respect to the distribution of σ. Furthermore, define the Rademacher complexity of $\mathcal{F}$ to be

$$R_n(\mathcal{F})=E_{\sigma ,S}\{\underset{f\in \mathcal{F}}{\text{sup}}\frac{1}{n}{\displaystyle \sum _{i=1}^n{\sigma }_{i}f({\mathit{x}}_i,y_i)}\}.$$

Another key step in the proof is to notice that the indicator function in (16) is discontinuous, thus it is difficult to bound the corresponding Rademacher complexity directly. To overcome this challenge, we can consider a continuous upper bound of the indicator function. In particular, for any $\widehat{\mathit{f}}$, let I_κ be defined as follows

$$I_{\kappa }\{\widehat{\mathit{f}}(\mathit{x}),y\}=\{\begin{array}{ll}1\hfill & \text{if }y\ne {\widehat{y}}_{\widehat{\mathit{f}}}(\mathit{x}),\hfill \\ 1-\frac{1}{\kappa }{min}_{j\ne y}\langle \widehat{\mathit{f}}(\mathit{x}),{\mathit{W}}_y-{\mathit{W}}_j\rangle \hfill & \text{if }y={\widehat{y}}_{\widehat{\mathit{f}}}(\mathit{x})\text{and}{min}_{j\ne y}\langle \widehat{\mathit{f}}(\mathit{x}),{\mathit{W}}_y-{\mathit{W}}_j\rangle \le \kappa ,\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}$$

where κ is a small positive number to be determined later. One can verify that I_κ is a continuous upper bound of the indicator function in (16). In the following proof, we focus on bounding the Rademacher complexity of I_κ, where $\widehat{\mathit{f}}$ is obtained from the optimization problems (3) and (6).

Our goal is to show that with probability at least 1 − δ (0 < δ < 1), $E[I_{\kappa }\{\widehat{\mathit{f}}(\mathit{X}),Y\}]$ is bounded by the summation of its empirical evaluation, the Rademacher complexity of the function class $\mathcal{F}$, and a penalty term on δ. The proof of Theorem 2 consists of two major steps. In particular, we have the following two lemmas.

Lemma 2

Let $R_n(\mathcal{F})$ and ${\widehat{R}}_n(\mathcal{F})$ be defined with respect to the I_κ function. Then, with probability at least 1−δ,

$$E[I_{\kappa }\{\widehat{\mathit{f}}(\mathit{X}),Y\}]\le \frac{1}{n}{\displaystyle \sum _{i=1}^n{I}_{\kappa }}\{\widehat{\mathit{f}}({\mathit{x}}_i),y_i\}+2R_n(\mathcal{F})+T_n(\delta ),$$ (17)

where T_n(δ) = {log(1/δ)/n}^1/2.

Moreover, with probability at least 1 − δ,

$$E[I_{\kappa }\{\widehat{\mathit{f}}(\mathit{X}),Y\}]\le \frac{1}{n}{\displaystyle \sum _{i=1}^n{I}_{\kappa }\{\widehat{\mathit{f}}({\mathit{x}}_i),y_i\}+2{\widehat{R}}_n(\mathcal{F})+3T_n(\delta /2)}.$$

Lemma 3

Let s = 1/λ. In linear learning, when we use the L₁ penalty, the empirical Rademacher complexity ${\widehat{R}}_n(\mathcal{F})\le \frac{s}{\kappa }\sqrt{\frac{2\text{log}(2pk-2p)}{n}}$, and when we use the L₂ penalty, ${\widehat{R}}_n(\mathcal{F})\le \{2(k-1){(ps)}^{1/2}\}/(\kappa n^{1/4})+\{2{(ps)}^{1/2}\}{\left(\text{log}[e+e\{2p(k-1)\}]/(n^{1/2})\right)}^{1/2}/(\kappa n^{1/4})$. for kernel learning with separable kernel functions, the empirical Rademacher complexity ${\widehat{R}}_n(\mathcal{F})\le \frac{s(k-1)}{\kappa \sqrt{n}}$.

Proof of Lemma 2

The proof consists of three parts. For the first part, we use the McDiarmid inequality (McDiarmid, 1989) to bound the left hand side of (17), in terms of its empirical estimation, plus the expectation of their supremum difference, E(ϕ), which is to be defined below. For the second part, we show that E(ϕ) is bounded by the Rademacher complexity using symmetrization inequalities (van der Vaart and Wellner, 2000). For the third part, we prove that one can bound the Rademacher complexity using the empirical Rademacher complexity.

For a given sample S, we define

$$\varphi (S)=\underset{\mathit{f}\in \mathcal{F}}{\text{sup}}\left(E[I_{\kappa }\{\widehat{\mathit{f}}(\mathit{X}),Y\}]-\frac{1}{n}{\displaystyle \sum _{i=1}^n{I}_{\kappa }\{\widehat{\mathit{f}}({\mathit{x}}_i),y_i\}}\right).$$

Let $S^{(i,\mathit{x})}=\{({\mathit{x}}_1,y_1),\dots ,({\mathit{x}}_i^{\prime },y_i),\dots ,({\mathit{x}}_n,y_n)\}$ be another sample from P(X,Y), where the difference between S and S^(i,x) is only on the x value of their ith pair. By definition, we have

$$|\varphi (S)-\varphi (S^{(i,\mathit{x})})|=|\underset{\mathit{f}\in \mathcal{F}}{\text{sup}}\left(E[I_{\kappa }\{\widehat{\mathit{f}}(\mathit{X}),Y\}]-\frac{1}{n}{\displaystyle \sum _S{I}_{\kappa }\{\widehat{\mathit{f}}({\mathit{x}}_i),y_i\}}\right)-\underset{\mathit{f}\in \mathcal{F}}{\text{sup}}\left(E[I_{\kappa }\{\widehat{\mathit{f}}(\mathit{X}),Y\}]-\frac{1}{n}{\displaystyle \sum _{S^{(i,\mathit{x})}}{I}_{\kappa }\{\widehat{\mathit{f}}({\mathit{x}}_i),y_i\}}\right)|.$$

For simplicity, suppose that f^S is the function that achieves the supremum of ϕ(S). We note that the case of no function achieving the supremum can be treated analogously, with only additional discussions on the arbitrarily small difference between ϕ(f) and its supremum. Thus, we omit the details here. We have that,

$$\begin{gathered} |\varphi (S)=\varphi (S^{(i,\mathit{x})})|\le |E[I_{\kappa }\{{\mathit{f}}^S(\mathit{X}),Y\}]-\frac{1}{n}{\displaystyle \sum _S{I}_{\kappa }\{{\mathit{f}}^S({\mathit{x}}_i),y_i\}}-E[I_{\kappa }\{{\mathit{f}}^S(\mathit{X}),Y\}] \\ +\frac{1}{n}{\displaystyle \sum _{S^{(i,\mathit{x})}}{I}_{\kappa }\{{\mathit{f}}^S({\mathit{x}}_i),y_i\}}|.=\frac{1}{n}|{\displaystyle \sum _S{I}_{\kappa }\{{\mathit{f}}^S({\mathit{x}}_i),y_i\}}-{\displaystyle \sum _{S^{(i,\mathit{x})}}{I}_{\kappa }\{{\mathit{f}}^S({\mathit{x}}_i),y_i\}}|\le \frac{1}{n}. \end{gathered}$$

Next, by the McDiarmid inequality, we have that for any t > 0, pr[ϕ(S)−E{ϕ(S) ≥ t] ≤ exp[−(2t²)/{2n(1/n)²}], or equivalently, with probability at least 1 – δ, ϕ(S))− E{ϕ(S) ≤ T_n(δ). Consequently, we have that with probability at least 1 – δ, $E[I_{\kappa }\{{\mathit{f}}^S(\mathit{X}),Y\}]\le n^{-1}{\displaystyle {\sum }_{i=1}^n{I}_{\kappa }\{\widehat{\mathit{f}}({\mathit{x}}_i),y_i\}}+E\{\varphi (S)\}+T_n(\delta )$. This completes the first part of the proof.

For the second part, we bound E{ϕ(S)} by the corresponding Rademacher complexity. To this end, define $S^{\prime }=\{({\mathit{x}}_i^{\prime },y_i^{\prime });i=1,\dots ,n\}$ as an independent duplicate sample of size n with the identical distribution as S. Denote by E_S the action of taking expectation with respect to the distribution of S, and define $E_{S^{\prime }}$ analogously. By definition, we have that $E_{S^{\prime }}[n^{-1}{\displaystyle {\sum }_{S\prime }{I}_{\kappa }\{\widehat{\mathit{f}}({\mathit{x}}_i^{\prime }),y_i^{\prime }\}|S}]=E[I_{\kappa }\{\widehat{\mathit{f}}(\mathit{X}),Y\}]$, and $E_{S^{\prime }}[n^{-1}{\displaystyle {\sum }_S{I}_{\kappa }\{\widehat{\mathit{f}}({\mathit{x}}_i),y_i\}|S}]=n^{-1}{\displaystyle {\sum }_S{I}_{\kappa }\{\widehat{\mathit{f}}({\mathit{x}}_i),y_i\}}$. then, by Jensen’s inequality and the property of σ, we have that

$$E\{\varphi (S)\}=E_S(\underset{f\in \mathcal{F}}{\text{sup}}{E}_{S^{\prime }}[\frac{1}{n}{\displaystyle \sum _{S^{\prime }}{I}_{\kappa }\{\widehat{\mathit{f}}({\mathit{x}}_i^{\prime }),y_i^{\prime }\}-\frac{1}{n}{\displaystyle \sum _S{I}_{\kappa }\{\widehat{\mathit{f}}({\mathit{x}}_i),y_i\}}}]|S)\le E_{S,S^{\prime }}[\underset{f\in \mathcal{F}}{\text{sup}}\frac{1}{n}{\displaystyle \sum _{S^{\prime }}{I}_{\kappa }\{\widehat{\mathit{f}}({\mathit{x}}_i^{\prime }),y_i^{\prime }\}-\frac{1}{n}{\displaystyle \sum _S{I}_{\kappa }\{\widehat{\mathit{f}}({\mathit{x}}_i),y_i\}}}]=E_{S,S^{\prime },\sigma }[\underset{f\in \mathcal{F}}{\text{sup}}\frac{1}{n}{\displaystyle \sum _{S^{\prime }}{\sigma }_i{I}_{\kappa }\{\widehat{\mathit{f}}({\mathit{x}}_i^{\prime }),y_i^{\prime }\}-\frac{1}{n}{\displaystyle \sum _S{\sigma }_i{I}_{\kappa }\{\widehat{\mathit{f}}({\mathit{x}}_i),y_i\}}}]\le 2R_n\{\mathcal{F}(p,k,s)\}.$$

Hence the second part is proved.

In the third step, we need to bound $R_n(\mathcal{F})$ using ${\widehat{R}}_n(\mathcal{F})$. This step is analogous to the first part, and we omit the details here. Briefly speaking, one can apply the McDiarmid inequality on ${\widehat{R}}_n(\mathcal{F})$ and the corresponding expectation $R_n(\mathcal{F})$. Similar to the first part of this proof, we can show that with probability at least 1 − δ, $R_n(\mathcal{F})\le {\widehat{R}}_n(\mathcal{F})+2T_n(\delta )$.

The final results of Lemma 2 can be obtained by choosing the confidence 1 − δ/2 in the first and third steps, and combining the inequalities of the three steps. □

Proof of Lemma 3

First, we prove that for the obtained $\widehat{\mathit{f}}$, $J(\widehat{\mathit{f}})\le s$. To see this, notice that for β_j = 0 and β_j,0 = 0, we have

$$\frac{1}{n}{\displaystyle \sum _{i=1}^n{I}_{\kappa }\{\mathit{f}({\mathit{x}}_i),y_i\}\le 1.}$$

On the other hand, $\widehat{\mathit{f}}$ is the solution to the optimization problems in (3) or (6), hence

$$\lambda J(\widehat{\mathit{f}})\le \frac{1}{n}{\displaystyle \sum _{i=1}^n{I}_{\kappa }\{\widehat{\mathit{f}}({\mathit{x}}_i),y_i\}+\lambda J(\widehat{\mathit{f}})}\le \frac{1}{n}{\displaystyle \sum _{i=1}^n{I}_{\kappa }\{\mathit{f}({\mathit{x}}_i),y_i\}},$$

which yields $J(\widehat{\mathit{f}})\le s$.

For the L₁ penalized learning, one can bound the corresponding Rademacher complexity ${\widehat{R}}_n(\mathcal{F})$ in the following way. In particular, by Lemma 4.2 in Mohri et al (2012), we have that ${\widehat{R}}_n(\mathcal{F})$ is upper bounded by

$$\frac{1}{\kappa }{\widehat{R}}_n^{\ast }(\mathcal{F})=\frac{1}{\kappa }{E}_{\sigma }\left\{\underset{{\displaystyle {\sum }_{j=1}^{k-1}\Vert {\mathit{\beta }}_j{\Vert }_1<s}}{\text{sup}}\frac{1}{n}{\displaystyle \sum _{i=1}^n{\sigma }_i\{{\displaystyle \sum _{j=1}^{k-1}{\mathit{x}}_i^T{\mathit{\beta }}_j}\}}\right\},$$ (18)

because the continuous indicator function is Lipschitz with constant 1/κ, and elements in W_j are bounded by 1. Without loss of generality, we can rewrite (18) as the following

$$\frac{1}{\kappa }{\widehat{R}}_n^{\ast }\{\mathcal{F}(p,k,s)\}=\frac{1}{\kappa }{E}_{\sigma }\{\underset{\Vert \gamma {\Vert }_1<s}{\text{sup}}\frac{1}{n}{\displaystyle \sum _{i=1}^n{\sigma }_i{\gamma }^T{\mathit{x}}_i^{\ast }}\},$$

where γ can be treated as a vector that contains all the elements in β_j for j = 1,…,k − 1, and ${\mathit{x}}_i^{\ast }$ is defined accordingly. Next, by Theorem 10.10 in Mohri et al (2012), we have that ${\widehat{R}}_n^{\ast }\{\mathcal{F}(p,k,s)\}\le s\sqrt{\frac{2\text{log}(2pk-2p)}{n}}$. Thus, ${\widehat{R}}_n^{\ast }\{\mathcal{F}(p,k,s)\}\le \frac{s}{\kappa }\sqrt{\frac{2\text{log}(2pk-2p)}{n}}$ for L₁ penalized linear learning.

For L₂ penalized learning, the proof is analogous to that of Lemma 8 in Zhang and Liu (2014), and we omit the details here.

For kernel learning, notice that one can include the intercept in the original predictor space (i.e., augment x to include a constant 1 before the other predictors), and define a new kernel function accordingly. This new kernel is also positive definite and separable with a bounded kernel function. By Mercer’s Theorem, this introduces a new RKHS $\mathcal{H}$. Next, by a similar argument as for (18), we have that the original Rademacher complexity is upper bounded by

$$\frac{1}{\kappa }{\widehat{R}}_n^{\ast }(\mathcal{F})=\frac{1}{\kappa }{E}_{\sigma }\left[\underset{{\displaystyle {\sum }_j\Vert f_j{\Vert }_{\mathcal{H}}^2\le s}}{\text{sup}}\frac{1}{n}{\displaystyle \sum _{i=1}^n{\sigma }_i}\{{\displaystyle \sum _{j=1}^{k-1}{f}_j({\mathit{x}}_i)}\}\right],\le \frac{k-1}{\kappa }{E}_{\sigma }\left[\underset{\Vert f{\Vert }_{\mathcal{H}}^2\le s}{\text{sup}}\frac{1}{n}{\displaystyle \sum _{i=1}^n{\sigma }_{i}f({\mathit{x}}_i)}\right],\le \frac{k-1}{\kappa }\frac{s}{\sqrt{n}},$$

where the last inequality follows from Theorem 5.5 in Mohri et al (2012). Hence, we have that for kernel learning, ${\widehat{R}}_n(\mathcal{F})\le \frac{s(k-1)}{\kappa \sqrt{n}}$.

The proof of Theorem 2 is thus finished by combining Lemmas 2 and 3, and the fact that the continuous indicator function I_κ is an upper bound of the indicator function for any κ.