Quantum measurement of a rapidly rotating spin qubit in diamond

Single-qubit sensing in a physically rotating reference frame with defect centers in diamond.

Abstract

A controlled qubit in a rotating frame opens new opportunities to probe fundamental quantum physics, such as geometric phases in physically rotating frames, and can potentially enhance detection of magnetic fields. Realizing a single qubit that can be measured and controlled during physical rotation is experimentally challenging. We demonstrate quantum control of a single nitrogen-vacancy (NV) center within a diamond rotated at 200,000 rpm, a rotational period comparable to the NV spin coherence time T₂. We stroboscopically image individual NV centers that execute rapid circular motion in addition to rotation and demonstrate preparation, control, and readout of the qubit quantum state with lasers and microwaves. Using spin-echo interferometry of the rotating qubit, we are able to detect modulation of the NV Zeeman shift arising from the rotating NV axis and an external DC magnetic field. Our work establishes single NV qubits in diamond as quantum sensors in the physically rotating frame and paves the way for the realization of single-qubit diamond-based rotation sensors.

INTRODUCTION

Profound aspects of fundamental and applied physics can be probed with a single quantum system in a rotating frame, including geometric phase shifts due to rotation of a quantum system (1, 2), magnetic fields induced as a result of the link between rotation and Larmor precession (3), and magic-angle spinning, a nuclear magnetic resonance (NMR) technique used to control magnetic dipolar interactions (4). The nitrogen-vacancy (NV) center in diamond (5, 6) is an ideal solid-state qubit to study quantum physics in the rotating frame. In static, nonrotating frames, it has demonstrated success as a nanoscale detector of magnetic fields (7), electric fields (8), crystal strain (9), and temperature (10) in real-world sensing environments, such as within biological cells (11). An NV center in a physically rotating diamond brings these extensive quantum sensing modalities to the rotating frame and is predicted to accumulate a quantum mechanical Berry phase (12, 13), which underlies the operation of a proposed NV-diamond gyroscope (14). Rotating diamonds with large ensembles of NV centers have recently been used to explore magnetic pseudofields generated in the rotating frame (15). This work realizes quantum measurement of a single solid-state qubit in a diamond rotating with a period comparable to the spin coherence time, establishing an exemplar system for probing rotational effects at the single quantum level.

Our experiments offer the robust, well-defined environment of bulk diamond in which to study the effects of rotation on a single-spin qubit. Hybrid spin-optomechanical systems, consisting of NV-hosting micro- and nanodiamonds in optical (16–18) and ion traps (19), are of considerable interest for studying quantum superpositions of massive objects (20, 21) and could also be potentially used to explore rotation of qubits. However, free rotation of the qubit in trapped-nanodiamond experiments is difficult to control because it depends on the trapping (or measurement) laser and geometry of the nanodiamond itself (19, 22), scrambling the orientation of the NV axis. The typical coherence times of NVs hosted in nanodiamonds (T₂ < 1 μs) require extremely rapid rotations to study rotational physics in a genuinely quantum setting. We demonstrate control and optical state readout of a single NV qubit during rapid, well-controlled physical rotation and perform coherent quantum measurements over a significant fraction of the rotation period. We use quantum measurement in the rotating frame to measure an effect unique to a rotating NV center—time-varying Zeeman shifts arising from stationary-frame DC magnetic fields. Our work opens the study of frame-dependent effects to quantum sensing at the single-spin level with a robust, versatile quantum sensor.

RESULTS

Experimental setup

A schematic of our experiment is depicted in Fig. 1. The diamond sample contains well-separated single NV centers 3 μm below the surface, with the (111) NV axes oriented at 54.7° to the surface normal. The diamond is mounted on a high-speed electric motor that is capable of rotation speeds of up to 3.33 kHz (200,000 rpm) in this configuration, and a purpose-built scanning-objective confocal microscope is used to optically address the NV centers. For quantum state control, we use microwave fields tuned to the ground state m_S = 0↔m_S = −1 two-level system. The timing of laser and microwave pulses for state manipulation is controlled by a pulse generator triggered by a signal synchronous with the rotation of the diamond. We denote the rotation axis as z, nominally orthogonal to the plane of the diamond surface. For the experiments described in this work, we typically operate with a 6.2-G magnetic bias field parallel to z. At this field strength, the spin coherence time of the NV centers in the diamond is approximately T₂ ≈ 350 μs (see fig. S1), limited by carbon-13 nuclear spin bath dynamics.

Fig. 1. Experimental schematic and setup.

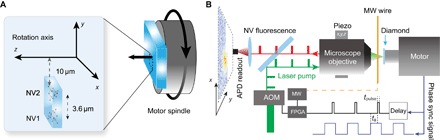
(A) A diamond containing single NV centers is mounted to the spindle of an electric motor that rotates at 3.33 kHz. Two NV centers located 3 μm below the diamond surface, separated by 3.6 μm, and located 10 μm from the center of the rotation axis (z) are considered in this work. (B) NV centers are optically prepared and addressed by a scanning confocal microscope: 532-nm excitation light is pulsed for a duration t_pulse synchronously with the motor rotation, and an avalanche photodiode (APD) collects the emitted photons from the NV center. A time delay t_φ between the motor synchronization edge and the optical pulse controls the instantaneous angle of the diamond imaged, and a wire located above the surface of the diamond is used to apply microwave (MW) pulses for state manipulation. Current-carrying coils (not shown) are used to apply magnetic fields along the x, y, and z axes. FPGA, field-programmable gate array.

Strobed confocal microscopy

An essential prerequisite to probing and manipulating the NV is to first locate it within the rapidly rotating diamond. Even when the host diamond is physically rotating with a period comparable to the spin coherence time of bulk diamond [T₂ = 0.1 to 1 ms (23), T₂⁻¹ ~ kHz], accessing the quantum properties of the NV under these conditions is still technically challenging. Quantum sensors must be initialized to a well-defined state, subjected to quantum state manipulation gates, and then read out with high fidelity after some sensing time (24). A single NV qubit located away from the center of rotation will execute circular motion, complicating optical addressing. We focus on two NV centers (NV1 and NV2; see Fig. 1A), separated by 3.6 μm and about r = 10 μm from the center of the diamond rotation (r = 0). Figure 2 shows a confocal image created by strobing the illumination synchronously with the rotation while the position of the microscope objective is scanned. A variable time delay t_φ between the motor synchronization signal and the laser pulse controls the instantaneous angle of the diamond and, hence, the position (and axis orientation) of the NV.

Fig. 2. Strobed confocal microscopy of NV centers.

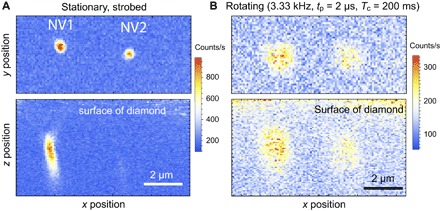
(A and B) NV1 and NV2 when stationary (A) and when rotating at high speed (B). Upper panels are x-y plane scans, whereas lower panels are x-z plane scans into the diamond. The color bar describes count rate at the experimental duty cycle of D = 0.67% (peak counts of 1 × 10⁵ recorded for D = 1). The stationary confocal images of NV1 and NV2 are strobed synchronously with an external 3.33-kHz signal from a function generator to yield an equivalent duty cycle to the rotating case. Counts are integrated for 200 ms at each pixel with the laser pulse duration t_pulse = 2 μs. (B) The optical illumination and collection are pulsed to be synchronous with the 3.33-kHz rotation of the diamond; blurring resulting from period jitter and wobble of the rotation is evident. NV1 was used for the remainder of the measurements described in this work.

The length of the laser pulse, t_pulse, determines the angular displacement and, thus, the resulting "smear" of the NV fluorescence during imaging (see fig. S2). With f_rot = 3.33 kHz (T_rot = 300 μs) and t_pulse = 2 μs, NV1 subtends an angle of 2.4° during the laser pulse. For our collection efficiency (assumed to be unchanged when rotating) and a laser power of 2.6 mW, we collect N_s = 1 × 10⁵ counts/s from a stationary NV under continuous illumination; we expect to measure N = N_st_pulse/T_rot ~ 700 counts/s when rotating at 3.33 kHz (a duty cycle of D = 0.67%). This maximum count rate is further reduced by noting that the fluorescence emitted by the NV is time-dependent because the NV samples the Gaussian intensity profile of the pumping laser beam (with 1/e² diameter d₀ ≈ 600 nm). We therefore typically measure about 350 counts/s when rotating at 3.33 kHz.

Figure 2 shows strobed confocal images of rotating NV centers with t_pulse = 2 μs, compared to stationary images. The two NVs are resolved and exhibit broadening due to jittering of the motor period and wobbling of the motor rotation axis: The characteristic 1/e² width is σ = 0.9 μm, compared to stationary images where σ = 0.3 μm. The timing jitter broadens the NV fluorescence azimuthally along its trajectory, and the wobble of the motor rotation axis broadens it primarily radially. For a laser pulse duration of 2 μs, the azimuthal smearing is less than the width due to the jitter of the rotational period (<0.4%) and the positional wobble of the rotation axis (see fig. S3). We characterized the motor rotation before attaching a diamond to the spindle and found the typical positional variation of a fiducial to be <1 μm at 3.33 kHz, consistent with the blurring we observed in the strobed confocal images in Fig. 2.

Quantum state preparation, readout, and control

In a stationary experiment, the quantum state occupation probability of the NV center is readily determined by measuring the fluorescence of the NV in some unknown superposition state relative to the fluorescence from a pure m_S = 0 state. When the NV is illuminated with green light, the state contrast is as high as 30% for a fully polarized m_S = ±1 state and then gradually reduces in time as the NV populations are pumped into a steady state. Normalized state populations can then be extracted from a single photoluminescence time series by comparing the fluorescence just after the laser turns on, when the contrast is highest, to some time after which the NV populations have reached steady state. Alternatively, the NV state can be determined by collecting separate fluorescence signals from the NV with and without microwave pulses applied (25). Both of these procedures repump the NV into the m_S = 0 state for subsequent experimental cycles. In our experiments, the NV moves during the laser preparation and readout. As it traverses the Gaussian spatial profile of the laser beam, the NV experiences an intensity with a time dependence comparable to the optical pumping dynamics responsible for state contrast and also emits fluorescence that is Gaussian in time. The state-dependent fluorescence of the NV that underlies state identification is therefore convolved with the time dependence of the laser intensity.

The emitted fluorescence from the moving NV is shown in Fig. 3. A microwave pulse is applied to an NV initially polarized into m_S = 0, creating an unknown superposition state. We then apply green excitation light and compare the fluorescence time series from the unknown state to that collected after another rotational period with no microwave pulses applied. After the second period, the NV has been repumped to the m_S = 0 bright state, and the fluorescence trace can then be used to compute the normalized contrast. We routinely observe contrasts of between 20 and 30% for resonant π pulses, indicating that the readout pulse adequately repumps the NV back to the bright state.

Fig. 3. Photoluminescence from a rapidly rotating NV center.

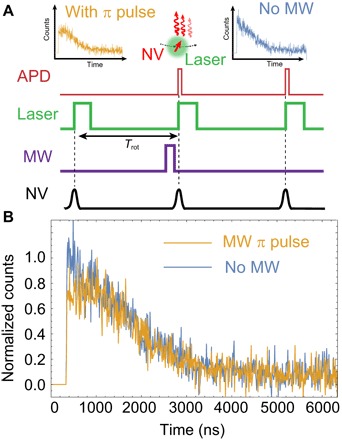
(A) The NV spin state is determined by collecting fluorescence after the application of a microwave pulse and comparing the photon counts to the same NV when in the m_S = 0 bright state. (B) The measured photoluminescence has a truncated Gaussian shape in time due to the motion of the NV through the laser beam. The initial fluorescence from the NV in the m_S = −1 dark state is approximately 20 to 30% lower than that after reinitialization into the m_S = 0 bright state.

The laser can be activated or extinguished at any time during transit through the spatial extent of the laser beam so that the NV sees a truncated Gaussian intensity profile. From a simple theoretical model (26, 27) of time-dependent optical pumping of the NV, we find that the optimum time to turn on the laser and achieve maximum signal-to-noise ratio is when the NV is almost directly under the center of the laser beam (see fig. S4).

Here, we have considered the case of a tightly focused laser beam originating from a high–numerical aperture objective, and many of the difficulties in state readout due to the transit of the NV through the beam could be mitigated by using a larger laser spot size. However, a larger laser spot size would also reduce the solid-angle collection efficiency and require more optical power. Our approach applies more generally to the resolution of single centers in the case of a diamond hosting more closely spaced NV centers. The effects of motion could also be mitigated somewhat with an NV center positioned closer to the rotational center.

To demonstrate quantum state control of the rotating NV, we vary the duration of the applied resonant microwave pulse (Fig. 3) and measure the emitted fluorescence to determine the spin state. We observe Rabi flopping between the m_S = 0 and m_S = −1 states, as shown in Fig. 4A, with a Rabi frequency of 3.6(2) MHz. We also performed measurements where we first apply a π pulse and then a second, variable-duration microwave pulse halfway through the rotation and observe the expected population oscillations with the NV initialized to the m_S = −1 state. Here, the microwave pulse flips the NV spin state after 150 μs of rotation when it is 20 μm from the laser preparation and readout region and has undergone a 180° rotation of the NV axis. The observation of Rabi oscillations initiated from the m_S = −1 state in Fig. 4B confirms that the NV state can be controlled far away from the preparation and readout region.

Fig. 4. Quantum state control of a rapidly rotating qubit.

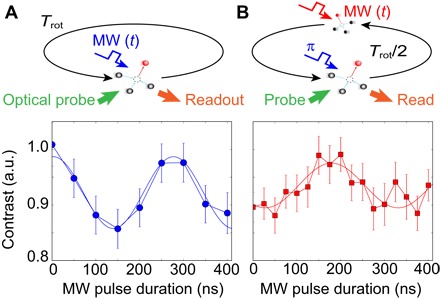
(A) Varying the duration of the microwave pulse in the sequence depicted in Fig. 3A results in time-domain Rabi oscillations, which we detect by computing the normalized fluorescence. a.u., arbitrary units. (B) We demonstrate quantum state control of the NV spin throughout the rotation by first applying a π pulse at t = 0 and then applying a variable duration microwave pulse at t = T_rot/2 at which the NV has moved 20 μm away from its initial position. We then observe Rabi oscillations with the NV initialized to the m_S = −1 state. Error bars are SE in computed fluorescence ratios from >10⁵ experimental repetitions.

Spin-echo interferometry of a rotating qubit

These results demonstrate the fundamental prerequisites to using an NV qubit as a rotating frame quantum sensor. We now apply these state control and readout techniques to quantum sensing in the rotating frame by performing spin-echo interferometry on the NV center and measure an effect unique to rotating NV centers: rotationally induced modulation of the NV Zeeman splitting. The NV axis is not parallel to the rotation axis for our diamond, and if B also makes an angle to the rotation axis, the vector projection of the bias magnetic field onto the NV axis changes as the diamond rotates. The NV then experiences an effective AC (eAC) magnetic field that oscillates at the motor frequency

$${\mathit{B}}_{\text{eff}}(\mathit{t})={\mathit{B}}_0\text{sin}{\mathrm{\theta }}_{\text{NV}}\text{sin}{\mathrm{\theta }}_{\mathit{B}}\text{cos}(2\mathrm{\pi }{\mathit{f}}_{\text{rot}}\mathit{t}+{\mathrm{\varphi }}_0)$$ (1)

where B₀ is the total magnetic field strength, f_rot is the rotation frequency, φ₀ is determined by the initial phase of the rotation, θ_B is the angle between the rotation axis and the magnetic field, and θ_NV = 54.7° is the angle between the rotation axis and the NV axis. The time-dependent Zeeman shift induced by the off-axis magnetic field can be detected using spin-echo interferometry (28) conducted in the rotating frame.

Evidence of ¹³C nuclear spins interacting with the NV can be detected in stationary spin-echo experiments, leading to a characteristic spin echo modulated at half the nuclear spin precession frequency (29). In our experiments, we applied a 6.2-G magnetic field along the z axis and measured the spin-echo signal (fig. S1). Although the first ¹³C contrast revival (τ_R =2 × 2π/γ_13CB₀ and γ_13C = 1.075 kHz/G) coincides with one rotation period at 3.33 kHz, when rotating the phase accumulated in a τ = 300 μs, the spin-echo experiment due to small (<0.01°) bias field misalignments is large enough to suppress the revival. In addition, the presence of rotationally induced effective magnetic fields shifts the rotating revival time away from the stationary revival time (15).

As shown in Fig. 5A, we consider partial rotations with the interrogation time τ short enough that the eAC field phase is slowly varying and the signal contrast has not collapsed because of the NV-¹³C interaction (τ < 60 μs). In this region, the microwave coupling is also reasonably uniform over the spatial region considered (a 12-μm arc). The final projective microwave pulse is then applied at the desired time τ, and state readout is performed after a time T_rot − τ after which the NV has completed the rotation and arrives beneath the laser.

Fig. 5. Quantum sensing with a single qubit in a physically rotating frame.

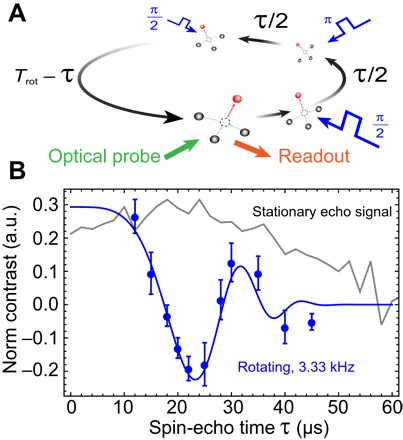
(A) We examine the phase accumulated over partial rotations by performing a spin-echo experiment for interrogation times τ < 60 μs. Once the final π/2 pulse has projected the NV into the basis state, we wait for the time remaining in the rotation for the NV to return to the preparation/readout region. (B) Unlike the stationary echo signal (gray), we observe nonzero phase accumulation for the rotating NV. The observed fringes originate from the time-varying projection of the magnetic field onto the NV axis due to misalignment from the rotation axis (data points). The observed signal is well described by an 88 ± 29–mG eAC field that is phase-locked to the diamond rotation (fitted line). Error bars are SE in computed fluorescence ratios averaged over three repeated experimental runs of ~10⁶ repetitions.

Figure 5B shows the spin-echo signal for a single NV rotating at 3.33 kHz, demonstrating the convergence of the quantum measurement and control protocols in the rotating frame described in this work. In comparison with the stationary echo signal, we observe fringes due to the presence of eAC fields. The spin-echo signal observed is consistent with the NV experiencing an eAC field (Eq. 1) of magnitude B₀sinθ_NVsinθ_B = 88 ± 29 mG, which corresponds to θ_B = 1.0 ± 0.3°. The uncertainty in the inferred field derives from the highly covariant nature of the parameters used to model the spin-echo signal in Fig. 5 and is not representative of the ultimate sensitivity of the technique. Modulating the NV Zeeman shift by rotation could, in principle, offer a simple alternative to existing schemes (30, 31) of surpassing T₂*-limited DC field sensitivities, pushing the relevant sensing time to T₂.

DISCUSSION

Our results establish the NV center as a tool to study the effects of physical rotation on individual quantum spins. These effects include rotationally induced strain, geometric phase (12, 13), and rotationally induced magnetic fields (3, 15, 32, 33), all important considerations for gyroscopic applications with NVs (14, 34). For the diamond used in this work, the ensemble dephasing time of T₂* ~ 5 μs results in a geometric phase of Φ = 2πf_rotT₂*m_S(1 − cosθ_NV) = 44 mrad for a Ramsey experiment and higher for a spin-echo sequence (12). Technical limitations due to the presence of eAC fields and ¹³C nuclei in our experiment make it difficult to discern a geometric phase from these systematics. These issues could be resolved using an isotopically pure diamond (23) with better field direction control. Rotation is typically an issue for motional sensors, such as nanodiamonds within biological cells (11), and a better understanding of the effect of rotation on single qubits could lead to more incisive quantum sensing in living organisms (35).

The quantum state manipulations in the physically rotating frame demonstrated here form the basis of new additions to the quantum sensing toolbox. Further extension to more complicated pulse sequences, with a concomitant increase in the incisiveness of the measurement, is therefore possible. A more direct investigation of the spin dynamics between a coupled NV–nuclear spin system, for example, using correlation spectroscopy (36), could analyze, with a single-spin sensor, the low- to zero-field transition between competing decoherence mechanisms in the nuclear spin bath (15).

Rotation could potentially improve the coherence, and hence, the precision, of quantum sensors. Magic-angle spinning is used in NMR experiments to narrow transition linewidths: Rotation of a solid-state nuclear spin sample with B oriented at 54.7° emulates motional averaging of internuclear magnetic dipole-dipole interactions in liquids (4). Considerable effort has been aimed at implementing nanoscale NMR sensing with the NV center (37–39), and motional narrowing of proton NMR signals in liquids has been observed with NV centers (40). It would be interesting to explore the effect of rotation at the magic angle on the internuclear interactions, either between NMR target spins in solids or between nuclear spins (such as ¹³C) within the diamond, the latter potentially increasing the coherence time of the NV center itself.

MATERIALS AND METHODS

The NV center in diamond

In the absence of magnetic fields, the electron spin of the NV center is quantized along the NV axis forming a ground state spin-triplet system: degenerate m_S = ±1 states and m_S = 0 state separated by the zero-field splitting D_zfs = 2.87 GHz. Spin-conserving optical transitions from the ground state to an excited triplet state 1.945 eV higher in energy were efficiently driven with 532-nm light. The NV emitted red photons at the 638-nm zero-phonon line and in a broad vibrational sideband. Peak emission from NVs in the m_S = 0 ground state is 30% brighter than that from m_S = ±1 states due to an intersystem crossing that results in nonradiative relaxation from the m_S = ±1 states (26). The spin state of the NV can therefore be determined via the fluorescence contrast between the bright m_S = 0 and dark m_S = ±1 states (25).

Our diamond sample was a high-purity single crystal grown by chemical vapor deposition diamond and cut along the (100) plane, with a 50-μm layer of 99.8% ¹²C grown on the surface. The concentration of nitrogen impurities was <10 parts per billion. A 0.95-NA microscope objective (Olympus UMPlanFl) mounted on a three-axis piezoelectric stage (PI P-611.3S) focused a 532- nm laser light to a 600-nm spot size onto the diamond, which was mounted on a high-speed electric motor (Celeroton CM-2-500). Red fluorescence from NV emitters was collected by the same lens and directed onto an APD (PerkinElmer SPCM-15-14), in a confocal microscope configuration. Photon counts from the APD were time-tagged and processed by a FPGA (Opal Kelly XEM3005) before computer analysis with custom Python code.

A 20-μm-diameter copper wire located 100 μm above the surface of the diamond was used to produce microwave magnetic fields for state manipulation. Current-carrying coils aligned along the x, y, and z axes were used to apply a bias field along the z axis, and the x and y coils used to eliminate off-axis field components. The coils were driven by a Hameg HMP4030 power supply. Control pulses synchronous with the rotation of the diamond were provided by an Opal Kelly XEM6310 FPGA triggered by the coil-current phase synchronization signal from the motor converter (Celeroton CC-75-500). The FPGA pulsed the microwaves (produced by a Windfreak SynthHD) and laser by actuating high-speed microwave switches (Minicircuits ZASWA-2-50DR).

Spin state readout

We used high laser powers of up to 3 mW within a narrow laser spot size (I₀ ≈ 1 MW cm⁻²), well above the saturation intensity. We inferred the ability of the readout laser pulse to subsequently repump the NV to the bright state by comparing the fluorescence after readout for different states. Regardless of what state the NV was in before the first readout laser pulse, we observed the same photoluminescence trace with the second readout pulse.

Pulse fidelity during rotation

The (111)-oriented NV axis n is always 54.7° to the rotation axis in our experiment because our diamond is mounted on its (100) face. Unless the applied magnetic bias and microwave fields required for state manipulation are also parallel to the rotation axis, the Zeeman shift (∝ n · B) and microwave coupling (∝ |n × B_MW|) vary as the diamond rotates. Microwave pulses that interrogate the NV throughout the rotation can thus be off-resonant (in the case of large-field misalignments) or drive imperfect spin rotations when the Rabi frequency varies substantially. We aligned the magnetic field to the rotation axis to within 1°, which resulted in a uniform detuning throughout the rotation. For sequences using multiple microwave pulses, such as spin echo, we determined the Rabi frequency at each point in the rotation and calibrated the requisite pulse durations to achieve the desired spin rotations.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/5/eaar7691/DC1

section S1. Stationary spin-echo signal

section S2. Effect of laser pulse duration

section S3. Time-dependent optical pumping of the NV

section S4. Drift during experiments

fig. S1. Stationary spin-echo signal from NV1.

fig. S2. Fluorescence smearing due to longer pulse durations.

fig. S3. Estimation of motor period jitter.

fig. S4. Dependence of NV contrast on delay time.