Estimated Brain Tissue Response Following Impacts Associated With and Without Diagnosed Concussion

Abstract

Kinematic measurements of head impacts are sensitive to sports concussion, but not highly specific. One potential reason is these measures reflect input conditions only and may have varying degrees of correlation to regional brain tissue deformation. In this study, previously reported head impact data recorded in the field from high school and collegiate football players were analyzed using two finite element head models (FEHM). Forty-five impacts associated with immediately diagnosed concussion were simulated along with 532 control impacts without identified concussion obtained from the same players. For each simulation, intracranial response measures (Max principal strain, strain rate, von Mises stress, and pressure) were obtained for the whole brain and within four regions of interest (ROI; Cerebrum, Cerebellum, Brain Stem, Corpus Callosum). All response measures were sensitive to diagnosed concussion; however, large inter-athlete variability was observed and sensitivity strength depended on measure, ROI, and FEHM. Interestingly, peak linear acceleration was more sensitive to diagnosed concussion than all intracranial response measures except pressure. These findings suggest FEHM may provide unique and potentially important information on brain injury mechanisms, but estimations of concussion risk based on individual intracranial response measures evaluated in this study did not improve upon those derived from input kinematics alone.

INTRODUCTION

Great effort has been made to better comprehend the head impact biomechanics linked to mild Traumatic Brain Injury (TBI) and, more specifically, sport-related concussion (SRC). Studies conducted on animals and human cadavers first linked TBI, ranging from moderate brain injury to skull fracture, to intracranial pressure. Intracranial pressure recorded from these controlled translational impacts was then correlated to linear acceleration of the head, which was, at the time, a more robust measure.^{15, 16} Correspondingly, a wide variety of physical models have also been used to study the relationship between inertial loading and brain response.^{12, 28, 37} Through the use of computational modeling, rotational kinematics have been shown to have strong correlation to relative brain strain response,^{23, 35} and it is theorized that rotational velocity and acceleration during a head impact causes diffuse axonal injury (DAI) at the brain tissue level,²⁸ leading to altered neuronal function. These studies, along with countless others over the past 70 years, have established sound biomechanical principals underlying the mechanisms of TBI and DAI; however, the theories resulting from these studies may not be fully translatable to the mechanism of sports concussion, which presents in a wide spectrum of clinical signs and symptoms that likely relates to diverse pathophysiology.¹⁰

On-field measurements of head impact exposure (HIE; frequency, location, and kinematic response to head impacts) have provided key insights on the kinematics involved with diagnosed sports concussion.^{2, 3, 8, 9} Previously, we reported that peak linear and rotational acceleration from head impacts associated with diagnosed concussion are typically in the highest percentile of all impacts sustained in contact sports, but it was also common for head impacts to occur with equivalent kinematic composition without any identifiable injury.² Additionally, large inter-player variability was observed for concussion-associated impact severity even though mean severity levels were consistent with historically estimated injury thresholds.² Ultimately, these studies demonstrated that traditional measures of acceleration are sensitive to diagnosed sports concussion, but not highly specific. One potential explanation for this lack of specificity is head kinematic measures reflect input conditions only, and, depending on several personal and environmental variables, have varying degrees of correlation to regional brain motion and deformation.

Direct in-situ measurement of brain tissue deformation under conditions typically associated with brain injury is currently impractical, leaving finite element modeling of the brain as a primary means for obtaining this information.³³ Finite element head models (FEHM) have the potential to transform measures of head impact kinematics (i.e. magnitude, direction, and duration of head translation and rotation) into intracranial response metrics that are directly linked to brain injury. A number of FEHMs with varying levels of complexity and validation have been developed to simulate the brain response to impact.^{17, 21, 23, 25, 35–37} The Wayne State University Brain Injury Model (WSUBIM),^{36, 37} the KTH FE Human Head model,^{23, 31} the Total Human Model for Safety,²¹ and the Worcester Head Injury Model (WHIM)³⁸ have been used to investigate brain tissue deformation linked to concussion by modeling estimated head accelerations obtained from reconstructing videos of 58 professional American football players in the laboratory.^{29, 30} On-field head impact measurements offer an opportunity to evaluate the nuances of concussion events that are difficult to simulate in laboratory reconstructions, and several studies have successfully demonstrated proof-of-concept viability. With the SIMon FEHM, Takhounts et al ³⁵ simulated 24 high-magnitude, on-field head impacts that were recorded with instrumented football helmets; however, none of these events were linked to injury. Hernandez et al ¹⁷ used the KTH model to simulate two football head impact events associated with self-reported and diagnosed concussion that were measured with an instrumented mouth guard. Finally, McAllister et al ²⁵ simulated 10 on-field measured concussion cases from high school and collegiate football players using the Dartmouth Subject-Specific FE Human Head Model (SSM).

In addition to limitations related to applicability and/or size of their kinematic data sets, a significant drawback of all these studies is their focus on output from a single FEHM to report injury thresholds. Unfortunately, even head models that have undergone validation testing will likely produce significantly different brain response estimates due to discrepancies in material properties, geometries, and processing methods.¹⁸ These uncertainties, combined with each study using varied processing and analytical methods, have led to a wide range of postulated injury thresholds for concussive injury that cannot be easily or directly compared.

In this study, intracranial response measures were computed from an existing data set of directly measured head impacts sustained during sessions of high school and collegiate football by two FEHM, WHIM and SIMon, which have been previously compared over a range of kinematic conditions representing helmeted head impacts.¹⁸ The overarching aim of this study was to quantify common measures of brain tissue response, both regionally and globally, following head impacts associated with diagnosed concussion. We tested the hypotheses that: 1) model estimated intracranial response will be dependent on brain region of interest for head impacts sustained prior to concussion diagnosis and 2) individual model estimated intracranial response measures will be more sensitive and specific to diagnosed concussion than peak kinematic measures alone.

MATERIALS AND METHODS

From 2005 to 2010, football players from eight collegiate and six high school teams were outfitted with instrumented helmets (Head Impact Telemetry (HIT) System; Simbex, Lebanon, NH; Riddell Inc, Chicago IL) to record measures of HIE. During that time, medical personnel at each institution diagnosed 105 concussions sustained by 95 individuals.³ Through a multi-institutional, collaborative agreement, these data were consolidated to provide the most comprehensive HIE dataset available to study the biomechanical basis of mild TBI.² Detailed descriptions of the overall study methodology pertaining to subject participation, head impact exposure instrumentation and monitoring, and concussion diagnosis has been previously reported along with analyses of the HIE data.^{2, 3} For completeness, a brief description of these study components is provided below along with more detailed discussion of modeling methods and subsequent data analysis pertinent to this report. Approval for data collection and reduction was received from the Institutional Review Board at each participating institution.

Head Impact Exposure

Helmet Instrumentation

Each helmet was equipped with a wireless head-measurement unit containing six single-axis accelerometers, data acquisition hardware, and a rechargeable battery. The unit’s foam accelerometer mounting system is specifically tuned and positioned to isolate head acceleration from helmet acceleration.²⁴ When any one of the six accelerometers exceeded a threshold of 14.4g, 40ms of data (8ms pre-trigger and 32ms post-trigger) from all accelerometers were recorded, time stamped, and transmitted to a sideline computer for processing, assessment of data quality, and storage. To date, this instrument has been used to record in situ head impacts from a large cross section of male and female athletes participating in several sports (e.g. football, ice hockey, soccer, and boxing) and skill classifications (i.e. youth, high school, college, and professional). Multiple assessments of the on-field data collection, processing, and data reduction techniques have been conducted as part of a multiphase validation process that has included laboratory testing,^{1, 7, 11, 24} video correlation of on-field events,^{5, 11} and multi-site field trials.^{4, 8, 9, 11, 34}

Clinical Diagnosis

Concussion in this study was defined as an alteration in mental status, as reported or observed by the player or team’s medical staff, resulting from a blow to the head which may or may not have involved loss of consciousness.^{2, 3} A certified athletic trainer or team physician at each participating institution was responsible for medical care, and concussions were diagnosed and treated independent of study protocol. When a concussion was diagnosed, the medical staff provided anecdotal descriptions of the events surrounding injury (e.g., description of the impact, method of identifying the injury, and on-field observations regarding clinical presentation) along with the date of injury, the suspected time of injury, the approximate time of diagnosis, day of symptom resolution, and player anthropometrics (age, height, and weight).

As previously reported, not all cases of concussion were preceded by a single, observable impact that could be directly associated with the injury.³ In many cases, symptoms were either observed or reported outside of play, thus bringing into question the role of cumulative impact exposure on brain injury. Because available FEHM have not been validated for modeling a series of impacts over time, this analysis focuses solely on 45 of the 105 injury cases classified as immediately diagnosed concussion (i.e. a single identifiable head impact preceded onset of symptoms that led to the player being immediately removed from play without re-entry).

Control Impact Selection

Due to the significant computational cost of FEHM (each impact required approximately 60 and 42 minutes for simulation using the WHIM and SIMon, respectively), a representative dataset of control impacts was selected from the 161,732 impacts sustained by the same players on days when no concussion was identified. Control impacts were selected in a semi-randomized process by first identifying the percentage of impacts by impact location (Front – 37%; Back – 27%; Top – 19%; Side – 17%) and peak acceleration (62% < 25g; 28% from 25 – 50g; 7% from 50 – 75g; 2% from 75 – 100g; 1% > 100g) for the entire distribution. The control data set (n = 532) was then randomly selected in proportions that replicated the location and acceleration characteristics of the entire impact distribution (Table 1).

Table 1.

Kinematic measures for head impacts associated with and without diagnosed concussion recorded from collegiate and high school football players.

	Immediate Dx Concussion Impacts (n = 45)		Control Impacts (n = 532)
Post-Impact Kinematics	Median	25-75% interquartile range	Median	25-75% interquartile range
Peak linear acceleration (g)	108.6	92.2 – 136.8	24.5	16.01 – 43.5
Peak rotational acceleration (rad·s−2)	4,364	3,210 – 6,022	1,274	850 – 2,178

Head Impact Processing

Historically, commercially available HIT System hardware has been paired with a simulated-annealing optimization algorithm that solves directly for linear acceleration magnitude.⁷ Rotational acceleration is then calculated about two axes of rotation using the modeled equations of motion for force acting on the head, the anterior–posterior and medial–lateral components of the peak linear acceleration vector, and the directly measured relationship between linear and rotational acceleration for on-field head impacts.³² For this analysis, recorded acceleration data for each head impact was post-processed using a custom, six degree of freedom Expanded Processing Algorithm (6DOF-EPA),⁶ which solved for X, Y, and Z components of both linear and rotational acceleration required as input to the FEHM. Acceleration was defined in a fixed Cartesian coordinate system at the head center of gravity following right-hand rule with the X direction towards the front of the head, the Y direction towards the left ear, and the Z direction towards the top of the head. Biofidelity of this approach was confirmed through laboratory verification experiments similar to those previously reported for other HIT System variants (see Appendix).

Measures of impact location were obtained using commercial HIT System processing techniques that optimize the direction of measured acceleration to discern the contact site directional vector in spherical coordinates. Impacts were then discretized into one of four general locations – Front, Back, Side, and Top.^{8, 14}

In addition to standard HIT System verification methods for data quality that were applied at the time of collection,^{1, 9} all kinematic data used in this study were visually reviewed post-processing to verify time series data matched theoretical patterns for rigid body head acceleration.

Finite Element Brain Models

The differences in available FEHM are vast, varying widely in anatomical complexity, material properties, boundary conditions, and computational methods for extracting and calculating tissue response metrics. In this study, the Worcester Head Injury Model (WHIM) and Simulated Injury Monitor (SIMon) were selected as representative models to provide a range of potential intracranial response measures. These models were identified because they have been previously used in brain injury studies focused on sports concussion,^{19, 35} they were derived from differing anatomical source data, provide direct output that could be compared without model modification, and, importantly, their output has been previously parametrically compared over a spectrum of kinematic conditions representing helmeted head impacts.¹⁸

The Worcester Head Injury Model (WHIM)

Details of the WHIM (formerly known as the Dartmouth Head Injury Model) used in this study (Figure 1) have previously been reported, including description of model development, mesh quality, assignment of material properties and boundary conditions.^{19, 38} The model was created from high-resolution T1-weighted magnetic resonance images of concussed collegiate football and hockey players. WHIM-estimated response has been verified against relative brain-skull displacement and intracranial pressure responses from cadaveric experiments, as well as strain responses in a live human volunteer, with an overall biofidelity rating of “good” to “excellent”.^{19, 20}

Figure 1.

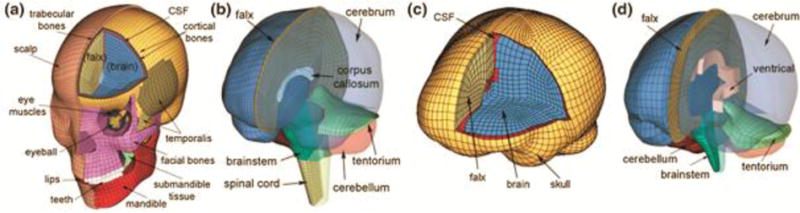
The WHIM (a, b) and SIMon (c, d) FEHM employed in this study with color-coded regions of interest (ROIs; cerebrum, cerebellum, and brainstem). The x-, y- and z-axis of the model coordinate system corresponds to the posterior-anterior, right-left, and inferior-superior direction, respectively.

Simulated Injury Monitor (SIMon)

Details of the development and verification of the second-generation SIMon, which is geometrically more detailed than its predecessor, have also been reported.³⁵ The model topology was derived from CT scans, which included major parts of the brain such as cerebrum, cerebellum, brainstem, ventricles, combined cerebrospinal fluid and pia arachnoid complex (PAC) layer, falx, tentorium, and parasagittal blood vessels (Figure 1). The model was then uniformly scaled to represent a 50th percentile male head. Kelvin-Maxwell viscoelastic properties were used for the brain. SIMon-estimated responses have been verified against brain-skull relative displacement and pressure responses in cadaveric head impacts, as reported.³⁵

Intracranial Response Measures and Data Reduction

Impacts were simulated using the WHIM and SIMon via Abaqus/Explicit (Version 2016; Dassault Systèmes, France) and LS-Dyna (Livermore Software Technology Corp., Livermore. CA), respectively, on a multi-core Linux cluster (Intel Xeon X5560, 2.80 GHz, 126 GB memory, using 8 CPUs) with a temporal resolution of 1 ms. For each impact, element-wise maximum principal strain, strain rate, von Mises stress, and pressure were obtained. Element-wise product of maximum principal strain and its rate was computed at every temporal point.²² For all response variables, peak magnitudes at each element, regardless of the time of occurrence, were extracted. For strain-related responses, we computed their volume-weighted regional averages for the whole-brain, cerebrum, cerebellum, brainstem, and corpus callosum.²⁰ For pressure, the 95th percentile maximum positive (coup) and negative pressure (contrecoup) magnitudes were determined to avoid potential numerical issues.

Data Analysis

To characterize brain tissue response associated with concussion, descriptive statistics were calculated – including minimum, maximum, median, and 25-75% interquartile range – for impacts preceding immediately diagnosed concussion. Data were reduced for each intracranial response measure generated globally for both FEHM (i.e. whole brain) and within each available, model-specified ROI. Distributions of whole brain response measures obtained from each model were then compared to assess whether outcomes were dependent on the model employed. Because all response measures except for max principal strain (WHIM), coup pressure (WHIM, SIMon), and contrecoup pressure (SIMon) failed tests for normality (Lilliefors test; p < 0.05), Kruskal-Wallis nonparametric analysis of variance tests were employed. The same statistical test was used within model to determine if peak tissue response is concentrated within a specific ROI for diagnosed concussions. When appropriate, a post-hoc Dunn’s multiple comparison test was performed to determine where concentrations of strain, stress, and pressure exist within the brain.

Regression analysis was used to assess relationships between peak resultant linear and rotational acceleration and whole brain intracranial response measures from each model. The coefficient of determination (r²) was calculated for each regression as a measure of goodness of fit.

Receiver Operating Characteristic (ROC) curves were generated from the concussion and control datasets to evaluate the sensitivity and specificity of each global response measure to the diagnosis of concussion. For each ROC curve, the null hypothesis of the true area under the curve (AUC), equaling 0.5 (same as guessing), was tested. Hanley’s method for comparing area under ROC curves were used to test if any single intracranial response measure is more sensitive to diagnosed concussion than the others.

Statistical analyses were performed with custom Matlab scripts (2015a, MathWorks, Natick, MA) in combination with built-in statistical toolbox functions. A significance level of α = 0.05 was set a-priori for each statistical test.

RESULTS

Large inter-athlete variation in FEHM estimated intracranial response was observed for athletes diagnosed with concussion (Figure 2). Measures obtained from WHIM were significantly higher for maximum principal strain (p < 0.001), maximum principal strain × max principal strain rate (p = 0.035), and contrecoup pressure (p < 0.003) with estimations ranging between 0.06 – 0.32 (WHIM) and 0.05 – 0.33 (SIMon), 0.58 – 24.42 (WHIM) and 0.42 – 21.82 (SIMon), and −28.83 – −115.81 kPa (WHIM) and −23.08 – −82.00 kPa (SIMon) respectively. WHIM estimated maximum principal strain rate (WHIM: 12.88 – 103.06, SIMon: 10.65 – 75.93; p = 0.066), von mises stress (WHIM: 0.31 – 10.38, SIMon: 0.49 – 3.57; p = 0.082), and coup pressure (WHIM: 24.75 – 169.73, SIMon: 23.28 – 98.50; p = 0.075) were also higher than SIMon, but differences did not reach significance.

Figure 2.

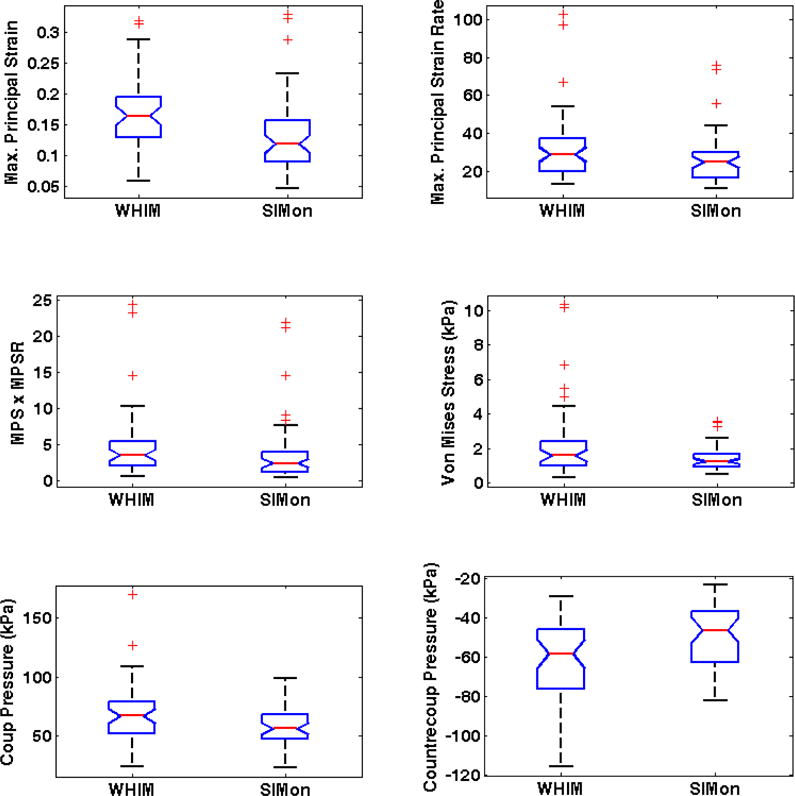
FEHM estimated intracranial response (whole brain) for head impacts sustained prior to immediately diagnosed concussion.

Peak impact kinematics significantly (p < 0.001) predicted linear increases in FEHM estimated intracranial response measures (Figure 3). For both FEHM, increasing peak rotational acceleration was a strong predictor of each response measure except coup (WHIM: r² = 0.331; SIMon: r² = 0.363) and contrecoup pressure (WHIM: r² = 0.312; SIMon: r² = 0.336). The coefficients of determination were slightly higher for SIMon (r² = 0.871 – 0.920) than WHIM (r² = 0.791 – 0.923), with the strongest correlation found between maximum principal strain rate and peak rotational acceleration. Peak linear acceleration was highly correlated with SIMon estimated coup pressure (r² = 0.881) and modestly correlated with WHIM estimated coup pressure (r² = 0.658) and SIMon estimated countercoup pressure (r² = 0.606). Correlation was weak for all other interactions between peak linear acceleration and intracranial response measures (WHIM: r² = 0.263 – 0.386); SIMon: r² = 0.248 – 0.363).

Figure 3.

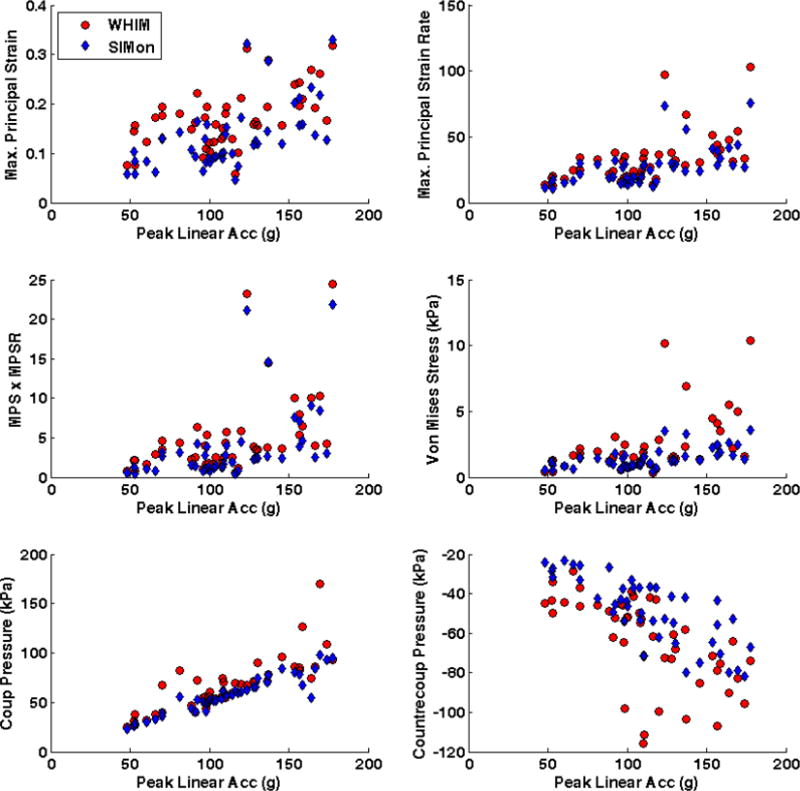
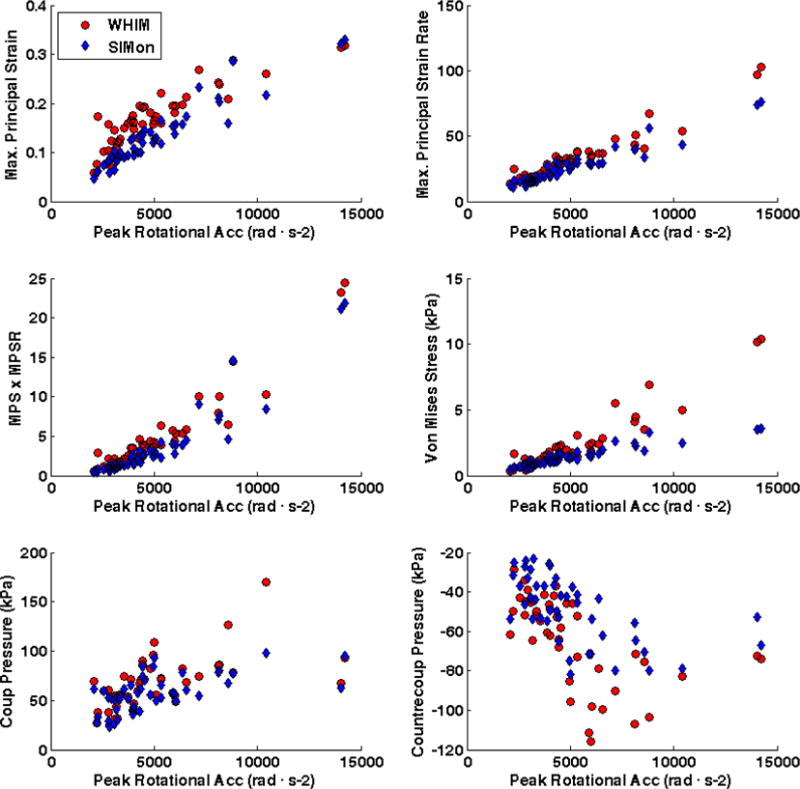
Correlation between peak impact kinematics (Top – Linear Acceleration; Bottom – Rotational Acceleration) and FEHM estimated intracranial response for head impacts sustained prior to diagnosed concussion.

For impacts associated with diagnosed concussion, both FEHM calculated intracranial response measures that were significantly different among ROIs with the exception of SIMon estimated contrecoup pressure (p = 0.361). Maximum principal strain, maximum principal strain rate, and maximum principal strain × max principal strain rate were highest in the cerebrum, followed by the brainstem, corpus callosum (WHIM only), and cerebellum (Table 2). Von mises stress estimated by WHIM followed the same ordering by magnitude, while SIMon estimated higher stress in the cerebellum. Coup pressure was again highest in the cerebrum, followed by the corpus callosum (WHIM only), cerebellum, and brain stem. Contrecoup pressure was highest in the corpus callosum and lowest in the cerebellum (WHIM only).

Table 2.

Median and interquartile range (25 – 75%) of FEHM estimated intracranial response for head impacts preceding diagnosed concussion.

Intracranial Response of Dx Concussion (n = 45)	FEHM – Regions of Interest (ROI)
	Whole Brain		Cerebrum (C)		Cerebellum (CB)		Brain Stem (BS)		Corpus Callosum (CC)		P Value	Post-hoc
WHIM
Max. Principal Strain	0.16	[0.13 – 0.20]	0.18	[0.14 – 0.21]	0.09	[0.06 – 0.11]	0.14	[0.12 – 0.22]	0.13	[0.09 – 0.16]	< 0.001	C,BS,CC > CB; C > CC
Max. Principal Strain Rate	28.82	[19.76 – 37.17]	30.53	[20.48 – 37.33]	19.23	[13.94 – 26.72]	30.18	[24.21 – 49.56]	25.68	[16.51 – 33.65]	< 0.001	C,BS > CB
MPS × MPSR	3.55	[2.06 – 5.45]	3.89	[2.25 – 5.78]	1.13	[0.63 – 2.15]	3.03	[1.95 – 7.78]	2.53	[1.25 – 3.70]	< 0.001	C,BS,CC >CB
Von Mises Stress (kPa)	1.59	[0.98 – 2.45]	1.79	[1.06 – 2.56]	0.59	[0.35 – 0.98]	1.25	[0.77 – 3.11]	1.15	[0.67 – 1.66]	< 0.001	C,BS,CC > CB
Coup Pressure (kPa)	67.12	[52.41 – 79.30]	69.69	[48.27 – 81.48]	17.51	[4.7 – 36.85]	11.58	[3.20 – 31.56]	28.53	[21.38 – 40.99]	< 0.001	C > CB,BS,CC
Contrecoup Pressure (kPa)	−58.27	[−76.14 – −45.62]	−48.61	[−75.19 – −35.85]	−47.57	[−63.37 – −28.93]	−50.12	[−59.47 – −28.32]	−25.97	[−36.82 – −12.53]	< 0.001	CC > CB, BS > C
SIMon
Max. Principal Strain	0.12	[0.09 – 0.16]	0.14	[0.1 – 0.18]	0.06	[0.04 – 0.07]	0.1	[0.07 – 0.14]		—	< 0.001	C > CB,BS; BS > CB
Max. Principal Strain Rate	24.78	[16.27 – 29.63]	29.45	[19.77 – 38.05]	16	[10.72 – 22.85]	20.98	[16.08 – 38.39]		—	< 0.001	C > CB; BS > CB
MPS × MPSR	2.42	[1.23 – 3.92]	3.25	[1.53 – 6.25]	0.7	[0.28 – 1.03]	1.52	[0.80 – 3.88]		—	< 0.001	> CB,BS; BS > CB
Von Mises Stress (kPa)	1.27	[0.93 – 1.66]	2.37	[1.66 – 3.13]	1.97	[1.24 – 2.49]	1.44	[1.01 – 2.12]		—	< 0.001	C > BS
Coup Pressure (kPa)	56.39	[47.97 – 68.35]	58.09	[46.64 – 74.15]	13.07	[2.99 – 35.00]	8.44	[2.21 – 29.14]		—	< 0.001	C > CB,BS
Contrecoup Pressure (kPa)	−46.14	[−62.88 – −36.79]	−34.32	[−52.85 – −26.61]	−38.43	[−50.59 – −22.27]	−49.11	[−60.70 – −18.24]		—	0.361	–

Similar trends were observed for both FEHM when regional intracranial stress and strain response measures were grouped by impact location. In the cerebrum, the highest stress and strain measures were associated with impacts to the Back of the head, followed by Front, Top, and Side. The same trend was observed for the cerebellum and corpus callosum (WHIM only), albeit at lower magnitudes. Higher concentrations of stress and strain in the brainstem were associated with impacts to the Front of the head, followed by Back, Side, and Top. Rank ordering of both coup and contrecoup pressure by impact location was not consistent for the two FEHM, with undiscernible trends due to the large intra-subject variability.

The area under the ROC curves generated for peak linear acceleration (AUC = 0.968), peak rotational acceleration (AUC = 0.929), and each global intracranial response measure (WHIM: 0.915 – 0.948; SIMon: 0.917 – 0.963) were higher than 0.5 (p < 0.001), demonstrating that both impact kinematics and FEHM-estimated response were statistically better than guessing whether an impact was associated with diagnosed concussion (Figure 4). Coup pressure was the most sensitive WHIM measure, but it was not significantly more predictive than the other WHIM global response measures (p > 0.123). Similarly, coup pressure obtained from the SIMon FEHM was the most sensitive measure (AUC = 0.963, p = 0.041) followed by contrecoup pressure (AUC = 0.958, p = 0.105) with the former reaching a level of significantly higher prediction. AUC for all ROI-specific intracranial response measures estimated by both FEHM were also greater than 0.5; however, greater variation was observed (WHIM: 0.672 – 0.938; SIMon: 0.645 – 0.955) and no regional measure significantly improved upon global model prediction. Of all measures, peak linear acceleration was found to be the most sensitive, with a significantly better predictive capability than all intracranial response measures other than WHIM and SIMon estimated coup (p = 0.174 and 0.392, respectively) and contrecoup pressure (p = 0.148 and 0.213, respectively).

Figure 4.

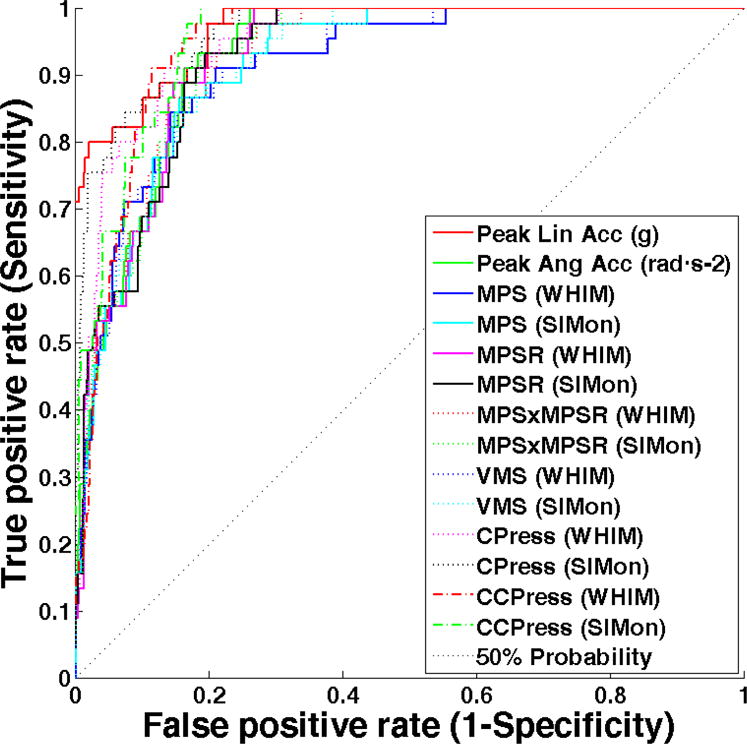
Receiver Operating Characteristic (ROC) curves indicating the sensitivity and specificity of peak kinematic measures and intracranial response estimated from two FEHM. A 50% probability line is included to indicate the level of guessing (50 – 50 chance). Peak linear acceleration, coup pressure, and SIMon estimated contrecoup pressure are the most sensitive measures to immediately diagnosed concussion.

DISCUSSION

The definition of concussion is continuously evolving – as is clinical perspective on the best methods for diagnosis, treatment, and recovery.²⁷ Broadly stated, concussion is caused by a direct blow to the head or body with an “impulsive force” transmitted to the head, resulting in short-lived, functional impairment of the neurologic system that manifests itself in a wide range of clinical and cognitive symptoms. The sequence of events leading up to and kinematics following head contact resulting in injury can also be extremely complex and diverse, particularly in an athletic environment.^{2, 3} This study, which sought to expound upon that complexity, used two FEHM and a robust kinematic data set of previously reported on-field measured head impacts to establish a range of brain tissue response measures associated with diagnosed concussion. Additionally, we derived the relationships between peak head acceleration, impact location, and six intracranial response measures within four regions of the brain, confirmed the hypothesis that model estimated intracranial response is dependent on brain region of interest, and rejected the hypothesis that individual intracranial response measures are more sensitive and specific to diagnosed concussion than peak kinematic measures.

For specific regions of the brain, the highest concentrations of strain, strain rate, and stress were found within the cerebrum followed by brain stem, corpus callosum, and cerebellum, respectively. Coup pressure was also highest in the cerebrum and brain stem; however, WHIM estimated higher values in the cerebellum than corpus callosum. Contrecoup pressure was distributed evenly across all ROI. Interestingly, these relationships did not differ for the selected control impacts, thus suggesting impact magnitude may be the primary single impact factor influencing concussion injury across all players, with other kinematic components such as direction playing a secondary role. When considering individual injuries, however, FEHMs have the ability to provide higher resolution for understanding mechanisms of injury at the finite tissue level than input kinematics alone (Figure 5). For example, recent studies have investigated the clinical potential of advanced modeling measures such as white matter anisotropy, an impact-induced injury to white matter neural tracts, and strain measures of the entire white matter.^{13, 19, 38} These measures, in addition to regionally estimated concentrations of stress, strain, and pressure, may be better predictors of an individual’s signs and symptoms of concussion than either input kinematics or global intracranial response measures.

Figure 5.

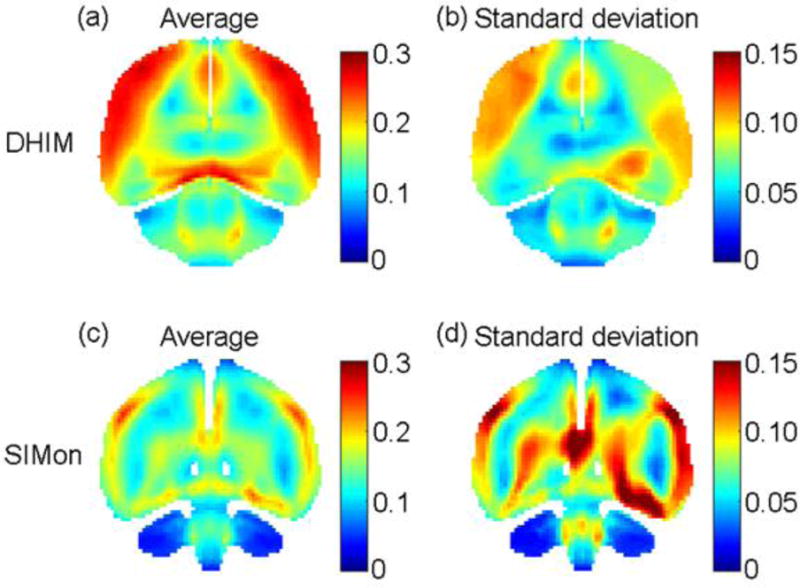
Average peak maximum principal strain (a and c) along with standard deviation (b and d) on a representative resampled coronal plane for 45 head impacts classified as immediately diagnosed concussion using the WHIM and SIMon (top and bottom rows, respectively)

Previous analyses of this on-field kinematic data set developed injury risk curves from all diagnosed concussions (n=105) and all impacts sustained by those athletes not associated with concussion (n=161,732).³ The ROC curves presented in this study were created with a control subset of non-concussive impacts sustained by these athletes, therefore the subsequent results do not represent concussion risk; however, since the control dataset is representative of all impacts not associated with concussion, the AUC stated for each metric is a true reflection of its specificity and between-measure comparisons made in this analysis are valid. While all measures of model estimated tissue were significant predictors of immediately diagnosed concussion, global intracranial response measures were not found to be more predictive than input kinematics alone. FEHM can provide significantly more resolution for understanding mechanisms of injury at the finite tissue level; however, higher resolution leads to more variation and less specificity. While a high resolution tool may be useful in differentiating these cases on an individual level, the diversity and complexity of these measures are less likely to be predictive of all injuries.

A significant relationship was found between all kinematic and model response interactions. Linear acceleration had the strongest correlation with coup and contrecoup pressure while rotational acceleration had the strongest correlation with strain-related measures. These relationships between input conditions and estimated tissue responses, which are in close agreement with prior work by Zhang³⁷ and Ji,¹⁸ are deterministic based on model architecture, selected tissue parameters, and assumed boundary conditions of human anatomy. For example, WHIM was found to produce higher absolute values for all intracranial response measures than SIMon, most likely due to differences in material properties chosen for the brain tissue and its larger anatomical size as compared to SIMon. It remains unknown, however, which model output better reflects in-vivo response. Availability of empirically obtained brain tissue properties is extremely limited, and assumptions are required when creating models. Because of this, due diligence is necessary when relating inter-model results across studies, and, as previously reported by Ji, incorporating multiple models is recommended when feasible.²⁰

Large variation was found between athletes for each obtained intracranial response measure; however, median values for concussion were not always consistent with preceding laboratory and pilot studies. For example, using the WSUBIM and nine simulated injury cases, Zhang predicted a coup and contrecoup pressure range of 53 – 130 kPa and −48 – −128 kPa, respectively, which is encompassing of the median values obtained from WHIM (67.12 and −58.27 kPa) and SIMon (56.39 and −46.14 kPa), but distributionally higher.³⁷ With the same FEHM and an expanded data set (n = 22), Viano reported median values for strain (0.448) and strain rate (81.5) in the midbrain which were well in excess of the median estimated by WHIM (0.16 and 28.82) and SIMon (0.12 and 24.78).³⁶ Similarly, when Takhounts employed the SIMon FEHM to simulate 24 on-field impacts not linked to concussion, the median strain obtained was magnitudes higher at 0.675 (range of 0.076 – 0.956).³⁵ Several practical reasons for intraplayer variation in this study exist, such as the wide range of peak linear and rotational accelerations preceding concussion (Figure 6), location of contact distributed over the entire head, and the diverse clinical presentation of athletes included in this study. It is not as clear, however, why the discrepancy exists between median tissue response measures reported in recent sports-impact modeling studies, but there are many potential sources such as differences in model construction, input kinematics, and varying methods for calculating each measure of interest.

Figure 6.

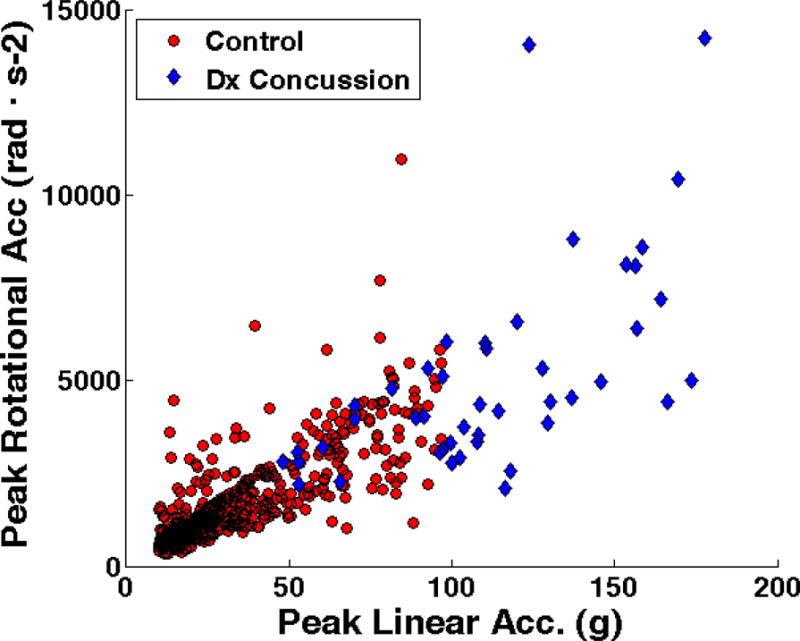
Kinematic measures for head impacts associated with and without diagnosed concussion sustained by 45 collegiate and high school football players.

Several limitations in this study are notable. Diagnosis of concussion is a clinical determination based on an interpretation of signs and symptoms. For this multi-institutional, multi-year study, it was not feasible to control for inherent clinical variation. Additionally, there is potential for cumulative impact history contributing to the manifestation of symptoms; however, potential effects were mitigated in this study by restricting the analysis to only immediately diagnosed concussions. Another limitation was that multivariate models were not developed. For this analysis we intentionally focused on independent measures to establish a baseline understanding of injury biomechanics. As has been shown with kinematic measures, though, FE model predictions may improve if composite metrics were created, both globally and between ROI. Other potential limitations surrounding modeling of on-field head impacts include differences in segmentation of ROI between FEHM; material properties and model features relative to subject population of high school and collegiate male football players (i.e. FEHM scaled to 50^th percentile male head); biological variance within the athlete cohort and unknown deviation from FEHM-assumed brain properties; and differences in processing methods for intracranial response measures between studies (e.g. calculation of coup and contrecoup pressure).

These findings suggest that FEHM have the ability to provide unique and potentially important information relative to the mechanisms of brain injury; however, FEHM estimated intracranial response measures evaluated in this study did not provide more sensitivity and specificity to diagnosed concussion than input kinematics. It has been shown that concussion is a clinical syndrome with a wide range of functional and symptomatic changes including cognitive impairment in the absence of specific somatic complaints.^{10, 26} Contact sport athletes are exposed to a wide range of impact conditions, and it is unlikely that any single pathophysiological process is associated with the entire spectrum of injury as it is currently defined. We recommend further research should be conducted to: 1) Expand on-field kinematic datasets and clinical outcome measures to enable correlation of regional intracranial response measures with specific and quantifiable signs and symptoms of injury; 2) Develop more advanced injury metrics from regional intracranial response measures and determine if these metrics increase sensitivity and specificity to concussion; and 3) Expand approach for model development to include additional verification data that is more relevant to impacts sustained in sporting environments, as most models are verified with high-severity cadaveric impacts or low-severity inertial events.

APPENDIX

Commercially available Head Impact Telemetry (HIT) System technology for American football (Sideline Response System, Riddell Inc., Chicago IL) acquires head acceleration data from six nonorthogonal, normally oriented, single-axis accelerometers fitted against a player’s head. Traditionally, acceleration data acquired following head contact are post-processed with a simulated-annealing optimization algorithm that numerically iterates rigid-body dynamics equations to obtain peak linear acceleration magnitude at the head center of gravity.³ Rotational acceleration is then calculated about two axes of rotation using the modeled equations of motion for force acting on the head, the anterior–posterior and medial–lateral components of the peak linear acceleration vector, and the directly measured relationship between linear and rotational acceleration for on-field head impacts.¹³ As part of a multi-phase validation process, multiple laboratory assessments of the HIT System have been conducted to verify accuracy and precision of these processing and data reduction techniques.^{2, 3, 6, 10}

As available, these data are insufficient input to finite element head models, which require independent temporal components of both linear and rotational acceleration about the head center of gravity to estimate brain tissue response following impact. To overcome this limitation, recorded acceleration data for each head impact in the accompanying study was post-processed using a custom, six degree of freedom expanded processing algorithm (6DOF-EPA). The development of 6DOF-EPA, which is based on a technique previously verified and implemented in research-only HIT System variants that utilized tangentially oriented accelerometers (i.e. boxing, soccer, ice hockey, and football), is described below.^{1, 3, 7, 12} To verify accuracy of this approach, previously published HIT System experimental data obtained through laboratory testing was reprocessed and compared to acceleration data measured by a Hybrid III (HIII) anthropomorphic test device.²

Expanded Processing Algorithm

6DOF-EPA directly solves for linear and rotational head accelerations about the head center of gravity using data obtained from six accelerometers placed normal to the surface of the head. By assuming rigid body dynamics, the acceleration of any point (i) on the head $({\overrightarrow{a}}_i)$ undergoing linear and rotational acceleration is projected on the sensing axis of the accelerometer $({\overrightarrow{r}}_{ai})$:

$$\Vert a_i\Vert ={\overrightarrow{r}}_{ai}·\stackrel{\rightharpoonup }{H}+{\overrightarrow{r}}_{\dot{a}}·(\stackrel{\rightharpoonup }{a}\times {\stackrel{\rightharpoonup }{r}}_i)+{\overrightarrow{r}}_{\dot{a}}·\left({\overrightarrow{\omega }}_i\times \left({\overrightarrow{\omega }}_i\times {\stackrel{\rightharpoonup }{r}}_i\right)\right)$$ (1)

where $\overrightarrow{H}$ is the linear acceleration vector at the head center of gravity (CG), ${\overrightarrow{r}}_i$ is the position vector of point i relative to head CG, $\stackrel{\rightharpoonup }{\alpha }$ is the rotational acceleration of the head, and $\overrightarrow{\omega }$ is the angular velocity of the head. Iterative optimization can then be used to solve for the linear acceleration $(\overrightarrow{H})$, rotational acceleration (α), and rotational velocity (ω) that minimizes the sum of square error between each accelerometer value and the expected acceleration:

$$min{{\displaystyle {\sum }_{i=1}^n\left[\Vert a_i\Vert -{\overrightarrow{r}}_{ai}·{\stackrel{\rightharpoonup }{H}}_E+{\overrightarrow{r}}_{\dot{a}}·({\stackrel{\rightharpoonup }{a}}_E\times {\stackrel{\rightharpoonup }{r}}_i)+{\stackrel{\rightharpoonup }{r}}_{\dot{a}}·\left({\overrightarrow{\omega }}_E\times ({\overrightarrow{\omega }}_E\times {\stackrel{\rightharpoonup }{r}}_i)\right)\right]}}^2$$ (2)

where n is the number of accelerometers, ${\overrightarrow{H}}_E$ is the estimated linear acceleration of the head CG, and ${\stackrel{\rightharpoonup }{\alpha }}_E$ and ${\overrightarrow{\omega }}_E$ are the estimated rotational acceleration and velocity vectors, respectively.

For the commercially available HIT System processing algorithm, rotational and centripetal acceleration is neglected based on an assumption that the accelerometer sensing axis is not radially oriented to the acceleration vector. Additionally, a single optimization is performed at the time of peak acceleration. Thus reducing Equation 2 to the following:

$$min{{\displaystyle {\sum }_{i=1}^n\left[\Vert a_i\Vert -{\overrightarrow{r}}_{ai}·{\stackrel{\rightharpoonup }{H}}_k\right]}}^2$$ (3)

where k is a discrete point in time (e.g. time of peak acceleration). While not accounting for rotational components contributes to overall measurement error and reducing the number of optimizations limits temporal resolution, this assumption provides a robust optimization solution and an acceptable level of measurement accuracy and processing time for on-field use.²

For 6DOF-EPA, a piecewise processing procedure was adopted to maintain established accuracy and integrity of peak linear acceleration measurements, obtain X, Y, and Z linear acceleration time series, and directly solve for X, Y, and Z rotational acceleration. Three serial processing steps were created to obtain: 1) Peak Linear Head Acceleration – Single iterative optimization of Equation 3 to solve for peak linear head acceleration and impact location, 2) Linear Acceleration Time Series – Iterative optimizations of Equation 3 for discrete points in time. For the HIT System, which records 40 ms of data at 1000 Hz, this requires 40 optimizations for a single head impact. Peak linear acceleration obtained from Step 1 is included as a known optimization parameter, and 3) Rotational Acceleration Time Series - Iterative optimizations of Equation 2 for each discrete point in time. Centripetal acceleration is considered negligible, and temporal components of linear acceleration obtained from Step 2 are included as known parameters. While computationally taxing (i.e. 81 optimizations for a single head impact), this approach best leverages available information obtained from the HIT System hardware to obtain the independent, temporal linear and rotational head acceleration data required for FEBM.

Experimental Data

Laboratory reconstructions were previously conducted to correlate head impact kinematics recorded by the commercially available HIT System and an instrumented Hybrid III headform under conditions that simulated impact velocities and locations associated with National Football League head impacts.² Four impact sites, designated as A, B, C, and D, were impacted with a pneumatic linear ram at four target speeds (4.4, 7.4, 9.3, and 11.2 m/s) to represent onfield impacts associated with and without concussion (Figure 1). Three to five trials were conducted at each site and speed, resulting in 54 impacts available for review.

Acceleration data obtained from the HIT System for each impact was post-processed with 6DOF-EPA, providing X, Y, and Z components of both linear and rotational acceleration. Resultant time series were calculated from component data, and peak measures were defined by the maximum time series acceleration. Corresponding HIII acceleration data, which was obtained from 9 accelerometers positioned in a 3-2-2-2 configuration was unchanged from previous published reports.^{2, 11} Direction was defined for both measurement devices following right-hand rule in a fixed Cartesian coordinate system at the head center of gravity (i.e. positive X direction towards the front of the head, positive Y towards the left ear, and positive Z towards the top of the head).

Figure 1.

Four primary impact sites were (A, B, C, and D) were identified as points of contact that most frequently result in mTBI for NFL athletes. Each site was impacted at four target speeds: 4.4, 7.4, 9.3, and 11.2 m/s.

Verifying Accuracy of 6DOF-EPA Peak Output

Following methods described in the previous evaluation, linear regression analysis was performed to assess correlation between peak linear and angular acceleration measures from the 6DOF-EPA and HIII. As described in the previous evaluation, all regressions were performed both on the entire data set and by impact site using equation 4:

$$y=mx+y_0$$ (4)

where x is the HIII measure, y is the HIT System measure, and the linear slope, m, is the relationship between the measurements. For all conditions, y₀ was constrained to be zero since both systems have a baseline output of zero when not impacted. The coefficient of determination (r²) was also calculated for each regression as a measure of goodness of fit. Slopes of the fit trendlines and coefficients of determination are summarized in Table 1. For reference, previously published results obtained with the commercially available HIT System processing algorithm are included. As defined, there was no change in peak linear acceleration. Modestly higher correlations were obtained for peak rotational acceleration, with the largest improvement occurring at the A impact site.

Table 1.

Results from linear regression analysis between HIT System and HIII impact measures. The relationship between measures (m) and coefficient of determination (r²) are shown for peak accelerations obtained at all impact sites. Previously published results when using commercially available HIT System processing are included for reference.²

	A		B		C		D		Overall A-B-C-D
	m	r2	m	r2	m	r2	m	r2	m	r2
Linear Acc. (historical)	1.055	0.930	0.995	0.822	1.084	0.987	0.969	0.875	1.009	0.903
Linear Acc. (6DOF – EPA)	1.055	0.930	0.995	0.822	1.084	0.987	0.969	0.875	1.009	0.903
Rotational Acc. (historical)	0.549	0.415	0.917	0.961	1.170	0.981	1.125	0.710	0.939	0.528
Rotational Acc. (6DOF-EPA)	0.770	0.726	0.895	0.930	1.047	0.974	1.050	0.608	0.942	0.718

Verifying Biofidelity of 6DOF-EPA Temporal Output

The Normalized Integral Square Error (NISE) was developed to quantitatively measure the similarity of time history response produced by two anthropomorphic test devices.⁵ It has since been employed by FE model developers to assess biofidelity of model estimated tissue response with direct measurements obtained through experimental methods.^{4, 8, 9} A detailed account of these calculations and their derivation has been previously described.^{4, 5, 9}

Briefly, the NISE method is used to evaluate three aspects of time history curves – amplitude difference (N-amp), shape difference (N-shape), and phase shift (N-phase). Because the NISE method produces Error Measures (EM) that are equal to zero when strong correlation exits, it has become common practice to calculate a Correlation Score (equation 5) that range from 0 to 100, with higher scores equating to higher correlation.

$$C{S}_{N-\mathit{amp}}=100\times \left(1-\left|E{M}_{N-\mathit{amp}}\right|\right)$$ (5)

Correlation scores can then be used to classify performance according to the following biofidelity rating:^{4, 9}

Excellent:	86 ≤ CS < 100
Good:	65 ≤ CS < 86
Fair:	44 ≤ CS < 65
Marginal:	26 ≤ CS < 44
Unacceptable:	0 ≤ CS < 26

For this analysis, CS were calculated for all component and resultant accelerations and grouped by impact site. Only CS_N-amp and CS_N-shape were considered, as simultaneous triggering of the two measurement systems was not feasible in the experimental design.

Overall, average CS values indicated excellent correlation for all component and resultant acceleration time series except for the shape of rotational acceleration in the Z direction which was in the marginal biofidelity range (Table 2). Marginal correlation for Z rotation shape was due primarily to relatively small Z acceleration contributions at A, B, and C sites where rotation occurred primarily about the X and Y axes. This was especially the case for low velocity impacts, as indicated by the high within-site standard deviations observed. For all other impact sites, component and resultant CS had excellent to good biofidelity except for CS_N-amp linear acceleration in the C direction which had fair correlation. Again, reduced correlation was due primarily to minimal linear acceleration contribution in the X direction for side of the head impacts.

Table 2.

Mean and standard deviation of CS values for linear and rotational acceleration at the head center of gravity.

	A		B		C		D		Overall A-B-C-D
	CSN-amp	CSN-shape	CSN-amp	CSN-shape	CSN-amp	CSN-shape	CSN-amp	CSN-shape	CSN-amp	CSN-shape
Linear Acc.
X dir.	98.82 (1.80)	99.46 (1.88)	92.58 (3.90)	80.84 (17.62)	61.43 (6.83)	100.00 (0.01)	92.72 (3.86)	99.56 (0.47)	87.09 (14.70)	95.47 (11.30)
Y dir.	82.54 (22.38)	98.12 (3.68)	99.30 (0.91)	99.82 (0.44)	99.63 (0.48)	99.60 (0.58)	91.86 (7.89)	99.97 (0.09)	93.17 (12.97)	99.44 (1.86)
Z dir.	91.24 (5.53)	96.28 (7.38)	88.55 (7.81)	100.00 (0.00)	93.21 (8.82)	97.70 (4.48)	91.41 (10.84)	75.54 (10.98)	91.14 (8.68)	90.51 (13.03)
Resultant	95.63 (3.59)	98.92 (2.20)	97.52 (2.13)	99.60 (0.80)	97.47 (3.17)	99.93 (0.16)	96.15 (2.24)	99.93 (0.13)	96.63 (2.82)	99.64 (1.15)
Rotational Acc.
X dir.	80.10 (18.88)	99.71 (0.69)	95.71 (4.56)	100.00 (0.00)	99.17 (0.80)	99.93 (0.14)	96.43 (4.02)	100.00 (0.00)	93.25 (11.64)	99.92 (0.34)
Y dir.	98.48 (2.11)	61.96 (21.15)	91.37 (16.06)	97.02 (4.62)	86.56 (9.85)	91.62 (11.31)	88.23 (8.87)	99.90 (0.19)	90.84 (10.93)	88.99 (18.60)
Z dir.	85.33 (15.01)	18.04 (43.28)	97.88 (2.65)	53.57 (24.44)	79.51 (10.22)	49.82 (19.13)	94.29 (3.76)	93.46 (5.89)	89.81 (11.16)	34.33 (60.42)
Resultant	91.58 (9.31)	97.97 (4.68)	99.55 (0.59)	86.81 (9.45)	95.05 (3.63)	99.67 (0.73)	95.83 (2.51)	99.99 (0.02)	95.54 (5.49)	96.54 (7.17)