Abstract
We develop a combined experimental-mathematical framework to investigate heterogeneity in the context of breast cancer treated with doxorubicin. We engineer a cell line to over-express the multi-drug resistance 1 protein (MDR1), an ATP-dependent pump that effluxes intracellular drug. Co-culture experiments mixing the MDR1-overexpressing line with its parental line are evaluated via fluorescence microscopy. To quantify the impact of population heterogeneity on therapy response, these data are analyzed with a coupled pharmacokinetics/pharmacodynamics model. The proliferation and death rates of each line vary with co-culture condition (the relative fraction of each cell line at the time of seeding). For example, the death rate in the parental line under low-dose doxorubicin treatment is increased from 0.64 (±0.22) × 10−2 hr−1 to 1.46 (±0.58) × 10−2 hr−1 with increasing fractions of MDR1-overexpressing cells. The growth rate of the MDR1-overexpressing line increases 29% as its relative fraction is decreased. Simulations of the pharmacokinetics/pharmacodynamics model suggest increased efflux from MDR1-overexpressing cells contributes to the increased death rate in the parental cells. Experimentally, the death rate of parental cells is constant across co-culture conditions under co-treatment with an MDR1 inhibitor. These data indicate that intercellular pharmacokinetic variability should be considered in analyzing treatment response in heterogeneous populations.
Keywords: oncology, pharmacology, mathematical modeling
1. Introduction
The advent of precision medicine has brought significant advances to oncology. The majority of these efforts have leveraged genetics to classify and pharmaceutically target cancers13. While the genetic-centric approach has great merit in appropriately selecting therapies and identifying new pharmaceutical targets, it overlooks a host of patient- and tumor-specific measures that influence therapy response. For example, the microenvironment of the tumor alters response34, delivery of therapy to tumors is variable as tumor perfusion is limited19, and patient-specific pharmacokinetic properties vary35. Further, tumors demonstrate intratumoral heterogeneity that evolves over time33. Tumors are composed of a diverse cell populations that demonstrate differences in phenotypes, such as gene expression and sensitivity to anti-cancer agents12,17. This intratumoral heterogeneity affects the response of tumors to therapy21. It is an ongoing challenge in clinical oncology to quantify tumor heterogeneity to adjust therapy choice, dose, and frequency to account for evolving tumor behavior in the individual patient.
Tumor initiation and progression has long been described as an evolutionary process in which the tumor is composed of discrete clones that are selected according to their relative fitness29. The fitness of a clone is defined by its interactions with neighboring clones and the microenvironment25. These inter-clonal interactions include those defined in ecology such as competition, under which clones compete for a limited resource, and mutualism, in which clonal interactions provide a benefit to each clone21. Some interactions result in selective sweeps, in which a single clone expands to dominate a neoplasm. Alternatively, non-autonomous behavior, in which driver mutations in one clone confer benefit to neighboring clones, selects for heterogeneous populations to maximize tumor population fitness, often to the detriment of the patient. For example, in a small cell lung cancer model, clonal heterogeneity was found to enhance tumor proliferation and metastatic potential8.
The dynamics of cancer progression have been a target of mathematicians for decades2,28. A host of both stochastic and deterministic models have been proposed to describe the evolution of a tumor in response to therapy and to optimize treatment approaches10,14,37. These computational models are often complemented by flow-cytometry or histology to quantify distinct clonal populations within a tumor and the interaction among those clones3,9,31. These techniques have been leveraged to quantify how both genetic and non-genetic heterogeneity influence tumor behavior20,22. While models of heterogeneous populations include terms to describe the interactions among populations, additional research is needed to elucidate the specific biophysical bases of those interactions. Such mechanisms could include paracrine signaling 8 or biomechanical forces 36. We recently proposed and validated a coupled pharmacokinetic/pharmacodynamic (PK/PD) model to predict the temporal response of a homogeneous cell population to a temporally-varying treatment timecourse23. We hypothesize that variable pharmacokinetic properties among clones serves as an additional means of interclonal interaction and influences the treatment response of heterogeneous population.
A goal of mathematical modeling is to abstract the key features of a physical system to succinctly describe its behavior in a series of mathematical equations. In this way, the system can be simulated in silico to further understand system behavior, generate specific, experimentally-testable hypotheses, and guide experimental design. In this work, we describe a coupled experimental-mathematical modeling approach to develop and parameterize a mathematical model describing treatment response in heterogeneous cell populations. We investigate this problem in triple negative breast cancer cell lines subject to standard-of-care doxorubicin therapy. We leverage two cell lines: a doxorubicin-sensitive line and a doxorubicin-resistant, multi-drug resistance protein 1 (MDR1)-overexpressing line. MDR1 is a surface membrane pump that actively effluxes drug from cells, decreasing intracellular drug accumulation and conferring resistance to anthracyclines (including doxorubicin), taxanes, and several other agents24. Each cell line is engineered to be distinguished via fluorescence imaging, which is utilized to monitor cell population dynamics. We build on a coupled pharmacokinetic/pharmacodynamic model of doxorubicin treatment response 23 to quantify how sensitive and resistant cell lines respond to treatment independently and in combination. Finally, we leverage mathematical models to predict aspects of treatment response in heterogeneous cell populations.
2. Materials and Methods
2.1 Cell Lines
The MDA-MB-468 triple negative breast cancer cell line was obtained through American Type Culture Collection (ATCC, Manassas, VA) and maintained in culture according to ATCC recommendations. The line was virally transduced to express a monomeric red fluorescence protein (mRFP)-tagged H2B protein as described previously12. The H2BmRFP-expressing MDA-MB-468 cell line was again transduced to express green fluorescent protein (GFP)-tagged MDR1 (ABCB1 gene, Origene Technologies, Rockville, MD). Following transduction, the cell line was cultured in 100 nM doxorubicin for two weeks to select a doxorubicin-resistant phenotype. The H2BmRFP MDA-MB-468 and the double positive H2BmRFP, MDR1GFP MDA-MB-468 cell lines are denoted as parental and resistant, respectively. Sample images of each cell line are shown in Figure 1.
Figure 1.
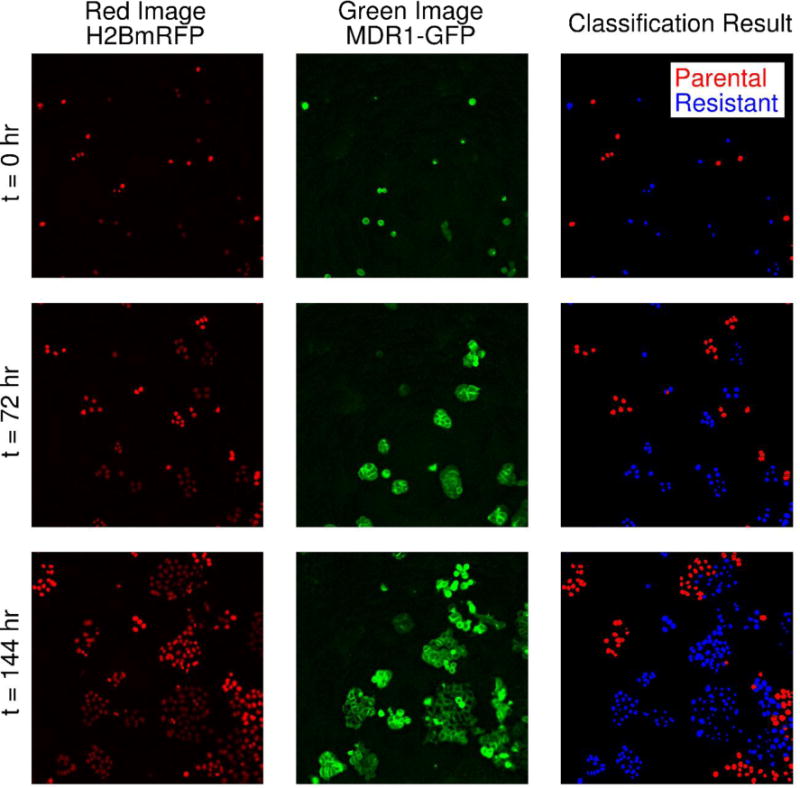
Sample image time series of parental and resistant cell lines and illustration of the counting and classification scheme. Both the parental and resistant cell lines are engineered to express a nuclear H2BmRFP label (left column). The resistant line additionally expresses a GFP-tagged MDR1 protein (middle column). Note that these fluorophores are stably expressed as the images show the same area over six days. The nuclear image (left column) is used for cell segmentation and counting. A SVM classifier is used to classify each detected cell as parental or resistant in co-culture conditions using the GFP image (middle column). A sample segmentation and classification result is shown in the right column. In this example, the resistant cells are colored blue and the parental line is shown in red. The classifier is able to accurately identify each cell line semi-automatically. (Placed in Section 2.4)
2.2 Chemicals
Doxorubicin is a standard-of-care cytotoxic agent used in the treatment of several malignancies, including triple negative breast cancer. Doxorubicin canonically induces DNA damage by intercalating DNA bases, stabilizing the topoisomerase II complex, and increasing free radical formation15. Doxorubicin hydrochloride was obtained from Sigma Aldrich and diluted to a stock concentration of 1 mM in saline.
Tariquidar (TQR) is a third-generation MDR1 inhibitor that non-competitively inhibits MDR1 function26. TQR was purchased from Selleckchem (Boston, MA) and dissolved to a 1 mM stock concentration in DMSO. Both doxorubicin and TQR were stored in 250 μL aliquots at −80 °C.
2.3 Treatment Response Assays
The response of each cell line to doxorubicin was measured using previously-published dose response assays23. Briefly, cells were added to 96-well microtiter plates at 5,000 cells per well. Cells were treated with doxorubicin concentrations ranging from 10 to 2,500 nM. Doxorubicin was removed via media replacement after 24 hours. These experimental conditions were designed such that the areas under the concentration of doxorubicin curves overlapped those observed in vivo. Live cells were imaged daily via fluorescent microscopy for up to two weeks following treatment. For these studies, fluorescence microscopy images were collected using a Synentec Cellavista High End platform (SynenTec Bio Services, Münster, Germany) with a 20× objective and tiling of 25 images. For each imaging session, cells were transferred from the incubator to the microscope and returned immediately following imaging. During all imaging sessions, cells were maintained in standard growth media (Leibovitz’s L-15 media supplemented with 10% fetal bovine serum). In this way, cell populations could be observed over time. Two co-registered channels of data were collected for these experiments: a red channel to image H2BRFP and a green channel to image the MDR1GFP. At least three replicates of each treatment condition were collected. Media was refreshed every three days for the duration of each experiment to ensure sufficient growth conditions.
The response of each cell line was assessed using the above assay. To investigate the behavior of heterogeneous populations, the parental and resistant lines were co-cultured in the microtiter plate at several ratios totaling 5,000 cells per well. For example, to simulate a tumor composed of 20% resistant cells, 1,000 resistant cells were added to 4,000 cells from the parental line. The response of these co-culture conditions was measured in the same way as above. Several co-culture conditions were investigated, ranging from 20% to 80% (in increments of 20-25%) resistant cells.
2.4 Image Processing
Nuclei were segmented and counted in MATLAB (Natick, MA) using a fully automated, watershed-based method12. A classification scheme was developed to identify resistant cells (GFP-expressing) in heterogeneous populations. Each identified nucleus and its surrounding area was described by an image feature vector (described below), and a support vector machine (SVM) was used to classify each cell nucleus as either parental or resistant. A SVM defines a hyperplane to optimally separate two classes6. The SVM was trained using image feature vectors from a subset of cells identified in parental-only and resistant-only control experiments. In all, the training set consisted of 10,000 feature vectors corresponding to 5,000 parental and 5,000 resistant cells. A 10-fold cross validation approach was used to train and tune the SVM.
Each cell identified via segmentation was described by a feature vector focusing on the intensity of the green channel image. For each identified nucleus, the average GFP intensity around the nucleus was calculated within a bounding box. Three bounding box sizes were used: 20×20, 30×30, and 40×40 pixels. Additionally, a radial intensity histogram was computed around each identified nucleus. The histogram summarizes the distribution of image intensities as a function of radial distance from the center of the nucleus, and this feature has been used to identify circular objects11. The histogram consisted of twenty bins, each containing of the average intensity over 5 pixel-wide rings with increasing radii centered on the nucleus. Finally, the distance from the nucleus to peak GFP intensity was calculated. We hypothesized that these features would capture the brightness patterns of the resistant cells. Briefly, resistant cells are characterized by a ring of MDR1-GFP a set distance from the nucleus (see Figure 1 for examples). The peak seen for parental cells near a resistant cell would be farther from the nucleus than the distance seen for resistant cells.
To classify images in the test set (i.e., cells in co-cultured wells), the above features were calculated for each identified nucleus and classified with the trained SVM. In this way, the image processing pipeline outputs the cell counts of both the parental and resistant lines. To establish the performance characteristics of the trained classifier, we defined a unique validation set consisting of approximately 28,000 cells (16,000 parental and 12,000 resistant cells). The sensitivity and specificity of the classifier when applied to this validation set is reported.
2.5 Treatment Response Model
We previously proposed and validated a coupled pharmacokinetic/pharmacodynamic model of doxorubicin treatment response in vitro23. The model incorporates measured doxorubicin pharmacokinetic and pharmacodynamic rates and allows for prediction of treatment response to a wide range of treatment conditions on a cell-line specific basis. This model is extended to account for the two cell populations present in the current experimental system. A compartment model is used to describe doxorubicin pharmacokinetics:
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
where CE (t), CF,c (t), and CB,c (t) are the concentrations of doxorubicin in the extracellular, free, and bound compartments, respectively, in cell line c (parental, P, or resistant, R) at time t. Both the free and bound compartments are defined to share the same physical space (intracellular). The free compartment represents drug that has diffused into the cell, while the bound compartment represents drug that has bound to DNA. The kij,c parameters are rate constants that describe the movement of doxorubicin between each of these compartments in each cell line; for example, kFE,R describes the rate of drug transfer from the free, intracellular compartment of the resistant cell line to the extracellular compartment. Similar definitions apply to kEF,R, kFB,R, kEF,P, kFE,P, and kFB,P. The volumes of the intracellular and extracellular compartments are denoted with vI,c and vE,c, respectively.
The pharmacodynamics model is similarly extended from that presented in previous work23 to include both parental and resistant cells. Specifically, we define the temporal change of a population consisting of a specified fraction of resistant cells, f, to a delivered doxorubicin dose, D, for all time, t as follows:
| (6) |
| (7) |
| (8) |
where NT is the total population size, NP is the number of parental cells, and NR is the number of resistant cells. kp,c and kd,c are the proliferation and death rates for cell line c, respectively. θ is the carrying capacity describing the maximum number of cells that can be supported by the experimental system. Dose, D, is defined as the maximum bound concentration of drug following treatment and is calculated by simulating the pharmacokinetics model using an experimentally-defined extracellular doxorubicin concentration timecourse. Co-culture condition, f, is defined by the fraction of each cell line at the time of seeding. As cell line behavior was observed to vary as a function of co-culture conditions, all model parameters are allowed to vary with f. Additionally, kd,c and θ are dose-specific. The death rate, kd,c, for each population can assume either of the following forms:
| (9) |
| (10) |
Eq. (9) assumes an immediate transition to a constant post-treatment death rate, kd,a. Eq. (10) assumes a smooth induction to and recovery from a maximal death rate, kd,b. r describes the rate at which treatment response is induced. A weighted averaging approach is used to combine these two models (i.e., Eqs. (6) – (8) with the death rate in Eq. (9) and Eqs. (6) – (8) with the death rate in Eq. (10) into a single best-fit model. The Akaike information criterion (AIC) is used to calculate the weight of each model. The AIC is a measure of model likelihood that balances goodness of fit with the number of free parameters. This is a common approach for multimodal inference5,7, and additional information on the model and model averaging approach can be found in previous work23.
2.6 Treatment Response Model Fitting
The two-species pharmacodynamics model, Eqs. (6) – (8), is fit to data by minimizing the following objective function, G(x):
where x is the set of parameters to be estimated, Yt,c is the measured cell counts at time t for cell line c, is the model-estimated cell counts at time t for cell line c when the model is evaluated with parameters x, and ti and tf are the initial and final timepoints respectively. c represents the parental cell line (P), resistant cell line (R), or total cell count (T). Specifically, the proliferation rate (kp,R, kp,P) and all dose-response parameters (kd,R, kd,P) for each cell line are optimized to fit the data. Data from each co-culture and treatment condition are fit independently using the trust region reflective algorithm, a nonlinear least squares optimization routine, implemented in MATLAB. To ensure the stability and accuracy of the fitting approach, the model was simulated with user-defined initial conditions and model parameter values, and the optimization routine was used to recover model parameters from the simulated data. Results of this simulation study are reported in Supplementary Materials. Model fits are compared to the measured response for each cell line, and the mean percent error across all timepoints is reported for the best-fit model. We define the mean percent error over all timepoints as the average of the model-data mismatches, which are calculated at each experimental timepoint. Specifically, we define the mean percent error (MPE):
where y is the observed cell count, is the model predicted cell count, and n is the number of timepoints in the experiment. We utilize the mean percent error as a summary statistic to quantitatively describe the goodness of fit of the model to the cell population timecourse data.
2.7 Simulation of Pharmacokinetics in Heterogeneous Cell Populations
The pharmacokinetics model is simulated to explore the movement of drug between the parental and resistant populations. Specifically, the accumulation of drug in the parental cells (CB,P) over a range of co-culture conditions is simulated. For these simulations, both cell lines are assumed to have identical pharmacokinetic parameters, except for the doxorubicin efflux parameter (kFE,R and kFE,P). To assess the effect of the efflux rate on the accumulation of drug in the parental cell line, a range of kFE,R values were simulated while holding kFE,P constant. To simulate a range of co-culture conditions, the total intracellular volume (vI,R + vI,P) was held constant while altering the relative volumes of the intracellular compartment of the resistant and parental cell lines. Proportional changes in kEF,P and kEF,R were made to reflect the changing volumes of the intracellular compartments. Doxorubicin primarily diffuses into cells, and diffusion, described by kEF, is proportional to membrane permeability and surface area. As we assume the cell surface area per unit volume for each cell line is constant in all co-culture conditions, the changing intracellular volumes require corresponding changes in total cell surface areas. For a simulation consisting of a fraction f of resistant cells and influx rate kEF, kEF,P = (1 – f) kEF and kEF,R = f kEF. This adjustment ensures that for each cell line the accumulation of drug per unit cell volume is constant in all co-culture conditions. A complete list of parameter values is shown in Table 1.
Table 1.
Properties for pharmacokinetic simulation. (Placed in Section 2.7)
2.8 Modulation of Pharmacokinetics in Heterogeneous Cell Populations
We hypothesize that doxorubicin efflux from the resistant line contributes to increased parental cell death in co-culture experiments. To test this hypothesis experimentally, the efflux of drug via MDR1 in the resistant cell line is inhibited with TQR. By inhibiting the effect of this pump, we hypothesize that the death rate of the parental population to doxorubicin should be independent of the presence of resistant cells. The treatment response assay described in Section 2.3 is repeated with 1 μM of TQR applied one hour prior to doxorubicin therapy and throughout the course of the assay. Notably, low concentrations of doxorubicin (50 and 100 nM) are used to avoid saturating the death rate. These data are fit with the pharmacodynamic model, and the hypothesis is assessed by measuring the change in the death rate of the parental population (kd,P) as a function of the percentage of resistant cells at the time of seeding.
3. Results
3.1 Cell Counting Results
A representative image set and corresponding segmentation and classification results are shown in Figure 1. The tuned SVM correctly classified 98.5% of cells in the training set. In the separate validation set, the classifier achieved a sensitivity of 0.942 with a specificity 0.994.
3.2 Model Fits
The treatment response model was fit to each co-culture and treatment condition. Model fits are superimposed on the total population cell counts in Figure 2. The model accurately captured the total cell count over a wide range of co-culture and treatment conditions with a mean percent error of 10.1% across all data points. Additionally, the model accurately described the dynamics of each cell line in co-culture conditions. Cell counts of the resistant and parental lines under a range of co-culture conditions at a representative doxorubicin treatment are shown in Figure 3. The best-fit model is overlaid on these data. The mean percent errors over all timepoints of the model fits to the parental and resistant lines are 17.2% and 8.9%, respectively. Of note, the high error rates of the parental line are concentrated in conditions of high cell death with relatively low cell counts.
Figure 2.
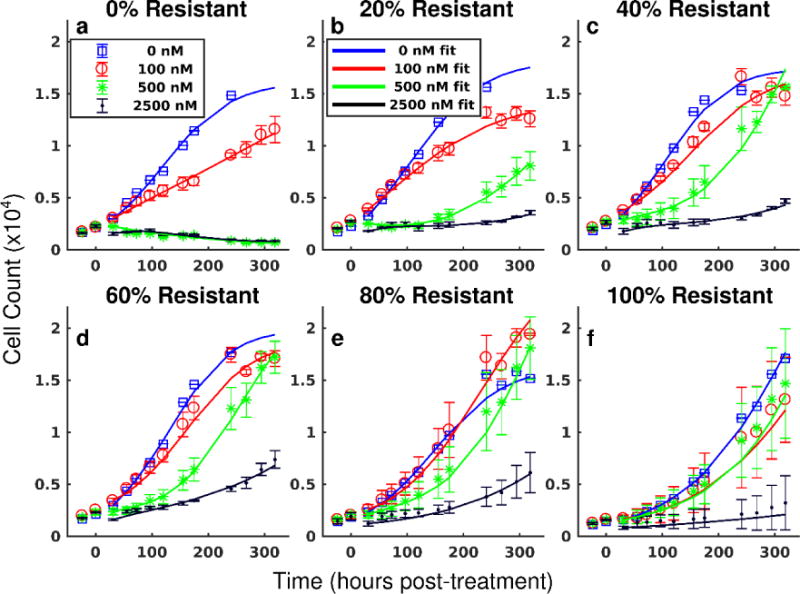
Treatment response in heterogeneous cell populations and pharmacodynamic model fits. The total cell counts (sum of resistant and parental cells) over time and corresponding 95% confidence intervals are shown for in a representative set of doxorubicin treatments and co-culture conditions. Each treatment condition is fit by Eqs. (6) – (8) as described in Section 2.6, and the model fit is overlaid on the data (smooth lines color-coded to data in all panels). The parental line is more sensitive to doxorubicin therapy relative to the resistant line. Complete population regression of the parental line is seen for doxorubicin treatments ≥ 500 nM (a). The cell populations demonstrate increasing resistance to therapy as the fraction of resistant cells increases (b – e). The resistant cell line continues to proliferate under 500 nM doxorubicin (f). The proposed model can describe the observed pharmacodynamics. (Placed in Section 3.1)
Figure 3.
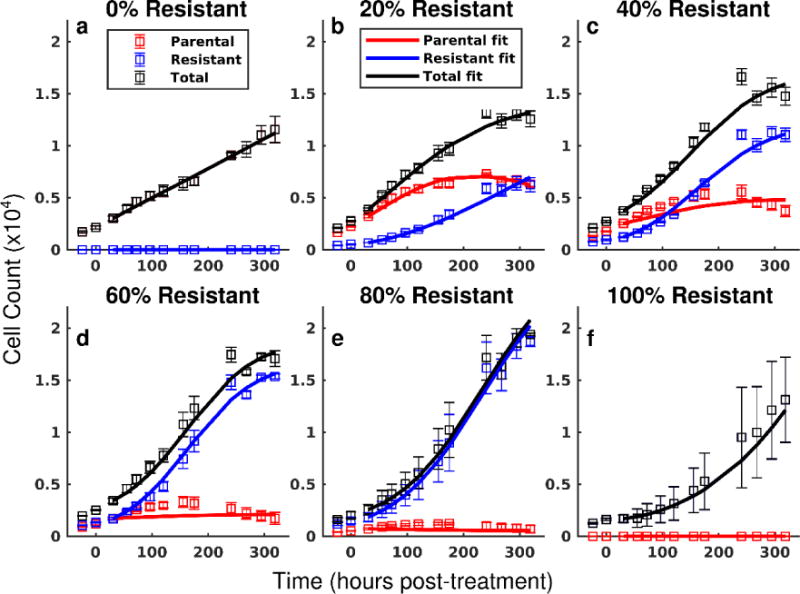
Model fits for each cell line in several co-culture conditions following treatment with 100 nM of doxorubicin. In the current experimental approach, each cell line can be quantified throughout the course of the experiment. The cell counts of the parental (red) and resistant (blue) lines with 95% confidence intervals are shown following treatment with 100 nM doxorubicin. The total cell counts with 95% confidence intervals are shown in black. Eqs. (6) – (8) are fit to these data as described in Section 2.6, and the best-fit model is overlaid on the observed cell counts (smooth line color-coded to data in all panels). While the parental line demonstrates continued positive proliferation in monoculture (a), the net proliferation rate of the parental line decreases with increasing fractions of resistant cells (b – e). The resistant line demonstrates positive growth in all conditions (b – f). (Placed in Section 3.1)
Prior to doxorubicin treatment, the parental and resistant cell lines displayed exponential growth in monoculture with proliferation rates (kp) of 2.07 (±0.08) × 10−2 hr−1 and 1.72 (±0.04) × 10−2 hr−1, respectively (the bounds here and below correspond to the 95% confidence interval of the parameter estimates). The proliferation rate of the resistant line increases as the percent of resistant cells at the time of seeding decreases. Conversely, the proliferation rate of the parental line decreases as the percent of resistant cells increases. The proliferation rate of each species as a function of the percentage of resistant cells is shown in Figure 4. For example, in an untreated control with 75% resistant cells, the parental proliferation rate decreases 30% from its monoculture rate to 1.45 (±0.07) ×10−2 hr−1. In the untreated 25% resistant culture control, the proliferation rate of the resistant line increases 29% from its monoculture rate to 2.22 (±0.07) × 10−2 hr−1. The mean percent error of the model fits in these untreated conditions were 9.1% and 14.9% for the resistant and parental lines, respectively.
Figure 4.
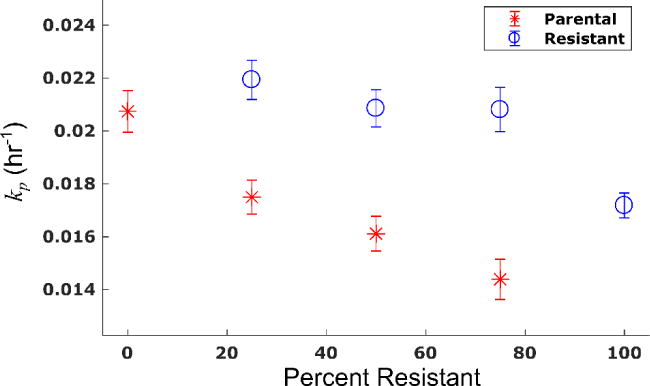
Proliferation rate of each cell line changes as a function of co-culture condition. The proliferation rate of each cell line and corresponding 95% confidence interval are estimated from control experiments (no doxorubicin). These rates are shown as a function of the percentage of resistant cells at the time of seeding. The proliferation rate of the resistant cell line increases as the fraction of resistant cells decreases. Conversely, the proliferation rate of the parental cell line decreases as the fraction of resistant cells increases. (Placed in Section 3.2)
Each cell line demonstrated a concentration-dependent response to doxorubicin. The parameter fits with 95% confidence intervals from a representative experimental replicate are shown in Tables S1 and S2 for the parental and resistant lines, respectively. The death rate of the parental cell line (kd,P) appears to saturate to approximately 2.0 × 10−2 hr−1 at high doxorubicin doses (≥ 500 nM) (this is the death rate in Eq. (9)). A similar trend was noted in the death rate derived from Eq. (10) (see Tables S1 and S2)). Notably, the death rate in the parental cells for the 100 nM treatment condition increases with the number of resistant cells present in the population. In the parental-only condition, the death rate is 0.64 (±0.22) × 10−2 hr−1. This rate increases to 1.46 (±0.58) × 10−2 hr−1 when the population consists of 80% resistant cells. Increasing death rate in the parental population with increasing numbers of resistant cells was noted in all experimental replicates (Figure 7a). The resistant cell line demonstrates decreased sensitivity to doxorubicin therapy relative to the parental line. For example, the death rate in the resistant line under 100 nM treatment (0.31 (±0.20) × 10−2 hr−1) is half that observed in the parental line.
Figure 7.
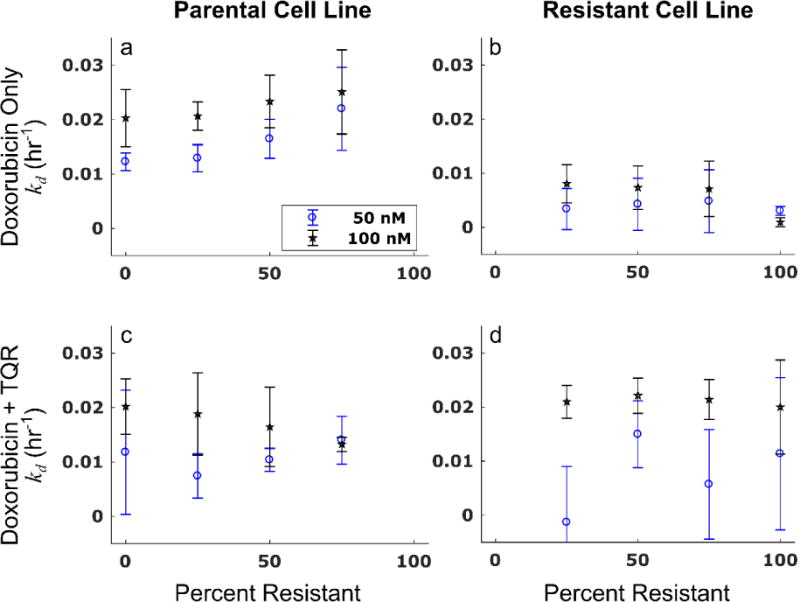
The death rate in the parental population is constant as a function of co-culture condition when the MDR1 pump is inhibited. Cells under various co-culture conditions were treated with doxorubicin only or a combination of doxorubicin and 1 μM TQR, which inhibits MDR1 function. The treatment response of these populations were then observed over time as described in Section 2.8. The treatment response model was fit to the treatment response timecourses. The death rate and corresponding 95% confidence interval from these model fits for each cell line (left and right columns for parental and resistant lines, respectively) are reported under the doxorubicin-only condition (top row) and the doxorubicin + TQR condition (bottom row). The death rate in the parental cell line appears to increase with increasing percentages of resistant cells (a). The resistant cell line is relatively insensitive to doxorubicin treatment as demonstrated by the low death rates in (b). The assay is repeated with the addition of 1 μM TQR to doxorubicin. The addition of TQR reverses the trend observed in a, and the response to therapy in the parental line appears constant as a function of co-culture condition (c). The death rate of the resistant cell line increases significantly with addition of TQR (d). (Placed in Section 3.4)
In Figure 5, the net proliferation rate (kp - kd) for each species is shown as a function of the percentage of resistant cells at the time of seeding. The increase in the death rate in the parental cell line is compounded by the decreasing proliferation rate, creating a synergistic effect leading to a significantly decreased net proliferation rate with increasing fractions of resistant cells. Further, the increased proliferation rate in the resistant line is greater than the effect of doxorubicin, causing an increasing net proliferation rate with decreasing fractions of resistant cells.
Figure 5.
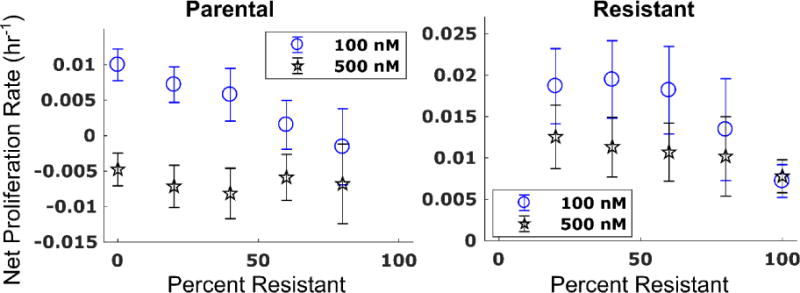
Net proliferation rate of the parental (left) and resistant (right) cell lines as a function of the number of resistant cells present at the time of seeding. Eqs. (6) – (8) were fit to each cell line in each co-culture and treatment condition. The net proliferation rate (kp - kd,a) with corresponding 95% confidence intervals under 100 and 500 nM of doxorubicin is shown for each cell line as a function of the percentage of resistant cells. Sensitivity to doxorubicin in the parental cell line increases with increasing fractions of resistant cells as demonstrated by the significant decrease in net proliferation rate under 100 nM of treatment with increasing fractions of resistant cells (left). The net proliferation rate of the parental line appears saturated at approximately −0.5 × 10−2 hr−1 under treatment with 500 nM doxorubicin. Conversely, the net proliferation rate of the resistant line increases with decreasing numbers of resistant cells (right). This indicates that the increase in proliferation rate in the resistant line more than offsets the effects of low-dose doxorubicin. (Placed in Section 3.2)
3.3 Pharmacokinetics Simulation
Based on the results of section 3.2, it is clear that the presence of resistant cells increases the sensitivity of parental cells to treatment. Simulation of the pharmacokinetic model predicts an increase in drug accumulation (up to 15%) in the parental cell line (CB,P) in the presence of resistant cells. Simulation results are shown in Figure 6. As the accumulation of doxorubicin is proportional to therapy response23, these simulations are consistent with the decreased net proliferation rate of the parental line with increasing fractions of resistant cells seen in Figure 5 and Table S1. A synergistic effect of the efflux rate of the resistant cells (kFE,R) and the fraction of resistant cells present in the co-culture condition in increasing the accumulation of drug in the parental line is observed. The magnitude of this effect is proportional to kEF. Additionally, no difference in CB,P is observed when kFE,R = kFE,P. This suggests that the response of the parental line to therapy would be independent of the presence of resistant cells if kFE,R were decreased to match kFE,P.
Figure 6.
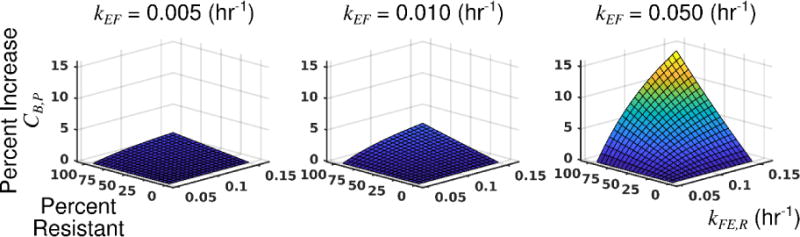
Pharmacokinetics model predicts increased doxorubicin accumulation in the parental cell line with increasing efflux rate in the resistant line (kFE,R) and increasing fractions of resistant cells. The pharmacokinetics model was simulated to assess the effect of kFE,R and the fraction of resistant cells on the accumulation of drug in the parental cells (CB,P). In these simulations, the drug binding rate was equal for each cell line (kFB,R = kFB,P), and the diffusion rate into each cell line was equal (kEF,R = kEF,P = kEF). The fraction of resistant cells in the population was varied between 0 (entirely parental) and 0.95. The efflux rate for the resistant cells (kFE,R) was varied between 0.05 and 0.15 hr−1. The efflux rate for the parental population (kFE,P) was fixed at 0.05 hr−1. All other parameter values are specified in Table 1. The drug accumulation in the parental cell line (CB,P) is normalized to the minimum simulated value in each plot to show the percent increase in drug accumulation as the fraction of resistant cells, kEF, and kFE,R are varied. As the percentage of resistant cells increase, there is an increase in the drug accumulation in parental cells. This accumulation is further increased as kFE,R increases. The magnitude of this effect is proportional to the simulated value of kEF. (Placed in Section 3.3)
3.4 MDR1 Inhibition
The co-culture treatment response experiments were repeated with addition of 1 μM TQR, and the treatment response model was fit to the resulting timecourses. The mean percent errors over all timepoints and treatment conditions of the model fits to the parental and resistant lines in these experiments are 6.5% and 5.9%, respectively. The death rate of the resistant cell line increased with the addition of TQR. For example, under treatment with 100 nM doxorubicin, the death rate of the resistant line increased an order of magnitude from 0.093 (±0.084) × 10−2 hr−1 to 2.00 (±0.87) × 10−2 hr−1 with addition of TQR. Contrary to the previous observation that the death rate of the parental line increases with increasing numbers of resistant cells, the death rate of the parental line appears constant across co-culture conditions with addition of TQR. These results are illustrated in Figure 7. This observation is consistent with the prediction of the PK model. By equalizing the efflux rate of the two cell lines through use of TQR, the death rate of the parental cell population appears independent of the presence of resistant cells. Of note, while treatment with TQR appeared to restore the linearity of the death rate with respect to co-culture condition in the parental population, the proliferation rate of each cell line still varied with respect to co-culture condition (Figure 8). The model described these untreated control data well with mean percent errors of 9.7% and 7.0% for the parental and resistant lines, respectively.
Figure 8.
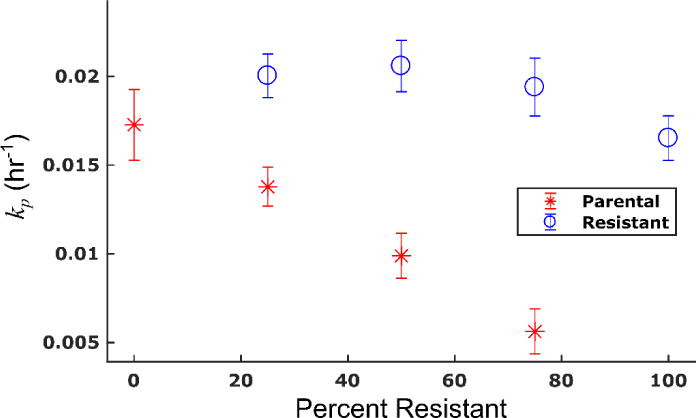
Proliferation rates of parental and resistant cell lines under treatment with TQR. Proliferation rates were estimated from control (i.e., no doxorubicin) treatment response studies with 1 μM TQR. The proliferation rate of the parental line decreases with increasing fractions of resistant cells. Conversely, the proliferation rate of the resistant cells increases slightly as the fraction of resistant cells decreases. This is consistent with the observation in Figure 4. (Placed in Section 3.4)
4. Discussion
We have established an experimental-mathematical modeling framework to investigate the response of heterogeneous cell populations to doxorubicin therapy. We found that treatment response of heterogeneous cell populations is non-linear in that model parameters change as a function of population composition. Specifically, over a range of clinically-relevant doses, the death rate of parental cells is increased in the presence of resistant cells. Further, the proliferation rate of the resistant cell line increases with decreasing fractions of resistant cells, and the proliferation rate of the parental cells is depressed with increasing fractions of resistant cells. We have proposed and validated a pharmacokinetics-based mechanism contributing to the nonlinearities in the observed death rates. We believe this framework to be a useful tool to systematically investigate the behavior of heterogeneous systems and to characterize quantitatively how heterogeneity affects therapy response.
Both the growth and death rates of each cell line are altered in co-culture conditions. The MDR1-overexpressing cell line demonstrates increased resistance to doxorubicin treatment relative to the parental cell line, and this difference is accentuated in co-culture. When grown together, the resistant line grows more quickly, and the parental cell line is further sensitized to doxorubicin therapy. We posit these observations largely agree with the ligand-capture hypothesis of cell competition27. Briefly, the ligand-capture hypothesis assumes: 1) the ligand is in limiting supply; 2) the ligand is a survival signal; and 3) partial withdrawal of the ligand triggers apoptosis.
The differing proliferation rates could be explained through competition for growth nutrients. Specifically, the MDR1 pump is ATP-dependent, and in other MDR1-positive cell lines, glucose uptake and ATP consumption are significantly increased relative to MDR1-negative cell lines4,32. Potentially, with transduction of MDR1, the resistant cells evolve an improved ability to capture nutrients from the environment to support the metabolic demands of the pump. The enhanced growth rate of resistant cells seen at low fractions of resistant cells may arise due to a decrease in competition for nutrients with fewer resistant cells. Conversely, the decreasing proliferation rate of the parental cells in the presence of resistant cells may arise due to the increased nutrient consumption by the resistant cells. Indeed, ATP generation mechanisms have been shown as a basis for cellular competition30. The proposed model can be extended to describe these effects through inclusion of metabolic rates into the proliferation rate. Just as the death rate was defined to account for varying drug concentrations, the proliferation rate can be defined to include the availability of nutrients (similar to the model proposed by Silva and colleagues32).
The enhanced death rate of the parental line requires a slight modification of the ligand-capture hypothesis, which we denote as the ligand-rejection hypothesis. We assume again that the ligand (in this case drug) is in limiting supply. However, the ligand is a cell death signal, and addition of ligand induces death. Cells that are able to reject or metabolize ligand will out-compete those that avidly consume the ligand. This is indeed the behavior predicted by simulations of the extended pharmacokinetic model in Figure 6 and validated with the experiments presented in Figure 7. We hypothesize that this pharmacokinetic-based mechanism may also contribute to responses to targeted anti-cancer agents. Biophysical processes of ligand transport underlie both the ligand-capture and ligand-rejection hypotheses. As demonstrated in this work, these physical processes can be described by a parsimonious set of equations, and simulations can be run to guide interventions to control heterogeneous populations.
We proposed and validated a mechanism that contributes to the increasing death rates in the parental cell line in co-culture conditions. Simulation of the pharmacokinetic model suggested that increasing the efflux rate of the resistant cell line increased drug accumulation within the parental cells. The increased accumulation would subsequently increase the death rates of the parental line in co-culture conditions. These simulations generated a specific hypothesis (i.e., response of the parental cell line is independent of the presence of resistant cells if the MDR1 pump is inhibited) that could be tested experimentally. Indeed, when MDR1 function is inhibited with TQR, the death rate of the parental cell line appears constant across co-culture conditions (Figure 7c). These data indicate that variable cellular pharmacokinetics contribute to the nonlinear death rate of parental cells. These data do not exclude alternative hypotheses explaining the observed increase in death rate (e.g., cell-cell signaling, extrusion of toxic metabolites from the resistant line, or impaired DNA repair mechanisms in the parental line secondary to nutrient depletion). Indeed, these additional interactions may be necessary as the increase in drug accumulation predicted by the PK model may not entirely explain the increase in death rate in co-culture conditions. Additional studies are needed to more precisely quantify the contribution of PK heterogeneity to the increased death rate.
While the variability in cell line pharmacokinetics is significant in predicting treatment response in the engineered cell populations in this work, these observations remain to be tested in additional cell lines and in vivo. Further, the proposed pharmacokinetic interaction does not preclude the presence of additional inter-clonal interactions that alter treatment response. For example, cells can secrete factors to stimulate growth and transfer resistance to previously-sensitive cells1. The spatial dependency of the clonal interactions observed in this study remains to be investigated. Indeed, local cell densities have been found to affect treatment response in vitro16. Finally, the hypothesized metabolism-based competition driving differing proliferation rates in co-culture conditions requires further exploration. With these limitations come opportunities to iteratively increase the complexity of the experimental-modeling framework to quantify the magnitude of these effects. Indeed, a major goal of mathematical modeling is to construct models that distill the relevant biology into a parsimonious set of equations. The framework proposed in this work provides a rich platform from which these equations can be constructed.
Supplementary Material
Acknowledgments
We thank the National Institutes of Health for funding through: NCI R01 CA138599, NCI R01 CA186193, NCI U01 CA174706, NIGMS T32 GM007347, NCI F30 CA203220, and NCI K25 CA204599. We thank CPRIT for RR160005; T.E.Y. is a CPRIT Scholar in Cancer Research.
Footnotes
Performance Site:
Department of Biomedical Engineering, Vanderbilt University, 5824 Stevenson Center, Nashville, TN 37232
Conflicts of Interest
The authors declare no conflict of interest.
References
- 1.Aldonza MBD, Hong J-Y, Lee SK. Paclitaxel-resistant cancer cell-derived secretomes elicit ABCB1-associated docetaxel cross-resistance and escape from apoptosis through FOXO3a-driven glycolytic regulation. Exp Mol Med. 2017;49:e286. doi: 10.1038/emm.2016.131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Altrock PM, Liu LL, Michor F. The mathematics of cancer: integrating quantitative models. Nat Rev Cancer. 2015;15:730–745. doi: 10.1038/nrc4029. [DOI] [PubMed] [Google Scholar]
- 3.Bhang HC, Ruddy DA, Krishnamurthy Radhakrishna V, Caushi JX, Zhao R, Hims MM, Singh AP, Kao I, Rakiec D, Shaw P, Balak M, Raza A, Ackley E, Keen N, Schlabach MR, Palmer M, Leary RJ, Chiang DY, Sellers WR, Michor F, Cooke VG, Korn JM, Stegmeier F. Studying clonal dynamics in response to cancer therapy using high-complexity barcoding. Nat Med. 2015;21:440–448. doi: 10.1038/nm.3841. [DOI] [PubMed] [Google Scholar]
- 4.Broxterman HJ, Pinedo HM, Kuiper CM, Schuurhuis GJ, Lankelma J. Glycolysis in P-glycoprotein-overexpressing human tumor cell lines Effects of resistance-modifying agents. FEBS Lett. 1989;247:405–410. doi: 10.1016/0014-5793(89)81380-8. [DOI] [PubMed] [Google Scholar]
- 5.Buckland ST, Burnham KP, Augustin NH. Model Selection: An Integral Part of Inference. Biometrics. 1997;53:603–618. [Google Scholar]
- 6.Burges CJC. A Tutorial on Support Vector Machines for Pattern Recognition. Data Min Knowl Discov. 1998;2:121–167. [Google Scholar]
- 7.Burnham KP, Anderson DR. Model Selection and Multimodel Inference: a Practical Information-theoretic Approach. New York: Springer; 2002. [Google Scholar]
- 8.Calbo J, van Montfort E, Proost N, van Drunen E, Beverloo HB, Meuwissen R, Berns A. A Functional Role for Tumor Cell Heterogeneity in a Mouse Model of Small Cell Lung Cancer. Cancer Cell. 2011;19:244–256. doi: 10.1016/j.ccr.2010.12.021. [DOI] [PubMed] [Google Scholar]
- 9.Carmona-Fontaine C, Deforet M, Akkari L, Thompson CB, Joyce JA, Xavier JB. Metabolic origins of spatial organization in the tumor microenvironment. Proc Natl Acad Sci U S A. 2017;114:2934–2939. doi: 10.1073/pnas.1700600114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Chmielecki J, Foo J, Oxnard GR, Hutchinson K, Ohashi K, Somwar R, Wang L, Amato KR, Arcila M, Sos ML, Socci ND, Viale A, de Stanchina E, Ginsberg MS, Thomas RK, Kris MG, Inoue A, Ladanyi M, Miller VA, Michor F, Pao W. Optimization of dosing for EGFR-mutant non-small cell lung cancer with evolutionary cancer modeling. Sci Transl Med. 2011;3:90ra59. doi: 10.1126/scitranslmed.3002356. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Davies ER. Computer and Machine Vision: Theory, Algorithms, Practicalities. 2012:1–912. doi: 10.1007/978-1-84882-935-0. [DOI] [Google Scholar]
- 12.Frick PL, Paudel BB, Tyson DR, Quaranta V. Quantifying heterogeneity and dynamics of clonal fitness in response to perturbation. J Cell Physiol. 2015;230:1403–1412. doi: 10.1002/jcp.24888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Garraway LA. Genomics-Driven Oncology: Framework for an Emerging Paradigm. J Clin Oncol. 2013;31:1806–1814. doi: 10.1200/JCO.2012.46.8934. [DOI] [PubMed] [Google Scholar]
- 14.Gatenby RA, Vincent TL. An Evolutionary Model Of Carcinogenesis. Cancer Res. 2003;63:6212–6220. [PubMed] [Google Scholar]
- 15.Gewirtz DA. A critical evaluation of the mechanisms of action proposed for the antitumor effects of the anthracycline antibiotics adriamycin and daunorubicin. Biochem Pharmacol. 1999;57:727–741. doi: 10.1016/s0006-2952(98)00307-4. [DOI] [PubMed] [Google Scholar]
- 16.Greene JM, Levy D, Herrada SP, Gottesman MM, Lavi O. Mathematical Modeling Reveals That Changes to Local Cell Density Dynamically Modulate Baseline Variations in Cell Growth and Drug Response. Cancer Res. 2016;76:2882–2890. doi: 10.1158/0008-5472.CAN-15-3232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Heppner GH. Tumor Heterogeneity. Cancer Res. 1984;44:2259–2265. [PubMed] [Google Scholar]
- 18.Jackson TL. Intracellular accumulation and mechanism of action of doxorubicin in a spatio-temporal tumor model. J Theor Biol. 2003;220:201–213. doi: 10.1006/jtbi.2003.3156. [DOI] [PubMed] [Google Scholar]
- 19.Jain RK. Normalizing tumor microenvironment to treat cancer: bench to bedside to biomarkers. J Clin Oncol. 2013;31:2205–18. doi: 10.1200/JCO.2012.46.3653. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kreso A, O’Brien CA, van Galen P, Gan OI, Notta F, Brown AMK, Ng K, Ma J, Wienholds E, Dunant C, Pollett A, Gallinger S, McPherson J, Mullighan CG, Shibata D, Dick JE. Variable Clonal Repopulation Dynamics Influence Chemotherapy Response in Colorectal Cancer. Science (80−) 2013;339:543–548. doi: 10.1126/science.1227670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Marusyk A, Polyak K. Tumor heterogeneity: Causes and consequences. Biochim Biophys Acta - Rev Cancer. 2010;1805:105–117. doi: 10.1016/j.bbcan.2009.11.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Marusyk A, Tabassum DP, Altrock PM, Almendro V, Michor F, Polyak K. Non-cell-autonomous driving of tumour growth supports sub-clonal heterogeneity. Nature. 2014;514:54–8. doi: 10.1038/nature13556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.McKenna MT, Weis JA, Barnes SL, Tyson DR, Miga MI, Quaranta V, Yankeelov TE. A Predictive Mathematical Modeling Approach for the Study of Doxorubicin Treatment in Triple Negative Breast Cancer. Sci Rep. 2017;7:5725. doi: 10.1038/s41598-017-05902-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Mechetner E, Kyshtoobayeva A, Zonis S, Kim H, Stroup R, Garcia R, Parker RJ, Fruehauf2 JP. Levels of Multidrug Resistance (MDR1) P-Glycoprotein Expression by Human Breast Cancer Correlate with in Vitro Resistance to Taxol and Doxorubicin. Clin Cancer Res. 1998;4:389–398. [PubMed] [Google Scholar]
- 25.Merlo LMF, Pepper JW, Reid BJ, Maley CC. Cancer as an evolutionary and ecological process. Nat Rev Cancer. 2006;6:924–935. doi: 10.1038/nrc2013. [DOI] [PubMed] [Google Scholar]
- 26.Mistry P, Stewart AJ, Dangerfield W, Okiji S, Liddle C, Bootle D, Plumb JA, Templeton D, Charlton P. In Vitro and in Vivo Reversal of P-Glycoprotein-mediated Multidrug Resistance by a Novel Potent Modulator, XR9576. Cancer Res. 2001;61:749–758. [PubMed] [Google Scholar]
- 27.Moreno E. Is cell competition relevant to cancer? Nat Rev Cancer. 2008;8:141–147. doi: 10.1038/nrc2252. [DOI] [PubMed] [Google Scholar]
- 28.Nowak MA, Sigmund K. Evolutionary Dynamics of Biological Games. Science (80−) 2004;303:793–799. doi: 10.1126/science.1093411. [DOI] [PubMed] [Google Scholar]
- 29.Nowell P. The clonal evolution of tumor cell populations. Science (80−) 1976;194:23–28. doi: 10.1126/science.959840. [DOI] [PubMed] [Google Scholar]
- 30.Pfeiffer T, Schuster S, Bonhoeffer S. Cooperation and Competition in the Evolution of ATP-Producing Pathways. Science (80−) 2001;292:504–507. doi: 10.1126/science.1058079. [DOI] [PubMed] [Google Scholar]
- 31.Prasanphanich AF, White DE, Gran MA, Kemp ML. Kinetic Modeling of ABCG2 Transporter Heterogeneity: A Quantitative, Single-Cell Analysis of the Side Population Assay. PLoS Comput Biol. 2016;12:e1005188. doi: 10.1371/journal.pcbi.1005188. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Silva AS, Kam Y, Khin ZP, Minton SE, Gillies RJ, Gatenby RA. Evolutionary Approaches to Prolong Progression-Free Survival in Breast Cancer. Cancer Res. 2012;72:6362–6370. doi: 10.1158/0008-5472.CAN-12-2235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Swanton C. Intratumor Heterogeneity: Evolution through Space and Time. Cancer Res. 2012;72:4875–4882. doi: 10.1158/0008-5472.CAN-12-2217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Trédan O, Galmarini CM, Patel K, Tannock IF. Drug resistance and the solid tumor microenvironment. J Natl Cancer Inst. 2007;99:1441–54. doi: 10.1093/jnci/djm135. [DOI] [PubMed] [Google Scholar]
- 35.Weinshilboum R, Wang L. Pharmacogenomics: bench to bedside. Nat Rev Drug Discov. 2004;3:739–748. doi: 10.1038/nrd1497. [DOI] [PubMed] [Google Scholar]
- 36.Yu H, Mouw JK, Weaver VM. Forcing form and function: biomechanical regulation of tumor evolution. Trends Cell Biol. 2011;21:47–56. doi: 10.1016/j.tcb.2010.08.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Zhao B, Hemann MT, Lauffenburger DA. Modeling Tumor Clonal Evolution for Drug Combinations Design. Trends in cancer. 2016;2:144–158. doi: 10.1016/j.trecan.2016.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


