Characterizing permuted block randomization as a big stick procedure

Abstract

There are numerous approaches to randomizing patients to treatment groups in clinical trials. The most popular is permuted block randomization, and a newer and better class, which is gaining in popularity, is the so-called class of MTI procedures, which use a big stick to force the allocation sequence back towards balance when it reaches the MTI (maximally tolerated imbalance). Three prominent members of this class are the aptly named big stick procedure, Chen's procedure, and the maximal procedure. As we shall establish in this article, blocked randomization, though not typically cast as an MTI procedure, does in fact use the big stick as well. We shall argue that its weaknesses, which are well known, arise precisely from its improper use, bordering on outright abuse, of this big stick. Just as rocket powered golf clubs add power to a golf swing, so too does the big stick used by blocked randomization hit with too much power. In addition, the big stick is invoked when it need not be, thereby resulting in the excessive prediction for which permuted blocks are legendary. We bridge the gap between the MTI procedures and block randomization by identifying a new randomization procedure intermediate between the two, namely based on an excessively powerful big stick, but one that is used only when needed. We shall then argue that the MTI procedures are all superior to this intermediate procedure by virtue of using a restrained big stick, and that this intermediate procedure is superior to block randomization by virtue of restraint in when the big stick is invoked. The transitivity property then completes our argument.

1. Introduction

There are numerous approaches to randomizing patients to treatment groups in clinical trials, the most popular of these being permuted block randomization, which holds a near monopoly on how trials are randomized in practice [1], [2], [3], [4], [5]. For example, randomization.com, when used in this context, offers only what it calls “randomly permuted blocks” and no other alternatives [6]. Even so authoritative a document as the International Conference on Harmonization Guideline E9 (Statistical Principles for Clinical Trials, February 5, 1998) [7] recommends randomizing subjects in blocks. Given this popularity and near ubiquity of permuted block randomization, one might expect, on this basis alone, that the permuted blocks design is also, in some sense, optimal, since it is fair to ask why it would be used so often if this was not the case. Unfortunately, this is actually not the case, and for this reason many competitors have been proposed [2], [3], [8], [9], [10]. One newer and better class, which is gaining in popularity, is the so-called class of MTI procedures, which use a big stick to force the allocation sequence back towards balance when it reaches the MTI (maximally tolerated imbalance). Four prominent members of this class are the aptly named big stick procedure [11], Chen's procedure [12], the maximal procedure [13], [14], and the block urn design [3] which shares many desirable properties with the maximal procedure.

As we shall establish in this article, permuted block randomization, though not typically cast as an MTI procedure, does in fact use the big stick as well. We shall argue that its well-known inability to ensure comparable comparison groups arises precisely from its improper use, bordering on outright abuse, of this big stick. Just as rocket powered golf clubs add power to a golf swing, so too does the big stick used by permuted block randomization hit with too much power. In addition, the big stick is invoked when it need not (and should not) be, thereby resulting in the excessive prediction, selection bias (which can arise even in the absence of any malice or intention to bias the trial), and baseline imbalances for which permuted blocks are legendary [4], [5]. These are two distinct abuses of the big stick that lead to excess vulnerability to prediction.

Consideration of the two weaknesses together may tend to muddy the waters, so we try here to bring clarity by isolating each one, and considering it on its own merits. This allows us to bridge the gap between the MTI procedures and block randomization by identifying a new randomization procedure that serves as the missing link, intermediate between the two, namely based on an excessively powerful big stick (alluded to in Ref. [15]), but one that is used only when needed. We shall then argue that the MTI procedures are all superior to this intermediate procedure by virtue of using a restrained big stick, and that this intermediate procedure is superior to block randomization by virtue of restraint in when the big stick is invoked. The transitivity property then completes our argument.

2. Rocket powered big sticks

Let us suppose that we can agree on a boundary. A chess board has 64 squares, so a piece may not legally move any further than that. The dimensions of a soccer field are marked off in advance of the game, so that all parties can agree on where the line is drawn, so to speak. These are examples of reflective boundaries. If a bishop moves to the perimeter (outside) of the chess board, then the next time it moves, that move has to be away from that boundary, not over it. Likewise, barring a red card, when a soccer player dribbles the ball to the edge of the soccer field, his or her next move (with respect to that boundary; we consider movement up and down the line to be no movement at all with respect to that line, as in projecting a two-dimensional space onto one dimension) must be away from that edge, and not over it. This much is clear, and there is also a rather clear parallel with allocation sequences when viewed as random walks.

The question before us is how far away from the boundary (as defined by the MTI condition) must one be sent upon reaching it? The rules of chess, for example, could be modified so that any time a king, queen, rook, bishop, or knight reaches any edge of the board (with the possible exception of the starting position), it must travel from there directly towards one of the central four squares, much the same way that the reflecting barrier works in monopoly, with the “go to jail” property serving as the boundary and the jail itself serving as center. In monopoly, the piece does not simply move back one property; it gets sent all the way back.

Nor is monopoly the only such example; in black jack, get to 21 and keep going and you get sent all the way back to zero (busted, as some call it). In soccer, the rules could state that whenever the ball reaches the edge of the field, it must be taken from there to the center circle. That would, of course, dampen the excitement surrounding corner kicks. Chess, soccer, black jack, and monopoly are just examples. We cannot on that basis make a determination regarding what is and is not appropriate for randomization in clinical trials, as the situations are entirely different. The games are presented as parallels only to illustrate the distinction between forced returns to the center and forced returns towards the center. Strictly on its own merits, which one makes more sense in our context, randomization in clinical trials? The standard big stick, to knock the allocation sequence back towards balance by one unit, or the super charged big stick that blasts the sequence all the way back towards perfect balance each time it dares to reach the edge? We cannot answer this question in a vacuum. Rather, we must consider the purpose of the reflecting boundary. Why is it so important that the boundary not be crossed? And is there commensurate harm caused by mere proximity to the boundary? Or is it instead a threshold effect, kicking in only when the boundary is actually crossed?

The key idea here is chronological bias [16], which has been adequately described in the literature. Briefly, we do not wish to allow the numbers of patients allocated to each treatment group to differ by too much at any one point in time, because this, coupled with time trends in key indicators of disease severity, can result in a substantial baseline imbalance across treatment groups, or confounding. Operationally, we deal with this by specifying a maximum tolerated imbalance (MTI). This is the reflecting boundary.

For example, even though one does not generally speak of an MTI when permuted blocks are used, blocks of size four (with two treatment groups) will induce an MTI of two. In general, when permuted blocks are used with any fixed block size (and two treatment groups), the MTI is half that block size. When varied block sizes are used, the MTI is half the largest block size (with two treatment groups), or the largest block size divided by the number of treatment groups (assuming equal allocation). In full generality, although this rarely comes up, the MTI induced by the use of permuted blocks, with arbitrary number of treatment groups and arbitrary allocation ratios, is the product of the largest block size and the largest allocation ratio for any one treatment group. So, for example, with three treatment groups, and varied block sizes of five and ten, with allocations in the ratio of 2:2:1, the MTI is (10) (2/5) = 4, since this randomization plan exposes us to the risk of an initial sequence of four consecutive allocations to A.

It is objectively clear that large imbalances at any point in time can lead to problems, as already discussed. It is less clear where to draw the line, since this is not really a binary phenomenon. If we use an MTI of four, then is this to suggest that an imbalance of three (or even four itself) is not a problem? What if we keep hitting the MTI boundary again and again, so we reach this level of imbalance fairly often during the course of the patient allocation process? One could certainly argue that there is harm done not only by crossing the MTI threshold but also by pressing right up against it repeatedly, especially if these swings are always in the same direction.

That is to say that if the MTI is three, then AAABBBAAABBBAAABBB might be considered a problematic allocation sequence, even while not crossing the boundary and therefore not being disallowed, since the accession numbers associated with treatment group A are systematically smaller than those associated with treatment group B. In other words, there are systematically more early allocations to treatment A and fewer to treatment B, so therefore this allocation sequence might also be considered worse than AAABBBBBBAAAAAABBB, which hits the boundary equally often, but hits both sides of the MTI boundary, rather than hitting the same side repeatedly, so that imbalances go in both directions over the course of the trial, rather than always going in the same direction. There would be an equal number of overall imbalances, but these are at least spread more evenly across the two treatment groups.

But is this enough of a problem to merit the draconian measures used to curtail it? If these sequences (and others like them) could be avoided with no dire consequences, then we would be in favor of eliminating them. But there is a cost, and a rather steep one at that. Each forced allocation is a deterministic allocation, and these are predictable, and have the potential to lead to selection bias by eliminating the possibility of allocation concealment [10]. It is not possible to simultaneously eliminate both chronological bias and selection bias [9]. So which one represents the more serious threat to the integrity of the trial? It seems fairly clear that selection bias is the more serious issue, since it can be steered in a preferred direction by a zealous investigator. That is, it is a true bias. But chronological bias, despite its name (a misnomer, actually), is not a bias. It is equally likely to go either way, and it is hard to imagine any plausible scenario under which an investigator exploits it to create a bias intentionally, in a preferred direction.

At least it is hard to imagine such a scenario without also positing simultaneous selection bias, because the investigator would need to know in advance that there are more early allocations to A and more late ones to B (thereby violating allocation concealment) to then influence the future stream of patients enrolled so that healthier ones are enrolled early and sicker ones are enrolled late. This is not the usual paradigm by which selection bias works, as the usual way involves selecting sicker or healthier patients for a specific allocation known or suspected to be A or B, rather than following a general trend. If we can accept that chronological bias cannot be manipulated for gain without also being able to predict future allocations and, therefore, engaging in selection bias, then we would have to consider selection bias to be the more serious threat, and if that is the cost of controlling chronological bias, then the cure is worse than the disease.

3. The rocket big stick randomization procedure

We already noted, in Section 1, that the permuted blocks procedure can be obtained from an MTI procedure by modifying two aspects of how the big stick is used. In other words, the two procedures can be said to be twice removed from each other. This raises the obvious question of what a randomization procedure would look like if it were just once removed from either one. Of course, there are two such intermediate procedures, or at least there would seem to be, but in fact one implies the other. That is, the periodic forced returns to perfect balance that characterize permuted block randomization also imply that this must be the case when the MTI is reached. Therefore, we cannot have the second condition without the first, but we can consider the first without the second. That is, we can define new randomization procedures based on the rocket-powered big stick.

In particular, the rocket big stick procedure would use equal allocation to both treatment groups until the MTI is reached, at which point the next few allocations are all forced (deterministic) to completely restore the balance. Likewise, the rocket version of Chen's procedure would go with equal allocation when the group sizes are equal, the specified biasing probability p when the group sizes are not equal but the MTI has not been reached since the last return to perfect balance, and the rocket big stick once the MTI is reached. Before we consider the merits of these procedures, we first note that it would not make sense to define the rocket big stick as sending the pendulum all the way to the far side, rather than just to perfect balance. In other words, the rocket big stick we consider forces BBB after AAA (if the MTI is three), but does not force BBBBBB, as it could, because if it did (which may seem like the intuitive form of a rocket big stick), then that would have to be followed by AAAAAA, and we see that the entire remainder of the allocation sequence would be deterministic. This would be glorified alternation, and alternation is certainly frowned upon, since it is not even randomization [17].

If we accept the earlier arguments in favor of preferring the control of selection bias to the control of chronological bias, then we must conclude that the standard big stick procedure is superior to the rocket big stick procedure, and also that the standard version of Chen's procedure is superior to the rocket version. There simply is insufficient compensation to warrant the excessive prediction associated with the rocket versions of these procedures. Of course, we could also modify Chen's procedure so that two biasing probabilities are specified, p1 when ascending the imbalance mountain (towards imbalance; the last sojourn at perfect balance was more recent than the last sojourn at the MTI boundary) and p2 when coming down the imbalance mountain (towards balance; the last sojourn at the MTI boundary was more recent than the last sojourn at perfect balance). Presumably, p2 would be more extreme than p1. So, for example, on the way up the smaller group might have a 70% allocation probability and on the way down an 80% probability. This would tend to push the allocation in the direction opposite to the one that resulted in hitting the last MTI boundary.

It is also possible to modify Chen's procedure so that the biasing probabilities used are sensitive to the number of times each boundary has been reached so far. With an MTI of three, AAABBBAAABBB might, despite the equal group sizes, use a biasing probability to encourage (without forcing) an allocation to B, in recognition of the imbalance in the frequency of visits to the two boundaries. We might even base the biasing probabilities on some measure of the difference between the two CDFs, similar to the Smirnov test for ordered categorical data. But this is for future work. For now, we note that the rocket versions of the standard methods are not improvements.

4. Capricious use of the big stick

What is it that keeps the rocket version of Chen's procedure (with suitably chosen biasing probabilities) from coinciding exactly with the permuted blocks procedure? It turns out that, while both use the same rocket big stick, there is still one difference between the two. Namely, Chen's procedure, with either the standard big stick or the rocket big stick, invokes this big stick only when the MTI is reached. Permuted block randomization, in contrast, invokes it even when the MTI is not reached. If the MTI is two, and we start with ABA, then the MTI is not reached, and either form of Chen's procedure would allow for freedom. But the permuted blocks approach would invoke the big stick even here. And, what is worse, excessive force is used even here, as in, if an MTI of three is never reached, but the imbalance does get to two, then the stick hits all the way to zero.

It may be true that parole involves regular checking in with the parole officer, so there is precedent for these forced returns. Nevertheless, they are not an appealing feature of an allocation procedure, as they result in deterministic (predictable) allocations whose harm far outweigh any benefit in attaining perfect balance more often than would otherwise be the case. We could easily modify either the big stick procedure or Chen's procedure to include these forced returns home on a regular basis, but we do not do so because we recognize that this would represent a degradation of the method, and not an improvement. Parsimony is the key when it comes to forcing deterministic allocations.

5. Transitivity

In Section 3 we argued that the standard version of the big stick procedure is superior to the rocket version, and, likewise, the standard version of Chen's procedure is also superior to its rocket version. This seems rather clear. In Section 4 we argued that even the rocket version of Chen's procedure is superior to the permuted blocks procedure. We can summarize by noting that Chen's procedure is objectively superior to the rocket Chen procedure which in turn is objectively superior to the permuted blocks procedure when we consider vulnerability to prediction. Before we go on, we shall demonstrate this superiority, both with a tabular display (Table 1) and with a graphical display.

Table 1.

Visual comparison of the randomization techniques.

Randomization	Specifics of the big stick invoked
Procedure	Frequency	Power
MTI Procedures	Appropriate	Appropriate
Rocket Big Stick	Appropriate	Inappropriate
Permuted Blocks	Inappropriate	Inappropriate

Table 1 illustrates the above considerations, specifically that the rocket big stick invokes the big stick only when it should, which is to say only when the MTI boundary is reached. However, the stick it uses is too powerful, and on this basis it is inferior to the standard big stick procedure. Moreover, the permuted blocks procedure also uses too powerful a big stick, but in addition to this, it also invokes this overly powerful big stick at the wrong times, as in, when the MTI boundary has not even been reached. For example, if the MTI is three, then the sequence ABBB never reaches this MTI, since the sequence of imbalances is 1012, all remaining less than three. Nevertheless, the permuted blocks procedure would, at this point, invoke the big stick, and force the next allocation to be A, ABBBA, nor would it even be satisfied here, as it would also force the next allocation after that to also be A, ABBBAA, thereby demonstrating both the inappropriate use of the big stick and the overly powerful big stick.

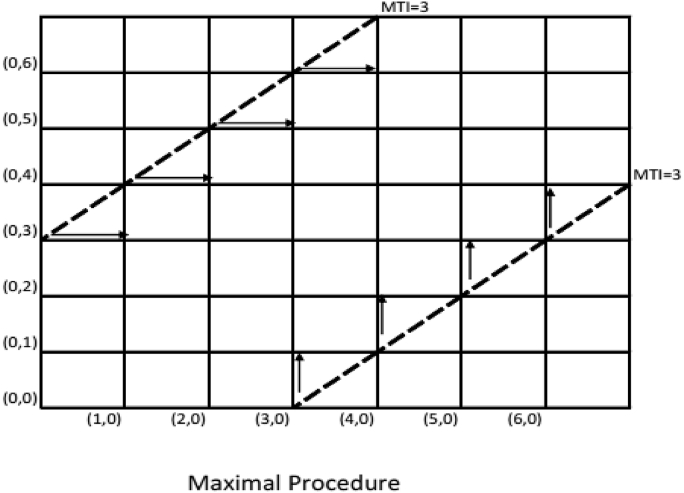
Table 1 may help some readers to understand the major differences among the three classes of randomization procedures, but graphical representations can also help to compare and contrast them. With this in mind, we present path maps of each randomization procedure. Fig. 1 shows the path map for the MTI procedures, including the maximal procedure. Note that the word “maximal” in the title refers to the set of admissible allocation sequences, and not to the set of restrictions, which, perhaps somewhat paradoxically, are not maximal but rather minimal. We see from Fig. 1 that only at the MTI are there any forced allocations. This is, of course, part and parcel of what it means to be an MTI randomization procedure, the very definition. Recall that fewer forced allocations translates into less prediction and more allocation concealment, which in turn translates into less selection bias and more comparable treatment groups.

Fig. 1.

Path Map For The Maximal Procedure. Arrows indicate forced allocations and dashed lines indicate MTI boundary.

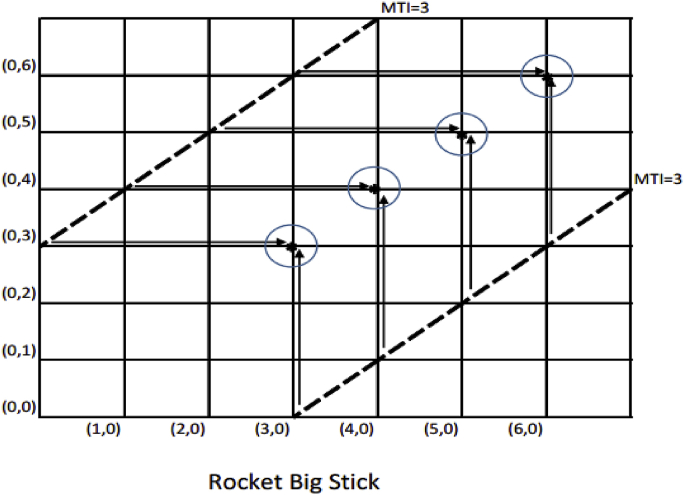
Fig. 2 is the path map for the rocket big stick procedure. We note a few differences between it and Fig. 1. Though it does remain the case that the big stick is invoked only at the MTI boundary (three, in this case), now the arrows are longer to indicate that once the big stick is invoked, it forces the sequence all the way back to the bull's eye at perfect balance (on the 45° angle line). Note that the rocket big stick randomization procedure is not Markovian; the transition probabilities depend on more than just the current location. If, e.g., the sequence is at (3,2), then the next allocation is forced to go to (3,3) only if we arrived at (3,2) by passing through (3,0). Otherwise, it is not deterministic. We have circled the home bases (so to speak) that serve as the destinations of the rocket big stick when it is invoked.

Fig. 2.

Path map for the rocket big stick procedure.

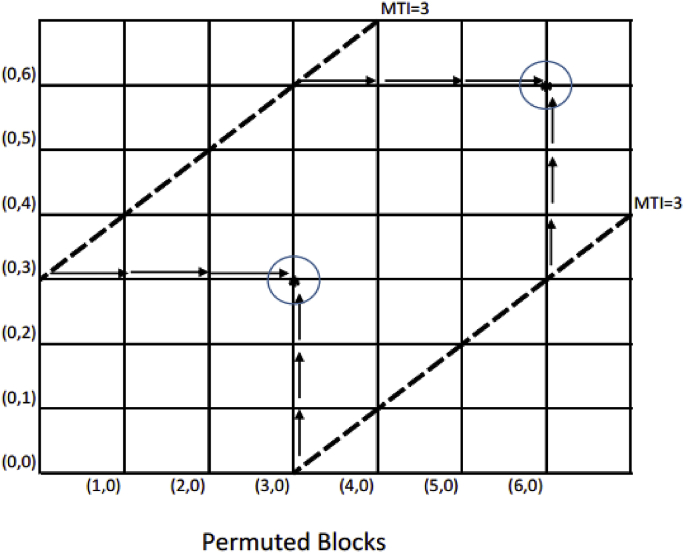
Fig. 3 displays the path map for the permuted blocks randomization procedure. Notice that there are now two home bases, instead of the four we saw with the rocket big stick procedure. This is because now it is no longer conditional; every sequence must pass through the point (3,3), whether or not it already hit the MTI boundary. Because of this, points such as (4,2), which are reachable when using either an MTI procedure or the rocket big stick procedure, are not reachable when using the permuted blocks procedure. The forced returns to perfect balance are not free; they come at a price, and a rather steep one at that. These forced returns to perfect balance are attained with deterministic allocations that are predictable, thereby violating true allocation concealment (even when allocation concealment is claimed), and expose the trial to the potential for selection bias.

Fig. 3.

Path map for permuted block randomization.

We now have a visual display to help understand why the MTI procedures are superior to their rocket big stick counterparts, which in turn are superior to permuted blocks randomization. There might be some small benefit in the control of chronological bias of the permuted blocks procedure to the rocket Chen procedure, but this needs to be established, as does any similar superiority along this dimension of the rocket versions to the standard versions. Even if this is the case, overall superiority still follows superiority with regard to prediction, since this is a larger effect, and since it is the more important bias to control. By transitivity, we conclude that the MTI procedures are objectively superior to the permuted blocks procedure, which should no longer be used in practice.

6. Summary and conclusions

Despite the analogies to games in discussing clinical trial allocation sequences, clinical trials themselves are not a game. They have consequences, in that their results go on to inform future medical decisions, and this remains true whether these results reflect reality or not. Therefore, it is clear that tangible harm results when trials produce results that do not reflect reality. Though one can never be sure that the trial results do reflect reality, one can at least do all that is possible to help that outcome along. Doing so necessarily means using the best research methods possible. There simply is no room in serious medical research for anything less than the best research methods. This obvious fact should have eliminated permuted block randomization from use a long time ago, but instead its use continues unabated. This highlights the fact that self-regulation does not work. Researchers cannot be granted carte blanche to essentially do whatever they want. We see clearly, and not only with regards to randomization methods, that far too many researchers will, when left to their own devices, use the research method with which they are most familiar [18]. Others will select the method that produces the most favorable outcome, or at least that can be expected to [19]. The actual rigor of the method plays no role whatsoever in these choices, for some researchers, as long as they can justify the choice. This is a problem even if we cannot say that this applies to most researchers. One is one too many, and there have been documented cases, but moreover, even in the absence of documented cases, it is still a problem if the system allows for such abuse. Loopholes need to be closed irrespective of how often they are exploited. Society needs demonstrably reliable trials, and this comes from systems that disallow abuses, rather than from having to rely on the good intentions of all researchers.

Unfortunately, real standards are almost never imposed externally, so it is not at all difficult to justify the use of even a fatally flawed method. The most common justification seems to be that the method in question is an industry standard, as in, everyone else is using it too. So precedent reigns supreme, and the standards that are imposed deal more with conformity than with actual methodological rigor. Everyone else uses permuted blocks randomization, so it must be OK. It is difficult to dislodge a precedent that is so entrenched. Just exposing it as fatally flawed ought to be enough, but in reality, much more is needed. We look forward to the day when the powers that be start to use that power to effect changes that will result in a system that simply does not allow for the use of such fatally flawed research methods. In the meantime, we hope to 1) point out the flaws in permuted block randomization; 2) provide the logical basis for using more appropriate randomization methods, as we do here; and 3) remove barriers, to the extent possible, that serve to keep permuted block randomization in use. To this end, we note that there is now a publicly available R program [20] that can be used to implement the three MTI randomization procedures discussed here, namely the big stick procedure, Chen's procedure, and the maximal procedure.