On clinical trials with a high placebo response rate

Abstract

The basic problem that causes the frequent failure of a standard randomized parallel placebo-controlled clinical trial with a high placebo response rate is the underestimation of the treatment effect by the observed relative treatment difference. A two-period sequential parallel enrichment design has been proposed where the first period is a standard parallel design and at the end of the first period, the placebo non-responders are identified and re-randomized in the second period. Based on such a design, available methods have primarily focused on testing either the first period treatment null hypothesis or the global null hypothesis defined as the joint period 1 and period 2 treatment effect null hypothesis by a test statistic which is either derived from a combined statistic or defined directly as a weighted z-score where the weights are functions of some population and design parameters satisfying certain power optimality criterion. However, in some cases, it is not clear what their combined statistics are estimating and in others, the combined statistics are estimating the apparent treatment effect; but generally, there is no discussion of the need to provide a proper assessment of the treatment effect for the intended study population. It should be clear that an appropriate assessment of the treatment effect for the intended study population is critical for the benefit/risk analysis as well as the proper dosage recommendation. Any benefit/risk analysis and dosage recommendation that are based on an apparent treatment effect from a standard parallel design such as the first period of a sequential parallel enrichment design tend to underestimate the benefit/risk ratio which in turn may lead to overdosing recommendation. It is the purpose of this paper to introduce the concept of an adjusted treatment effect which is derived by adjusting the apparent treatment effect from the first period of a sequential parallel enrichment design with information from the second period subject to a consistency condition. The adjustment properly compensates for the high placebo response rate. It is proposed that this adjusted treatment effect should be used to assess the treatment effect for the intended study population and should be the basis for the benefit/risk analysis and the dosage recommendation.

1. Introduction

The basic reason for the failure of many standard randomized parallel placebo-controlled clinical trials with high placebo response rate is that the observed relative treatment difference only provides an estimate of an apparent treatment effect since the treatment effect has been diminished by the presence of a substantial proportion of placebo responders in the population. The full treatment effect cannot be directly estimated by the relative treatment difference. An appropriate assessment of the full treatment effect is critical for making a risk/benefit analysis and dosage recommendation. The primary purpose of this paper is to propose a method for adjusting the apparent treatment effect to account for the high placebo response rate within the framework of a doubly randomized delayed start (DRDS) design as discussed in Liu et al. [1] which improves upon the earlier sequential parallel design (SPD) of Fava et al. [2].

2. Background

2.1. The sequential enrichment design

The problem of a high placebo response rate in clinical trials occurs in several therapeutic areas, but it is most often observed in trials involving subjects with psychiatric disorders. In these populations of subjects with psychiatric disorders, the placebo response rate has been estimated to vary from 30% to 50%. Trials in these therapeutic areas often failed because in a standard randomized parallel placebo-controlled trial, the observed relative treatment difference only provides an estimate of an apparent treatment effect which does not reflect the full treatment effect due to the dilution resulting from the presence of a substantial proportion of placebo responders. This problem has been known for quite some time. Temple [3] had suggested an enrichment design whereby subjects responding to placebo in a run-in period are excluded from a second period during which placebo non-responders are re-randomized to treatment and placebo in a parallel design. The purpose of Temple's enrichment design is merely to show that the treatment is effective in some subpopulation and in this case in the subpopulation of placebo non-responders. However, one problem with this enrichment design is that the claim of treatment effectiveness cannot be readily extended to the entire intended study population. Another problem with this design is that if the treatment is to be indicated for the enriched subpopulation, then in actual clinical practice, a patient has to be given placebo first to verify his/her placebo response status before the treatment can be prescribed; however, this would entail an ethical dilemma.

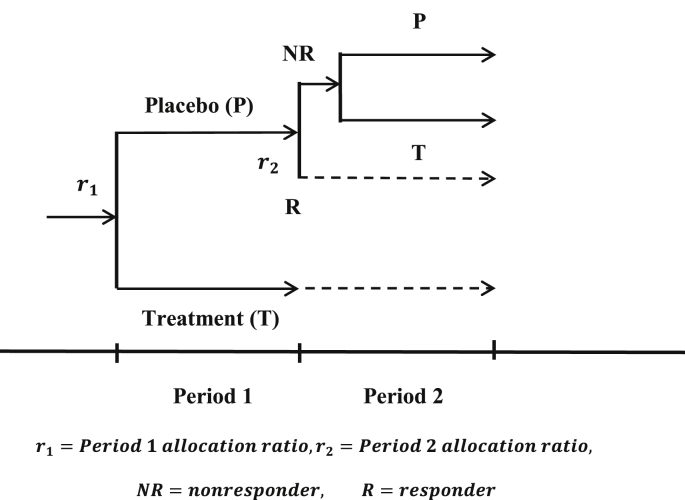
Fava et al. [2] proposed a SPD design where subjects are randomized to a treatment group and two placebo groups in the first period. At the end of the first period, the non-responders in one placebo group will be given treatment in the second period, while the non-responders in the other placebo group will continue with placebo in the second period. The subjects in the treatment group in the first period will continue on the treatment in the second Period. It should be noted that in the original proposed SPD design, the randomization in Period 2 refers to the original randomization conducted at the beginning of the first period. The lack of a re-randomization in the second period poses potential imbalance in key covariates between the two placebo non-responder groups at the end of the second period if there is a differential placebo dropout rate between the two placebo arms. Such imbalance may introduce bias and cause difficulty in the statistical inference. Liu et al. [1] proposed a doubly randomized delayed start (DRDS) design which was presented earlier at the 2010 BASS Conference. This DRDS design involves randomizing the subjects to treatment and placebo in the first period and then re-randomizing the placebo non-responders identified at the end of the first period based on some pre-specified response threshold to treatment and placebo in the second period. The terms “delayed start” were used for the obvious application of this design to trials involving progressive diseases. A simple diagram of such a design is depicted in Fig. 1.

Fig. 1.

A basic DRDS design for assessing treatment effect in trials with a high placebo response rate.

Chen et al. [4] considered a SPD design with re-randomization in the second period which they termed a SPD-ReR design. Now, the original SPD design has since also been revised to include re-randomization in the second period. In this paper, the DRDS design may refer to a SPD ReR design or a SPD design with re-randomization if found appropriate, and for convenience, some of the terminologies and notations used in Liu et al. [1] are adopted. The DRDS design has been accepted by the regulatory agencies as an innovative design. However, the regulatory agencies have raised issues with various proposed methods of analysis. In order to address these issues, a new statistical methodology is proposed here that includes the DRDS design and a statistical approach for this design that differs from the currently available methods.

2.2. Some key issues associated with the current methods for a DRDS design

There are a few important conceptual and technical issues related to the problem of a high placebo response rate in a DRDS design that have not been mentioned nor discussed by the previous authors. These basic issues need to be satisfactorily resolved before a DRDS design can be applied to phase 3 trials to obtain the evidence of effectiveness required. These issues will now be discussed and they will be addressed in the new approach to be proposed in Section 4.

2.2.1. Issue 1

The customary view considers the standard randomized parallel double blind placebo-controlled design as the design of choice because the relative treatment difference from such a design reflects the net treatment effect over and beyond what is expected of a placebo which should be minimal for this view to be valid. In a study population that has a substantial proportion of placebo responders, the relative treatment difference is only an apparent treatment difference, because it ignores the mitigating effect of the presence of a high placebo response rate on this treatment difference. This is the primary reason why many such trials have failed in the past. In a DRDS design, this same problem is present in the first period. Therefore, clearly the apparent treatment effect from the first period would be underestimating the full treatment effect. Another problem inherent in the above view is that even if perchance the apparent treatment effect shows the treatment is superior to placebo, any dosage recommendation based on an apparent dose–response relationship would likely lead to overdosing. Hence, for these two reasons alone, an appropriate assessment of the treatment effect adjusting for high placebo response rate is needed.

2.2.2. Issue 2

A problem that is born of the above view is present in the current proposed methods of analysis of a DRDS design. These methods variously proposed to estimate the apparent treatment effect of Period 1 by a combined statistic, which is defined as a weighted combination of the apparent treatment effect of Period 1 and the enriched treatment effect of Period 2 under some assumptions. For example, in Huang and Tamura [5], a score test is derived under the constancy assumption which requires that the enriched treatment effect of Period 2 be equal to the apparent treatment effect of Period 1, while for binary outcome, in Tamura and Huang [8], the combined statistic is derived under the monotonicity condition which assumes that each placebo responder is also a treatment responder. In each instance, the assumption may be invalid or unnecessarily stringent. Furthermore, the combined statistic is used to derive a combination test for testing either the apparent treatment null hypothesis of Period 1, or a global null hypothesis which is defined as the joint apparent treatment null of Period 1 and the enriched treatment null of Period 2. Even if these assumptions are appropriate, the rejection of these null hypotheses by these combination tests would not have solved the problem discussed under Issue 1 above.

2.2.3. Issue 3

A problem that arises as a result of the two issues discussed above is that the weights used in the combined statistics are functions not only of the population parameters, but also some DRDS design parameters, in particular the placebo to treatment allocation ratios in Period 1 and Period 2. One can place more weight on Period 2 treatment effect estimate in the combined statistic by simply increasing the allocation ratio in Period 1. Such bias is present even when the allocation ratio in Period 1 is equal to 2 as is the case in most of the DRDS designs used in these earlier papers. Such potential bias causes concern over these combined statistics and is interpreted as biasing the estimate of the apparent treatment effect of Period 1. Such misleading use of the Period 2 result and a misleading interpretation of the purpose of the second period of a DRDS design is unfortunate and should be corrected.

2.2.4. Issue 4

Assuming for the moment that a combined statistic with weights that are independent of the allocation ratios has been defined. Then, one needs to know what this combined statistic is estimating and how to interpret it. Is the combined statistic estimating a treatment effect for the intended study population? Does the treatment effect represent an appropriate assessment of the full treatment effect in the intended study population? Does the treatment effect adjust for the presence of placebo responders in the intended study population? Interpretability of the estimate of a combined statistic is crucial in its acceptability as an estimate of the full treatment effect for the intended study population. Such interpretation is lacking for the combined statistics in most of the current available methods, except for those cases where the combined statistics are meant to estimate the apparent treatment effect of Period 1 as discussed in Issue 2 above.

2.2.5. Issue 5

Assuming that a combined statistic is estimating the true treatment effect for the intended study population as discussed in Issue 4, one problem that may arise is that it is possible for the combined statistic to show a positive combined treatment effect, yet the estimate of the apparent treatment effect from Period 1 may be negative. This kind of inconsistency is not a desirable outcome, since it suggests that the treatment effect may be substantially worse than placebo among the placebo responders. This issue is also not addressed relative to the combined statistics in the current available methods in addition to their problems as discussed above although it is related to the monotonicity condition introduced in Tamura et al. [8].

2.2.6. Issue 6

In all of the currently available methods, Period 2 of a DRDS design is simply viewed as a trial independent of Period 1. However, realistically, the probability structure underlying Period 2 in a DRDS design is conditional in nature. The sample cohorts in Period 2 represent placebo non-responders in Period 1 who are re-randomized in Period 2 into treatment and placebo groups. Therefore, the distributions of the response variables for these cohorts in Period 1 and Period 2 are singly truncated bivariate normal distributions where the Period 1 placebo responses of these cohorts have been truncated at some pre-specified threshold. Hence, the distributions of these cohorts in Period 2 are conditional distributions with the condition specified by the truncation of their placebo response in Period 1 at some threshold. Thus, the treatment effect at the end of Period 2 will be conditional in nature which has some interesting and useful properties that are not available or apparent under the unconditional probability structure.

To address the above issues, a new approach is proposed in this paper. The probability structure underlying a DRDS design is first developed in Section 3. Then, in Section 4, the key concept of an adjusted treatment effect will be defined as a specific weighted treatment effects from Period 1 and Period 2 where the weights are independent of the allocation ratios and any design parameters. This adjusted treatment effect can be interpreted as an adjustment of the apparent treatment effect from Period 1 by appropriately accounting for the presence of placebo responders in the intended study population. Period 2 of a DRDS design provides the information needed to make this adjustment possible. Therefore, this adjusted treatment effect provides an appropriate assessment of the full treatment effect for the intended study population. Then, in Section 5, a new combined statistic can be derived directly from the definition of the adjusted treatment effect so that it will provide an unbiased estimate of the adjusted treatment effect. The combination test derived from this combined statistic will then be used to test the adjusted treatment null hypothesis. In addition to this combination test, a new consistency measure is introduced in Section 6, which can be viewed as a natural generalization of the monotonicity condition for a continuous outcome. A consistency null hypothesis is defined from this consistency measure and a consistency test is derived to test the consistency of the treatment effects from the two periods which is now a condition needed for excluding the situation where the adjusted treatment effect is positive while the apparent treatment effect of Period 1 is negative. Finally, in Section 7, a joint test, which is defined as the simultaneous testing of both the adjusted treatment null by the combination test and the consistency null by the consistency test, is proposed for demonstrating that a treatment is effective for the intended study population. It is shown that this joint test controls the type I error strongly under most of the scenarios encountered in practice. In addition, it is shown that if a particular application scenario appears to fall in certain range that suggests potential inflation in type I error may be expected, then one can control the expected inflation of this type I error by increasing the allocation ratio r₁ to a level >2. It should be noted that since the weights used to define the combined statistic is independent of the allocation ratios, a DRDS design is free to choose any allocation ratios in Period 1 and Period 2 as long as they satisfy certain inequalities that are usually met in any practical application. Once the joint null has been rejected, then the estimated adjusted treatment effect derived from the combined statistic should represent an appropriate assessment of the full treatment effect for the intended study population. In Section 8, a simulated DRDS designed trial is presented for illustration. A summary discussion concludes the paper in Section 9.

3. The DRDS design and its underlying probability structure

Before introducing the adjusted treatment effect, it is important to first discuss the probability structure underlying a DRDS design. The previous authors have essentially adopted the view that the two periods in a DRDS design may be considered as two independent trials. In this section, a trial using the basic DRDS design is described and the probability structure behind this design is discussed which forms the basis for the proposed methodology. It will become clear that this underlying probability structure is crucial in establishing the needed properties for the proposed test statistics. In addition, it will be relevant at the study design stage.

Consider a trial with a DRDS design as shown in Fig. 1. Let Ω = Ω₁ denote the intended study population, and assume that there is a subpopulation of placebo responders Ω_R even though this subpopulation can't be characterized prior to the start of the trial. Let Ω_NR denote the placebo non-responder subpopulation. Let T denote an experimental treatment and P the placebo. In Period 1, n₁ subjects are randomly assigned to T and P in a placebo-to-treatment allocation ratio of r₁ ≥ 1 with n_1,T subjects assigned to treatment T and n_1,P = r₁n_1,T subjects assigned to placebo P, where n₁ = n_1,P + n_1,T. Let X₁ denote a continuous clinical response variable of interest, X_1,T and X_1,P the response variables under the treatment T and the placebo P respectively. Let $X_{1,P}\sim N({\mu }_{1,P},{\sigma }_{1,P}^2)$ and $X_{1,T}\sim N({\mu }_{1,T},{\sigma }_{1,T}^2)$ be normally distributed with the mean and variance (μ_1,P, ${\sigma }_{1,P}^2)$ and (μ_1,T, ${\sigma }_{1,T}^2)$ respectively. For simplicity and without much loss in generality, it will be assumed that${\sigma }_{1,P}^2={\sigma }_{1,T}^2={\sigma }_1^2$. Let Δ₁ = μ_1,T − μ_1,P denote the relative treatment difference in Period 1.

Let {x_1,P,i, i = 1,2,. . . , n_1,P} and {x_1,T,j, j = 1,2,. . . , n_1,T} denote the observed sample responses from the placebo and treatment groups respectively. Then, ${\widehat{\text{Δ}}}_1=\left({\hat{\mu }}_{1,T}-{\hat{\mu }}_{1,P}\right)\sim N\left({\Delta }_1,{\sigma }_1^2/n_{1,T}{R}_1\right)$, where${\hat{\mu }}_{1,P}=1/n_{1,P}\sum _{i=1}^{n_{1,P}}{x}_{1,P,i}$, ${\hat{\mu }}_{1,T}=1/n_{1,T}\sum _{j=1}^{n_{1,T}}{x}_{1,T,j}$, and $R_1=r_1/(1+r_1)=n_{1,P}/(n_{1,P}+n_{1,T})$ is the fraction of placebo subjects among the entire sample of n₁ subjects.

When the variances ${\sigma }_1^{2}and{\sigma }_2^2$ for ${\widehat{\text{Δ}}}_1$ and ${\widehat{\text{Δ}}}_2$ from Period 1 and Period 2 are considered unknown as is usually the case, then one may estimate these unknown variances by their respective pooled sample variances given by ${\hat{\sigma }}_1^2=\left((n_{1,T}-1){\hat{S}}_{1,T}^2+(n_{1,P}-1){\hat{S}}_{1,P}^2\right)/\left(n_{1,T}+n_{1,P}-2\right)$ and ${\hat{\sigma }}_2^2=\left(\left(n_{2,T}-1\right){\hat{S}}_{2,T}^2+\left(n_{2,P}-1\right){\hat{S}}_{2,P}^2\right)/\left(n_{2,T}+n_{2,P}-2\right)$ where

$${\hat{S}}_{1,T}^2=\frac{1}{\left(n_{1,T}-1\right)}\sum _{i=1}^{n_{1,T}}{\left(X_{1,T,i}-{\overline{X}}_{1,T}\right)}^2,{\hat{S}}_{1,P}^2=\frac{1}{\left(n_{1,P}-1\right)}\sum _{i=1}^{n_{1,P}}{\left(X_{1,P,i}-{\overline{X}}_{1,P}\right)}^2$$

$${\hat{S}}_{2,T}^2=\frac{1}{\left(n_{2,T}-1\right)}\sum _{i=1}^{n_{2,T}}{\left(X_{2,T,i}-{\overline{X}}_{2,T}\right)}^2,{\hat{S}}_{2,P}^2=\frac{1}{\left(n_{2,P}-1\right)}\sum _{i=1}^{n_{2,P}}{\left(X_{2,P,i}-{\overline{X}}_{2,P}\right)}^2$$

At the end of Period 1, a pre-specified criterion will be applied to determine the response status of each placebo subject who completed the trial. This criterion may be translated into a threshold c in the range of the response variable X₁. At the end of Period 1, placebo subjects who are identified as responders, that is, if X_1,P > c, and along with the placebo dropouts will be excluded from the second period of the study. Those placebo subjects classified as non-responders, that is, X_1,P < c, will be re-randomized to treatment and placebo at the start of Period 2 in a placebo-to-treatment allocation ratio of r₂ ≥ 1. For practical consideration, r₂ is set to the value 1 in the present paper as is the case in most applications for obvious reason. It will also be assumed that the proportion of placebo non-responders among the placebo dropouts in Period 1 is similar to their population proportion. For simplicity, it is assumed here that there were no placebo dropouts. Let $\tau =(c-{\mu }_{1,P})/{\sigma }_{1,P}$ be the placebo response threshold standardized relative to the placebo response distribution in Period 1. Let n₂ equal the number of placebo non-responders who completed Period 1 of the study and $\gamma =\text{Φ}\left(\tau \right)=\text{Φ}\left((c-{\mu }_{1,P})/{\sigma }_{1,P}\right)$ denote the population proportion of placebo non-responders in Ω = Ω₁. Then, the ratio$\hat{\gamma }=n_2/n_{1,P}$ should be a consistent estimate of the parameter Φ(τ) in the absence of placebo dropouts, or under the above assumption if placebo dropouts are present.

At the start of Period 2, the n₂ placebo non-responders from Period 1 will be re-randomized to treatment and placebo under equal allocation r₂ = 1. Then, it follows that $n_{2,T}=n_{2,P}=n_2/(1+r_2)=\gamma n_{1,P}/(1+r_2)=\gamma n_{1,T}{r}_1/(1+r_2)=n_{1,T}\gamma R_{\mathrm{1,2}}$, where$R_{\mathrm{1,2}}=r_1/(1+r_2)$.

Now without loss in generality and for obvious reason, consider relabeling the entire placebo sample in Period 1 as follows:

$$\left\{X_{1,P,i},i=\mathrm{1,2},...,n_{2,T},n_{2,T}+1,n_{2,T}+2,...,n_2,n_2+1,n_2+2,...,n_{1,P}\right\}$$

where the first n_2,T placebo subjects {X_1,P,i, i = 1,2,. . . , n_2,T} are placebo non-responders that have been re-randomized in Period 2 to treatment, and the next set of n_2,P placebo subjects {X_1,P,i, i = n_2,T + 1, n_2,T + 2,. . . ,n₂,} are placebo non-responders that have been re-randomized in Period 2 to placebo, while the remainder of the placebo sample {X_1,P,i, i = n₂ + 1,n₂ + 2, . . . , n_1,P} are the placebo subjects who were placebo responders (or placebo dropouts if any, although it is assumed none here) in Period 1. Note that under equal allocation in Period 2, $n_{2,P}=n_{2,T}=(n_{2,P}+n_{2,T})/2=n_2/2=\gamma n_{1,P}/2$.

Assuming that the randomization in Period 1 holds, the placebo sample should be representative of the population Ω = Ω₁. If the entire placebo sample at the end of Period 1 were re-randomized in Period 2 to treatment, then the pair of response variables (X_1,P,X_2,T) should follow a bivariate normal distribution $\left(X_{1,P},X_{2,T}\right)\sim N({\mu }_{12,T},{\text{Σ}}_{12,T})$, where ${\mu }_{12,T}=\left(\begin{array}{c}{\mu }_{1,P}\\ {\mu }_{2,T}\end{array}\right)$ and ${\text{Σ}}_{12,T}=\left(\begin{array}{cc}{\sigma }_{1,P}^2& {\rho }_T{\sigma }_{1,P}{\sigma }_{2,T}\\ {\rho }_T{\sigma }_{1,P}{\sigma }_{2,T}& {\sigma }_{2,T}^2\end{array}\right)$ upon assuming that ${\sigma }_{1,P}^2={\sigma }_{1,T}^2={\sigma }_1^2$, ${\sigma }_{2,P}^2={\sigma }_{2,T}^2={\sigma }_2^2$, and ρ_T is the correlation corr(X_1,P, X_2,T), where X_2,T is the response variable in Period 2 under the treatment T. Similarly, if the entire placebo sample at the end of Period 1 were re-randomized in Period 2 to placebo, then the pair of response variables (X_1,P, X_2,P) should follow a bivariate normal distribution $\left(X_{1,P},X_{2,P}\right)\sim N({\mu }_{12,P},{\text{Σ}}_{12,P})$, where ${\mu }_{12,P}=\left(\begin{array}{c}{\mu }_{1,P}\\ {\mu }_{2,P}\end{array}\right)$ and${\text{Σ}}_{12,P}=\left(\begin{array}{cc}{\sigma }_{1,P}^2& {\rho }_P{\sigma }_{1,P}{\sigma }_{2,P}\\ {\rho }_P{\sigma }_{1,P}{\sigma }_{2,P}& {\sigma }_{2,P}^2\end{array}\right)$ upon assuming that ${\sigma }_{1,P}^2={\sigma }_{1,T}^2={\sigma }_1^2$, ${\sigma }_{2,P}^2={\sigma }_{2,T}^2={\sigma }_2^2$, and ρ_P is the correlation corr(X_1,P, X_2,P), where X_2,P is the response variable in Period 2 under the placebo P. Indeed, in this case, one may even assume that${\sigma }_{1,P}^2={\sigma }_{2,P}^2,{\sigma }_{1,T}^2={\sigma }_{2,T}^2$ and hence${\sigma }_1^2={\sigma }_2^2$. It should be pointed out that if the treatment is not effective, then it is likely that ρ_P=ρ_T, i.e., ρ_P − ρ_T = 0. Otherwise, if the treatment is more effective than placebo, then one should expect that ρ_P≥ρ_T, i.e., ρ_P−ρ_T ≥ 0.

3.1. Truncated distributions of the two placebo non-responder cohorts in period 2

However, in a DRDS design, since only the placebo non-responders at the end of Period 1 are re-randomized to placebo and treatment in Period 2. Therefore, for the cohort of placebo non-responders who were re-randomized to treatment in Period 2 denoted by (P → T), the sample pairs {(X_1,P,i, X_2,T,i), i = 1, 2, . . ., n_2,T} would follow a singly truncated bivariate normal distribution

$$\left(\left(X_{1,P}|X_{1,P}<c\right),\left(X_{2,T}|X_{1,P}<c\right)\right)\sim N\left({\mathit{\mu }}_{12,\mathit{T}|{\mathit{X}}_{1,\mathit{P}}<\mathit{c}},{\mathbf{\Sigma }}_{12,\mathit{T}|{\mathit{X}}_{1,\mathit{P}}<\mathit{c}}\right)$$

where

$${\mathit{\mu }}_{12,\mathit{T}|{\mathit{X}}_{1,\mathit{P}}<\mathit{c}}=\left(\begin{array}{c}{\mu }_{1,P|{\mathit{X}}_{1,\mathit{P}}<\mathit{c}}\\ {\mu }_{2,T|{\mathit{X}}_{1,\mathit{P}}<\mathit{c}}\end{array}\right)=\left(\begin{array}{c}{\mu }_{1,P}-{\sigma }_{1,P}\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)\\ {\mu }_{2,T}-{\rho }_T{\sigma }_{2,T}\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)\end{array}\right)$$

$$\begin{array}{l}{\mathbf{\Sigma }}_{\left(12,\mathit{T}|{\mathit{X}}_{1,\mathit{P}}<\mathit{c}\right)}=\left(\begin{array}{cc}var\left(X_{1,P}\right|X_{1,P}<c)& cov(X_{1,P},X_{2,T}|X_{1,P}<c)\\ cov(X_{1,P},X_{2,T}|X_{1,P}<c)& var\left(X_{2,T}\right|X_{1,P}<c)\end{array}\right)\\ =\left(\begin{array}{ll}{\sigma }_{\left(1,P|X_{1,P}<c\right)}^2& {\rho }_{\left(T|X_{1,P}<c\right)}{\sigma }_{\left(1,P|X_{1,P}<c\right)}{\sigma }_{\left(2,T|X_{1,P}<c\right)}\\ {\rho }_{\left(T|X_{1,P}<c\right)}{\sigma }_{\left(1,P|X_{1,P}<c\right)}{\sigma }_{\left(2,T|X_{1,P}<c\right)}& {\sigma }_{\left(2,T|X_{1,P}<c\right)}^2\end{array}\right)\end{array}$$

where the elements of the variance-covariance matrix are given by

$${\sigma }_{1,P|X_{1,P}<c}^2=var\left(X_{1,P}\text{|}{X}_{1,P}<c\right)=\left[1-\tau \frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}-{\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)}^2\right]{\sigma }_{1,P}^2$$

$${\sigma }_{2,T|X_{1,P}<c}^2=var\left(X_{2,T}\right|X_{1,P}<c)=\left({\rho }_T^2\left[1-\tau \frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}-{\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)}^2\right]{\sigma }_{1,P}^2+(1-{\rho }_T^2)\right){\sigma }_{2,T}^2$$

$${\sigma }_{2,P|X_{1,P}<c}^2=var\left(X_{2,P}\right|X_{1,P}<c)=\left({\rho }_P^2\left[1-\tau \frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}-{\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)}^2\right]{\sigma }_{1,P}^2+(1-{\rho }_P^2)\right){\sigma }_{2,P}^2$$

$$cov\left(X_{1,P},X_{2,T}\text{|}{X}_{1,P}<c\right)={\rho }_T\left[1-\tau \frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}-{\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)}^2\right]{\sigma }_{1,P}{\sigma }_{2,T}$$

and ${\rho }_{T|X_{1,P}<c}$ is the correlation for the truncated (P → T) cohort given by

$${\rho }_{T|{\mathit{X}}_{\mathbf{1,}\mathit{P}}<\mathit{c}}=\frac{cov\left(X_{1,P},X_{2,T}\text{|}{X}_{1,P}<c\right)}{\sqrt{var\left(X_{1,P}\text{|}{X}_{1,P}<c\right)}\sqrt{var\left(X_{2,T}\text{|}{X}_{1,P}<c\right)}}=\frac{{\rho }_T}{\sqrt{\left({\rho }_T^2{\sigma }_{1,P}^2+\frac{(1-{\rho }_T^2)}{\left[1-\tau \frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}-{\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)}^2\right]}\right)}}$$

Now in practice, the variances var(X_1,P|X_1,P<c), var(X_2,T|X_1,P<c) and the cov(X_1,P, X_2,T|X_1,P<c) may be estimated by their respective sample variances and the sample covariance given by

$$\begin{array}{l}{S}_{X_{1,P|X_{1,P}<c}}^2=\frac{1}{n_{2,T}-1}\sum _{i=1}^{n_{2,T}}{\left(X_{1,P,i}-{\hat{X}}_{\left(1,P|X_{1,P}<c\right)}\right)}^2\\ S_{X_{2,T|X_{1,P}<c}}^2=\frac{1}{n_{2,T}-1}\sum _{i=1}^{n_{2,T}}{\left(X_{2,T,i}-{\hat{X}}_{\left(2,T|X_{1,P}<c\right)}\right)}^2\text{and}\\ S_{(X_{1,P},X_{2,T}|X_{1,P}<c)}=\frac{1}{n_{2,T}-1}\sum _{i=1}^{n_{2,T}}{X}_{1,P,i}^{\ast }{X}_{2,T,i}^{\ast },\text{where}\\ X_{1,P,i}^{\ast }=X_{1,P,i}-{\hat{X}}_{\left(1,P|X_{1,P}<c\right)},X_{2,T,i}^{\ast }=X_{2,T,i}-{\hat{X}}_{\left(2,T|X_{1,P}<c\right)}\text{and}\\ {\hat{X}}_{1,P|X_{1,P}<c}=\frac{1}{n_{2,T}}\sum _{i=1}^{n_{2,T}}\left(X_{1,P,i}|X_{1,P}<c\right)\text{and}\\ {\hat{X}}_{2,T|X_{1,P}<c}=\frac{1}{n_{2,T}}\sum _{i=1}^{n_{2,T}}\left(X_{2,T,i}|X_{1,P}<c\right)\text{.}\end{array}$$

The sample correlation is given by${\hat{\rho }}_{T|X_{1,P}<c}=S_{(X_{1,P},X_{2,T}|X_{1,P}<c)}/\sqrt{S_{X_{1,P|X_{1,P}<c}}^2}\sqrt{S_{X_{2,T|X_{1,P}<c}}^2}$.

Similarly, for the cohort of placebo non-responders who are re-randomized to placebo, denoted by, (P → P) in Period 2, the sample pairs $\left\{\left(X_{1,P,n_{2,T}+i},X_{2,P,i}\right),i=1,2,...,n_{2,P}\right\}$ also follows a singly truncated bivariate normal distribution with

$$\left(\left(X_{1,P}|X_{1,P}<c\right),\left(X_{2,P}|X_{1,P}<c\right)\right)\sim N\left({\mathit{\mu }}_{12,\mathit{P}|{\mathit{X}}_{1,\mathit{P}}<\mathit{c}},{\mathbf{\Sigma }}_{12,\mathit{P}|{\mathit{X}}_{1,\mathit{P}}<\mathit{c}}\right)$$

where

$${\mathit{\mu }}_{12,\mathit{P}|{\mathit{X}}_{1,\mathit{P}}<\mathit{c}}=\left(\begin{array}{c}{\mu }_{1,P|X_{1,P}<c}\\ {\mu }_{2,P|X_{1,P}<c}\end{array}\right)=\left(\begin{array}{c}{\mu }_{1,P}-{\sigma }_{1,P}\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)\\ {\mu }_{2,P}-{\rho }_P{\sigma }_{2,P}\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)\end{array}\right)$$

$${\mathbf{\Sigma }}_{12,\mathit{P}|{\mathit{X}}_{1,\mathit{P}}<\mathit{c}}=\left(\begin{array}{cc}var\left(X_{1,P}\right|X_{1,P}<c)& cov(X_{1,P},X_{2,P}|X_{1,P}<c)\\ cov(X_{1,P},X_{2,P}|X_{1,P}<c)& var\left(X_{2,P}\right|X_{1,P}<c)\end{array}\right)$$

the expressions for the elements of the above variance-covariance matrix ${\mathbf{\Sigma }}_{12,\mathit{P}|{\mathit{X}}_{1,\mathit{P}}<\mathit{c}}$ are similar to the previous expressions derived for the (P → T) cohort and will not be repeated here.

Now, with the underlying conditional probability structure for a DRDS design as described above, the Period 2 expected treatment effect is now given by the conditional (truncated) mean difference

$$\begin{array}{c}\left({\Delta }_2|X_{1,P}<c\right)={\mu }_{2,T|X_{1,P}<c}-{\mu }_{2,P|X_{1,P}<c}=\left[{\mu }_{2,T}-{\rho }_T{\sigma }_{2,T}\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)\right]-\left[{\mu }_{2,P}-{\rho }_P{\sigma }_{2,P}\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)\right]\\ =\left({\mu }_{2,T}-{\mu }_{2,P}\right)+\left({\rho }_P{\sigma }_{2,P}-{\rho }_T{\sigma }_{2,T}\right)\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)\end{array}$$ (1)

which may be estimated by the observed mean difference given by

$$\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)={\hat{\mu }}_{2,T|X_{1,P}<c}-{\hat{\mu }}_{2,P|X_{1,P}<c}$$

where

$${\hat{\mu }}_{2,T|X_{1,P}<c}={\hat{X}}_{2,T|X_{1,P}<c}=\frac{1}{n_{2,T}}\sum _{i=1}^{n_{2,T}=n_{2,P}}\left(X_{2,T,i}\right|X_{1,P}<c)$$

and

$${\hat{\mu }}_{2,P|X_{1,P}<c}={\hat{X}}_{2,P|X_{1,P}<c}=\frac{1}{n_{2,P}}\sum _{i=1}^{n_{2,P}=n_{2,T}}\left(X_{2,P,i}\right|X_{1,P}<c)$$

Thus,

$$\begin{array}{c}E\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)=E\left({\hat{\mu }}_{2,T|X_{1,P}<c}-{\hat{\mu }}_{2,P|X_{1,P}<c}\right)=\left({\Delta }_2|X_{1,P}<c\right)\\ =\left({\mu }_{2,T}-{\mu }_{2,P}\right)+({\rho }_P{\sigma }_{2,P}-{\rho }_T{\sigma }_{2,T})\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\end{array}$$

Note that in the above expression for$E\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)$ or Eq. (1), if the duration of Period 1 is relatively short, then the first term (μ_2,T − μ_2,P) = (μ_1,T − μ_1,P) which is the apparent treatment effect from Period 1, and hence the increase in the expected treatment effect in Period 2 would come from the second term $({\rho }_P{\sigma }_{2,P}-{\rho }_T{\sigma }_{2,T})\phi \left(\tau \right)/\text{Φ}\left(\tau \right)$ which is 0 when there is no treatment effect and should be positive when the treatment is effective, since in that case, one expects that (ρ_Pσ_2,P − ρ_Tσ_2,T) > 0. Eq. (1) will be important as will be seen later.

Some of the above expressions are well-known (see e.g., Johnson and Kotz [9], Gajjar and Subrahmaniam [10], Rosenbaum [11], Shah and Parikh [12] and Tallis [13]) and others can be derived from them.

3.2. The joint distribution of $\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|{\mathit{X}}_{1,\mathit{P}}<\mathit{c}\right)\right)$

Now with the above derivation of the expressions for the various distribution parameters for the conditional distributions as a function of the distribution parameters of their underlying unconditional distributions for the two cohorts (P → T) and (P → P) in Period 2, one can establish the following lemma within the framework of a DRDS design.

Lemma

For a DRDS design, the treatment effect estimates ${\widehat{\text{Δ}}}_1$ and $\left({\widehat{\text{Δ}}}_2\right|X_{1,P<c})$ from Period 1 and Period 2 follow an asymptotically normal bivariate distribution$\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)\sim \mathbf{\Phi }({\mathit{\mu }}_{12},{\mathbf{\Sigma }}_{12})$, where the means are given by

$${\mathit{\mu }}_{12}=\left(\begin{array}{c}{\Delta }_1\\ \left({\Delta }_2\right|X_{1,P}<c)\end{array}\right)=\left(\begin{array}{c}{\mu }_{1,T}-{\mu }_{1,P}\\ {\mu }_{2,T|X_{1,P}<c}-{\mu }_{2,P|X_{1,P}<c}\end{array}\right)=\left(\begin{array}{c}{\mu }_{1,T}-{\mu }_{1,P}\\ \left({\mu }_{2,T}-{\mu }_{2,P}\right)+({\rho }_P{\sigma }_{2,P}-{\rho }_T{\sigma }_{2,T})\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\end{array}\right)$$

and the variance-covariance matrix is given by

$${\mathbf{\Sigma }}_{12}=\left(\begin{array}{cc}var\left({\hat{\Delta }}_1\right)& cov\left({\hat{\Delta }}_1,\left({\hat{\Delta }}_2|X_{1,P}<c\right)\right)\\ cov\left({\hat{\Delta }}_1,\left({\hat{\Delta }}_2|X_{1,P}<c\right)\right)& var\left({\hat{\Delta }}_2|X_{1,P}<c\right)\end{array}\right)$$

where

$$var\left({\widehat{\text{Δ}}}_1\right)=\frac{{\sigma }_1^2}{n_{1,T}{R}_1},assumingthat{\sigma }_{1,T}^2={\sigma }_{1,P}^2={\sigma }_1^2$$ (2)

$$var\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)=var\left({\hat{\mu }}_{2,T|X_{1,P}<c}-{\hat{\mu }}_{2,P|X_{1,P}<c}\right)=\frac{1}{n_{2,T}}\left(var\left(X_{2,T}\right|X_{1,P}<c)+var\left(X_{2,P}\right|X_{1,P}<c)\right)$$ (3)

where

$$var\left(X_{2,T}|X_{1,P}<c\right)=\left({\rho }_T^2\left[1-\tau \frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}-{\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)}^2\right]{\sigma }_{1,P}^2+(1-{\rho }_T^2)\right){\sigma }_{2,T}^2$$ (4)

$$var\left(X_{2,P}|X_{1,P}<c\right)=\left({\rho }_P^2\left[1-\tau \frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}-{\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)}^2\right]{\sigma }_{1,P}^2+(1-{\rho }_P^2)\right){\sigma }_{2,P}^2$$ (5)

and

$$cov({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2\right|X_{1,P}<c))=cov(({\hat{\mu }}_{1,T}-{\hat{\mu }}_{1,P}),({\hat{\mu }}_{2,T|X_{1,P}<c}-{\hat{\mu }}_{2,P|X_{1,P}<c}))=\frac{1}{n_{1P}}\left(cov(X_{1,P},X_{2,P}|X_{1,P}<c)-cov(X_{1,P},X_{2,T}|X_{1,P}<c)\right)\to 0$$ (6)

asymptotically where the covariance terms cov(X_1,P,X_2,P|X_1,P<c) and cov(X_1,P, X_2,T| X_1,P<c) are as given previously.

The proof of this lemma will be omitted since these expressions can be directly derived from the preceding conditional distribution parameters for the two cohorts (P → P) and (P → T).

Note that for the conditional (truncated) variances and covariance, one can use their sample variance and covariance as estimates.

3.3. An example of a DRDS design

Table 1 displays a summary of the data from a very small completed phase II study based on a DRDS design as described in Fig. 1. Using the conditional probability structure described above, the data from Period 1 of this study will be used later as the basis for illustrating the proposed method with a simulated trial using a DRDS design. In addition, selected power and sample size calculations for the combination and consistency tests will also be based on the data from this table.

Table 1.

Hypothetical Distributions of a HDRS₁₇ Subscale Score based on an Early Phase 2 Major Depressive Disorder Trial using a DRDS Design with Parameter Values: r₁ = 2, π = 0.60, γ = 0.40, r₂ = 1.

Period 1
μ1T	σ1T	μ1P	σ1P	Δ1	σ1
3.30	2.44	3.00	2.40	0.30	2.42
Period 2
μ2T	σ2T	μ2P	σ2P	Δ2	σ2
3.90	1.95	2.80	2.00	1.10	1.98

4. The adjusted treatment effect

4.1. The reason for adjusting the apparent treatment effect Δ₁

In a trial with high placebo response rate, the first problem encountered is the inability to characterize the subpopulation of placebo responders Ω_R. Therefore, if a traditional randomized parallel design is used, such as the first period of a DRDS design, then the high placebo response rate in the intended study population Ω = Ω₁ would obviously reduce the treatment effect because it is measured as a relative difference Δ₁ = μ_1,T − μ_1,P between the treatment and placebo groups, a problem that is all too familiar in an active control trial. If placebo responders are present in substantial proportion, then this relative difference will become much smaller. This reduced treatment effect termed the apparent treatment effect in a parallel design is the reason why many such trials had failed in the past.

To further elaborate on this problem, assume for the moment that one is able to characterize the placebo responders Ω_R and the placebo non-responders Ω_NR relative to a response variable X ∼ N(μ, σ²) and a response threshold c, where larger values of the response variable X represent better outcomes. Let $\tau =(c-\mu )/\sigma$, then α_NR = Φ(τ) would be the proportion of placebo non-responders in Ω = Ω₁. Let $X_{R,T}\sim N({\mu }_{R,T},{\sigma }_{R,T}^2)$ and $X_{R,P}\sim N({\mu }_{R,P},{\sigma }_{R,P}^2)$ denote the response distribution for treatment T and placebo P respectively in Ω_R, and $X_{NR,T}\sim N({\mu }_{NR,T},{\sigma }_{NR,T}^2)$ and $X_{NR,P}\sim N({\mu }_{NR,P},{\sigma }_{NR,P}^2)$ denote the response distribution for treatment T and placebo P respectively in Ω_NR. Furthermore, let Δ_R = μ_R,T − μ_R,P and Δ_NR = μ_NR,T − μ_NR,P denote the respective treatment effects in Ω_R and Ω_NR. Under homogeneity, the apparent treatment effect Δ₁ in Period 1 of a DRDS design can be defined as a simple weighted average of Δ_R and Δ_NR given by Δ₁ = α_RΔ_R + α_NRΔ_NR. Clearly, when the proportion of placebo responders α_R is low, then the apparent treatment effect Δ₁ is close to Δ_NR and the impact of Δ_R would be small. On the other hand, when the placebo response rate α_R is relatively high, then the impact of Δ_R would be great on the apparent treatment effect Δ₁. In this latter case, the apparent treatment effect Δ_R due to the placebo response in Ω_R results in the apparent treatment effect Δ₁. Therefore, this suggests that one should adjust the weights α_R and α_NR in Δ₁ = α_RΔ_R + α_NRΔ_NR in an objective manner to account for the high placebo response rate in Ω_R which is reflected in the apparent treatment effect Δ_R. In the next section, an adjusted treatment effect is defined which represents an adjustment of the weights in Δ₁ = α_RΔ_R + α_NRΔ_NR to account for the impact of the presence of placebo responders in Ω = Ω₁.

4.2. An adjusted treatment effect

Recall that for simplicity and without loss in generality, one may assume that${\sigma }_{1,P}^2={\sigma }_{1,T}^2$ which is also suggested by the first period data in the example given in Table 1. Denote this common variance by${\sigma }_1^2$, and hence ${\sigma }_{{\widehat{\text{Δ}}}_1}^2={\sigma }_1^2/(n_{1,T}{R}_1)$ Similarly, one may assume that in Period 2, the conditional variances are equal, i.e., ${\sigma }_{2,T|X_{1,P}<c}^2=var\left(X_{2,T}\text{|}{X}_{1,P}<c\right)={\sigma }_{2,P|X_{1,P}<c}^2=var\left(X_{2,P}\text{|}{X}_{1,P}<c\right)={\sigma }_2^2$, which is also suggested by the data in the example given in Table 1, although it was not assumed to be so in the earlier expression for ${\sigma }_{\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)}^2$, and hence here one has ${\sigma }_{\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)}^2={\sigma }_2^2/(n_{2,T}{R}_2)$. If one were to combine the treatment effect estimate${\widehat{\text{Δ}}}_1$ from Period 1 and$\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)=\left({\hat{\mu }}_{2,T|X_{1,P}<c}-{\hat{\mu }}_{2,P|X_{1,P}<c}\right)$ from Period 2 using weights defined through their inverse variances following the method of weighted least square [14], then the least square estimator of the treatment effect is given by

$$\widehat{\text{Δ}}={\alpha }_1{\widehat{\text{Δ}}}_1+{\alpha }_2\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)$$ (7)

where the coefficients α₁ and α₂ are given in general by

$${\alpha }_1=1-{\alpha }_2$$

where

$${\alpha }_2=\frac{\frac{{\sigma }_1^2}{n_{1,T}{R}_1}-cov({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2\right|X_{1,P}<c))}{\frac{{\sigma }_1^2}{n_{1,T}{R}_1}+\frac{{\sigma }_2^2}{n_{2,T}{R}_2}-2cov({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2\right|X_{1,P}<c))}$$ (8)

Now, since $cov({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2\right|X_{1,P}<c))\to 0$ asymptotically as noted earlier, hence under large sample, α₂ may be approximately given by

$${\alpha }_2=\frac{\frac{{\sigma }_1^2}{n_{1,T}{R}_1}}{\frac{{\sigma }_1^2}{n_{1,T}{R}_1}+\frac{{\sigma }_2^2}{n_{2,T}{R}_2}}=\frac{\frac{n_{1,T}\gamma R_{12}{R}_2}{{\sigma }_2^2}}{\frac{n_{1,T}{R}_1}{{\sigma }_1^2}+\frac{n_{1,T}\gamma R_{12}{R}_2}{{\sigma }_2^2}}=\frac{1}{1+{\left(\frac{{\sigma }_2}{{\sigma }_1}\right)}^2\frac{1}{\gamma }\left(\frac{R_1}{R_{12}{R}_2}\right)}$$

where under a DRDS design, n_2,T = n_1,TγR₁₂ and γ = Φ(τ) is the population proportion of placebo non-responders which can be consistently estimated by the fraction of placebo subjects remained at the end of Period 1 who are placebo non-responders exclusive of the placebo responders and placebo dropouts and under the previous assumptions.

Now, in a DRDS design, for practical reasons, the following restrictions on the allocation ratios are expected 1 ≤ r₂ ≤ r₁. Hence, based on this restriction, the ratio $\left(R_1/(R_{12}{R}_2)\right)$ in the above expression for α₂ achieves its maximum value of 2 which is the value actually attained under the case of equal allocations, when r₁ = r₂ = 1.

Therefore, one can define

$${\alpha }_2=\frac{1}{1+{\left(\frac{{\sigma }_2}{{\sigma }_1}\right)}^2\frac{2}{\gamma }}\text{and}{\alpha }_1=1-{\alpha }_2$$ (9)

which will minimize the weight placed on ${\Delta }_{2|X_{1,P}<c}$, the expected treatment effect from Period 2.

The coefficients in Eq. (9) are the weights that will be used to define the adjusted treatment effect in the following definition.

Definition 1: Under a DRDS design, the adjusted treatment effect is defined as the convex combination

$$\Delta ={\alpha }_1{\Delta }_1+{\alpha }_2\left({\Delta }_2|X_{1,P}<c\right)$$ (10)

where the coefficients α₁ = α₁(γ,σ₁,σ₂) and α₂ = α₂(γ,σ₁,σ₂) are as defined in Eq. (9).

Note that the weights as defined above assumes that $cov({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2\right|X_{1,P}<c))\to 0$ and it would be valid in a DRDS design with the conditional probability structure discussed above under large sample as shown in the Lemma. However, for small samples, the weights may not be appropriate and the combined statistics as defined may not be valid and should be interpreted with caution, particularly when the covariance $cov({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2\right|X_{1,P}<c))$ is negative suggesting that the Period 1 apparent treatment effect and the Period 2 treatment effect are not consistent. This inconsistency will be discussed later under a consistency condition to be introduced.

In addition, the weights defined in Eq. (9) for the adjusted treatment effect as defined in Eq. (10) are dependent on the population parameters $\gamma ,{\sigma }_1$ and${\sigma }_2$, but they are independent of any design parameters particularly the allocation ratios r₁ and r₂. This is important because if the weights are dependent on the allocation ratios, then one can easily bias the results in favor of the treatment by increasing the allocation ratio r₁ and thus placing greater and greater weights on the Period 2 results. In fact, when the weights are dependent on the allocation ratios, the combined statistic will provide an estimate that is biased in favor of the treatment even when r₁ = 2 and r₂ = 1 which are the allocation ratios used in the SPD design of Fava et al. [3] and the DRDS design of Liu et al. [1].

Remark 1: It is important to emphasize again that the adjusted treatment effect is independent of the allocation ratios in the class of DRDS designs that are subject to the restriction 1 ≤ r₂ ≤ r₁. More importantly, the coefficient α₂ represents the smallest possible weight assigned to Δ₂ under a DRDS design subject to the above restriction and α₂ is actually attained under the case of a DRDS design with equal allocation. Also, with α₂ so defined, the actual DRDS design can still assume allocation ratios other than equal allocation provided the allocation ratios satisfy the above restriction. Therefore, with the weights α₁ and α₂ as defined in Eq. (9), there is no possibility for a DRDS design that is subject to the above allocation ratio restriction to introduce bias into the adjusted treatment effect by over-weighting the treatment effect (Δ₂|X_1,P<c) from the enriched subpopulation of the placebo non-responders from Period 2 by increasing the allocation ratio r₁ in favor of placebo in Period 1 and thereby overweighting the Period 2 results. Even though the coefficient α₂ is the weight actually attained under equal allocations r₁ = r₂ = 1 which does not involve overweighting the Period 2 results, it would be an unlikely configuration to be adopted in practical applications. Thus, if a given DRDS design adopts an allocation ratio r₁ > 1, it will only improve the precision of estimates, but will not affect the estimate of the adjusted treatment effect as defined in Eq. (10) above.

The weights used in the current combined statistics are implicitly dependent on the allocation ratios, although they are not noted as such. However, Tamura et al. [8] discussed the combined statistic with a view to estimating the treatment effect. But the authors' combined statistic is actually defined as an estimate of the apparent treatment effect Δ₁ which is not solving the basic problem at hand. Furthermore, the authors prefer weights that are dependent on the allocation ratios which are clearly not appropriate. Therefore, with any allocation r₁ > 1, these combined statistics would tend to bias the results in favor of the treatment by placing more weight on (Δ₂|X_1,P < c) from Period 2.

Remark 2: The weights defined in Eq. (9) for the adjusted treatment effect as defined in Eq. (10) are independent of the allocation ratios r₁ and r₂ as long as they satisfy the constraint 1 ≤ r₂ ≤ r₂. This property allows one to freely choose a DRDS design with any allocation ratios r₁ and r₂ as long as they satisfy the constraint 1 ≤ r₂ ≤ r₂. This flexibility has a very interesting, unintended and useful property in assuring type I error control of the joint test which will be discussed in Section 7.2.

Note: It is important to point out that the combined statistic as given in Eq. (7) will not necessarily retain the efficiency property of a least square estimator in light of the weights as defined in Eq. (9) unless it is a DRDS design with equal allocation ratios. But this may be the trade-off that one has to consider if one wishes to be able to define an adjusted treatment effect where the weights are independent of the DRDS design parameters, particularly, the allocation ratios, so that the adjusted treatment effect is not biased in favor of the treatment by placing more weights on the enriched treatment effect from Period 2. This latter seems to be a more important issue than optimal efficiency consideration, because an appropriate definition of adjusted treatment effect is critical and would allow a proper assessment of the treatment effect for the intended study population.

4.3. Interpretation of the adjusted treatment effect

As noted earlier, if one were able to characterize the subpopulation Ω_R of placebo responders and the subpopulation Ω_NR of placebo non-responders, then for the overall study population Ω in Period 1 of a DRDS design, the overall apparent treatment effect Δ₁ can be expressed as

$${\Delta }_1={\alpha }_R{\Delta }_R+{\alpha }_{NR}{\Delta }_{NR}$$ (11)

Then, the adjusted treatment effect given by Eq. (10) becomes

$$\Delta ={\alpha }_1{\Delta }_1+{\alpha }_2\left({\Delta }_2|X_{1,P}<c\right)={\alpha }_1\left[{\alpha }_R{\Delta }_R+{\alpha }_{NR}{\Delta }_{NR}\right]+{\alpha }_2\left({\Delta }_2|X_{1,P}<c\right)$$

under the assumption that the distribution of the placebo responders/non-responders among the placebo dropouts, if any, is the same as its population distribution, which implies that (Δ₂|X_1,P < c) ≅ Δ_NR. Hence, it follows that

$$\begin{array}{l}\Delta \cong {\alpha }_1{\alpha }_R{\Delta }_R+({\alpha }_2+{\alpha }_1{\alpha }_{NR}){\Delta }_{NR}\\ \cong \left(1-{\alpha }_2\right){\alpha }_R{\Delta }_R+\left({\alpha }_2+\left(1-{\alpha }_2\right){\alpha }_{NR}\right){\Delta }_{NR},since{\alpha }_1=(1-{\alpha }_2)\\ \cong \left({\alpha }_R-{\alpha }_2{\alpha }_R\right){\Delta }_R+({\alpha }_{NR}+{\alpha }_2(1-{\alpha }_{NR})){\Delta }_{NR}\\ \cong \left({\alpha }_R-{\alpha }_2{\alpha }_R\right){\Delta }_R+\left({\alpha }_{NR}+{\alpha }_2{\alpha }_R\right){\Delta }_{NR},since{\alpha }_R=1-{\alpha }_{NR}\end{array}$$ (12)

Upon comparing Eq. (11) and Eq. (12), one notes that the adjusted treatment effect Δ as defined in Eq. (10) can be viewed as a weighted average of Δ_R and Δ_NR as in Eq. (11) for Δ₁ except the weights now have been changed in the following manner: The weight for Δ_R has been decreased by the fractional amount α₂α_R while the weight for Δ_NR has been increased by the same fractional amount α₂α_R. Therefore, Eq. (12) shows that the adjusted treatment effect Δ can be viewed as a weighted average of the treatment effect Δ_R and Δ_NR and hence represents a treatment effect for the intended MDD study population Ω = Ω₁. The fraction α₂α_R represents the amount of adjustment needed to account for the presence of placebo responders Ω_R in Ω = Ω₁.

On the other hand, Eq. (12) can also be rearranged as follows:

$$\begin{array}{l}\Delta \cong \left({\alpha }_R-{\alpha }_2{\alpha }_R\right){\Delta }_R+\left({\alpha }_{NR}+{\alpha }_2{\alpha }_R\right){\Delta }_{NR}\\ \cong \left({\alpha }_R{\Delta }_R+{\alpha }_{NR}{\Delta }_{NR}\right)+{\alpha }_2\left[{\alpha }_R\left({\Delta }_{NR}-{\Delta }_R\right)\right]\\ \cong {\Delta }_1+{\alpha }_2\left[{\alpha }_R\left({\Delta }_{NR}-{\Delta }_R\right)\right]\end{array}$$ (13)

Now from Eq. (13), one can see that if there are no placebo responders, i.e., Ω_R = Ø, then α_R = 0 and Δ = Δ₁. That is, the adjusted treatment effect Δ and the apparent treatment effect Δ₁ are identical and hence no adjustment is really needed.

Now if Ω_R ≠ Ø, then it is expected that Δ_NR > Δ_R. In this case, then [α_R(Δ_NR − Δ_R)] represents the total amount of expected treatment effect Δ_NR that is not observed due to the placebo response in Ω_R. Now, because Δ_NR = Δ₂, one can view [α_R(Δ_NR − Δ_R)] = [α_R(Δ₂ − Δ_R)] as the equivalent amount of treatment effect from Period 2 that has been nullified by the placebo response in Ω_R. Then, it follows that α₂[α_R(Δ₂ − Δ_R)] represents the appropriately weighted amount of [α_R(Δ₂− − Δ_R)] from Period 2 that needs to be added to the apparent treatment effect Δ₁ from Period 1 to account for the presence of placebo responders Ω_R. Hence, the quantity α₂[α_R(Δ_NR − Δ_R)] represents the appropriate adjustment that needs to be made to the apparent treatment effect Δ₁ to account for the presence of placebo responders.

5. The combination test

For a DRDS design, under large sample, consider the adjusted treatment effect Δ = α₁Δ₁ + α₂(Δ₂|X_1,P < c) as given in Definition 1 above. The adjusted treatment null hypothesis and its alternative are defined as follows:

$$\begin{array}{l}{H}_{o,Adj}:\Delta ={\alpha }_1{\Delta }_1+{\alpha }_2\left({\Delta }_2|X_{1,P}<c\right)\le 0vs.H_{a,Adj}:\Delta \\ ={\alpha }_1{\Delta }_1+{\alpha }_2\left({\Delta }_2|X_{1,P}<c\right)>0\end{array}$$ (14)

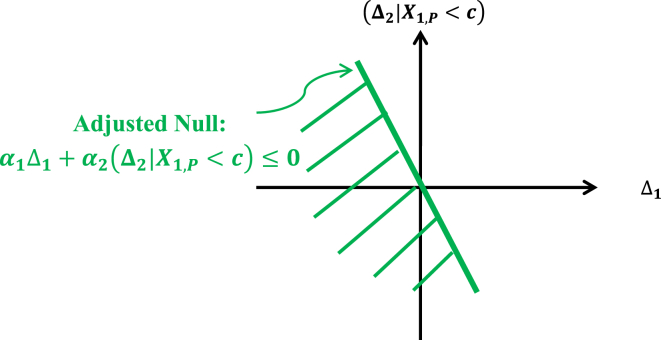
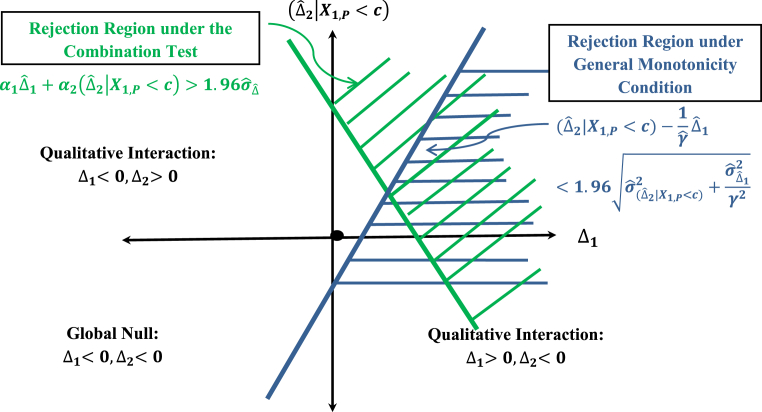
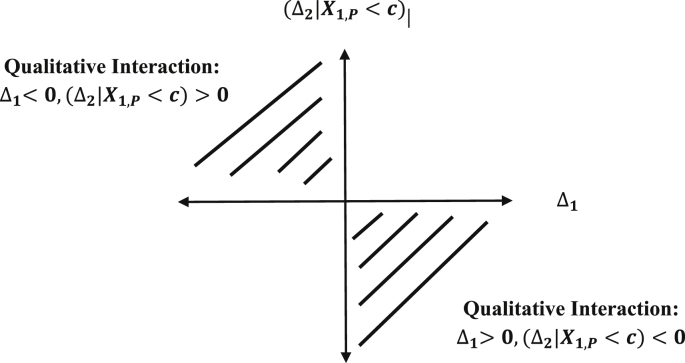
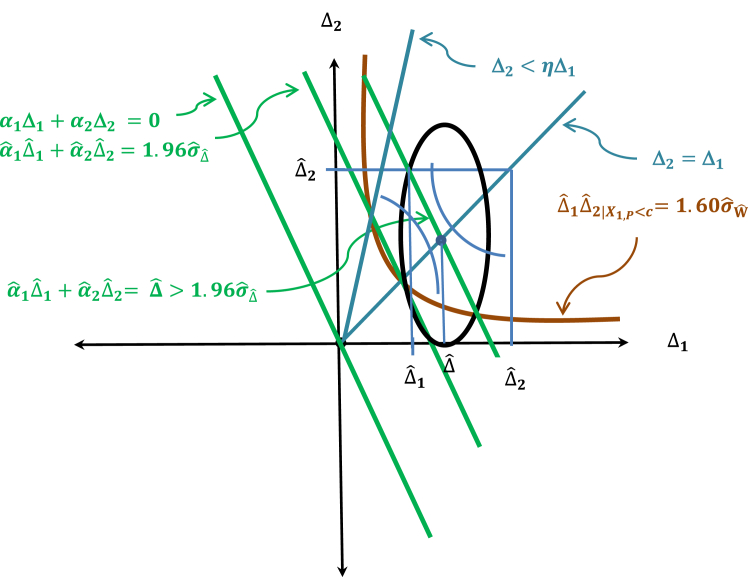
It should be pointed out that the above adjusted null hypothesis is a stronger null hypothesis than the global null hypothesis defined by {(Δ₁,(Δ₂|X_1,P < c))|Δ₁ ≤ 0 & (Δ₂|X_1,P c) ≤ 0}, because the parameter space defined by the adjusted null is a half-space in the product space Δ₁ × (Δ₂|X_1,P < c) below a straight line that goes through the origin (0,0) defined by α₁Δ₁ + α₂(Δ₂|X_1,P < c) = 0 and it covers the global null space which is the third quadrant of the product space Δ₁ × (Δ₂|X_1,P < c) as illustrated in Fig. 2.

Fig. 2.

Region of the parameter space for the adjusted treatment null.

Let the estimate of the adjusted treatment effect Δ be given by the least square estimator as defined by Eq. (7) with weights defined by Eq. (9):

$$\widehat{\text{Δ}}={\alpha }_1{\widehat{\text{Δ}}}_1+{\alpha }_2\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)$$

Then, it follows that

$$E\left(\widehat{\text{Δ}}\right)={\alpha }_{1}E\left({\widehat{\text{Δ}}}_1\right)+{\alpha }_{2}E\left(\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)={\alpha }_1{\Delta }_1+{\alpha }_2\left({\text{Δ}}_2|X_{1,P}<c\right)=\Delta$$

and

$$var\left(\widehat{\text{Δ}}\right)={\text{Σ}}_{\hat{\Delta }}^2={\alpha }_1^{2}var\left({\widehat{\text{Δ}}}_1\right)+{\alpha }_2^{2}var\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)+2{\alpha }_1{\alpha }_{2}cov\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)$$

where $var\left({\widehat{\text{Δ}}}_1\right)$, $var\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)$ and $cov\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)$ are as given in the earlier lemma.

The combination test for testing the adjusted null hypothesis is then given by

$$\hat{Z}=\frac{\left(\hat{\Delta }-\Delta \right)}{\sqrt{var\left(\hat{\Delta }\right))}}\text{,}$$

where $\widehat{\text{Δ}}$, $\Delta$ and $var\left(\hat{\Delta }\right)$ are as given above.

Note: It is important to point out that the adjusted treatment effect Δ and its estimate $\widehat{\text{Δ}}$ are independent of the allocation ratios r₁ and r₂, but the variance of $\widehat{\text{Δ}}$ does depend on the allocation ratios. This is fine, since the variance of$\widehat{\text{Δ}}$ should take into account the actual allocation ratios in the design. This will not affect the estimate of the adjusted treatment effect, but only its precision.

5.1. The type I error for the combination test

The type I error for the combination test is given by

$$\alpha =P\left(\hat{Z}>c_{\alpha }|H_{o,Adj}\right)=P\left({\hat{Z}}_o>c_{\alpha }\right)$$

where

$${\hat{Z}}_o=\left(\frac{\left(({\alpha }_1{\widehat{\text{Δ}}}_1+{\alpha }_2\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right))\right)}{\sqrt{var\left({\alpha }_1{\widehat{\text{Δ}}}_1+{\alpha }_2\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)}}\right)$$

$$var\left({\alpha }_1{\widehat{\text{Δ}}}_1+{\alpha }_2\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)={\alpha }_1^2\left(\gamma ,{\sigma }_1,{\sigma }_2\right)var\left({\widehat{\text{Δ}}}_1\right)+2{\alpha }_1{\alpha }_{2}cov\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)+{\alpha }_2^2\left(\gamma ,{\sigma }_1,{\sigma }_2\right)var\left(\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)$$

Note that from the following relationship previously derived,

$$cov\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)=\frac{1}{n_{1P}}\left(cov(X_{1,P},X_{2,P}|X_{1,P}<c)-cov(X_{1,P},X_{2,T}|X_{1,P}<c)\right)$$

which may be estimated by the sample covariance from the two cohorts (P → P) and (P → T).

The type I error control for the combination test is illustrated in Table 8

Table 8.

Powers for the Combination, the Consistency and the Joint Tests at c_α = 1.96, c_{0.05, W} = 1.60 for the Specified DRDS Design Parameter Values and the Hypothetical Distributions of a HDRS₁₇ Subscale Score (DRDS Design Parameter Values: r₁ = 2, r2 = 1, γ = 0.44, c = 2.75 for First Scenario, γ = 0.42, c = 2.50 for Second Scenario).

μ1T	μ1P	Δ1	σ1	ρP	ρT	Δ2|C	σ2|C	N1	P (${\hat{Z}}_o$>c0.025|Ha)	P (${\hat{W}}_o$>c0.05,W|Ha)	P (${\hat{Z}}_o$>c0.025, ${\hat{W}}_o$> c0.050,W|Ha)
3.50	3.50	0.00	2.42	0.80	0.80	1.48	3.23	750	0.025	0.050	0.001
3.50	3.10	0.40	2.42	0.80	0.20	1.48	3.23	750	0.81	0.74	0.66
								840	0.85	0.79	0.73
								990	0.91	0.85	0.82
				0.80	0.50	0.96	3.32	750	0.71	0.66	0.51
								840	0.76	0.71	0.58
								990	0.82	0.78	0.68
3.30	3.00	0.30	2.42	0.80	0.20	1.43	3.18	750	0.64	0.55	0.41
								840	0.69	0.59	0.47
								990	0.76	0.66	0.57
				0.80	0.50	0.88	3.28	750	0.51	0.46	0.26
								840	0.56	0.50	0.31
								990	0.63	0.57	0.39

5.2. The power and sample size for the combination test

The power of the combination test at a specified alternative (Δ₁, Δ₂) in the first quadrant is given by

$$1-\beta =P\left({\hat{Z}}_o>c_{\alpha }/H_{a,Adj}:\left({\Delta }_1,{\Delta }_2\right)in1stQuadrant,{\rho }_P>{\rho }_T\right)=P\left({\hat{Z}}_a>c_{\alpha }-\frac{{\alpha }_1{\Delta }_1+{\alpha }_2\left({\text{Δ}}_2|X_{1,P}<c\right)}{{\text{Σ}}_{\widehat{\text{Δ}},a}}|H_{a,Adj}:\left({\Delta }_1,{\Delta }_2\right)in1stQuadrant,{\rho }_P>{\rho }_T\right)$$

where ${\hat{Z}}_a=\left({\alpha }_1{\widehat{\text{Δ}}}_1+{\alpha }_2\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)-\left({\alpha }_1{\Delta }_1+{\alpha }_2\left({\Delta }_2|X_{1,P}<c\right)\right)/{\text{Σ}}_{\widehat{\text{Δ}},a}\sim N\left(\mathrm{0,1}\right)$ and ${\text{Σ}}_{\widehat{\text{Δ}},a}={\text{Σ}}_{\widehat{\text{Δ}},o}$.

From the above power function, one can derive the sample size formula as follows:

$$n_{1T}={\left(\frac{c_{\alpha }+c_{1-\beta }}{{\alpha }_1{\Delta }_1+{\alpha }_2\left({\Delta }_2|X_{1,P}<c\right)}\right)}^2\left({\alpha }_1^2\frac{{\sigma }_1^2}{R_1}+{\alpha }_2^2\frac{{\sigma }_{{\widehat{\text{Δ}}}_2|X_{1P}<c}^2}{\gamma R_{12}}+2{\alpha }_1{\alpha }_2{\rho }_{\mathrm{1,2}}\frac{{\sigma }_1}{\sqrt{R_1}}\frac{{\sigma }_{{\widehat{\text{Δ}}}_2|X_{1P}<c}}{\sqrt{\gamma R_{12}}}\right)$$

Note: Alternatively, instead of the power and sample size formulas given in the above equations, one can actually find the power and sample size formulae via the bivariate normal probability integral below:$1-\beta ={\int }_{-\infty }^{\infty }{\phi }_{{\hat{V}}_1}\left(x\right)\left(1-{\int }_{-\infty }^{\frac{\left(c_{\alpha }\sqrt{1+{\left(\frac{{\alpha }_1^{\ast }}{{\alpha }_2^{\ast }}\right)}^2}-\left(\frac{{\alpha }_1^{\ast }}{{\alpha }_2^{\ast }}{U}_1+U_2\right)-\frac{{\alpha }_1^{\ast }}{{\alpha }_2^{\ast }}x\right)-{\rho }_{\mathrm{1,2}}x}{\sqrt{1-{\rho }_{\mathrm{1,2}}^2}}}\phi \left(y\right)dy\right)dx$where ${\alpha }_1^{\ast }={\alpha }_1{\sigma }_1/\sqrt{n_{1,T}{R}_1}$, ${\alpha }_2^{\ast }={\alpha }_2{\sigma }_2/\sqrt{n_{2,T}{R}_2}$ and φ and Φ represent the standard normal density and cumulative distribution functions.

Table 2, .Table 3, Table 8 provide the power and sample size for selected scenarios and DRDS design parameter values based on the HDRS17 Anxiety and Somatization subscale score data given in Table 1.

Table 2.

Selected Powers and Sample Sizes at One-sided α = 0.025 for the Combination Test at the Specified DRDS Design Parameter Values and the Hypothetical Distributions of a HDRS17 Subscale Score under Treatment and Placebo as given in Table 1 (DRDS Design Parameter Values: r₁ = 2, r₂ = 1, c = 2.50, γ = 0.42), Δ = α₁*Δ₁ + α₂*Δ_2|C.

μ1T	μ1P	Δ1	σ1	ρP	ρT	Δ2|C	σ2|C	Δ	1 − β	N1	n1T	n2T
3.30	3.00	0.30	2.42	0.80	0.20	1.43	3.18	0.42	80%	960	320	134
									85%	1098	366	154
									90%	1287	429	180
				0.80	0.50	0.88	3.28	0.38	80%	1338	446	187
									85%	1587	529	222
									90%	1893	631	265

Table 3.

Selected Powers and Sample Sizes at One-sided α = 0.025 for the Combination Test at the Specified DRDS Design Parameter Values and the Hypothetical Distributions of a HDRS₁₇ Subscale Score under Treatment and Placebo as given in Table 1 (DRDS Design Parameter Values: r₁ = 2, r₂ = 1, c = 2.75, γ = 0.44), Δ = α₁*Δ₁ + α₂*Δ_2|C.

μ1T	μ1P	Δ1	σ1	ρP	ρT	Δ2|C	σ2|C	Δ	1-β	N1	n1T	n2T
3.50	3.10	0.40	2.42	0.80	0.20	1.48	3.23	0.52	80%	636	212	93
									85%	720	240	106
									90%	838	280	123
				0.80	0.50	0.96	3.32	0.46	80%	819	273	120
									85%	936	312	137
									90%	1095	365	161

5.3. The monotonicity condition

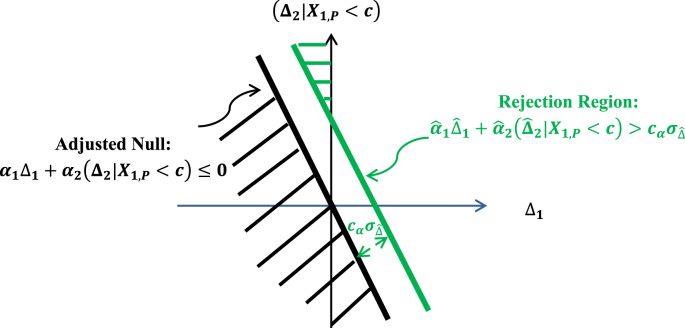
The rejection region for the adjusted treatment null hypothesis as defined by the combination test is depicted in Fig. 3 below.

Fig. 3.

Rejection region of the combination test.

Fig. 3 shows that there is still a small area shaded green in Fig. 2 under the rejection region that is situated inside the second quadrant. This suggests that even though the probability is small, the adjusted treatment null may be rejected by the combination test, but the Period 1 treatment effect Δ₁ may be negative. From Eq. (11), one can see that a negative Δ₁ suggests that the treatment may perform worse than placebo in the subpopulation Ω_R. Now in the subpopulation Ω_R, the placebo acts like an active control trial in a non-inferiority trial. In a non-inferiority trial, a treatment is still considered effective if it performs no worse than placebo by a given non-inferiority margin δ > 0. So, what would be an equivalent non-inferiority margin for assessing the effectiveness of a treatment effect in the subpopulation Ω_R of placebo responders?

As a condition required for a treatment effectiveness claim to be extendable to the intended study population, Tamura et al. [8] introduced a monotonicity condition for the case under binary outcome. This monotonicity condition simply requires each placebo responder also responds to treatment. Under binary outcome, this monotonicity condition is equivalent to requiring that the treatment be at least as effective as placebo. Now for continuous outcome, this monotonicity condition does not rule out the possibility that the treatment could perform worse than the placebo. Therefore, what should then be the monotonicity condition? Now if one were to require that the treatment should perform at least as effective as placebo, then this is equivalent to requiring the treatment to show superiority to an active control, and hence would be too stringent. On the other hand, if one were simply to require that each placebo responder also responds to treatment, then under this condition, the treatment can still perform worse than placebo. But then what would be a corresponding non-inferiority margin in this case?

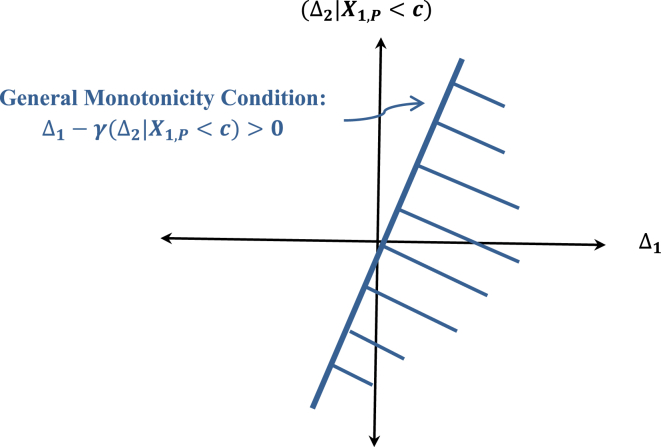
From Eq. (9), one can see that the condition that requires the treatment to be at least as effective as placebo can be stated as the following equivalent condition:

$${\Delta }_1={\alpha }_R{\Delta }_R+{\alpha }_{NR}{\Delta }_{NR}>\gamma \left({\Delta }_2|X_{1,P}<c\right)\text{or}\left({\Delta }_2|X_{1,P}<c\right)<\frac{1}{\gamma }{\Delta }_1$$ (15)

since under the earlier assumptions on the placebo dropouts if any, α_NR = γ = Φ(τ) and Δ_NR = Δ₂. This condition in Eq. (15) is depicted in Fig. 4.

Fig. 4.

Region defined by the general monotonicity condition.

It is clear that this condition is quite stringent and besides this superiority condition is also not required for a non-inferiority trial. Therefore, a less stringent monotonicity condition is needed, a condition that allows the treatment to perform no worse than placebo by a non-inferiority margin. An obvious general monotonicity condition is to require that

$$\left({\Delta }_2|X_{1,P}<c\right)<\eta {\Delta }_1,\text{for}\text{some}\eta >\frac{1}{\gamma }$$ (16)

The slope η can be viewed here as the equivalent of a non-inferiority margin δ. But how should η be determined? This would be a challenging problem. But even the general monotonicity condition as defined by Eq. (16) is very stringent if the condition is required to be tested as illustrated in Fig. 5.

Fig. 5.

Rejection region under the combination test and the rejection region under the general monotonicity condition.

Note that in the general monotonicity conditions defined by Eq. (16), a constraint is placed on the expected Period 2 treatment effect (Δ₂|X_1,P < c). This constraint is really not necessary because from Eq. (1),

$$\left({\Delta }_2|X_{1,P}<c\right)=\left({\mu }_{2,T}-{\mu }_{2,P}\right)+\left({\rho }_P{\sigma }_{2,P}-{\rho }_T{\sigma }_{2,T}\right)\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)\cong {\Delta }_1+\left({\rho }_P{\sigma }_{2,P}-{\rho }_T{\sigma }_{2,T}\right)\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)$$ (17)

and it is seen from Eq. (17) that the magnitude of the expected Period 2 treatment effect (Δ₂|X_1,P < c) is determined by the magnitude of the Period 1 treatment effect Δ₁ and the term $\left({\rho }_P{\sigma }_{2,P}-{\rho }_T{\sigma }_{2,T}\right)\left(\phi \left(\tau \right)/\text{Φ}\left(\tau \right)\right)$ the magnitude of which in turn is determined by the standard deviations σ_2,P=σ_1,P, σ_2,T=σ_1,T, the correlations ρ_P and ρ_T and the hazard ratio $\left(\phi \left(\tau \right)/\text{Φ}\left(\tau \right)\right)$, and it cannot be arbitrarily large.

Therefore, if such constraint imposed by the above condition is not necessary, then one should consider relaxing the condition by letting η → ∞. Now as one lets η → ∞, the line (Δ₂|X_1,P < c) = ηΔ₁ → the (Δ₂|X_1,P < c) – axis. This then naturally leads to the consistency condition which will be introduced in the next section as the condition required for the treatment effectiveness claim to be extendable to the intended study population Ω₁ in lieu of a general monotonicity condition defined by Eq. (16).

5.4. A measure of consistency

In a DRDS design, what is consistency and why is it necessary? As discussed in Section 5.4, even if the combination test rejects the adjusted null hypothesis, one may still not be able to claim that the treatment is effective for the intended population because the pair of treatment effect (Δ₁,Δ₂) may be located in the second quadrant in the Δ₁ × (Δ₂|X_1,P < c) parameter space meaning that Δ₁ could be negative. To remedy this problem, a general monotonicity condition as defined by Eq. (16) can be proposed. But as discussed in Section 5.4, this general monotonicity condition is too stringent. In this section, an alternative consistency test is introduced to test for the consistency between the treatment effects Δ₁ and (Δ₂|X_1,P < c). However, the consistency test alone does not permit one to conclude that the treatment effects are positive in both periods. It requires the joint rejection of the adjusted null and the consistency null by their respective tests. Therefore, the simultaneous rejection of the adjusted null and the consistency null would be required for one to conclude that the pair of treatment effect (Δ₁,(Δ₂|X_1,P < c)) lies in the first quadrant of the parameter space Δ₁ × (Δ₂|X_1,P < c).

This consistency test jointly with the combination test may provide sufficient evidence for one to conclude that the pair of treatment effect (Δ₁,(Δ₂|X_1,P < c)) lies in the first quadrant, that is, both Δ₁ and (Δ₂|X_1,P < c) are positive. Once this is established, then the treatment effectiveness claim as represented by the adjusted treatment effect can be extended to the intended study population and the adjusted treatment effect estimates can then be used in the benefit/risk analysis and in proper dosage recommendation.

Note that under finite samples, if the pair (Δ₁,(Δ₂|X_1,P < c)) is inconsistent with Δ₁ < 0, then the optimal efficiency of the combined statistic under equal allocation case may be lost. However, as noted earlier, since in practice, equal allocation is unlikely to be used, maintenance of efficiency may be a moot point and is of secondary concern compared to a proper assessment of the treatment effect. But in any case, one should interpret the combined statistic with caution in light of such inconsistency. This suggests that consistency is an important condition needed for the validity and interpretability of the combined statistic.

5.5. The consistency test

Let the consistency measure Γ between Δ₁ and (Δ₂|X_1,P < c) be defined as Γ = Δ₁(Δ₂|X_1,P < c). Then the consistency null and alternative hypotheses are defined as:

$$H_{o,C}:\text{Γ}={\Delta }_1\left({\text{Δ}}_2|X_{1,P}<c\right)\le 0vs.H_{o,C}:\text{Γ}={\Delta }_1\left({\text{Δ}}_2|X_{1,P}<c\right)>0$$ (18)

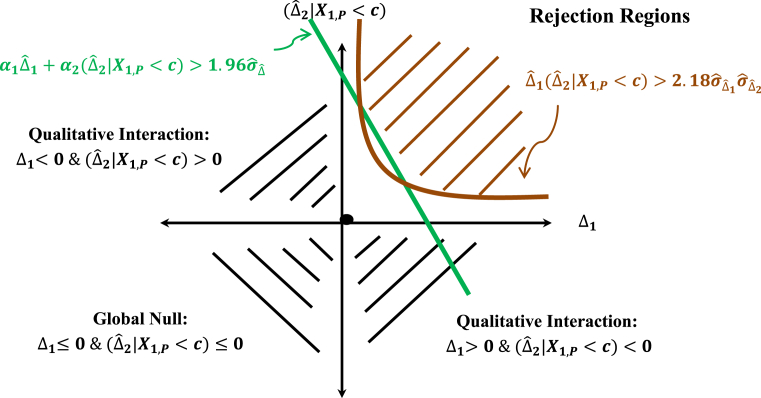
The consistency null hypothesis is depicted by the shaded region in Fig. 6.

Fig. 6.

Region of the parameter space for the consistency null.

Now consider the following statistic:

$$\widehat{\text{Γ}}={\widehat{\text{Δ}}}_1\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)-\widehat{cov}\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)$$

Then, one has

$$E\left(\widehat{\text{Γ}}\right)=E\left({\widehat{\text{Δ}}}_1\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)-cov\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)\right)={\Delta }_1\left({\Delta }_2|X_{1,P}<c\right)$$

The variance of$\widehat{\text{Γ}}$ is given approximately asymptotically by

$$var\left(\widehat{\text{Γ}}\right)=\left[var\left({\widehat{\text{Δ}}}_1\right)var\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right]+co{v}^2\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)+\left[{\left({\Delta }_2|X_{1,P}<c\right)}^{2}var\left({\widehat{\text{Δ}}}_1\right)\right]+\left[{\Delta }_1^{2}var\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right]+\left[4{\Delta }_1\left({\Delta }_2|X_{1,P}<c\right)cov\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)\right]+{\Delta }_1^2{\left({\Delta }_2|X_{1,P}<c\right)}^2$$

The consistency test for the consistency hypothesis defined by Eq. (18) is then given by

$$\hat{W}=\frac{\widehat{\text{Γ}}-E\left(\widehat{\text{Γ}}\right)}{\sqrt{var\left(\widehat{\text{Γ}}\right)}}\text{,}$$

where $\widehat{\text{Γ}},E\left(\widehat{\text{Γ}}\right)$ and $var\left(\widehat{\text{Γ}}\right)$ are given above, with $cov\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)$ estimated by $\widehat{cov}\left({\hat{\Delta }}_1,\left({\hat{\Delta }}_2|X_{1,P}<c\right)\right)=\frac{1}{n_{1P}}\left(S_{X_{1,P}<c,X_{2,P}|X_{1,P}}-S_{X_{1,P}<c,X_{2,T}|X_{1,P}}\right)$ where $S_{X_{1,P}<c,X_{2,P}|X_{1,P}}$ and $S_{X_{1,P}<c,X_{2,T}|X_{1,P}}$are the sample covariance estimates for $cov\left({\hat{\mu }}_{1,P|X_{1,P}<c},{\hat{\mu }}_{2,P|X_{1,P}<c}\right)$ and $cov\left({\hat{\mu }}_{1,P|X_{1,P}<c},{\hat{\mu }}_{2,T|X_{1,P}<c}\right)$ for the two cohorts $\left(P\to P\right)$ and $\left(P\to T\right),$ since as previously noted,

$$cov\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)=\frac{1}{n_{1P}}\left(cov(X_{1,P},\left(X_{2,P}\right|X_{1,P}<c))-cov(X_{1,P},\left(X_{2,T}\right|X_{1,P}<c))\right)$$

5.6. The type I error for the consistency test

The type I error for the consistency test is given under asymptotic normality by

$$\alpha =P\left(\hat{W}>c_{\alpha ,W}|H_{o,C}\right)=P\left(\frac{\left[{\hat{\Delta }}_1\left({\hat{\Delta }}_2|X_{1,P}<c\right)-\widehat{cov}\left({\hat{\Delta }}_1,\left({\hat{\Delta }}_2|X_{1,P}<c\right)\right)\right]-\text{Γ }}{\sqrt{var\left(\widehat{\text{Γ}}\right)}}>c_{\alpha ,W}|H_{o,C}\right)\text{,}$$

where $var\left(\widehat{\text{Γ}}\right)$ as derived above and $\text{Γ}={\Delta }_1\left({\text{Δ}}_2|X_{1,P}<c\right)$.

Note that at the boundary of the consistency null, the type I error assumes its maximum at (Δ₁,(Δ₂|X_1,P<c)) = (0,0) and$cov\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)=0$. Therefore, the type I error for the consistency test evaluated at its maximum is given by

$$\alpha =P\left(\frac{{\hat{\Delta }}_1\left({\hat{\Delta }}_2|X_{1,P}<c\right)-\widehat{cov}\left({\hat{\Delta }}_1,\left({\hat{\Delta }}_2|X_{1,P}<c\right)\right)}{\sqrt{var\left(\widehat{\text{Γ}}|H_{o,C}\right)}}>c_{\alpha ,W}\right)$$

where

$$var\left(\widehat{\text{Γ}}|H_{o,C}\right)=\left[var\left({\hat{\Delta }}_1\right)var\left({\hat{\Delta }}_2|X_{1,P}<c\right)\right]+\left[{\left({\text{Δ}}_2|X_{1,P}<c\right)}^{2}var\left({\hat{\Delta }}_1\right)\right]+\left[{\Delta }_1^{2}var\left({\hat{\Delta }}_2|X_{1,P}<c\right)\right]$$

Analogously, the above type I error can also be evaluated asymptotically via bivariate normal integral as

$$\alpha =P\left({\hat{U}}_1{\hat{U}}_2>c_{\alpha ,W}\right)=P\left({\hat{U}}_2>\frac{c_{\alpha ,W}}{{\hat{U}}_1}|H_{o,C}\right)=P\left({\hat{U}}_2>\frac{c_{\alpha ,W}}{{\hat{U}}_1}|\left(U_1,U_2\right)=\left(\mathrm{0,0}\right),{\text{ρ}}_{\mathrm{1,2}}=0\right)=\frac{1}{2}+{\int }_{-\infty }^0\text{φ}\left(z_1\right)\text{Φ}\left(\frac{c_{\alpha ,W}}{z_1}\right)d{z}_1-{\int }_0^{\infty }\text{φ}\left(z_1\right)\text{Φ}\left(\frac{c_{\alpha ,W}}{z_1}\right)d{z}_1,\text{with}{\hat{U}}_1=\frac{{\widehat{\text{Δ}}}_1}{\frac{{\sigma }_1}{\sqrt{n_{1,T}{R}_1}}},{\hat{U}}_2=\frac{\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)}{\frac{\sqrt{var\left(X_{2|X_{1,P}<c}\right)}}{\sqrt{n_{2,T}{R}_2}}}$$

Since ${\hat{W}}_o={\hat{U}}_1{\hat{U}}_2$ is not normally distributed and has a distribution with heavy tail, its critical values are somewhat larger for the same significance level α as compared to the critical values from a normal distribution. Critical values for selected levels of significance are given in Table 4.

Table 4.

Critical values for the consistency test ${\hat{W}}_o$ at selected significance level α.

α	cα,W
0.001	5.08
0.005	3.60
0.010	2.98
0.025	2.18
0.050	1.60
0.075	1.26
0.100	1.03

In light of the proposed procedure of testing both the adjusted treatment null hypothesis by the combination test ${\hat{Z}}_o$ and the consistency null hypothesis by the consistency test${\hat{W}}_o$, a rejection of the adjusted treatment null by the test ${\hat{Z}}_o$ implies that (Δ₁,(Δ₂|X_1,P < c)) does not lie in the third quadrant which effectively reduces the nominal α level of the consistency test ${\hat{W}}_o$ by half. Therefore, it is suggested that the type I error rate for the consistency test ${\hat{W}}_o$ be held at the one-sided significance level of α = 0.05 corresponding to a critical value of c_0.05,W = 1.60. This yields an effective significance level of α = 0.025 for the consistency test${\hat{W}}_o$ under the joint testing procedure. This is the significance level that is used subsequently in generating the various sample size and power calculations for the consistency test${\hat{W}}_o$.

Table 8 suggests that the type I error rate for the consistency test is controlled at the one-sided 0.05 level.

The rejection region of the consistency test is depicted in Fig. 7. It shows that the rejection region defined by the consistency test (region in the first and third quadrants) and the combination test (region in the first, second and fourth quadrants defined by the green line) consists of the shaded parabolic region in brown in the first quadrant which represents the intersection of the two rejection regions.

Fig. 7.

Rejection regions under the combination and consistency tests.

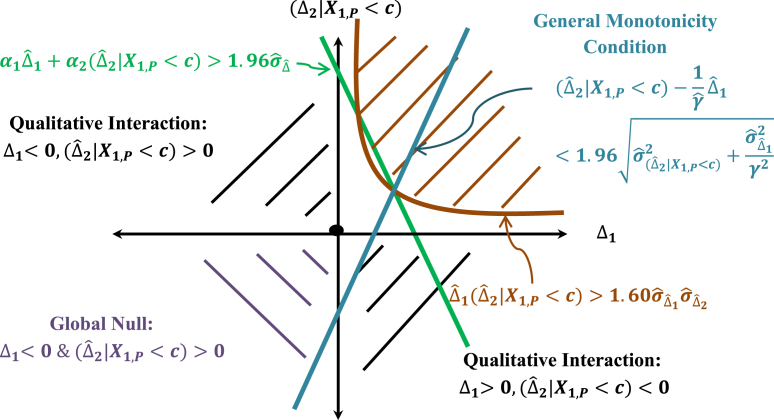
Fig. 8 shows that the rejection region under the combination test and the consistency test is less stringent than the rejection region required by the general monotonicity condition as defined by Eq. (16). The consistency condition here may be viewed as equivalent to a non-inferiority margin in an active control trial (see the discussion in Section 5.4 where the consistency condition may be viewed as the limiting general monotonicity condition).

Fig. 8.

Rejection regions in the alternative space.

5.7. The power and sample size for the consistency test

The Power of the Consistency Test is given by:

$$1-\beta =P({\hat{W}}_o>c_{\alpha }|H_{a,C})=P\left(\frac{{\widehat{\text{Δ}}}_1\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)-\widehat{cov}\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)}{\sqrt{var\left({\hat{W}}_o\right)}}>c_{\alpha ,W}|H_{a,C}\right)$$

where $var\left({\hat{W}}_o\right)=var\left({\widehat{\text{Δ}}}_1\right)var\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)$.

Hence,where

$$1-\beta =P\left({\hat{W}}_a>\frac{c_{\alpha ,W}\sqrt{var\left({\hat{W}}_o\right)}-{\Delta }_1\left({\Delta }_2|X_{1,P}<c\right)}{\sqrt{var\left({\hat{W}}_a\right)}}|H_{a,C}\right)\text{,}$$

where

$${\hat{W}}_a=\left[{\hat{\Delta }}_1\left({\hat{\Delta }}_2|X_{1,P}<c\right)-\widehat{cov}\left({\hat{\Delta }}_1,\left({\hat{\Delta }}_2|X_{1,P}<c\right)\right)-\text{Γ}\right]/\sqrt{var\left({\hat{W}}_a\right)}\text{,}$$

and $\text{Γ}={\Delta }_1\left({\Delta }_2|X_{1,P}<c\right)$.

$$var\left({\hat{W}}_a\right)=var\left({\hat{W}}_o\right)+co{v}^2\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)+{\left({\Delta }_2|X_{1,P}<c\right)}^{2}var\left({\widehat{\text{Δ}}}_1\right)+{\Delta }_1^{2}var\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)+4{\Delta }_1\left({\Delta }_2|X_{1,P}<c\right)cov\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)+{\Delta }_1^2{\left({\Delta }_2|X_{1,P}<c\right)}^2$$

Note that the power may be evaluated by viewing ${\widehat{\text{Δ}}}_{1}and\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)$ as having an asymptotic bivariate normal distribution given by

$$\begin{array}{l}1-\beta =P\left({\hat{V}}_2>\frac{R-U_1{U}_2-U_2{\hat{V}}_1}{U_1+{\hat{V}}_1}|H_{a,C}\right)\\ =\underset{-\infty }{\overset{\infty }{\int }}{\phi }_{{\hat{V}}_1}\left(x\right)\underset{\frac{R-U_1{U}_2-U_{2}x-{\rho }_{\mathrm{1,2}}x\left(x+U_1\right)}{\left(x+U_1\right)\sqrt{1-{\rho }_{\mathrm{1,2}}^2}}}{\overset{\infty }{\int }}\phi \left(y\right)dydx\end{array}$$

where

$$R=\left(c_{\alpha ,W}\sqrt{1+{\rho }_{\mathrm{1,2}}^2+U_1^2+U_2^2}+{\rho }_{\mathrm{1,2}}\right)$$

where $U_i=\frac{{\Delta }_i}{\frac{{\sigma }_i}{\sqrt{n_{i,T}{R}_i}}}$, i = 1,2 and ( ${\hat{V}}_1,{\hat{V}}_2)\sim \mathit{N}({\mathit{\mu }}_{\mathrm{1,2}},{\mathbf{\Sigma }}_{\mathrm{1,2}}^2)$ where${\mathit{\mu }}_{\mathrm{1,2}}=\left(\begin{array}{c}0\\ 0\end{array}\right)$ and ${\mathbf{\Sigma }}_{\mathrm{1,2}}^2=\left(\begin{array}{cc}1& {\rho }_{\mathrm{1,2}}\\ {\rho }_{\mathrm{1,2}}& 1\end{array}\right)$ and ${\rho }_{\mathrm{1,2}}=corr\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)={\rho }_{{\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)}$ as derived earlier.

By substituting the above expressions for U_i, i = 1, 2 and noting that n_2,T = n_1,TγR₁₂, then one can evaluate the above probability integral for the power at a given sample size. n_1,T.

Conversely, to calculate the sample size, one can just solve the above equation implicitly for n_1,T at a given power (1 − β). Some selected powers and sample sizes are given in Table 5, Table 6, Table 8 based on the example in Table 1.

Table 5.

Selected Powers and Sample Sizes at One-sided α = 0.05 for the Consistency Test ${\hat{W}}_o$ at the Specified DRDS Design Parameter Values and the Hypothetical Distributions of a HDRS₁₇ Subscale Score under Treatment and Placebo as given in Table 1 (DRDS Design Parameter Values: r₁ = 2, r₂ = 1, c = 2.75, γ = 0.44) Γ = Δ₁*Δ₂.

μ1T	μ1P	Δ1	σ1	ρP	ρT	Δ2|C	σ2|C	Γ	1 − β	N1	n1T	n2T
3.50	3.10	0.40	2.42	0.80	0.20	1.48	3.23	0.59	80%	825	275	121
									85%	954	318	140
									90%	1083	361	159
				0.80	0.50	0.96	3.32	0.38	80%	1032	344	151
									85%	1176	392	172
									90%	1389	463	204

Table 6.

Selected Powers and Sample Sizes at One-sided α = 0.05 for the Consistency Test ${\hat{W}}_o$ at the Specified DRDS Design Parameter Values and the Hypothetical Distributions of a HDRS₁₇ Subscale Score under Treatment and Placebo as given in Table 1 (DRDS Design Parameter Values: r₁ = 2, r₂ = 1, c = 2.50, γ = 0.42) Γ = Δ₁*Δ_2|C.

μ1T	μ1P	Δ1	σ1	ρP	ρT	Δ2|C	σ2|C	Γ	1 − β	N1	n1T	n2T
3.30	3.00	0.30	2.42	0.80	0.20	1.43	3.18	0.43	80%	1128	376	158
									85%	1323	441	185
									90%	1605	535	225
				0.80	0.50	0.88	3.28	0.26	80%	1377	459	193
									85%	1587	529	222
									90%	1893	631	265

6. The joint test

As mentioned in the preceding section, both the combination test and the joint test are necessary for establishing the effectiveness of a treatment for the intended study population Ω = Ω₁ in a DRDS design. A joint test is proposed here for simultaneously testing the adjusted treatment null by the combination test and the consistency null by the consistency test. Upon the simultaneous rejection of this pair of null hypotheses, one can then derive an estimate of the adjusted treatment effect along with its confidence interval, and an estimate of the consistency of the treatment effects from Period 1 and Period 2 along with its confidence interval. The adjusted treatment effect represents the apparent treatment effect of Period 1 having been adjusted for the presence of high placebo response rate. The consistency condition is viewed as a generalization of the general monotonicity condition and a rejection of the consistency null would permit the extension of the effectiveness of the adjusted treatment effect to the intended study population.

Table 9a, Table 9b, Table 9c provide the type I error, power and sample size needed for some selected configurations for purpose of illustration. These data can be generated by integrating the combination test and the consistency test through the bivariate normal probability integral since both tests are jointly defined in terms of ${\Delta }_1$ and (Δ₁|X_1,P<c).

Table 9a.

Type I Error Rate for Joint Test at a Boundary Point on the Positive (Δ₂|c)-Axis for Selected Parameter Values of ρ_T, ρ_P, σ₁ and τ (DRDS Design Parameter Values: r₁ = 2, r₂ = 1) (Δ, Γ) = (α₁*Δ₁ + α₂*(Δ₂|X_1,P < c)_, Δ₁ (Δ₂|X_1,P < c)) P (${\hat{Z}}_a$ > c_0.025 - α₂ (Δ₂|X_1,P < c)/std ($\widehat{\text{Δ}}$) & ${\hat{W}}_o$> c_0.025,W |(0, Δ₂|X_1,P < c)).

ρP	ρT	σ1	κ	τ	γ = Φ(τ)	ϕ(τ)/Φ(τ)	Δ2|X1,P < c	Type I error rate
0.80	0.20	2.40	1.0	−0.60	0.274	1.215	1.75	0.0041
				−0.30	0.382	0.998	1.44	0.0047
				0.00	0.500	0.798	1.15	0.0049
				0.30	0.618	0.618	0.89	0.0047
				0.60	0.726	0.459	0.66	0.0040
			0.5	−0.60	0.274	1.215	2.04	0.0050
				−0.30	0.382	0.998	1.68	0.0058
				0.00	0.500	0.798	1.34	0.0061
				0.30	0.618	0.618	1.04	0.0057
				0.60	0.726	0.459	0.77	0.0048
		1.20	1.0	−0.60	0.274	1.215	0.87	0.0074
				−0.30	0.382	0.998	0.72	0.0089
				0.00	0.500	0.798	0.57	0.0094
				0.30	0.618	0.618	0.44	0.0086
				0.60	0.726	0.459	0.33	0.0069
			0.5	−0.60	0.274	1.215	1.02	0.0141
				−0.30	0.382	0.998	0.84	0.0174
				0.00	0.500	0.798	0.67	0.0184
				0.30	0.618	0.618	0.52	0.0166
				0.60	0.726	0.459	0.39	0.0129

Table 9b.

Type I Error Rate for Joint Test at a Boundary Point on the Positive (Δ₂|c)-Axis for Selected Parameter Values of ρ_T, ρ_P, σ₁ and τ (DRDS Design Parameter Values: r₁ = 2, r₂ = 1, N₁ = 990) (Δ, Γ) = (α₁*Δ₁ + α₂*(Δ₂|X_1,P < c)_, Δ₁ (Δ₂|X_1,P < c)) P (${\hat{Z}}_a$>c_0.025 - α₂ (Δ₂|X_1,P < c)/std ($\widehat{\text{Δ}}$) & ${\hat{W}}_o$> c_0.025,W |(0, Δ₂|X_1,P < c)).

ρP	ρT	σ1	κ	τ	γ = Φ(τ)	ϕ(τ)/Φ(τ)	Δ2|X1,P < c	Type I error rate
0.90	0.10	2.40	1.0	−0.60	0.274	1.215	2.33	0.0054
				−0.30	0.382	0.998	1.92	0.0064
				0.00	0.500	0.798	1.53	0.0068
				0.30	0.618	0.618	1.19	0.0063
				0.60	0.726	0.459	0.88	0.0052
			0.5	−0.60	0.274	1.215	2.48	0.0058
				−0.30	0.382	0.998	2.04	0.0068
				0.00	0.500	0.798	1.63	0.0072
				0.30	0.618	0.618	1.26	0.0067
				0.60	0.726	0.459	0.94	0.0055
		1.20	1.0	−0.60	0.274	1.215	1.17	0.0124
				−0.30	0.382	0.998	0.96	0.0153
				0.00	0.500	0.798	0.77	0.0161
				0.30	0.618	0.618	0.59	0.0146
				0.60	0.726	0.459	0.44	0.0114
			0.5	−0.60	0.274	1.215	1.24	0.0236
				−0.30	0.382	0.998	1.02	0.0285
				0.00	0.500	0.798	0.81	0.0296
				0.30	0.618	0.618	0.63	0.0269
				0.60	0.726	0.459	0.47	0.0210

Table 9c.

Type I Error Rate for Joint Test at a Boundary Point on the Positive (Δ₂|c)-Axis for Selected Parameter Values of ρ_T, ρ_P, σ₁ and τ (DRDS Design Parameter Values: r₁ = 1, 2, 3, r₂ = 1, N₁ = 990) (Δ, Γ) = (α₁*Δ₁ + α₂*(Δ₂|X_1,P < c)_,Δ₁(Δ₂|X_1,P < c)) P (${\hat{Z}}_a$>c_0.025 - α₂ (Δ₂|X_1,P < c)/std ($\widehat{\text{Δ}}$) & ${\hat{W}}_o$> c_0.025,W |(0, Δ₂|X_1,P < c)).

ρP	ρT	σ1	κ	r1	τ	γ = Φ(τ)	ϕ(τ)/Φ(τ)	Δ2|X1,P < c	Type I error rate
0.90	0.10	2.40	0.5	1.0	−0.60	0.274	1.215	2.48	0.0072
					−0.30	0.382	0.998	2.04	0.0086
					0.00	0.500	0.798	1.63	0.0091
					0.30	0.618	0.618	1.26	0.0083
					0.60	0.726	0.459	0.94	0.0067
				2.0	−0.60	0.274	1.215	2.48	0.0058
					−0.30	0.382	0.998	2.04	0.0068
					0.00	0.500	0.798	1.63	0.0072
					0.30	0.618	0.618	1.26	0.0067
					0.60	0.726	0.459	0.94	0.0055
				3.0	−0.60	0.274	1.215	2.48	0.0048
					−0.30	0.382	0.998	2.04	0.0056
					0.00	0.500	0.798	1.63	0.0059
					0.30	0.618	0.618	1.26	0.0056
					0.60	0.726	0.459	0.94	0.0047
		1.20	0.5	1.0	−0.60	0.274	1.215	1.24	0.0298
					−0.30	0.382	0.998	1.02	0.0341
					0.00	0.500	0.798	0.81	0.0359
					0.30	0.618	0.618	0.63	0.0321
					0.60	0.726	0.459	0.47	0.0251
				2.0	−0.60	0.274	1.215	1.24	0.0236
					−0.30	0.382	0.998	1.02	0.0285
					0.00	0.500	0.798	0.81	0.0296
					0.30	0.618	0.618	0.63	0.0269
					0.60	0.726	0.459	0.47	0.0210
				3.0	−0.60	0.274	1.215	1.24	0.0186
					−0.30	0.382	0.998	1.02	0.0229
					0.00	0.500	0.798	0.81	0.0241
					0.30	0.618	0.618	0.63	0.0219
					0.60	0.726	0.459	0.47	0.0170

6.1. The joint test $({\hat{\mathit{Z}}}_{\mathit{o}}>{\mathit{c}}_{0.025},{\hat{\mathit{W}}}_{\mathit{o}}>{\mathit{c}}_{0.05,\mathit{W}})$

Since the test of the adjusted null hypothesis by the combination test alone is deemed not sufficient to establish the effectiveness of the treatment for the intended population in Period 1, it is proposed that a joint testing of the adjusted null hypothesis by the combination test ${\hat{Z}}_o$ at α = 0.025 and the consistency null hypothesis by the consistency test ${\hat{W}}_o$ at α = 0.05 should be performed. When both the adjusted null and the consistency null have been rejected by their respective tests${\hat{Z}}_o$ and${\hat{W}}_o$, then one may conclude that the treatment effect pair (Δ₁,(Δ₂|X_1,P<c)) is located in the first quadrant and the treatment effects for both Period 1 and Period 2 are positive and consistent. The combination test can then provide an estimate of the adjusted treatment effect and its associated 95% confidence interval given by $\widehat{\text{Δ}}={\hat{\alpha }}_1{\widehat{\text{Δ}}}_1+{\hat{\alpha }}_2\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)$where

$$\left({\hat{\alpha }}_1{\hat{\Delta }}_1+{\hat{\alpha }}_2\left({\hat{\Delta }}_2|X_{1,P}<c\right)\right)\pm 1.96\sqrt{var\left({\hat{\alpha }}_1{\hat{\Delta }}_1+{\hat{\alpha }}_2\left({\hat{\Delta }}_2|X_{1,P}<c\right)\right)}$$

where

$$var\left({\hat{\alpha }}_1{\hat{\Delta }}_1+{\hat{\alpha }}_2\left({\hat{\Delta }}_2|X_{1,P}<c\right)\right)={\hat{\alpha }}_1^2\frac{{\sigma }_1^2}{n_{1,T}{R}_1}+{\hat{\alpha }}_2^2\frac{var\left(\left({\hat{\Delta }}_2|X_{1,P}<c\right)\right)}{n_{2,T}}+2{\hat{\alpha }}_1{\hat{\alpha }}_{2}cov\left({\hat{\Delta }}_1,\left({\hat{\Delta }}_2|X_{1,P}<c\right)\right)$$

where${\sigma }_1^2$ and $var\left(\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)$ may be estimated by the sample variances${\hat{\sigma }}_1^2\text{and}\widehat{var}\left(\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)$, the latter via the sample variances from the two cohorts (P→P) and (P→T) for var(X_2,T|X_1,P<c) and var(X_2,P|X_1,P<c), the covariance $cov\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)$ can also be estimated by the sample covariance for the two cohorts (P→P) and (P→T), and the weights α_i may be estimated by ${\hat{\alpha }}_i={\alpha }_i\left(\hat{\gamma },{\hat{\sigma }}_1,\sqrt{\widehat{var}\left(\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)}\right)$, for i = 1, 2.

The magnitude of the consistency measure also provides supportive information for the strength of the consistency.

Fig. 9 provides a graphical description of the estimate of the adjusted treatment effect in relation to the joint test and the general monotonicity condition. It shows that the estimated adjusted treatment effect $\widehat{\text{Δ}}={\hat{\alpha }}_1{\widehat{\text{Δ}}}_1+{\hat{\alpha }}_2\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)$ appears as the coordinates of the point$(\widehat{\text{Δ}},\widehat{\text{Δ}})$ which is the intersection of the line ${\hat{\alpha }}_1{\Delta }_1+{\hat{\alpha }}_2\left({\text{Δ}}_2|X_{1,P}<c\right)=\widehat{\text{Δ}}$ and the 45° diagonal line. The point $\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)$ satisfies the general monotonicity condition Δ₂<ηΔ₁ as shown in Fig. 9, but if the slope η is smaller, then$\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)$ may very well not satisfy the corresponding monotonicity condition. In addition, if one is required to test the general monotonicity condition, then it would be even more stringent. Thus, it is clear from Fig. 9 that the general monotonicity condition as defined by Eq. (16) is unnecessarily restrictive, and the consistency condition should be preferred.

Fig. 9.

Estimate of the adjusted treatment effect under the joint test.

The power of the joint test (${\hat{Z}}_o>c_{0.025},{\hat{W}}_o>c_{0.05,W})$ is given in Table 7 and in the last column of Table 8. As expected, the power will be relatively low.

Table 7.

Selected Powers and Sample Sizes at One-sided α = 0.025 for the Joint Test (${\hat{Z}}_o,{\hat{W}}_o$) at the Specified DRDS Design Parameter Values and the Hypothetical Distributions of a HDRS₁₇ Subscale Score under Treatment and Placebo as given in Table 1 (DRDS Design Parameter Values: r₁ = 2, r₂ = 1, c = 2.75, γ = 0.44) (Δ, Γ) = α₁*Δ₁ + α₂*Δ₂,Δ₁Δ_2|C).

μ1T	μ1P	Δ1	σ1	ρP	ρT	Δ2|C	σ2|C	(Δ, Γ)	1 − β	N1	n1T	n2T
3.50	3.10	0.40	2.42	0.80	0.20	1.48	3.23	(0.52, 0.59)	80%	951	317	139
									85%	1056	352	155
									90%	1194	398	175
				0.80	0.50	0.96	3.32	(0.46, 0.38)	80%	1218	406	179
									85%	1350	450	198
									90%	1524	508	224

6.2. The type I error control of the joint test

The control of the type I error of the joint test will be investigated in this section.

It suffices to show that the type I error of the joint test is controlled at the positive (Δ₂|X_1,P<c) – axis. Let (0, (Δ₂|X_1,P<c)) be a point on the positive (Δ₂|X_1,P<c) – axis on the boundary of the joint null.

It is desired to show that

$$\alpha =P\left({\hat{Z}}_a>c_{\alpha }-\frac{{\alpha }_2\left({\text{Δ}}_2|X_{1,P}<c\right)}{\sqrt{V_{Z_a}}},{\hat{W}}_o>c_{\alpha ,W}\right)\le 0.025$$

where $V_{Z_a}=var\left({\hat{\alpha }}_1{\hat{\Delta }}_1+{\hat{\alpha }}_2\left({\hat{\Delta }}_2|X_{1,P}<c\right)|\left(0,\left({\text{Δ}}_2|X_{1,P}<c\right)\right)\right)$

First, consider the probability

$$P\left({\hat{Z}}_a>c_{\alpha }-\frac{{\alpha }_2\left({\text{Δ}}_2|X_{1,P}<c\right)}{\sqrt{V_{Z_a}}}\right)$$ (19)

where,

$$V_{Z_a}=var\left({\hat{\alpha }}_1{\hat{\Delta }}_1+{\hat{\alpha }}_2\left({\hat{\Delta }}_2|X_{1,P}<c\right)|H_{o,Adj}:\left(0,\left({\text{Δ}}_2|X_{1,P}<c\right)\right)\right)={\hat{\alpha }}_1^{2}var\left({\widehat{\text{Δ}}}_1\right)+{\hat{\alpha }}_2^{2}var\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)+2{\hat{\alpha }}_1{\hat{\alpha }}_{2}cov\left({\widehat{\text{Δ}}}_1,\left({\widehat{\text{Δ}}}_2|X_{1,P}<c\right)\right)$$

$$\left({\Delta }_2|X_{1,P}<c\right)=\left({\mu }_{2,T}-{\mu }_{2,P}\right)+\left({\rho }_P{\sigma }_{2,P}-{\rho }_T{\sigma }_{2,T}\right)\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)\cong {\Delta }_1+\left({\rho }_P{\sigma }_{2,P}-{\rho }_T{\sigma }_{2,T}\right)\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)$$

Therefore, at the boundary point (0, (Δ₂|X_1,P<c)), sinceΔ₁ = 0, one has

$$\left({\Delta }_2|X_{1,P}<c\right)\cong \left({\rho }_P{\sigma }_{2,P}-{\rho }_T{\sigma }_{2,T}\right)\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)$$ (20)

Now without loss in generality, it has been assumed that σ_2,P = σ_2,T = σ_1,T = σ_1,P = σ₁, therefore Eq. (20) reduces to

$$\left({\Delta }_2|X_{1,P}<c\right)\cong {\sigma }_1\left({\rho }_P-{\rho }_T\right)\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)$$ (21)

Consider now the variance and covariance terms in the denominator in Eq. (19).

$$var\left({\widehat{\text{Δ}}}_1\right)=\frac{{\sigma }_1^2}{n_{1,T}{R}_1},assumingthat{\sigma }_{1,T}^2={\sigma }_{1,P}^2={\sigma }_1^2$$

$$\begin{array}{l}var\left({\hat{\Delta }}_2|X_{1,P}<c\right)=var\left({\hat{\mu }}_{2,T|X_{1,P}<c}-{\hat{\mu }}_{2,P|X_{1,P}<c}\right)\\ =\frac{1}{n_{2,T}}\left(var\left(X_{2,T}|X_{1,P}<c\right)+var\left(X_{2,P}|X_{1,P}<c\right)\right)\\ =\frac{{\sigma }_1^2}{n_{2,T}}\left(2+\left(\left({\rho }_P^2+{\rho }_T^2\right)\left(\left[1-\tau \frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}-{\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)}^2\right]{\sigma }_1^2-1\right)\right)\right),\text{which}\end{array}$$

follows from Eqn. (4) and Eqn. (5), since

$$\begin{array}{l}var\left(X_{2,T}|X_{1,P}<c\right)=\left({\rho }_T^2\left[1-\tau \frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}-{\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)}^2\right]{\sigma }_{1,P}^2+\left(1-{\rho }_T^2\right)\right){\sigma }_{2,T}^2\\ var\left(X_{2,P}|X_{1,P}<c\right)=\left({\rho }_P^2\left[1-\tau \frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}-{\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)}^2\right]{\sigma }_{1,P}^2+\left(1-{\rho }_P^2\right)\right){\sigma }_{2,P}^2\end{array}$$

and from the further assumptions that ${\sigma }_{2,P}={\sigma }_{2,T}={\sigma }_{1,T}={\sigma }_{1,P}={\sigma }_1$.

Now,

$$\begin{array}{l}cov\left({\hat{\Delta }}_1,\left({\hat{\Delta }}_2|X_{1,P}<c\right)\right)\\ =\frac{1}{n_{1P}}\left(cov(X_{1,P},X_{2,P}|X_{1,P}<c)-cov(X_{1,P},X_{2,T}|X_{1,P}<c)\right),\text{since}\\ {\hat{\Delta }}_1={\hat{\mu }}_{1,T}-{\hat{\mu }}_{1,P}\text{and}\left({\hat{\Delta }}_2|X_{1,P}<c\right)={\hat{\mu }}_{2,T|X_{1,P}<c}-{\hat{\mu }}_{2,P|X_{1,P}<c}.\\ =\frac{1}{n_{1P}}\left({\rho }_P{\sigma }_{2,P}-{\rho }_T{\sigma }_{2,T}\right)\left[1-\tau \left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)-{\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)}^2\right]{\sigma }_{1,P},\text{since}\\ cov\left(X_{1,P},X_{2,P}|X_{1,P}<c\right)={\rho }_P\left[1-\tau \left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)-{\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)}^2\right]{\sigma }_{1,P}{\sigma }_{2,P}\text{and}\\ cov\left(X_{1,P},X_{2,T}|X_{1,P}<c\right)={\rho }_T\left[1-\tau \left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)-{\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)}^2\right]{\sigma }_{1,P}{\sigma }_{2,T}.\\ =\frac{1}{n_{1T}{r}_1}\left({\rho }_P{\sigma }_{2,P}-{\rho }_T{\sigma }_{2,T}\right)\left[1-\tau \left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)-{\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)}^2\right]{\sigma }_{1,P}\\ =\frac{{\sigma }_1^2}{n_{1T}{r}_1}\left({\rho }_P-{\rho }_T\right)\left[1-\tau \left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)-{\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)}^2\right],\text{under}\text{the}\text{further}\\ \text{assumptions}\text{that}{\sigma }_{2,P}={\sigma }_{2,T}={\sigma }_{1,T}={\sigma }_{1,P}={\sigma }_1\end{array}$$

Hence,

$$\begin{array}{l}\alpha =P\left({\hat{Z}}_a>c_{\alpha }-\frac{{\alpha }_2\left({\text{Δ}}_2|X_{1,P}<c\right)}{\sqrt{V_{Z_a}}}|\left(0,\left({\Delta }_2|X_{1,P}<c\right)\right)\right)\\ =P\left({\hat{Z}}_a>c_{\alpha }-\frac{\sqrt{n_{1,T}}\left({\rho }_P-{\rho }_T\right)\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)}{\sqrt{V_{Z_a}}}\right)\end{array}$$ (22)

where now

$$V_{Z_a}={\left(\frac{{\alpha }_1}{{\alpha }_2}\right)}^2\frac{1}{R_1}+\frac{1}{\gamma R_{12}}\left(2+\left(\left({\rho }_T^2+{\rho }_T^2\right)\left[h\left(\tau \right){\sigma }_1^2-1\right]\right)\right)+2\left(\frac{{\alpha }_1}{{\alpha }_2}\right)\frac{1}{r_1}\left({\rho }_P-{\rho }_T\right)h\left(\tau \right)$$

with $h\left(\tau \right)=\left[1-\tau \frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}-{\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)}^2\right]$.

The power given by Eq. (22) for the combination test is essentially a function of the population parameters ρ_P and ρ_T from the two cohorts (P → P) and (P → T), the variance${\sigma }_1^2$, and the standardized response threshold τ. The hazard $\left(\phi \left(\tau \right)/\text{Φ}\left(\tau \right)\right)$ and γ = Φ(τ) are in turn influenced by the parameter τ. The design parameters may be considered as fixed.

Type I Error rate at a boundary point (0,(Δ₂|X_1,P < c)) on the positive (Δ₂|X_1,P<c)- axis which is in the consistency null space but in the alternative space of the adjusted treatment null is given by

$$P\left({\hat{Z}}_a>c_{\alpha }-\frac{{\alpha }_2\left({\text{Δ}}_2|X_{1,P}<c\right)}{\sqrt{V_{Z_a}}}\&{\hat{W}}_o>c_{\alpha ,W}|\left(0,\left({\Delta }_2|X_{1,P}<c\right)\right)\right)=P\left({\hat{Z}}_a>c_{\alpha }-\frac{{\alpha }_2\left({\text{Δ}}_2|X_{1,P}<c\right)}{\sqrt{V_{Z_a}}}|\left(0,\left({\Delta }_2|X_{1,P}<c\right)\right)\right)\times P\left({\hat{W}}_o>c_{\alpha ,W}|\left(0,\left({\Delta }_2|X_{1,P}<c\right)\right)\right)$$

since ${\hat{Z}}_a$ and ${\hat{W}}_o$ are asymptotically independent.

$$\le P\left({\hat{Z}}_a>c_{\alpha }-\frac{\sqrt{n_{1,T}}\left({\rho }_P-{\rho }_T\right)\left(\frac{\phi \left(\tau \right)}{\text{Φ}\left(\tau \right)}\right)}{\sqrt{V_{Z_a}}}\right)\times 0.05\text{,}$$

where $V_{Z_a}$ is as given above.

Table 9a, Table 9b, Table 9c provide the type I error rates for the joint test at boundary points on the positive (Δ₂|X_1,P < c) – axis derived from selected values of the parameters ρ_P, ρ_T, σ₁ = σ_1,P, $\kappa ={\sigma }_{1,T}/{\sigma }_{1,P}={\sigma }_{2,T}/{\sigma }_{2,P}$ and τ with the allocation ratios fixed at r₁ = 2 and r₂ = 1 as in the Example given in Table 1.

It can be seen from the first panels of Table 9a, Table 9b which are based on the example given in Table 1 that the type I error rates are controlled for various response thresholds. Under the scenarios in the first panels of these tables, the type I errors are controlled. The lower panels of Table 9a, Table 9b show that when the standard deviation σ₁ = σ_1,P decreases, the type I error rate increases and even more so when the ratio κ = σ_1,T/σ_1,P decreases. This is because the variance in the denominator of the test statistic is getting smaller. However, in practical applications, the ratio κ = σ_1,T/σ_1,P is not expected to deviate too much from 1 as shown by the example in Table 1. There are some inflation when the correlations ρ_P = 0.90, ρ_T = 0.10 and σ₁ = σ_1,P = 0.5 as shown in the bottom panel of Table 9b. However, interestingly, as Table 9c below shows, the type I error inflation under these scenarios can be controlled if one increases the allocation ratio r₁.

As Table 9c illustrates, under these scenarios, the greatest type I error inflation occurs under equal allocation ratios and the type I error starts to decrease as the allocation ratio r₁ increases while holding r₂ = 1. The reason why the type I error starts to decrease as the allocation ratio r₁ increases is because for a fixed total sample size N₁, the sample size n_1,T allocated to treatment decreases as r₁ increases. This results in a net decrease in the second term on the right side of the power formula in Eq. (22) and a corresponding reduction in power. This fact holds true across all scenarios. Therefore, from these tables, it appears that the type I error rate of the joint test is controlled at the one-sided 0.025 level under most reasonable scenarios where the correlations are not too extreme and the ratio κ = σ_1,T/σ_1,P is expected not to deviate too much from 1, when the allocation ratios are fixed at r₁ = 2 and r₂ = 1. If in a given application, it appears that it may fall into a neighborhood of some scenarios where the type I error of the joint test may be inflated, one can consider increasing the allocation ratio r₁ from 2 to a higher level so that the type I error will be under control. This is an interesting and unexpected useful property which is a byproduct of the fact that the weights in the adjusted treatment effect are independent of the allocation ratios so a DRDS design has the flexibility in the choice of the allocation ratios r₁ and r₂ as long as they satisfy the constraint 1 ≤ r₂ ≤ r₁. Also note that the allocation ratio of r₁ = 1 is unlikely to be adopted in practice, so the increase in r₁ should only be considered relative to those scenarios where the type I error appears to be inflated under a DRDS design with an allocation ratio r₁ = 2 ≥ r₂ ≥ 1.

In summary, Table 9a, Table 9b, Table 9c show that the type I error rate of the joint test is controlled under most practical situations with the allocation ratios fixed at r₁ = 2 and r₂ = 1. In a given application, under a DRDS design with allocation ratio r₁ = 2 and r₂ = 1, if the situation appears to fall in one of the scenarios where type I error inflation is anticipated, then one may consider increasing the allocation ratio r₁ to a level greater than 2 so that the type I error will be controlled. However, as discussed above, the type I error is expected to be under control in most practical applications.

6.3. Hypothetical example on HDRS₁₇ Anxiety and Somatization subscale score data

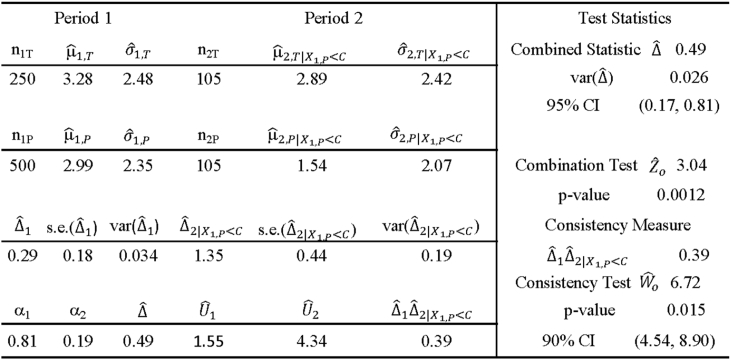
The hypothetical values presented in Table 1 are those of the distributional parameters of the HDRS₁₇ Subscale score for treatment and placebo that are derived on the basis of an exploratory early phase 2 study with a DRDS design in subjects with major depressive disorder. Although the sample size for this study is very small, they are adequate for the purpose of illustration in this paper.

Using the Period 1 data in Table 1 for the distributional parameters of the HRDS₁₇ subscale score under treatment and placebo, a major depressive disorder trial with a DRDS is simulated, where the DRDS design parameters assumed the values of r₁ = 2, π = 0.58, γ = 0.42, r₂ = 1, and a Period 1 sample size of N₁ = 750. For simplicity, it is assumed that the placebo dropout rate is 0 in this simulated trial. Assuming a correlation between${\widehat{\text{Δ}}}_1$ and ${\widehat{\text{Δ}}}_2$ of ρ_1,2 = 0, this sample size was chosen to have about 69% power for the combination test, 59% power for the consistency test and 48% power for the joint test. Thus, the sample size selected is somewhat underpowered for the tests. A summary of the DRDS study design features and the simulated trial outcome statistics are given in Table 10.

Table 10.

Summary Statistics from a Simulated MDD Trial with the Specified DRDS Design Parameter Values and the Hypothetical Distributions of a HDRS₁₇ Subscale Score under Treatment and Placebo as given in the First Row of Table 1, Table 3 (r₁ = 2, R₁ = 2/3, π = 0.58, γ = 0.42, r₂ = 1, R₂ = 1/2) (c_α = 1.96, c_α,W = 1.60, N1 = 750 with 70%, 59%, 48% Power for ${\hat{Z}}_o,{\hat{W}}_o,\left({\hat{Z}}_o,{\hat{W}}_o\right)$) (μ_1T = 3.30, σ_1T = 2.44, μ_1P = 3.00, σ_1P = 2.40).

From the results of the simulated trial given in Table 10, one obtains the following results for the combination test${\hat{Z}}_o$ and the consistency test${\hat{W}}_o$:

The combined statistic is given by $\widehat{\text{Δ}}={\alpha }_1{\widehat{\text{Δ}}}_1+{\alpha }_2{\widehat{\text{Δ}}}_2=0.49$ with a standard error of $s.e.\left(\widehat{\text{Δ}}\right)=0.16$ and a 95% CI of (0.17, 0.81). The combination Test: ${\hat{Z}}_o=3.04$ has a p-value of p = 0.0012. For the consistency test, one has${\hat{U}}_1=1.55,{\hat{U}}_2=4.34$ and ${\hat{W}}_o=6.72$ with a p-value of p = 0.015 with 90% CI of (4.54, 8.90).

Thus, the estimate of an adjusted treatment effect of 0.49 given by the combined statistic $\widehat{\text{Δ}}$ is obtained as a result of adjusting for the presence of placebo responders by increasing the weight α_NR= = 0.42 placed on Δ_NR to the weight 0.53 by an amount α₂α_R = 0.19(0.58) = 0.11.

This simulated trial shows that the apparent treatment effect Δ₁ for Period 1 is estimated to be${\widehat{\text{Δ}}}_1=0.29$, and the adjusted treatment effect Δ is estimated to be$\widehat{\text{Δ}}=0.49$. The consistency test${\hat{W}}_o=6.72$ with a p-value of 0.015 shows that the Period 1 and Period 2 treatment effect estimates${\widehat{\text{Δ}}}_1=0.29$ and${\widehat{\text{Δ}}}_2=1.35$ are consistent. Therefore, the evidence supports the adjusted treatment effect of Δ=0.49 as the treatment effect for the intended study population Ω.

7. Summary discussion

In psychiatric trials, the presence of a relatively high proportion of placebo responders has caused many trials using a traditional randomized parallel placebo-controlled trial to fail because the treatment effect as measured by the relative treatment difference has been diluted. Various authors (Liu et al. [1], Fava et al. [3], Chen et al. [4], Huang and Tamura [5], Ivanova et al. [6], Tamura and Huang [7] and Tamura et al. [8]) have proposed a DRDS design in an attempt to resolve this problem. In their proposed methods, a combination test with certain power optimality criterion to either test the apparent treatment null hypothesis of Period 1or global null hypothesis which is defined as the joint apparent treatment null of Period 1 and the enriched treatment null of Period 2. The weights used in the combined statistics depend on the DRDS design allocation ratios and the combined statistics may provide biased estimates of the apparent treatment effect. More importantly, it is believed that the apparent treatment effect should not be the basis for evaluating the effectiveness of the treatment since the true treatment effect has been mitigated on account of the presence of placebo responders. It can underestimate the risk/benefit ratio and it can lead to overdosing recommendation. In this paper, the concept of an adjusted treatment effect is introduced which is a weighted combination of the apparent treatment effects from Period 1 and the treatment effect from Period 2 in a DRDS design where the weights are independent of the DRDS design allocation ratios. The adjusted treatment effect is invariant in the class of DRDS design subject to the restriction that 1 ≤ r₂ ≤ r₁ which will be satisfied in practical applications. It is shown that the adjusted treatment effect can be interpreted as an adjustment of the apparent treatment effect of Period 1 by a quantity that represents an appropriately weighted amount of the treatment effect (as represented by the treatment effect from Period 2) that has been nullified by the presence of placebo responders. Therefore, the adjusted treatment effect as defined does not bias the assessment of the treatment effect in favor of the treatment. Thus, Period 2 of a DRDS design should not be viewed as providing enriched treatment effect in order to bias the adjusted treatment effect through the combined statistic, but rather as providing a measure of the treatment effect in the absence of placebo response which is exactly the information needed to make the proper adjustment. The independence of the weights from the allocation ratios in a DRDS design would allow the design to retain its flexibility in its choice of allocation ratios subject to a certain minor restriction which is needed to assure the type I error control of the joint test.

A new combined statistic is derived to test the adjusted treatment null hypothesis. In order for the adjusted treatment effectiveness claim to be extendable to the intended study population, a consistency measure is introduced to assess the consistency between the treatment effects from the two periods. The general monotonicity condition which has been suggested by some as a criterion for extendibility of the treatment effectiveness claim to the intended study population appears to be too stringent because it is analogous to requiring the treatment to be at least as effective as the control in an active control trial. It is shown that the consistency condition is a natural generalization of the monotonicity condition and it is less stringent and does not require the specification of a non-inferiority margin. It is suggested that the rejection of the consistency null by the consistency test should provide the additional evidence needed to be able to extend the adjusted treatment effectiveness claim to the intended study population.

Therefore, a joint test consisting of the combination test and the consistency test is proposed for testing the adjusted null and the consistency null. In most practical applications, the type I error of the joint test should be under control. Indeed the conditional probability structure underlying a DRDS design shows that the Period 2 treatment effect cannot be arbitrarily large. However, in a given application, if specific scenario suggests that the type I error may be inflated, then an appropriate choice of the allocation ratios can be selected for the DRDS design to assure the type I error control. The independence of the weights in the adjusted treatment effect from the allocation ratios in a DRDS design subject to a certain minor restriction would allow a DRDS design to retain this needed flexibility in its choice of the allocation ratios. The power of the joint test is not expected to be high and therefore the proposed methodology is not expected to increase efficiency compared to a standard randomized parallel design. But the proposed method would allow an unbiased estimate of the adjusted treatment effect which represents an appropriate assessment of the true treatment effect in the intended study population which is something that a standard randomized parallel design can never provide.

A successful outcome based on the proposed methodology should provide the confidence required of the evidence provided by a DRDS design to support the treatment effectiveness claim for the intended study population. The estimated adjusted treatment effect should also provide crucial information needed for making appropriate benefit/risk analysis and dosage recommendation.